Презентация на тему: "Объемы. Соотношения между единицами измерения объема"

Объемы. Соотношения между единицами измерения объема

Прозвенел и смолк звонок,

Начинается урок.

Друг на друга посмотрели

И за парты дружно сели.

Повторение

• Найдите объем куба с ребром 4 см.

( V = 4 ³ =64 см ³ )

• Найдите площадь всей поверхности куба с ребром 4 см.

( S =4·4·6=96 см ² )

Повторение

• Найдите площадь боковой поверхности куба с ребром 4 см.

( S =4·4·4=64 см ² )

• Высота комнаты 3 м, ширина 5 м, а длина 6 м. Сколько кубических метров воздуха находится в комнате?

( V =3·5·6=90 см ³ )

Повторение

• Бак для воды имеет форму прямоугольного параллелепипеда. Его три измерения: 3 дм, 5 дм, 4 дм. Найдите объем бака для воды. Сколько литров воды входит в этот бак?

( V =3·5·4=60 дм ³ =60 л)

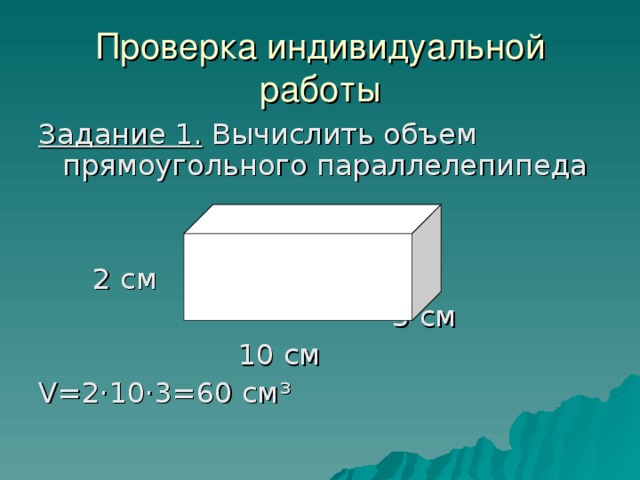
Проверка индивидуальной работы

Задание 1. Вычислить объем прямоугольного параллелепипеда

2 см

3 см

10 см

V =2·10·3=60 см ³

Проверка индивидуальной работы

Задание 2. Вычислите площадь всей поверхности куба.

5 см

S =5·5·6=150 см ²

Проверка индивидуальной работы

Задание 3. Вычисли площадь боковой поверхности прямоугольного параллелепипеда.

5 см 2 см

9 см

S =2·5·9+ 2·2·5=90+20=110 см ²

Прочитайте записи

5 см, 8 дм³, 10 м, 6 га, 7 л, 21 а,

9 м², 25 см³, 2 км

Назовите единицы измерения объема

1 см³= 1000 мм³

1дм³= 1000 см³= 1 л

1м³= 1000 дм³= 1 000 000 см³

Решение задач

№ 827

Длина аквариума 80 см, ширина 45 см, а высота 55 см. Сколько литров воды надо влить в этот аквариум, чтобы уровень воды был ниже верхнего края аквариума на 10 см.

Анализ задачи

• Что требуется найти в задаче?

(В задачи требуется найти сколько литров воды входит в аквариум)

• Какую форму имеет аквариум?

(Аквариум имеет форму прямоугольного параллелепипеда)

Анализ задачи

• Назовите три его измерения.

(Длина 80 см, ширина 45 см, высота 55 см)

• Что нужно вычислить, чтобы узнать, сколько воды входит в аквариум?

(Чтобы узнать, сколько воды входит в аквариум надо вычислить его объем)

Анализ задачи

• Какое есть дополнительное условие?

(Нужно чтоб уровень воды был ниже верхнего края аквариума на 10 см)

• Как вы это понимаете?

(Нужно высоту уменьшить на 10 см)

Решение:

1) 55-10=45 (см) – высота уровня воды

2) 80·45·45=162 000 (см³)

3) 162 000 см³ = 162 дм³ = 162 л

Ответ: в аквариум надо влить 162 л воды.

Решение задачи

№ 828

Прямоугольный параллелепипед (рис. 88) разделен на две части. Найдите объем и площадь поверхности всего параллелепипеда и обеих его частей. Равен ли объем параллелепипеда сумме объемов его частей? Можно ли это сказать о площадях их поверхностей? Объясните почему.

Анализ задачи

• Рассмотрите первую картинку.
• Назовите три измерения прямоугольного параллелепипеда.

(Длина – 10 см, ширина – 6 см, высота – 8 см)

• Можно ли по этим данным вычислить объем и площадь поверхности?

(Да)

Анализ задачи

• Какие формулы мы будем использовать?

( V =авс, S = 2ав+2вс+2ас)

• Вычислите объем и площадь поверхности.

( V =8·10·6=480 см³

S =10·6·2+8·10·2+6·8·2=120+160+96=376 см²)

Анализ задачи

• Рассмотрите вторую и третью картинку и аналогично вычислите объем и площадь поверхности прямоугольного параллелепипеда.

( V 1 =8·3·6=144 см³

S 1 =3·6·2+3·8·2+8·6·2=36+48+96 =180 см²

V 2 =8·7·6=336 см³

S 2 =7·8·2+8·6·2+6·7·2=112+96+84 =292 см²)

Анализ задачи

• Проверьте, равен ли объем параллелепипеда сумма объемов его частей.

( V = V + V

144+336=480 см³)

• Можно ли это сказать о площадях их поверхностей?

( S≠S + S

180+292=472 см², 376≠472)

Решение задачи

№ 824

Найдите объем куба, если площадь его поверхности равна 96 см².

Анализ задачи

• Что известно в задаче?

(В задаче известна площадь поверхности куба)

• Что требуется найти?

(Требуется найти объем куба)

• Из чего складывается площадь всей поверхности?

(Площадь всей поверхности складывается из суммы площадей всех граней)

Анализ задачи

• Сколько граней у куба?

(У куба 6 граней)

• Что вы можете о них сказать?

(Грани представляют собой 6 равных квадратов)

• Как найти площадь одной грани?

( S =а²)

Анализ задачи

• Какую формулу удобно использовать для вычисления объема?

V = S ·с

1) 96:6=16(см²) – площадь основания

2) 16·4=64 (см³)

Ответ: объем куба 64 см³.

Подведение итогов урока

• Расскажите, как запомнить соотношение единиц измерения объема?

(Единицы измерения объема кубические, значит, линейные единицы измерения возводим в куб)

Подведение итогов урока

• Назовите формулы для вычисления объема.

( V =авс – нахождение объема прямоугольного параллелепипеда

V =а³ - нахождение объема куба)

Домашнее задание

№ 841,№844, №846 (в,г)