Презентация о квадратичной функции.

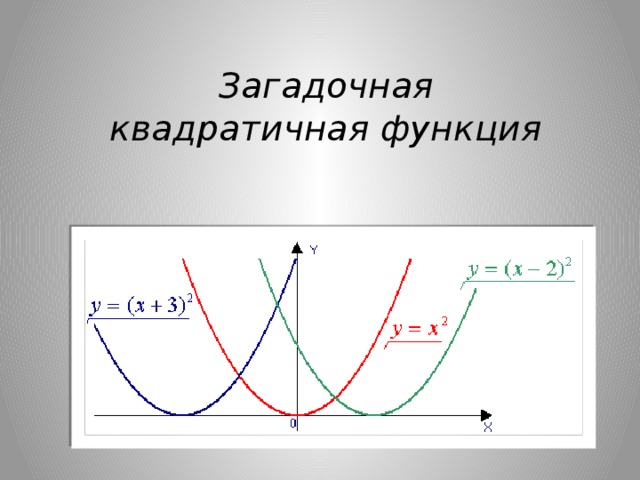
Загадочная квадратичная функция

• Цель: Научиться применять знания свойства квадратного трехчлена при выполнении нестандартных заданий.

• Задачи исследования:

• 1.Рассмотреть свойства квадратичной функции, выходящие за рамки школьных знаний.
• 2.Научиться решать квадратное уравнение с параметром, а также неравенства и системы.

• Предмет: Квадратичная функция
• Объект: Задания на квадратичную функцию с параметром
• Выдвигаемая гипотеза: Знание свойств квадратичной функции помогает при решении заданий с параметром

• Методы исследования

-  теоретические :  сравнение  анализ систематизация формализация

- эмпирические:   изучение литературы по проблеме защиты информации поиск информации в Интернете

• Продукт: Памятка для решения квадратных уравнений с параметром

Исторические сведения

• Линии второго порядка - плоские линии, прямоугольные координаты точек которых удовлетворяют алгебраическому уравнению второй степени. Средь линий второго порядка различают: параболы, гиперболы, эллипсы (также окружности).
• Линии второго порядка возникли как сечения конических поверхностей.

• Приступил к изучению конических сечений - парабола, гипербола, эллипс, ученик знаменитого Платона, древнегреческий математик Менехм (IV в. до н.э.). Захотев решить задачу об удвоении куба, Менехм задумался: «А что случится, если разрезать конус плоскостью, перпендикулярной его образующей?». Таким образом, изменив угол при вершине прямого кругового конуса, Менехм получил три вида кривых: эллипс — если угол при вершине конуса острый; парабола — если угол прямой; одну ветвь гиперболы — если угол тупой.

• Название кривых придумал не Менехм. Дал представление о них геометр древности Аполлоний Пергский, посвятивший замечательным кривым трактат из восьми книг «Конические сечения» («О кониках»).
• Аполлоний отобразил, что кривые можно получить, проводя различные сечения несменяемого кругового конуса, причем какого угодно. При надлежащем наклоне секущей плоскости удается обрести все типы конических сечений. Если считать, что конус не заканчивается в вершине, а проектируется на нее, тогда у некоторых сечений образуется две ветви.

Определение квадратичной функции

• Квадратичная функция  — функция вида  

, где  a, b, c некоторые числа.

• Выделим полный квадрат

0 и влево, если  x 0  2) сдвига вдоль оси ОY на  y 0  единиц (вверх, если  y 0   0 и вниз, если  y 0  Точка с координатами ( x 0 ;  y 0 ) называется  вершиной  параболы. " width="640"

Теорема Виета

• Для того чтобы числа x 1 , x 2 , были решениями уравнения ax 2 +bx+c=0 необходимо и достаточно, чтобы x 1 +x 2 =-b/a; x 1 x 2 =c/a.
• Графиком квадратичной функции является парабола, получаемая из графика функции y  =  ax 2  с помощью двух параллельных переносов:

1) сдвига вдоль оси ОХ на  x 0  единиц (вправо, если  x 0  0 и влево, если  x 0 

2) сдвига вдоль оси ОY на  y 0  единиц (вверх, если  y 0   0 и вниз, если  y 0  

• Точка с координатами ( x 0 ;  y 0 ) называется  вершиной  параболы.

0 и a0, то уравнение умеет два действительных различных корня, знаки которых при c0 одинаковые и противоположны знаку коэффициента b, а при c2.Если D=0 и a0,то уравнение имеет действительные и равные между собой корни, знак которых противоположен знаку коэффициента b; 3.Если D0, то уравнение не имеет действительных корней; " width="640"

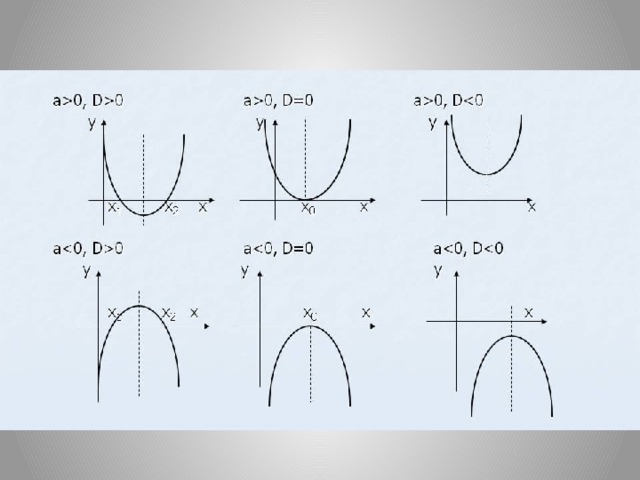
Свойства корней квадратного трёхчлена

• Приведенные теоремы позволяют сформулировать следующие свойства корней квадратного уравнения, часто применяемые при решении задач с параметрами:

1.Если D0 и a0, то уравнение умеет два действительных различных корня, знаки которых при c0 одинаковые и противоположны знаку коэффициента b, а при c

2.Если D=0 и a0,то уравнение имеет действительные и равные между собой корни, знак которых противоположен знаку коэффициента b;

3.Если D0, то уравнение не имеет действительных корней;

0 и D=0, то левая часть уравнения есть полный квадрат и, наоборот, если левая часть уравнения есть полный квадрат, то a0, а D=0; " width="640"

• Замечание.  Аналогично устанавливаются и свойства корней квадратного уравнения и для a

4.Если в квадратном уравнении поменять местами коэффициенты a и c, то получим уравнение, корни которого обратны корням данного;

5.Если в квадратном уравнении поменять знак коэффициента b, то получим уравнение, корни которого противоположны корням данного;

6.Если в квадратном уравнении коэффициенты a и c разных знаков, то уравнение имеет действительные корни;

7.Если a0 и D=0, то левая часть уравнения есть полный квадрат и, наоборот, если левая часть уравнения есть полный квадрат, то a0, а D=0;

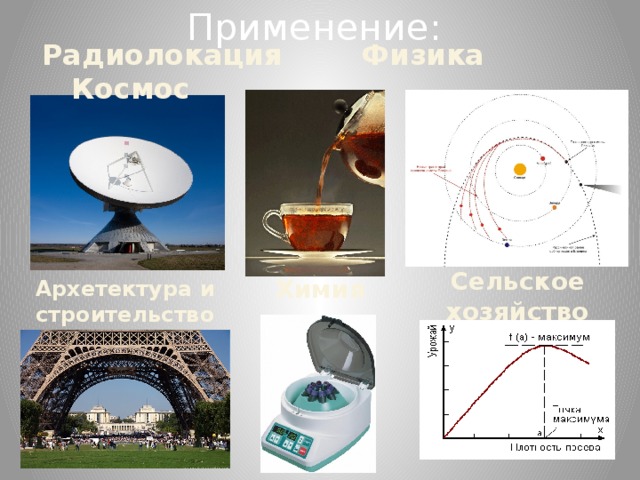
Применение:

Радиолокация Физика Космос

Архетектура и строительство

Химия

Сельское хозяйство

Что такое параметр?

• Параметр  - математическая величина, входящая в математическую формулу и сохраняющая своё постоянное значение лишь в условиях данной задачи. При решении таких задач необходимо привести ответ для каждого значения параметра. Принято обозначать неизвестные последними буквами латинского алфавита (х, у, z…), параметры – первыми буквами ( а, в, с…). Задачи с параметрами решаются теми же приемами, что и аналогичные задачи без параметра. При решении используются аналитические и графические способы. Задачи с параметрами входят в экзаменационную работу за 9 класс, поэтому мы решили поближе познакомиться с данными задачами.
• Определение .  Квадратным уравнением с параметром  а  называется уравнение вида    , где А(а), В(а), С(а)   – данные функции от параметра  а , рассматриваемые на пересечении их областей определения.
• В частности, некоторые из коэффициентов или свободный член могут быть числами.

Примеры решений заданий с параметром

• Найти сумму целых значений числа p, при которых вершина параболы y = 1/3x 2  – 2p+ 12p расположена выше оси Ox.

0). Так как вершина параболы лежит выше оси Ox, то парабола не пересекает ось абсцисс. " width="640"

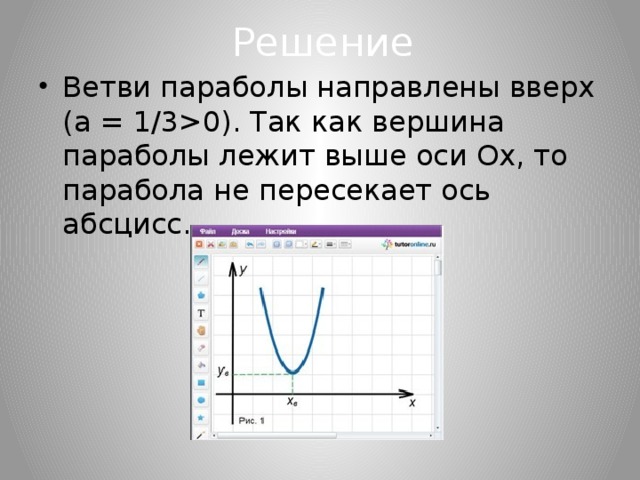
Решение

• Ветви параболы направлены вверх (a = 1/30). Так как вершина параболы лежит выше оси Ox, то парабола не пересекает ось абсцисс.

• Значит, функция y = 1/3x 2  – 2px + 12p не имеет нулей, а уравнение 1/3x 2  – 2px + 12p = 0 не имеет корней.
• Это возможно, если дискриминант последнего уравнения окажется отрицательным.
• Вычислим его: D/4 = p 2  – 1/3·12p = p 2  – 4p; p 2  – 4p
• Сумма целых значений числа p из промежутка (0; 4): 1 + 2 + 3 = 6.

Ответ: 6.

• Постройте график функции    и определите, при каких значениях параметра  a  он имеет ровно две общие точки с пря­мой  y  =  a .

Решение

• Построим график функции  y  = − x 2  − 4 x  − 4 на промежутке (−∞; −1), график функции  y  =  x  на промежутке [−1; 1] и график функции  y  = 2 −  x  на промежутке (1; +∞).

• Прямая  y  =  a  имеет с построенным графиком ровно две общие точки при  a  a  

Ответ:  a   a  

Заключение

• В заключение можно сказать, что многие процессы описываются квадратичной функцией, что в основе многих устройств лежат свойства параболы, связанные с её фокусом, т. е. способностью отражать и собирать лучи. Конечно, использование свойств параболы не ограничивается всем вышеизложенным, можно встретить много примеров в науке и технике, астрономии. В данной работе я попыталась рассказать, что некоторые формы устройств, приборов выбраны не просто так, что без математики не обойтись ни в одной области науки, техники и в повседневной жизни.

Спасибо за внимание!