Презентация "Решение задач с применением Пифагоровых троек"

Решение задач

с применением

пифагоровых троек.

Зубко Елена Федоровна учитель математики

ГУ «Школы-гимназии № 18 отдела образования акимата г. Костаная»

Пифагорово число или

(пифагорова тройка) –

комбинация из трех целых чисел

х, у, z, удовлетворяющих соотношению Пифагора

х 2 + у 2 = z 2

Египетский треугольник

5

3

4

Примитивные тройки

(3, 4, 5)

(5, 12, 13)

(8, 15, 17)

(7, 24, 25)

(20, 21, 29)

(12, 35, 37)

(9, 40, 41)

(3, 4, 5) - (6, 8, 10)

(9, 12, 15)

(12,16, 20)

( 15,16,25)

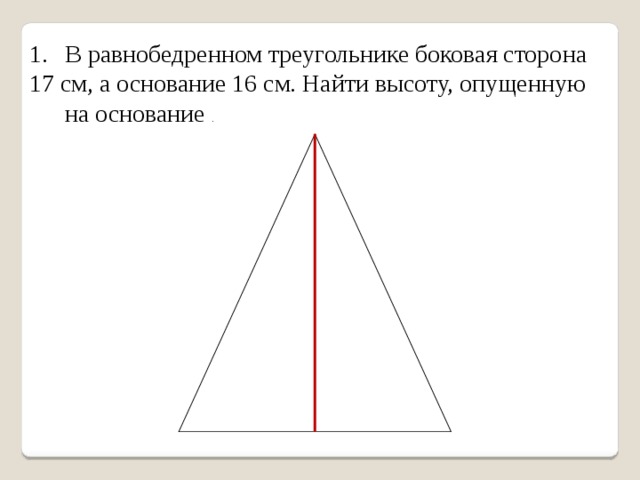
• В равнобедренном треугольнике боковая сторона

17 см, а основание 16 см. Найти высоту, опущенную на основание .

2.В прямоугольном треугольнике катеты равны

5 и 12. Найти длину медианы , проведенной к гипотенузе.

3. Гипотенуза прямоугольного треугольника равна 26, а катеты относятся как 5: 12. Найти наибольший катет

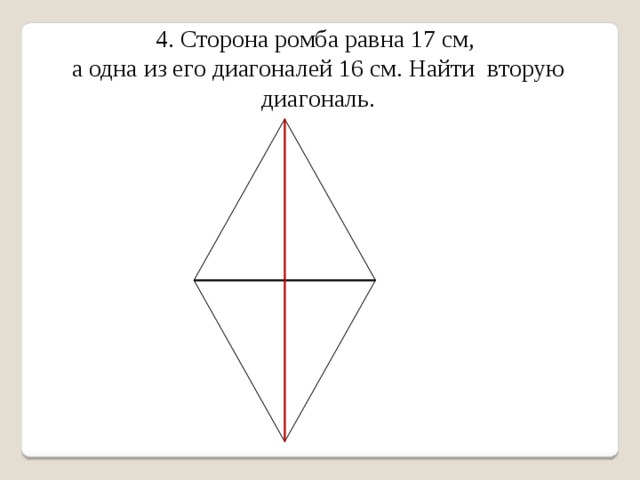
4. Сторона ромба равна 17 см,

а одна из его диагоналей 16 см. Найти вторую диагональ.

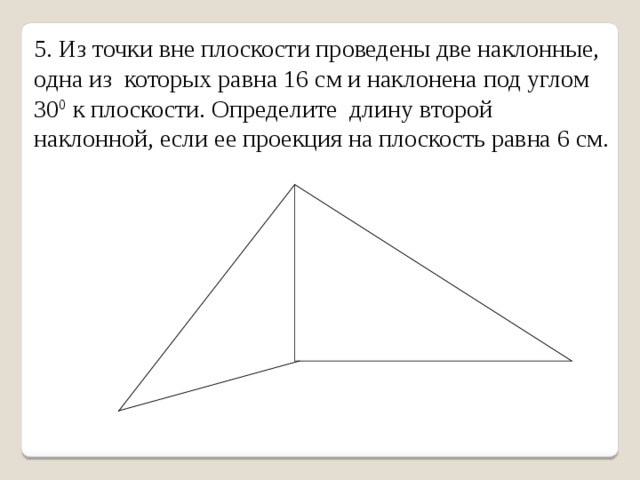
5. Из точки вне плоскости проведены две наклонные, одна из которых равна 16 см и наклонена под углом 30 0 к плоскости. Определите длину второй наклонной, если ее проекция на плоскость равна 6 см.

6. Точка М удалена от плоскости правильного многоугольника на расстоянии 15 см. Найти расстояние от этой точки до вершин многоугольника, если площадь круга, описанного около

него равна 64п

7. Высота прямоугольного параллелепипеда равна 8 см, а стороны оснований 5 и 6 см. Вычислите площадь сечения, проведенного через сторону меньшего основания и противоположную ей сторону верхнего основания.

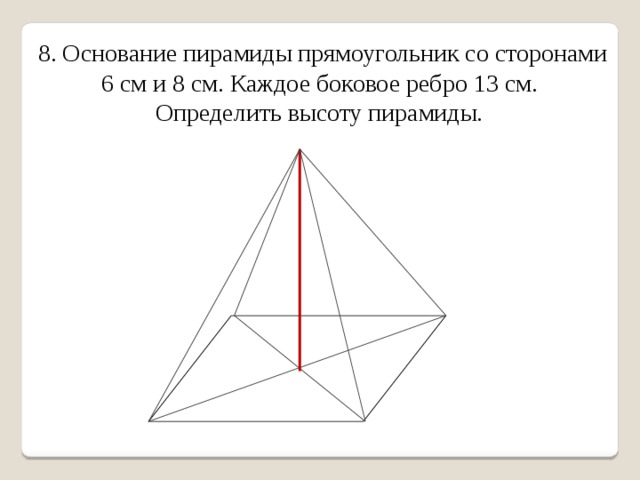
8. Основание пирамиды прямоугольник со сторонами 6 см и 8 см. Каждое боковое ребро 13 см.

Определить высоту пирамиды.

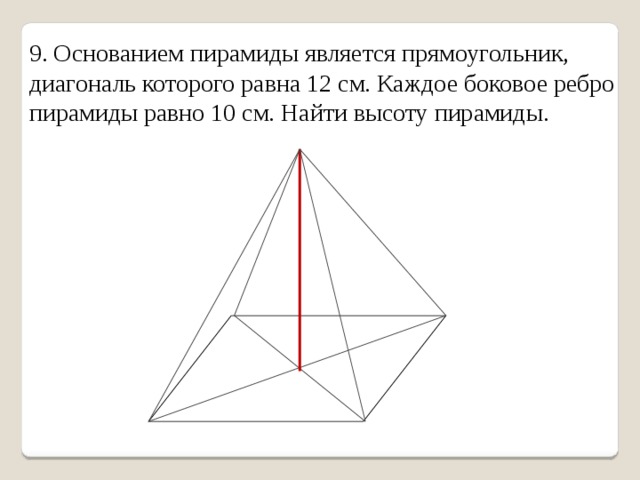
9. Основанием пирамиды является прямоугольник, диагональ которого равна 12 см. Каждое боковое ребро пирамиды равно 10 см. Найти высоту пирамиды.

10. Найти площадь круга вписанного в многоугольник, лежащий в основании пирамиды, если высоты боковых граней равна 25 см , а высота пирамиды 24 см.

11. Диагональ осевого сечения цилиндра 13 см, высота 5 см. Найти площадь боковой поверхности цилиндра.

12. Диаметр основания цилиндра 4 см, высота 3 см. Определить диагональ осевого сечения цилиндра.

13.Длина радиуса основания конуса 3м, высота 4 м. Определить образующую конуса.

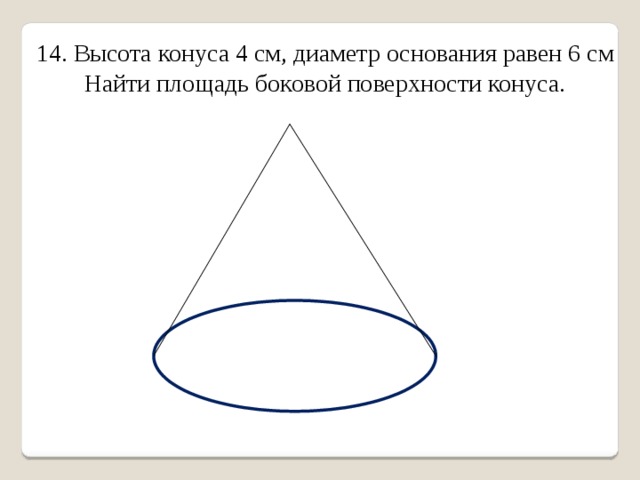
14. Высота конуса 4 см, диаметр основания равен 6 см Найти площадь боковой поверхности конуса.

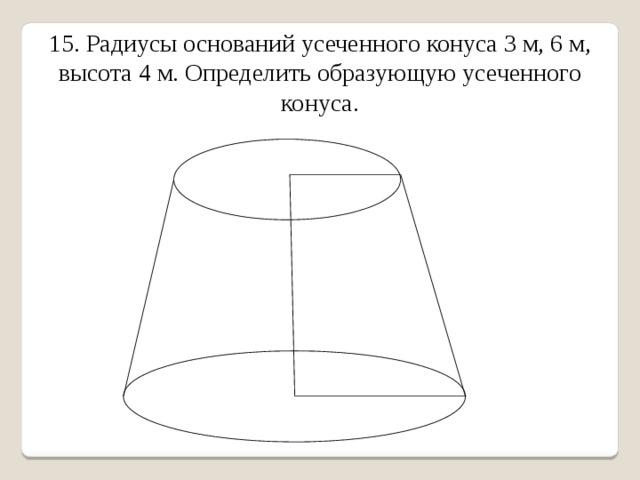
15. Радиусы оснований усеченного конуса 3 м, 6 м, высота 4 м. Определить образующую усеченного конуса.

16. В шаре с радиусом 41см на расстоянии 9 см от центра проведено сечение. Найти площадь этого сечения.

17. На поверхности шара даны три точки. Прямолинейные расстояния между ними 6,8,10. Радиус шара 13. Найти расстояние от центра шара до плоскости, проходящей через эти точки.

18. Гипотенуза прямоугольного треугольника равна 20. Найдите его катеты, если один из них на 4 см больше другого.

А) 7 и 13

в) 12 и 14

с) 24 и 4

д) 12 и 16

е) 11 и 9

19. В прямоугольном треугольнике сумма катетов равна 17, длина гипотенузы 13. Найдите катеты.

А) 11 и 6

в) 10 и 7

с) 9 и 8

д) 12 и 5

е) 13 и 4

Из точки к плоскости проведены

две наклонные, равные 10см и 17 см.

найдите проекции этих наклонных, если точка находится на расстоянии

8 см от плоскости

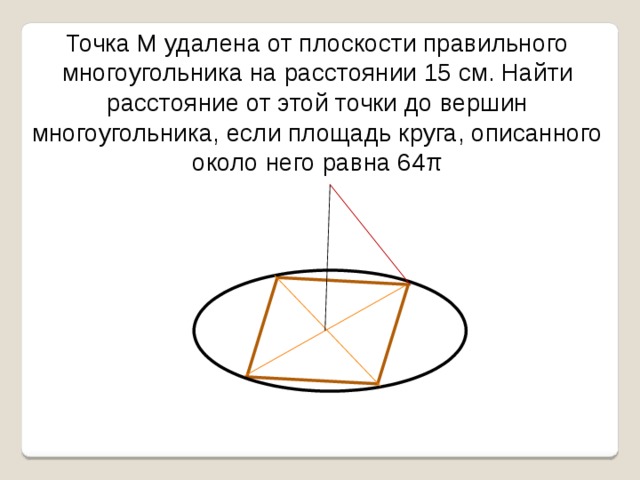
Точка М удалена от плоскости правильного многоугольника на расстоянии 15 см. Найти расстояние от этой точки до вершин многоугольника, если площадь круга, описанного около него равна 64π

Найдите значения тригонометрических функций угла , если известно, что:

α – угол первой четверти

Найдите значения тригонометрических функций угла , если известно, что:

α – угол первой четверти

Решение задач

с применением

пифагоровых троек.

Зубко Елена Федоровна учитель математики

ГУ «Школы-гимназии № 18 отдела образования акимата г. Костаная»