Просмотр содержимого документа
«Презентация "Треугольники" обобщающее повторение»

Треугольники.
Презентация для обобщающего повторения и подготовке к ГИА
Презентацию подготовила
Скосырская Л.Г.
Учитель математики 1 категории
Мкоу Красноярская сош

Содержание:
- Треугольники
- медиана, высота и биссектриса
- Виды треугольников
- Углы в треугольниках
- Признаки равенства треугольников
- Подобие треугольников
- Площади и периметры треугольников
- Средняя линия в треугольниках
- Другие фигуры из треугольников
- Треугольники в природе

- Биссектриса - отрезок, соединяющий вершину треугольника с противоположной стороной и делящий угол на 2 равных угла.
СМ – биссектриса. ∟ВСМ = ∟МСА
- Медиана – отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
ВК – медиана. АК=КС
- Высота – перпендикуляр, проведенный из вершины треугольника к противоположной стороне.
АН – высота. ∟АНС = 90˚
А
М
К
В
Н
С

треугольники
Треугольник - геометрическая фигура, состоящая из 3 точек, не лежащих на одной прямой, и отрезков, их соединяющих
А, В, С – вершины
А
С
В

Виды треугольников
- Прямоугольные
- Тупоугольные
- Остроугольные
- Равнобедренные
- Равносторонние

Прямоугольный треугольник- треугольник, у которого один из углов = 90 °
В
У прямоугольного треугольника
АВ и АС – катеты (стороны прямоугольного треугольника, образующие прямой угол)
ВС – гипотенуза (сторона прямоугольного треугольника, лежащая против прямого угла)
Свойс тва
С
А

Свойства прямоугольного треугольника
- Катет прямоугольного треугольника, лежащий против угла 30˚, равен половине гипотенузы
- Гипотенуза всегда больше катета
- Сумма острых углов прямоугольного треугольника = 90˚
- Теорема Пифагора
квадрат гипотенузы равен сумме квадратам катетов
с² = а² + в²

Тупоугольный треугольник- это треугольник, у которого один из углов больше 90 °
Остроугольный треугольник - это треугольник, у которого все углы меньше 90 °

Равнобедренный треугольник
Равнобедренный треугольник -треугольник, у которого две стороны равны. Равные стороны называют боковыми, а третью- основанием.
Свойства:
- Углы при основании равны
- Биссектриса, проведенная
к основанию, является медианой и высотой.
Б с
О т
К о
О р
В о
А н
Я а
основание
Равносторонний треугольник
Равносторонний треугольник – это треугольник, у которого все стороны равны

Внешний угол треугольника – угол, смежный с каким-нибудь углом этого треугольника
Свойства внешнего угла треугольника:
- Внешний угол равен сумме углов треугольника, несмежных с ним.
- Сумма внешнего и смежного угла равна 180˚
Теорема о сумме углов треугольника .
Сумма углов треугольника ровнав180˚
Смежный
угол
Внешний угол

Признаки равенства треугольников
ТРЕУГОЛЬНИКИ ПОДОБНЫ
- Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
- Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней угла другого треугольника, то такие треугольники равны.
- Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Подобие треугольников
β
- Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами равны, то такие треугольники подобны
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами равны, то такие треугольники подобны
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами равны, то такие треугольники подобны
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами равны, то такие треугольники подобны
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами равны, то такие треугольники подобны
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами равны, то такие треугольники подобны
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами равны, то такие треугольники подобны
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами равны, то такие треугольники подобны
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами равны, то такие треугольники подобны
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны
΄
β΄
΄
∟ =∟΄
∟ β=∟β΄
∆ αbc~∆α΄b΄c ΄
γ
α
b
γ΄
b΄
α΄
α∕α΄=b∕b΄
∟ γ=∟γ΄
∆ αbc~∆α΄b΄c ΄
α
b
c
b΄
α΄
c΄
α∕α΄=b∕b΄=c∕c΄ ∆αbc~∆α΄b΄c ΄

Ѕ и Р треугольников
H- высота, проведенная к стороне а
Р=a+b+c
- Ѕ=½ah
- Ѕ=a²√3 : 4 (для равностороннего )
- Ѕ=½αb (для прямоугольного треугольника)
- Ѕ=½αb sinγ
- Ѕ=√p(p-α)(p-b)(p-c)
h
a
а
а
γ
в
р - полупериметр
Р=( а + в + с) : 2
в
а
с
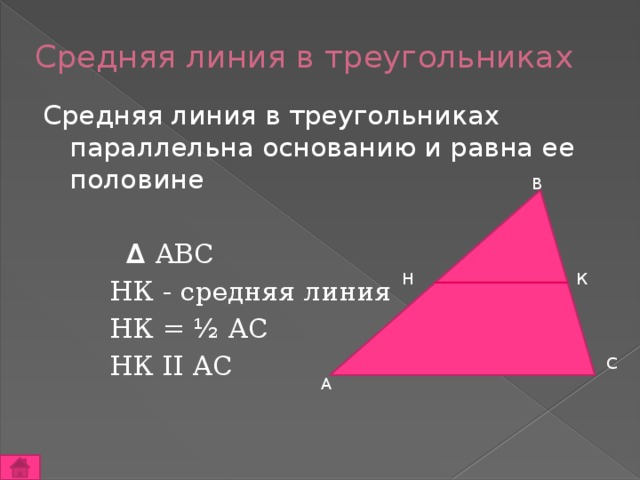
Средняя линия в треугольниках
Средняя линия в треугольниках параллельна основанию и равна ее половине
∆ АВС
НК - средняя линия
НК = ½ АС
НК ΙΙ АС
В
Н
К
С
А
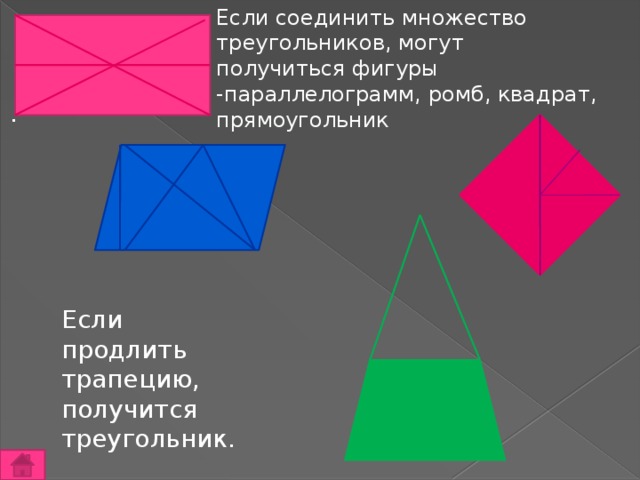
Если соединить множество треугольников, могут получиться фигуры -параллелограмм, ромб, квадрат, прямоугольник
.
Если продлить трапецию, получится треугольник.

Треугольники в природе































