Презентация «Углы в пространстве»

Углы в пространстве

Подготовила

Пискарева Р.И.,

учитель математики

МОУ «Гимназия №1»

г.Железногорска Курской обл.

Оглавление

• Углы между двумя прямыми
• Угол между плоскостями
• Угол между прямой и плоскостью
• Пирамида Хеопса (Хуфу)

Углы между двумя прямыми

• Углом между двумя пересекающимися прямыми называется наименьший из углов, образованных при пересечении прямых.
• 0°
• Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся.
• Две прямые называются перпендикулярными, если угол между ними равен 90°.
• Угол между параллельными прямыми считается равным нулю.

При нахождении угла используют:

• Формулу для нахождения угла  между прямыми m и l , если стороны a и b треугольника ABC соответственно параллельны этим прямым;
• Формулу или в координатной форме для нахождения угла φ между прямыми m и l , если векторы и параллельны соответственно этим прямым; в частности, для того что бы прямые m и l были перпендикулярны, необходимо и достаточно, чтобы или
• Ключевые задачи.

Пример 1:

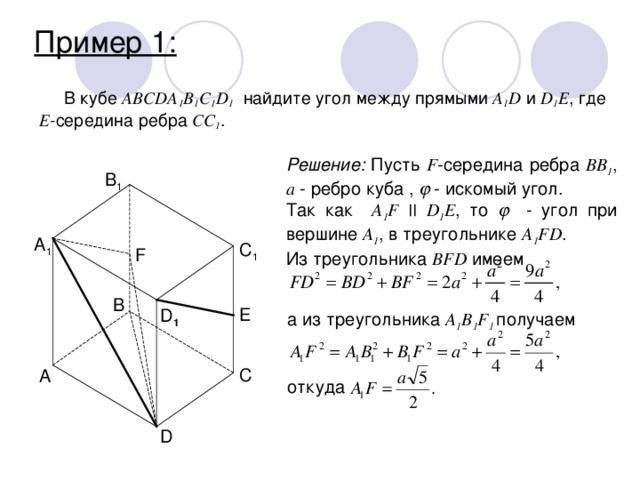
В кубе ABCDA 1 B 1 С 1 D 1 найдите угол между прямыми A 1 D и D 1 E , где Е -середина ребра CC 1 .

Решение: Пусть F -середина ребра BB 1 , а - ребро куба ,  - искомый угол.

Так как A 1 F || D 1 E , то  - угол при вершине A 1 , в треугольнике A 1 FD .

Из треугольника BFD имеем

B 1

A 1

C 1

F

B

E

D 1

a из треугольника A 1 B 1 F 1 получаем

C

A

откуда

D

Пример 1:

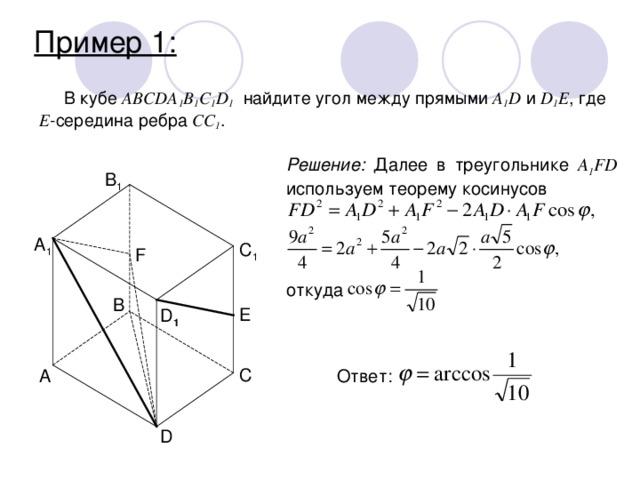
В кубе ABCDA 1 B 1 С 1 D 1 найдите угол между прямыми A 1 D и D 1 E , где Е -середина ребра CC 1 .

Решение: Далее в треугольнике A 1 FD используем теорему косинусов

B 1

A 1

C 1

F

откуда

B

E

D 1

C

A

Ответ:

D

Пример 2:

В единичном кубе ABCDA 1 B 1 С 1 D 1 найдите угол между прямыми AE и DF , Где E и F – точки, расположенные на ребрах CD и C 1 D 1 так, что

Решение: Введем прямоугольную систему координат, как указано на рисунке. Тогда A (0;0;0), D (1;0;0),

B 1

C 1

z

F

A 1

D 1

y

C

B

где  - искомый угол.

E

A

D

x

Ответ:

Пример 3:

Ключевая задача (теорема косинусов для трёхгранного угла)

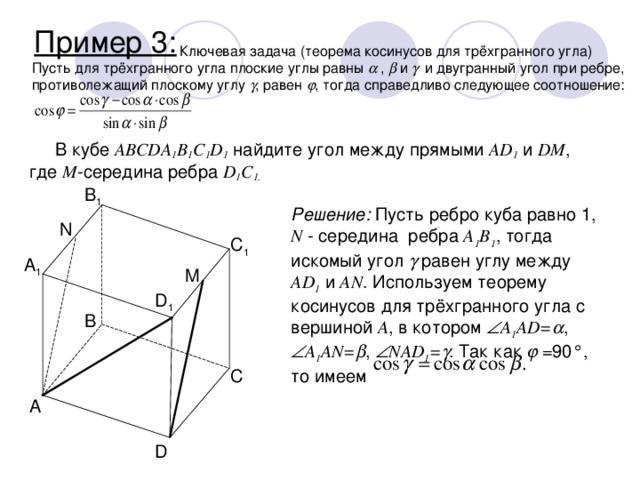
Пусть для трёхгранного угла плоские углы равны  ,  и  и двугранный угол при ребре, противолежащий плоскому углу  , равен  , тогда справедливо следующее соотношение:

В кубе ABCDA 1 B 1 C 1 D 1 найдите угол между прямыми AD 1 и DM , где M -середина ребра D 1 C 1.

B 1

Решение: Пусть ребро куба равно 1, N - середина ребра A 1 B 1 , тогда искомый угол  равен углу между AD 1 и AN . Используем теорему косинусов для трёхгранного угла с вершиной A , в котором  A 1 AD=  ,  A 1 AN=  ,  NAD 1 =  . Так как  =90°, то имеем

N

C 1

A 1

M

D 1

B

C

A

D

Пример 3:

Ключевая задача (теорема косинусов для трёхгранного угла)

Пусть для трёхгранного угла плоские углы равны  ,  и  и двугранный угол при ребре, противолежащий плоскому углу  , равен  , тогда справедливо следующее соотношение:

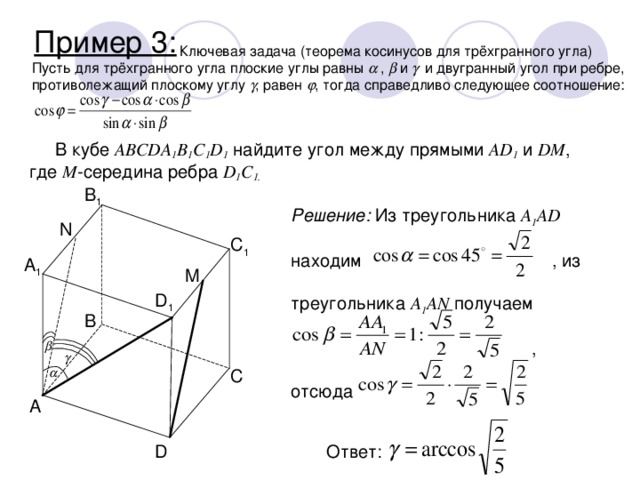
В кубе ABCDA 1 B 1 C 1 D 1 найдите угол между прямыми AD 1 и DM , где M -середина ребра D 1 C 1.

B 1

Решение: Из треугольника A 1 AD находим , из треугольника A 1 AN получаем , отсюда

N

C 1

A 1

M

D 1

B







C

A

D

Ответ:

Угол между прямой и плоскостью

• Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и её проекцией на данную плоскость.
• 0 o  ( a ;  )
• Угол между взаимно перпендикулярной прямой и плоскостью равен 90 o
• Если прямая параллельна плоскости (или лежит в ней), то угол между ними считается равным 0 0

Угол между прямой l и плоскостью  можно вычислить:

• Если этот угол удаётся включить в прямоугольный треугольник в качестве одного из острых углов;
• По формуле где
• Используя координатно-векторный, векторный метод по формуле или в координатной форме - вектор нормали плоскости  , - направляющий вектор прямой l ; прямая l плоскость  параллельны тогда и только тогда, когда
• Ключевая задача

Пример 1:

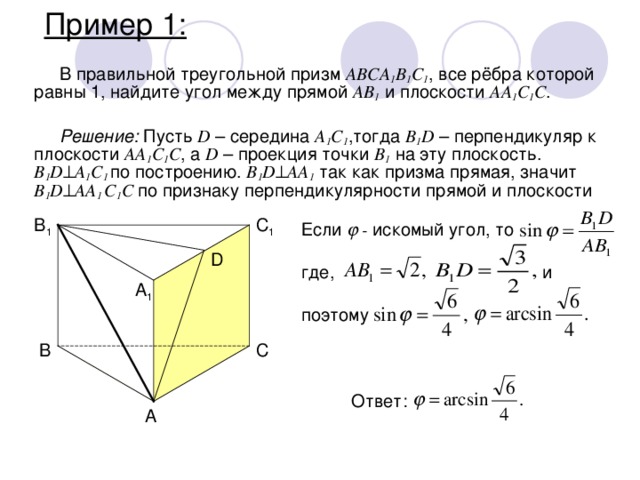
В правильной треугольной призм ABCA 1 B 1 C 1 , все рёбра которой равны 1, найдите угол между прямой AB 1 и плоскости AA 1 C 1 C .

Решение: Пусть D – середина A 1 C 1 ,тогда B 1 D – перпендикуляр к плоскости AA 1 C 1 C , а D – проекция точки B 1 на эту плоскость. B 1 D  A 1 C 1 по построению. B 1 D  AA 1 так как призма прямая, значит B 1 D  AA 1 C 1 C по признаку перпендикулярности прямой и плоскости

B 1

C 1

Если  - искомый угол, то

где, и

поэтому

D

A 1

B

C

Ответ:

A

Пример 2:

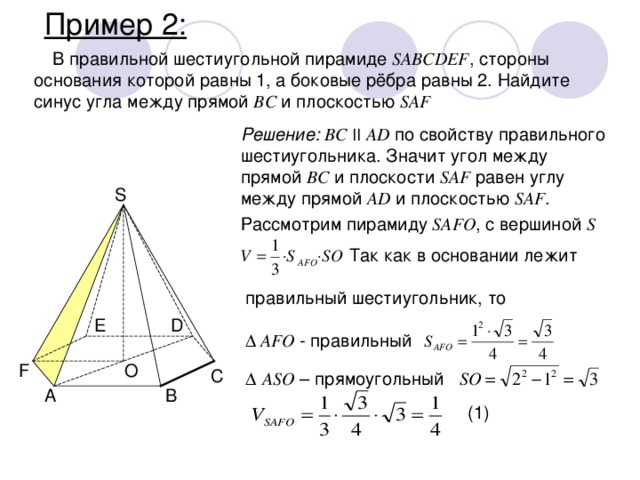
В правильной шестиугольной пирамиде SABCDEF , стороны основания которой равны 1, а боковые рёбра равны 2. Найдите синус угла между прямой BC и плоскостью SAF

Решение: BC || AD по свойству правильного шестиугольника. Значит угол между прямой BC и плоскости SAF равен углу между прямой AD и плоскостью SAF .

Рассмотрим пирамиду SAFO , с вершиной S

S

Так как в основании лежит

правильный шестиугольник, то

∆ AFO - правильный

∆ ASO – прямоугольный

E

D

F

O

C

B

A

(1)

Пример 2:

В правильной шестиугольной пирамиде SABCDEF , стороны основания которой равны 1, а боковые рёбра равны 2. Найдите синус угла между прямой BC и плоскостью SAF

Решение: Рассмотрим пирамиду OAFS ,

с вершиной O . , где

OH – перпендикуляр проведённый из точки O к плоскости SAF

S

S

2

2

D

E

H

K

F

A

1

F

O

C

A

B

(2)

Пример 2:

В правильной шестиугольной пирамиде SABCDEF , стороны основания которой равны 1, а боковые рёбра равны 2. Найдите синус угла между прямой BC и плоскостью SAF

Решение: Так как находим объем одной пирамиды двумя способами, то сравнивая равенства 1 и 2 делаем вывод

S

 HAO – угол между прямой AO и плоскостью SAF значит синус угла между прямой BC и плоскостью SFA равен

E

D

H

O

F

C

A

B

Ответ:

Пример 3: Координатно-векторный метод

В единичном кубе ABCDA 1 B 1 C 1 D 1 найдите угол между прямой AD 1 и плоскостью  , проходящей через точки A 1 , E и F , где точка E - середина ребра C 1 D 1 , а точка F лежит на ребре DD 1 , так, что D 1 F=2DF .

Решение: Введём прямоугольную систему координат, как указано на рисунке. Тогда

A (0;0;0), A 1 (0;0;1), D 1 ( 1;0;1),

z

A 1

B 1

E

D 1

C 1

Пусть - вектор,

A

B

Перпендикулярный плоскости  ,

 - искомый угол. Тогда

F

y

C

D

x

Пример 3: Координатно-векторный метод

В единичном кубе ABCDA 1 B 1 C 1 D 1 найдите угол между прямой AD 1 и плоскостью  , проходящей через точки A 1 , E и F , где точка E - середина ребра C 1 D 1 , а точка F лежит на ребре DD 1 , так, что D 1 F=2DF .

Решение: Вектор найдём из условий перпендикулярности этого вектора векторами и ,т.е из условий

z

A 1

B 1

E

D 1

или

C 1

Пусть x = 2, тогда y = -4, z = 3 и

A

B

F

Так как

y

то

C

D

Ответ:

x

Пример 3: Векторный метод

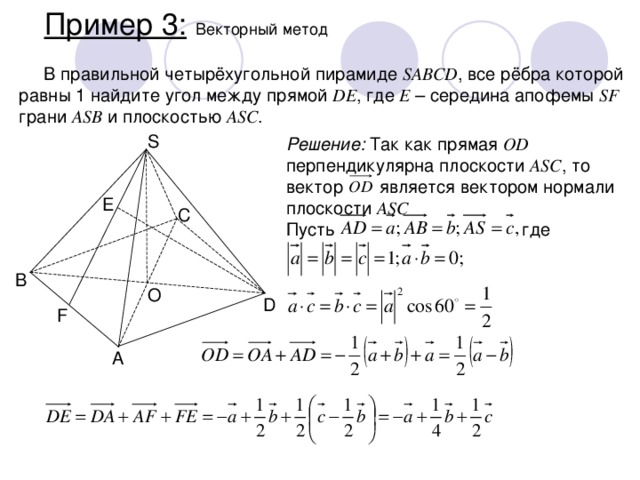
В правильной четырёхугольной пирамиде SABCD , все рёбра которой равны 1 найдите угол между прямой DE , где E – середина апофемы SF грани ASB и плоскостью ASC .

S

Решение: Так как прямая OD перпендикулярна плоскости ASC , то вектор является вектором нормали плоскости ASC

Пусть где

E

C

B

O

D

F

A

Пример 3: Векторный метод

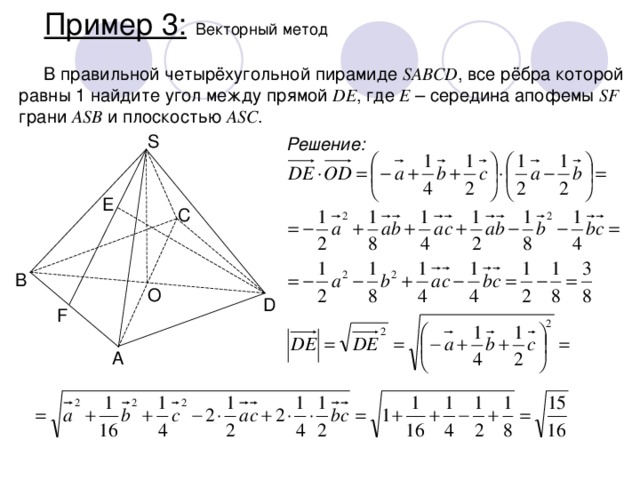
В правильной четырёхугольной пирамиде SABCD , все рёбра которой равны 1 найдите угол между прямой DE , где E – середина апофемы SF грани ASB и плоскостью ASC .

S

Решение:

E

C

B

O

D

F

A

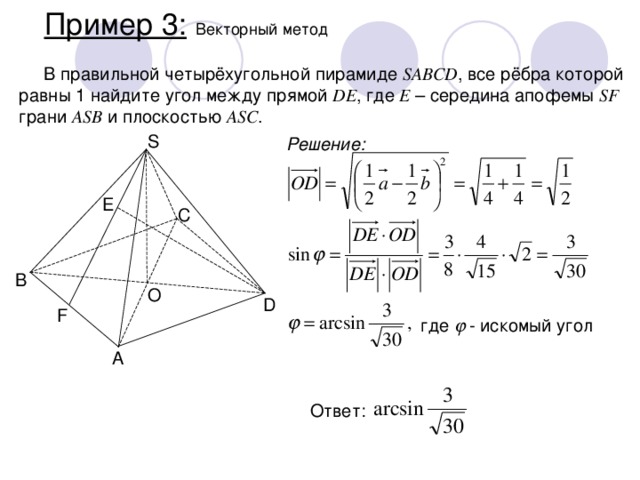
Пример 3: Векторный метод

В правильной четырёхугольной пирамиде SABCD , все рёбра которой равны 1 найдите угол между прямой DE , где E – середина апофемы SF грани ASB и плоскостью ASC .

S

Решение:

E

C

B

O

D

F

где  - искомый угол

A

Ответ:

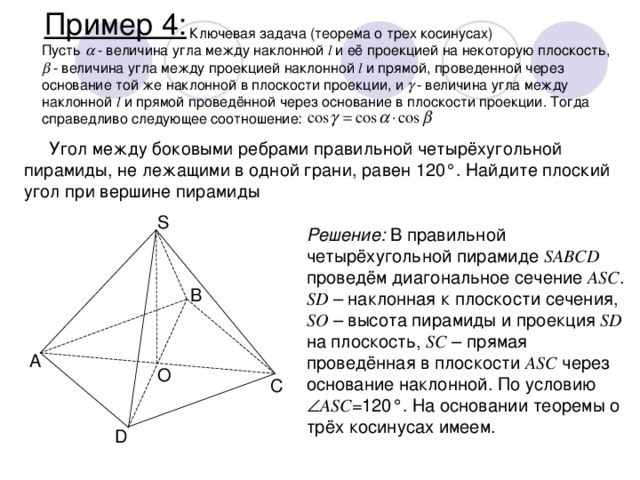
Пример 4:

Ключевая задача (теорема о трех косинусах)

Пусть  - величина угла между наклонной l и её проекцией на некоторую плоскость,  - величина угла между проекцией наклонной l и прямой, проведенной через основание той же наклонной в плоскости проекции, и  - величина угла между наклонной l и прямой проведённой через основание в плоскости проекции. Тогда справедливо следующее соотношение:

Угол между боковыми ребрами правильной четырёхугольной пирамиды, не лежащими в одной грани, равен 120°. Найдите плоский угол при вершине пирамиды

S

Решение: В правильной четырёхугольной пирамиде SABCD проведём диагональное сечение ASC . SD – наклонная к плоскости сечения, SO – высота пирамиды и проекция SD на плоскость, SC – прямая проведённая в плоскости ASC через основание наклонной. По условию  ASC =120°. На основании теоремы о трёх косинусах имеем.

B

A

O

C

D

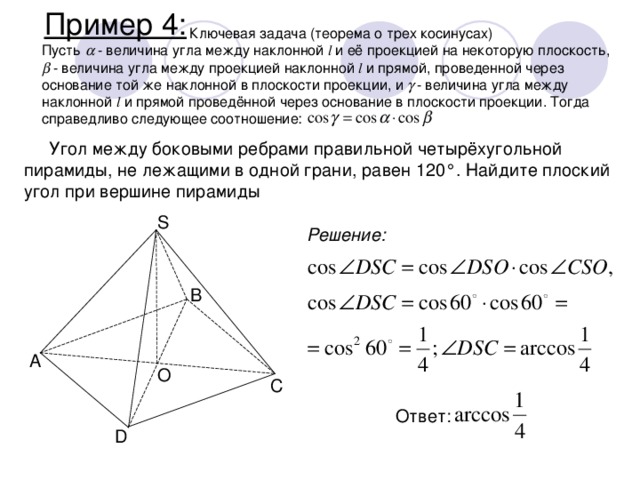
Пример 4:

Ключевая задача (теорема о трех косинусах)

Пусть  - величина угла между наклонной l и её проекцией на некоторую плоскость,  - величина угла между проекцией наклонной l и прямой, проведенной через основание той же наклонной в плоскости проекции, и  - величина угла между наклонной l и прямой проведённой через основание в плоскости проекции. Тогда справедливо следующее соотношение:

Угол между боковыми ребрами правильной четырёхугольной пирамиды, не лежащими в одной грани, равен 120°. Найдите плоский угол при вершине пирамиды

S

Решение:

B

A

O

C

Ответ:

D

Угол между плоскостями

• Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру.
• Величина двугранного угла принадлежит промежутку (0°;180°) .
• Величина угла между пересекающимися плоскостями принадлежит промежутку (0°;90°].
• Угол между двумя параллельными плоскостями считается равным 0°.

Способы нахождения угла между плоскостями:

• Как угол между прямыми, лежащими в этих плоскостях и перпендикулярным к линии их пересечения.
• По формуле , где S - площадь фигуры Ф , расположенной в плоскости  , S’ - площадь проекции фигуры Ф на плоскость  .
• По формуле или в координатной форме где - вектор нормали плоскости - вектор нормали плоскости
• Используя ключевые задачи.

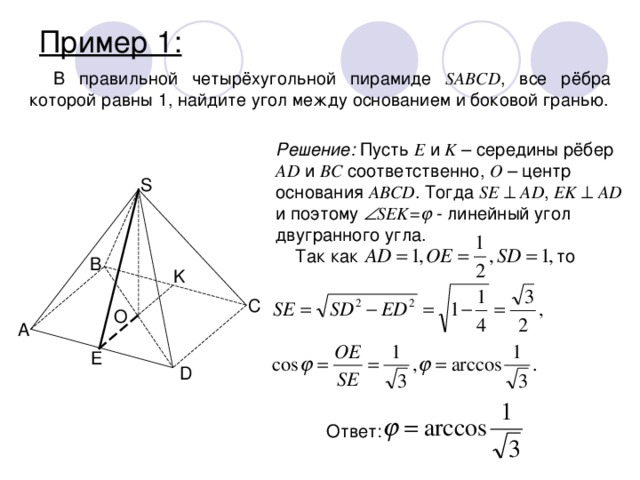
Пример 1:

В правильной четырёхугольной пирамиде SABCD , все рёбра которой равны 1, найдите угол между основанием и боковой гранью.

Решение: Пусть Е и K – середины рёбер AD и BC соответственно, O – центр основания ABCD . Тогда SE  AD , EK  AD и поэтому  SEK=  - линейный угол двугранного угла.

Так как то

S

В

K

C

O

А

E

D

Ответ:

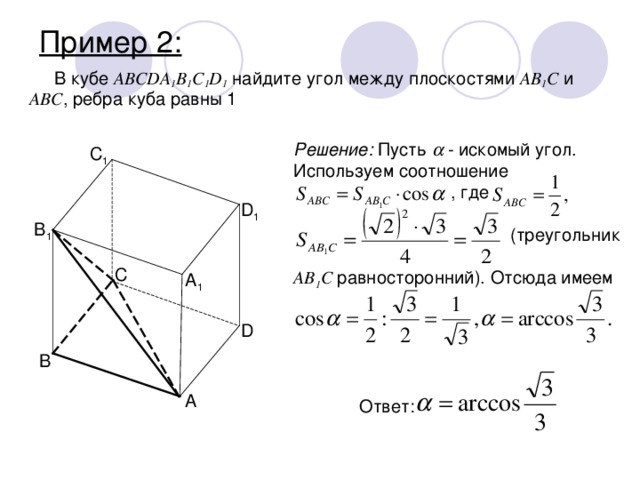
Пример 2:

В кубе ABCDA 1 B 1 C 1 D 1 найдите угол между плоскостями AB 1 C и ABC , ребра куба равны 1

Решение: Пусть  - искомый угол. Используем соотношение , где (треугольник AB 1 C равносторонний). Отсюда имеем

C 1

D 1

B 1

C

A 1

D

B

A

Ответ:

Пример 3:

Найдите угол между плоскостями 2 x +3 y +6 z -5=0 и 4 x +4 y +2 z -7=0.

Решение: Рассмотрим векторы и перпендикулярные к данным плоскостям. Искомый угол найдём по формуле

Так как то откуда

Ответ:

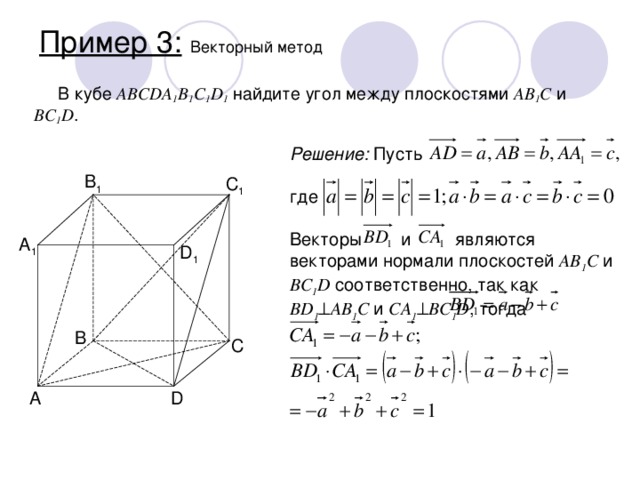
Пример 3: Векторный метод

В кубе ABCDA 1 B 1 C 1 D 1 найдите угол между плоскостями AB 1 C и BC 1 D .

Решение: Пусть где

Векторы и являются векторами нормали плоскостей AB 1 C и BC 1 D соответственно, так как BD 1  AB 1 C и CA 1  BC 1 D , тогда

B 1

C 1

A 1

D 1

B

C

A

D

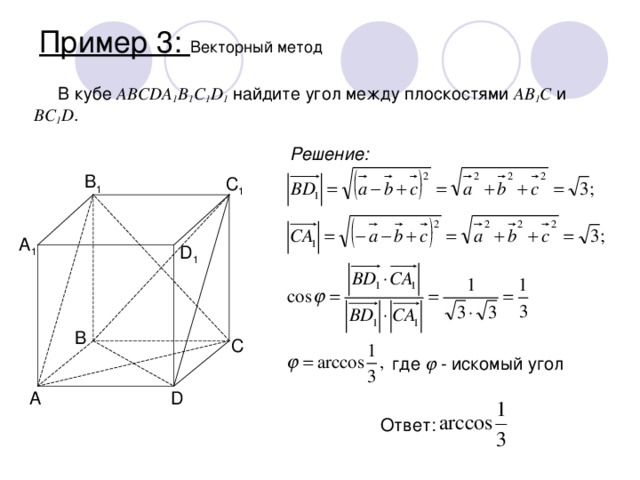
Пример 3: Векторный метод

В кубе ABCDA 1 B 1 C 1 D 1 найдите угол между плоскостями AB 1 C и BC 1 D .

Решение:

B 1

C 1

A 1

D 1

B

C

где  - искомый угол

A

D

Ответ:

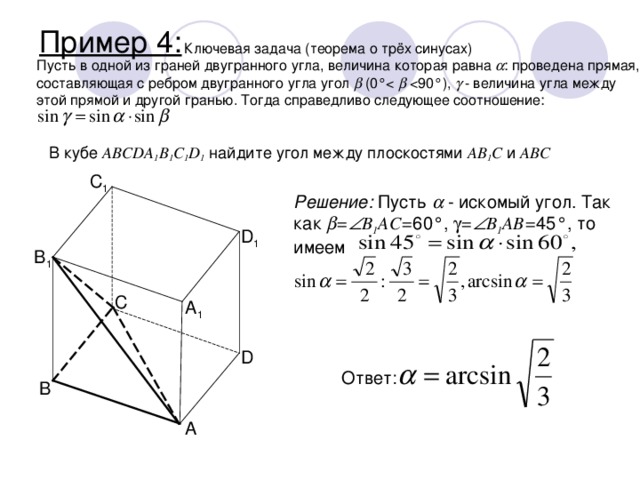
Пример 4:

Ключевая задача (теорема о трёх синусах)

Пусть в одной из граней двугранного угла, величина которая равна  : проведена прямая, составляющая с ребром двугранного угла угол  (0°   - величина угла между этой прямой и другой гранью. Тогда справедливо следующее соотношение:

В кубе ABCDA 1 B 1 C 1 D 1 найдите угол между плоскостями AB 1 C и ABC

C 1

Решение: Пусть  - искомый угол. Так как  =  B 1 AC= 60°,  =  B 1 AB= 45°, то имеем

D 1

B 1

C

A 1

D

Ответ:

B

A

Пирамида Хеопса (Хуфу)

Великая Пирамида Хеопса (ХУФУ) (около 2590-2568 годы до н .э.) последнее оставшееся чудо из древнего списка семи чудес света, является фантастическим шедевром инженерного искусства, не только благодаря своим гигантским размерам… Считается что Пирамида Хеопса весит 6,3 миллиона тонн и содержит строительного материала больше, чем ушло на сооружение всех соборов, церквей, и часовень в Англии. Сегодня Пирамида Хеопса(ХУФУ) состоит из 203 рядов каменно кладки, имеет высоту 146,6 метров, длина бокового ребра изначально была 230,3 метра. Площадь основания изначально 53000 метра квадратных или 5,3 га. Общий объем пирамиды 2,58 млн.метров кубических, средняя масса каменных блоков 2,5 тонн, самый тяжелый блок 15 тонн, Количество блоков около 2,5 млн. По подсчетам общий вес пирамиды около 6,25 млн тонн. Первоначально пирамида была облицована более твердым, чем основные блоки, белым известняком. Верх пирамиды венчал позолоченный камень-пирамидион. Облицовка сияла на Солнце персиковым цветом словно»сияющее чудо, которому сам бол Солнца РА ,казалось, отдал все свои лучи.»

Великая пирамида Хеопса (ХУФУ) имеет вид правильной пирамиды с высотой 147 метров и стороной основания 230 метров.

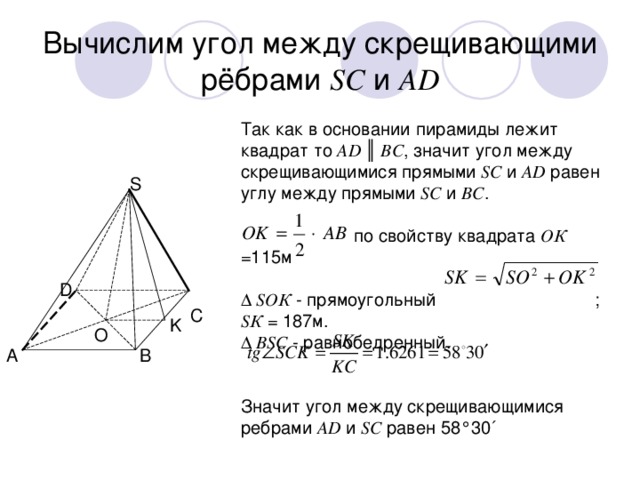
Вычислим угол между скрещивающими рёбрами SC и AD

Так как в основании пирамиды лежит квадрат то AD ║ ВС , значит угол между скрещивающимися прямыми SC и AD равен углу между прямыми SС и ВС .

по свойству квадрата ОК =115м

∆ SОК - прямоугольный ; SК = 187м.

∆ ВSС - равнобедренный.

Значит угол между скрещивающимися ребрами AD и SС равен 58°30´

S

D

C

K

O

A

B

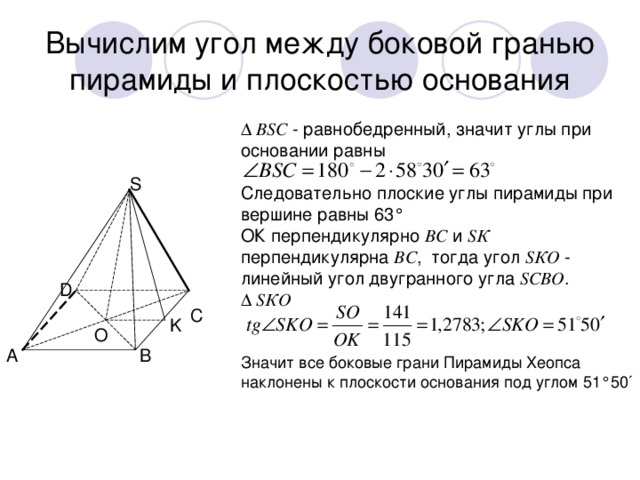
Вычислим угол между боковой гранью пирамиды и плоскостью основания

∆ ВSС - равнобедренный, значит углы при основании равны

Следовательно плоские углы пирамиды при вершине равны 63°

ОК перпендикулярно ВС и SК перпендикулярна ВС , тогда угол SКО - линейный угол двугранного угла SСВО .

∆ SКО

Значит все боковые грани Пирамиды Хеопса наклонены к плоскости основания под углом 51°50´

S

D

C

K

O

A

B

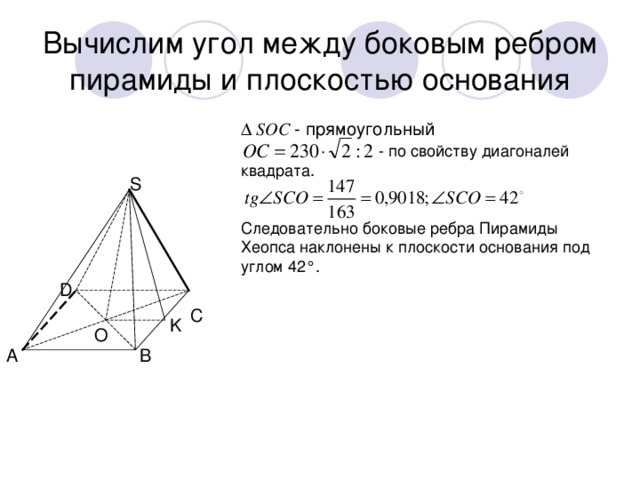
Вычислим угол между боковым ребром пирамиды и плоскостью основания

∆ SОС - прямоугольный

- по свойству диагоналей квадрата.

Следовательно боковые ребра Пирамиды Хеопса наклонены к плоскости основания под углом 42°.

S

D

C

K

O

A

B