Применение Формулы Пика для вычисления площади фигур, изображенных на клетчатой бумаге

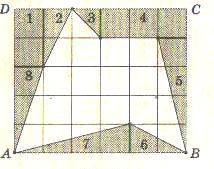
Итак, наш сюжет будет разворачиваться на обычном листке клетчатой бумаги. Линии, идущие по сторонам клеток, образуют сетку - палетку, а вершины клеток – узлы этой сетки. Нарисуем на листе многоугольник с вершинами в узлах (Рис.1) и найдем его площадь. Чтобы оценить площадь многоугольника, нарисованного на клетчатой бумаге, достаточно подсчитать, сколько клеток покрывает этот многоугольник (площадь клетки мы принимаем за единицу). Искать площадь можно по-разному.

Если дан многоугольник, то его можно разбить на такие части, которые пересекаются только по границам и площадь каждой из которых легко находится. Например: Разбиваем многоугольник на трапецию и треугольник как показано на рисунке 2. Его площадь будет равна сумме площади треугольника и трапеции. S= * 4 + * 2 * 4 = 20 + 4 =24 (см²)

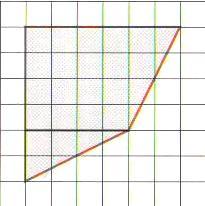
И спользованный нами способ несложен, но, он годится не для всяких многоугольников. Так , как многоугольник на рисунке 3 уже нельзя разбить на фигуры, как мы это делали с предыдущим многоугольником. Для этого существует другой способ вычисления площади.

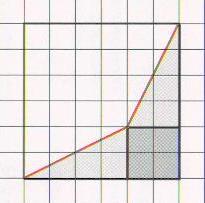
Давайте «схитрим»: вычислим площадь заштрихованной фигуры, которая «дополняет» наш многоугольник до прямоугольника. (Рис.4) Заштрихованная фигура легко разбивается на квадрат и прямоугольные треугольники, и ее площадь вычисляется без усилий. S= 6² – 2 * – 2² = 36 – 8 – 4 =24 (см²)

Я нашел свой способ решения, не указанный в литературе. Разбиваем многоугольник на трапецию и треугольник, как на рисунке 5. Присоединяем получившийся прямоугольный треугольник к трапеции так, чтобы получился прямоугольник. Вычисляем площадь получившегося прямоугольника: S= 4*6 = 24 (см²). Она равна площади данного многоугольника.

Подобные задачи как видим не очень сложные. Главное здесь – быть внимательным и аккуратным при проведении элементарных вычислении.

Я задумался, а нет ли универсальной формулы позволяющей находить площадь многоугольника без разбиения и дополнения?

ОСНОВНАЯ ЧАСТЬ. ФОРУЛА ПИКА

В истории черпаем мы мудрость,

В поэзии – остроумие,

В математике – проницательность.

Ф.Бэкон

О казывается, площади многоугольников, вершины которых расположены в узлах сетки, можно вычислять по формуле, связывающей их площадь с количеством узлов, лежащих внутри и на границе многоугольника. Эта замечательная и простая формула называется формулой Пика. Открыл ее немецкий математик Георгий Александр Пик в 1899г.

S=B + Г/2 – 1

Где S – площадь многоугольника, выраженная в площадях единичных квадратиков сетки, Г – количество узлов сетки, лежащих на границе многоугольника, а В – количество узлов сетки, лежащих внутри многоугольника

1.ПРЯМОУГОЛЬНИК С ВЕРШИНАМИ В УЗЛАХ И СТОРОНАМИ,

ИДУЩИМИ ПО ЛИНИЯМ СЕТКИ,

Связь между площадью фигуры и количеством узлов, попавших в эту фигуру, особенно ясно видна в случае прямоугольника.

Пусть ABCD – прямоугольник с вершинами в узлах и сторонами, идущими по линиям сетки (Рис.5) .Обозначим через B количество узлов, лежащих внутри прямоугольника, а через Г – количество узлов на его границе. Сместим сетку на пол клетки вправо и пол клетки вниз. Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из B узлов «контролирует» целую клетку смещенной сетки, каждый из Г – четырех граничных не угловых узла – половинок клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника S равна S= B + + 4* ¼ = B + Г/2 – 1

Итак, для прямоугольников с вершинами в узлах и сторонами, идущими по линиям сетки, мы установили формулу S= B + Г/2 – 1 . Оказывается, эта формула верна не только для прямоугольников, но и для произвольных многоугольников с вершинами узлах сетки!

Найдем площадь данной фигуры по формуле Пика. (Рис.5)

S ; внутри четырехугольника 17 узлов сетки, на границе – 16 узлов.

(Рис.5)

ПРОИЗВОЛЬНЫЙ МНОГОУГОЛЬНИК С ВЕРШИНАМИ В УЗЛАХ

Мы только что убедились в том, что формула Пика верна для рассмотренного примера. Докажем справедливость формулы Пика для произвольного многоугольника с вершинами в узлах.

Обозначим через S_м площадь многоугольника М с вершинами в узлах, а через П_м- величину B_м + – 1, где B_м – число узлов внутри М, а Г_м – число узлов на границе. Тогда формулу Пика можно записать в виде S_м=П_м.

Доказательство формулы разобьем на несколько шагов.

Шаг 1.

Е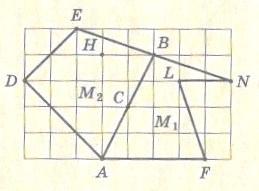 сли многоугольник М с вершинами в узлах сетки разрезан на 2 многоугольника М₁ и М₂, также имеющих вершины только в узлах сетки, то П_м = П_м1 + П_м2.

Пусть многоугольник М разрезан на многоугольники М₁ и М₂ с вершинами в узлах отрезком АВ (Рис.6). Все узлы, кроме тех, которые попадают на отрезок АВ, дают одинаковый вклад в левую и правую части формулы. Рассмотрим узлы, лежащие на

отрезке АВ. Если такой узел лежит между А и В (например, С), то для многоугольника М он внутренний, а для многоугольника М₁ и М₂ – граничный. Поэтому его вклад в П_м равен 1, а в каждое из выражений П_м1 и П_м2 – по 0,5, то есть вклады такого узла в П_м и П_м1 + П_м2 равны!

Наконец рассмотрим узлы А и В. Они граничные как для М, так и для М₁ и М_2. Поэтому вклад каждого из этих узлов в П_м равен 0,5 а в П_м1+П_м2 – единице. Значит, суммарный вклад узлов А и В в П_м равен 1, что на 1 меньше, чем их вклад в П_м1+П_м2. Но П_м= B_м + – 1, а

П_м1+П_м2 = (B_м1 + – 1) + (B_м2 + – 1) .

Из общего «вклада» всех узлов П_м вычитается 1, а из П_м1+П_м2 вычитается 2, и это компенсирует разницу вкладов узлов А и В! Итак, П_м=П_м1+П_м2

Шаг 2.

Если многоугольник М с вершинами в узлах сетки разрезан на два многоугольника М₁ и М₂ (тоже с вершинами в узлах) и формула верна для каких-то двух из многоугольников М,М₁,М₂, то она верна и для третьего многоугольника.

Пусть, например, она верна для М₁ и М_2, то есть S_м1 = П_м1, S_м2 = П_м2. Тогда (по первому шагу) S_м = S_м1+S_м2 = П_м1 + П_м2, но (по первому шагу) последнее выражение равно П_м, а равенство S_м=П_м и есть формула Пика.

Ш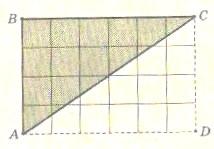 аг 3.

Докажем формулу Пика для прямоугольного треугольника с вершинами в узлах сетки и катетами, лежащими на линиях сетки. Треугольник АВС достроим до прямоугольника АВСD (Рис.7) . Для прямоугольников формула Пика верна: S_ABCD = П_АBCD. Согласно первому шагу П_ABCD=П_ABC + П_ACD , П_ABC=П_ACD, так что П_ABCD=2П_ABC. Но S_ABCD=2S_ABC. Поэтому S_ABC=П_ABC.

Ш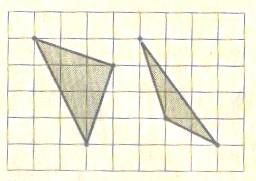 аг 4.

Формула Пика верна для произвольного треугольника с вершинами в узлах сетки.

Рассмотрев рисунок 8, легко понять: любой такой треугольник можно получить, «отрезав» от некоторого прямоугольника со сторонами, идущими по линиям сетки несколько прямоугольников и прямоугольных треугольников с катетами на линиях сетки. А так как формула Пика верна для прямоугольников и прямоугольных треугольников, то (вспомним шаг 2) она верна и для исходного треугольника.

Мы доказали, что если многоугольник можно разрезать на треугольники с вершинами в узлах сетки, то для него верна формула Пика.

ЗАКЛЮЧЕНИЕ.ФОРМУЛА ПИКА И ЗАДАНИЯ ЕГЭ

Часть B Единого Государственного Экзамена содержит задачи, связанные с понятием площади, в частности В6.Задача В6 – действия с фигурами, координатами и векторами. Самое популярное задание В6 – это найти площадь многоугольника с вершинами в узлах квадратной сетки. 1 см на 1 см. Теперь мы можем решить это задание тремя способами.

Подобные задачи не очень сложные. Главное здесь – быть внимательным и аккуратным при проведении элементарных вычислений. Для самоконтроля полезно решить задачу нахождения площади хотя бы двумя способами. Разумеется, результаты должны совпадать.

ВЫВОДЫ

1. Я рассмотрел различные подходы к решению задачи по нахождению площади произвольного многоугольника с вершинами в узлах сетки.

2. Доказал формулу Пика, по которой можно найти площадь такого многоугольника через количество узлов на границе и внутри его.

Своими знаниями я хочу поделиться с учащимися 10-11 классов, которые сейчас готовятся к Единому Государственному Экзамену.

ЛИТЕРАТУРА

1. Н.Б Васильев. Вокруг формулы Пика // Квант. – 1984. – №12. – с.39 – 43

2. Калейдоскоп «Кванта». Площадь // Квант. – 1991. – №7.

3. . Формула Площади. // Квант.- 1985. – №3. – с.32-33

4. Н.Жарковская, Е.Рисс Геометрия клетчатой бумаги. Формула Пика // Математика. Приложение к газете «1 сентября». – 2009. - №23

5. С.Дворянинов. Готовимся к ЕГЭ. Задача В6 – действия с фигурами координатами и векторами. // Математика. Приложение к газете «1 сентября». – 2011. - №5.- с.24 – 25

6. Материалы ЕГЭ