© 2019, ДУДИНСКАЯ ИРИНА НИКОЛАЕВНА 6918 102
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 07.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Был в сети 01.09.2024 19:53
ДУДИНСКАЯ ИРИНА НИКОЛАЕВНА
учитель математики
6 лет
1 436
42 238 
Специализация
Применение графов
Категория:
Математика
23.01.2019 00:37
Просмотр содержимого документа
«Применение графов»
2
ПРИМЕНЕНИЕ ГРАФОВ ПРИ РЕШЕНИИ ЛОГИЧЕСКИХ ЗАДАЧ
Актуальность этой темы обусловлена тем, что теория графов стала в настоящее время простым, доступным и мощным средством решения вопросов, относящихся к широкому кругу проблем. Графы, благодаря наглядности, позволяют представить соотношение между событиями и объектами событий, что упрощает решение многих занимательных задач.
Цель данной работы рассмотреть возможность применения графов при решении логических задач и разработать алгоритм их решения.
Решение логических задач предполагает сложный мыслительный процесс. Это построение цепочки точных рассуждений с правильными промежуточными и итоговыми умозаключениями. Условия логических задач часто многословно и содержит противоречивые высказывания. А использование графов позволяет решать эти задачи начиная с пятого класса. К тому же изучение теории графов развивает у учащихся навыки абстрактного и логического мышления, творческий подход к решению, помогает им свободнее пользоваться различными языковыми средствами математики и демонстрирует прикладную сторону математики.
В этой работе логические задачи переведены на язык графов.
1. Основные положения теории графов
Граф состоит из двух множеств: конечного множества элементов – вершин, и конечного множества элементов – ребер. Геометрически граф – это структура, состоящая из разбросанных в пространстве точек (вершин), соединенных системой линий (ребер). При изображении графа не имеет значения расположение вершин на плоскости, кривизна и длина ребер. Любой граф в абстрактном смысле эквивалентен некоторому геометрическому графу. Геометрический граф является удобным представлением любых графов. 
Граф, который можно начертить на плоскости таким образом, чтобы его ребра пересекались только в вершинах, называется плоским графом. Граф, на котором указано направление каждого его ребра, (что обычно показывается стрелкой) называется ориентированным графом. 
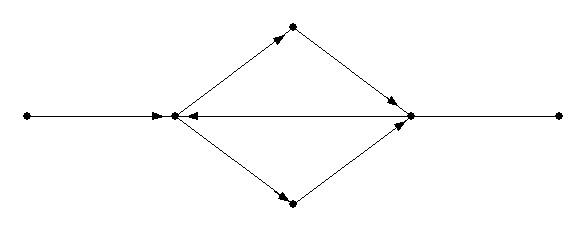
Линия на графе, быть может проходящая даже по нескольку раз через одни и те же вершины, не содержащая одних и тех же ребер, называется цепью.
Замкнутая цепь, которая начинается и оканчивается в одной и той же вершине, называется циклом АFЕДFВСА.
Если каждую вершину графа можно соединить с любой другой его вершиной некоторой цепью, то граф называется связным. В теории графов предполагают, что рассматриваемые графы являются связными.
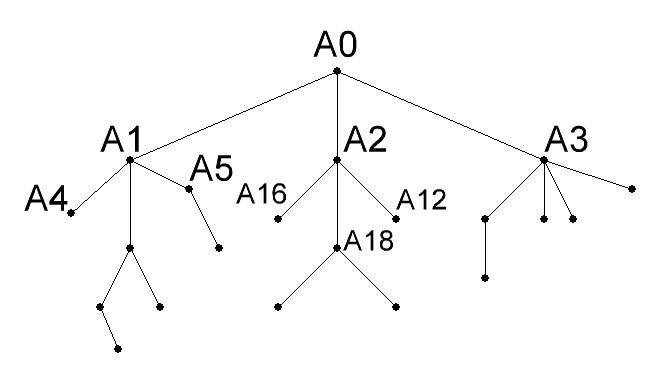
Деревом называется связной граф, не содержащий циклов. Такой граф не имеет кратных ребер. Для каждой пары его вершин существует единственная соединяющая их цепь.
Каждый граф имеет хроматическое число. Хроматическим числом графа называется наименьшее количество красок, с помощью которых можно так раскрасить вершины графа, что любые две вершины, соединенные ребром, окрашиваются при этом в разные цвета рис. Хроматическое число любого графа, расположенного на плоскости не больше четырех.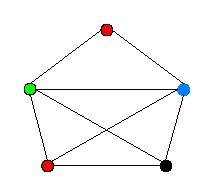 
2. Решение задач с помощью графов
Будем считать, что граф – это совокупность объектов со связями между ними. Объекты (элементы множества) представим как вершины, а связи между ними как ребра. Для удобства иллюстрации условия задачи, вершины графа заменим кругами или прямоугольниками там, где это целесообразно.
1. Команда космического корабля должна состоять из командира, пилота и врача. На пост командира притендуют 3 кандидата: К1, К2, К3; на пост пилота тоже 3 кандидата: Р1, Р2, Р3; а на пост врача 2 кандидата: В1, В2. При изучении психологической совместимости членов экипажа выяснилось, что:
– К1 несовместим с Р2 и В1; – Р2 несовместим с В2;
– К2 несовместим с Р3; – Р3 несовместим с В1.
– К3 несовместим с Р3 и В2;
Сколько вариантов экипажей возможно сформировать?
Решение
Для решения данной задачи построим граф-дерево, вершинами которого являются члены экипажа, а ребрами выражена совместимость членов экипажей.
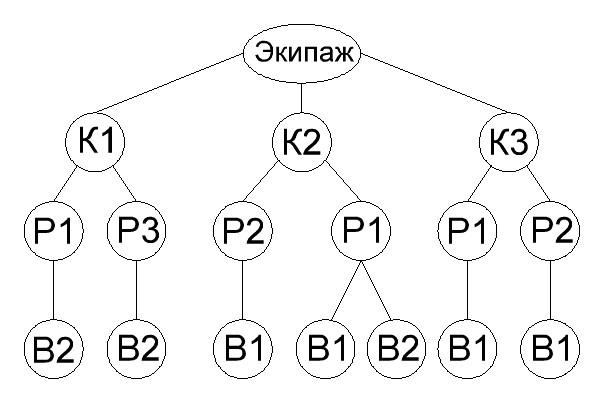
Ответ: 7 вариантов.
2. Марина, Лариса, Жанна и Катя умеют играть на разных инструментах (пианино, виолончели, гитаре, скрипке), но каждая только на одном. Они же знают иностранные языки (английский, французский, немецкий и испанский), но каждая только один. Известно:
1. Девушка, которая играет на гитаре, говорит по-испански.
2. Лариса не играет ни на скрипке, ни на виолончели и не знает английского.
3. Марина не играет ни на скрипке, ни на виолончели и не знает ни немецкого, ни английского.
4. Девушка, которая говорит по-немецки, не играет на виолончели.
5. Жанна знает французский язык, но не играет на скрипке.
Кто на каком инструменте играет, и какой иностранный язык знает?
Решение
Построим граф, вершинами которого являются имена девочек, названия языков и инструментов, а ребрами – информация о девочках. По условию задачи между элементами множеств существует взаимно-однозначное соответствие. Вершины, соответствующие именам девочек, соединяем с вершинами, соответствующими названиям языков или инструментов сплошными направленными отрезками-ребрами, если девочки ими владеют, в противном случае – пунктирными. Так «Ж» соединим с «Ф» (условие 5), а «Г» можем соединить с «И»(условие 1) сплошными ребрами. «Л» соединяем с «С», «В», «А» (условие 2); «М» соединяем с «С», «В», «Н» и «А» ( условие 3); «Н» с «В» ( условие 4); «Ж» с «С» (условие 5) пунктирными ребрами.
На построенном графе видно, что Марина знает испанский язык и играет на гитаре. Лариса знает немецкий язык, значит, Катя владеет английским. Лариса играет на пианино, Жанна – на виолончели, значит, Катя играет на скрипке.
Ответ: Марина знает испанский и играет на гитаре, Лариса знает немецкий и играет на пианино, Жанна знает французский и играет на виолончели, Катя знает английский и играет на скрипке.
3. В 7 и 8 классах надо провести занятия по алгебре, геометрии, русскому языку и истории (по одному занятию по каждому предмету). Занятия по каждому предмету проводятся с каждым классом отдельно. Занятия по алгебре и по геометрии ведет преподаватель X, по русскому языку — преподаватель Y , по истории — преподаватель Z. Найти минимальное число уроков, в которые можно провести все занятия, и составить соответствующее расписание.
Решение
Построим граф с вершинами А7, А8, Р8, И8, Г8, Г7, И7 и Р7 (буква соответствует предмету, а цифра — классу). Соединим ребрами вершины, соответствующие урокам, которые нельзя проводить одновременно.
|
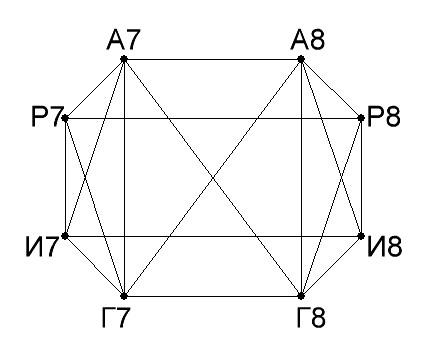
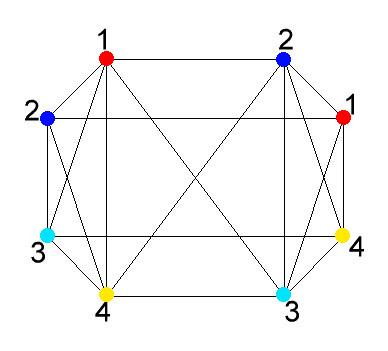
| 7 класс | 8 класс |
| 1 урок | Алгебра | Русский язык |
| 2 урок | Русский язык | Алгебра |
| 3 урок | История | Геометрия |
| 4 урок | Геометрия | История |
Ответ: 4 урока.
2.1. Алгоритм решения задач при помощи графов
- проанализировать условие задачи;
- определить, что известно;
- составить граф:
- проанализировать граф, найти все возможные решения или доказать, что их нет.
Математика, как и любой другой предмет, необходима для разностороннего развития учеников и полноценной реализации их возможностей в будущей самостоятельной жизни. И, следовательно, обучение должно быть поставлено таким образом, чтобы повысить удельный вес самостоятельной познавательной деятельности в процессе обучения. Мотивацией для самообразования является успех.
Использование графов, благодаря наглядности, облегчает решение логических задач и делает его простым, лаконичным и доступным всем учащимся, что дает им уверенность в своих силах и повышает интерес к математике. А так как решение логических задач развивает нестандартное мышление, умение анализировать и обобщать данные, искать возможные пути решения, формировать стратегию, проверять данные на достоверность, то уровень знаний учащихся повышается.
Познакомив учащихся, с возможностью решении логических задач при помощи графов, я увидела их интерес. Поэтому провела турнир по решению логические задач при помощи графов. Подобрав соответствующие задачи, мы пригласили на турнир по решению логических задач учащихся, знакомых с теорией графов и не знакомых с ней. Результат превзошел ожидания. Учащиеся, решавшие задачи при помощи графов, справились со всеми заданиями раньше отведенного времени, а учащиеся не знакомые с теорией графов, не успели решить до 40% задач.
Практическая значимость изучения теории графов состоит в возможности применения полученных знаний при решении логических задач, в межпредметных дисциплинах и повседневной жизни; использования результатов исследования в виде презентаций учителями-предметниками в качестве вспомогательного материала при проведении интегрированных уроков по различным учебным дисциплинам и на внеклассных занятиях по математике.
Список использованной литературы
1.Оре.О. “Графы и их применение” - М.ИЗД.ЛКИ. 2007. – 184 с.
2.Свами М., Тхуласираман К. Графы ,сети и алгоритмы. – М.Изд. «Мир» ,1984 – 454 с.
3.Емеличев В.А. ,Мельников О.И. ,Сарванов В.И. ,Тышкевич Р.И. Лекции по теории графов. – М. «Наука», 1990 - 384 с
4.Бассакер Р. Саати Т. – Конечные графы и сети . – М. Изд. «Наука» ,1974 - 388 с.
5.Кристофидес Н. Теория графов. Алгоритмический и подход . М .Изд. «Мир » 1978 -432 с
6.Уилсон Р. Введение в теорию графов . - М. Изд. «Мир». 1977 г.- 208 с.
7.Абрахамс Дж. Каверли Дж. Анализ электрических цепей методом графа
М.Изд. «Мир » - 1967 г. – 175 с.
8.Татт У. Теория графов М. Изд. « Мир » . 1988 г. - 424 с.
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
