Применение комплексных чисел в расчете физических величин

Применение комплексных чисел в расчете физических величин. Расчет комплекса сопротивления при последовательном и параллельном соединении.

Так как комплексные числа геометрически представляются векторами на плоскости, то все векторные физические величины могут быть охарактеризованы при помощи комплексных чисел. Особенно широкое применение комплексные числа получили в электротехнике при расчете электрических цепей, основные характеристики которых являются гармоническими колебаниями.

Как известно, значение величины, изменяющейся по законам гармонических колебаний с амплитудой V, угловой частотой (угловой скоростью) и начальной фазой , задается уравнением 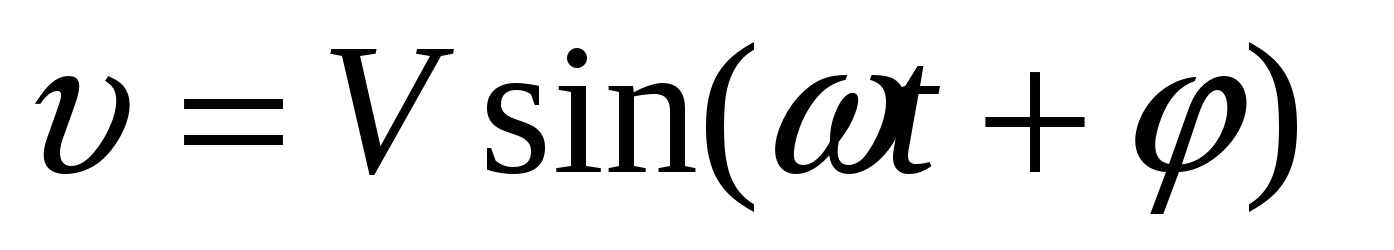(1) , где t время.

В частности, переменное напряжение задается уравнением .

При стандартной частоте 50 Гц угловая частота является постоянным числом 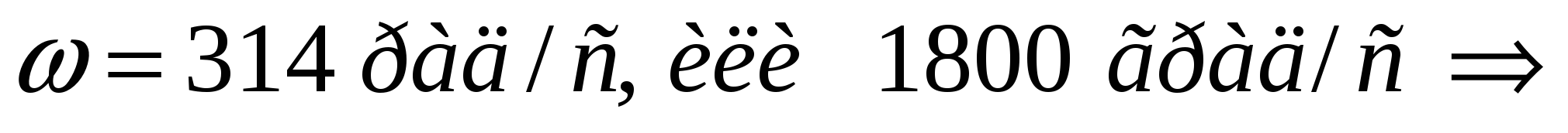уравнение (2) определяется двумя параметрами -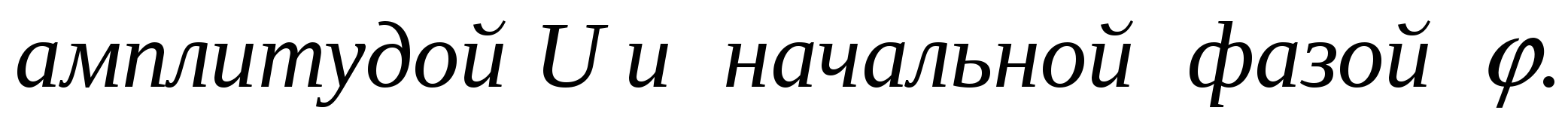

Аналогичная ситуация имеет место для уравнения тока .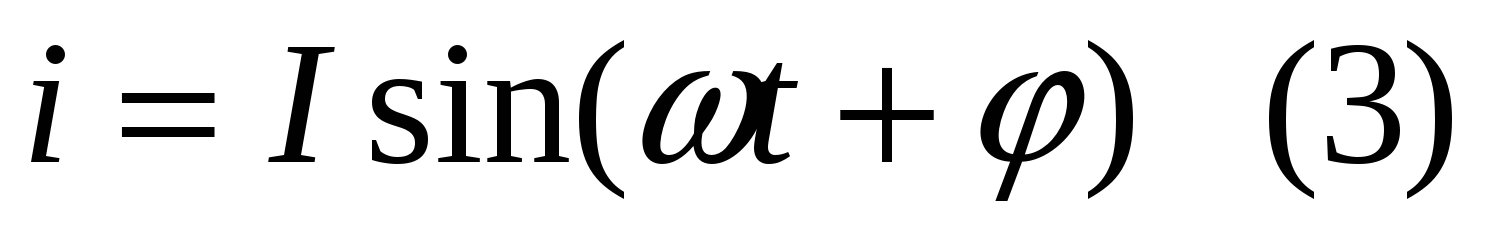

Каждому уравнению (2) можно сопоставить комплексное число, модуль которого равен амплитуде колебания. Т.е.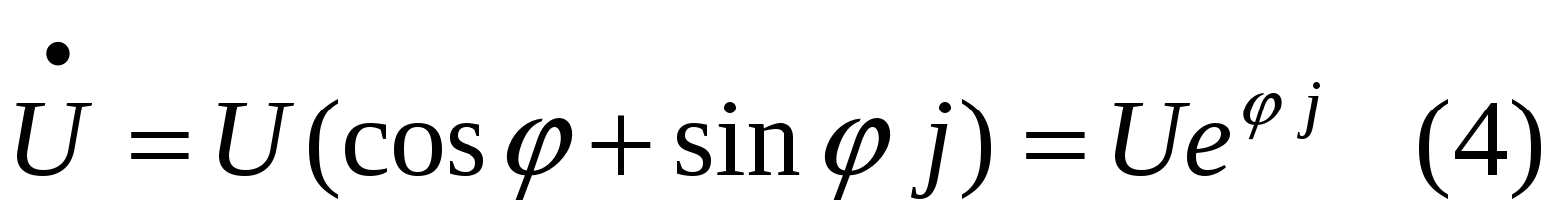

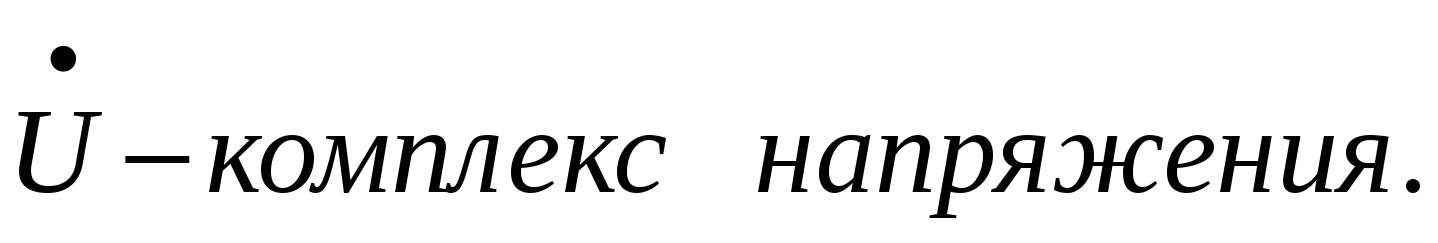
Аналогично определяется комплекс тока 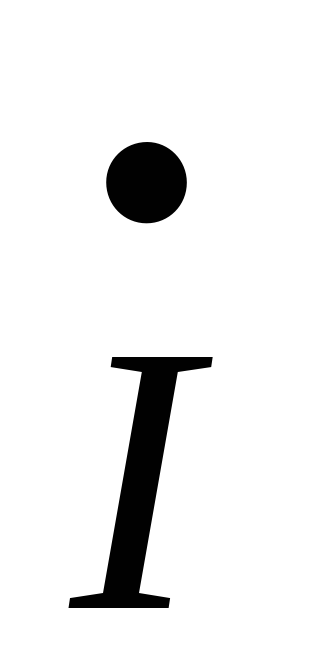. Т.е.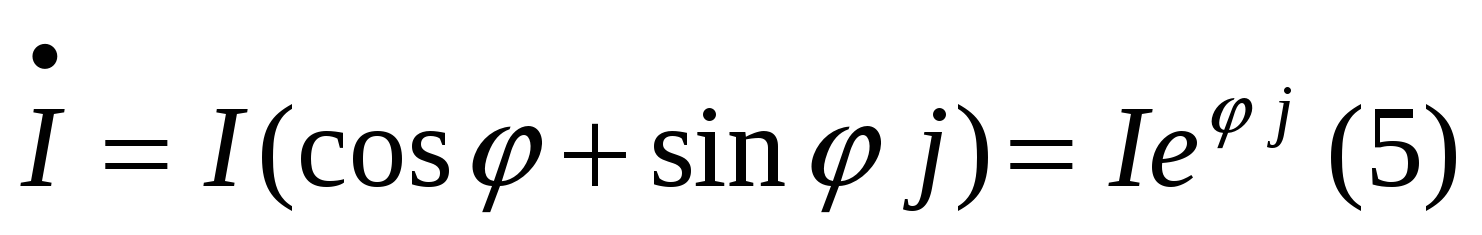

Теорема 1. Сумма двух гармонических колебани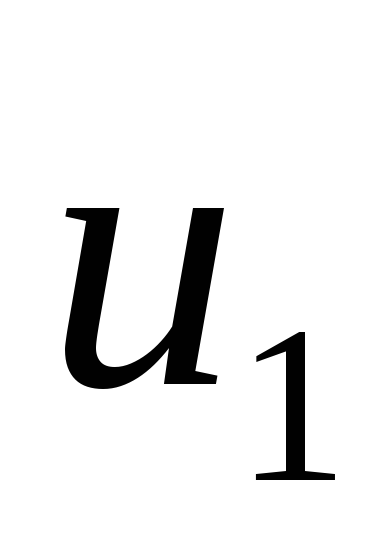й и 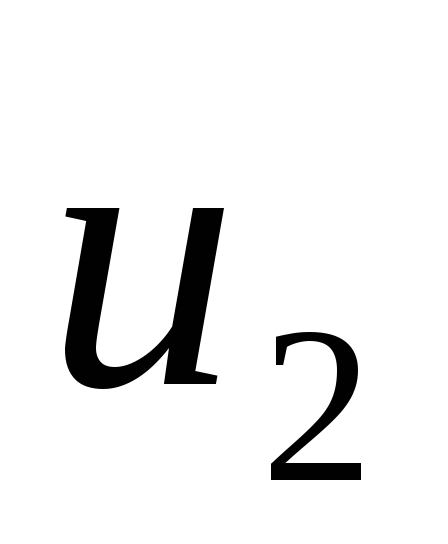с одной и той же угловой частотой является также гармоническим колебанием с той же угловой частотой , которому соответствует комплексное число , равное сумме комплексных чисел и 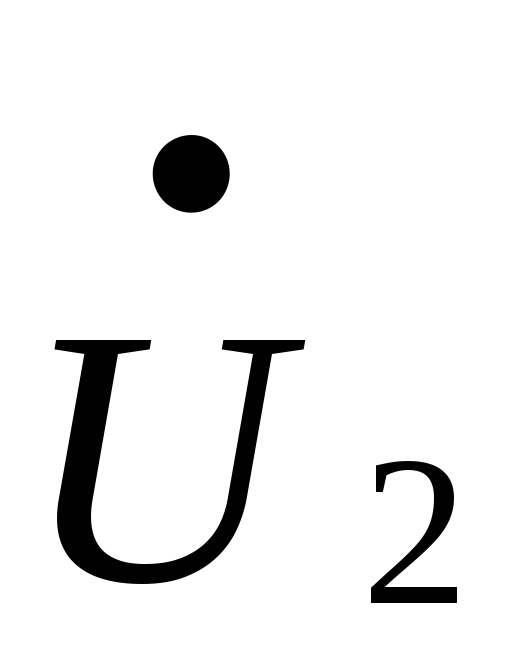(соответствующих величинам 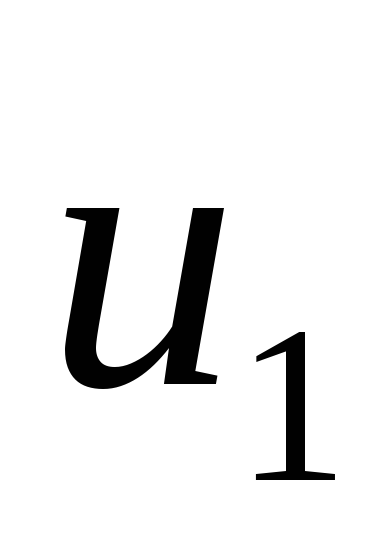и ).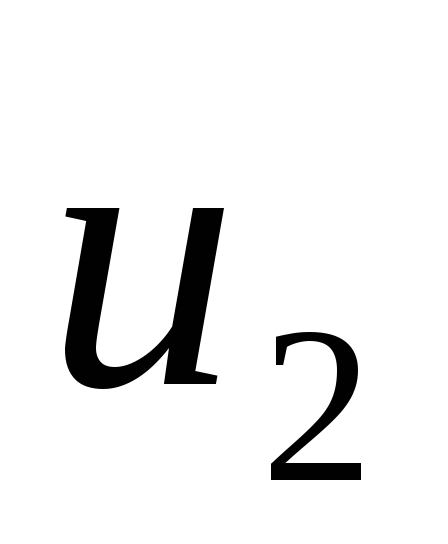

Замечание. При последовательном соединении в цепи 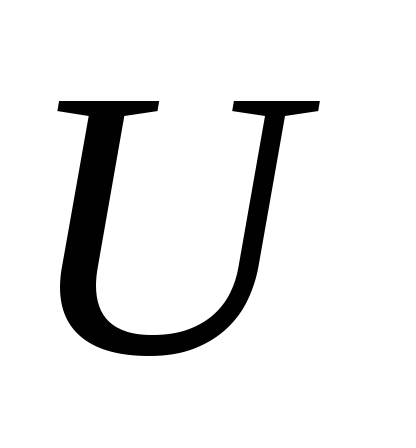меняется, а постоянно. При параллельном соединении в цепи наоборот.

(комплекс сопротивления)

Пример 1. Рассчитать комплекс сопротивления цепи переменного тока с частотой 50Гц, если 3 генератора соединены последовательно.

Решение: (суммарное напряжение)

Ответ:

Пример 2. Рассчитать комплекс сопротивления цепи переменного тока с частотой 50Гц, если 3 генератора соединены параллельно.

Решение:

Ответ: