Применение метода рационализации при решении неравенств и систем

Применение метода рационализации при решении неравенств и систем неравенств

Метод рационализации заключается

в замене сложного выражения F(x) на

более простое выражение G(x) ,

при которой

неравенство G(x)v0 равносильно

неравенству F(x)v0 в

области определения выражения F(x).

0,h 1, f0, g0), а – фиксированное число (a0, a 1). " width="640"

Выделим некоторые выражения F

и соответствующие им

рационализирующие выражения G,

где f,g,h,p,q – выражения с

переменной x (h0,h

1, f0, g0),

а – фиксированное число (a0, a

1).

Выражение F

1

1а

Выражение G

2

1б

2а

3

2б

4

4а

5

6

Некоторые следствия с учетом области

определения неравенства:

*

*

*

*

Пример 1.

Решить неравенство:

Решение:

+

-

+

-

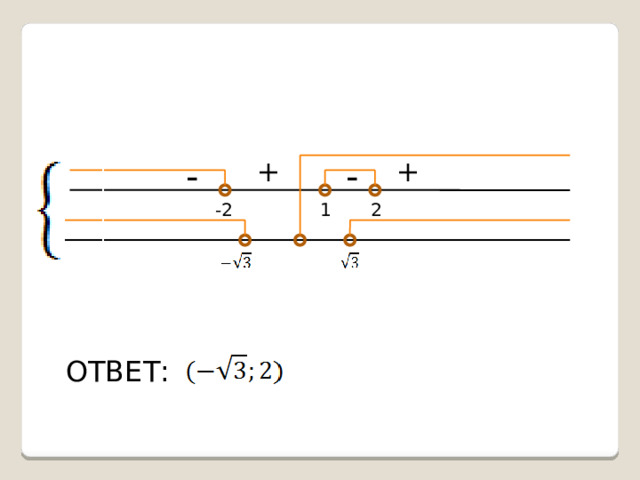
1

2

-2

ОТВЕТ:

Пример 2.

Решить неравенство:

Решение:

+

-

-

-

+

+

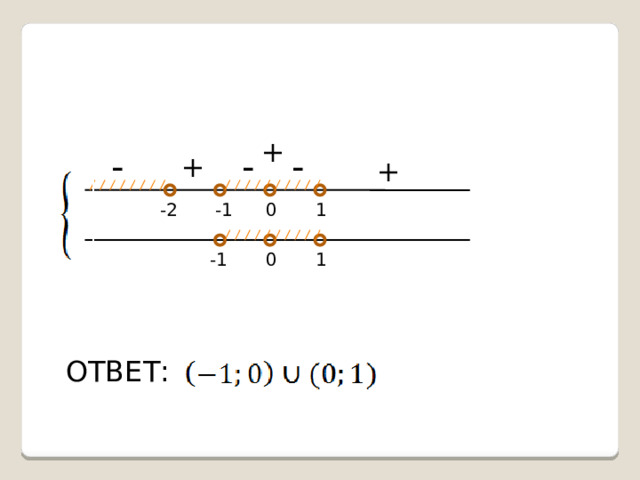
0

1

-1

-2

-1

0

1

ОТВЕТ:

Решить неравенства:

Пример 3.

Пример 4.

Пример 5.

Пример 6.

ОТВЕТ

ОТВЕТ

ОТВЕТ

ОТВЕТ

Пример 7.

Пример 8.

Пример 9.

ОТВЕТ

ОТВЕТ

ОТВЕТ

Решить систему неравенств:

1.

2.

3.

Решить неравенство

(из сборника МИОО):

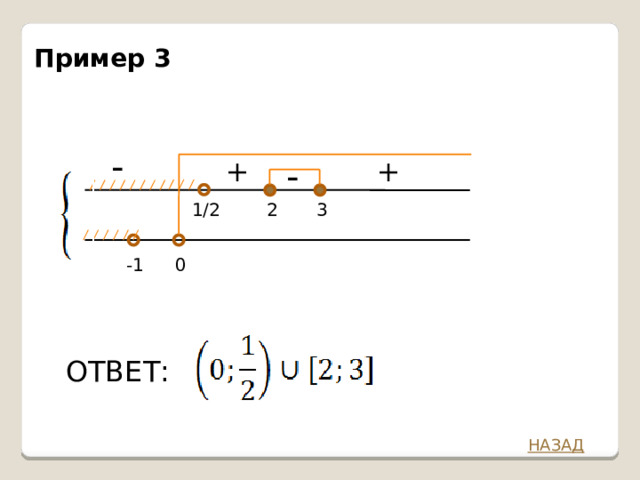
Пример 3

-

+

-

+

1/2

2

3

0

-1

ОТВЕТ:

НАЗАД

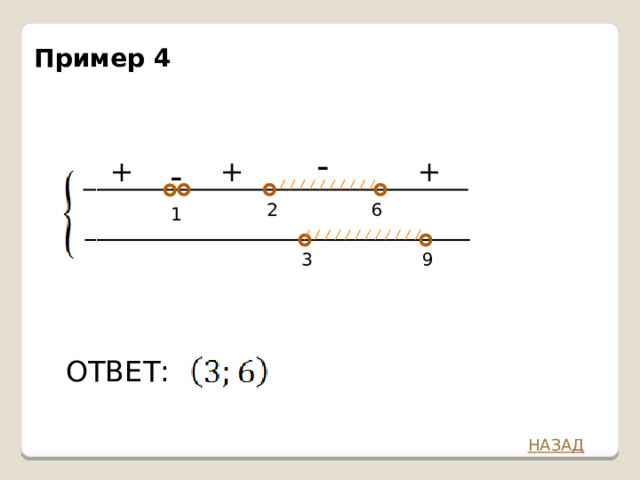
Пример 4

-

+

-

+

+

6

2

1

3

9

ОТВЕТ:

НАЗАД

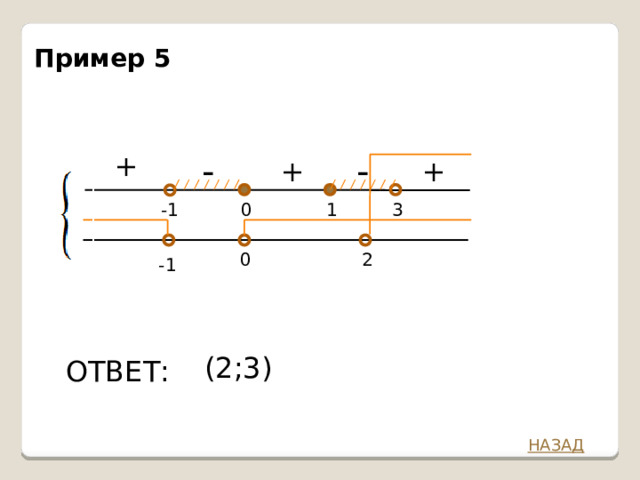
Пример 5

-

+

-

+

+

0

1

3

-1

2

0

-1

(2;3)

ОТВЕТ:

НАЗАД

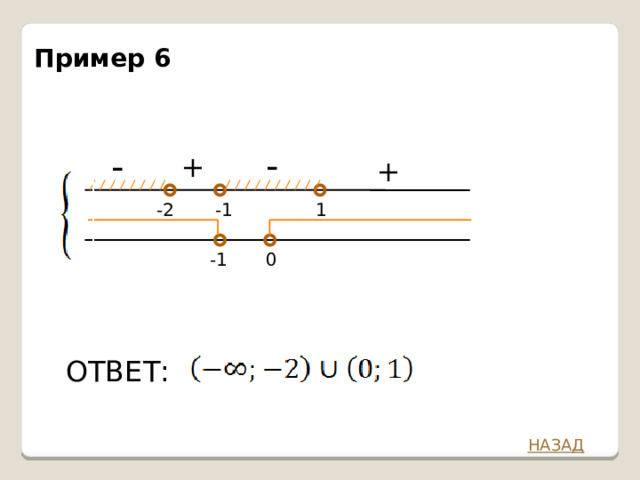
Пример 6

-

-

+

+

-2

-1

1

0

-1

ОТВЕТ:

НАЗАД

Пример 7

-

+

-

+

+

-3

-1

1

0

4

-1/2

ОТВЕТ:

НАЗАД

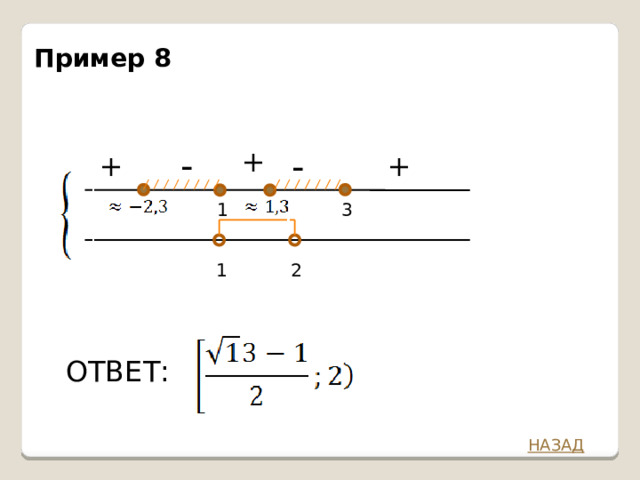
Пример 8

-

+

-

+

+

3

1

2

1

ОТВЕТ:

НАЗАД

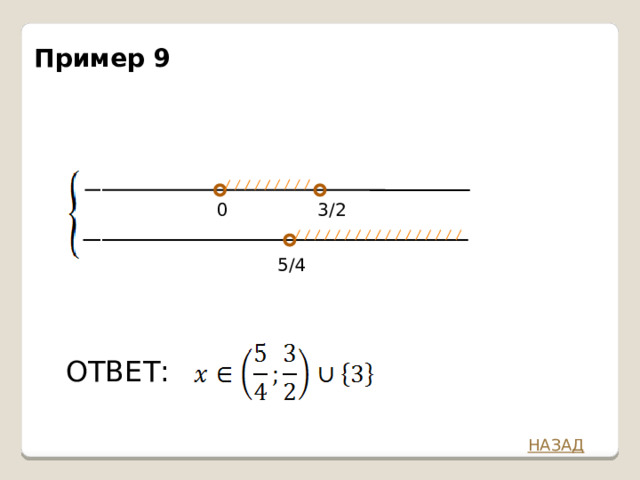
Пример 9

0

3/2

5/4

ОТВЕТ:

НАЗАД