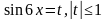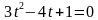Дата:
Тема: Применение основных тригонометрических формул для решения уравнений
Цели: продолжить формирование навыков решения тригонометрических уравнений; научить применять основные тригонометрические формулы при решении.
Ход урока
-
АКТУАЛИЗАЦИЯ ЗНАНИЙ
Самостоятельная работа
-
ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА
Откройте тетради, запишите сегодняшнее число и тему урока. Перейдите по ссылке и посмотрите видеоурок:
http://1tvcrimea.ru/content/domashnee-zadanie-10-klass-algebra-literatura-biologiya-vypusk-ot-8042020
-
ПРАКТИЧЕСКАЯ ЧАСТЬ
Пример 1. Решить уравнение:
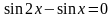
Решение. Применим формулу синуса двойного угла 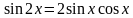 , получим:
, получим:
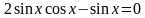
Вынесем общий множитель за скобку:
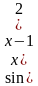
Решим распадающееся уравнение, запишем в виде совокупности:
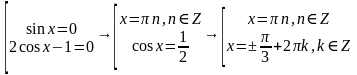
Ответ: 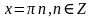 ;
; 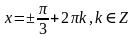 .
.
Пример 2. Решить уравнение:
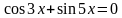
Решение. Используем формулу приведения для 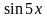 , чтобы уравнение было относительно одной функции:
, чтобы уравнение было относительно одной функции:
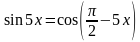
Перепишем уравнение в виде:
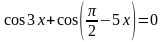
Далее применим формулу суммы косинусов, получим:
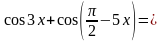
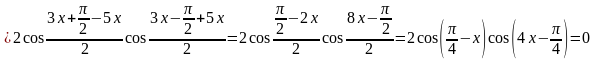
Снова пришли к распадающемуся уравнению, решим его:

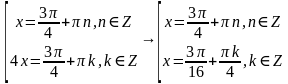
Ответ: 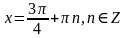 ;
; 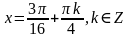 .
.
Пример 3. Решить уравнение:
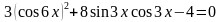
Решение. Применим формулу синуса двойного угла, получим:
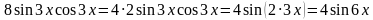
Уравнение пока еще зависит от двух функций, поэтому применим к косинусу основное тригонометрическое тождество, получим:
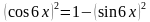
Тогда исходное уравнение примет вид:
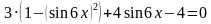
Раскроем скобку, приведем подобные и умножим на « -1 »:
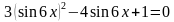
Получили квадратное уравнение относительно 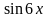 . Выполним замену:
. Выполним замену: 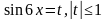
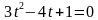

Оба значения подходят. Вернемся к замене:
Ответ: ; .
Пример 4. Решить уравнение:
Решение. Применим формулу синуса двойного угла:
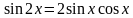
Применим основное тригонометрическое тождество:
Перепишем уравнение в виде:
Преобразуем:
Разделим на  , получим:
, получим:
Введем замену  , получим:
, получим:


Тангенс – функция не ограничена, поэтому оба корня подходят. Вернемся к замене:
Ответ: ; .
-
ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ
Домашнее задание: выучить теорию, №11.19 (б, г, е).







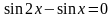
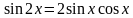 , получим:
, получим: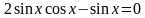
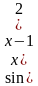
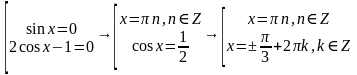
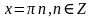 ;
; 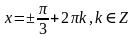 .
.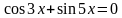
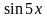 , чтобы уравнение было относительно одной функции:
, чтобы уравнение было относительно одной функции: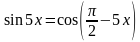
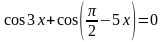
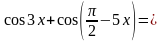
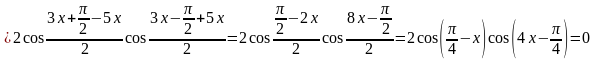

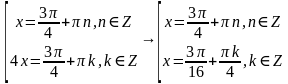
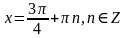 ;
; 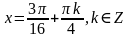 .
.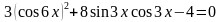
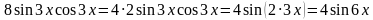
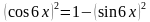
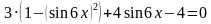
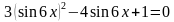
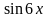 . Выполним замену:
. Выполним замену: