Муниципальное бюджетное образовательное учреждение
Терновская обще образовательная школа №2
Миллеровского района Ростовской области
ПРАКТИКО-ОРИЕНТИРОВАННЫЕ ЗАДАНИЯ КАК СРЕДСТВО ПОВЫШЕНИЯ МОТИВАЦИИ ШКОЛЬНИКОВ НА УРОКАХ МАТЕМАТИКИ
Козуренко Юлия Сергеевна
учитель математики,
учитель первой категории,
2024
Введение
В современном школьном математическом образовании особое внимание уделяется подготовке учеников к применению математических знаний в решении разнообразных проблем, возникающих в реальной жизни за пределами учебного процесса.
Формирование у школьников универсальных навыков, необходимых для решения жизненных и профессиональных задач, является одной из ключевых целей Федерального государственного образовательного стандарта. Прикладной аспект математического образования также находит отражение в контрольно-измерительных материалах для ОГЭ и ЕГЭ.
Цель исследования — разработать задания с практико-ориентированным содержанием для повышения мотивации школьников на уроках математики в 5–6 классах.
Объект исследования — процесс обучения математике в 5–6 классах.
Предмет исследования — практико-ориентированные задания, способствующие реализации прикладной направленности курса математики.
В соответствии с проблемой, целью, объектом и предметом исследования выдвигается следующая гипотеза: систематическое использование практико-ориентированных задач в процессе обучения математике повысит мотивацию учеников к изучению предмета.
Для достижения цели были поставлены следующие задачи:
изучить научно-методическую литературу и опыт работы учителей математики;
разработать этапы решения практико-ориентированных задач;
подобрать и составить практико-ориентированные задачи, решаемые с помощью составления уравнений и по алгоритму;
апробировать разработанные задачи;
выявить влияние практико-ориентированных задач на мотивацию учеников.
Для решения поставленных задач были использованы следующие методы исследования:
изучение и анализ научно-методической и учебной литературы по теме исследования;
наблюдение за учебной деятельностью учеников;
педагогический эксперимент;
качественный анализ результатов исследования.
Практическая значимость исследования заключается в разработке системы практико-ориентированных задач и методики обучения их решению. Эти материалы могут быть использованы в практической деятельности учителей при работе с учениками основной школы.
В современном образовательном процессе школьный курс математики имеет практическую направленность. Это означает, что в процессе обучения математике школьники решают задачи, которые имеют практическое применение в повседневной жизни.
Такая практика показывает, что ученики с интересом воспринимают и решают задачи, которые имеют практическое применение. Это даёт возможность реализовать общедидактические принципы в обучении математике.
Практическая направленность школьного курса математики направлена на повышение качества математического образования учеников. Она также помогает применять математические знания в повседневной жизни и в будущей профессиональной деятельности.
Кроме того, усиление практической направленности в обучении математике положительно влияет на качество самого обучения математике.
Практическая направленность в обучении математике предполагает ориентацию на тесную связь с жизнью, основами других наук и подготовку учеников к использованию математических знаний в будущей профессиональной деятельности. Она включает в себя реализацию связей с другими предметами, такими как физика, химия, география и другие. Также она направлена на формирование математического мышления и деятельности.
На уроках необходимо обеспечивать органическую связь между изучаемым теоретическим материалом и задачами, чтобы ученики понимали их значимость и перспективы использования.
Известно, что одним из ключевых условий успешной деятельности и достижения целей в любой области является мотивация. Она основана на потребностях и интересах личности. Чтобы ученики были мотивированы к учёбе, необходимо сделать обучение привлекательным процессом.
Однако есть и трудности: учителю необходимо освоить другие предметы, а практические задачи обычно требуют больше времени, чем теоретические.
Важную роль в реализации практической направленности обучения математике играют задачи.
К прикладным задачам предъявляются определённые требования:
содержание задач должно отражать математические и не математические проблемы и их взаимосвязь;
задачи должны соответствовать программе курса и служить достижению целей обучения;
понятия и термины, используемые в задачах, должны быть доступны для учеников;
содержание задач должно соответствовать реальности;
способы и методы решения задач должны быть приближены к практическим методам и приёмам;
Однако выполнить все эти требования в рамках одного учебного предмета невозможно.
Эту проблему можно решить с помощью интегрированных уроков с другими предметами. Это усилит практическую направленность и повысит мотивацию учеников.
Опыт показывает, что проведение таких уроков, как «Диаграммы» (математика и география, 6 класс), «Задачи на движение» (математика и физика, 7 класс), «Задачи на смеси, сплавы и растворы» (математика и химия, 8 класс) и других, способствует развитию познавательной и исследовательской деятельности учеников.
Работа учителя и ученика в этом случае становится продуктивной, что способствует повышению мотивации к предмету.
На своих уроках я стараюсь организовать учебный процесс так, чтобы он способствовал развитию умений учеников:
самостоятельно определять цели своего обучения и планировать пути их достижения;
соотносить свои действия с планируемыми результатами и контролировать свою деятельность в процессе достижения результата;
организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками;
формулировать, аргументировать и отстаивать своё мнение.
Современный урок — это урок, на котором ученики чувствуют себя уверенно, урок открытия истины, поиск и осмысление которой происходит в совместной деятельности учителя и ученика — урок активных действий.
Использование задач, направленных на практику, в обучении математике в школе не только способствует реализации прикладных аспектов программы, но и повышает мотивацию учащихся.
Практико-ориентированная деятельность подразумевает связь школьного курса с реальными жизненными ситуациями. Это позволяет развивать у учеников навыки, необходимые для применения математических знаний в практических задачах.
Для успешного решения прикладных задач необходимо овладеть тремя ключевыми умениями:
Выделить основные характеристики задачи.
Определить взаимосвязи между этими характеристиками.
Учесть ограничения, накладываемые на характеристики.
В работах таких авторов, как Ю. М. Колягин, В. В. Фирсов и Л. М. Фридман, уделяется большое внимание методике решения прикладных задач.
Цель учителя математики — показать, как математические концепции применяются для понимания явлений и процессов, изучаемых в естественных и общественных науках. Для этого необходимо:
Определить темы в курсе математики, которые наиболее ярко демонстрируют мировоззренческие основы.
Выделить темы из курсов химии, физики и других дисциплин, где можно использовать математический аппарат.
Выбрать и разработать методы обучения, соответствующие поставленной цели.
Определить формы применения математических методов и понятий в других дисциплинах.
Однако следует помнить, что задачи с практическим содержанием не могут стать основой для создания единой дидактической системы, которая бы охватывала весь теоретический материал, изучаемый на уроках математики.
Практико-ориентированные задачи — это математические задачи, в которых описываются ситуации из реальной жизни. Они направлены на формирование практических навыков использования математических знаний и умений, необходимых в повседневной жизни. В том числе, такие задачи могут включать элементы краеведения и производственных процессов.
Решение задач такого типа требует построения модели реальной ситуации, описанной в задаче. Это требует высокого уровня математической подготовки и является результатом обучения, который можно назвать общекультурным.
Практико-ориентированные задачи имеют ряд особенностей:
Значимость результата, что мотивирует ученика к познанию.
Условие задачи сформулировано в виде сюжета, ситуации или проблемы, для решения которой необходимо использовать знания из разных областей, включая математику, другие предметы или жизненный опыт.
Информация и данные в задаче могут быть представлены в различных формах, таких как рисунок, таблица, схема, диаграмма или график. Это требует умения распознавать объекты.
Указание области применения результата, полученного при решении задачи.
Некоторые задачи, содержащиеся в школьных учебниках, могут быть отнесены к задачам с практическим содержанием. Однако ни один учебник не может полностью охватить все связи школьного курса с производительным трудом. Поэтому необходимо дополнять предлагаемые в учебнике упражнения составленными задачами.
Сельская школа имеет все возможности для того, чтобы связать обучение и воспитание учащихся на уроках математики с сельскохозяйственным трудом. Я хотел бы представить вам несколько групп практико-ориентированных задач, которые можно разделить на следующие этапы:
Анализ текста задачи.
Перевод текста на математический язык.
Установление связей между данными и вопросом.
Составление плана решения задачи.
Реализация плана решения.
Проверка и оценка решения задачи.
Задачи с экологическим содержанием, 5-6 класс [3, с.15-16]:
Задача №1.В нашей области водится много бобров. Бобр – крупнейший грызун, ведёт полуводный образ жизни и обитает по лесным рекам, сооружает из ветвей или ила домики, делает плотины длиной 5-6 м. Вдоль плотин с удивительной равномерностью расположены бобровые хатки.
Задание 1. Узнать длину тела бобра в дециметрах вам поможет удивительный квадрат
| 
| 5,9 | 6,3 | 3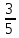 |
| 2,3 | 2,7 | 0 |
| 3,7 | 4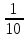 | 1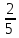 |
1) из первой строки выберите наименьшее число.
2) из второй строки выберите наибольшее число.
3) из третьей строки выбери не наименьшее, не наибольшее.
4) найдите сумму этих чисел: 3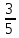 + 2,7 + 3,7 = 10 (дм).
+ 2,7 + 3,7 = 10 (дм).
Вы нашли длину тела бобра.
Задание 2. Длинные и острые зубы бобра помогают ему легко и быстро перегрызть дерево. Дерево диаметром 12 см бобр перегрызает за 3 мин. Сколько времени понадобится бобру, чтобы свалить 7 деревьев, из которых два дерева толщиной по 12 см, два – по 20 см и остальные – по 28 см.
Решение: 6+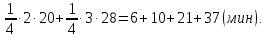
Задача №2. Средняя продолжительность жизни россиян составляет 68 лет, причём 8% из этих лет мы проживаем за счёт медицины. На сколько лет врачи продлевают жизнь?
Задача №3. Один гектар леса в течение года способен поглощать столько углекислого газа, сколько его выделяют 232 человека. Сколько процентов это составляет от общего числа людей, проживающих в Кировской области (в 2014 году численность составила 487 136 человек). Сколько гектаров леса должно находиться в пределах города, чтобы в чистоте содержать воздух города?
Ответ: примерно 0,05%; 2100 га.
Задача №4. Вырубая один гектар леса, наносят огромный урон составу воздуха. Ведь за один солнечный день 1 га леса поглощает из воздуха до 280 кг углекислого газа и выделяет до 200 кг кислорода. Также 1 га лиственного леса за год задерживает до 100 тонн пыли, хвойного – до 40 тонн.
Задание 1. Сколько кг углекислого газа поглощается в солнечные дни лесом в Кировской области в год, если считать, что солнечных дней в году примерно 97, а площадь лесов составляет 8,14 млн. га?
Задание 2. На сколько процентов больше поглощается углекислого газа, чем выделяется кислорода?
Задание 3. Сколько тонн пыли за полгода задерживают 4055,1 тыс. га хвойных и 3519,8 тыс. га лиственных лесов Кировской области?
Задача №5. Объёмы выполняемых лесовосстановительных работ в Кировской области обеспечивают своевременное восстановление лесов на вырубаемых площадях и сокращение непокрытых лесной растительностью земель лесного фонда. В 2016 году мероприятия по воспроизводству лесов выполнены на площади 35012 га при годовом плане 26699 га. На сколько процентов перевыполнен план по воспроизводству лесов? Ответ: на 31%
Задача №6. За 2016 год в рамках осуществления федерального государственного лесного надзора (лесной охраны) лесного фонда Кировской области было выявлено 6910 нарушений лесного законодательства, в том числе 303 случаев незаконных рубок лесных насаждений. Объем незаконно заготовленной древесины составил 17,0 тыс. куб. м.
Задание 1. Сколько % составляют случаи незаконной вырубки лесных насаждений от общего числа выявленных нарушений? Ответ:4,4%
Задание 2. Вычислите стоимость ущерба от незаконно заготовленной древесины, если стоимость 1 куб.м составляет примерно 8, 2 тыс. руб.?
Задача №7.Раскрываемость незаконных рубок леса в Кировской области в 2016 г. составляет 56,4% от общего количества случаев. В течение года возбуждено 169 уголовных дел по ст. 260 УК РФ. Найдите общее количество нарушений.
Задачи на растворы и сплавы (6-7 класс)
Задача №1. Для приготовления блюда требуется на 50 г воды добавить 100 г 6%-го уксуса. У хозяйки имеется только 12%-й уксус. Сколько граммов 12%-го уксуса ей нужно добавить на 50 г воды, чтобы получить раствор нужной концентрации?
Ответ: 25 г.
Задача №2. Сколько граммов воды нужно добавить к 180 г сиропа, содержащего 25% сахара, чтобы получить сироп, концентрация которого равна 20% ?
Ответ: 45 г.
Задача №3. Два спиртовых раствора борной кислоты одинаковой массы слили в один сосуд. Раствор какой концентрации получили в результате, если первый раствор был 5%-ный, а второй 1%-ный ?
Задача №4. Сплавили 40 г золота одной пробы и 60 г золота другой пробы и получили золото 62 пробы. Какой пробы было золото первого и второго слитков, если при сплаве их поровну получается золото 61 пробы ? (Проба – это процентное содержание чистого золота.)
Ответ: 56 пробы и 66 пробы.
Задача №5. Имеется два сплава с разным содержанием меди: в первом содержится 70%, а во втором-40% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 50% меди?
Ответ: 1:2.
Составление уравнений при решении текстовых задач традиционно вызывают затруднения у учащихся. Поэтому учителю трудно организовать самостоятельную работу учеников, которые нуждаются в постоянной помощи учителя.
Предлагаемые задания [4 с. 15-18] помогут в решении этой проблемы. Задачи, сгруппированные по сюжетам, сопровождаются указаниями, которые помогут ученикам составить уравнение и получить правильный ответ. Для подготовленных учащихся предлагаются дополнительные вопросы.
При работе с такими задачами полезно выделять как самостоятельный этап доведение решения задачи до уравнения или системы уравнений, поскольку именно этот этап наиболее труден.

















