Пример расчёт неразветвленной цепи переменного тока
Построить векторную диаграмму, по заданным активным и реактивным сопротивлениям цепи: R1 = 2 Ом, XC1 = 3 Ом, R2 = 14 Ом, XC2 = 12 Ом, XL3 = 18 Ом и напряжению равному U=65 В. Определить активную, реактивную и полную мощность. Найти индуктивные и емкостные сопротивления.
Решение:
Из заданных приёмников составляем неразветвлённую цепь (рис 1.1).
Определяем активные и реактивные сопротивления всей цепи:
R = R1 + R2 = 2 + 14 = 16 Ом;
X = -XC1 – XC2 + XL3 = -3 – 12 + 18 = 3 Ом.

Полное сопротивление всей цепи тогда определяем из выражения:
Z = 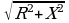 =
= 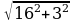 = 16,3 Ом.
= 16,3 Ом.
Ток в цепи будет общим для всех приёмников и определится по закону Ома:
I = U / Z = 65 / 16,3 = 3,99 A.
Угол сдвига фаз между напряжением и током определяется по синусу
sin = X / Z или тангенсу tg = X / R,
так как эти функции являются нечётными и определяют знак угла “плюс” или “минус”. Положительный знак угла указывает на активно-индуктивный (или чисто индуктивный) характер нагрузки, а отрицательный знак угла указывает на активно-ёмкостный (или чисто ёмкостный) характер. Таким образом, угол сдвига фаз между напряжением и током определим по синусу
Sin = X / Z = 3 / 16 = 0,184; = 10,6; Cos = 0,983.
Напряжения на участках цепи определяем также из формулы закона Ома:
UR1 = I ·R1 = 3,99 · 2 = 7,98 B;
UC1 = I · XC1 = 3,99 · 3 = 12 B;
UR2 = I · R2 = 3,99 · 14 = 55,9 B;
UC2 = I · XC2 = 3,99 · 12 = 47,9 B;
UL3 = I · XL3 = 3,99 · 18 = 71,8 B.
Р
ис.1.1
Определяем активные и реактивные мощности участков цепи:
P1 = I2 ·R1 = 3,992 ·2 = 31,8 Вт;
P2 = I2 · R2 = 3,992 · 14 = 223 Вт;
QC1 = I2 ·XC1 = 3,992 · 3 = 47,8 вар;
QC2 = I2 · XC2 = 3,992 · 12 = 191 вар;
QL3 = I2 · XL3 = 3,992 · 18 = 287 вар.
Активная, реактивная и полная мощности всей цепи соответственно будут равны:
P = P1 + P2 = 31,8 + 223 = 254,8 Вт;
Q = -QC1 – QC2 + QL3 = -47,8 – 191 + 287 = 48,2 вар;
S = 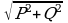 =
= 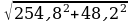 = 259 BA.
= 259 BA.
Полную, активную и реактивную мощности всей цепи можно определить также по другим формулам:
S = U · I = 65 ·3,99 = 259 ВА;
Р = S · Cos = 259 * 0,983 = 254,8 Вт;
Q = S · Sin = 259 * 0,184 = 47,9 вар.
Эти два способа определения мощностей могут быть взаимоповерочными и при сходимости результатов указывать на правильность произведённых расчётов.
Определяем ёмкости и индуктивность участков. Угловая частота ω = 2 πf = 2 · 3,14 ·50 = 314 с –1.
L3 = Xl3/ = 18/314 = 0,0573 Гн;
 C1 = 1/Xc1=1/(314*3)= 0,00106 Ф = 1060 мкФ;
C1 = 1/Xc1=1/(314*3)= 0,00106 Ф = 1060 мкФ;
C2 = 1/Xc2=1/(314*12)= 0,000265 Ф = 265 мкФ.
Для построения векторной диаграммы задаёмся масштабами тока и напряжения, которые будут соответственно равны MI = 0,5 A/см и MU = 10 B/см.
Построение топографической векторной диаграммы начинаем с вектора тока, который откладываем вдоль положительной горизонтальной оси координат. Векторы напряжений на участках строятся в порядке обтекания их током с учётом того, что векторы напряжений на активных элементах 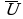 R1 и
R1 и 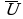 R2 совпадают по фазе с током и проводятся параллельно вектору тока; вектор напряжения на индуктивности
R2 совпадают по фазе с током и проводятся параллельно вектору тока; вектор напряжения на индуктивности 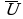 L3 опережает ток по фазе на угол 900 и поэтому откладывается на чертеже вверх по отношению к току; векторы напряжений на ёмкостях
L3 опережает ток по фазе на угол 900 и поэтому откладывается на чертеже вверх по отношению к току; векторы напряжений на ёмкостях 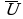 C1 и
C1 и 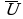 С2 отстают от тока по фазе на угол 900 и откладываются на чертеже вниз по отношению к току.
С2 отстают от тока по фазе на угол 900 и откладываются на чертеже вниз по отношению к току.
Р
ис. 1.2
Вектор напряжения между зажимами цепи проводится с начала вектора тока в конец вектора 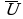 L3. На векторной диаграмме отмечаем треугольник напряжений ОАВ, из которого активная составляющая напряжения
L3. На векторной диаграмме отмечаем треугольник напряжений ОАВ, из которого активная составляющая напряжения
Ua = UR1 + UR2 = 7,95 + 55,9 = 63,88 B;
и реактивная составляющая напряжения
Up = -UC1 – UC2 + UL3 = -12 – 47,9 + 71,8 = 11,9 B.
Таким образом, напряжение между зажимами цепи равно
U = 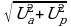 =
= 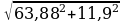 = 65 B.
= 65 B.
Топографическая векторная диаграмма построена на рис 1.2








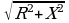 =
= 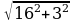 = 16,3 Ом.
= 16,3 Ом. 
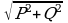 =
= 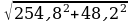 = 259 BA.
= 259 BA.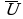 R1 и
R1 и 
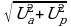 =
= 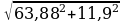 = 65 B.
= 65 B.



















