- 9 -
Школьное методическое объединение «МИФ»
Интегрированный физико-математический проект
«Применение математического аппарата к решению физических задач с использованием различных методов»
Автор: Гордин Андрей – 11 класс
Научное руководство:
Скобелева Майя Борисовна,
учитель математики;
«Математика – царица всех наук и служанка физики»(с)
Показателем владения тем или иным навыком является способность применять его к решению кардинально отличающихся друг от друга задач в различных ситуациях. Точно так же, показателем владения математическими методами является умение применить их к решению большого количества прикладных задач. При этом, основным в умении решить задачу различными способами является возможность выбрать из них в данных условиях наиболее рациональный. Что подтверждает незыблемую взаимосвязь абстрактности математики с реальностью окружающего нас мира.
В работе:
1) Рассмотрены разнообразные способы решения одной задачи, с анализом эффективности и рациональности их применения.
2) Отобраны и разобраны задачи по различным темам физики, решающиеся путем применения однотипного математического приема.
Цели работы:
Применить различные методы решения к одной задаче.
Отработать технику решения физических задач одним из математических методов.
Выработать систему анализа эффективности применения различных математических методов к решению физических задач.
Задачи:
Исследовать возможности решений одной физической задачи при применении различных методов.
Оценить эффективность методов, определить их характерные особенности.
Решить графическим методом ряд физических задач.
Сравнить эффективность применения данного метода в различных случаях, оценить его положительные и отрицательные стороны.
Описать основные признаки физических задач, рационально решаемых графическим методом, обосновать критерии отбора.
Исследуем возможность решения одной физической задачи различными методами.
Шофёр резко затормозил при скорости автомобиля 72 км/ч.
Дорога горизонтальная, коэффициент трения скольжения 0,5.
Исследуем эту ситуацию.
1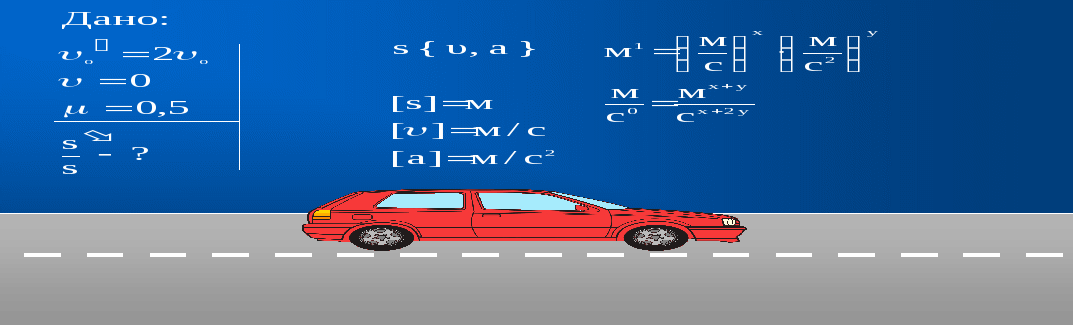 .Во сколько раз изменится тормозной путь, если начальная скорость машины увеличится в 2 раза?
.Во сколько раз изменится тормозной путь, если начальная скорость машины увеличится в 2 раза?
В ышеприведённый способ решения носит название:
ышеприведённый способ решения носит название:
«Метод размерностей»
Он позволяет определить вид пропорциональных отношений между величинами задачи. С его помощью можно решать задачи на нахождение отношений между двумя величинами.
2. Найдём ускорение автомобиля.
Д ля этого запишем второй закон Ньютона, применительно к данной ситуации и найдём проекции векторов на координатные оси. Затем, выполнив стандартные алгебраические преобразования, вычислим модуль ускорения автомобиля.
ля этого запишем второй закон Ньютона, применительно к данной ситуации и найдём проекции векторов на координатные оси. Затем, выполнив стандартные алгебраические преобразования, вычислим модуль ускорения автомобиля.
3. Найдём тормозной путь автомобиля.
Воспользуемся для этого графическим методом решения задач.
Я напомню вам его суть.
Графики играют здесь не вспомогательную роль, как, например, в случае приближенного решения уравнений. В случае использования графического метода решения задач графики являются полноправной математической моделью процесса.
Графический метод особенно удобен в тех случаях, когда нужно (или можно) связать некоторую величину со скоростью ее изменения в зависимости от некоторого параметра (не обязательно времени) и с самим этим параметром. Иначе говоря, если у нас есть зависимость вида 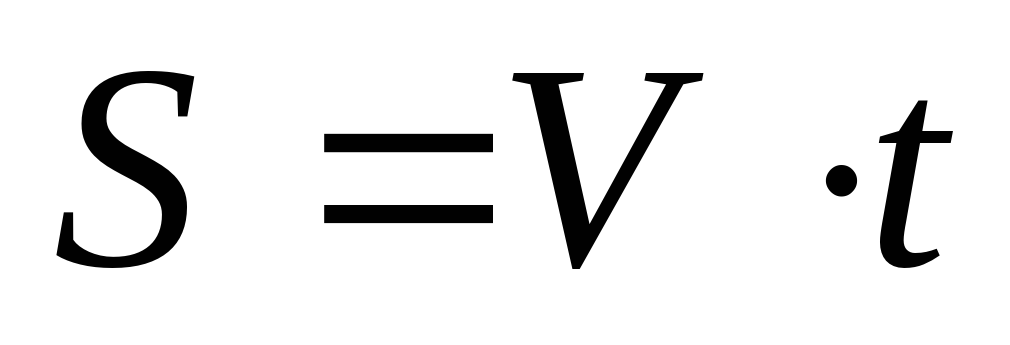 ,
, 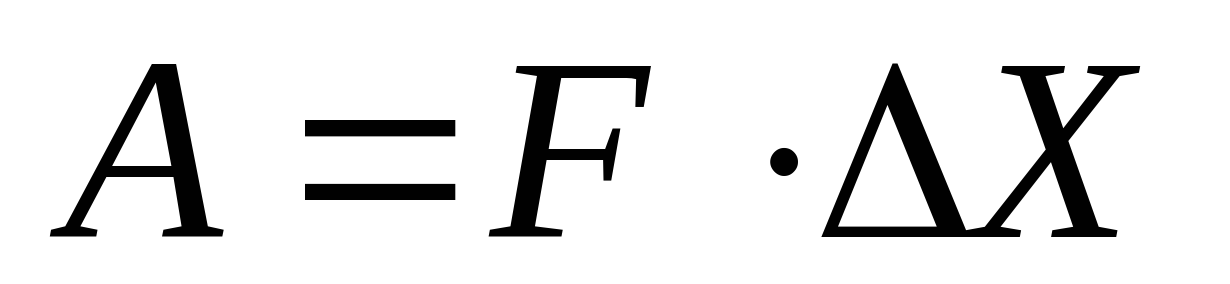 ,
, 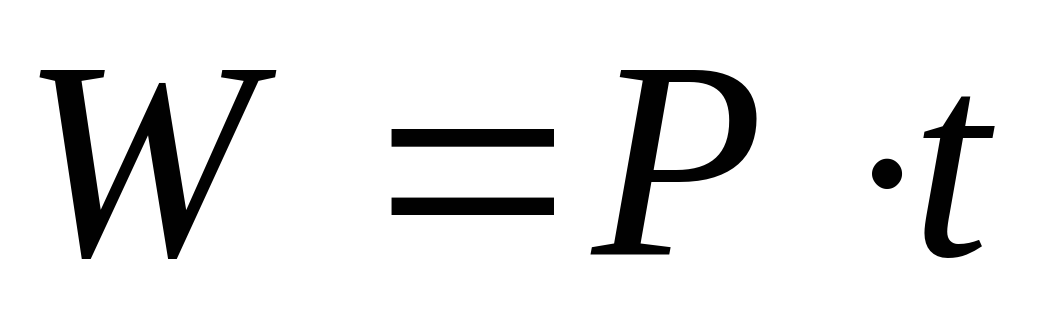 или
или 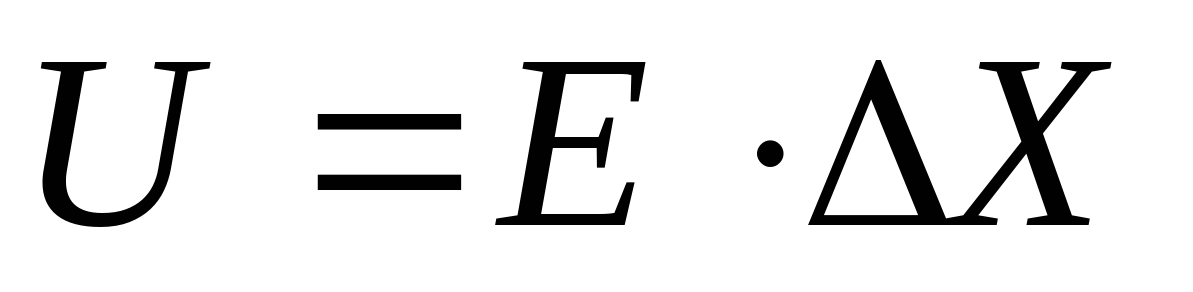 , можно попробовать использовать графическую модель процесса для получения необходимых уравнений.
, можно попробовать использовать графическую модель процесса для получения необходимых уравнений.
Д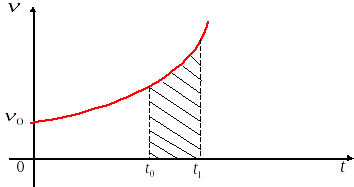 ля примера рассмотрим график зависимости скорости от времени.
ля примера рассмотрим график зависимости скорости от времени.
Путь, пройденный за какой-либо промежуток времени, численно равен площади фигуры, ограниченной осью времени, графиком скорости и двумя вертикальными отрезками,
проведёнными из точек, соответствующих началу и концу данного промежутка времени, т. е. площади заштрихованной криволинейной трапеции.
В общем случае её можно вычислить по формуле:
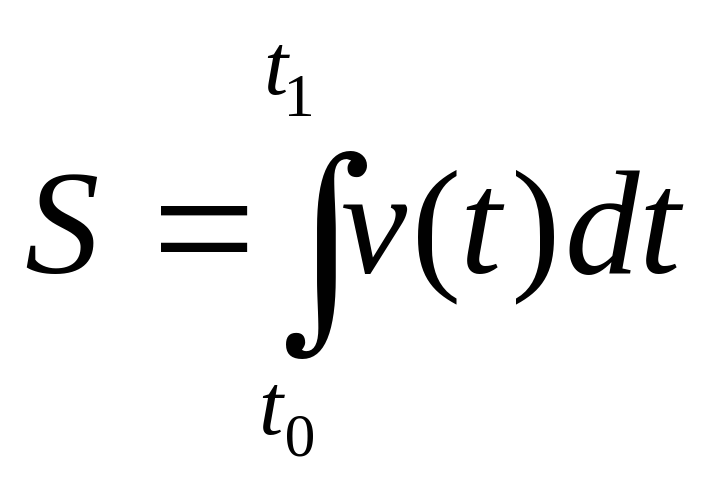
В случае, когда зависимость скорости от времени выражается классической алгебраической функцией, криволинейная трапеция превращается геометрическую фигуру, площадь которой мы можем вычислить, используя, знакомые нам из курса геометрии формулы.
В нашей ситуации движение прямолинейное равноускоренное, а значит, зависимость скорости от времени является линейной функцией. Построив её график и найдя площадь получившегося прямоугольного треугольника, мы численно вычислим длину тормозного пути. 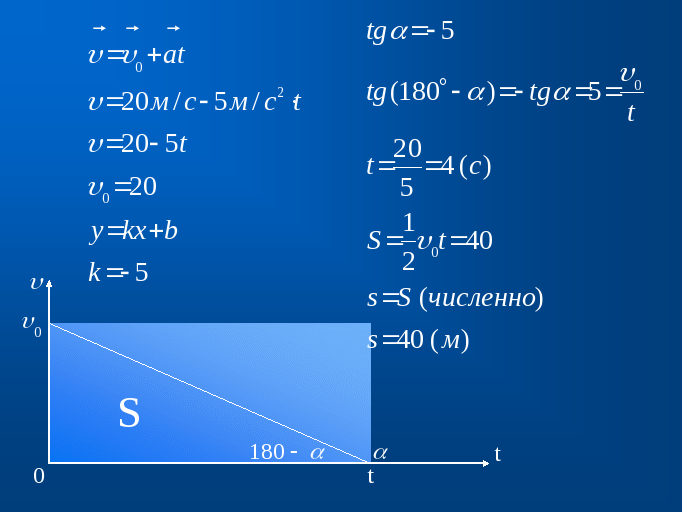
О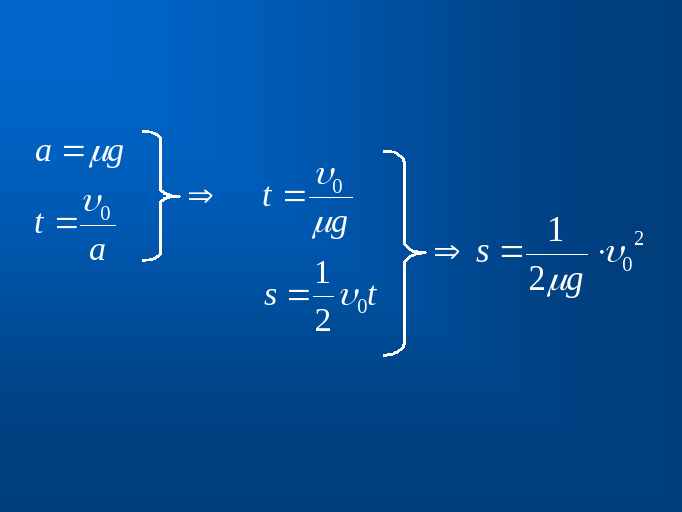 бъединив все полученные при исследовании формулы, мы видим, что тормозной путь пропорционален квадрату начальной скорости с коэффициентом пропорциональности
бъединив все полученные при исследовании формулы, мы видим, что тормозной путь пропорционален квадрату начальной скорости с коэффициентом пропорциональности 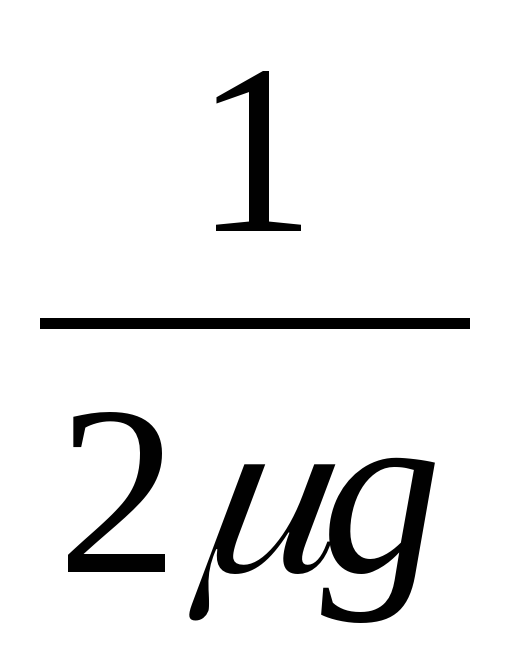 , который зависит от коэффициента трения, т. е. от характеристик резины и дорожного покрытия.
, который зависит от коэффициента трения, т. е. от характеристик резины и дорожного покрытия.
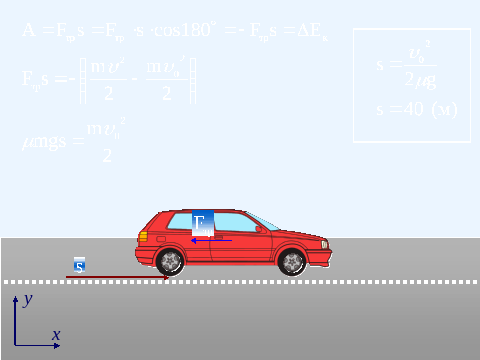
Есть ещё один способ решения этой задачи. Работу в данном случае совершает сила трения. С одной стороны, она равна скалярному произведению вектора силы трения на вектор перемещения, а так как мы видим, что они противоположно направлены, то косинус угла между ними равен -1. С другой стороны, работа равна изменению кинетической энергии автомобиля. Мы помним, что конечная скорость автомобиля равна 0, а значит, путём несложных алгебраических преобразований получаем формулу для вычисления тормозного пути.
Критерии рациональности
применения того или иного метода:
Самый важный – время, затрачиваемое на решение задачи.
Далее, немаловажной является необходимость владения специфическими знаниями и навыками (законы физики, умение брать интегралы и т. п.).
Простота производимых действий и объём работы – как правило, находятся в обратной пропорциональности.
Затрачиваемые умственные и творческие усилия.
Необходимость применения знаний из дисциплин различной степени смежности.
Универсальность метода, точность и полнота полученного результата.
Выводы:
Овладение различными способами решения задач – не самоцель, а возможность выработать более глубокое понимание проблемы.
Одной из основных задач в жизни человека является выбор наиболее рациональных способов решения возникающих проблем.
Выработка критериев оценки рациональности того или иного метода применительно к конкретной проблеме является задачей нетривиальной и требующей детального анализа.
Список литературы
1) Энциклопедия для детей. Том 16. Физика. Ч.1. биография физики. Путешествие вглубь материи. Механическая картина мира / Глав. ред. В.А.Володин. – М.: Аванта+, 2000.-448 с.
2) Энциклопедия для детей. Том 14.техника / Глав. ред. М.Д.Аксёнова. – М.: Аванта+, 2000.-688 с.
3) Элементарный учебник физики. Учеб. пособие. В 3 т. / Под ред. Г.С.Ландсберга: Т. 1. Механика. Теплота. Молекулярная физика. –
12-е изд. – М.: ФИМАЛИТ, 2000г.-608 с.
4) Физика: механика: 9 кл.: Учеб. для углубленного изучения физики / М.М.Балашов, А.И.Гомонова, А.Б.Долинский и др.; Под ред. Г.Я.Мякишева. – М.: Дрофа, 1996.-496 с.
5) Работа Гундырева В. Б. «ИНЖЕНЕР- «Физик», «Лирик» или просто волшебник».





 .Во сколько раз изменится тормозной путь, если начальная скорость машины увеличится в 2 раза?
.Во сколько раз изменится тормозной путь, если начальная скорость машины увеличится в 2 раза? ышеприведённый способ решения носит название:
ышеприведённый способ решения носит название:  ля этого запишем второй закон Ньютона, применительно к данной ситуации и найдём проекции векторов на координатные оси. Затем, выполнив стандартные алгебраические преобразования, вычислим модуль ускорения автомобиля.
ля этого запишем второй закон Ньютона, применительно к данной ситуации и найдём проекции векторов на координатные оси. Затем, выполнив стандартные алгебраические преобразования, вычислим модуль ускорения автомобиля. ля примера рассмотрим график зависимости скорости от времени.
ля примера рассмотрим график зависимости скорости от времени. 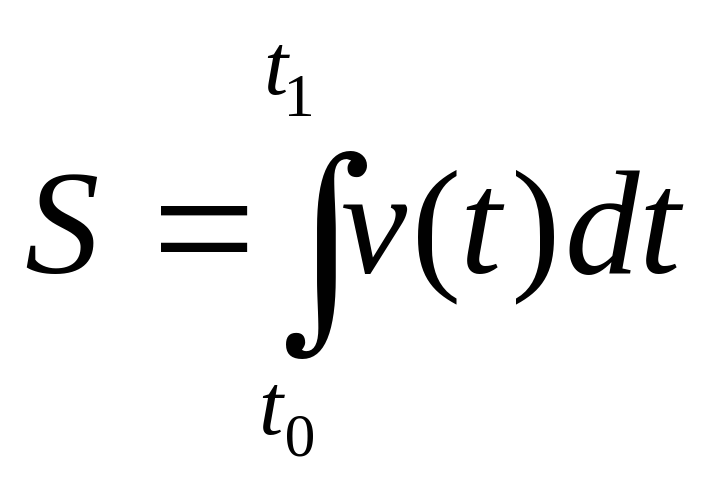

 бъединив все полученные при исследовании формулы, мы видим, что тормозной путь пропорционален квадрату начальной скорости с коэффициентом пропорциональности
бъединив все полученные при исследовании формулы, мы видим, что тормозной путь пропорционален квадрату начальной скорости с коэффициентом пропорциональности 










