

Дидактические проекты уроков по математике

МИНИСТЕСТВО ПРОСВЕЩЕНИЯ РЕСПУБЛИКИ МОЛДОВА
ГЛАВНОЕ УПРАВЛЕНИЕ ОБРАЗОВАНИЯ ФЭЛЕШТСКОГО РАЙОНА
Теоретический лицей имени А. С. Пушкина г. Фэлешть


| 
| Преподаватель математики: Дьячук Габриэлла (Высшая дидактическая степень).
|
2015-2016 учебный год
Преподаватель математики
Дата проведения: 1 февраля 2016 года.
Класс: 11 «б» (реальный профиль)
Предмет: Математика
Учитель: Дьячук Габриэлла
Номер урока в системе уроков: 12 урок.
Продолжительность урока: 45 минут.
Глава (Модуль V):Приложения производной.
Субъект урока: Применение производной в физике, геометрии, экономике.
Специфические компетенции:3: 3.2, 3.5, 3.6, 3.7
Цели урока: В конце урока учащиеся будут способны:
Ц1: вычислять производные элементарных и
сложных функций;
Ц2:распознавать и применять правила вычисления
производных при решении различных задач;
Ц3:решать задачи с применением уравнения
касательной к графику функций;
Ц4:использовать приобретенные знания и умения в
практической деятельности для решения
геометрических, физических и практических задач;
Ц5:оценивать критически свою деятельность на уроке,
отстаивать свою точку зрения.
Тип урока: Урок обобщения, анализа-синтеза
знаний.
К концу урока ученик будет способен
О1 – распознавать и классифицировать по различным критериям элементарные функции.
О2 – распознавать в различных контекстах функции и находить их производные.
О3 – анализировать решение задачи и объяснять полученный математический результат на социальном языке .
Дидактические технологии:
Формы обучения: фронтальная, индивидуальная.
Методы и приемы: анализ, синтез, обобщение, эвристическая беседа, работа в группах .
Дидактические материаллы: учебник И.Акири «Математика 11 класс», проектор, компьютер, доска, мел.
Дидактические технологии:
1)Методы обучения: Анализ, синтез и обобщение;
метод упражнений; беседа.
2)Формы обучения: Фронтальная, индивидуальная,
групповая.
3)Оборудование: Компьютеры,
компьютерная презентация в
Microsoft Power Point
проектор, экран,
оценочные листы, раздаточный
и справочный материал.
Оценивание: а) Виды оценивания: текущее оценивание;
б) Формы, методы оценивания: устные и
письменные вопросы и упражнения;
самостоятельная работа;
самопроверка.
План урока:
Организационный момент: проверка готовности класса к уроку (мел, доска)..
Вступительное слово учителя (2 мин.)
1 .Актуализация опорных знаний (10 мин.):
Постановка целей урока.
Математический диктант
Проверка домашней работы
( правильное решение проектируется на экран)
( 5 мин.)
2. Осмысление
Устная разминка( 3мин)
Самостоятельная работа (15 мин.)
3.Рефлексия.
Подведение итогов урока. (5 мин.)
Задание на дом, заполнение оценочных листов (2 мин.)
Резерв (дополнительные задания из тестов « Готовимся к БАКу» ).
Ход урока
Вступительное слово учителя.
-Здравствуйте ребята! Прошу вас сесть!
Организационный момент.
Проверка явки учащихся.
Проверка готовности учащихся к уроку.
Создание эмоционального настроя у учащихся на работу.
Учитель: Сегодня у нас заключительный урок по теме « Применения производной», на котором мы должны, систематизируя знания и умения, подготовиться к контрольной работе.
( Постановка целей урока, проектируются проектором .)
Учитель: Перед нами стоит задача – показать знание формул и теоретического материала по теме и умение применять производную при решении практических задач .
Учитель: Производная относится к числу математических понятий, которые носят межпредметный характер, и широко применяются в физике, химии, биологии, в технике и других отраслях наук. Изучение материала по теме урока имеет принципиально важное значение, так как здесь показывается приложение производной к решению различных физических и технических задач, то есть возможности применения элементов дифференциального исчисления в описании и изучении процессов и явлений реального мира.
Вопрос 1. В чем заключается геометрический смысл первой производной?
Ответ ученика: Геометрический смысл производной состоит в следующем: если к графику функции y=f(x) в точке с абсциссой  можно провести касательную не параллельную оси у, то f’(x) выражает угловой коэффициент касательной. k=f’(x0)=
можно провести касательную не параллельную оси у, то f’(x) выражает угловой коэффициент касательной. k=f’(x0)=
Вопрос 2. В чем заключается физический смысл первой производной?
Ответ ученика: Физический (механический) смысл производной состоит в следующем. Если S(t)- закон прямолинейного движения тела, то производная выражает мгновенную скорость в момент времени t: V=S’(t).
Вопрос 3. В чем заключается физический смысл второй производной?
Ответ ученика: 
Учитель: На практике во многих отраслях науки используется обобщение этого равенства: Если некий процесс протекает по закону S=S(t),то S’(t)- выражает скорость протекания этого процесса в момент времени t.
Примеры из физики: q’(t)=I; a=V’(t)
Производная – это скорость роста функции.
Мощность – это производная работы по времени P = A' (t).
Сила тока – производная от заряда по времени I = g' (t).
Сила – есть производная работы по перемещению F = A' (x).
Теплоемкость – это производная количества теплоты по температуре C = Q' (t).
Давление – производная силы по площади P = F'(S)
Длина окружности – это производная площади круга по радиусу lокр=S'кр(R).
Темп роста производительности труда – это производная производительности труда по времени.
Успехи в учебе? Производная роста знаний.
Например. Обсуждая успехи учащегося, преподаватель математики так отозвался о нем: “Он очень мало знает, но у него положительная производная”. Он хотел сказать, что скорость приращения знаний у учащегося положительная, а это есть залог того, что знания возрастут.
Чтоб увеличить скорость приращения знаний, ВЫПОЛНИМ ТЕСТ.
Выполните задание:На столе у каждого учащегося находятся карточки с тестом:
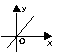
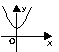
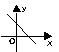
1)Нужно указать пары “функция – график производной этой функции”.
| График производной Функция | 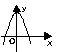
| 
| 
| 
| 
| 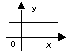
|
| у = 2х – х3
| | | | | | |
| 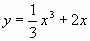
| | | | | | |
| 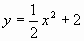
| | | | | | |
| 
| | | | | | |
| у = 2х – 7
| | | | | | |
| у = 2х + х4
| | | | | | |
| График производной Функция | 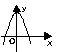
| 
| 
| 
| 
| 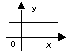
|
| у = 2х – х3 y/ = 2 – 3х2 | + | | | | | |
| 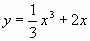
y / = х2 + 2 | | | + | | | |
| 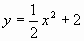
y/ = х | | + | | | | |
|
 у / = 2 - х | | | | + | | |
| у = 2х – 7 у / = 2 | | | | | | + |
| у = 2х + х4 у / = 2 + 4х3 | | |
|
| + |
|
-Анализируя ваши письменные работы, самая часто встречающая ошибка-это производная сложной функции. Формулу производной сложной функции мы повторили в начале урока. ( Надо последовательно представить ее в виде элементарных функций и взять производную по известным правилам). Закрепим это на практике.
2)Вариант 1. Найти производные функций.
| № | Задание | Ответы |
| А | В | С |
| 1 | 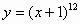
| 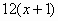
| 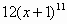
| 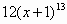
|
| 2 | 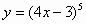
| 
| 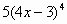
| 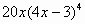
|
| 3 | 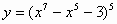
| 
| 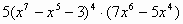
| 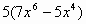
|
| 4 | 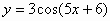
| 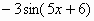
| 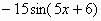
| 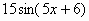
|
| 5 | 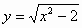
| 
| 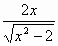
| 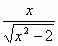
|
Теперь выполним самостоятельно вариант 2 и ответы запишем в таблицу.
Вариант 2. . Найти производные функций
| № | Задание | Ответы |
| А | В | С |
| 1 | 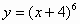
| 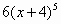
| 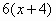
| 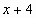
|
| 2 | 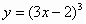
| 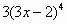
| 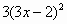
| 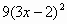
|
| 3 | 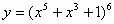
| 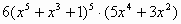
| 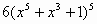
| 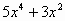
|
| 4 | 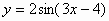
| 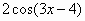
| 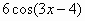
| 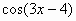
|
| 5 | 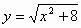
| 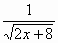
| 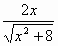
| 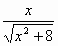
|
| № задания | 1 | 2 | 3 | 4 | 5 |
| № ответа | А | С | А | В | С |
II. Проверка домашнего задания.
Учащиеся обмениваются тетрадями и поверяют решение, которое отображается на экране.
На дом заданы примеры: №2(б),№10,№6(а)
Ответы домашней работы №2(б),№10,№6(а) спроецированы проектором.
№ 10.Найти силу F, действующую на материальную точку массой m, которая движется по закону S(t )=4 t3 – t2 при t=3 сек.
Ответ: a(t) =24t-2, a(3)=70 (m/s 2 ), F(t)=70m (H)
№ 2(б).Напишите уравнение касательной к графику функции f: D -R в точке с абсциссой х0 =2/3, f(x)= lg2 ( 3x-1).
Ответ : f ( 2/3 )=lg2 1 =0, тогда y=0 .
( Определите угловой коэффициент касательной? К=0, касательная параллельна или совпадает с осью ОХ)
№6(а).Решить на множестве R неравенство f / (х) 0 , если :
f(x) = x3 – 6x2 + 3x .
Ответ: при х��
 ��
��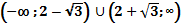
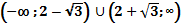
-Ученики индивидуально проверяют ответы и ставят (самоконтроль) оценку однокласснику в лист его контроля. (У каждого ученика имеется лист контроля, критерий оценки за домашнюю работу и образец листа контроля в раздаточном материале к уроку.)
Лист контроля (в приложении)
Демонстрационный материал. Презентация 5 минут. Свойства производной.
Применим наши теоретические знания на практике:
Задача №1. Командиру межгалактического космического корабля, движущемуся по закону 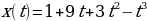 , сообщили о том, что приборы зафиксировали неопознанный летающий объект, стремительно приближающийся к кораблю. Чтобы избежать столкновения, необходимо максимально увеличить скорость. Каким должно быть ускорение корабля в момент, когда скорость станет максимальной?
, сообщили о том, что приборы зафиксировали неопознанный летающий объект, стремительно приближающийся к кораблю. Чтобы избежать столкновения, необходимо максимально увеличить скорость. Каким должно быть ускорение корабля в момент, когда скорость станет максимальной?

 , при t=1 скорость максимальна a(1)=0.
, при t=1 скорость максимальна a(1)=0.
Задача №2. Оборот предприятия за истекший год описывается через функцию
 , где
, где 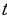 –месяцы,
–месяцы, 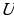 -миллионы лей. Исследуйте оборот предприятия.
-миллионы лей. Исследуйте оборот предприятия.
Решение: Исследуем оборот предприятия с помощью производной:
 Определим вторую производную: U′′(t)=0,9t-4 и третью:
Определим вторую производную: U′′(t)=0,9t-4 и третью:  Момент наименьшего оборота при
Момент наименьшего оборота при  =0, т.е.при t=8,9.Наименьший оборот был на девятом месяце. Первая производная показывает экстремальное изменение оборота. Из U′′(t)=0 следует t=4,4. Так как U″′(t)0, то на пятом месяце имеется сильное снижение оборота. Точки перегиба важны в экономике, так как именно по ним можно определить, в какой конкретно момент произошло изменение.
=0, т.е.при t=8,9.Наименьший оборот был на девятом месяце. Первая производная показывает экстремальное изменение оборота. Из U′′(t)=0 следует t=4,4. Так как U″′(t)0, то на пятом месяце имеется сильное снижение оборота. Точки перегиба важны в экономике, так как именно по ним можно определить, в какой конкретно момент произошло изменение.
Так, например, по решению предложенной задачи можно сделать выводы:
В начале исследуемого периода у предприятия было снижение оборота.
Предприятие пыталось выйти из этого состояния и для этого использовало
определенные средства. На пятом месяце (точка перегиба) что-то было предпринято и предприятие стало выходить из кризиса, а на девятом месяце стало набирать обороты.
Задача №3.Способность человека развить и понимать пространственные концепции задается законом  , t – возраст
, t – возраст  .
.
Найдите скорость улучшения понимания пространственных понятий когда человеку 9 лет и 16 лет. Определите знак ускорения. Вывод.
Работа в группах:
1 группа
Количество вещества в человеческой коже которое отвечает за эластичность кожи задано следующей законом  , где t – возраст в годах.
, где t – возраст в годах.
Найдите Q когда t=0, t=25, t=100 лет. Вывод.
С какой скоростью меняется концентрация этого вещества, на что указывает минус?
2 групп
Мяч подброшенный ребёнком вверх, будет находиться через t секунд на высоте
 метров ( от поверхности Земли).
метров ( от поверхности Земли).
С какой высоты подбрасывается мяч? Определите начальную скорость  . Через сколько секунд мяч упадет на Землю?
. Через сколько секунд мяч упадет на Землю?
3 группа
Оценка прибыли компании выражается следующей функцией
 (тыс. евро) t – момент времени в годах.
(тыс. евро) t – момент времени в годах.
Найти величину прибыли при t=0 и через год, скорость изменения прибыли, для каких значений t прибыль убывает, а для каких t возрастает ?.
«Изучение производных поможет Вам быстро и правильно принимать решения в различных ситуациях, так как Вы уже учитесь думать, преодолевать трудности и рассуждать, а это всё ведет к приобретению мудрости.»
Задача Докажите, что уравнение 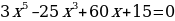 имеет только один действительный корень.
имеет только один действительный корень.
Указание: Рассмотрим функцию  и найдем её интервалы монотонности.
и найдем её интервалы монотонности.
Имеем: 
Задача . При извержении вулкана камни горной породы выбрасываются перпендикулярно вверх с начальной скоростью 120 м/с. Какой наибольшей высоты достигнут камни, если сопротивлением ветра пренебречь?
Решение: Вещество выбрасывается перпендикулярно вверх. Высота камня  функция времени:
функция времени:  =
= . Откуда следует:
. Откуда следует:  . Следовательно,
. Следовательно, 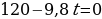 и
и  . Тогда
. Тогда 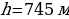 , т.е. камни горной породы достигают уровня
, т.е. камни горной породы достигают уровня  от края вулкана. ю
от края вулкана. ю
VI. Подведение итогов урока
Подводятся итоги каждого этапа урока.
Ответы на вопросы учащихся.
Объявление и комментирование оценок
Подумайте и ответьте на такие вопросы:
Где применяется производная?
Как вы думаете нужно ли нам знать как применять производную? В вашей профессии она нужна?
VII. Домашнее задание:
Повторить метод интервалов из 10кл.
Домашнее задание
Придумать и решить задачу на применение производной.
Выучить правила дифференцирования §2-§4 из Модуля V.
Выполнить упражнение № 2,4 и5 из проверочной работы на стр.134,уровень Б и дополнительную карточку.
Резерв На рисунках изображены графики функций и касательные к ним в точке а. Укажите функцию, производная которой в точке а равна 1?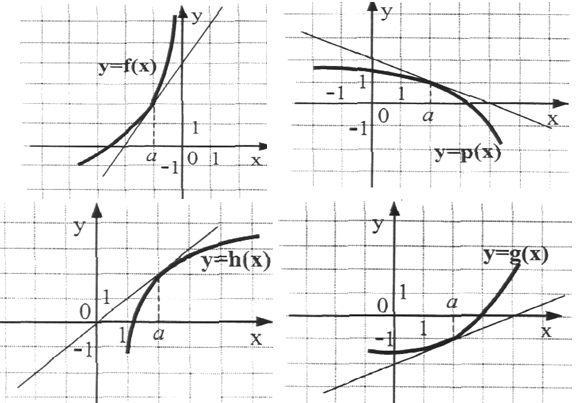














 можно провести касательную не параллельную оси у, то f’(x) выражает угловой коэффициент касательной. k=f’(x0)=
можно провести касательную не параллельную оси у, то f’(x) выражает угловой коэффициент касательной. k=f’(x0)=






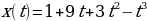 , сообщили о том, что приборы зафиксировали неопознанный летающий объект, стремительно приближающийся к кораблю. Чтобы избежать столкновения, необходимо максимально увеличить скорость. Каким должно быть ускорение корабля в момент, когда скорость станет максимальной?
, сообщили о том, что приборы зафиксировали неопознанный летающий объект, стремительно приближающийся к кораблю. Чтобы избежать столкновения, необходимо максимально увеличить скорость. Каким должно быть ускорение корабля в момент, когда скорость станет максимальной?
 , при t=1 скорость максимальна a(1)=0.
, при t=1 скорость максимальна a(1)=0. , где
, где 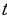 –месяцы,
–месяцы, 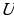 -миллионы лей. Исследуйте оборот предприятия.
-миллионы лей. Исследуйте оборот предприятия. Определим вторую производную: U′′(t)=0,9t-4 и третью:
Определим вторую производную: U′′(t)=0,9t-4 и третью:  Момент наименьшего оборота при
Момент наименьшего оборота при  =0, т.е.при t=8,9.Наименьший оборот был на девятом месяце. Первая производная показывает экстремальное изменение оборота. Из U′′(t)=0 следует t=4,4. Так как U″′(t)0, то на пятом месяце имеется сильное снижение оборота. Точки перегиба важны в экономике, так как именно по ним можно определить, в какой конкретно момент произошло изменение.
=0, т.е.при t=8,9.Наименьший оборот был на девятом месяце. Первая производная показывает экстремальное изменение оборота. Из U′′(t)=0 следует t=4,4. Так как U″′(t)0, то на пятом месяце имеется сильное снижение оборота. Точки перегиба важны в экономике, так как именно по ним можно определить, в какой конкретно момент произошло изменение. , t – возраст
, t – возраст  .
. , где t – возраст в годах.
, где t – возраст в годах. метров ( от поверхности Земли).
метров ( от поверхности Земли). . Через сколько секунд мяч упадет на Землю?
. Через сколько секунд мяч упадет на Землю? (тыс. евро) t – момент времени в годах.
(тыс. евро) t – момент времени в годах.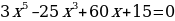 имеет только один действительный корень.
имеет только один действительный корень. и найдем её интервалы монотонности.
и найдем её интервалы монотонности. 
 функция времени:
функция времени:  =
= . Откуда следует:
. Откуда следует:  . Следовательно,
. Следовательно, 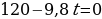 и
и  . Тогда
. Тогда 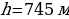 , т.е. камни горной породы достигают уровня
, т.е. камни горной породы достигают уровня  от края вулкана. ю
от края вулкана. ю











