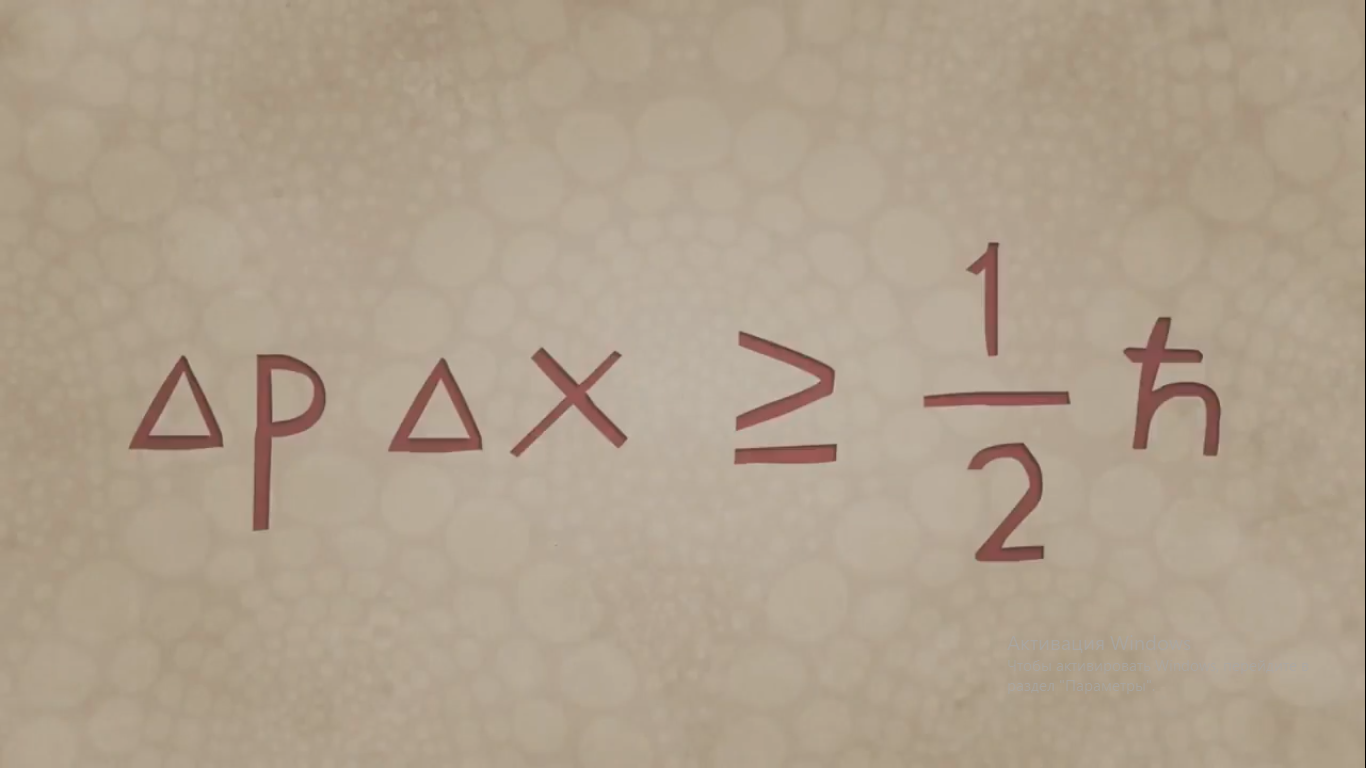Принцип неопределенности Гейзенберга. Квантовая физика

Принцип неопределенности Гейзенберга - одна из немногих идей квантовой физики, которые проникли в массовое сознание.

Принцип гласит, что невозможно одновременно знать и точное положение , и точную скорость объекта , и как метафора встречается повсюду – от литературы до спортивных комментариев .

Неопределенность часто считается следствием самого измерения: измерение положения объекта меняет его скорость, и наоборот.

Но настоящая причина гораздо глубже и удивительнее.

Принцип неопределенности существует,

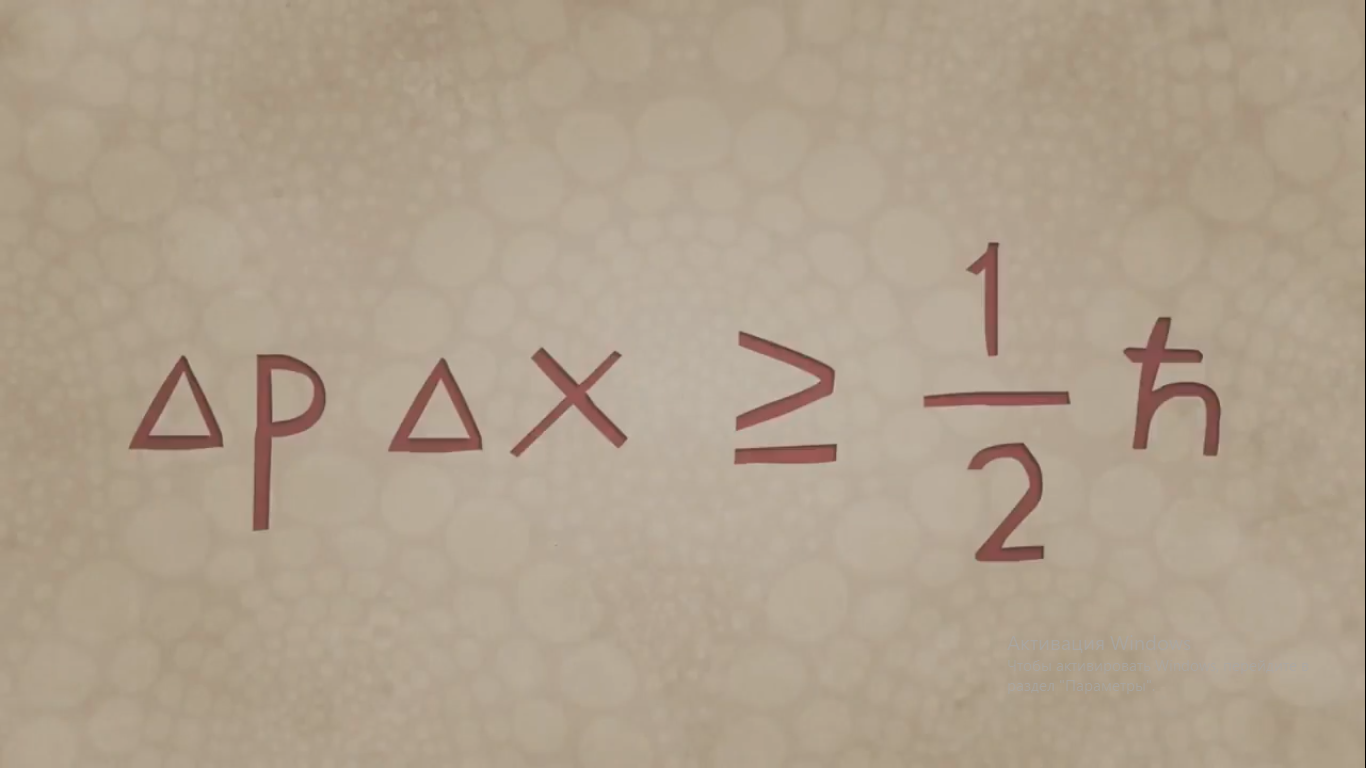
потому что всё во Вселенной ведет себя одновременно и как волна, и как частица.

В квантовой механике точное место и точная скорость объекта не имеют смысла.

Чтобы это понять, надо разобраться, что значит вести себя как волна или как частица.

По определению, в любой момент времени частица находится в одном месте.

На графике вероятности нахождения объекта в определенном месте это выглядит как пик: 100% в одной точке, ноль во всех остальных.

Волна же - это возмущение ,распространяющееся в пространстве, как рябь на поверхности водоема.

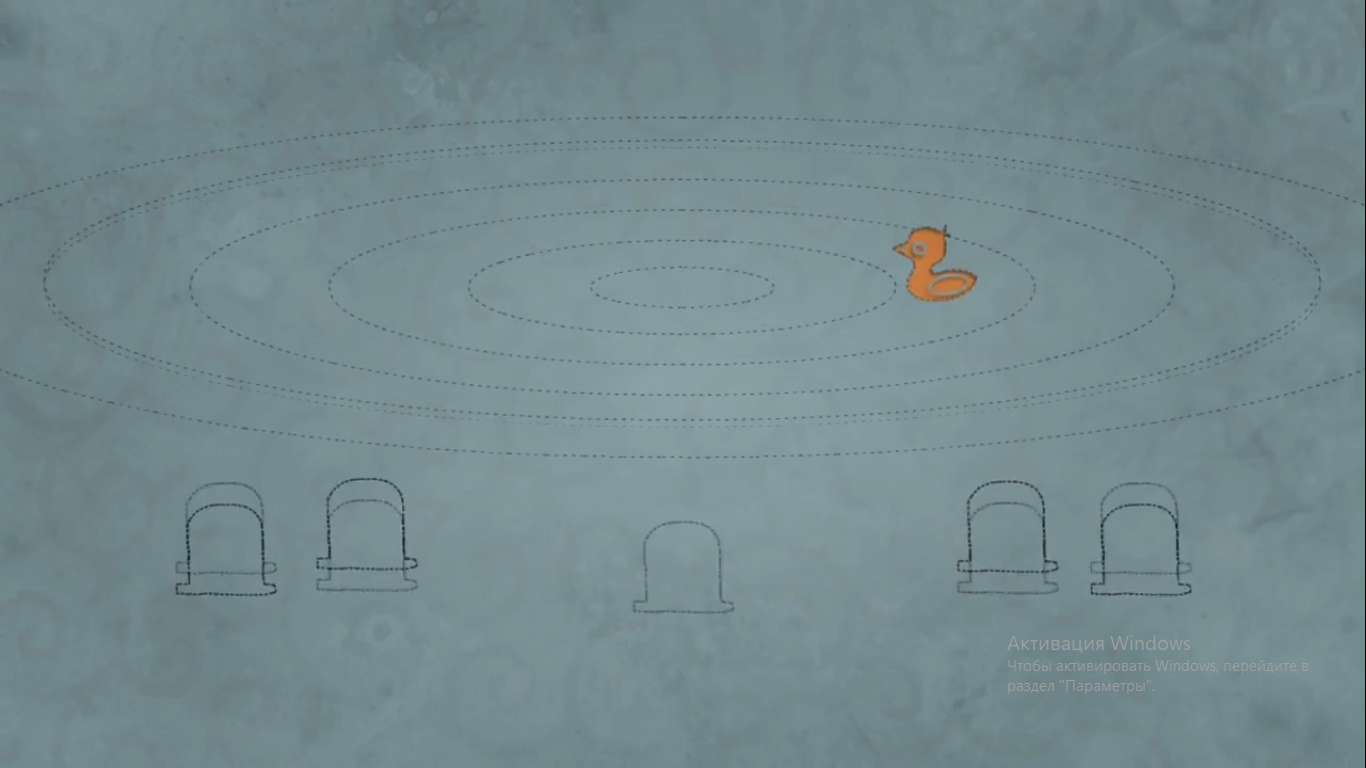
Можно четко распознать общие признаки волн и, что еще важнее, длину одной волны, т.е. расстояние между соседними пиками

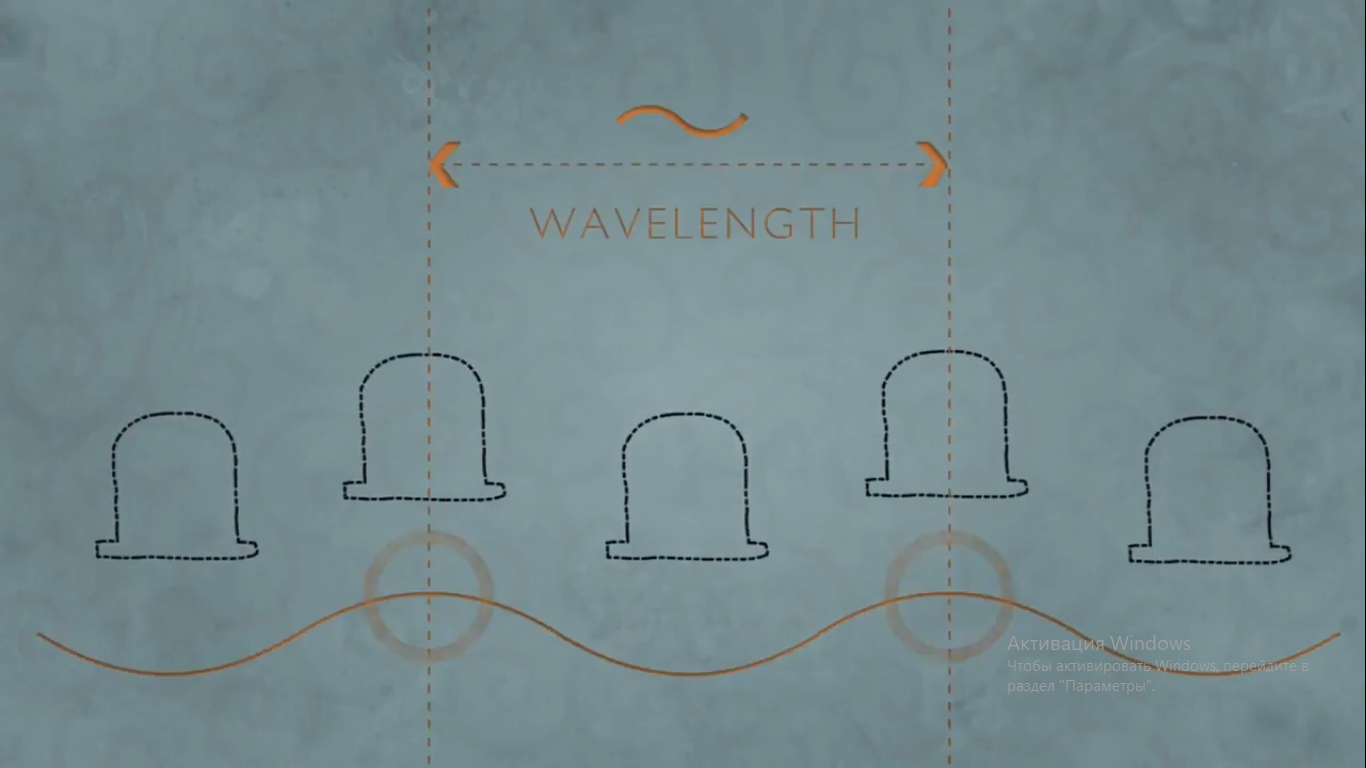
или соседними ложбинами.

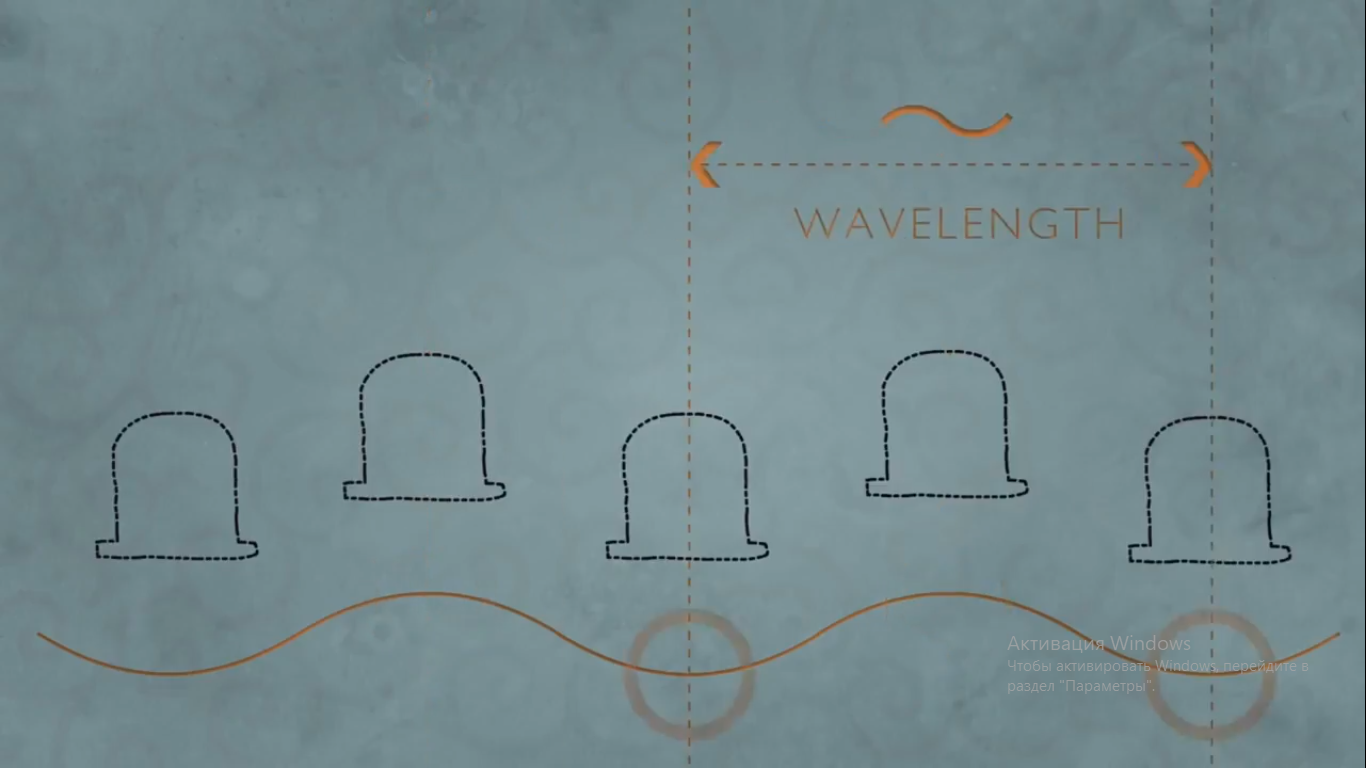
Но при этом нельзя показать ее точное местонахождение. У нее всегда есть вероятность находиться во многих местах.

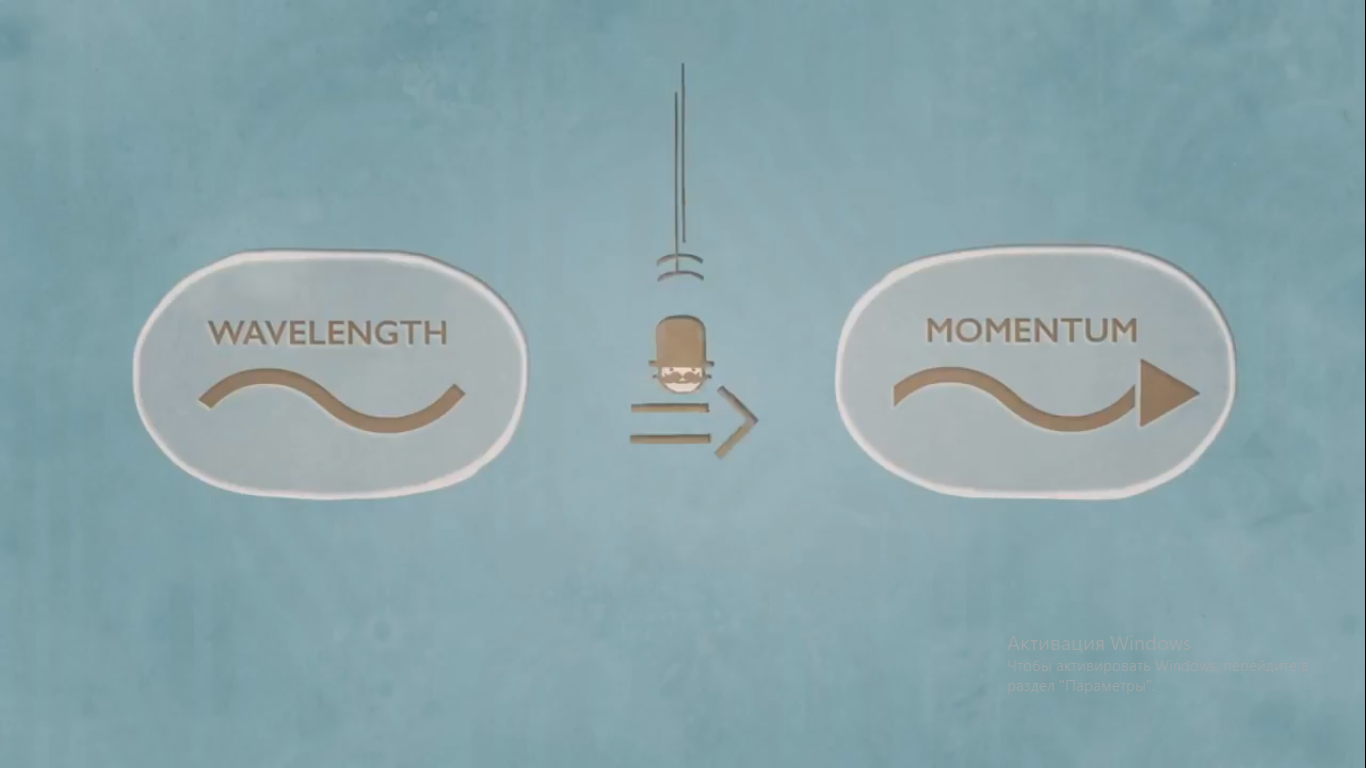
Для квантовой физики длина так важна, потому что она связана с импульсом объекта - массой , умноженной на скорость.

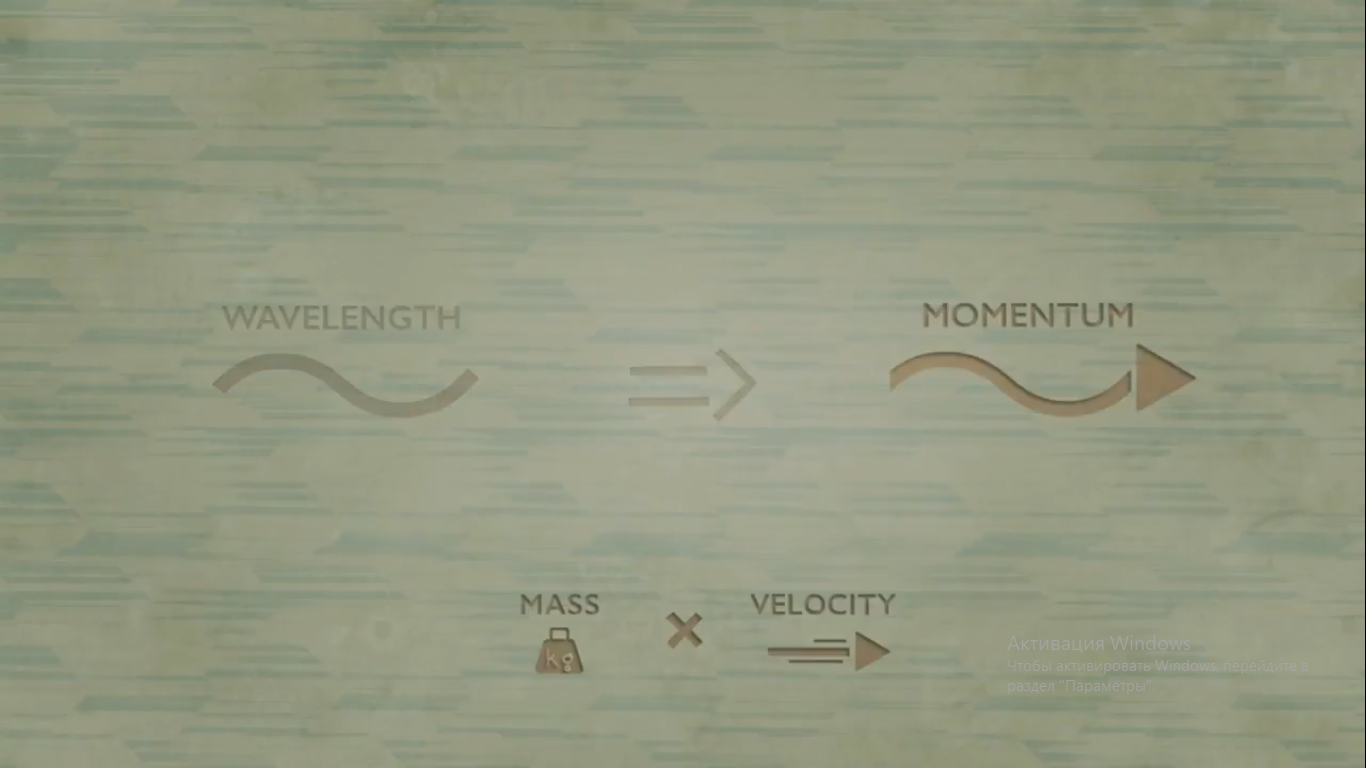
Быстро движущийся объект обладает большим импульсом, который соответствует очень малой длине волны.

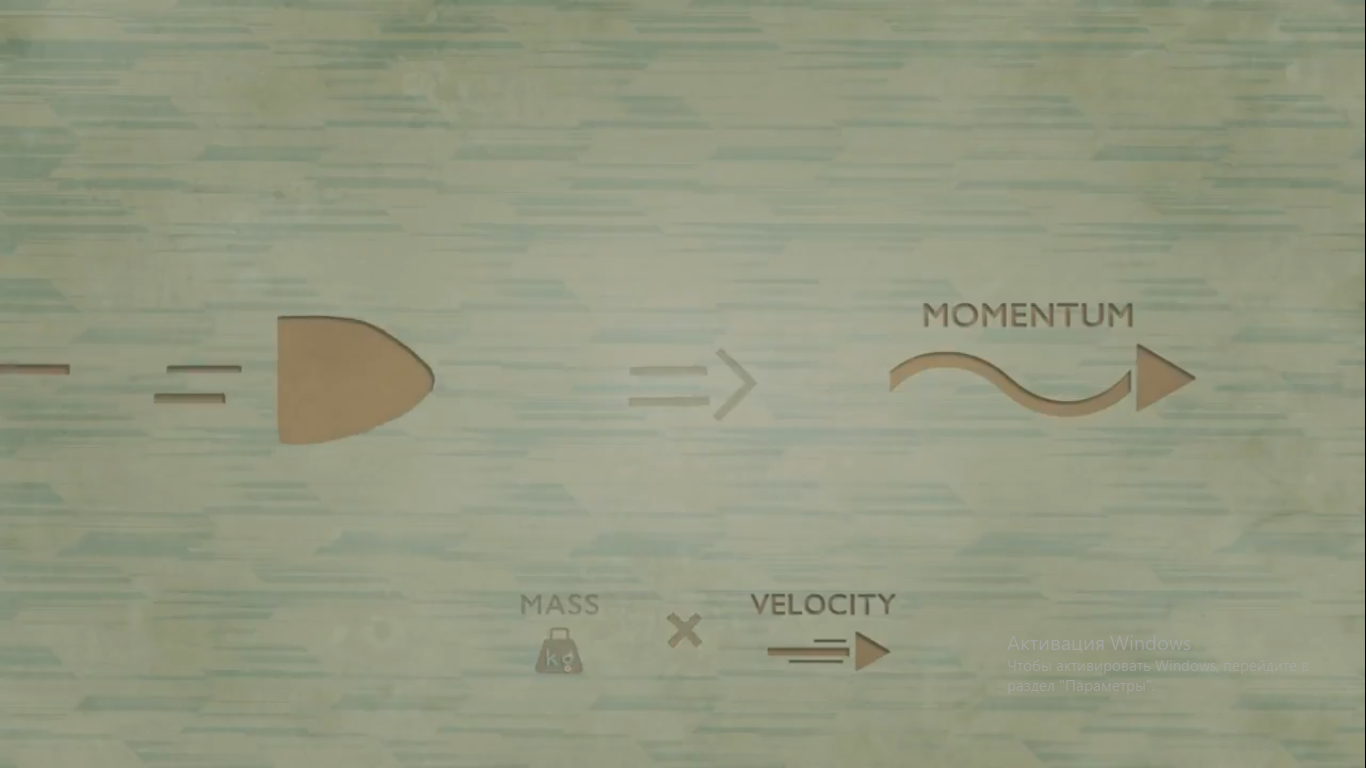
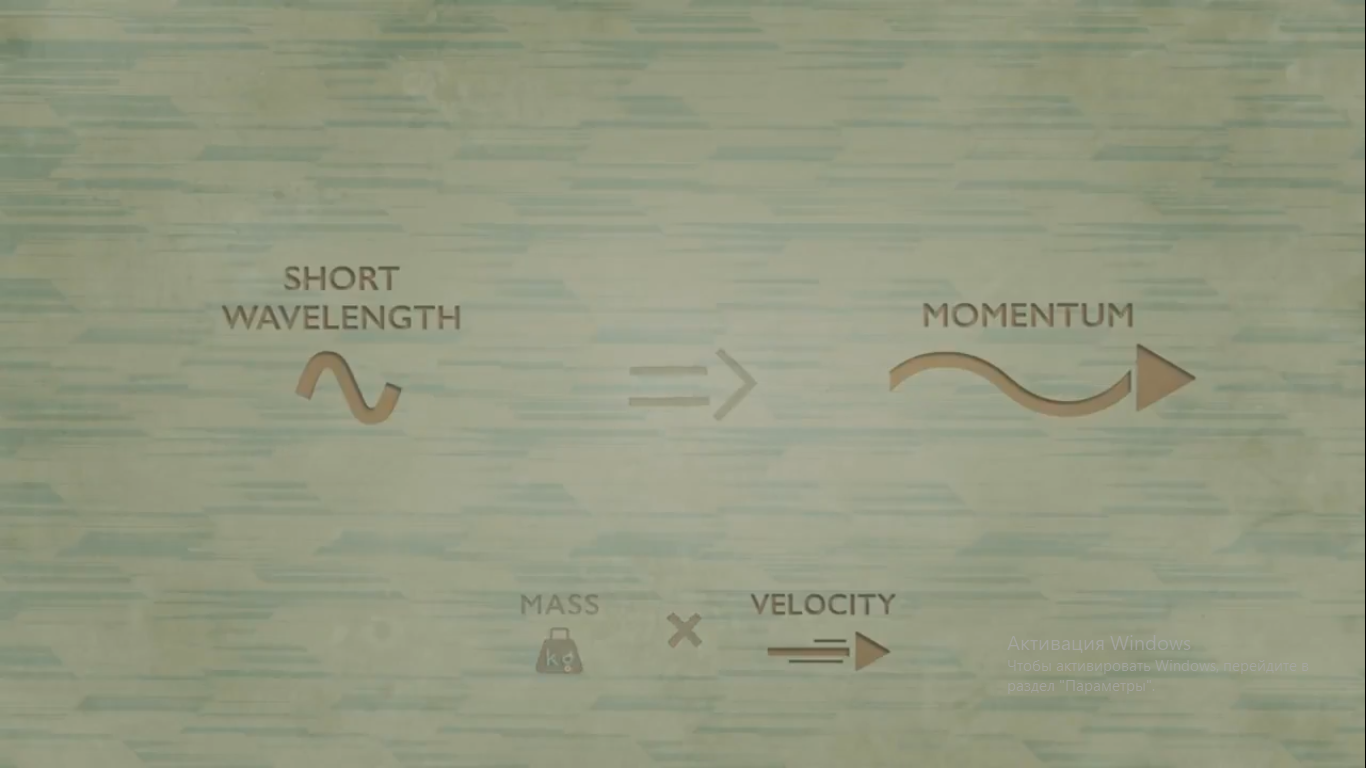
Объект с большой массой имеет большой импульс, даже если не движется быстро, что опять-таки соответствует малой длине волны. Вот почему мы не замечаем волновой природы привычных объектов.

У бейсбольного мяча в воздухе длина в одну миллиардную от триллионной триллионной метра слишком мала для обнаружения .

У таких маленьких тел, как атомы и электроны длину волны вполне можно измерить экспериментальным путем.

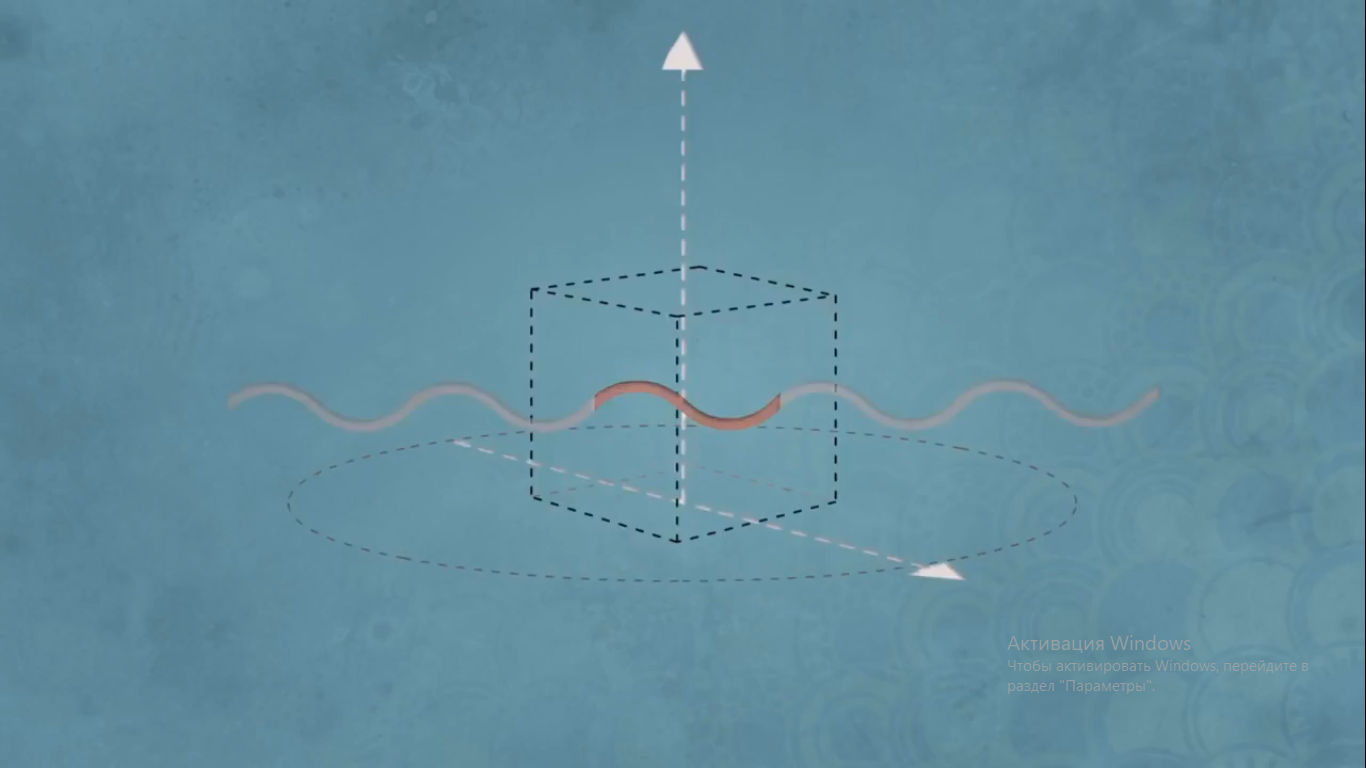
Итак, у волны можно измерить ее длину, а значит и ее импульс, но четкого местонахождения у нее нет.

Мы можем точно определить положение частицы,

но длины волны у нее нет , а значит , неизвестен и ее импульс.

Чтобы у частицы были и положение, и импульс , надо совместить обе картинки

получив на графике волну, но на очень маленьком отрезке.

Как это сделать?

Путем сложения волн с разными длинами, что обеспечит вероятность наличия у квантового объекта различных импульсов.

При сопоставлении двух волн мы видим , что в местах , где пики совпадают , образуется большая волна, а в других местах пик одной волны заполняет ложбину другой.

В результате участки с волнами чередуются с участками, где ничего нет.

При добавлении третьей волны промежутки , где волны гасят друг друга, становятся длиннее.

С четвертой они еще больше удлиняются , а участки с волнами сужаются.

Если продолжать добавлять волны,

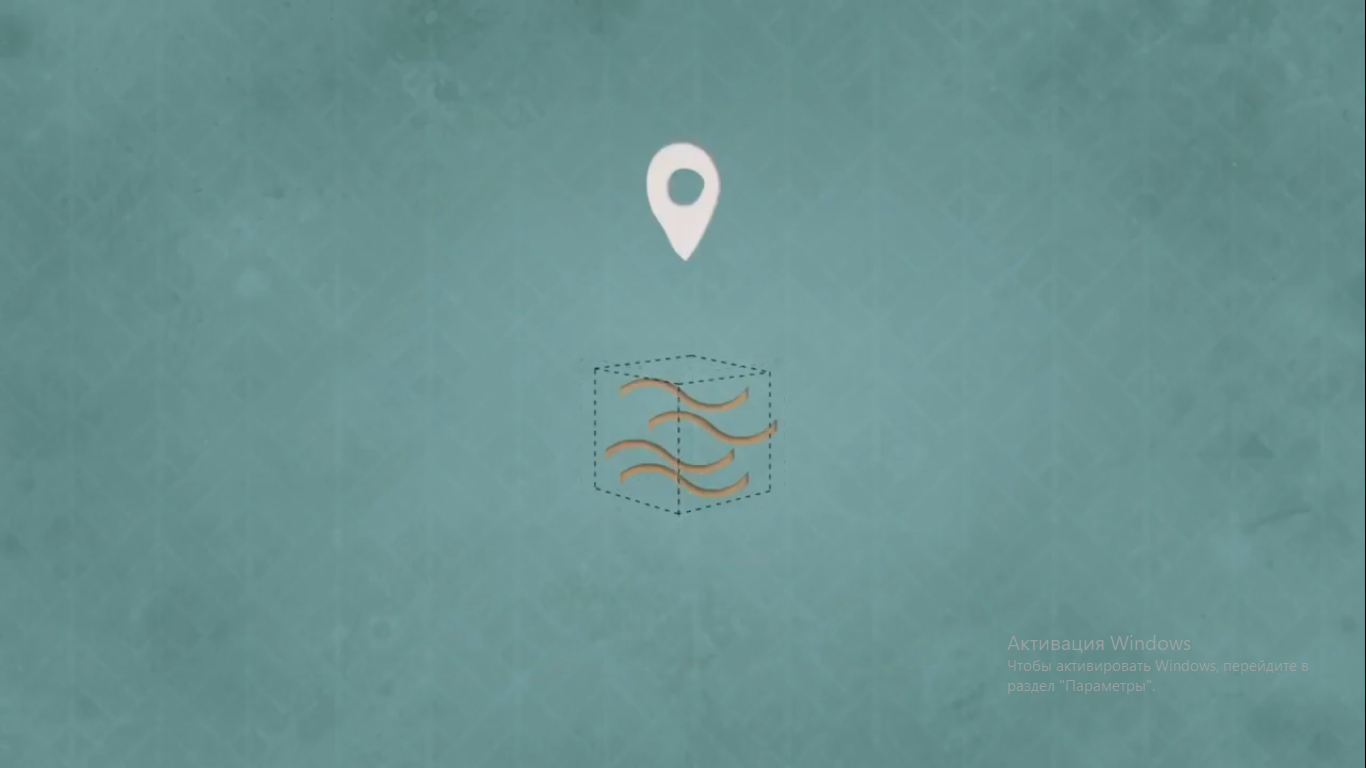
можно получить волновой пакет с определенной длинной волны на одном малом участке.

Это квантовый объект , имеющий природу как волны, так и частицы, но добившись этого, мы лишаемся определенности относительно как положения, так и импульса. Положение теперь не ограничивается одной точкой.

Существует вероятность его нахождения в некоторой области вокруг центра волнового пакета, полученного путем сложения множества волн, а значит имеется некая вероятность его обнаружения по импульсу , соответствующему любой из них. Теперь и положение, и импульс являются неопределенными, и эти неопределенности взаимосвязаны.

Чтобы уменьшить неопределенность положения за счет уменьшения волнового пакета, надо добавить больше волн, но это увеличит неопределенность импульса.

А чтобы точнее определить импульс , нужен бОльший волновой пакет, что увеличит неопределенность положения.

Это и есть принцип неопределенности Гейзенберга,

впервые сформулированный немецким физиком Вернером Гейзенбергом еще в 1927г.

Эта неопределенность- не следствие несовершенства измерений,

а неизбежный результат объединения свойств волны и частицы.

Принцип неопределенности- это не просто объективный предел самих измерений. Это предел совместимости свойств, присущих этому объекту, являющийся фундаментальным принципом организации самой Вселенной.