Призма и его свойства 10 класс

Призма

Призма

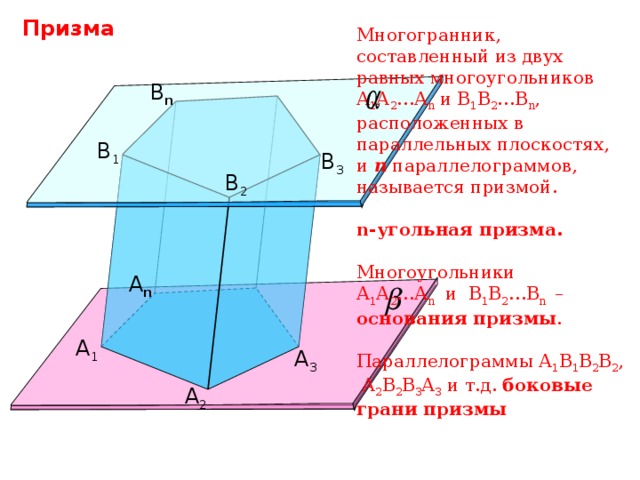
Многогранник, составленный из двух равных многоугольников А 1 А 2 …А n и В 1 В 2 …В n , расположенных в параллельных плоскостях, и n параллелограммов, называется призмой.

n-угольная призма.

Многоугольники

А 1 А 2 …А n и В 1 В 2 …В n – основания призмы .

Параллелограммы А 1 В 1 В 2 В 2 , А 2 В 2 В 3 А 3 и т.д. боковые грани призмы

B n

B 1

B 3

B 2

А n

А 1

А 3

А 2

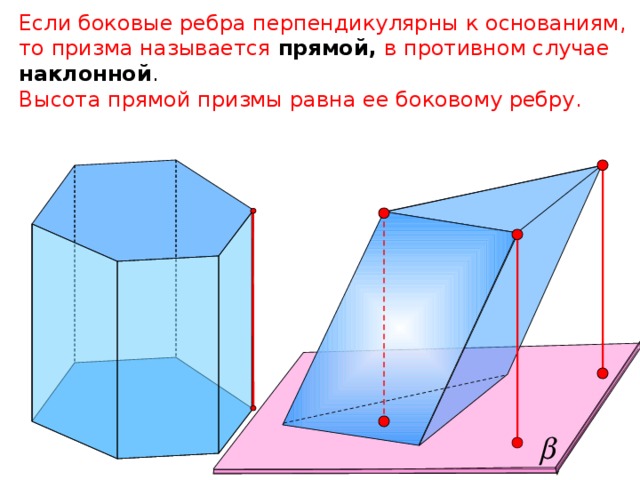
Если боковые ребра перпендикулярны к основаниям, то призма называется прямой, в противном случае наклонной .

Высота прямой призмы равна ее боковому ребру.

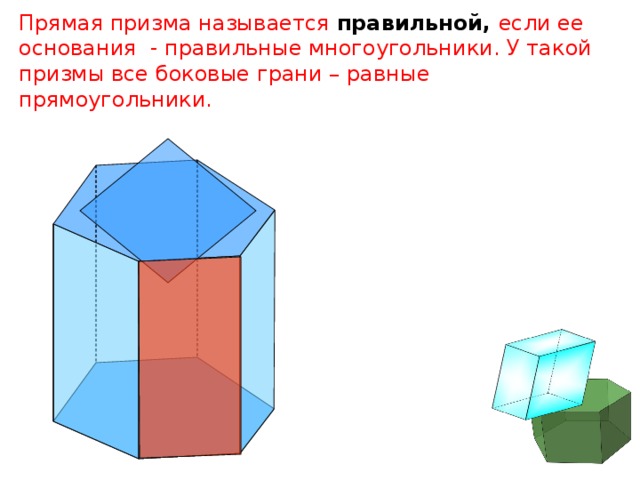
Прямая призма называется правильной, если ее основания - правильные многоугольники. У такой призмы все боковые грани – равные прямоугольники.

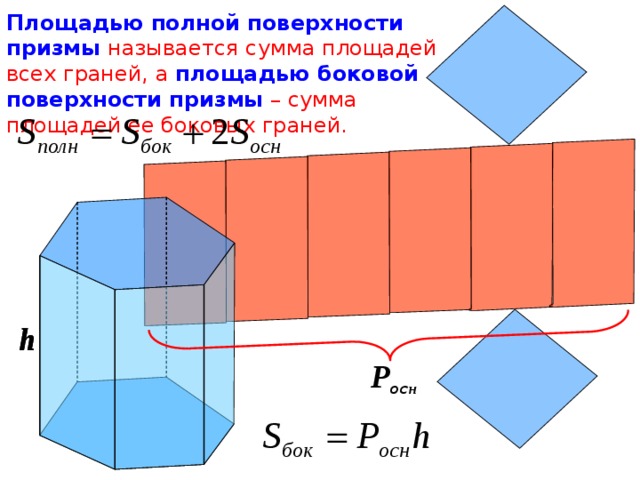
Площадью полной поверхности призмы называется сумма площадей всех граней, а площадью боковой поверхности призмы – сумма площадей ее боковых граней.

h

h

P oc н

Теорема о площади боковой поверхности прямой призмы

Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы

S бок. = Р осн. · h

Доказательство.

Боковые грани прямой призмы – прямоугольники, основания которых – стороны основания призмы, а высоты равны высоте h призмы.

S бок. = A 1 A 2 · h + A 2 A 3 · h + A 3 A 4 · h + … + A n-1 A n · h =

= (A 1 A 2 + A 2 A 3 + A 3 A 4 + … + A n-1 A n ) · h = P осн. · h

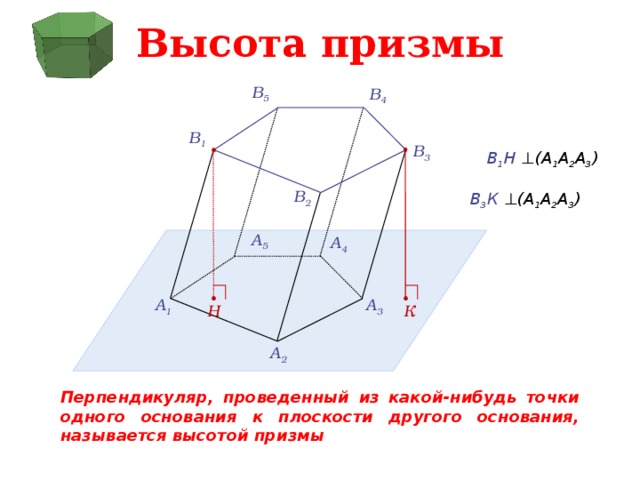
Высота призмы

В 5

В 4

В 1

В 3

В 1 Н ⊥ (А 1 А 2 А 3 )

В 2

В 3 К ⊥ (А 1 А 2 А 3 )

A 5

A 4

A 3

A 1

К

Н

A 2

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы

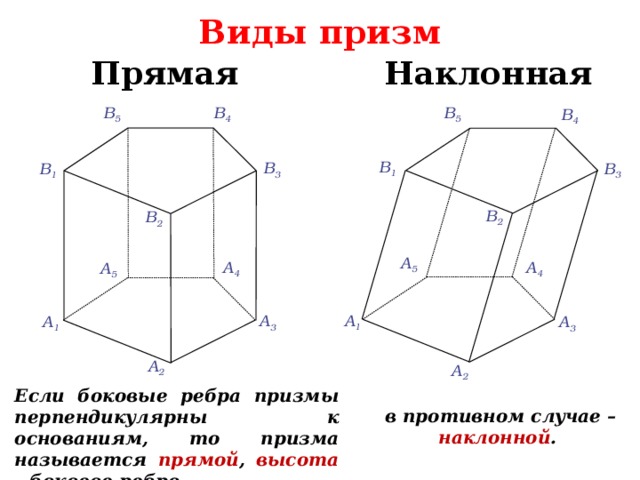
Виды призм

Прямая

Наклонная

В 4

В 5

В 5

В 4

В 1

В 3

В 3

В 1

В 2

В 2

A 5

A 4

A 4

A 5

A 1

A 3

A 1

A 3

A 2

A 2

Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой , высота – боковое ребро

в противном случае – наклонной .

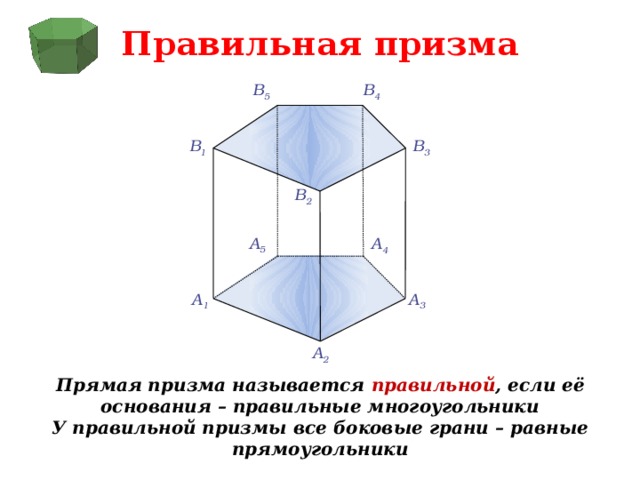
Правильная призма

В 5

В 4

В 3

В 1

В 2

A 5

A 4

A 3

A 1

A 2

Прямая призма называется правильной , если её основания – правильные многоугольники

У правильной призмы все боковые грани – равные прямоугольники

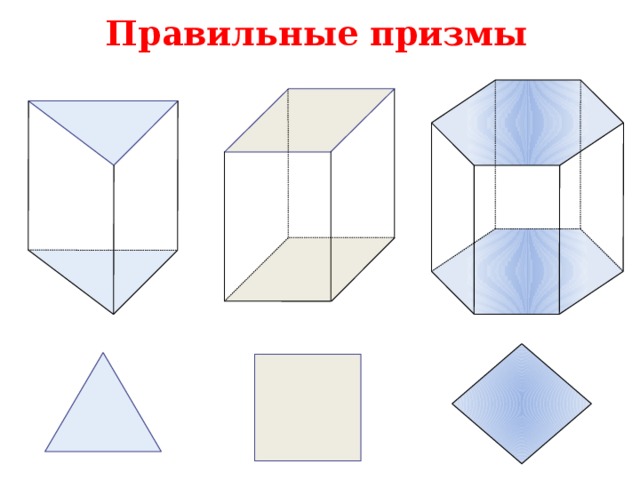
Правильные призмы

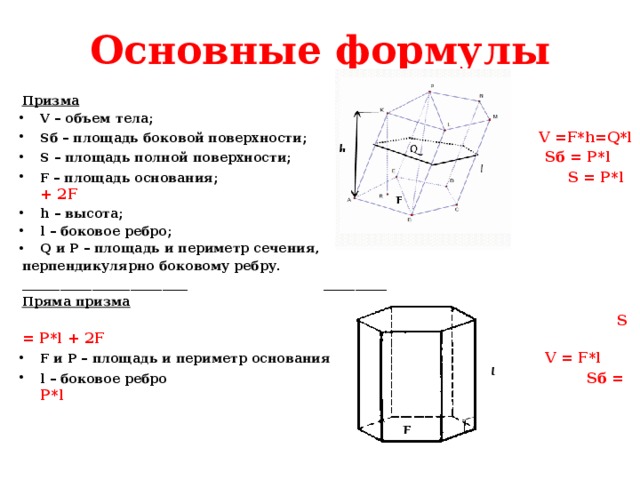
Основные формулы

Призма

• V – объем тела;
• Sб – площадь боковой поверхности; V =F*h=Q*l
• S – площадь полной поверхности; Sб = P*l
• F – площадь основания; S = P*l + 2F
• h – высота;
• l – боковое ребро;
• Q и P – площадь и периметр сечения,

перпендикулярно боковому ребру.

__________________________ __________

Пряма призма

S = P*l + 2F

• F и P – площадь и периметр основания V = F*l
• l – боковое ребро Sб = P*l

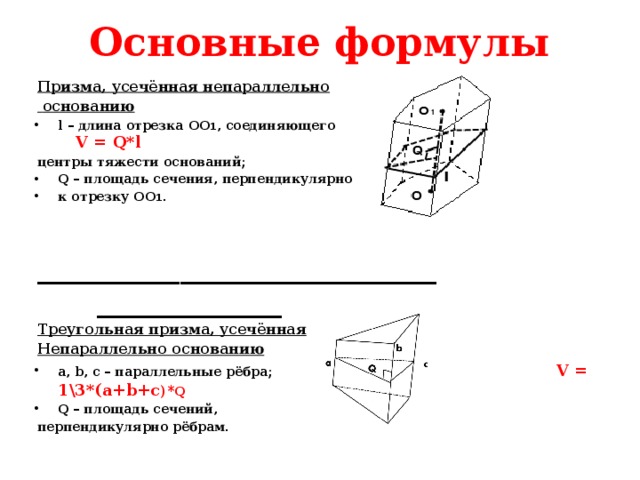
Основные формулы

Призма, усечённая непараллельно

основанию

• l – длина отрезка OO 1 , соединяющего V = Q*l

центры тяжести оснований;

• Q – площадь сечения, перпендикулярно
• к отрезку OO 1 .

____________________________ _____________

Треугольная призма, усечённая

Непараллельно основанию

• a, b, c – параллельные рёбра; V = 1\3*(a+b+c )* Q
• Q – площадь сечений,

перпендикулярно рёбрам.

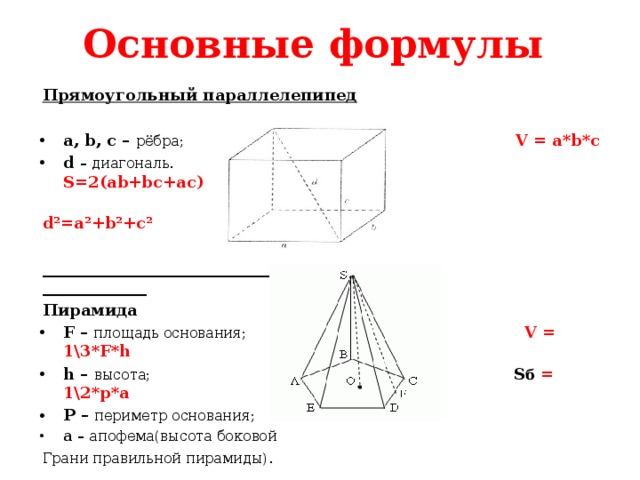
Основные формулы

Прямоугольный параллелепипед

• a, b, c – рёбра; V = a*b*c
• d – диагональ. S=2(ab+bc+ac)

d²=a²+b²+c²

______________________________ _____________

Пирамида

• F – площадь основания; V = 1\3*F*h
• h – высота; S б = 1\2*p*a
• P – периметр основания;
• a – апофема(высота боковой

Грани правильной пирамиды) .

Задания

• Найдите расстояние между вершинами D и B 1 прямоугольного параллелепипеда, для которого AB=AA 1 =17,5; AD=17,5
• Дам прямоугольный параллелепипед ABCDA 1 B 1 C 1 D 1 , для которого АА 1 =17, АВ=19, AD=17.
• Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 48 и 14. Площадь её поверхности равно 728. Найдите высоту призмы.

• 1. Решение:

1) ρ(B1,D)=B1D – диагональ

2) d²=a²+b²+c²(в прямом парал-де).

3) т.к. AD=17,5 , AA1=AB=17,5

B1D²=AB²+AD²+AA1²

B1D==

=2*17,5=35

Ответ: B1D = 35 ед.

• 2. Решение:

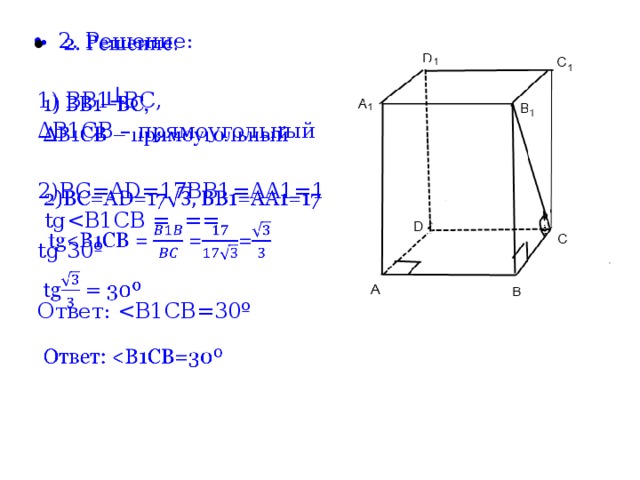
1) BB1┴BC,

∆ B1CB – прямоугольный

2)BC=AD=17BB1=AA1=17

tg

tg 30º

Ответ:

BB1 = 2) ∆ABC – основание. AC = = = = = 50 3) S∆ABC = 1\2 * AB * BC = 1\2 * 14 * *48 = 7*48 = 336 4) P ∆ABC = 50+48+14= 112 5) BB1 = = = = = 0, 5 Ответ: 0,5 ед. " width="640"

• 3. Решение:

1)AA1=BB1=CC1 – высота.

Sп.п. = Pосн.*BB1+2*Sосн =

BB1 =

2) ∆ABC – основание.

AC = = =

= = 50

3) S∆ABC = 1\2 * AB * BC = 1\2 * 14 *

*48 = 7*48 = 336

4) P ∆ABC = 50+48+14= 112

5) BB1 = = = =

= 0, 5

Ответ: 0,5 ед.

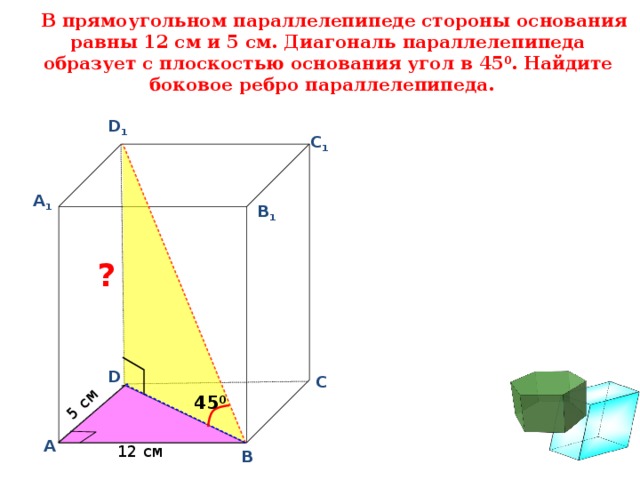
5 см

В прямоугольном параллелепипеде стороны основания равны 12 см и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол в 45 0 . Найдите боковое ребро параллелепипеда.

D 1

С 1

А 1

В 1

?

D

С

45 0

А

12 см

В

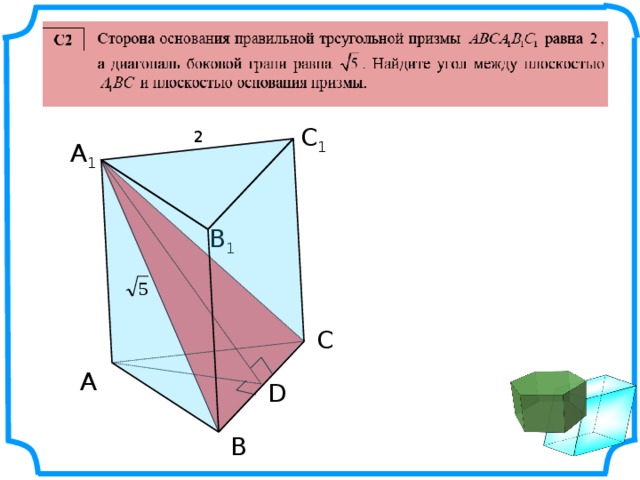
С 1

2

А 1

В 1

С

А

D

В

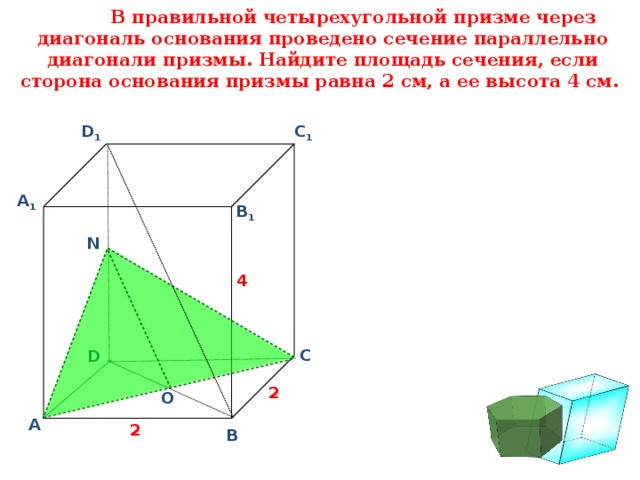
В правильной четырехугольной призме через диагональ основания проведено сечение параллельно диагонали призмы. Найдите площадь сечения, если сторона основания призмы равна 2 см, а ее высота 4 см.

D 1

С 1

А 1

В 1

N

4

С

D

2

O

А

2

В

Ответы к задачам.

• 1) 96 см 2 .
• 2) 300см 2 .
• 3) (450 +50 ) см 2 .

• 4) 408 см 2 .
• 5) 1464 см 2 .
• 6) 168 см 2 .