Муниципальное общеобразовательное учреждение Ветлужскаяшкола №2
Лист Мёбиуса
Выполнил
ученик 8 «а» класса
Ягилев Иван
Руководитель
учитель математики
Максимова Татьяна Анатольевна
Ветлуга 2017
Оглавление
Введение ……………………………………………………………… 3
Историческая справка ………………………………………………... 6
Глава I. Лист Мёбиуса ……………………………………………….. 9
Что такое лист Мёбиуса ………………………………………….. 9
Свойства листа Мёбиуса ……………………………………......... 9
Практическое применение ………………………………………. 11
Глава II. Практическая часть ……………………………………….. 23
Изготовление листа Мёбиуса …………………………………... 23
Опыты с листом Мёбиуса ……………………………………….. 24
Экспериментальные выводы …………………………………….. .28
Заключение …………………………………………………………… 29
Литература…………………………………………………………….. 30
Сайты сети Интернет …………………………………………………. 30
Введение
В наше время актуально изучение различных свойств предметов и их нестандартных применений. Я рассмотрела применение листа Мебиуса в науке и технике. Уже сейчас лента Мебиуса находит различное применение в быту: абразивные ремни для заточки инструментов, красящие ремни для печатающих устройств, ременные передачи, магнитофонные ленты и т.д.
Кроме того, существует гипотеза, что наша Вселенная вполне вероятно замкнута в ту же самую ленту согласно теории относительности – чем больше масса, тем больше кривизна пространства.
Есть гипотеза, что спираль ДНК сама по себе тоже является фрагментом ленты Мебиуса, и только поэтому генетический код так сложен для расшифровки и восприятия.
В ходе исследования я узнала, что основателем топологии считают ученого Августа Фердинанда Мёбиуса.
ходе исследования я узнала, что основателем топологии считают ученого Августа Фердинанда Мёбиуса.
Сама топология, можно сказать, началась именно с листа Мёбиуса. Меня заинтересовала эта тема. И я решил узнать больше о науке топологии, а именно о листе Мёбиуса.
Актуальность работы заключается в применении математических знаний в практической деятельности человека, связи математики с другими сферами человеческого познания.
Гипотеза – лист Мёбиуса обладает свойствами, которые применяют не только в геометрии, физике, технике, но даже в повседневной жизни.
Объект исследования - лист Мёбиуса.
Методы исследования – анализ, сравнительная характеристика, аналогия, обобщение, эксперимент.
Результат исследования - применение полученных знаний на практике.
Цель - исследовать лист Мебиуса как один из объектов топологии.
Для достижения поставленной цели необходимо выполнить следующие задачи:
познакомиться с историей ленты Мебиуса;
изготовить ленту Мебиус;
изучить и исследовать свойства ленты Мебиуса;
установить области применения листа Мебиуса.
Основные этапы исследования:
постановка проблемы;
изучение литературы с целью получения информации о листе Мёбиуса;
сбор собственного материала;
проведение экспериментов;
оформление результатов исследования в альбом;
создание мультимедийной презентации.
Целевая аудитория. Я думаю, что моя работа будет интересна любознательным ученикам 7-11 классов. Учителя математики могут использовать материал как на уроках, так и во внеурочной деятельности.
Историческая справка
За последнее столетие большое влияние на ряд совершенно различных областей знания приобрела новая ветвь геометрии – топология. Топология занимается изучением свойств фигур (или пространств), которые сохраняются при непрерывных деформациях, таких, например, как растяжение, сжатие или изгибание.
Наука эта молодая и потому озорная. Иначе не скажешь о тех правилах игры, которые в ней приняты. Любую фигуру тополог имеет право сгибать, скручивать, сжимать и растягивать – делать с ней всё что угодно, только не разрывать и не склеивать. И при этом он будет считать, что ничего не произошло, все её свойства остались неизменными. С точки зрения тополога баранка и кружка - это одно и то же. Сжимая и растягивая кусок резины, можно перейти от одного из этих тел ко второму.

Рис.1
А вот баранка и шар - разные объекты: чтобы сделать отверстие, надо разорвать резину. Для тополога не имеют никакого значения ни расстояния, ни углы, ни площади. А что же его интересует? Самые общие свойства фигур, которые не изменяются ни при каких преобразованиях. Поэтому иногда топологию называют «геометрией непрерывности». Топология имеет не метрический, а качественный характер.
Первые важные наблюдения и точные топологические соотношения были найдены ещё Эйлером, Гауссом и Риманом, однако термин «топология» впервые появился в 1847 году в работе Листинга. Тем не менее, без преувеличения можно сказать, что топология как раздел науки основана в конце XIX века А. Пуанкаре. А её головокружительный взлёт стал одним из самых неожиданных явлений в развитии математики ХХ века.
На весь мир известна история про гениального математика Григория Перельмана, доказавшего теорему Пуанкаре, который отказался от Нобелевской премии в миллион долларов. Учёный объяснил, почему же он не взял заслуженную премию: «Я знаю, как управлять Вселенной. И скажите – зачем же мне бежать за миллионом
Более ста лет светлые умы бились над доказательством гипотезы Пуанкаре.
Суть её такова: любой трёхмерный объект, например, стакан можно преобразовать в шар путём одной только деформации, то есть его не нужно будет ни разрезать, ни склеивать. Иными словами, Пуанкаре предположил, что пространство не трёхмерно, а содержит значительно большее число измерений, если трехмерная поверхность в чем-то похожа на сферу, то ее можно расправить в сферу. Утверждение Пуанкаре называют «Формулой Вселенной» из-за его важности в изучении сложных физических процессов в теории мироздания и из-за того, что оно дает ответ на вопрос о форме Вселенной. Перельман математически это доказал.

Сама топология, можно сказать, началась именно с листа Мёбиуса. Август Фердинанд Мёбиус (1790-1868) - ученик знаменитого математика Гаусса. Как и многие другие математики, Мебиус начинал свою карьеру астрономом, затем только в возрасте 68 лет он сделал открытие в области геометрии - односторонние поверхности, одна из которых – лист Мёбиуса. Свое открытие Мёбиус разделил с другим учеником Гаусса – Листингом (1808-1882), который опубликовал свою работу на три года раньше, чем Мёбиус – в 1862 году. И
Рис. 2
стория открытия ленты Мёбиуса очень интересна. Все началось с того, что однажды служанка сшила неправильно концы ленты. Разглядывая ленту, профессор обнаружил, чтоу ленточки нет изнанки, получилась односторонняя кольцевая поверхность.
Глава I. Лист Мёбиуса
Что такое лист Мёбиуса?
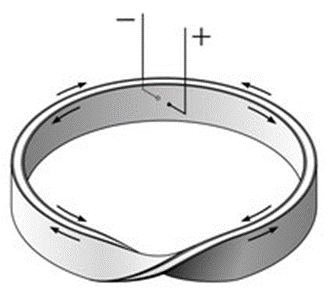
Лента Мёбиуса - топологический объект, простейшая неориентируемая поверхность с краем, односторонняя при вложении в обычное трехмерное евклидово пространство. Это - научное определение данной геометрической фигуры.
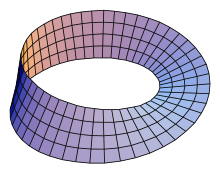 А если говорить проще, то лист Мёбиуса – это лента, которую скрепили, перекрутив на 180. Получив одностороннюю поверхность, без «изнанки».
А если говорить проще, то лист Мёбиуса – это лента, которую скрепили, перекрутив на 180. Получив одностороннюю поверхность, без «изнанки».
Лента, из которой делается лист, имеет две стороны, а сам лист Мёбиуса имеет одну сторону.
Рис.3
2. Свойства листа Мёбиуса
Давайте рассмотрим свойства ленты. Основными свойствами ленты Мебиуса являются:
односторонность,
непрерывность,
связность,
“Хроматический номер”
ориентированность
Рассмотрим эти свойства подробнее.
Односторонность
В своей работе «Об объёме многогранников» Август Мёбиус описал геометрическую поверхность-лист Мёбиуса, обладающую совершенно невероятным свойством: она имеет только одну сторону!
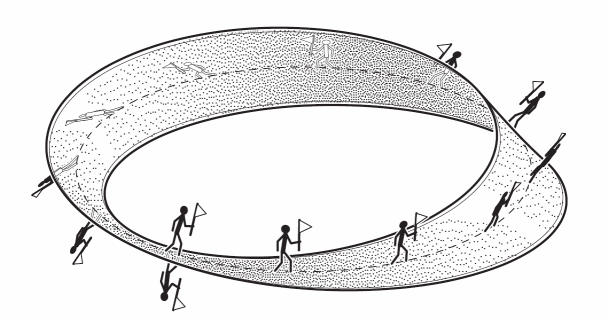
Представьте себе, что по наружной поверхности обычного кольца путешествует муравей. Если муравей не пересекает рёбра, а идёт вдоль листа, он вернётся в исходную точку, обойдя наружную поверхность. На ленте Мёбиуса путешествие муравья будет длиться вдвое дольше: муравей, не пересекая рёбер, обойдёт обе поверхности – наружную и внутреннюю.
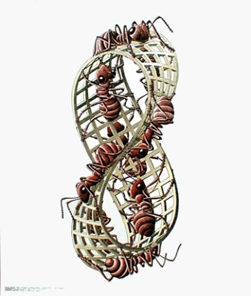 Рис.8
Рис.8
| И хотя лист Мёбиуса имеет одну сторону, в каждом поперечном сечении эта поверхность имеет "внешнюю" и "внутреннюю" стороны, которые по ходу движения вдоль ленты переходят друг в друга.
|  Рис.9 Рис.9
|
Непрерывность
На листе Мёбиуса любая точка может быть соединена с любой другой точкой и при этом не придётся переходить через край ленты. Разрывов нет –
полная непрерывность.
Связность
Если квадрат разрезать от стороны к стороне, то он, естественно, распадётся на два отдельных куска. Чтобы разделить кольцо на две части, нужно уже два разреза. Таким образом, квадрат– односвязен, а кольцо – двусвязно. Если разрезать лист Мёбиуса вдоль, то он превратится не в два не связанных с собою кольца, а в одну целую ленту. Таким образом, лист Мёбиуса двусвязен.
«Хроматический номер»
Хроматический номер - это максимальное число областей, которые можно нарисовать на поверхности так, чтобы каждая из них имела общую границу со всеми другими. Хроматический номер листа Мёбиуса равен шести.
Свойства, отсутствующие у ленты Мёбиуса.
Ориентированность
 Так, если бы человек смог путешествовать по всем изгибам листа Мёбиуса, то когда он вернулся бы в исходную точку, он превратился в своё зеркальное отражение.
Так, если бы человек смог путешествовать по всем изгибам листа Мёбиуса, то когда он вернулся бы в исходную точку, он превратился в своё зеркальное отражение.
Рис.10
3. Практическое применение
Лист Мёбиуса и его свойства применяют в различных областях.
Техника. Лист Мебиуса и сейчас продолжает будоражить умы изобретателей. Во многих странах мира запатентованы на его основе удивительные механизмы. Я приведу лишь некоторые примеры.
К инолента
инолента
В
Рис.11
1923 году выдан патент изобретателю Ли де Форсу, который предложил записывать звук на киноленте без смены катушек, сразу с двух сторон.
Кассеты
П ридуманы кассеты для магнитофона, где лента перекручивается и склеивается в кольцо, при этом появляется возможность записывать или считывать информацию сразу с двух сторон, что увеличивает ёмкость кассеты и соответственно время звучания.
ридуманы кассеты для магнитофона, где лента перекручивается и склеивается в кольцо, при этом появляется возможность записывать или считывать информацию сразу с двух сторон, что увеличивает ёмкость кассеты и соответственно время звучания.
Рис.12
Шлифовальная лента
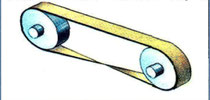 В 1969 году советский изобретатель Губайдуллин предложил бесконечную шлифовальную ленту в виде листа Мёбиуса.
В 1969 году советский изобретатель Губайдуллин предложил бесконечную шлифовальную ленту в виде листа Мёбиуса.
Рис.13.
Матричный принтер
В о многих матричных принтерах красящая лента также имеет вид листа Мёбиуса для увеличения её ресурса.
о многих матричных принтерах красящая лента также имеет вид листа Мёбиуса для увеличения её ресурса.
Рис.14
А втомобиль Toyota MOB
втомобиль Toyota MOB Б
Рис.15
оллид Мёбиуса выполнен испанским дизайнером Хорхе Марти Видала и сочетает в себе красоту и загадку ленты Мёбиуса. Уникальная форма кузова обеспечивает гоночной машине хорошую аэродинамику.
 Резистор Мёбиуса
Резистор Мёбиуса
Э
Рис.16
то недавно изобретённый электронный элемент, который не имеет собственной индуктивности. Благодаря этому, срок службы техники увеличивается в разы.
В виде парадоксальной геометрической фигуры можно, оказывается, изготовить лопасти бетономешалки или обычного бытового миксера — энергозатраты снизятся на одну пятую, а качество бетона (или кондитерского крема) улучшится.

Рис.17

Несколько лет назад ленте Мёбиуса нашли ещё одно применение - она стала играть роль пружины, вот только пружины особенной. Как известно взведённая пружина срабатывает в противоположном направлении. Лента Мёбиуса же, поправ все законы, направления срабатывания не меняет. Такая пружина могла бы стать бесценной в заводных игрушках –своего рода вечный двигатель.
Архитектура
П роект здания библиотеки в Казахстане.
роект здания библиотеки в Казахстане.
В
Рис.18
настоящее время рассматривается проект постройки библиотеки в виде листа Мёбиуса в Казахстане.
Изгибы здания образуют лист Мёбиуса, таким образом внутреннее пространство переходит во внешнее и обратно; подобным образом стены переходят в крышу, а крыша трансформируется обратно в стены. Естественный свет проникает во внутренние коридоры сквозь геометрические отверстия во внешней оболочке, создавая прекрасно освещённые пространства, идеальные для чтения.
Идея для аттракционов (американские горки).
А ттракцион “Американские горки” напоминает форму листа Мебиуса. В Москве находятся самые большие в мире американские горки инвертированного типа, где человек сидит в подвешенном кресле, а его ноги находятся в воздухе. Скорость - 81 км/ч, высота 30 м. Высота, по сравнению с зарубежными аналогами, невелика, но это с лихвой окупается обилием спиралей, колец и мёртвых петель.
ттракцион “Американские горки” напоминает форму листа Мебиуса. В Москве находятся самые большие в мире американские горки инвертированного типа, где человек сидит в подвешенном кресле, а его ноги находятся в воздухе. Скорость - 81 км/ч, высота 30 м. Высота, по сравнению с зарубежными аналогами, невелика, но это с лихвой окупается обилием спиралей, колец и мёртвых петель.
Рис.19
Живопись
Л
Рис. 20
ист Мёбиуса служил вдохновением для скульптур и для графического искусства. Известный голландский художник М. Эшер (1898-1971) особенно любил его и посвятил несколько своих литографий этому математическому объекту. Одна из известных — лист Мёбиуса, показывает муравьёв, ползающих по поверхности ленты Мёбиуса.

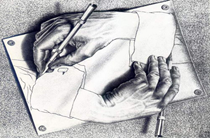
Рис. 21
Рис. 22
Граффити
С
Рис. 23
овременная лента Мёбиуса нарисована на одной из стен в Праге, Чехия.
По ленте двигаются два типа машин: танки и строительно-дорожная техника. Символ современной цивилизации: разрушаем-строим-разрушаем-строим.

Скульптура
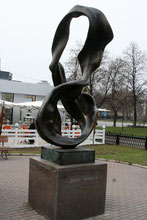
В Москве, на Комсомольском проспекте около кинотеатра “Горизонт” находится памятник “Ленте Мёбиуса”. Памятник был установлен в 1997 году. Авторы памятника: скульптор А.З.Налич, архитектор О.Н.Иванченко и строитель Г.Л.Федорков
Рис. 24
В Екатеринбурге на улице Свердлова установлен памятник листу Мёбиуса в 2008 году. Скульптор Адуашвили
Екатеринбурге на улице Свердлова установлен памятник листу Мёбиуса в 2008 году. Скульптор Адуашвили
Рис. 25
Логотипы и символы
Логотип компании Woolmark
Л оготип был создан в 1964 году в результате дизайнерского конкурса. Член жюри Franco Grignani не устоял и предложил свой вариант, спрятавшись под псевдонимом Francesco Seraglio. Данный логотип напоминает лист
оготип был создан в 1964 году в результате дизайнерского конкурса. Член жюри Franco Grignani не устоял и предложил свой вариант, спрятавшись под псевдонимом Francesco Seraglio. Данный логотип напоминает лист
Мебиуса и является символом вечности и
г
Рис. 26
ибкости компании.
Символ переработки
М еждународный символ переработки представляет собой Лист Мёбиуса. Перерабо́тка (другие термины: вторичная переработка, рециклинг отходов, рециклирование и утилизация отходов) — повторное использование или возвращение в оборот отходов производства или мусора.
еждународный символ переработки представляет собой Лист Мёбиуса. Перерабо́тка (другие термины: вторичная переработка, рециклинг отходов, рециклирование и утилизация отходов) — повторное использование или возвращение в оборот отходов производства или мусора.
Н
Рис. 27
аиболее распространена вторичная, третичная и т. д. переработка в том или ином масштабе таких материалов, как стекло, бумага, алюминий, асфальт, железо, ткани и различные виды пластика. Также с глубокой древности используются в сельском хозяйстве органические сельскохозяйственные и бытовые отходы.
Символ математики

Лист Мёбиуса считают символом современной математики, так как именно он дал толчок новым математическим исследованиям.
Рис. 28
Одежда и обувь
Туфли
С
Рис. 29
озданная в 2003 году архитектором Рэм Ди Колхаазом и обувщиком Галахадом Кларком компания United Nude специализируется на выпуске инновационной дизайнерской обуви. Одной из наиболее удачных разработок компании являются туфли Mobius, названные так в честь геометра Августа Мебиуса и его идеи односторонней поверхности. Идея туфель такова: кожаный верх туфель и подошва представляют собой единую ленту, закрученную определенным образом.
Шарф Мёбиуса

Инетресная вещь - шарф Мёбиуса, появившаяся в гардеробах 21 века. Шарф Мёбиуса можно сделать самому, связав концы шарфа и перекрутив на один оборот.
Рис. 30
Мебель
Книжная полка Infinity
Д
Рис. 31
изайнер Джоб Келевий сломал форму, когда разрабатывал свой книжный шкаф Инфинити. Используя математическую концепцию Лемниската, и что-то похожее на ленту Мебиуса, в полке Инфинити дизайнер воплотил физическое представление о бесконечности. Это значит, что если вы прочитали все книги с этой полки, считайте, что вы постигли всю бесконечность литературы.

Стол Мёбиуса
Стол с одной поверхностью, за которым можно стоять, сидеть и на котором можно удобно лежать.
Рис. 32
Диван Мёбиуса
Р
Рис. 33
одившееся под девизом "Двойное кресло - двойное удовольствие", кресло-диван Moebius Double Armchair создано дизайнером Gaеtan Van de Wyer из Бельгии и несет в себе свежее видение мебели для влюбленных.
Парфюм
| 
Рис. 34
| 
Рис. 35
| 
Рис. 36
|
| Духи Bugatti
Компания Bugatti начала выпуск не только сверхдорогих автомобилей, но и духов. Каждый флакончик, сделанный из хрусталя и покрытый настоящим золотом выполнен в виде необычного листа Мёбиуса, который имеет лишь одну сторону. Цена духов Bugatti составляет 3500 евро. | Духи Loewe Quzas, Quizas, Quizas Осенью 2011 года вышла багровая версия аромата, флакон которой обернут лентой Мебиуса – символом круговорота страстей в природе. | Духи UFO Limited Edition, Kenzo Презентация аромата Kenzo состоялась в 2009 году на ретроспективной выставке работ Рона Арада (Ron Arad) в парижском Центре Помпиду. Именно этот художник и архитектор придумал космический дизайн флакона в виде ленты Мебиуса. Он разработан так, чтобы точь-в-точь поместиться в ладонь. «Неопознанный ароматический объект» существует в количестве всего 180 экземпляров и стоит $188. |
Украшения
Необычный вид листа Мёбиуса приглянулся и ювелирам. Часто украшения напоминают математический объект.


Рис. 37
Рис. 38
Спорт
 Ручной эспандер "Робур"
Ручной эспандер "Робур"
О
Рис. 39
дна из любимых вещей всех школьных учителей физкультуры, которая по их собственному выражению «тренирует не только мышцы кисти, но и мышцу мозга". Кистевой эспандер от студии Артемия Лебедева повторяет форму ленты Мёбиуса. Отличное средство для снятия стресса, размышлений о бесконечности и просто полезный способ занять руки.
Природа и жизнь
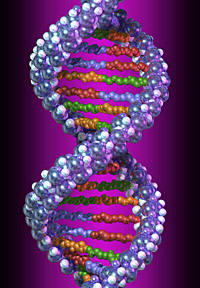 Есть гипотеза, что спираль ДНК сама по себе тоже является фрагментом ленты Мебиуса и только поэтому генетический код так сложен для расшифровки и восприятия. Больше того - такая структура вполне логично объясняет причину наступления биологической смерти - спираль замыкается сама на себя и происходит самоуничтожение.
Есть гипотеза, что спираль ДНК сама по себе тоже является фрагментом ленты Мебиуса и только поэтому генетический код так сложен для расшифровки и восприятия. Больше того - такая структура вполне логично объясняет причину наступления биологической смерти - спираль замыкается сама на себя и происходит самоуничтожение.
И
Рис. 40
менем Мёбиуса назван кратер на обратной стороне Луны.
Литература
Иногда научно – фантастические рассказы предполагают, что наша вселенная может быть некоторым обобщенным листом Мёбиуса. В рассказе автора А.Дж. Дейча, бостонское метро строит новую линию, маршрут которой становится настолько запутанным, что превращается в ленту Мёбиуса, после чего на этой линии начинают исчезать поезда, появляясь снова только через несколько месяцев.
Ленте Мёбиуса посвящают стихи:
Наталия Юрьевна Иванова
Лист Мёбиуса - символ математики,
Что служит высшей мудрости венцом…
Он полон неосознанной романтики:
В нем бесконечность свернута кольцом.
В нем – простота, и вместе с нею – сложность,
Что недоступна даже мудрецам:
Здесь на глазах преобразилась плоскость
В поверхность без начала и конца.
Здесь нет пределов, нет ограничений,
Стремись вперед и открывай миры,
Почувствуй силу новых ощущений,
Прими познанья высшего дары:
Познай любовь и ненависть изведай,
Низвергнись в ад – тотчас увидишь рай.
Ты в одночасье насладись победой,
И горечь пораженья испытай.
На грани бесконечного блаженства,
Испытывая суеверный страх,
Найдешь свой путь. Достигнув совершенства,
Окажешься в таинственных мирах.
И, вдохновленный этим дерзновеньем,
По экспоненте поднимаясь в высь,
Ты ощутишь восторг освобожденья,
Почувствуешь, как возникает Мысль.
Покажется, что распростерлась Вечность,
Что взломан Мироздания пароль.
И вдруг твое стремленье в бесконечность
Тебя вернет к исходной точке: в ноль.
Как о порог, об этот ноль споткнешься.
Но как бы ни был прежний путь тернист,
Вновь выбирай (и ты не ошибешься!)
Путь в бесконечность – Мёбиуса лист!
Фокусы
Более 100 лет лист Мёбиуса используется для показа различных фокусов и развлечений. Удивительные свойства листа демонстрировались даже в цирке, где подвешивались яркие ленты, склеенные в виде листов Мёбиуса. Фокусник дотрагивался зажигалкой до средней линии каждой ленты, которая была выполнена из специального покрытия. Огненная дорожка превращала первую ленту в более длинную, а вторую - в две ленты, продетая одна в другую.
Простой фокус можно сделать самому - завязать на шарфе узел, не выпуская из рук его концов.Это можно сделать так. Положите шарф на стол. Скрестите руки на груди. Продолжая держать их в таком положении, нагнитесь к столу и возьмите поочередно по одному концу шарфа каждой рукой. После того как руки будут разведены, в середине шарфа сам собой получится узел. Пользуясь топологической терминологией, можно сказать, что руки зрителя, его корпус и шарф образуют замкнутую кривую в виде “трехлистного” узла. При разведении рук узел только перемещается с рук на платок.
Глава II. Практическая часть.
1. Изготовление Листа Мёбиуса
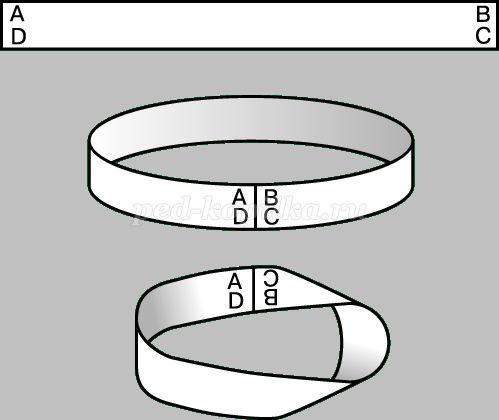
Рис. 41
Лист не относится к числу простых геометрических фигур. Чтобы сделать такую ленту достаточно рассмотреть рисунок. На нем изображен бумажный лист, с вершинами ABCD. Накладываем вершины так, чтобы точка Aсовпала с точкой B, а точка D совпала с точкой C. Перед склеиванием необходимо перекрутить ленту один раз (на 180). Получилось бумажное кольцо, под названием «Лист Мёбиуса». Он получается из прямоугольника, у которого длина намного больше ширины (например, в 10 раз – 30 × 3 см).
Для проведения опытов я изготовила бумажные полосы длиной 30 см и шириной 3 см. Чтобы понять, в чём особенность листа Мёбиуса, я проводила опыты с обычным бумажным кольцом и с перекрученным (листом Мёбиуса).
2. Опыты
| Кольцо | Лист Мёбиуса |
| Опыт № 1 |
| Поставим точку на одной стороне каждого кольца и начертим непрерывную линию вдоль него, пока не придём снова в отмеченную точку. |
| Р езультат: Внешняя сторона полностью обведена, а внутренняя - нет. езультат: Внешняя сторона полностью обведена, а внутренняя - нет.
Рис. 41
| Результат: Непрерывная линия прошла по всем сторонам, вернувшись на исходную точку. 
Рис. 42
|
|
| Вывод: Лист Мёбиуса обладает только одной стороной. Односторонность. |
| Опыт № 2 |
| Поставить двух человек, идущих навстречу друг другу, на разных сторонах кольца и заставить их встретиться, не пересекая границ. |
| Р езультат: Бедные люди будут ходить по одной стороне и никогда не пересекутся. езультат: Бедные люди будут ходить по одной стороне и никогда не пересекутся.
Рис. 43
|  Р Р
Рис. 44 езультат: Люди в скором времени придут навстречу друг другу, то есть встретятся.
|
|
| Вывод: Непрерывность. На листе Мёбиуса любая точка может быть соединена с любой другой точкой, не пересекая краев ленты (не прерываясь). |
| Опыт № 3 |
| Закрасить непрерывной линией только один край колец. |
| Результат: Один край закрашен, другой край нет. 
Рис. 45
| Р Рис. 46 езультат: Линия края получилась, непрерывно закрашена. 
|
|
| Вывод: Лист Мёбиуса имеет не только одну сторону, но и один край. |
| Опыт № 4 |
| Разрезание листа и кольца вдоль пополам, параллельно краям. |
| Результат: Получилось два одинаковых кольца, которые уже, чем исходное. Диаметр двух колец получился таким же, как диаметр первого кольца. 
Рис. 47
| Результат: Получилось одно скрученное кольцо в виде восьмерки. 
Рис. 48
|
|
| Вывод: Лист Мёбиуса двусвязен, если разрезать его вдоль, будет не два отдельных кольца, а одна целая лента. |
| Исследуем полученные поверхности: На полученных кольцах поставим точку на одной стороне каждого кольца и начертим непрерывную линию вдоль него, пока не придём снова в отмеченную точку.
|
| Результат: Непрерывная линия будет проходить по одной стороне кольца. 
Рис. 49
| Результат: Непрерывная линия будет проходить только по одной стороне кольца. Л ента Мёбиуса не получилась. ента Мёбиуса не получилась. Рис. 50
|
|
| Вывод: При таком разрезании, лента утрачивает свойства листа Мёбиуса. А именно непрерывность. |
| Опыт №5 |
| Разрезание фигур вдоль, отступив от края 1/3 ширины кольца. |
| Результат: Получилось два кольца. Одно уже, другое шире, но кольца имеют одинаковые диаметры. 
Рис. 51
| Р Рис. 52 езультат: Получилось два связанных друг с другом кольца, разной ширины. Одно скрученное, в виде восьмерки, а другое в виде обычного листа Мёбиуса.
|
| Исследуем полученные поверхности: На полученных кольцах поставим точку на одной стороне каждого кольца и начертим непрерывную линию вдоль него, пока не придём снова в отмеченную точку. |
| Результат: Непрерывная линия будет проходить только по одной стороне кольца.

Рис. 53
| Результат: Непрерывная линия проходит только по одной стороне большого кольца. Это - не лист Мёбиуса. По всей поверхности маленького кольца будет проходить непрерывная линия. Это-лист Мёбиуса. 
Рис. 54
|
| Опыт №6 |
| Проведем многократные перекручивания и разрезания. |
| Результат: Получится множество колец. | Результат: получится несколько перекрученных соединенных между собой колец. |
| Исследуем полученные поверхности: На полученных кольцах поставим точку на одной стороне каждого кольца и начертим непрерывную линию вдоль него, пока не придём снова в отмеченную точку. |
|
| Результат: Полученные поверхности не обладают свойствами листа Мебиуса. 
Рис. 55
|
3. Экспериментальные выводы
Свойства листа, полученные мной, в результате экспериментов подтверждают свойства, описанные в математической литературе:
Лист Мёбиуса имеет одну сторону (поверхность). Это подтверждают результаты опытов № 1, 2, 4.
Лист Мёбиуса имеет один край. Результат опыта № 3.
Лист Мёбиуса можно получить из прямоугольника, где длина значительно больше ширины, т. е. из полосы, ленты.
Если пустить по поверхности листа Мёбиуса движущиеся объекты, они будут двигаться бесконечно долго, т.е. поверхность непрерывна. Это подтверждают опыты № 2, 4.
Листу Мёбиуса присуще свойство – связность.
Лист Мёбиуса, как и любая топологическая фигура, не меняет своих свойств, пока её не разрезают, не разрывают, или не склеивают его отдельные куски.
Один край и одна сторона листа Мёбиуса не связаны с его положением в пространстве, с понятиями расстояния.
Заключение
Выполняя работу по изучению удивительного листа Мёбиуса, я узнала о жизни самого учёного, об истории уникального открытия. Не зря говорят: «Всё гениальное рядом». Открытие положило начало новому направлению в математике. Мною была изучена большая разнообразная информация. Она анализировалась и перерабатывалась.
Опыты с листом Мёбиуса увлекли не только меня, но и моих знакомых. Результаты были очевидны, поскольку эксперименты проводились с обычным кольцом и листом Мёбиуса. Так я узнала об удивительных свойствах листа Мёбиуса. Для меня это были маленькие открытия.
Таким образом, все поставленные задачи были выполнены.
Используя источники сети Интернет, я узнала, что лист Мёбиуса и его свойства применяют во всех сферах жизни человека.
Применение проекта и практическая значимость.
Я сумела получить интересный математический материал. В ходе работы я создала мультимедийную презентацию, в которую включены иллюстративные материалы о листе Мёбиуса.
Своими результатами исследования о листе Мебиуса я поделилась со своими одноклассниками. Думаю, что это их заинтересовало. Вообще я считаю, что моя работа будет интересна любителям математики для расширения математического кругозора. Ее можно использовать учителям математики, как на уроках, так и во внеклассной и кружковой работе.
Познакомившись с топологией, я узнала, что в настоящее время эта наука переживает период бурного развития, что она изучает объекты не только на плоскости, но и в 3D (бутылка Клейна).Возможно, меня ждут новые исследования, новые открытия.
Список литературы
Савин А. П. «Я познаю мир. Математика» «Издательство АСТ», 2001.
Депман И.Я. «За страницами учебника математики». Москва, изд. «Просвещение», 1989. 3. Энциклопедический словарь юного математика/Сост. А. П. Савин. -М.: Педагогика, 1985. 5. Банурин И.В. Геометрическое моделирование окружающего мира. – Москва: Терра, 2009 6. Майер В.А. Всё о кривых. – СПб.; Знание, 1999 7. Дорохов А.М. Геометрия в моём понимании. – М.20041.
8. М. Гарднер. Математические чудеса и тайны. – М: Наука, 1978.
9. Е.С. Смирнова. Курс наглядной геометрии. – М: Просвещение, 2002.
10. И.Ф. Шарыгин, Л.Н. Еранжиева. Наглядная геометрия. 5-6 класс. – М: Дрофа, 2000.
Сайты сети Интернет:
http://arbuz.uz/t_lenta.html
http://www.frei.ru/golos/books/
http://umiranie.chat.ru/sphere.htm
http://school-sector.relarn.ru/dckt/projects/ctrana/matric/t_lm1.htm
http://www.kvant.info/
http://www.websib.ru/noos/math/listmebiusa/
_ http://www.univer.omsk.su/omsk/Edu/Math/mmebius.htm
7







 ходе исследования я узнала, что основателем топологии считают ученого Августа Фердинанда Мёбиуса.
ходе исследования я узнала, что основателем топологии считают ученого Августа Фердинанда Мёбиуса.
 Сама топология, можно сказать, началась именно с листа Мёбиуса. Август Фердинанд Мёбиус (1790-1868) - ученик знаменитого математика Гаусса. Как и многие другие математики, Мебиус начинал свою карьеру астрономом, затем только в возрасте 68 лет он сделал открытие в области геометрии - односторонние поверхности, одна из которых – лист Мёбиуса. Свое открытие Мёбиус разделил с другим учеником Гаусса – Листингом (1808-1882), который опубликовал свою работу на три года раньше, чем Мёбиус – в 1862 году. И
Сама топология, можно сказать, началась именно с листа Мёбиуса. Август Фердинанд Мёбиус (1790-1868) - ученик знаменитого математика Гаусса. Как и многие другие математики, Мебиус начинал свою карьеру астрономом, затем только в возрасте 68 лет он сделал открытие в области геометрии - односторонние поверхности, одна из которых – лист Мёбиуса. Свое открытие Мёбиус разделил с другим учеником Гаусса – Листингом (1808-1882), который опубликовал свою работу на три года раньше, чем Мёбиус – в 1862 году. И  А если говорить проще, то лист Мёбиуса – это лента, которую скрепили, перекрутив на 180. Получив одностороннюю поверхность, без «изнанки».
А если говорить проще, то лист Мёбиуса – это лента, которую скрепили, перекрутив на 180. Получив одностороннюю поверхность, без «изнанки». Рис.8
Рис.8 Рис.9
Рис.9 Так, если бы человек смог путешествовать по всем изгибам листа Мёбиуса, то когда он вернулся бы в исходную точку, он превратился в своё зеркальное отражение.
Так, если бы человек смог путешествовать по всем изгибам листа Мёбиуса, то когда он вернулся бы в исходную точку, он превратился в своё зеркальное отражение. инолента
инолента ридуманы кассеты для магнитофона, где лента перекручивается и склеивается в кольцо, при этом появляется возможность записывать или считывать информацию сразу с двух сторон, что увеличивает ёмкость кассеты и соответственно время звучания.
ридуманы кассеты для магнитофона, где лента перекручивается и склеивается в кольцо, при этом появляется возможность записывать или считывать информацию сразу с двух сторон, что увеличивает ёмкость кассеты и соответственно время звучания. В 1969 году советский изобретатель Губайдуллин предложил бесконечную шлифовальную ленту в виде листа Мёбиуса.
В 1969 году советский изобретатель Губайдуллин предложил бесконечную шлифовальную ленту в виде листа Мёбиуса. о многих матричных принтерах красящая лента также имеет вид листа Мёбиуса для увеличения её ресурса.
о многих матричных принтерах красящая лента также имеет вид листа Мёбиуса для увеличения её ресурса.  втомобиль Toyota MOB
втомобиль Toyota MOB  Резистор Мёбиуса
Резистор Мёбиуса

 роект здания библиотеки в Казахстане.
роект здания библиотеки в Казахстане. ттракцион “Американские горки” напоминает форму листа Мебиуса. В Москве находятся самые большие в мире американские горки инвертированного типа, где человек сидит в подвешенном кресле, а его ноги находятся в воздухе. Скорость - 81 км/ч, высота 30 м. Высота, по сравнению с зарубежными аналогами, невелика, но это с лихвой окупается обилием спиралей, колец и мёртвых петель.
ттракцион “Американские горки” напоминает форму листа Мебиуса. В Москве находятся самые большие в мире американские горки инвертированного типа, где человек сидит в подвешенном кресле, а его ноги находятся в воздухе. Скорость - 81 км/ч, высота 30 м. Высота, по сравнению с зарубежными аналогами, невелика, но это с лихвой окупается обилием спиралей, колец и мёртвых петель.



 Екатеринбурге на улице Свердлова установлен памятник листу Мёбиуса в 2008 году. Скульптор Адуашвили
Екатеринбурге на улице Свердлова установлен памятник листу Мёбиуса в 2008 году. Скульптор Адуашвили оготип был создан в 1964 году в результате дизайнерского конкурса. Член жюри Franco Grignani не устоял и предложил свой вариант, спрятавшись под псевдонимом Francesco Seraglio. Данный логотип напоминает лист
оготип был создан в 1964 году в результате дизайнерского конкурса. Член жюри Franco Grignani не устоял и предложил свой вариант, спрятавшись под псевдонимом Francesco Seraglio. Данный логотип напоминает лист  еждународный символ переработки представляет собой Лист Мёбиуса. Перерабо́тка (другие термины: вторичная переработка, рециклинг отходов, рециклирование и утилизация отходов) — повторное использование или возвращение в оборот отходов производства или мусора.
еждународный символ переработки представляет собой Лист Мёбиуса. Перерабо́тка (другие термины: вторичная переработка, рециклинг отходов, рециклирование и утилизация отходов) — повторное использование или возвращение в оборот отходов производства или мусора. 






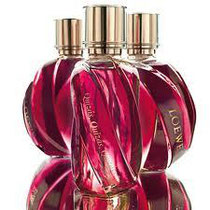



 Ручной эспандер "Робур"
Ручной эспандер "Робур" Есть гипотеза, что спираль ДНК сама по себе тоже является фрагментом ленты Мебиуса и только поэтому генетический код так сложен для расшифровки и восприятия. Больше того - такая структура вполне логично объясняет причину наступления биологической смерти - спираль замыкается сама на себя и происходит самоуничтожение.
Есть гипотеза, что спираль ДНК сама по себе тоже является фрагментом ленты Мебиуса и только поэтому генетический код так сложен для расшифровки и восприятия. Больше того - такая структура вполне логично объясняет причину наступления биологической смерти - спираль замыкается сама на себя и происходит самоуничтожение.
 езультат: Внешняя сторона полностью обведена, а внутренняя - нет.
езультат: Внешняя сторона полностью обведена, а внутренняя - нет.
 езультат: Бедные люди будут ходить по одной стороне и никогда не пересекутся.
езультат: Бедные люди будут ходить по одной стороне и никогда не пересекутся. Р
Р 




 ента Мёбиуса не получилась.
ента Мёбиуса не получилась.














