бюджетное учреждение профессионального образования
«Радужнинский политехнический колледж»
Использование графиков функций для решения задач
| Автор: | Адукова Хамис 26 группа, профессия «Делопроизводитель»
|
| Руководитель: | Озерова Руфина Кунакбаевна, Преподаватель математики и информатики
|
2018 год
Оглавление
| Введение | 3 |
| Глава1. Функции и их графики
| 5 |
История возникновения функции
| 6 |
|
|
|
|
Глава 2.Использование графиков функций для решения
| 8 |
| § 1. Решение уравнений | 8 |
| § 2. Решение систем уравнений | 9 |
| § 3. Решение неравенств с одной переменной | 11 |
| § 4. Решение неравенств с двумя переменными | 12 |
| Заключение | 14 |
| Список используемой литературы | 14 |
Введение
Изучение поведения функций и построение их графиков является важным разделом математики. Свободное владение техникой построения графиков часто помогает решать многие задачи и порой является единственным средством решения. Кроме того, умение строить графики функций представляет большой самостоятельный интерес.
Часто построение графиков связано с исследованием поведения функций. Однако необходимость построения графиков не ограничивается только этим. В ряде случаев графики облегчают нахождение решений уравнений и неравенств, сокращая и упрощая аналитические выкладки, и часто при этом являются единственным методом решения таких задач. Кроме того, графический метод нередко применяется и при решении многих прикладных задач.
Поэтому, объектом нашего исследования стали уравнения, неравенства, их системы и задачи, которые либо невозможно решить аналитическим способом, либо рационально решить графическим способом. Умение строить графики функций – одно из важнейших как в математике, так и в других науках. Навыки построений графиков функций необходимо приобретать в школе. В целом построение графиков основывается на знании графиков основных элементарных функций, и на основные методы построения графиков функций: параллельный перенос, отражение, деформация, комбинация переноса, отражения и деформации, функции, содержащие знак модуля, алгебраические операции над графиками функций, построение графиков сложных функций.
Исходя из этого, предметом нашего исследования стали функции и их графики.
Цель нашей работы – показать использование графиков при решении уравнений, неравенств, их систем, а также прикладных задач. Такое решение представляется целесообразным для оказания помощи выпускникам средних школ при их подготовке к вступительным экзаменам в вузы, студентам университетов и педагогических институтов при подготовке их к педагогической практике.
В работе представлено достаточное количество примеров, раскрывающих функционально-графический способ решения задач.
Тема нашей работы весьма актуальна, так как графический метод, опирающийся на знания функций, доступен для понимания школьников, хотя спектр применения методов, с помощью которых строятся графики функций, широк.
Глава 1. Функции и их графики
Переменная величина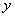 называется функцией переменной величины
называется функцией переменной величины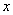 , если каждому значению
, если каждому значению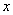 соответствует определенное значение
соответствует определенное значение 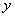 .
.
Множество всех тех значений, которые принимает аргумент 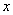 функции
функции 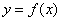 , называется областью определения этой функции.
, называется областью определения этой функции.
Множество всех тех значений, которые принимает сама функция 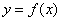 , называется областью значений (изменения) этой функции.
, называется областью значений (изменения) этой функции.
Функция 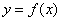 называется четной, если при всех значений
называется четной, если при всех значений 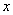 из области определения этой функции
из области определения этой функции 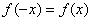 .
.
Функция 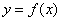 называется нечетной, если при всех значений
называется нечетной, если при всех значений 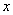 из области определения этой функции
из области определения этой функции 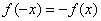 .
.
Область определения четной и нечетной функции симметрична относительно начала координат.
Функция 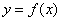 называется возрастающей (убывающей) на данном промежутке, если при произвольных двух различных значениях аргумента, из данного промежутка, большему значению аргумента соответствует большее (меньшее) значение функции.
называется возрастающей (убывающей) на данном промежутке, если при произвольных двух различных значениях аргумента, из данного промежутка, большему значению аргумента соответствует большее (меньшее) значение функции.
Функция 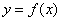 называется периодической, с периодом
называется периодической, с периодом 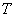 , где
, где 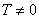 , если значение функции не изменяется при прибавлении числа
, если значение функции не изменяется при прибавлении числа 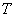 к любому допустимому значению аргумента:
к любому допустимому значению аргумента: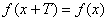 .
.
Функция 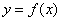 называется ограниченной, если можно указать такое положительное число
называется ограниченной, если можно указать такое положительное число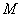 , что
, что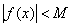 для всех значений
для всех значений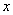 из области определения функции. Если же точка
из области определения функции. Если же точка 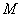 не существует, то функция называется неограниченной.
не существует, то функция называется неограниченной.
Графиком функции 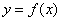 называется множество всех точек плоскости, координаты которых
называется множество всех точек плоскости, координаты которых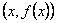 .
.
1.1 История возникновения функции
Понятие функции уходит своими корнями в ту далёкую эпоху, когда люди впервые поняли, что окружающие их явления взаимосвязаны. Они ещё не умели считать, но уже знали, что, чем больше оленей удастся убить на охоте, тем дольше племя будет избавлено от голода, чем сильнее натянута тетива лука, тем дальше полетит стрела, чем дольше горит костёр, тем теплее будет в пещере.
С развитием скотоводства и земледелия, ремесла и обмена увеличилось количество известных людям зависимостей между величинами.
Начиная с XVII в. одним из важнейших понятий является понятие функции. Оно сыграло и поныне большую роль в познании реального мира.
Идея функциональной зависимости восходит к древности, она содержится уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами, в первых формулах для нахождения площади и объема тех или иных фигур.
Однако явное и вполне сознательное применение понятия функции и систематическое изучение функциональной зависимости берут своё начало в XVIIв. в связи с проникновением в математику идеи переменных.
Чёткого представления понятия функции в XVII в. ещё не было, однако путь к первому такому определению проложил Декарт, который систематически рассматривал в своей «Геометрии» лишь те кривые, которые можно точно представить с помощью уравнений, притом преимущественно алгебраических. Постепенно понятие функции стало отождествляться таким образом с понятием аналитического выражения – формулы.
Слово «функция» (от латинского functio – совершение, выполнение) Лейбниц употреблял с 1673 г. в смысле роли (величина, выполняющая ту или иную функцию). Как термин в нашем смысле выражение «функция от x» стало употребляться Лейбницем и И. Бернулли.
Явное определение функции было впервые дано в 1718 г. одним из учеников и сотрудников Лейбница, выдающимся швейцарским математиком Бернулли: «Функцией переменной величины называют количество, образованное каким угодно способом из этой переменной величины и постоянных». Оно привело в восхищение престарелого Лейбница, увидевшего, что отход от геометрических образов знаменует новую эпоху в изучении функций. Многие из этих функций нельзя было явно выразить с помощью ранее известных операций. Поэтому один из самых замечательных математиков XVII в. Леонард Эйлер (1707 – 1783), вводя в своём учебнике понятие функции, говорит лишь, что «когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называются функциями вторых».
Леонард Эйлер во «Введении в анализ бесконечных» (1748) примыкает к определению своего учителя И. Бернулли несколько уточняя его. Определение Л. Эйлера гласит: « Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого количества и чисел или постоянных количеств». Так понимали функцию на протяжении почти всего XVII в. Даламбер, Лагранж и другие видные математики.
В формировании современного понимания функциональной зависимости приняли участие многие крупные математики. Описание функции, почти совпадающее с современным, встречается уже в учебниках математики начала XIX в. Активным сторонником такого понимания функции был Н.И. Лобачевский.
Определение функции:
Зависимость переменной y от переменной x называется функцией, если каждому значению x соответствует единственное значение у. Переменную x называют независимой переменной или аргументом, а переменную у – зависимой переменной. Значение у, соответствующее заданному значению x, называют значением функции.
Записывают: y =f(x) (читается: «Эф от икс»). Буквой f обозначается данная функция, т. е. функциональная зависимость между переменными x и y; f(x) есть значение функции, соответствующее значению аргумента х. Говорят также, что f(x) есть значение функции в точке х.
Все значения, которые принимает независимая переменная, образуют область определения функции.
Все значения, которые принимает функция f(x) (при x, принадлежащих области ее определения), образуют область значений функции.
Может возникнуть вопрос: почему мы обозначаем функцию символом f, и когда он появился. Этот символ изобрел в 1733 г. французский математик Клеро. А появился этот символ, когда формировался общий подход к понятию функции, когда потребовалось обозначение «функции вообще».
Глава 2. Использование графиков функций для решения задач
§1. Решение уравнений
Для того, чтобы найти решение уравнения с одним неизвестным графическим способом, нужно, перенеся все члены его в левую часть, представить это уравнение в виде f(x) = 0. После этого необходимо построить график функции y = f(x). Абсциссы точек пересечения или касания этого графика с осью x равны корням исходного уравнения. Если таких точек нет, то уравнение не имеет решений.
В ряде случаев при решении уравнений с одним неизвестным целесообразней воспользоваться другим методом. Для этого уравнение записывается в виде f1 (x) = f2 (x) и заменяется системой 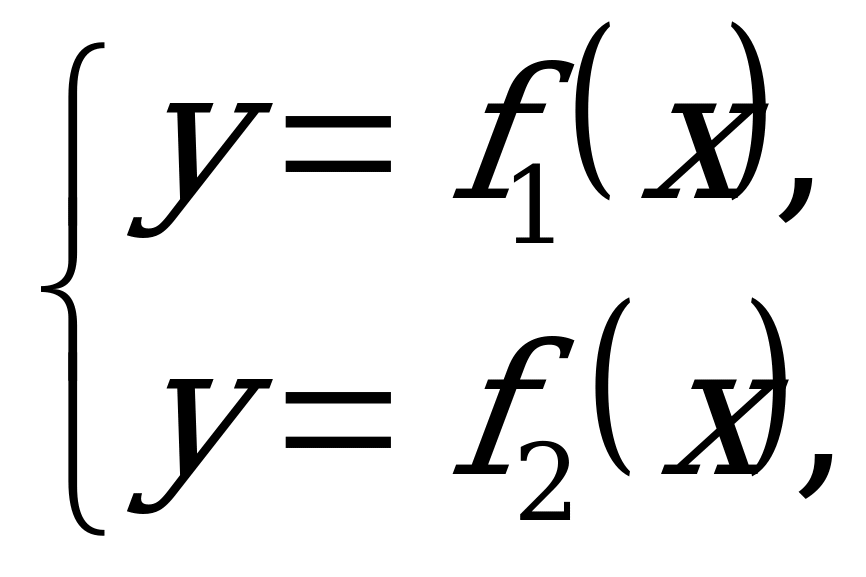 решаемой графически. Абсциссы точек пересечения или касания графиков f1(x) и f2(x) равны корням исходного уравнения.
решаемой графически. Абсциссы точек пересечения или касания графиков f1(x) и f2(x) равны корням исходного уравнения.
Пример 1. Решить уравнение 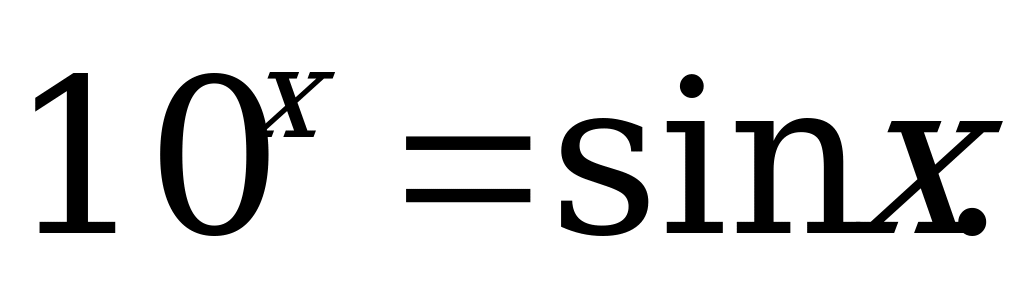 .
.
Решение. После построения графиков функций 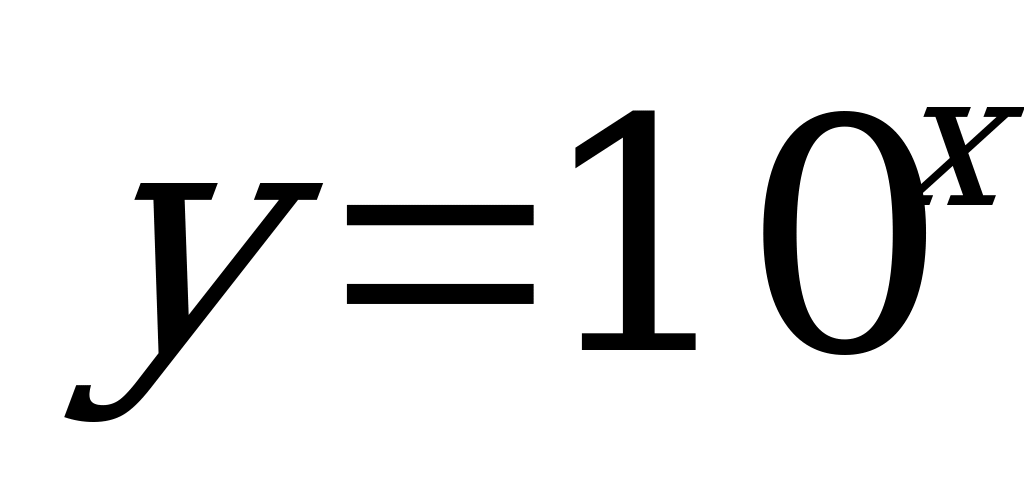 и
и 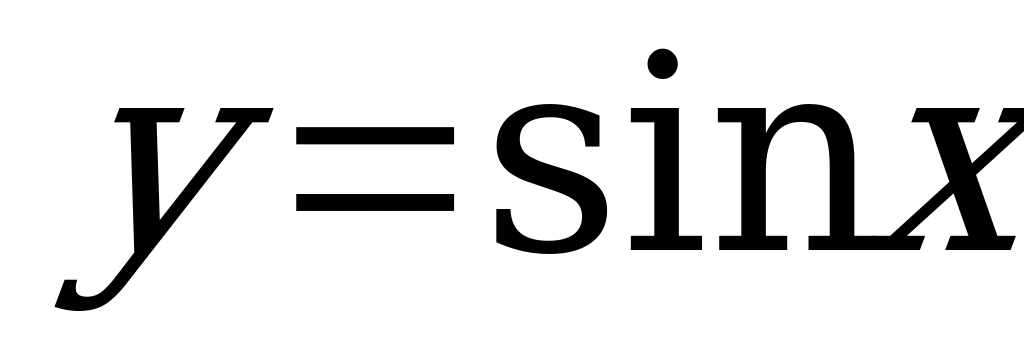 легко заметить, что уравнение имеет бесчисленное множество решений. Значения корней близки к
легко заметить, что уравнение имеет бесчисленное множество решений. Значения корней близки к 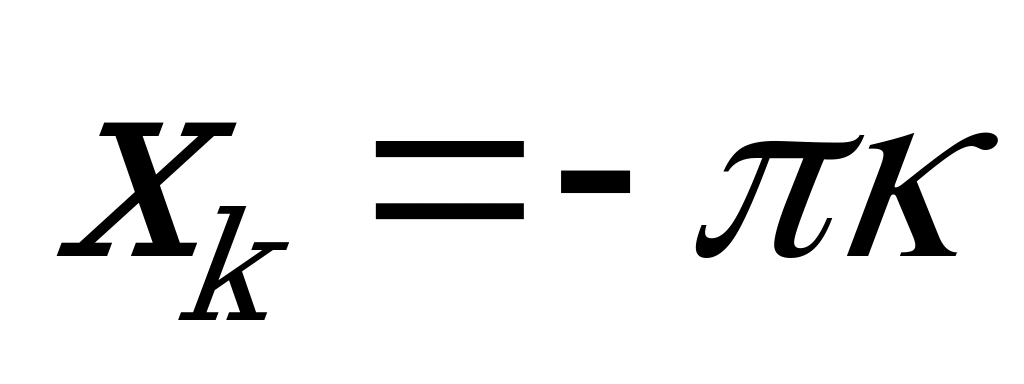 , где k = 1, 2, ... (рис. 1).
, где k = 1, 2, ... (рис. 1).
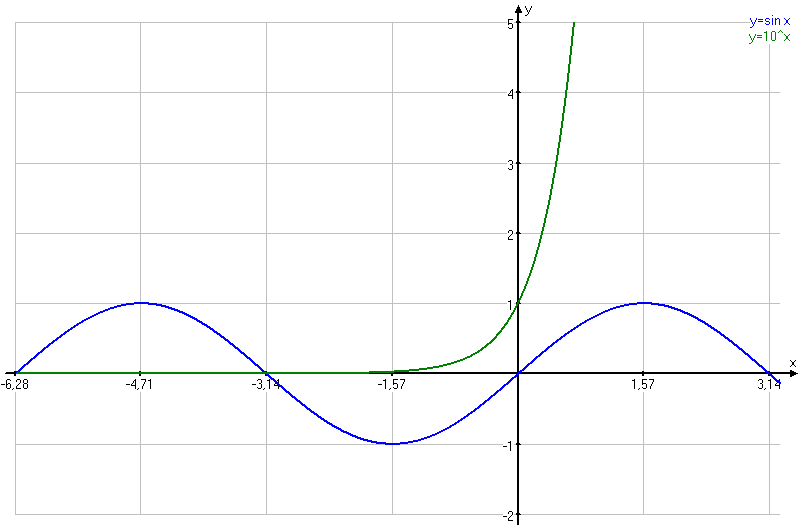
Рис. 1
Пример 2. Найти число корней уравнения sin x = lg x.
Решение. После построения графиков y=sinx и y=lg x становится очевидным, что это уравнение имеет три корня (рис. 2).
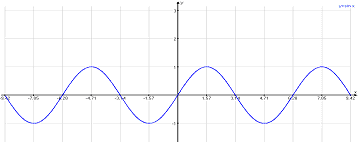
Рис. 2
§2. Решение систем уравнений
Каждое из уравнений системы 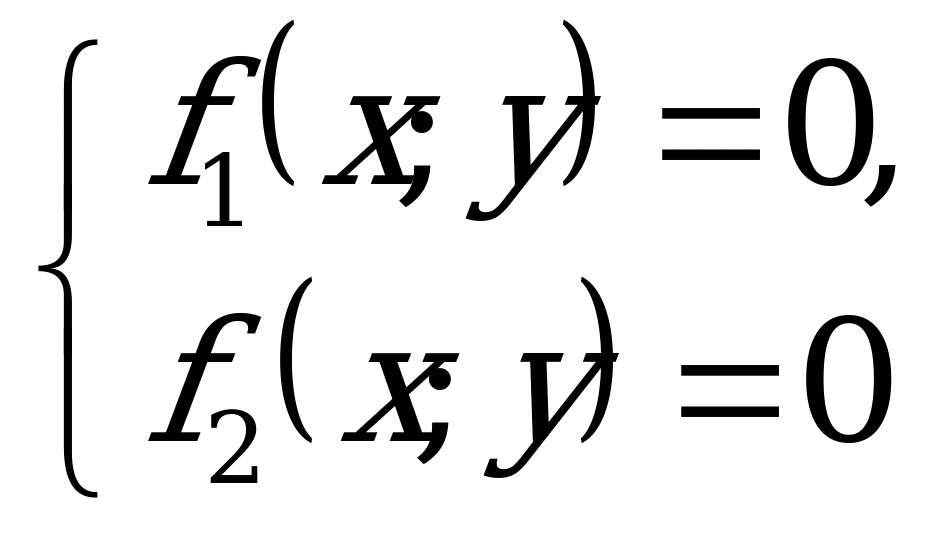
представляют собой функциональную зависимость между переменными x и y. Обе функции f1 и f2 могут быть изображены графически. Координаты x и y точек пересечения или касания этих графиков являются решением исходной системы уравнений. Число общих точек графиков равно количеству решений. Если общих точек нет, то система несовместна, т.е. не имеет решений.
Пример 3. Решить систему уравнений 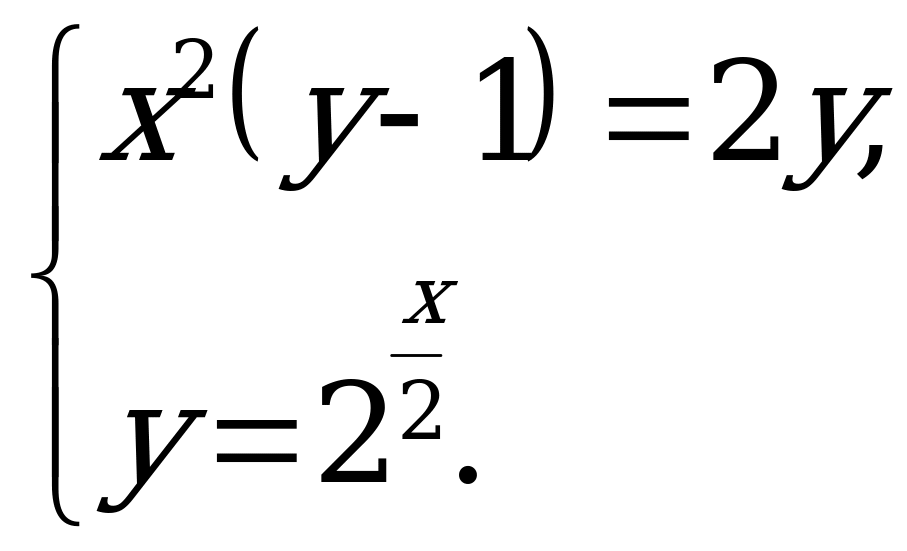
Решение. Уравнения, входящие в систему, удобно записать в виде
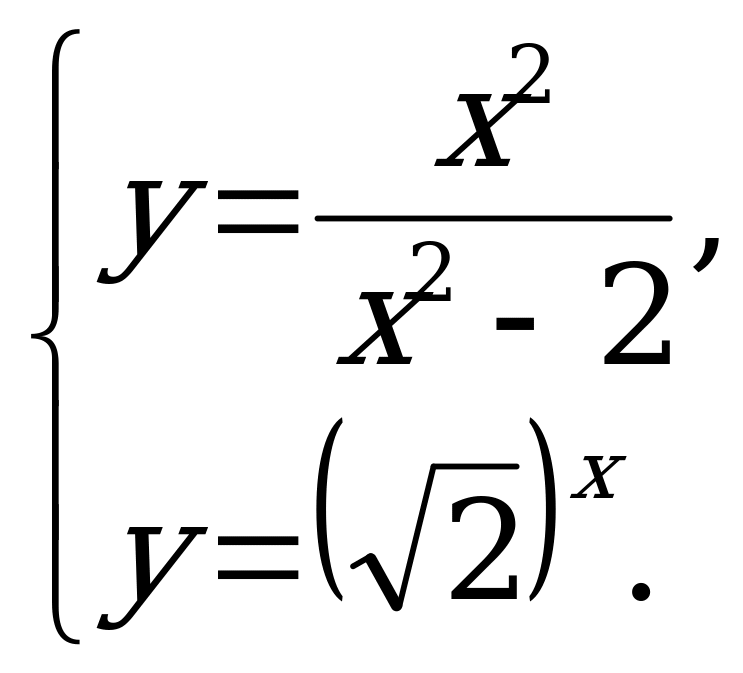
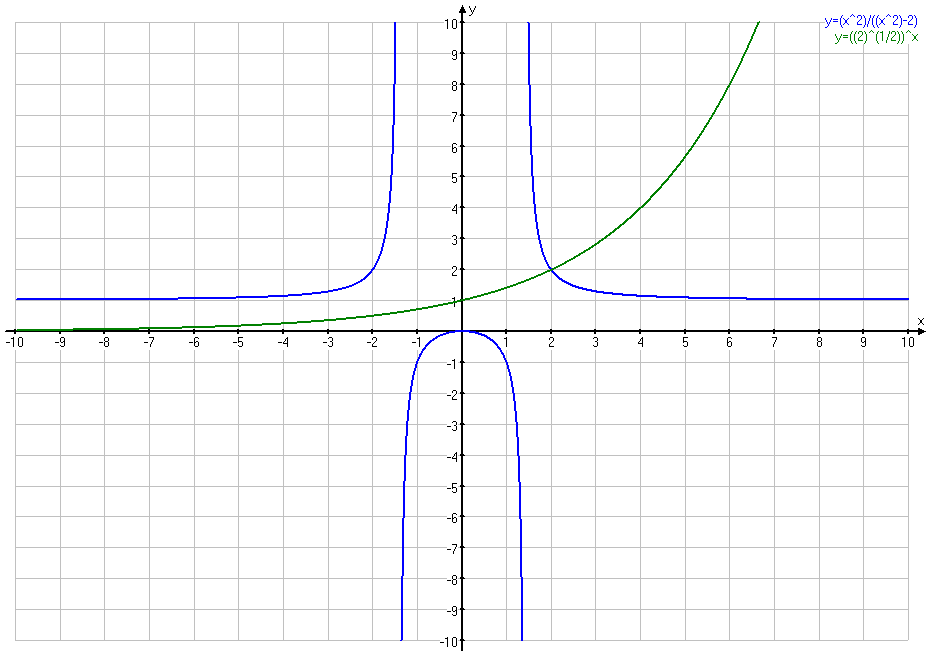
Рис. 3
Графики этих функций пересекаются в точке с координатами x = 2 и y = 2, значения которых являются решением исходной системы. Из рисунка 4 видно, что это решение единственно.
Пример 4. Решить систему уравнений 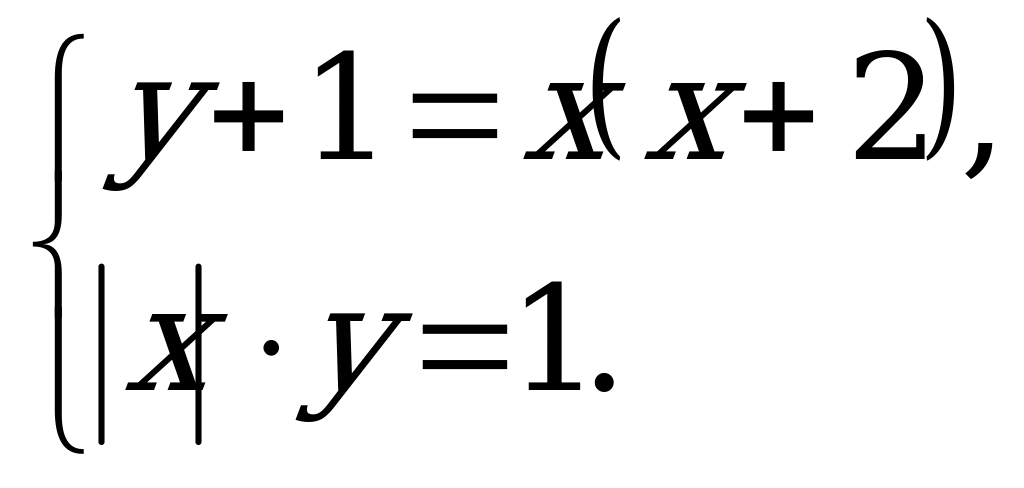
Решение. Для решения системы нужно построить графики функций 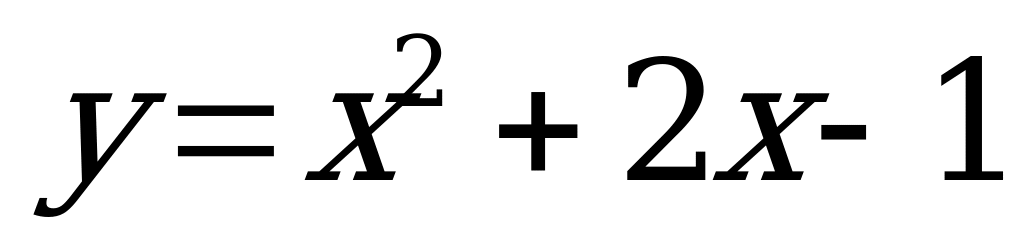 и
и 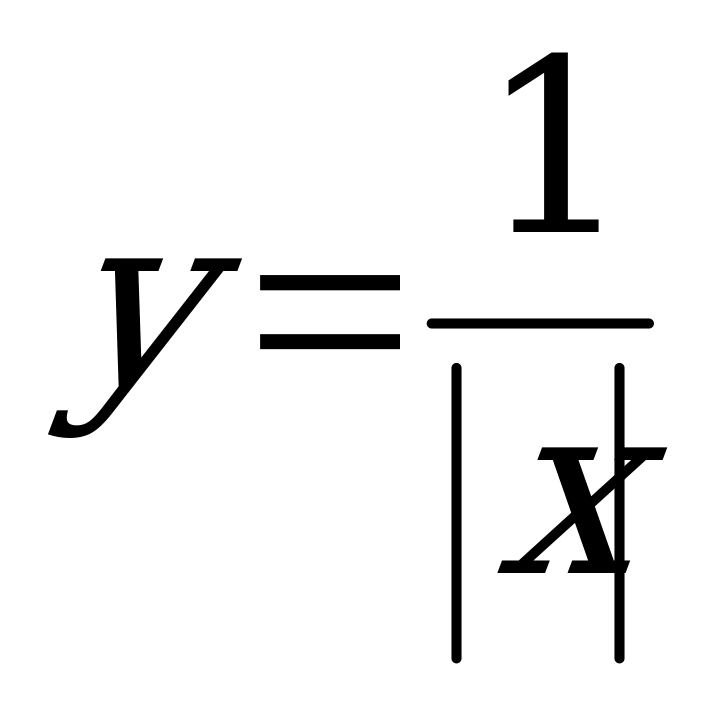 .
.
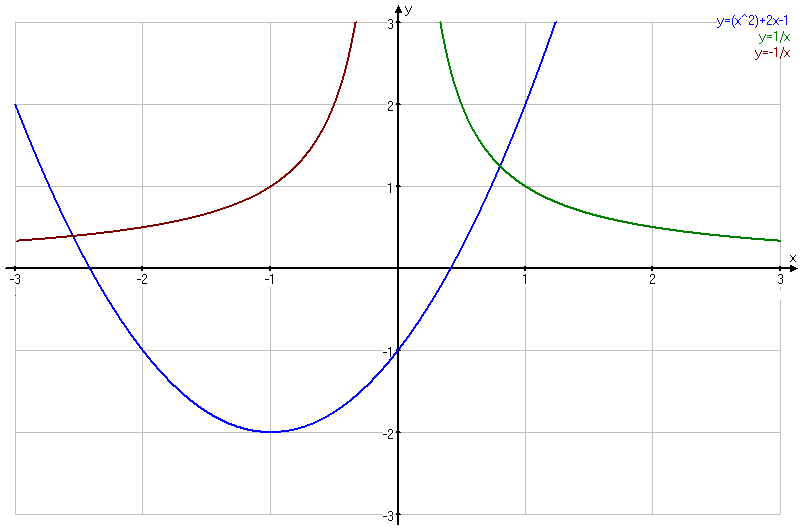
Рис. 4
Эти графики имеют две точки пересечения (рис. 5), т. е. система обладает двумя решениями, которые находятся приближённо: 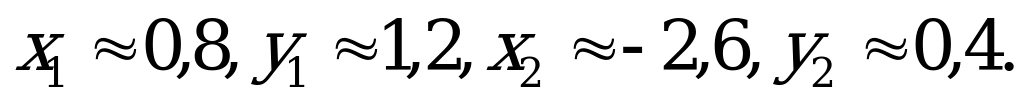
Пример 5. Решить систему уравнений 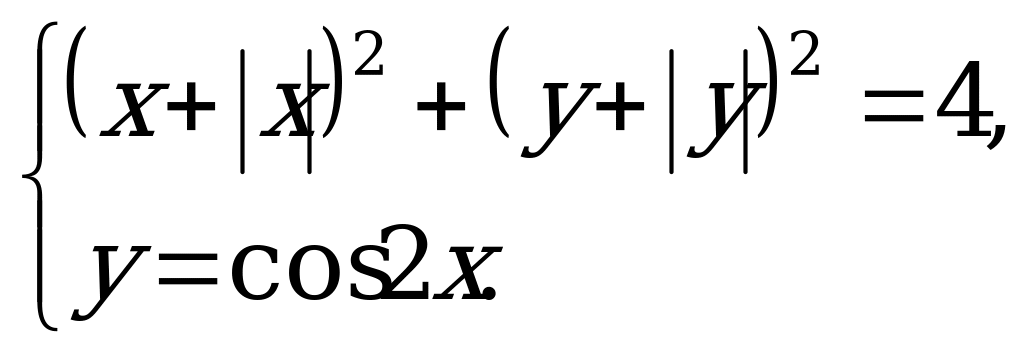
Решение. В первом квадрате первое уравнение системы может быть представлено в виде 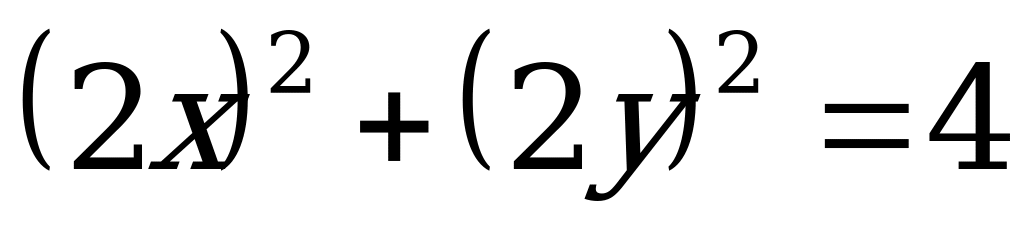 , т.е.
, т.е. 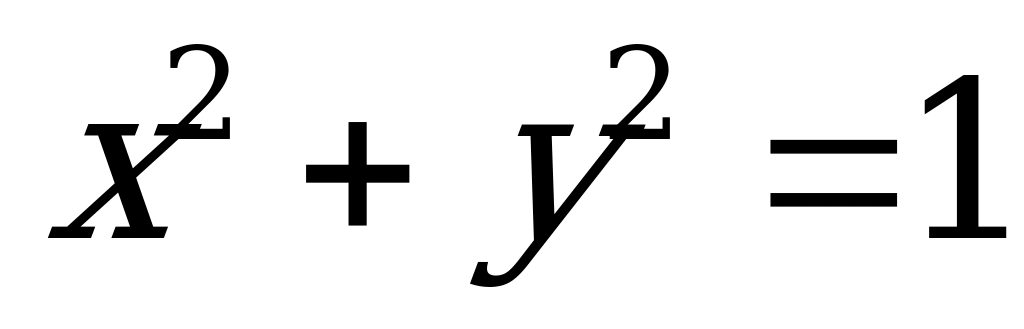 , поэтому здесь график представляет собой четверть окружности единичного радиуса с центром в начале координат. Если x ≤ 0, то y = 1 (прямая, параллельная оси Оx), а если y≤0, то x =1 (прямя, параллельная оси Оy). График функции y=cos2x очевиден.
, поэтому здесь график представляет собой четверть окружности единичного радиуса с центром в начале координат. Если x ≤ 0, то y = 1 (прямая, параллельная оси Оx), а если y≤0, то x =1 (прямя, параллельная оси Оy). График функции y=cos2x очевиден.
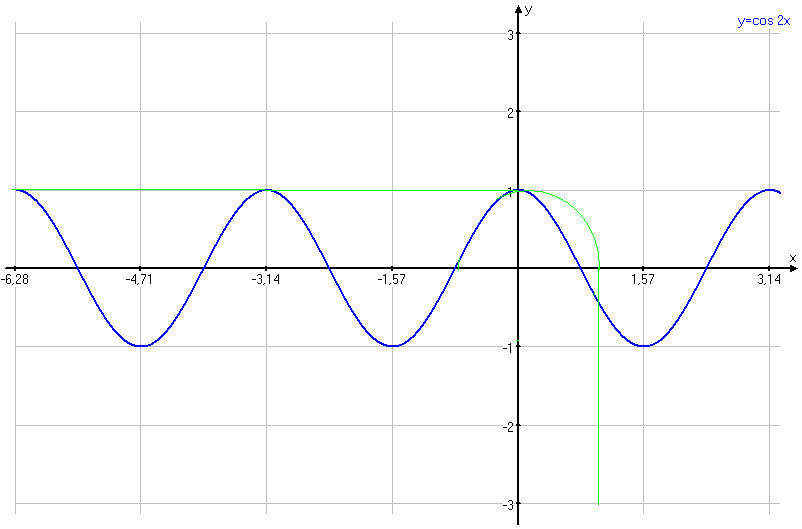
Рис. 5
Построенные графики (рис. 6) имеют одну точку пересечения и бесконечное множество точек касания, что соответствует множеству решений заданной системы уравнений:  и
и  , где k = 0, 1, 2, … .
, где k = 0, 1, 2, … .
§3. Решение неравенств с одной переменной
Наглядность, свойственная графическому методу, при решении неравенств еще более ценна, чем при решении уравнений. Способы решения остаются теми же. Сами же решения, в отличие от решений уравнений, чаще изображаются на графике не только отдельными точками, но и целыми участками числовой оси.
Пример 6. Решить неравенство 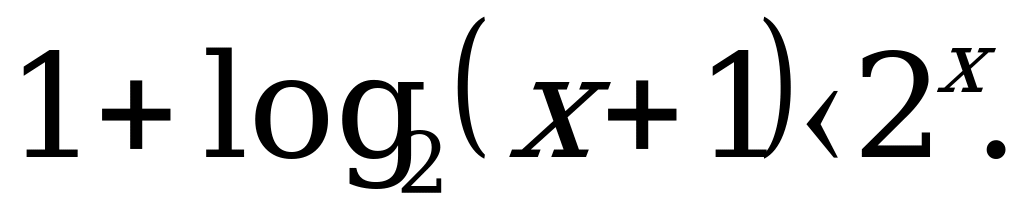
Решение. После построения графиков функций 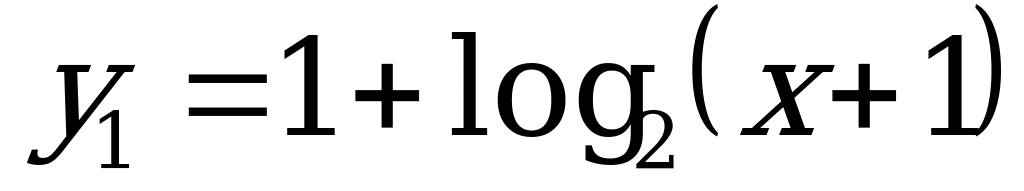 и
и 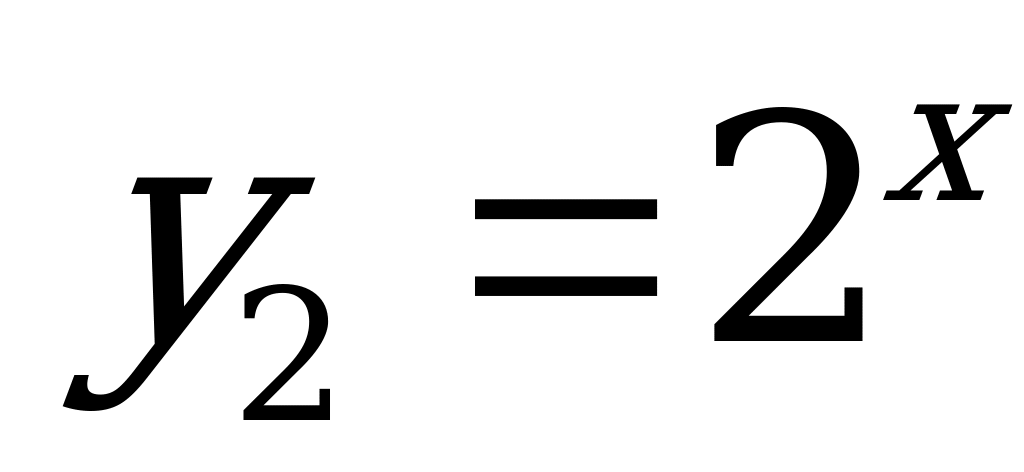 (рис. 9) записываем решение: -1x x
(рис. 9) записываем решение: -1x x
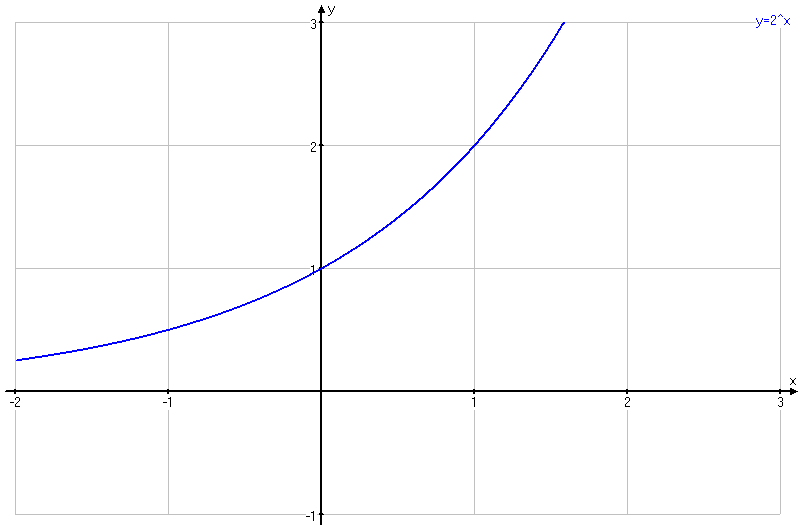
Рис. 6
§4. Решение неравенств с двумя переменными
Решением неравенства с двумя переменными x и y называется любая пfра чисел x0 и y0, удовлетворяющая этому неравенству. Графически это соответствует заданию точки с координатами (x0, y0). Совокупность всех точек, координаты которых удовлетворяют некоторому неравенству, называется областью его решений.
Для графического решения неравенства с двумя переменными необходимо построить график функции y=f(x) (для неравенства вида yf(x), y f(x),) или геометрическое место точек F(x, y)=0 (для неравенства вида F(x, y)≥0). Такие построения разбивают всю плоскость (x, y) на две или более областей. Область, в которой выполняется исходное неравенство, и представляют собой область его решений.
Пример 7. Решить неравенство 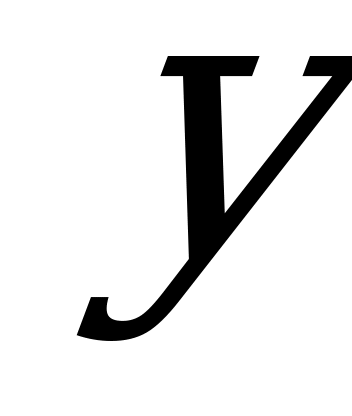
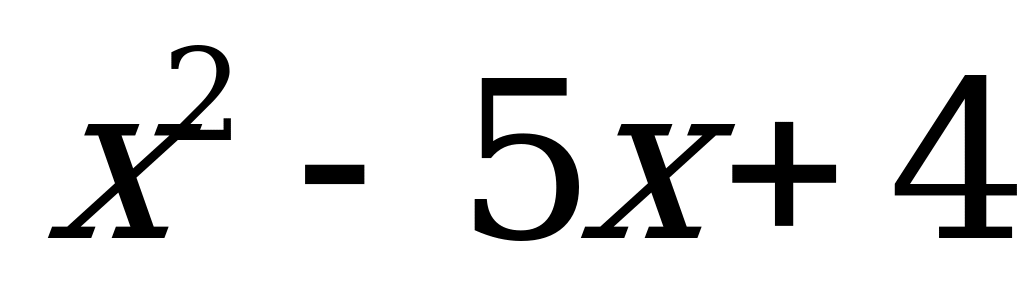
Решение. График функции 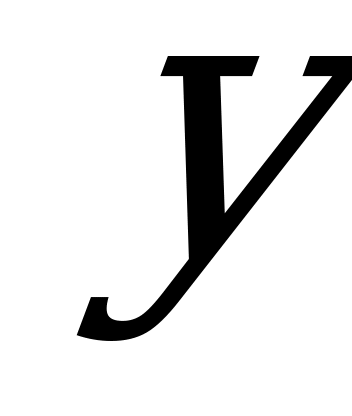 =
= 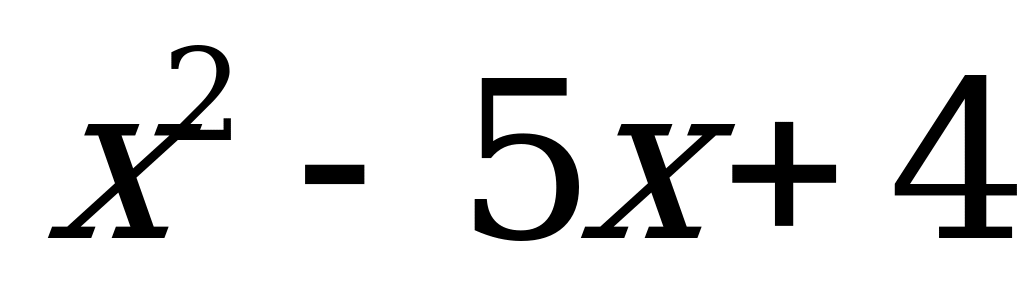 представляет собой параболу. Координаты любой точки, лежащей выше параболы, удовлетворяют заданному неравенству (на рис. 14 область решений неравенства закрашена, причем точки самого графика в эту область не входят).
представляет собой параболу. Координаты любой точки, лежащей выше параболы, удовлетворяют заданному неравенству (на рис. 14 область решений неравенства закрашена, причем точки самого графика в эту область не входят).
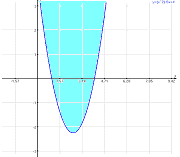
Рис. 7
Пример 8. Решить неравенство lg (y-x)≤0.
Решение. Это неравенство равносильно системе неравенств 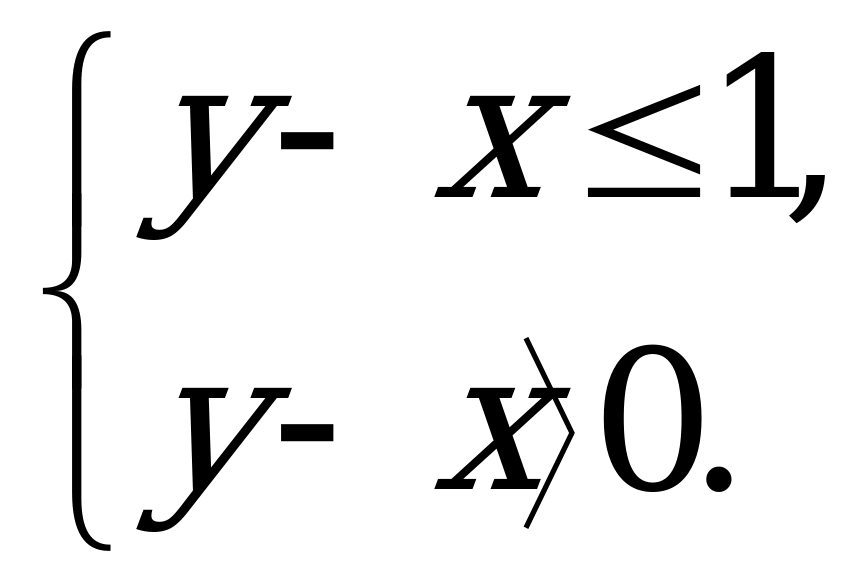
Графики функций y=x+1 и y=x представляют собой параллельные прямые. Областью решений неравенства y-x≤1 является полуплоскость, лежащая ниже прямой y=x+1, включая точки самой прямой (рис. 14).

Рис. 8
Область решения неравенства y-x0 – полуплоскость выше прямой y=x Общая часть этих полуплоскостей (или их пересечение), очевидно, содержит точки, удовлетворяющие обоим неравенствам. Следовательно, областью решений неравенства lg (y-x)≤0 является полоса, заключенная между двумя прямыми (закрашенная часть), причем одна из границ полосы – прямая y=x+1 – также входит в область решений.
Заключение
Курс математики предусматривает изучение различных способов решения уравнений и неравенств. Однако на вступительных экзаменах в ВУЗы всё чаще встречаются уравнения и неравенства, методы, решения которых выходят за рамки школьного учебника математики. В связи с этим, вполне целесообразно рассмотреть использование графиков для решения уравнений и неравенств на факультативных занятиях. Это и закрепление изученных свойств функций, и прекрасная демонстрация их применения на практике, и подготовка учащихся к вступительным экзаменам.
В данной работе представлены графические способы решения уравнений, неравенств, их систем и прикладных задач, которые наглядно объясняются геометрической интерпретацией, сопровождаются рисунками, а также достаточным количеством примеров.
Список используемой литературы
Дороднов А.М., Острецов И.Н. и др. Графики функций. Москва, 1972 г.
Егерев В.К. Радунский Б.А., Тальский Д.А. Методика построения графиков функций. Москва, 1970г.
Костюкова Н.К. Построение графиков рациональных функций. Москва,1998г.
Гурский И.П. Функции и построение графиков. Учпедгиз, 1961.
Гельфанд И.М., Глаголева Е.Г., Школ Э.Э. Функции и графики. «Наука»,1965.
Шилов Г.Е. Как строить графики? «Наука»,1965.
Сивашинский И.Х. Элементарные функции и графики. «Просвещение»,1965.
19

























