Бюджетное учреждение профессионального образования
«Радужнинский политехнический колледж»
ИНДИВИДУАЛЬНЫЙ ПРОЕКТ НА ТЕМУ:
«Определенный интеграл. Введение и некоторые приложения»
| Автор: | Ледяева Александра 26 группа, профессия «Делопроизводитель»
|
| Руководитель: | Озерова Руфина Кунакбаевна, Преподаватель математики и информатики
2018 год |
ВВЕДЕНИЕ
Курс математического анализа содержит разнообразный материал, однако, одним из его центральных разделов является определенный интеграл. Интегрирование многих видов функций подчас представляет собой одну из труднейших проблем математического анализа.
Вычисление определенного интеграла имеет не только теоретический интерес. К его вычислению сводятся иногда задачи, связанные с практической деятельностью человека.
Также понятие определенного интеграла широко используется в физике. Поэтому тема "Определенный интеграл и его приложения" вводится ещё в школьном курсе математики.
Все выше сказанное подчеркивает актуальность выбранной нами темы проектной работы.
Цель проекта состоит в изучении актуальности применения определенного интеграла и его приложений, а также широты его использования не только в математике, но и других науках, оценить ее практическую и теоретическую значимость.
Объектом проекта являются определенный интеграл и его приложения.фференциальный уравнение интеграл кривая
Для достижения указанной цели поставлены следующие задачи:
- изучить литературу по заданной теме;
- собрать теоретический и практический материал по теме;
- подвергнуть материал обобщению и систематизации.
Раскрытие темы проектной работы было проведено по следующему плану: определение определенного интеграла и его свойства, вычисление определенного интеграла и его приложения.
Глава 1. Определенный интеграл.
-
Определение определённого интеграла через сумму Римана.
Пусть функция  определена на отрезке
определена на отрезке 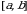 ,
, 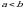 . Выполним следующие операции:
. Выполним следующие операции:
1. разобьем отрезок  точками
точками 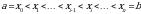 на n частичных отрезков
на n частичных отрезков 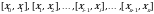 ;
;
2. в каждом из частичных отрезков 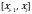 ,
, 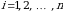 выберем произвольную точку
выберем произвольную точку 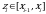 и вычислим значение функции в этой точке:
и вычислим значение функции в этой точке: 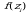 ;
;
3. найдем произведения  , где
, где 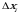 – длина частичного отрезка
– длина частичного отрезка 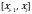 ,
, 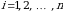 ;
;
4. составим сумму
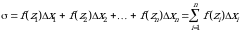 , (1)
, (1)
которая называется интегральной суммой Римана функции y = f(x) на отрезке [а, b]. С геометрической точки зрения интегральная сумма  представляет собой сумму площадей прямоугольников, основаниями которых являются частичные отрезки
представляет собой сумму площадей прямоугольников, основаниями которых являются частичные отрезки 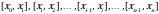 , а высоты равны
, а высоты равны 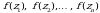 соответственно (рис. 1). Обозначим через
соответственно (рис. 1). Обозначим через  длину наибольшего частичного отрезка
длину наибольшего частичного отрезка 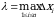 ;
;
5. найдем предел интегральной суммы, когда  .
.
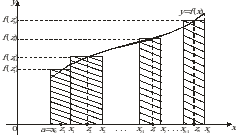
Рис. 1
Определение. Если существует конечный предел интегральной суммы (1) и он не зависит ни от способа разбиения отрезка  на частичные отрезки, ни от выбора точек
на частичные отрезки, ни от выбора точек 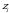 в них, то этот предел называется определенным интегралом от функции
в них, то этот предел называется определенным интегралом от функции  на отрезке
на отрезке  и обозначается
и обозначается 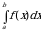 .
.
Таким образом, 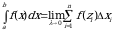 .
.
В этом случае функция 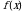 называется интегрируемой на
называется интегрируемой на  . Числа а и b называются соответственно нижним и верхним пределами интегрирования,
. Числа а и b называются соответственно нижним и верхним пределами интегрирования, 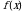 – подынтегральной функцией,
– подынтегральной функцией,  – подынтегральным выражением,
– подынтегральным выражением,  – переменной интегрирования; отрезок
– переменной интегрирования; отрезок  называется промежутком интегрирования.
называется промежутком интегрирования.
Условия существования определенного интеграла.
Необходимое условие: если функция интегрируема на отрезке  , но она ограничена на этом отрезке.
, но она ограничена на этом отрезке.
Достаточные условия: если функция 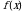 непрерывна на отрезке
непрерывна на отрезке  , то она интегрируема по этому отрезку; если функция
, то она интегрируема по этому отрезку; если функция 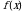 непрерывна на отрезке
непрерывна на отрезке  , за исключением конечного числа точек, и ограничена на этом отрезке, то она интегрируема по отрезку
, за исключением конечного числа точек, и ограничена на этом отрезке, то она интегрируема по отрезку  .
.
Теорема 1. Если функция  непрерывна на отрезке
непрерывна на отрезке  , то она интегрируема на этом отрезке.
, то она интегрируема на этом отрезке.
-
Геометрический смысл определенного интеграла.
Пусть на отрезке  задана непрерывная неотрицательная функция
задана непрерывная неотрицательная функция  . Криволинейной трапецией называется фигура, ограниченная сверху графиком функции y = f(x), снизу – осью Ох, слева и справа – прямыми x = a и x = b (рис. 2).
. Криволинейной трапецией называется фигура, ограниченная сверху графиком функции y = f(x), снизу – осью Ох, слева и справа – прямыми x = a и x = b (рис. 2).

Рис. 2
Определенный интеграл 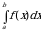 от неотрицательной функции
от неотрицательной функции  с геометрической точки зрения численно равен площади криволинейной трапеции, ограниченной сверху графиком функции
с геометрической точки зрения численно равен площади криволинейной трапеции, ограниченной сверху графиком функции  , слева и справа – отрезками прямых
, слева и справа – отрезками прямых 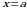 и
и  , снизу – отрезком
, снизу – отрезком  оси Ох.
оси Ох.
1.3. Основные свойства определенного интеграла
1.Значение определенного интеграла не зависит от обозначения переменной интегрирования:  .
.
2.Определенный интеграл с одинаковыми пределами интегрирования равен нулю: 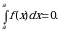
3.Если 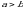 , то, по определению, полагаем
, то, по определению, полагаем 
4.Постоянный множитель можно выносить за знак определенного интеграла: 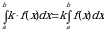
5.Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме определенных интегралов от этих функций:
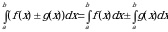 .
.
6.Если функция 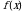 интегрируема на
интегрируема на  и
и 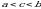 , то
, то
 .
.
7.(теорема о среднем). Если функция  непрерывна на отрезке
непрерывна на отрезке  , то на этом отрезке существует точка
, то на этом отрезке существует точка 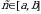 , такая, что
, такая, что 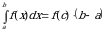 .
.
1.4. Формула Ньютона–Лейбница.
Вычисление определенных интегралов через предел интегральных сумм связано с большими трудностями. Поэтому существует другой метод, основанный на тесной связи, существующей между понятиями определенного и неопределенного интегралов.
Теорема 2. Если функция  непрерывна на отрезке
непрерывна на отрезке  и
и 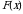 – какая-либо ее первообразная на этом отрезке, то справедлива следующая формула:
– какая-либо ее первообразная на этом отрезке, то справедлива следующая формула:
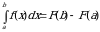 , (2)
, (2)
которая называется формулой Ньютона–Лейбница. Разность  принято записывать следующим образом:
принято записывать следующим образом:
 ,
,
где символ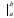 называется знаком двойной подстановки.
называется знаком двойной подстановки.
Таким образом, формулу (2) можно записать в виде:
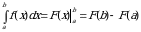 .
.
Нахождение определенных интегралов с помощью формулы Ньютона-Лейбница осуществляется в два этапа: на первом этапе находят некоторую первообразную 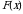 для подынтегральной функции
для подынтегральной функции 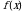 ; на втором – находится разность
; на втором – находится разность  значений этой первообразной на концах отрезка
значений этой первообразной на концах отрезка  .
.
Пример 1. Вычислить интеграл  .
.
Решение. Для подынтегральной функции  произвольная первообразная имеет вид
произвольная первообразная имеет вид 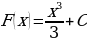 . Так как в формуле Ньютона-Лейбница можно использовать любую первообразную, то для вычисления
. Так как в формуле Ньютона-Лейбница можно использовать любую первообразную, то для вычисления
интеграла возьмем первообразную, имеющую наиболее простой вид: 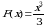 . Тогда
. Тогда 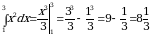 .
.
Ответ: 8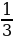
Пример 2. Вычислить интеграл 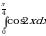 .
.
Решение. По формуле Ньютона-Лейбница имеем:
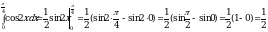 .
.
Ответ: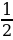
Глава 2. Некоторые приложения определенного интеграла.
2.1. Способы вычисления определенного интеграла.
Замена переменной в определенном интеграле: Теорема 3. Пусть функция 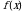 непрерывна на отрезке
непрерывна на отрезке  . Тогда, если: 1) функция
. Тогда, если: 1) функция 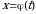 и ее производная
и ее производная 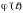 непрерывны при
непрерывны при 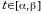 ; 2) множеством значений функции
; 2) множеством значений функции 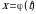 при
при 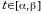 является отрезок
является отрезок  ; 3)
; 3) 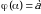 ,
,  , то справедлива формула
, то справедлива формула
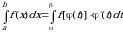 , (3)
, (3)
которая называется формулой замены переменной в определенном интеграле.
Заметим, что как и в случае неопределенного интеграла, использование замены переменной позволяет упростить исходный интеграл, приблизив его к табличному. При этом в отличие от неопределенного интеграла в данном случае нет необходимости возвращаться к исходной переменной интегрирования – достаточно лишь найти новые пределы интегрирования  и
и 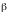 (для этого надо решить относительно переменной t уравнения
(для этого надо решить относительно переменной t уравнения 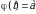 и
и  )).
)).
На практике часто вместо подстановки 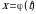 используют подстановку
используют подстановку 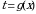 . В этом случае нахождение новых пределов интегрирования по переменной t упрощается:
. В этом случае нахождение новых пределов интегрирования по переменной t упрощается: 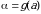 ,
, 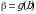 .
.
Пример 3. Вычислить интеграл 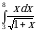
Решение. Введем новую переменную по формуле 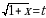 . Определим
. Определим  и
и 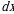 . Возведя в квадрат обе части равенства
. Возведя в квадрат обе части равенства 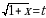 , получим
, получим 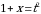 , откуда
, откуда 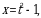
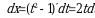 . Находим новые пределы интегрирования. Для этого в формулу
. Находим новые пределы интегрирования. Для этого в формулу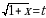 подставим старые пределы
подставим старые пределы  и
и 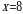 . Получим:
. Получим: 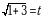 , откуда
, откуда  и, следовательно,
и, следовательно, 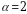 ;
; 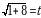 , откуда
, откуда 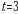 и, следовательно,
и, следовательно, 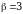 . Таким образом:
. Таким образом:
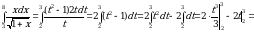
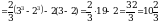 .
.
Ответ:10
Пример 4. Вычислить интеграл 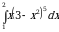 .
.
Решение. Положим 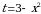 , тогда
, тогда  , откуда
, откуда 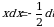 . Находим новые пределы интегрирования:
. Находим новые пределы интегрирования: 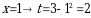 ;
; 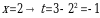 . Имеем:
. Имеем: 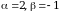 . Следовательно:
. Следовательно:
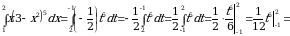
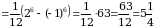 .
.
Ответ:5
Интегрирование по частям: Теорема 4. Пусть функции  и
и  имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке  . Тогда имеет место следующая формула интегрирования по частям:
. Тогда имеет место следующая формула интегрирования по частям:
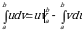 . (4)
. (4)
Доказательство: Так как 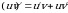 , то функция
, то функция  является первообразной для функции
является первообразной для функции 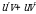 . Тогда по формуле Ньютона–Лейбница получаем
. Тогда по формуле Ньютона–Лейбница получаем
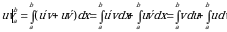 ,
,
откуда 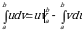 .
.
Пример 5. Вычислить  .
.
Решение. Положим 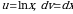 , отсюда
, отсюда 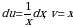 . По формуле (4) находим
. По формуле (4) находим

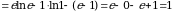 .
.
Ответ: 1
Пример 6. Вычислить 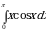 .
.
Решение. Пусть 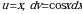 , тогда
, тогда 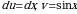 . Применяя формулу интегрирования по частям, получаем
. Применяя формулу интегрирования по частям, получаем
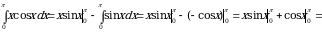
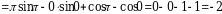 .
.
Ответ: -2
2.2. Вычисление площади плоской фигуры.
Пусть функция  неотрицательна и непрерывна на отрезке
неотрицательна и непрерывна на отрезке  . Тогда, согласно геометрическому смыслу определенного интеграла, площадь криволинейной трапеции, ограниченной сверху графиком этой функции, снизу – осью
. Тогда, согласно геометрическому смыслу определенного интеграла, площадь криволинейной трапеции, ограниченной сверху графиком этой функции, снизу – осью 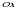 , слева и справа – прямыми
, слева и справа – прямыми 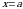 и
и  (см. рис. 2) вычисляется по формуле
(см. рис. 2) вычисляется по формуле
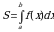 . (5)
. (5)
Пример 7. Найти площадь фигуры, ограниченной линией 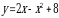 и осью
и осью 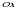 .
.
Решение. Графиком функции 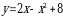 является парабола, ветви которой направлены вниз. Построим ее (рис. 3). Чтобы определить пределы интегрирования, найдем точки пересечения линии (параболы) с осью
является парабола, ветви которой направлены вниз. Построим ее (рис. 3). Чтобы определить пределы интегрирования, найдем точки пересечения линии (параболы) с осью 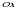 (прямой
(прямой  ). Для этого решаем систему уравнений
). Для этого решаем систему уравнений
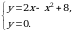
Получаем: 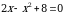 , откуда
, откуда  ,
, 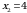 ; следовательно,
; следовательно,  ,
, 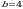 .
.
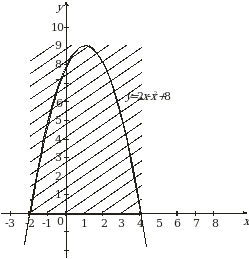
Рис. 3
Площадь фигуры находим по формуле (5):
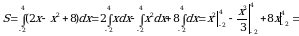
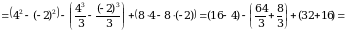
 (кв. ед.).
(кв. ед.).
Ответ: 36
Если функция  неположительная и непрерывна на отрезке
неположительная и непрерывна на отрезке  , то площадь криволинейной трапеции, ограниченной снизу графиком данной функции, сверху – осью
, то площадь криволинейной трапеции, ограниченной снизу графиком данной функции, сверху – осью 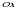 , слева и справа – прямыми
, слева и справа – прямыми 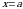 и
и  , вычисляется по формуле
, вычисляется по формуле
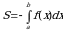 . (6)
. (6)
В случае если функция  непрерывна на отрезке
непрерывна на отрезке  и меняет знак в конечном числе точек, то площадь заштрихованной фигуры (рис. 4) равна алгебраической сумме соответствующих определенных интегралов:
и меняет знак в конечном числе точек, то площадь заштрихованной фигуры (рис. 4) равна алгебраической сумме соответствующих определенных интегралов: . (7)
. (7)
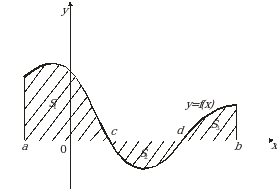
Рис. 4
Пример 8. Вычислить площадь фигуры, ограниченной осью 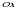 и графиком функции
и графиком функции 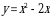 при
при 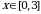 .
.
Решение. Сделаем чертеж (рис. 5).
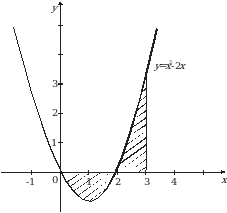
Рис. 5
Искомая площадь представляет собой сумму площадей  и
и 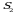 . Найдем каждую из этих площадей. Вначале определим пределы интегрирования, решив систему
. Найдем каждую из этих площадей. Вначале определим пределы интегрирования, решив систему 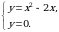 Получим
Получим 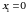 ,
, 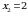 . Следовательно:
. Следовательно:
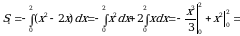
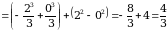 ;
;
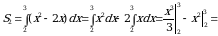
 .
.
Таким образом, площадь  заштрихованной фигуры равна
заштрихованной фигуры равна
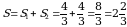 (кв. ед.).
(кв. ед.).
Ответ:2

Рис. 6
Пусть, наконец, криволинейная трапеция ограничена сверху и снизу графиками непрерывных на отрезке  функций
функций 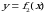 и
и  ,
,
а слева и справа – прямыми 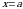 и
и  (рис. 6). Тогда ее площадь вычисляется по формуле
(рис. 6). Тогда ее площадь вычисляется по формуле
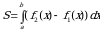 . (8)
. (8)
Пример 9.Найти площадь фигуры, ограниченной линиями  и
и 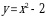 .
.
Решение. Данная фигура изображена на рис. 7. Площадь ее вычислим по формуле (8). Решая систему уравнений 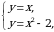 находим
находим 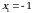 ,
, 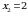 ; следовательно,
; следовательно, 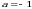 ,
, 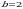 . На отрезке
. На отрезке 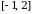 имеем:
имеем: 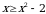 . Значит, в формуле (6) в качестве
. Значит, в формуле (6) в качестве 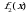 возьмем x, а в качестве
возьмем x, а в качестве 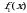 –
– 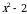 . Получим:
. Получим:

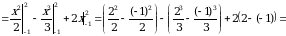
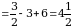 (кв. ед.).
(кв. ед.).
Более сложные задачи на вычисление площадей решают путем разбиения фигуры на непересекающиеся части и вычисления площади всей фигуры как суммы площадей этих частей.
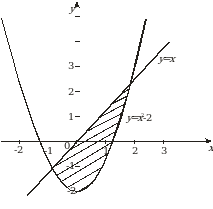
Рис. 7
Пример 10. Найти площадь фигуры, ограниченной линиями  ,
, 
 ,
,  .
.
Решение. Сделаем чертеж (рис. 8).
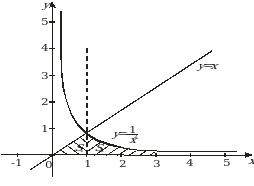
Рис. 8
Данную фигуру можно рассматривать как криволинейную трапецию, ограниченную снизу осью  , слева и справа – прямыми
, слева и справа – прямыми 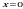 и
и 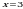 , сверху – графиками функций
, сверху – графиками функций  и
и  . Так как фигура ограничена сверху графиками двух функций, то для вычисления ее площади разобьем данную фигуру прямой
. Так как фигура ограничена сверху графиками двух функций, то для вычисления ее площади разобьем данную фигуру прямой 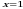 на две части (1 – это абсцисса точки пересечения линий
на две части (1 – это абсцисса точки пересечения линий  и
и  ). Площадь каждой из этих частей находим по формуле (5):
). Площадь каждой из этих частей находим по формуле (5):
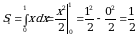 (кв.ед.);
(кв.ед.); 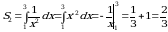 (кв. ед.). Следовательно:
(кв. ед.). Следовательно:
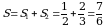 (кв. ед.).
(кв. ед.).
В заключение отметим, что если криволинейная трапеция ограничена прямыми  и
и 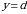 , осью
, осью 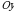 и непрерывной на
и непрерывной на 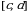 кривой
кривой 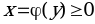 (рис. 9), то ее площадь находится по формуле
(рис. 9), то ее площадь находится по формуле
 , (9)
, (9)

х = (у)

Рис. 9
-
Длина дуги плоской кривой
Пусть кривая  , заданная уравнением
, заданная уравнением  , где
, где 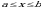 , лежит в плоскости
, лежит в плоскости  (рис. 10).
(рис. 10).

Рис. 10
Определение. Под длиной дуги  понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной стремится к бесконечности, а длина наибольшего звена стремится к нулю.
понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной стремится к бесконечности, а длина наибольшего звена стремится к нулю.
Если функция  и ее производная
и ее производная 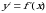 непрерывны на отрезке
непрерывны на отрезке 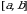 , то длина дуги кривой
, то длина дуги кривой  вычисляется по формуле
вычисляется по формуле
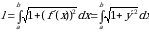 . (10)
. (10)
Пример 11. Вычислить длину дуги кривой 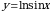 , заключенной между точками, для которых
, заключенной между точками, для которых 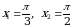 .
.
Решение. Из условия задачи имеем 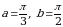 . По формуле (10) получаем:
. По формуле (10) получаем:
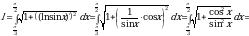
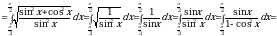
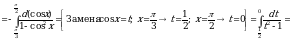
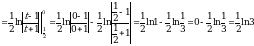 .
.
2.4.Объем тела вращения
Пусть криволинейная трапеция, ограниченная графиком непрерывной на отрезке 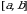 функции
функции  , осью
, осью 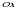 , прямыми
, прямыми 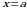 и
и  , вращается вокруг оси
, вращается вокруг оси 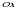 (рис. 11). Тогда объем полученного тела вращения вычисляется по формуле
(рис. 11). Тогда объем полученного тела вращения вычисляется по формуле
 . (11)
. (11)
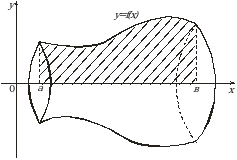
Рис. 11
Пример 12. Вычислить объем тела, полученного вращением вокруг оси 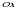 криволинейной трапеции, ограниченной гиперболой
криволинейной трапеции, ограниченной гиперболой 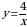 , прямыми
, прямыми 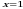 ,
, 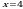 и осью
и осью 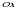 .
.
Решение. Сделаем чертеж (рис. 12).
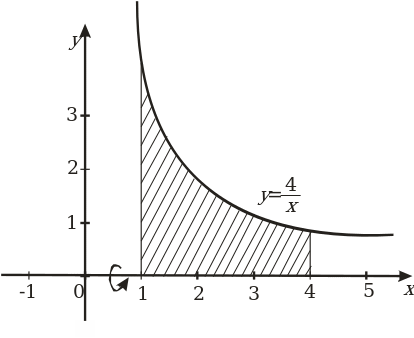
Рис. 12
Из условия задачи следует, что 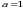 ,
, 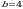 . По формуле (11) получаем
. По формуле (11) получаем
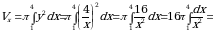
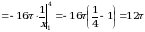 .
.
Ответ: 12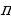 .
.
Объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной прямыми у = с и у = d, осью Оу и графиком непрерывной на отрезке 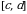 функции
функции  (рис. 13), определяется по формуле
(рис. 13), определяется по формуле
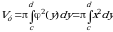 . (12)
. (12)

х = (у)
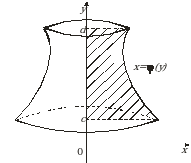
Рис. 13
Пример 13. Вычислить объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной линиями х2 = 4у, у = 4, х = 0 (рис. 14).
Решение. В соответствии с условием задачи находим пределы интегрирования: 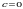 ,
, 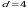 . По формуле (12) получаем:
. По формуле (12) получаем:
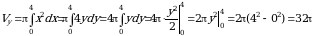 .
.
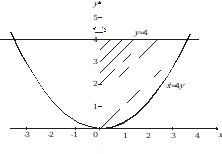
Рис. 14
Ответ: 32
ЗАКЛЮЧЕНИЕ
Рассмотренные выше примеры практических задач, дают нам ясное представление значимости определенного интеграла для их разрешимости.
Трудно назвать научную область, в которой бы не применялись методы интегрального исчисления, в общем, и свойства определенного интеграла, в частности. Так в процессе выполнения проектной работы нами были рассмотрены примеры практических задач в области геометрии. Конечно, это еще далеко не единственная наука, в которой используется интегральный метод для поиска устанавливаемой величины при решении конкретной задачи, и установлении теоретических фактов.
Также определенный интеграл используется для изучения собственно самой математики. Например, при решении дифференциальных уравнений, которые в свою очередь вносят свой незаменимый вклад в решение задач практического содержания. Можно сказать, что определенный интеграл – это некоторый фундамент для изучения математики. Отсюда и важность знания методов их решения.
Из всего выше сказанного понятно, почему знакомство с определенным интегралом происходит еще в рамках средней общеобразовательной школы, где ученики изучают не только понятие интеграла и его свойства, но и некоторые его приложения.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
-
Григорьев С.Г., Иволгина С.В. Математика / Григорьев С.Г., Иволгина С.В. – Москва, 2012г.
-
Григорьев В.П., Сабурова Т.Н. Сборник задач по высшей математике / Григорьев В.П., Сабурова Т.Н. – Москва, 2014г.
-
Башмаков М.И., Математика / Башмаков М.И. – Москва, 2015г.
-
Колмогоров, А.Н. Алгебра и начало математического анализа. Учебник для 10 - 11 кл. / А.Н. Колмогоров, А.М. Абрамов и др.- 17-е изд. - М.: Просвещение, 2008 г.
-
Виленкин, М.Я. Алгебра и математический анализ / М.Я. Виленкин, О.С. Ивашев, Мусатов, С.И. Шварцбурд, - Москва, 1993г.
-
Бермантт, А.Ф. Краткий курс математического анализа для вузов / А.Ф. Бермантт, И.Г. Араманови – М.: Наука, 1971. - 736с.
-
Власов, В.Г. Конспект лекций по высшей математике / В.Г. Власов, Москва Айрис, 1997г.
-
Иванов, А.А. Курс лекций по математике / А.А. Иванов
-
Ильин, В.А. Основы математического анализа, часть I / В.А. Ильин, Э.Г. Позняк – Москва, 1982г.
-
Никольский, С.Н. Элементы математического анализа / С.Н. Никольский – М.: Наука, 1981г.
-
Письменный, Д.Т. Конспект лекций по высшей математике / Д.Т. Письменный – M.: Айрис – пресс, 2003. – 288 c.






 определена на отрезке
определена на отрезке 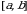 ,
, 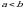 . Выполним следующие операции:
. Выполним следующие операции: точками
точками 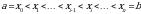 на n частичных отрезков
на n частичных отрезков 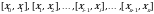 ;
;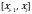 ,
, 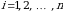 выберем произвольную точку
выберем произвольную точку 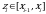 и вычислим значение функции в этой точке:
и вычислим значение функции в этой точке: 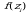 ;
; , где
, где 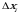 – длина частичного отрезка
– длина частичного отрезка 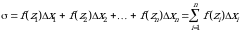 , (1)
, (1) представляет собой сумму площадей прямоугольников, основаниями которых являются частичные отрезки
представляет собой сумму площадей прямоугольников, основаниями которых являются частичные отрезки 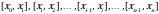 , а высоты равны
, а высоты равны 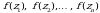 соответственно (рис. 1). Обозначим через
соответственно (рис. 1). Обозначим через  длину наибольшего частичного отрезка
длину наибольшего частичного отрезка 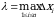 ;
; .
.
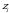 в них, то этот предел называется определенным интегралом от функции
в них, то этот предел называется определенным интегралом от функции 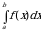 .
.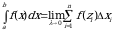 .
.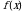 называется интегрируемой на
называется интегрируемой на  – подынтегральным выражением,
– подынтегральным выражением,  – переменной интегрирования; отрезок
– переменной интегрирования; отрезок 
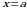 и
и  , снизу – отрезком
, снизу – отрезком  .
.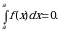
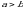 , то, по определению, полагаем
, то, по определению, полагаем 
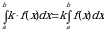
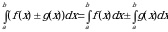 .
.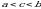 , то
, то .
.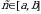 , такая, что
, такая, что 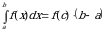 .
.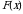 – какая-либо ее первообразная на этом отрезке, то справедлива следующая формула:
– какая-либо ее первообразная на этом отрезке, то справедлива следующая формула: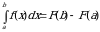 , (2)
, (2) принято записывать следующим образом:
принято записывать следующим образом: ,
,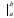 называется знаком двойной подстановки.
называется знаком двойной подстановки.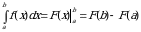 .
. значений этой первообразной на концах отрезка
значений этой первообразной на концах отрезка  .
. произвольная первообразная имеет вид
произвольная первообразная имеет вид 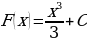 . Так как в формуле Ньютона-Лейбница можно использовать любую первообразную, то для вычисления
. Так как в формуле Ньютона-Лейбница можно использовать любую первообразную, то для вычисления 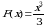 . Тогда
. Тогда 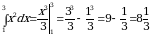 .
.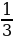
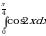 .
.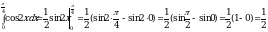 .
.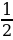
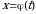 и ее производная
и ее производная 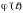 непрерывны при
непрерывны при 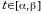 ; 2) множеством значений функции
; 2) множеством значений функции 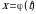 при
при 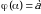 ,
,  , то справедлива формула
, то справедлива формула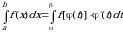 , (3)
, (3) и
и 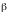 (для этого надо решить относительно переменной t уравнения
(для этого надо решить относительно переменной t уравнения 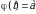 и
и  )).
)).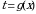 . В этом случае нахождение новых пределов интегрирования по переменной t упрощается:
. В этом случае нахождение новых пределов интегрирования по переменной t упрощается: 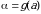 ,
, 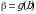 .
.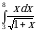
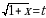 . Определим
. Определим 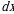 . Возведя в квадрат обе части равенства
. Возведя в квадрат обе части равенства 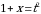 , откуда
, откуда 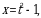
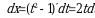 . Находим новые пределы интегрирования. Для этого в формулу
. Находим новые пределы интегрирования. Для этого в формулу и
и 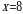 . Получим:
. Получим: 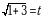 , откуда
, откуда  и, следовательно,
и, следовательно, 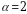 ;
; 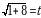 , откуда
, откуда 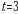 и, следовательно,
и, следовательно, 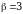 . Таким образом:
. Таким образом: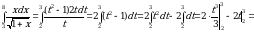
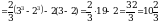 .
.
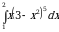 .
.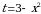 , тогда
, тогда  , откуда
, откуда 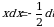 . Находим новые пределы интегрирования:
. Находим новые пределы интегрирования: 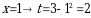 ;
; 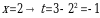 . Имеем:
. Имеем: 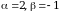 . Следовательно:
. Следовательно: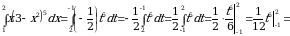
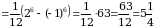 .
.
 и
и  имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке 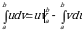 . (4)
. (4)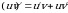 , то функция
, то функция  является первообразной для функции
является первообразной для функции 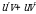 . Тогда по формуле Ньютона–Лейбница получаем
. Тогда по формуле Ньютона–Лейбница получаем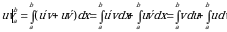 ,
, .
.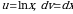 , отсюда
, отсюда 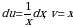 . По формуле (4) находим
. По формуле (4) находим
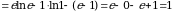 .
.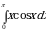 .
.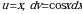 , тогда
, тогда 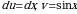 . Применяя формулу интегрирования по частям, получаем
. Применяя формулу интегрирования по частям, получаем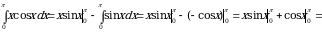
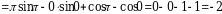 .
.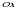 , слева и справа – прямыми
, слева и справа – прямыми 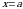 и
и  (см. рис. 2) вычисляется по формуле
(см. рис. 2) вычисляется по формуле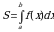 . (5)
. (5)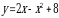 и осью
и осью 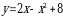 является парабола, ветви которой направлены вниз. Построим ее (рис. 3). Чтобы определить пределы интегрирования, найдем точки пересечения линии (параболы) с осью
является парабола, ветви которой направлены вниз. Построим ее (рис. 3). Чтобы определить пределы интегрирования, найдем точки пересечения линии (параболы) с осью  ). Для этого решаем систему уравнений
). Для этого решаем систему уравнений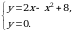
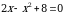 , откуда
, откуда  ,
, 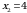 ; следовательно,
; следовательно,  ,
, 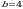 .
.
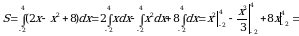
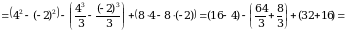
 (кв. ед.).
(кв. ед.).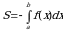 . (6)
. (6) . (7)
. (7)
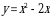 при
при 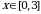 .
.
 и
и 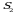 . Найдем каждую из этих площадей. Вначале определим пределы интегрирования, решив систему
. Найдем каждую из этих площадей. Вначале определим пределы интегрирования, решив систему 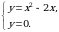 Получим
Получим 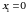 ,
, 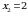 . Следовательно:
. Следовательно: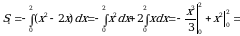
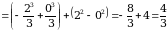 ;
;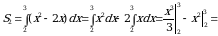
 .
. заштрихованной фигуры равна
заштрихованной фигуры равна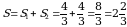 (кв. ед.).
(кв. ед.).
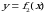 и
и  ,
, 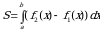 . (8)
. (8) и
и 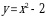 .
.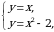 находим
находим 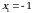 ,
, 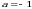 ,
, 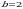 . На отрезке
. На отрезке 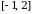 имеем:
имеем: 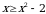 . Значит, в формуле (6) в качестве
. Значит, в формуле (6) в качестве 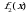 возьмем x, а в качестве
возьмем x, а в качестве 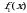 –
– 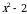 . Получим:
. Получим:
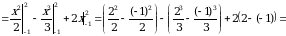
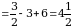 (кв. ед.).
(кв. ед.).

 ,
, 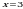 .
.
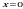 и
и 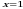 на две части (1 – это абсцисса точки пересечения линий
на две части (1 – это абсцисса точки пересечения линий 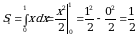 (кв.ед.);
(кв.ед.); 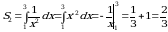 (кв. ед.). Следовательно:
(кв. ед.). Следовательно: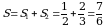 (кв. ед.).
(кв. ед.). и
и 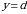 , осью
, осью 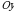 и непрерывной на
и непрерывной на  кривой
кривой  , (9)
, (9) 

 , заданная уравнением
, заданная уравнением  , где
, где 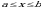 , лежит в плоскости
, лежит в плоскости  (рис. 10).
(рис. 10).
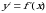 непрерывны на отрезке
непрерывны на отрезке 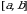 , то длина дуги кривой
, то длина дуги кривой 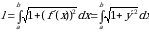 . (10)
. (10)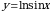 , заключенной между точками, для которых
, заключенной между точками, для которых 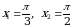 .
.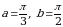 . По формуле (10) получаем:
. По формуле (10) получаем: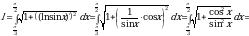
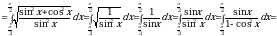
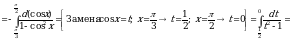
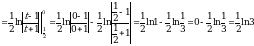 .
. . (11)
. (11)
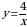 , прямыми
, прямыми 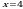 и осью
и осью 
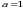 ,
, 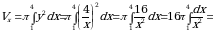
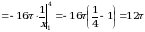 .
.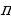 .
.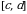 функции
функции 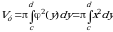 . (12)
. (12)
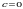 ,
, 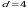 . По формуле (12) получаем:
. По формуле (12) получаем: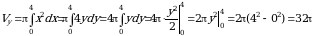 .
.