Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа №4
ГРУППОВОЙ ИТОГОВЫЙ ПРОЕКТ
НА ТЕМУ
«Теорема Пифагора»
Выполнили:
Прошина Наталия
Резник Виктория
Савченко Леонид
Литвинова Арина
ученики: 8 в класса
МБОУ СОШ №4
Руководитель проекта:
Зубенко Наталья Федоровна
учитель Математики
г. Светлоград, 2021 год
Содержание:
Введение..........................................................................................................3
Глава 1. Окружность.......................................................................................4
1.1.Теоремы и следствия, изучаемые в курсе 8-9 класса............................5
1.2.Исследование «Число π»........................................................................12
1.3.Теорема Птолемея...................................................................................13
Глава 2. Круг.................................................................................................14
Глава 3. Применение теорем окружности и круга при решении задач...15
Заключение....................................................................................................17
Список литературы........................................................................................18
Введение.
Чем же выделяется геометрия среди других разделов математики? Во-первых, геометрия - это древнейшая наука. Некоторые теоремы геометрии стали памятниками мировой культуры. Ярким примером является “Теорема Пифагора”, которая используется при доказательстве и решении большинства задач, связанных с прямоугольным треугольником.
Наша работа посвящается окружности и кругу. В этом проекте собрана вся самая важная информацию по этой теме. Благодаря этому она станет проще для понимания.
Цели:
Изучить окружность и круг, их составляющие, свойства, теоремы и использовать данные знания в решении задач.
Задачи:
-
Рассмотреть важнейшие теоремы и свойства.
-
Провести математическое исследование «Число π».
-
Применить полученные знания в решении задач.
Актуальность:
В структуру экзамена ОГЭ по математике входят геометрические задачи на всестороннее знание планиметрии. Особенностью работы над задачами является отсутствие единых алгоритмов решения, успех во многом зависит от накопленного учащимися опыта решения комбинированных планиметрических задач. Тем не менее, практика решения позволила выделить некоторые геометрические структуры, являющиеся вспомогательными ключами к поиску правильного решения. Одним из таких ключей является знание основных свойств и формул окружности и круга. В нашей работе собраны все основные свойства, теоремы и методы их применения на экзамене.
Глава 1. Окружность.
История возникновения и развития геометрического понятия «окружность».
Для первобытных людей важную роль играла форма окружавших их предметов. По форме и цвету они отличали съедобные грибы от несъедобных, пригодные для построек породы деревьев от тех, которые годятся лишь на дрова, вкусные орехи от горьких и т.д. Особенно вкусными казались им орехи кокосовой пальмы, похожие на шар. Специальных названий для геометрических фигур, конечно, не было. Говорили: “такой же, как кокосовый орех” или “такой же, как соль” и т.д. Так, овладевая окружающим их миром, люди знакомились с простейшими геометрическими фигурами.
Окружность и круг – это плоские фигуры. В Древней Греции круг и окружность считали венцом совершенства. “В каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе”. Это свойство окружности стало толчком к возникновению колеса.
Элементы окружности.
Радиус окружности – это отрезок, соединяющий центр окружности с любой её точкой (по - латыни – спица колеса).
Диаметр окружности – это хорда, проходящая через центр окружности (с греческого – “поперечник”).
Хорда окружности – отрезок, соединяющий любые две точки на окружности (с греческого – “струна”).
Дуга окружности – это часть окружности, ограниченная двумя точками.
Центральный угол — угол, образованный двумя радиусами. Центральный угол измеряется дугой, на которую опирается.
Вписанный угол — угол, вершина которого лежит на окружности, а стороны являются ее хордами.
Касательная — прямая, проходящая через точку окружности, перпендикулярно ее радиусу. Касательная имеет с окружностью только одну общую точку.
1.1.Теоремы и следствия, изучаемые в курсе 8-9 класса.
1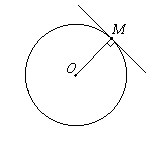 .Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
.Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
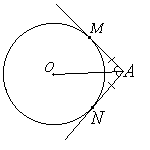
2.Отрезки касательных к окружности, проведённых из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
3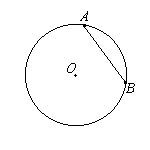 .Отрезок, соединяющий две точки окружности, называется её хордой. Хорда, проходящая через центр окружности, называется диаметром.
.Отрезок, соединяющий две точки окружности, называется её хордой. Хорда, проходящая через центр окружности, называется диаметром.
Свойства хорд.
Д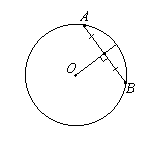 иаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.
иаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.

Дуги, заключённые между параллельными хордами, равны.
Е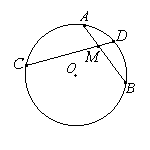 сли две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB =CM•MD.
сли две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB =CM•MD.
Свойства окружности.
Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку (касательная); иметь с ней две общие точки (секущая).
Ч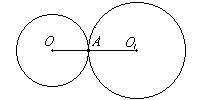 ерез три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
ерез три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
Точка касания двух окружностей лежит на линии, соединяющей их центры.
Т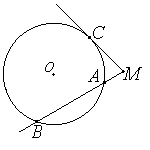 еорема о касательной и секущей.
еорема о касательной и секущей.
Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на её внешнюю часть:MC2 =MA•MB.
Т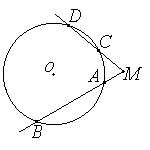 еорема о секущих.
еорема о секущих.
Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть: MA•MB = MC•MD.
 Углы в окружности.
Углы в окружности.
Ц ентральным углом в окружности называется плоский угол с вершиной в её центре.
ентральным углом в окружности называется плоский угол с вершиной в её центре.
У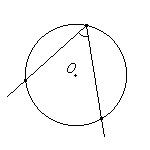 гол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом.
гол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом.
Любые две точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. Мерой дуги может служить мера соответствующего ей центрального угла.
Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.
Свойства углов, связанных с окружностью.
В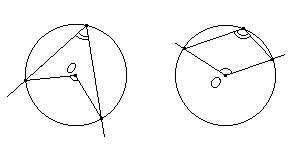 писанный угол либо равен половине соответствующего ему центрального угла, либо дополняет половину этого угла до 180°.
писанный угол либо равен половине соответствующего ему центрального угла, либо дополняет половину этого угла до 180°.
У глы, вписанные в одну окружность и опирающиеся на одну и ту же дугу, равны.
глы, вписанные в одну окружность и опирающиеся на одну и ту же дугу, равны.
В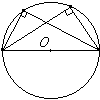 писанный угол, опирающийся на диаметр, равен 90°.
писанный угол, опирающийся на диаметр, равен 90°.
У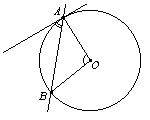 гол, образованный касательной к окружности и секущей, проведённой через точку касания, равен половине дуги, заключённой между его сторонами.
гол, образованный касательной к окружности и секущей, проведённой через точку касания, равен половине дуги, заключённой между его сторонами.
Длины и площади.
Длина окружности C радиуса R вычисляется по формуле:
C = 2 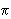 R.
R.
Площадь S круга радиуса R вычисляется по формуле:
S = 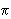 R2.
R2.
Д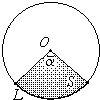 лина дуги окружности L радиуса R с центральным углом
лина дуги окружности L радиуса R с центральным углом 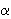 ,измеренным в радианах, вычисляется по формуле:
,измеренным в радианах, вычисляется по формуле:
L = R 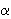 .
.
Площадь S сектора радиуса R с центральным углом в 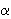 радиан вычисляется по формуле: S =
радиан вычисляется по формуле: S = 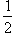 R2
R2 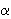 .
.
Вписанные и описанные окружности.
Окружность и треугольник.
Центр вписанной окружности — точка пересечения биссектрис треугольника, её радиус r вычисляется по формуле:
r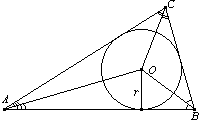 =
=  ,
,
где S — площадь треугольника, а  — полупериметр;
— полупериметр;
центр описанной окружности — точка пересечения серединных перпендикуляров, её радиус R вычисляется по формуле:
R = 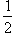
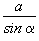 ,
,
R = 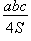 ;
;
Окружность и четырёхугольники
О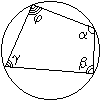 коло выпуклого четырёхугольника можно описать окружность тогда и только тогда, когда сумма его внутренних противоположных углов равна 180°:
коло выпуклого четырёхугольника можно описать окружность тогда и только тогда, когда сумма его внутренних противоположных углов равна 180°:

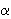 +
+ 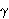 =
= 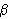 +
+ 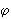 = 180°;
= 180°;
В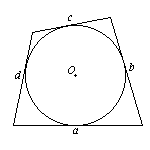 четырёхугольник можно вписать окружность тогда и только тогда, когда у него равны суммы противоположных сторон:
четырёхугольник можно вписать окружность тогда и только тогда, когда у него равны суммы противоположных сторон:
 a + c = b + d;
a + c = b + d;
Около параллелограмма можно описать окружность тогда и только тогда, когда он является прямоугольником;
Около трапеции можно описать окружность тогда и только тогда, когда эта трапеция — равнобедренная; центр окружности лежит на пересечении оси симметрии трапеции с серединным перпендикуляром к боковой стороне;
В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом.
Свойства вписанных углов.
Углы, связанные с окружностью
Т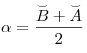 еорема (угол между пересекающимися хордами). Угол между двумя пересекающимися хордами равен полусумме высекаемых ими дуг:
еорема (угол между пересекающимися хордами). Угол между двумя пересекающимися хордами равен полусумме высекаемых ими дуг:
Т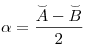 еорема (угол между секущими). Угол между двумя секущими, проведёнными из одной точки, равен полуразности большей и меньшей высекаемых ими дуг:
еорема (угол между секущими). Угол между двумя секущими, проведёнными из одной точки, равен полуразности большей и меньшей высекаемых ими дуг:
Т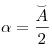 еорема (угол между касательной и хордой, проведённой через точку касания). Угол между касательной и хордой, проведённой в точку касания, равен половине дуги, стягиваемой этой хордой:
еорема (угол между касательной и хордой, проведённой через точку касания). Угол между касательной и хордой, проведённой в точку касания, равен половине дуги, стягиваемой этой хордой:
Теорема (угол между касательной и секущей).Угол между касательной и секущей равен полуразности высекаемых ими дуг: 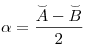 .
.
Теорема (угол между касательными). Угол между двумя касательными, проведёнными из одной точки, равен полуразности большей и меньшей высекаемых ими дуг: 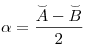 .
.
Отрезки, связанные с окружностью.
Теорема. Отрезки касательных к окружностям, проведённым из одной точки, равны:  , центр окружности лежит на биссектрисе угла
, центр окружности лежит на биссектрисе угла 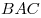 .
.
Теорема. Произведение секущей на её внешнюю часть есть для данной окружности величина постоянная и равная разности квадратов расстояния от точки пересечения секущих до центра окружности и радиуса окружности.
Теорема. Произведение отрезков, на которые делится хорда данной точкой, есть для данной окружности величина постоянная и равна разности квадратов радиуса окружности и расстояния от точки 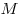 до центра окружности.
до центра окружности.
Теорема. Квадрат касательной равен произведению секущей на её внешнюю часть.
Теорема. Отношение хорды к синусу вписанного угла, который на неё опирается, равно двум радиусам (теорема синусов).
Окружность, вписанная в многоугольник.
Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник — описанным около этой окружности.
Теоремы:
-
Если в трапецию вписана окружность, то сумма оснований равна сумме боковых сторон, а средняя линия — полусумме боковых сторон: 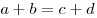 ,
, 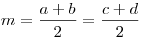 .
.
Окружность, описанная около четырёхугольника.
Если вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник — вписанным в эту окружность.
Теоремы:
-
Центром описанной окружности является точка пересечения серединных перпендикуляров к сторонам.
-
В любом четырёхугольнике, вписанном в окружность, сумма противоположных углов равна 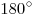 .
.
-
Из всех параллелограммов окружность можно описать около прямоугольника, квадрата.
Вневписанная окружность.
Вневписанная окружность — окружность, касающаяся одной стороны треугольника и продолжения двух других его сторон.
Теорема. Расстояние от вершины треугольника до точки касания вневписанной окружности с продолжением его боковой стороны равно полупериметру p: 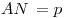 .
.
Примечание:точка касания вневписанной окружности со стороной треугольника делит его периметр пополам: 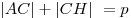 .
.
Следствие: 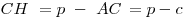 ,
, 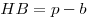 .
.
Теорема. Радиус вневписанной окружности, проведённый к стороне a, вычисляется по формуле:

1.2. Исследование «Число π»
Часто в практических задачах нужно узнать длину окружности. А как измерить длину окружности, если сама окружность – кривая линия, а единица измерения длины – отрезок? Есть несколько способов измерения длины окружности.
Многие учёные – математики пытались доказать, что это отношение есть число постоянное, не зависящее от размеров окружности, его стали обозначать греческой буквой π-ервая буква греческого слова “периферия” – круг.
С:d = π, где С – длина окружности, d – длина диаметра, отсюда и формула длины окружности C = πd или C = 2πr.
Изучив исследования учёных математиков, мы провели следующие измерения и вычисления«числа π»:
а) с помощью тонкой нити измерили длину окружности С некоторых предметов быта;
б) чтобы точнее найти длину диметра d, приложили этот предмет к листу бумаги и обвели карандашом, вырезали, свернули пополам, линия сгиба – это диаметр, измерили его с помощью линейки;
в) нашли отношение С:d, данные занесли в таблицу:
Таблица 1.
| Предметы | Длина окружности С | Диаметр d | Отношение С:d |
| Стакан | 22 см | 7 см | 3.1428 |
| Ведро | 82 см | 26 см | 3.1538 |
| Тарелка | 62 см | 19,5 см | 3,1794 |
| Кастрюля | 69 см | 22 см | 3.1363 |
| Бидон | 52 см | 16,5 см | 3,1515 |
Границы значения числа пи:
а) с помощью циркуля вписали круг в квадрат: если диаметр равен 1,то длина окружности равна π. Периметр квадрата со стороной 1 равен 4. Значит π меньше 4.
б) в этот же круг вписали правильный шестиугольник: диаметр круга снова 1, длина окружности равна π. Сторона правильного шестиугольника равна радиусу, т.е.0,5,а периметр равен 6·0,5=3,значит π больше 3
В результате мы убедились, что отношение длины окружности к ее диаметру (число π) есть число постоянное и 3 ‹ π ‹ 4 ,т.е. мы подтвердили исследования учёных – математиков.
1.3. Теорема Птолемея.
Эта теорема понадобилась александрийскому астроному Клавдию Птолемею, жившему во II в. н. э., для составления таблицы синусов, точнее, таблицы длин хорд. Частные случаи своей теоремы Птолемей использовал для составления своих таблиц, очень нужных для астрономических расчётов. Таблицы хорд Птолемея, сохранившиеся до наших дней, соответствуют таблице синусов от 0° до 90° (через 0,25°)- с пятью верными знаками после запятой.
В эпоху средневековья книга Птолемея, в которой содержались обширные сведения по астрономии, получила распространение в странах арабского Востока; астрономы называли её там “Аль Маджисти” “Величайшее”, отсюда и происходит её название “Альмагест”.
Теорема. Произведение диагоналей вписанного четырёхугольника равно сумме произведений его противоположных сторон.
Доказательство (близкое к доказательству самого Птолемея).
В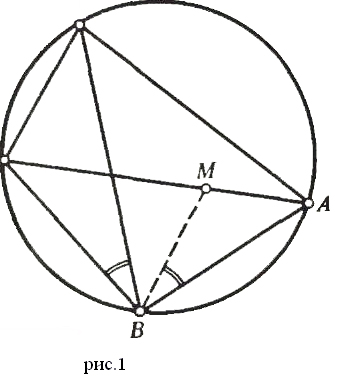 озьмём на диагонали АС точку М (рис.1) такую, что ABM=CBD. Поскольку CDB= MAB как вписанные, треугольники BCD и АВМ подобны. Поэтому ,
озьмём на диагонали АС точку М (рис.1) такую, что ABM=CBD. Поскольку CDB= MAB как вписанные, треугольники BCD и АВМ подобны. Поэтому ,
1)ABCD =АМBD
Из того, что ABD =MBC по построению, a BCM =ADB как вписанные, следует, что ABD ~ МВС.
Значит,
2) ADВС = BDСМ
Сложив почленно равенства (1) и (2), получим:
ABCD+ADВС= BD(AM + CM)=BDАC, что и требовалось доказать.
Глава 2.Круг.
Круг– это множество точек на плоскости, ограниченных окружностью (т.е. лежащих внутри окружности).
Сектор круга – область внутри круга, которая образована двумя радиусами и дугой между ними.
Сегмент круга – область, образованная в результате деления круга хордой, которая в свою очередь является частью секущей (прямой), пересекающей круг.
Свойства круга. -
Центр круга совпадает с центром ограничивающей его окружности. Чаще всего, обозначается буквой O.
-
Радиус круга (R) является, в т.ч., радиусом граничной окружности. Это отрезок, соединяющий центр круга с любой точкой, лежащей на его границе, т.е. на окружности.
Хорда, проходящая через центр круга называется его диаметром (d).
Формулы: -
П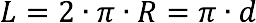 ериметр круга (L):
ериметр круга (L):
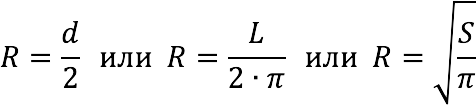
2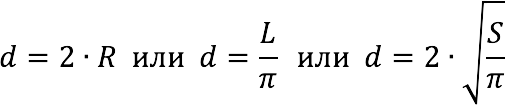 . Радиус круга (R):
. Радиус круга (R):
3. Диаметр круга (d):
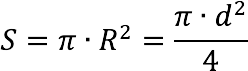
4. Площадь круга (S):

5. Площадь сектора (S):
Глава 3. Применение теорем окружности и круга при решении задач.
Задание 1. Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 83°. Найдите величину угла OMK. Ответ дайте в градусах.
Решение:
Н айдём угол OKM: OKM = 90° − 83° = 7°.
айдём угол OKM: OKM = 90° − 83° = 7°.
Треугольник OMK —равнобедренный, поэтому угол OMK равен углу OKM и равен 7°
Ответ: 7°.
Задание 2. Радиус вписанной в квадрат окружности равен 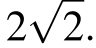 Найдите радиус окружности, описанной около этого квадрата.
Найдите радиус окружности, описанной около этого квадрата.
Р ешение:
ешение:
С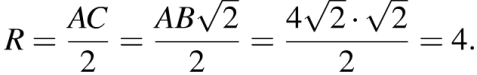 торона квадрата вдвое больше радиуса вписанной в него окружности. Поэтому
торона квадрата вдвое больше радиуса вписанной в него окружности. Поэтому 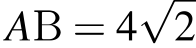 . Радиус описанной вокруг квадрата окружности равен половине его диагонали. Поэтому:
. Радиус описанной вокруг квадрата окружности равен половине его диагонали. Поэтому:
Ответ: 4.
Задание 3. Отрезок AB = 45 касается окружности радиуса 60 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
Решение:
Р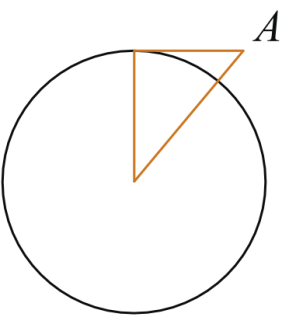 адиус окружности перпендикулярен касательной в точке касания. Из прямоугольного треугольника AOB по теореме Пифагора найдём
адиус окружности перпендикулярен касательной в точке касания. Из прямоугольного треугольника AOB по теореме Пифагора найдём 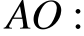
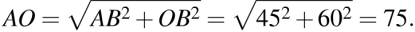
Н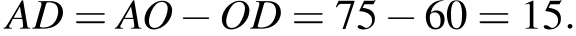 айдём
айдём 
Ответ: 15.
Задание 4. Сторона равностороннего треугольника равна 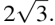 Найдите радиус окружности, вписанной в этот треугольник.
Найдите радиус окружности, вписанной в этот треугольник.
Р ешение:
ешение:
В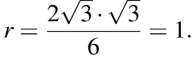 оспользуемся приведённой в справочных материалах формулой, связывающий сторону правильного треугольника и радиус окружности, вписанной в этот треугольник:
оспользуемся приведённой в справочных материалах формулой, связывающий сторону правильного треугольника и радиус окружности, вписанной в этот треугольник: 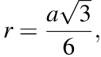 тогда:
тогда:
Ответ: 1.
Заключение.
На протяжении нашей работы мы прочитали и изучили материал по теме «Основные свойства и формулы окружности и круга». Мы ставили перед собой цель глубокого изучения данной темы и использование полученных знаний в решении задач. На наш взгляд данная тема является актуальной в наше время.
Геометрические построения являются неотъемлемой частью математического образования и основой заданий геометрической части ОГЭ. Задачи с окружностью и кругом представляют прекрасное средство для развития логического и абстрактного мышления.
С помощью одной только теоремы можно решить несколько заданий. Таким образом, знание основных свойств и теорем значительно сокращает время решения, а так же может добавить к итогу несколько баллов, что крайне важно.
Работая над данной темой, мы углубили и расширили свои знания об окружности, её элементах и свойствах.
В ходе исследования были решены следующие задачи:
-
Рассмотреть важнейшие теоремы и свойства.
-
Провести математическое исследование «Число π».
-
Применить полученные знания в решении задач.
Цель данного итогового проекта выполнена. Материал, приведённый в данной работе, может служить материалом для подготовки к ОГЭ.
Список литературы.
Геометрия. 7-9 классы: учеб. для общеобразоват. учреждений /Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 20-е изд. – М.: Просвещение, 2010. – 384 с.(стр.164-187)
Сайт – «Решу ОГЭ»
Открытый банк заданий.
Геометрия: учеб. Для 7-9 кл. общеобразоват. учреждений / А.В. Погорелов. – 2-е изд. – М.: Просвещение, 2001.
Интернет ресурс: http://matschool2005.narod.ru/Lessons/Lesson8.htm
https://www.bibliofond.ru/view.aspx?id=457106#text
Костовский, А.Н. Геометрические построения одним циркулем / А.Н. Костовский. – М.: Наука, 2014. – 122 с.
Костовский, А.Н. О возможности решения задач на построение одним циркулем с ограниченным раствором ножек / А.Н. Костовский. – М.: Наука, 2014. – 222 с.
Красс, М.С. Основы математики и её приложения в экономическом образовании / М.С. Красс. – М.: Дело, 2011. – 212 с.
http://www.univer.omsk.su/
https://www.fun4child.ru/1113-matematicheskie-stikhi






 .Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
.Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
 .Отрезок, соединяющий две точки окружности, называется её хордой. Хорда, проходящая через центр окружности, называется диаметром.
.Отрезок, соединяющий две точки окружности, называется её хордой. Хорда, проходящая через центр окружности, называется диаметром. иаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.
иаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.
 сли две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB =CM•MD.
сли две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB =CM•MD. ерез три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
ерез три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну. еорема о касательной и секущей.
еорема о касательной и секущей. еорема о секущих.
еорема о секущих. ентральным углом в окружности называется плоский угол с вершиной в её центре.
ентральным углом в окружности называется плоский угол с вершиной в её центре.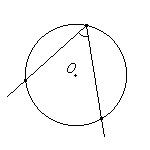 гол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом.
гол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом.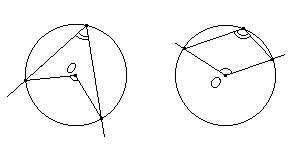 писанный угол либо равен половине соответствующего ему центрального угла, либо дополняет половину этого угла до 180°.
писанный угол либо равен половине соответствующего ему центрального угла, либо дополняет половину этого угла до 180°. глы, вписанные в одну окружность и опирающиеся на одну и ту же дугу, равны.
глы, вписанные в одну окружность и опирающиеся на одну и ту же дугу, равны. писанный угол, опирающийся на диаметр, равен 90°.
писанный угол, опирающийся на диаметр, равен 90°.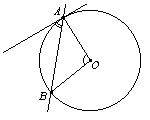 гол, образованный касательной к окружности и секущей, проведённой через точку касания, равен половине дуги, заключённой между его сторонами.
гол, образованный касательной к окружности и секущей, проведённой через точку касания, равен половине дуги, заключённой между его сторонами. лина дуги окружности L радиуса R с центральным углом
лина дуги окружности L радиуса R с центральным углом  =
=  коло выпуклого четырёхугольника можно описать окружность тогда и только тогда, когда сумма его внутренних противоположных углов равна 180°:
коло выпуклого четырёхугольника можно описать окружность тогда и только тогда, когда сумма его внутренних противоположных углов равна 180°: четырёхугольник можно вписать окружность тогда и только тогда, когда у него равны суммы противоположных сторон:
четырёхугольник можно вписать окружность тогда и только тогда, когда у него равны суммы противоположных сторон: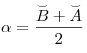 еорема (угол между пересекающимися хордами). Угол между двумя пересекающимися хордами равен полусумме высекаемых ими дуг:
еорема (угол между пересекающимися хордами). Угол между двумя пересекающимися хордами равен полусумме высекаемых ими дуг: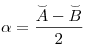 еорема (угол между секущими). Угол между двумя секущими, проведёнными из одной точки, равен полуразности большей и меньшей высекаемых ими дуг:
еорема (угол между секущими). Угол между двумя секущими, проведёнными из одной точки, равен полуразности большей и меньшей высекаемых ими дуг: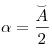 еорема (угол между касательной и хордой, проведённой через точку касания). Угол между касательной и хордой, проведённой в точку касания, равен половине дуги, стягиваемой этой хордой:
еорема (угол между касательной и хордой, проведённой через точку касания). Угол между касательной и хордой, проведённой в точку касания, равен половине дуги, стягиваемой этой хордой: озьмём на диагонали АС точку М (рис.1) такую, что ABM=CBD. Поскольку CDB= MAB как вписанные, треугольники BCD и АВМ подобны. Поэтому ,
озьмём на диагонали АС точку М (рис.1) такую, что ABM=CBD. Поскольку CDB= MAB как вписанные, треугольники BCD и АВМ подобны. Поэтому ,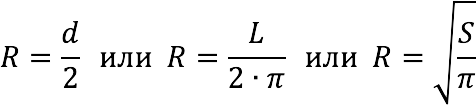
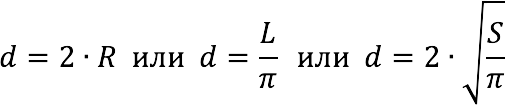 . Радиус круга (R):
. Радиус круга (R): айдём угол OKM: OKM = 90° − 83° = 7°.
айдём угол OKM: OKM = 90° − 83° = 7°. ешение:
ешение: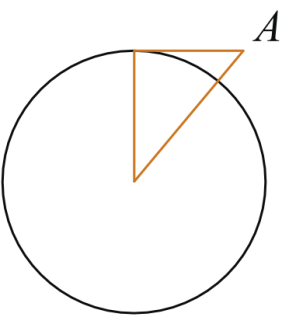 адиус окружности перпендикулярен касательной в точке касания. Из прямоугольного треугольника AOB по теореме Пифагора найдём
адиус окружности перпендикулярен касательной в точке касания. Из прямоугольного треугольника AOB по теореме Пифагора найдём  ешение:
ешение:

















