Муниципальное автономное образовательное учреждение «Лицей №14 имени Заслуженного учителя Российской Федерации А.М. Кузьмина»
ИНДИВИДУАЛЬНЫЙ ПРОЕКТ:
«Замечательные точки треугольника»
Выполнила:
Учащаяся 10 класса «К»
Островерхова Татьяна Сергеевна
Руководитель:
Андрющенко Алла Рудольфовна,
учитель математики
Тамбов, 2022
Оглавление
ВВЕДЕНИЕ 3
1. Задача Эйлера 5
2. Лемма Мансиона (лемма о трезубце) 10
3. Многообразие доказательств теорем о прямой и окружности Эйлера. 14
1. Доказательство теоремы об окружности Эйлера 2 способом. 14
2. Доказательство теоремы об окружности Эйлера 3 способом. 17
3. Доказательство теоремы о прямой Эйлера 2 способом. 18
4. Теорема Симсона. 20
5. Теорема Жергонна. 21
6. Решение задач на тему «Замечательные точки треугольника». 22
7. Заключение. 33
СПИСОК ЛИТЕРАТУРЫ 34
Приложение 1. 35
Приложение 2. 36
ВВЕДЕНИЕ
Треугольник – геометрическая фигура, неисчерпаемая для изучения. Более того, его исследование можно начать, используя лишь одно свойство, рассмотрение которого приведет к множеству других полезных фактов, теорем, понятий, связанных с треугольником, в частности, к его замечательным точкам.
Выходя за рамки школьной программы, которая рассматривает 4 основные замечательные точки треугольника (центроид, инцентр, ортоцентр, центр описанной окружности), существует также большое количество и других, не менее интересных для изучения, точек. В работах Евклида и Архимеда были доказаны и изложены свойства основных четырех точек треугольника, которые назвали «замечательными» или «особенными» только в 18 веке. Однако основоположники «новой геометрии треугольника»: Эйлер, Жергонн, Симсон, Мансион и другие смогли открыть новые замечательные точки, изучению которых и будет посвящен мой проект.
Актуальность этой темы состоит в необходимости расширения знаний о точках треугольника. Данную фигуру можно считать основой планиметарной геометрии. Знание о его точках, прямых, окружностях – залог решения задач с любыми фигурами любой сложности. Зачастую различные олимпиады проверяют способность учеников видеть и применять нестандартные, редкоиспользуемые теоремы о замечательных точках треугольника.
Цель исследования – рассмотреть и овладеть различными геометрическими свойствами замечательных точек треугольника, экспериментально-практически изучить многообразие доказательств теорем о данных точках, используя интерактивное приложение Geogebra.
Задачи:
Провести теоретическое исследование теорем о замечательных точках треугольника.
Ознакомиться с функциональными составляющими системы Geogebra.
Изучить созданные модели, проанализировать многообразие подходов к доказательству теорем.
Решить задачи на тему «Замечательные точки треугольника»
Создать видео, в которых будут продемонстрированы основные теоремы, выходящие за рамки школьного курса и решить задачи по данным темам.
Создать математическую игру для учащихся восьмых классов, с целью проверки знаний в интерактивной форме, по теме «Замечательные точки треугольника».
 Задача Эйлера
Задача Эйлера
Что такое Задача Эйлера? Это одна из красивейших задач геометрии, которая состоит из четырех подзадач, связанных с окружностью Эйлера и прямой Эйлера, и включает в себя понятие еще одной замечательной точке треугольника. Рассмотрим каждую из подзадач, докажем их.
Задача Эйлера:
Точки, симметричные точке Н пересечения высот (или их продолжений) относительно сторон треугольника и их середин, лежат на описанной окружности.
Теорема об окружности Эйлера (теорема об окружности девяти точек). Середины сторон, основания высот и середины отрезков, соединяющих точку Н с вершинами, лежат на одной окружности, центром которой является середина отрезка, соединяющая точку Н с центром описанной окружности, а ее радиус в два раза меньше радиуса описанной окружности (эта окружность называется окружностью Эйлера).
Точка пересечения медиан лежит на отрезках, соединяющих точку Н с центром описанной окружности. Прямая, на которой лежат 4 точки – точка Н, точка пересечения медиан, центр описанной окружности и центр окружности Эйлера, называется прямой Эйлера.
Точки, симметричные центру описанной окружности относительно прямых, содержащих средние линии треугольника, лежат на окружности Эйлера.
Первая подзадача.
Дано: Треугольник АВС; А1, В1, С1 – середины сторон ВС, СА, АВ; А2, В2, С2 – основания высот, проведенных к этим сторонам; А3, В3, С3 - середины отрезков АН, ВН, СН; А4, В4, С4 – точки, симметричные точке Н относительно сторон треугольника; А5, В5, С5 – точки, симметричные точке Н относительно середин этих сторон; А6, В6, С6 – точки, симметричные точке О относительно прямых В1С1, А1С1, А1В1; Н – точка пересечения высот; G – точка пересечения медиан.
 Доказательство:
Доказательство:


Первый случай
Рассмотрим первый случай, когда один из углов треугольника АВС, например, угол А, - прямой, то точки Н, В
4, С
4 совпадают с точкой А (высоты из В и С это соответственно отрезки ВА и АС), точка В
5 – с точкой С, а точка С
5 – с точкой В. Поскольку ∠ВА
4С=∠ ВА
5С= ∠А = 90°, то точки А, А
4, А
5 лежат на окружности с диаметром ВС. Таким образом, точки А
4, А
5, В
5, С
4, С
5 лежат на окружности, описанной около треугольника АВС.

Второй случай
Второй случай. Допустим, что треугольник АВС не является прямоугольным. Поскольку ∠АВ
2Н=∠АС
2Н =90°, то точки В
2 и С
2 лежат на окружности с диаметром АН. Следовательно, вписанные по отношению к этой окружности углы В
2АС
2 и В
2НС
2, а значит, и углы ВАС и ВНС, либо равны, либо составляют в сумме 180° (так как это противоположные углы во вписанном в окружность четырехугольнике АС
2НВ
2). В обоих случаях sin∠ВНС = sin∠ВАС.
Пусть R1 – радиус окружности, описанной около треугольника НВС. В соответствии с теоремой синусов ВС = 2 R1 sin∠ВНС =2 R1 sin∠ВАС. При этом sin∠ВНС = sin∠ВАС. Значит, R1= R. Из этого следует, что окружности, описанные около треугольника АВС и НВС, симметричны относительно прямой ВС и относительно середины отрезка ВС. Точка Н лежит на окружности, описанной около треугольника НВС. Следовательно, симметричные ей точки А4 и А5 лежат на окружности, описанной около треугольника АВС. Аналогично доказывается, что точки В4, В5, С4, С5 также лежат на этой окружности.
Вторая подзадача.

Вторая подзадача
Д  ано:
ано: Треугольник АВС; А
1,
В
1,
С
1 – середины сторон ВС, СА, АВ; А
2,
В
2, С
2 – основания высот, проведенных к этим сторонам; А
3,
В
3,
С
3 - середины отрезков АН, ВН, СН; А
4,
В
4,
С
4 – точки, симметричные точке Н относительно сторон треугольника; А
5,
В
5,
С
5 – точки, симметричные точке Н относительно середин этих сторон; А
6,
В
6,
С
6 – точки, симметричные точке О относительно прямых В
1С
1,
А
1С
1, А
1В
1; Н – точка пересечения высот, О – центр описанной окружности.
Доказательство:
Рассмотрим центральное подобие с центром H и коэффициентом ½. При этом подобии описанная окружность переходит в окружность радиуса R/2, центр O9, который является серединой отрезка ОН, а точки А5, В5, С5, А4, В4, С4, А, В, С описанной окружности переходят в точки А1, В1, С1 (середины сторон), А2, В2, С2 (основания высот), А3, В3, С3 (середины отрезков АН, ВН, СН). Следовательно, точки А1, В1, С1, А2, В2, С2, А3, В3, С3 лежат на окружности с центром О9 радиуса R/2. Утверждение доказано.
Третья подзадача.
Дано: Треугольник АВС; А1, В1, С1 – середины сторон ВС, СА, АВ; А2, В2, С2 – основания высот, проведенных к этим сторонам; Н – точка пересечения высот; G – точка пересечения медиан; О – центр описанной окружности.
Доказательство:
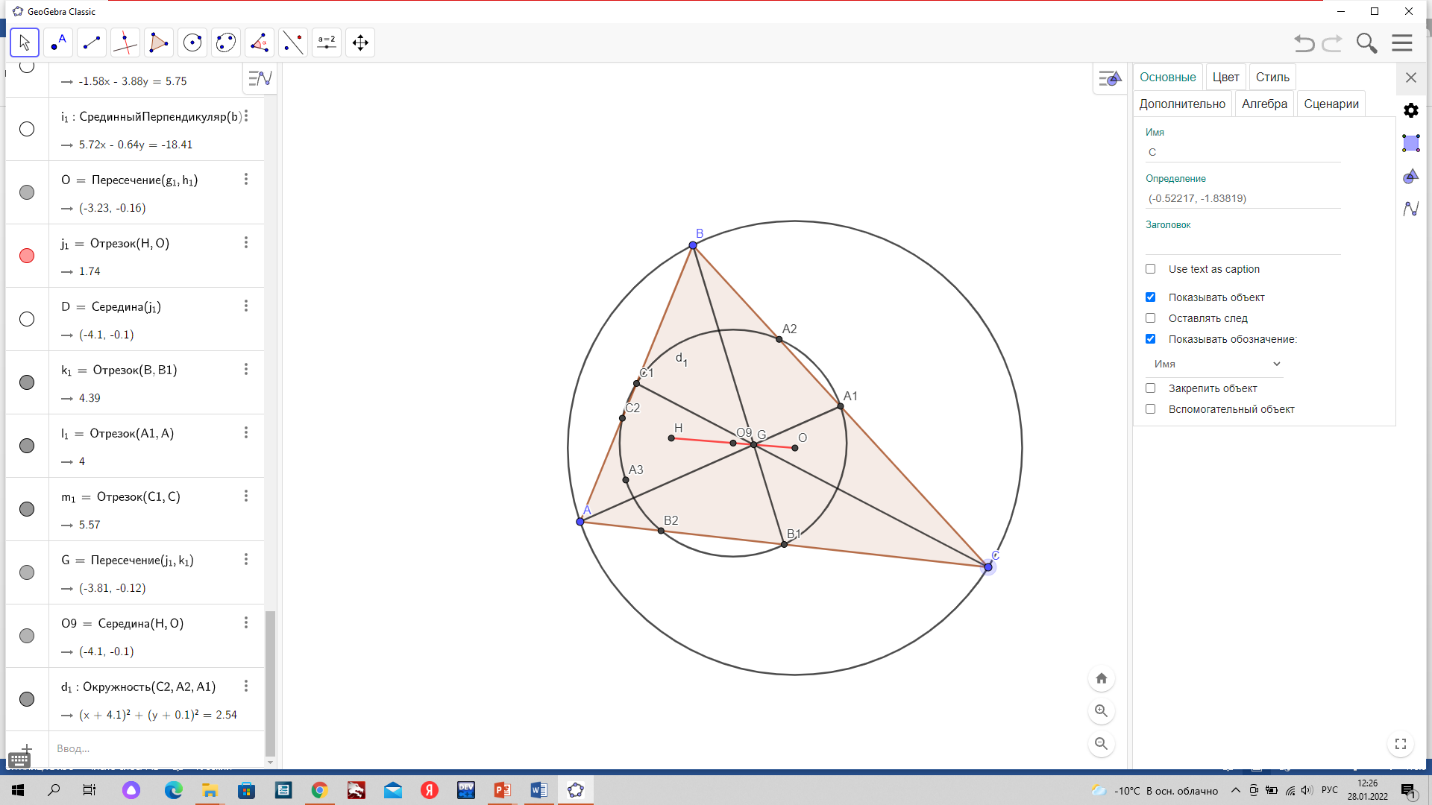

Третья подзадача
Рассмотрим центральное подобие с центром G и коэффициентом – ½. Медианы треугольника АВС делятся точкой G в отношении 1:2, поэтому при рассматриваемом центральном подобии вершины А, В, С перейдут в середины А
1,
В
1,
С
1 противоположных сторон. Следовательно, прямые, содержащие высоты треугольника, перейдут в прямые, перпендикулярные к его сторонам и проходящие через их середины, то есть в серединные перпендикуляры к сторонам. Поэтому точка Н перейдет в центр О описанной окружности. Это означает, что точка G лежит на отрезке ОН и делит его в отношении 1:2, считая от точки О. Что и требовалось доказать.
Четвертая подзадача.
Дано: Треугольник АВС; А1, В1, С1 – середины сторон ВС, СА, АВ; А2, В2, С2 – основания высот, проведенных к этим сторонам; А3, В3, С3 – середины отрезков АН, ВН, СН; А4, В4, С4 – точки, симметричные точке Н относительно сторон треугольника; А6, В6, С6 – точки, симметричные точке О относительно прямых В1С1, А1С1, А1В1; Н – точка пересечения высот, О – центр описанной окружности G – точка пересечения медиан.
Доказательство:


Четвертая подзадача
Было отмечено, что при центральном подобии с центром G и коэффициентом - ½ вершины А, В и С переходят в середины А
1,
В
1,
С
1 противоположных сторон, а точка Н переходит в точку О. Из этого следует, что а) окружность, описанная около треугольника АВС, переходит в окружность Эйлера; б) точки А
4,
В
4,
С
4 описанной окружности, симметричны точке Н относительно прямых ВС, СА, АВ, переходят в точки А
6,
В
6,
С
6 окружности Эйлера, симметричные точке О относительно прямых В
1С
1,
А
1С
1, А
1В
1. Таким образом, точки А
6,
В
6,
С
6 лежат на окружности Эйлера.
Лемма Мансиона (лемма о трезубце)
Рассмотрим лемму о трезубце, также называемую леммой о трилистнике и леммой Мансиона, — теорема в геометрии треугольника, связанная со свойствами вписанной, вневписанной и описанной окружностей треугольника.
Лемма Мансиона гласит: в треугольнике АВС, где I – центр вписанной окружности, а Iв – центр вневписанной окружности, касающейся стороны АС, биссектриса угла В пересекает описанную окружность треугольника АВС в точке L, то LA=LС=LI=LIB.
 Дано: Треугольник АВС, окружность, описанная около АВС, ВМ – биссектриса ∠В, BIB пересекает окружность в точке L, I – центр вписанной окружности, а Iв – центр вневписанной окружности.
Дано: Треугольник АВС, окружность, описанная около АВС, ВМ – биссектриса ∠В, BIB пересекает окружность в точке L, I – центр вписанной окружности, а Iв – центр вневписанной окружности.
Доказать: LA=LС=LI=LIB
Доказательство:

Лемма Мансиона
I – центр вписанной в треугольник АВС окружности, то есть центр пересечения биссектрис, значит ∠ABL = ∠CBL и являются вписанными, значит дуги AL, LC равны. Равные дуги стягивают равные хорды, следовательно, AL=LC.
Докажем, что треугольник ALI – равнобедренный. Обозначим ∠BAI=∠CAI=α; ∠ABI=∠CBI=β. ∠LAC = ∠CBL (вписанные углы, опирающие за одну дугу). ∠LAI= α+β= ∠AIL (он внешний для треугольника AIB). Значит треугольник ALI – равнобедренный, AL=LI.
Iв лежит на пересечении биссектрис внешних углов для угла ВАС, АСВ и угла В АIв – биссектриса, АI – биссектриса. Биссектрисы смежных углов перпендикулярны. Треугольник АIIв – прямоугольный, AL=LI, следовательно, IL=LIв (отрезок, проведенный из вершины прямого угла к гипотенузе и равный ее половине – медиана).
Значит LA=LС=LI=LIB, что и требовалось доказать.
Внешняя лемма о трезубце.
Точка пересечения биссектрисы внешнего угла В треугольнике АВС с его описанной окружностью равноудалена от точек А, С, IA, IC, где IA – центр вневписанной окружности, касающийся ВС, IC - центр вневписанной окружности, касающийся АВ.
Дано: треугольник АВС, ВN – биссектриса внешнего угла В, пересекается с описанной около треугольника АВС окружностью в точке N.
Доказать: NА=NС=NIC=IAN
Доказательство:
IA и Iс лежат на биссектрисах вертикальных углов, точки IA, Iс, В лежат на одной прямой.
Проведем NL (L – середина дуги АС, BL – биссектриса), данный отрезок – диаметр окружности, так как BL – биссектриса ∠АВС, а ВN – биссектриса ∠СВТ, эти углы смежные, а биссектрисы смежных углов перпендикулярны, значит ∠LBN опирается на диаметр.
NL – серединный перпендикуляр к АС. Рассмотрим треугольники ANL=LCN (NL- общая, AL=LC, так как равные хорды, ∠NLC = ∠ALN), значит AN=NC, N равноудалена от АС.
∠IAАIC – прямоугольный (биссектрисы смежных углов образуют прямой угол), аналогично ∠IAСIC – прямоугольный, значит около четырехугольника IAICСА можно описать окружность (IAIC виден под прямым углом), IAIC – диаметр. (см. рис. 1)


Рис. 1
Предположим, что середина диаметра – точка О1 (центр окружности). Центр описанной около четырехугольника окружности лежит в точке пересечения серединных перпендикуляров к его сторонам. NL – серединный перпендикуляр к AC, но центр должен обязательно находиться на диаметре. Эти две прямые пересекаются только в одной точке – N. (см. рис. 2)


Рис. 2
Значит IAN = NIC. В треугольнике IAАIC АN – медиана, равна половине гипотенузы, IAN = NIC= АN= СN. (см. рис. 3)
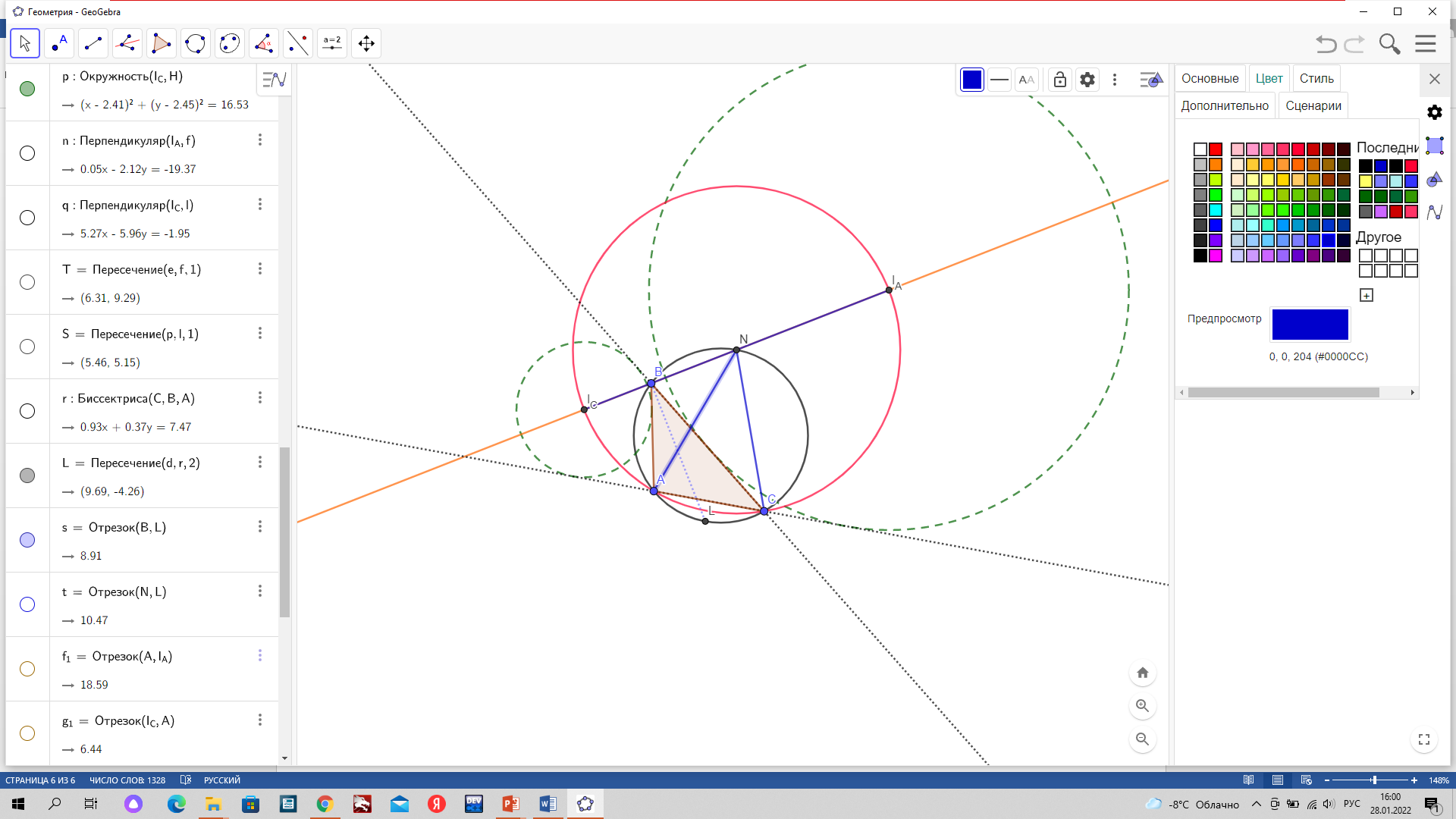

Рис. 3
Многообразие доказательств теорем о прямой и окружности Эйлера.
Рассмотрим еще несколько способов доказательства теоремы о замечательной точке треугольника – центре окружности Эйлера.
1. Доказательство теоремы об окружности Эйлера 2 способом.
Теорема: Основания трех высот треугольника, середины трех его сторон и середины трех отрезков, соединяющих вершины треугольника с ортоцентром, лежат на одной окружности.
Дано: Треугольник АВС, высоты АHA, АHВ, АHС, которые пересекаются в точке Н; К, N, L – середины AH, CH, BH соответственно. В1, А1, С1 – середины АС, ВС, АВ соответственно.
Доказать: HA, HВ, HС, К, N, L, В1, А1, С1 лежат на одной окружности (окружности Эйлера).
Доказательство:
1 часть через лемму о трезубце (см. рис. 4):
АHA, АHВ, АHС – биссектрисы треугольника НAHBHC – ортотреугольника треугольника АВС (высоты остроугольного треугольника являются биссектрисами его ортотреугольника).


Рис. 4
HС пересекает описанную около треугольника H
СH
ВH
А окружность. HСN пересекает ее точке N, H – центр вписанной окружности (пересечение биссектрис), С – центр вневписанной окружности (так как лежит на биссектрисе ∠H
ВH
СH
А и на биссектрисе внешнего угла H
ВH
АЕ (биссектриса смежного угла образует ∠АH
АС = 90° с прямой СHА)). По лемме Мансиона HN=NC, значит середина отрезка НС лежит на окружности, проходящей через H
С,
H
В,
H
А.
Аналогично с К, L.
2 часть через внешнюю лемму о трезубце (см. рис. 5):
Точка В1 - точка пересечения окружности Эйлера и биссектрисы внешнего угла HAHВF для треугольника, равноудалена от вершин А и С треугольника АВС по внешней лемме о трезубце.
Аналогично с точками А1, С1.
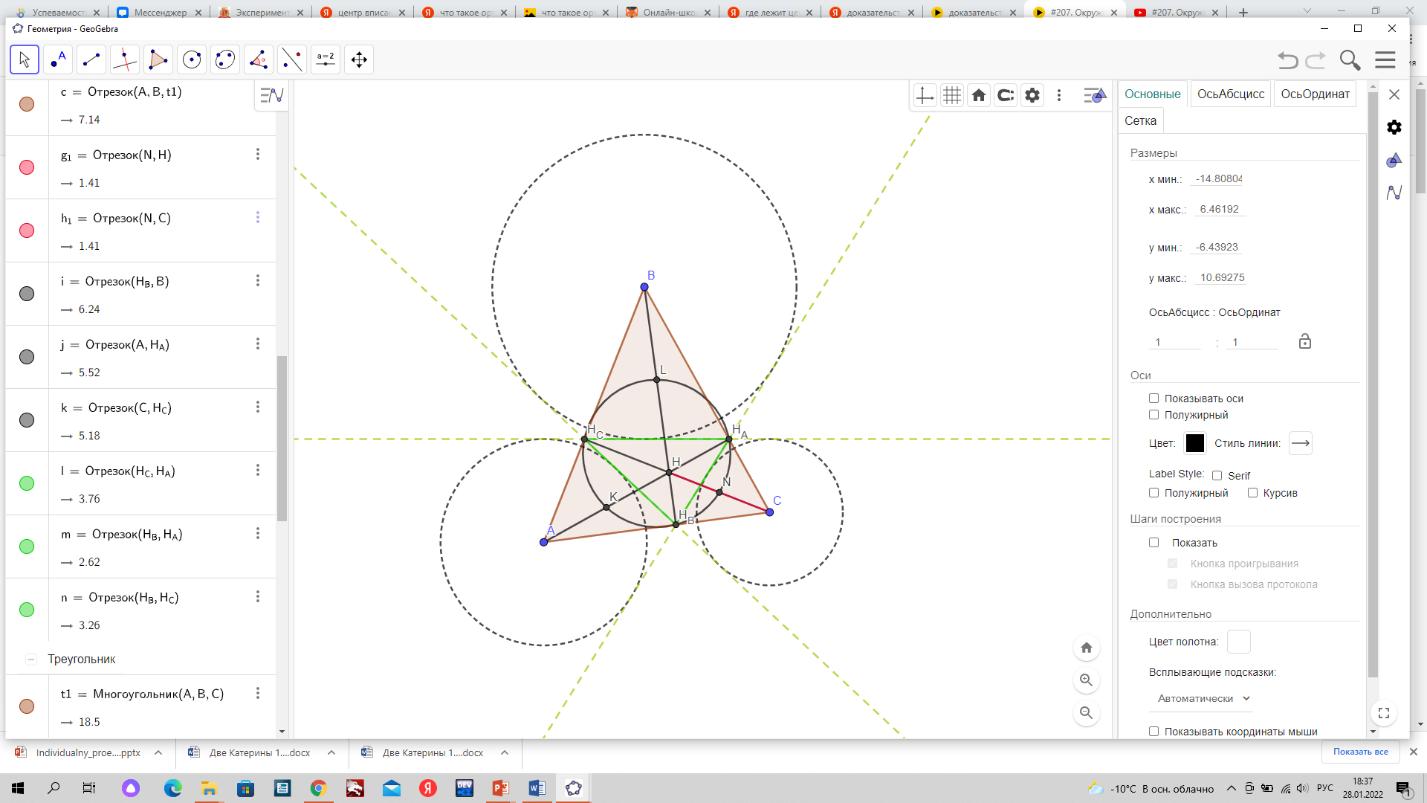

Рис. 5
Для следующего доказательства теорем об окружности и прямой Эйлера рассмотрим вспомогательную теорему.
Лемма: Если Н – ортоцентр треугольника АВС, ОМ1 – перпендикуляр, опущенный из центра О описанной окружности на сторону ВС, то АН = 2ОМ1. (см. рис. 6)
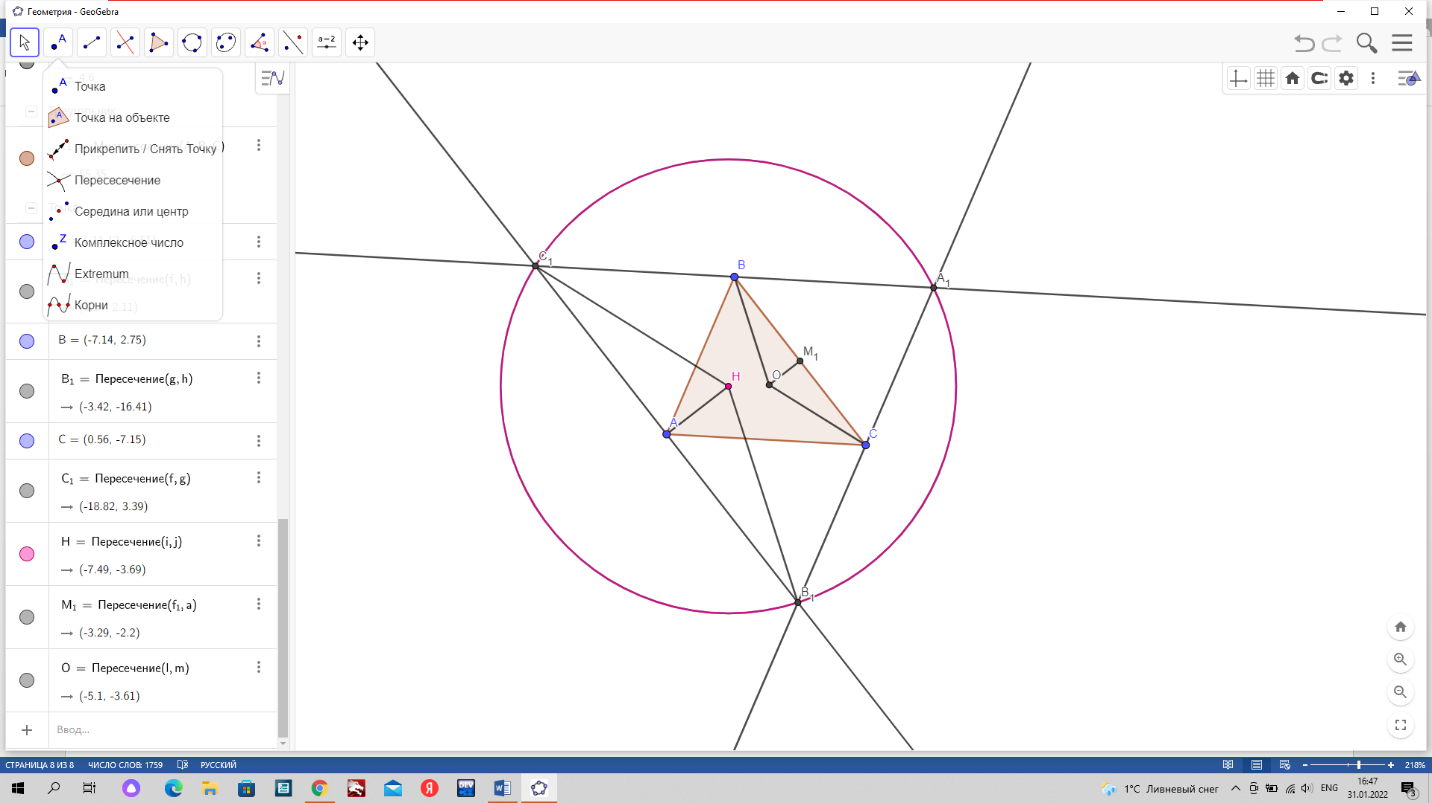 Дано: треугольник АВС, ОМ1 перпендикулярен ВС
Дано: треугольник АВС, ОМ1 перпендикулярен ВС
Доказать: АН = 2ОМ1
Доказательство:
Выполним дополнительное построение: через каждую вершины треугольника АВС проведем прямую, параллельную противолежащей стороне. Получаем треугольник А1В1С1.

Рис. 6
Ортоцентр Н треугольника АВС является центром описанной окружности треугольника А1В1С1 (по свойству ортоцентрического треугольника). Для этой окружности ∠В1НС1 является центральным, а ∠В1А1С1 – вписанным. Поскольку оба угла опираются на одну и ту же дугу, то ∠В1НС1 = 2∠В1А1С1.
∠В1А1С1 = ∠ВАС, как противолежащие углы параллелограмма АВА1С, поэтому ∠ВОС = 2∠ВАС = 2∠В1А1С1 = ∠В1НС1.
Поскольку В1С1 = 2ВС, то равнобедренные треугольники В1НС1 и СОВ подобны (по трем углам: ∠ВОС = ∠В1НС1, ∠В1С1Н = ∠ С1В1Н = ∠ВСО = ∠СВО) с коэффициентом подобия 2. Поскольку отрезки АН и ОМ1 – соответственные высоты подобных треугольников, то АН = 2ОМ1.
2. Доказательство теоремы об окружности Эйлера 3 способом.
Теорема: Середины сторон треугольника, основания его высот и середины отрезков, соединяющих вершины треугольника с его ортоцентром, лежат на одной окружности, радиус которой равен ½R, где R – радиус описанной окружности данного треугольника. Эту окружность называют окружностью девяти точек или окружностью Эйлера.
Дано: В треугольнике АВС точка Н- ортоцентр, точка О – центр описанной окружности, точка А1 – основание высоты, проведенной из вершины А, точка М1 – середины стороны СВ, точка К1 – середина отрезка АН.
Доказательство:
Согласно лемме, ОМ1 = ½ АН = К1Н. Поскольку АН||ОМ1 (АА1 перпендикулярен СВ, ОМ1 перпендикулярен СВ), то четырехугольники К1АОМ1 и НК1ОМ1 – параллелограммы. Пусть диагонали НК1ОМ1 пересекаются в точке F.
Заметим, что точка F – середина гипотенузы К1М1 прямоугольного треугольника А1К1М1. Следовательно, точки А1, К1, М1 лежат на окружности радиуса FК1 с центром в точке F.
Так как К1АОМ1 – параллелограмм, К1М1 = АО. Тогда FК1 = ½ОА = ½R.
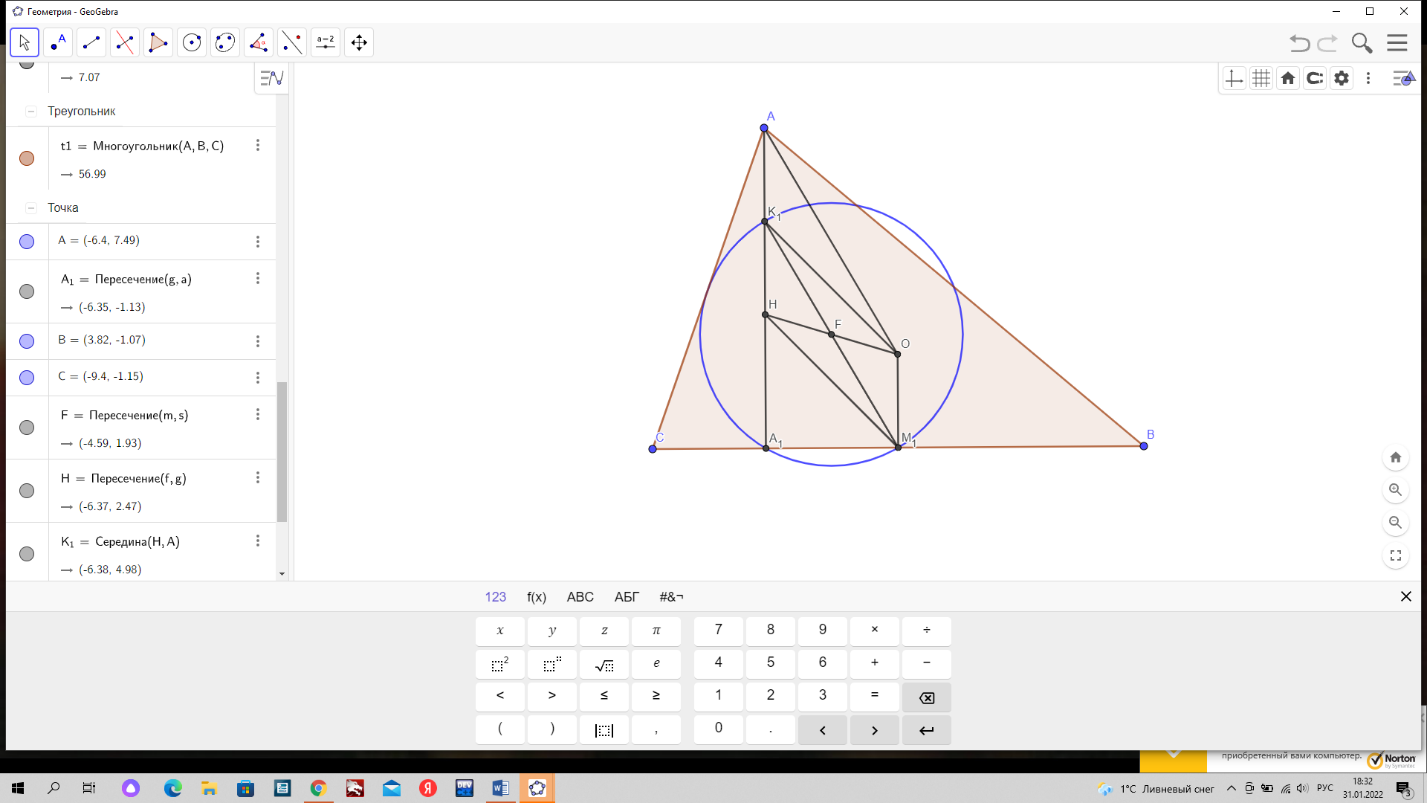 Следовательно, было доказано, что три точки – середина М1 стороны СВ, основание А1 высоты АА1 и середина К1 отрезка НА – лежат на окружности с центром в середине F отрезка НО и радиусом равным ½R.
Следовательно, было доказано, что три точки – середина М1 стороны СВ, основание А1 высоты АА1 и середина К1 отрезка НА – лежат на окружности с центром в середине F отрезка НО и радиусом равным ½R.

Рис. 7
Аналогично можно доказать, что другие тройки точек - В
1, М
2, К
2 и С
1, М
3, К
3, где точки В
1, С
1 – основания высот ВВ
1, СС
1 соответственно, точки М
2, М
3 – середины сторон АС и АВ соответственно, точки К
2, К
3 – середины отрезков НВ и НС

соответственно, - лежат на окружности радиуса ½R с центром в точке F. (см. рис. 7)

Рис. 8
Примечание. Доказательство теоремы для случая тупоугольного треугольника аналогично. (см. рис. 8)
3. Доказательство теоремы о прямой Эйлера 2 способом.
Теорема: В любом треугольнике центр описанной окружности, центроид и ортоцентр лежат на одной прямой, эту прямую называют прямой Эйлера. (см. рис. 9)
Дано: треугольник АВС, О – центр окружности, описанной около АВС, Н – ортоцентр, М – центроид, точка пересечения медиан, АМ1 – медиана проведенная из точки А к стороне ВС.
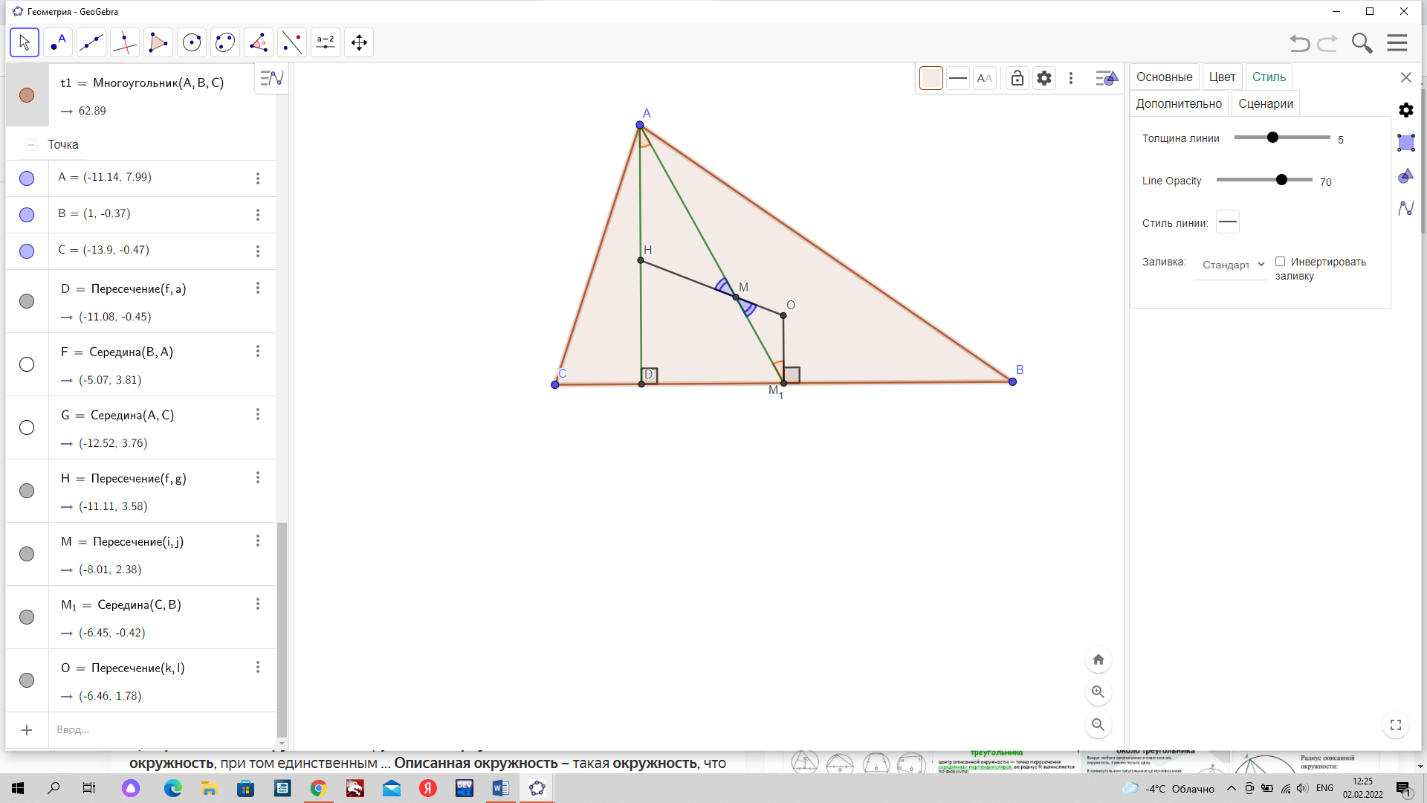 Доказать: О, Н, М лежат на одной прямой
Доказать: О, Н, М лежат на одной прямой
Доказательство:
Если данный треугольник АВС прямоугольный (∠С = 90°), то его ортоцентр – точка С, центр описанной окружности – середина гипотенузы АВ. Тогда все три точки, о которых сказано в теореме, принадлежат медиане, проведенной к гипотенузе.
Рассмотрим теорему для остроугольного треугольника.

Рис. 9
Пусть точка М – точка пересечения отрезков АМ
1 и НО. Поскольку АН||ОМ
1, то ∠НАМ = ∠ОМ
1М. ∠АМН = ∠М
1МО, так как вертикальные. Следовательно, треугольники НАМ и ОМ
1М подобны по первому признаку подобия треугольников. Отсюда

=

= 2.
Значит, точка М делит медиану АМ1 в отношении 2:1, считая от вершины А. Отсюда точка М – центроид треугольника АВС.
Доказательство для случая тупоугольного треугольника аналогично.
Обратим внимание на то, что был установлен факт принадлежности точек О, М и Н одной прямой, но и доказано равенство НМ = 2МО, которое является еще одним свойством замечательных точек треугольника (ортоцентр, центроид, центр окружности, описанной около треугольника).
Теорема Симсона.
Умение работать с прямой Симсона помогает при решении задач, которые требуют доказать, что три точки лежат на одной прямой.
Теорема. Основания перпендикуляров, опущенных на стороны треугольника (или их продолжения) из точки, лежащей на описанной около этого треугольника окружности, лежат на одной прямой. (см. рис. 10)
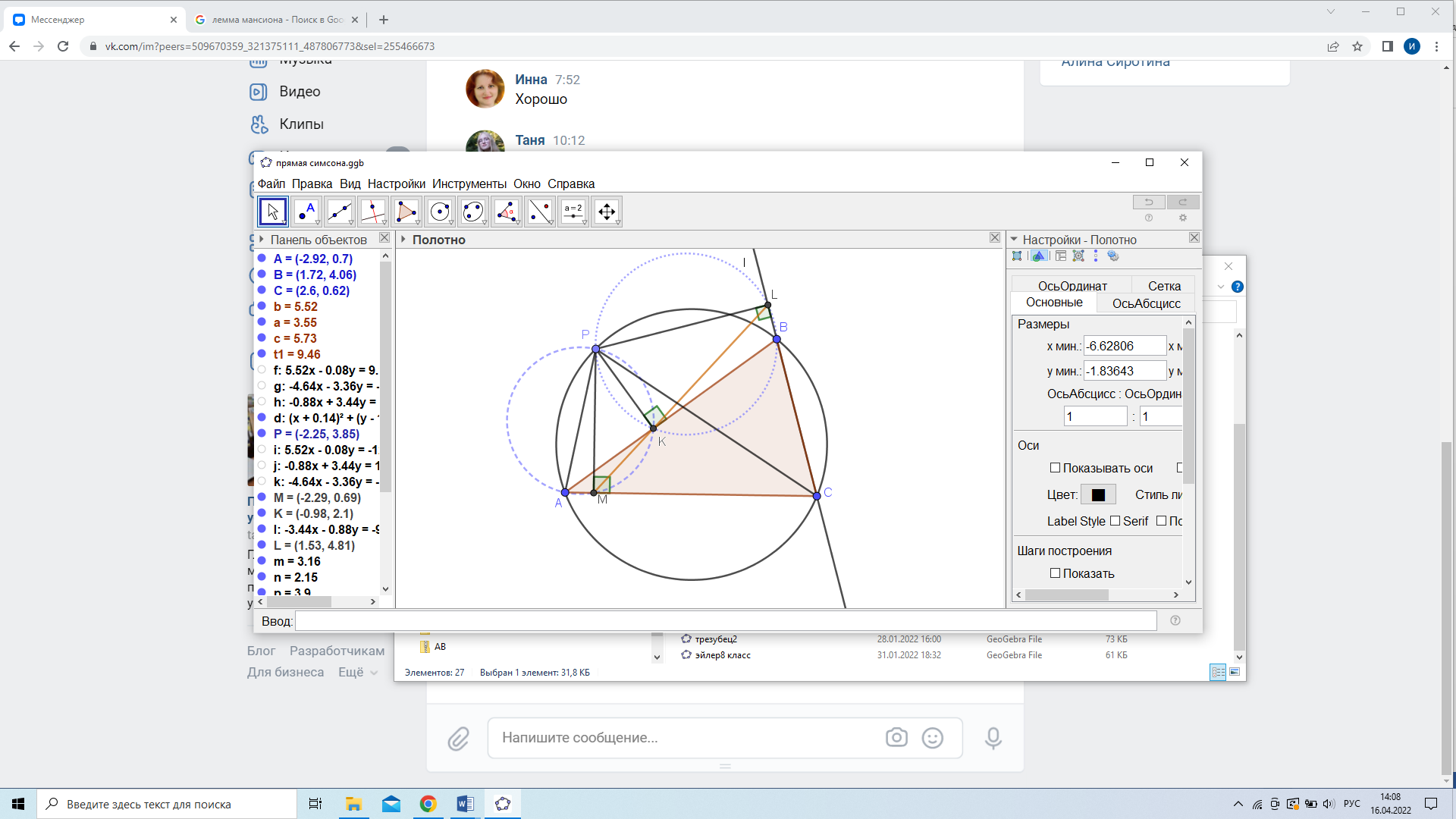

Рис. 10
Доказательство: Пусть точки М, К и L – основания перпендикуляров, опущенных из точки Р на прямые АС, АВ и ВС соответственно. Используя, что ∠АPС = ∠АВС (вписанные и опираются на одну дугу), докажем, что углы АКМ и BKL – вертикальные. Действительно, четырехугольники АМКР (AP виден из ∠AMP и ∠AKP под прямым углом) и МРLС (аналогично) – вписанные. Следовательно, ∠АРМ = ∠АКМ и ∠СРМ = ∠СLМ (вписанные, опирающиеся на одну дугу). Тогда ∠ВКL = ∠АВС – ∠СLМ = ∠АPС – ∠СPМ = ∠АРМ = ∠АКМ. Так как точки А, K и В лежат на одной прямой, то точки М, К и L также лежат на одной прямой. Чтобы не рассматривать различные случаи расположения точек K, L и М можно использовать ориентированные углы.
В некоторых случаях необходимые перпендикуляры, для прямой Симсона, «спрятаны» в виде середин отрезков или точек касания прямых и окружностей.
Теорема Жергонна.
Точка Жергонна — точка пересечения чевиан треугольника, соединяющих вершины треугольника с точками пересечения вписанной окружности и сторон треугольника.
Теорема: Три чевианы (отрезок в треугольнике, соединяющий вершину треугольника с точкой на противоположной стороне), соединяющие вершины треугольника с точками пересечения вписанной окружности и сторон треугольника, пересекаются в одной точке. (см. рис. 11)
Доказательство:
 Пусть D, E, F — точки пересечения вписанной окружности и сторон треугольника BC, AC и AB соответственно.
Пусть D, E, F — точки пересечения вписанной окружности и сторон треугольника BC, AC и AB соответственно.
AF=AE, BF=BD, CD=CE (свойство отрезков касательных, проведенных из одной точки, к окружности).
Следовательно:


Рис. 11
По теореме Чевы отрезки AD, BE и СF пересекаются в одной точке.
Решение задач на тему «Замечательные точки треугольника».
Задача 1. Исследование прямой Эйлера для остроугольного и тупоугольного треугольника.




Рис. 12.2
Рис. 12.1
Пусть AB BC CA. Легко проверить, что для остроугольного и тупоугольного треугольников точка H пересечения высот и центр O описанной окружности расположены именно так, как на рис. (т. е. для остроугольного треугольника точка O лежит внутри треугольника BHC
1, а для тупоугольного точки O и B лежат по одну сторону от прямой CH). Поэтому в остроугольном треугольнике прямая Эйлера пересекает наибольшую сторону AB и наименьшую сторону AC (см рис 12.1), а в тупоугольном треугольнике — наибольшую сторону AB и среднюю по длине сторону BC. (см. рис. 12.2)
Задача 2. Точки A2, B2 и C2 – середины высот AA1, BB1 и CC1 остроугольного треугольника ABC. Найдите сумму углов B2A1C2, C2B1A2 и A2C1B2. (Всероссийская олимпиада по математике, 1995)

Рис. 13
Решение: Пусть H – точка пересечения высот треугольника A BC, M – середина стороны AB. (см. рис. 13) Поскольку MB
2 и MA
2 – средние линии прямоугольных треугольников AB
1B и AA
1B, то ∠MB
2H = ∠AB
1B= 90
(MB
2 || AB
1), ∠MA
2H = ∠BA
1A= 90
° (MA
2 || BA
1), поэтому из точек B
2, A
2 и C
1 отрезок MH виден под прямым углом. Следовательно, эти точки лежат на окружности с диаметром MH. Четырёхугольник A
2B
2C
1H – вписанный, поэтому ∠A
2C
1B
2 = 180
°-∠A
2HB
2 = 180
°-∠A
1HB
1 = ACB, т.к. вокруг A
1HB
1С можно описать окружность, ∠A
1=∠B
1=90
°).
Аналогично
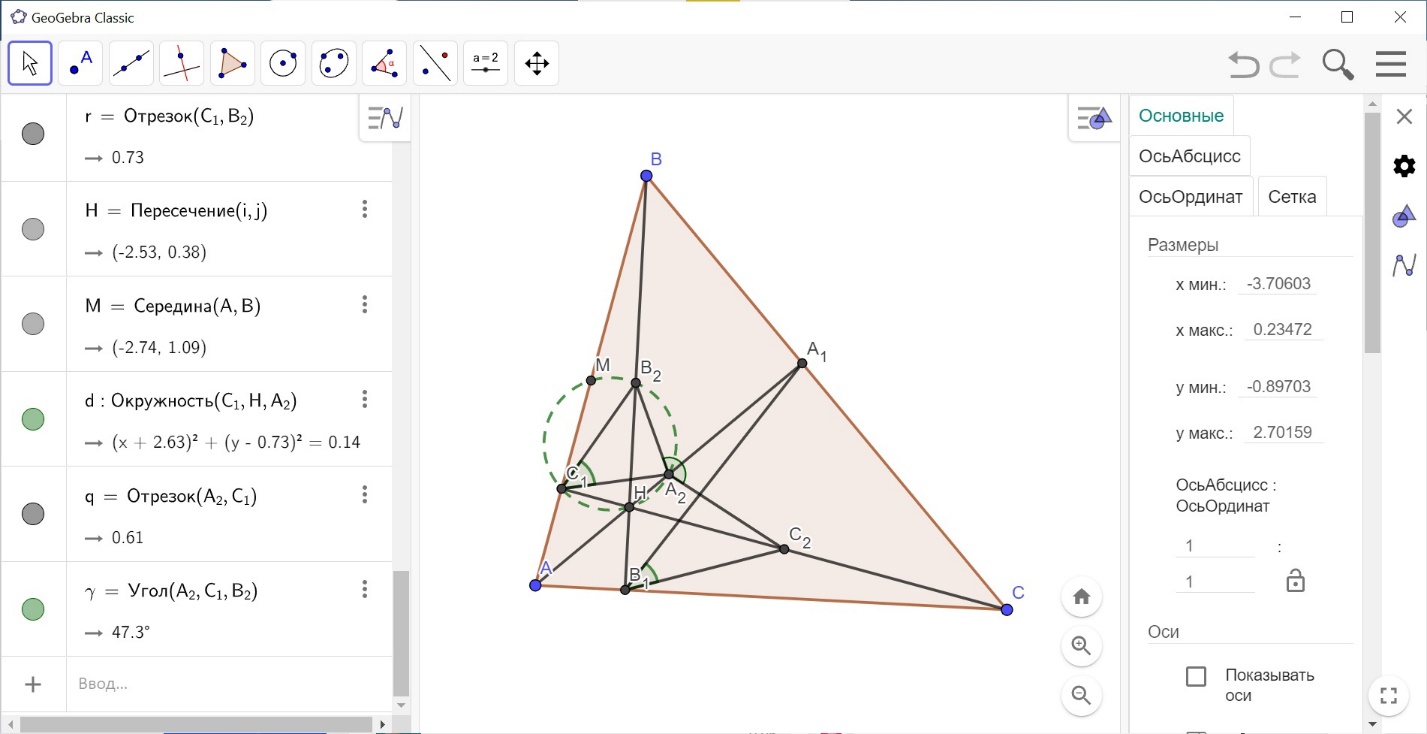
доказывается, что ∠B
2A
1C
2 = ∠BAC, ∠C
2B
1A
2 = ∠ABC.
Следовательно, ∠A
2C
1B
2+∠B
2A
1C
2+∠C
2B
1A
2= ∠ACB + ∠BAC + ∠ABC = 180
°.
Задача 3. Вписанная окружность касается сторон треугольника ABCв точках A1, B1 и C1. Докажите, что прямая Эйлера треугольника A1B1C1 проходит через центр описанной окружности треугольника ABC.


Рис. 14
Решение: Пусть O и I — центры описанной и вписанной окружностей треугольника ABC, H — ортоцентр треугольника A
1B
1C
1.(см. рис. 14) Проведем в треугольнике A
1B
1C
1 высоты A
1A
2, B
1B
2 и C
1C
2. Треугольник A
1B
1C
1 остроугольный (∠B
1A
1C
1 = (∠B + ∠C)/2
o). H — центр вписанной окружности треугольника A
2B
2C
2, т.к. A
1A
2, B
1B
2, C
1C
2 – биссектрисы треугольника A
2B
2C
2, которые пересекаются в Н, по свойству ортотреугольника. Рассмотрим касательную ВС к описанной около треугольника A
1B
1C
1 окружности. ∠B
1A
1C=1/2 дуги B
1A
1 = ∠B
1С
1A
1 (вписанный угол), ∠B
1С
1A
1 = ∠B
2C
2А
1 (B
2C
2 – сторона ортотреугольника), следовательно, ∠B
2C
2А
1 = ∠B
1A
1C – накрест лежащие при ВС, B
2C
2 и секущей C
2А
1, значит, ВС || B
2C
2. Аналогично и с другими сторонами ортотреугольника. Получается, что стороны треугольников ABC и A
2B
2C
2 параллельны, поэтому существует гомотетия, переводящая треугольник ABC в A
2B
2C
2. При этой гомотетии точка O переходит в точку I, а точка I — в точку H, поэтому прямая IH проходит через точку O.
 Задача 4. B остроугольном треугольнике ровно один из углов равен 60°. Докажите, что прямая, проходящая через центр описанной окружности и точку пересечения медиан треугольника, отсекает от него равносторонний треугольник. (Московская устная олимпиада по геометрии, 2006)
Задача 4. B остроугольном треугольнике ровно один из углов равен 60°. Докажите, что прямая, проходящая через центр описанной окружности и точку пересечения медиан треугольника, отсекает от него равносторонний треугольник. (Московская устная олимпиада по геометрии, 2006)

Рис. 15
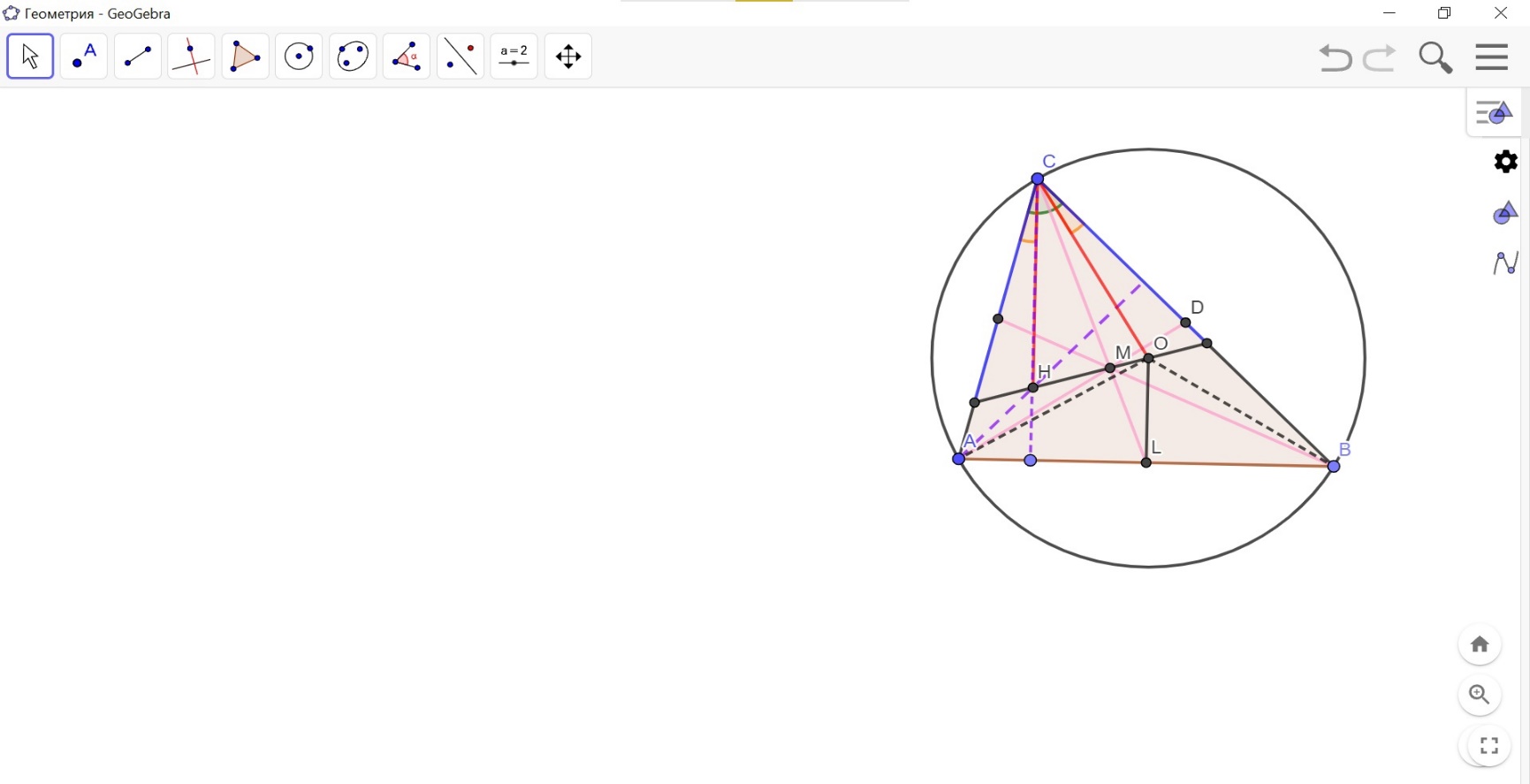
Решение: Пусть O — центр окружности, описанной около треугольника ABC, M — точка пересечения медиан этого треугольника, R — радиус описанной окружности. (см. рис. 15) Значит, OM — прямая Эйлера для треугольника ABC, поэтому она проходит через его ортоцентр H, при этом MH = 2MO. Треугольник ABC — остроугольный, поэтому O и H лежат внутри него. Построим OL перпендикулярно АВ. ∠ACB (вписанный в окружность) = ½∠AOB (центральный) = ∠AOL (треугольник АОВ – равнобедренный, ОА = ОВ, как радиусы), откуда OL = Rcos∠AOL = R cos∠ACB, следовательно, так как Н –точка пересечения высот, а ОL – перпендикуляр из центра описанной окружности к стороне, CH = 2OL = 2Rcos∠ACB.
Допустим, AC и ∠ACB = 60°, тогда CH = 2Rcos60° = R = CO. ∠ACH= ∠OCB, следовательно, биссектриса угла OCH совпадает с биссектрисой угла ACB. Значит, эта биссектриса перпендикулярна OH (так как треугольник СНО – равнобедренный, СН = СО), поэтому прямая OH отсекает на лучах CB и CA равные отрезки (создавая равнобедренный треугольник). ∠CAB ∠CBA и ∠HCA = 90°– ∠CAB (из прямоугольного треугольника), а ∠OCA = 90°– ∠CBA, значит ∠HCA ∠OCA. Таким образом доказывается, ∠HAC ∠OAC, следовательно, точка H лежит внутри треугольника OAC. Аналогично доказывается, что точка O лежит внутри треугольника HBC. Поэтому прямая OH, пересекая стороны AC и BC (а не их продолжения), отсекает от треугольника АВС равнобедренный треугольник с углом 60°, значит, являющийся равносторонним.
Задача 5. В треугольнике ABC проведены высоты BB1 и CC1. Докажите, что если ∠A = 45°, то B1C1 – диаметр окружности девяти точек треугольника ABC. (см. рис. 16)


Рис. 16
Решение: Диаметр описанной окружности треугольника ABC по теореме синусов равен
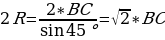
, значит, диаметр окружности девяти точек равен

, по теореме об окружности Эйлера. Треугольник AC
1B
1 подобен треугольнику ABC по двум углам. Так как отрезок ВС виден из ∠ВС
1С и ∠С
1В
1С под прямым углом, то около С
1В
1СВ можно описать окружность, ∠В
1С
1В + ∠В
1СВ = 180°, при этом ∠В
1С
1В + ∠В
1С
1А = 180°, следовательно, ∠В
1СВ = ∠В
1С
1А, ∠А=45° – общий. Коэффициент подобия:

, из прямоугольного треугольника АСС
1 данное отношение – cos 45°. Значит, В
1С
1 =

= диаметр окружности Эйлера. Поскольку точки B
1 и C
1 лежат на окружности девяти точек, то B
1C
1 – диаметр.
Задача 6. Высоты AA1, BB1 и CC1 остроугольного треугольника ABC пересекаются в точке H; точки A2, B2 и C2 – середины отрезков AH, BH и CH соответственно. Рассмотрим шестиугольник, образованный пересечением треугольников A1B1C1 и A2B2C2. Докажите, что его диагонали, соединяющие противоположные вершины, пересекаются в одной точке.
 Решение: Пусть M – точка пересечения отрезков B1C1 и A2C2, а N – отрезков A1C1 и B2C2. (см. рис. 17) Необходимо доказать, что ∠MHB1 = NHB2, это будет означать, что диагональ MN указанного шестиугольника проходит через точку H.
Решение: Пусть M – точка пересечения отрезков B1C1 и A2C2, а N – отрезков A1C1 и B2C2. (см. рис. 17) Необходимо доказать, что ∠MHB1 = NHB2, это будет означать, что диагональ MN указанного шестиугольника проходит через точку H.

Рис. 17
Обозначим ∠MHB
1 = α, ∠NHA
1 = β. Отрезок A
2C
2 – средняя линия треугольника AHC, поэтому A
2C
2 – серединный перпендикуляр к отрезку HB
1, значит, треугольник HMB
1 – равнобедренный, а так как высота BB
1 треугольника ABC делит пополам угол его ортотреугольника (свойство угла ортотреугольника), то ∠BB
1A
1 = ∠MB
1H = ∠MHB
1 = α. Точки A
1 и B
1 лежат на окружности с диаметром AB, поэтому ∠BAA
1 = ∠BB
1A
1 = α. Тогда ∠B
2A
2A
1 = ∠BB
1A
1 = α. Аналогично ∠A
2B
2B
1 = ∠NHA = β. По теореме о внешнем угле треугольника ∠A
1HB
2 = α + β, значит, ∠NHB
2 = ∠A
1HB
2 – ∠NHA
1 = (α + β) – β = α = ∠MHB
1. Так как B
1, Н, B
2 лежат на одной прямой, а ∠NHB
2 = ∠MHB
1, то M, N, H лежат на одной прямой. Аналогично доказывается, что и две остальные большие диагонали шестиугольника проходят через точку H.

Рис. 18
Задача 7. Дан треугольник ABC, O — центр его описанной окружности, O
1, O
2 и O
3 — точки, симметричные точке O относительно

прямых AB, BC и AC. Докажите, что середины сторон треугольника O
1O
2O
3 лежат на окружности девяти точек треугольника ABC.
Решение: Пусть A1, B1 и C1 — середины сторон соответственно BC, AC и AB, A2 — середина отрезка O1O3. (см. рис. 18) Поскольку A2C1 и A2B1 — средние линии треугольника O1OO3 (A2 — середина отрезка O1O3, ОВ1 = В1О3, С1О1 = С1О) то A2C1OB1 - параллелограмм. Поэтому ∠C1A2B1 = ∠C1OB1 = 180° - ∠A (около четырехугольника C1AB1О можно описать окружность, т.к. ∠АC1O = ∠OB1А = 90°), 180° - ∠A =180° - ∠C1A1B1 (C1A1B1А – параллелограмм). Тогда ∠C1A2B1 + ∠C1A1B1 = 180°.
Значит, точка A2 лежит на описанной окружности треугольника A1B1C1, т.е. на окружности девяти точек треугольника ABC. Аналогично для точек B2 и C2.
 Задача 8. В треугольнике АВС проведены высота BH и биссектриса BL. Точки Р и Q – основания перпендикуляров, опущенных из А на BL и из L на ВС соответственно. Докажите, что точки Н, Р и Q лежат на одной прямой. (Окружная олимпиада, Москва, 2006)
Задача 8. В треугольнике АВС проведены высота BH и биссектриса BL. Точки Р и Q – основания перпендикуляров, опущенных из А на BL и из L на ВС соответственно. Докажите, что точки Н, Р и Q лежат на одной прямой. (Окружная олимпиада, Москва, 2006)

Рис. 19
Доказательство: Заметим, что точки Н, Р и Q – это основания перпендикуляров, опущенных из точки L на прямые ВН, АР и ВС соответственно. (см. рис. 19) Поэтому достаточно доказать, что L лежит на окружности, описанной около треугольника, образованного этими прямыми. Это треугольник BDE, где D и Е – точки пересечения прямой АР с ВН и ВС соответственно. Так как ВР перпендикулярно АЕ, ВL – биссектриса, значит треугольник AЕВ – равнобедренный, АР = РЕ, следовательно, А и Е равноудалены от Р, т.е. треугольник ALE - равнобедренный, значит, ∠LAP = ∠LEP. Кроме того, ∠LAP = 90° - ∠ВLA = ∠LBD. Следовательно, ∠LED = ∠LBD, то есть точки L, D, В и E лежат на одной окружности. Значит, по теореме Симсона: Н, Р и Q – это основания перпендикуляров, опущенных из точки L, которая лежит на описанной около треугольника BDE окружности, на прямые ВН, АР и ВС соответственно, значит Н, Р и Q лежат на одной прямой.
Задача 9. Остроугольный треугольник ABC (AB ) вписан в окружность. Пусть M – точка пересечения его медиан, а AH – высота. Луч MH пересекает описанную около АВС окружность в точке A'. Докажите, что описанная окружность треугольника A'HB касается прямой AB. (Всероссийская олимпиада по математике 2014/2015) (см. рис. 20)


Рис. 20
Решение: Выберем на данной окружности точку D так, что AD || BC, тогда точки A и D симметричны относительно серединного перпендикуляра к BC (∠DAB = ∠BAD, опираются на большую дугу AD, значит трапеция BADС равнобокая, следовательно, серединный перпендикуляр к ВС – серединный перпендикуляр к AD). Пусть H' – проекция точки D на BC, а K – середина BC (АН – высота, АН || H'D). Из симметрии K также является серединой отрезка HH'. Кроме того, HH' = АD (АНH'D – прямоугольник).
Пусть X – точка пересечения отрезков AK и DH. Тогда треугольники ADX и KHX подобны (по вертикальному углу и ∠ADН = ∠XHK, как накрест лежащие при параллельных прямых НК и AD), откуда AX : KX = AD : KH = 2 : 1. Из данного соотношения, X – точка пересечения медиан треугольника ABC, то есть X = M. Таким образом, точки A', H, M и D лежат на одной прямой.
Заметим, что ∠ABH = ∠ABC = ∠BCD (так как трапеция BADС равнобокая); ∠BCD = ∠BA'D (вписанные и опираются на одну дугу BD); ∠BA'D = ∠BA'H. При этом ∠ABH образован прямой АВ и хордой ВН и равен ½ дуги ВН. Значит, что AB – касательная к описанной окружности треугольника BA'H.
 Задача 10. Пусть M и N – середины гипотенузы AB и катета BC прямоугольного треугольника ABC соответственно. Вневписанная окружность треугольника ACM касается стороны AM в точке Q, а прямой AC – в точке P. (см. рис. 21) Докажите, что точки P, Q и N лежат на одной прямой.
Задача 10. Пусть M и N – середины гипотенузы AB и катета BC прямоугольного треугольника ABC соответственно. Вневписанная окружность треугольника ACM касается стороны AM в точке Q, а прямой AC – в точке P. (см. рис. 21) Докажите, что точки P, Q и N лежат на одной прямой.

Рис. 21
Решение: 1 способ. Пусть D – центр вневписанной окружности треугольника ACM, P и Q – радиусы, проведенные из точки D на прямые AC и AB соответственно. Так как MN – медиана равнобедренного треугольника BMC (СМ = МВ = АМ, по свойству медианы прямоугольного треугольника), проведённая к основанию, то MN – биссектриса угла BMC, поэтому точка D лежит на прямой MN. Кроме того, MN – средняя линия треугольника ABC, значит, MN || AC. Таким образом, PCND – прямоугольник.
∠AMD = ∠CMN (образованы биссектрисой равных углов), ∠CMN = ∠ACM = α (накрест лежащие при АС и NM, средней линией АВС), тогда ∠PAD = ½ (180° – α), а ∠APN = ∠PCD = α/2 (CD – биссектриса угла ACM). Следовательно, ∠PAD + ∠APN = 90°, поэтому AD ⊥ PN. Поскольку точка Q симметрична точке P относительно прямой AD, то Q лежит на PN, что и требовалось.
2 способ. Заметим, что DN – серединный перпендикуляр к стороне BC, следовательно, ∠ABD = ∠DCM (из равных треугольников CMD, BMD) = ∠ACD. Отсюда следует другое решение задачи: точки A, C, B и D лежат на одной окружности, из точки D проведены перпендикуляры к АС, АВ, СВ, значит, точки P, Q и N (соответственно) лежат на прямой Симсона точки D.
 Задача 11. Окружность с центром I, вписанная в треугольник АВС, касается сторон АВ и ВС в точках С0 и А0 соответственно. Окружность, проходящая через точки В и I, пересекает стороны АВ и ВС в точках X и Y. (см. рис. 22) Докажите, что середина отрезка XY лежит на прямой А0С0.
Задача 11. Окружность с центром I, вписанная в треугольник АВС, касается сторон АВ и ВС в точках С0 и А0 соответственно. Окружность, проходящая через точки В и I, пересекает стороны АВ и ВС в точках X и Y. (см. рис. 22) Докажите, что середина отрезка XY лежит на прямой А0С0.

Рис. 22
Решение: Точка I лежит на биссектрисе угла B, следовательно, делит дугу XY пополам (так как угол А
0ВС
0 – вписанные и равен дуге, на которую опирается). Пусть B
0 - середина хорды XY. Тогда IB
0 - серединный перпендикуляр к XY (хорды IX и IY равны, стягивают равные дуги).
I - точка на окружности, описанной около треугольника BYЧ. IA0, IB0, IC0 - перпендикуляры, опущенные на стороны треугольника XBY. Основания перпендикуляров A0, B0, C0 лежат на прямой Симсона.
Задача 12. Биссектрисы углов А и В треугольника АВС пересекают описанную окружность треугольника в точках А1 и В1. Вписанная  окружность касается сторон АС и ВС в точках А2 и В2. Докажите, что А1В1 || А2В2. (см. рис. 23)
окружность касается сторон АС и ВС в точках А2 и В2. Докажите, что А1В1 || А2В2. (см. рис. 23)

Рис. 23
Решение: По лемме Мансиона (центр вневписанной окружности лежит на АА
1, биссектриса угла пересекает описанную около АВС окружность в А
1) отрезки ВА
1, А
1С, А
1I равны. Аналогично АВ
1 = В
1I = В
1С. Из этого следует, что четырехугольник СВ
1А
1I – дельтоид, так как он образован двумя равнобедренными треугольниками с разными боковыми сторонами и с общим основанием. В дельтоиде диагонали перпендикулярны, значит, IC перпендикулярно А
1В
1. Рассмотрим четырехугольник IА
2СВ
2. В нем IА
2 = IВ
2, как радиусы, СА
2 = СВ
2, отрезки касательных, проведенных из одной вершины. Значит данный четырехугольник тоже дельтоид, в нем диагональ IC перпендикулярна А
2В
2. Следовательно, А
1В
1 || А
2В
2.
 Задача 13. Пусть А0 и С0 – середины дуг ВС и АВ описанной окружности треугольника АВС, не содержащих третьей вершины треугольника. Найдите угол В треугольника, у которого отрезок А0С0 касается вписанной окружности треугольника АВС. (Региональный этап 2007). (см. рис. 24)
Задача 13. Пусть А0 и С0 – середины дуг ВС и АВ описанной окружности треугольника АВС, не содержащих третьей вершины треугольника. Найдите угол В треугольника, у которого отрезок А0С0 касается вписанной окружности треугольника АВС. (Региональный этап 2007). (см. рис. 24)

Рис. 24
Решение: С0А = С0В = С0I по лемме о трезубце (АА0 – биссектриса, А0 лежит на описанной около АВС окружности). Аналогично ВА0 = А0С = А0I. Значит С0ВА0I – дельтоид, так как образован двумя равнобедренными треугольниками с разными боковыми сторонами и с общим основанием.
Следовательно, С0А0 перпендикулярно BI, так как диагонали дельтоида, С0А0 пересекает BI в точке К. К – точка касания вписанной окружности и С0А0. Диагонали дельтоида делят друг друга точкой пересечения пополам, ВК = КI. N – точка касания вписанной окружности, IN перпендикулярно ВС. В треугольнике BIN: BI = 2*IN, так как он прямоугольный, то угол IВN = 30°. Значит, искомый угол АВС равен 60°.
Заключение.
В ходе работы над проектом я изучила, освоила различные теоремы о замечательных точках треугольника. Используя данные методы можно решать сложные и нестандартные задачи, а также экономить значительную часть времени на их решение. Умение видеть в задачах замечательные точки, теоремы, подводящие к ним, является очень полезным навыком. Мне удалось выполнить все поставленные задачи.
Мною были подготовлены видео-уроки по теме «Замечательные точки треугольника», в которых я раскрыла три основные изученные мною теоремы и разобрала по каждой несколько задач (Приложение 1). Также я составила и провела математическую игру по изученной теме для учащихся восьмых классов (Приложение 2). Я смогла освоить навык не только решения задач на тему «Замечательные точки треугольника», но и создания новых задач для школьников.
СПИСОК ЛИТЕРАТУРЫ
Прасолов В. В. Задачи по планиметрии. — 4-е изд., дополненное — М.: Изд-во Московского центра непрерывного математического образования, 2001. — 584 с.
Система задач по геометрии Р.К. Гордина, режим доступа: https://zadachi.mccme.ru/2012/#&page1
Геометрия. 10 -11 классы: учебник для общеобразовательных учреждений: базовый и профильный уровни / [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.] – 22-е издание – М.: Просвещение, 2013. – 255 с.
Приложение 1.
https://youtu.be/Nosm2n49zgg
https://youtu.be/GMZP9wViznw
https://youtu.be/I5E_wMdlOKI
Приложение 2.
Задачи для математической игры.
Дан треугольник АВС, проведены высоты, которые пересекаются в точке Н. Найдите радиус окружности, образованной серединами отрезков ВН, СН, АН, если радиус описанной около АВС окружности равен 126 см. (ответ 63 см)
В треугольнике АВС высоты пересекаются в точке Н. Наименьшие расстояние от Н до точки, лежащей на высоте, проведенной из А, и принадлежащей окружности Эйлера равно 6. Найдите НВ2, где В2 – основание высоты из В на АС, а угол С равен 45°. (ответ 6  )
)
В прямоугольном треугольнике АВС из прямого угла А проведена высота АН = 2. Найти ВН, если угол С равен 30°. (ответ  )
)
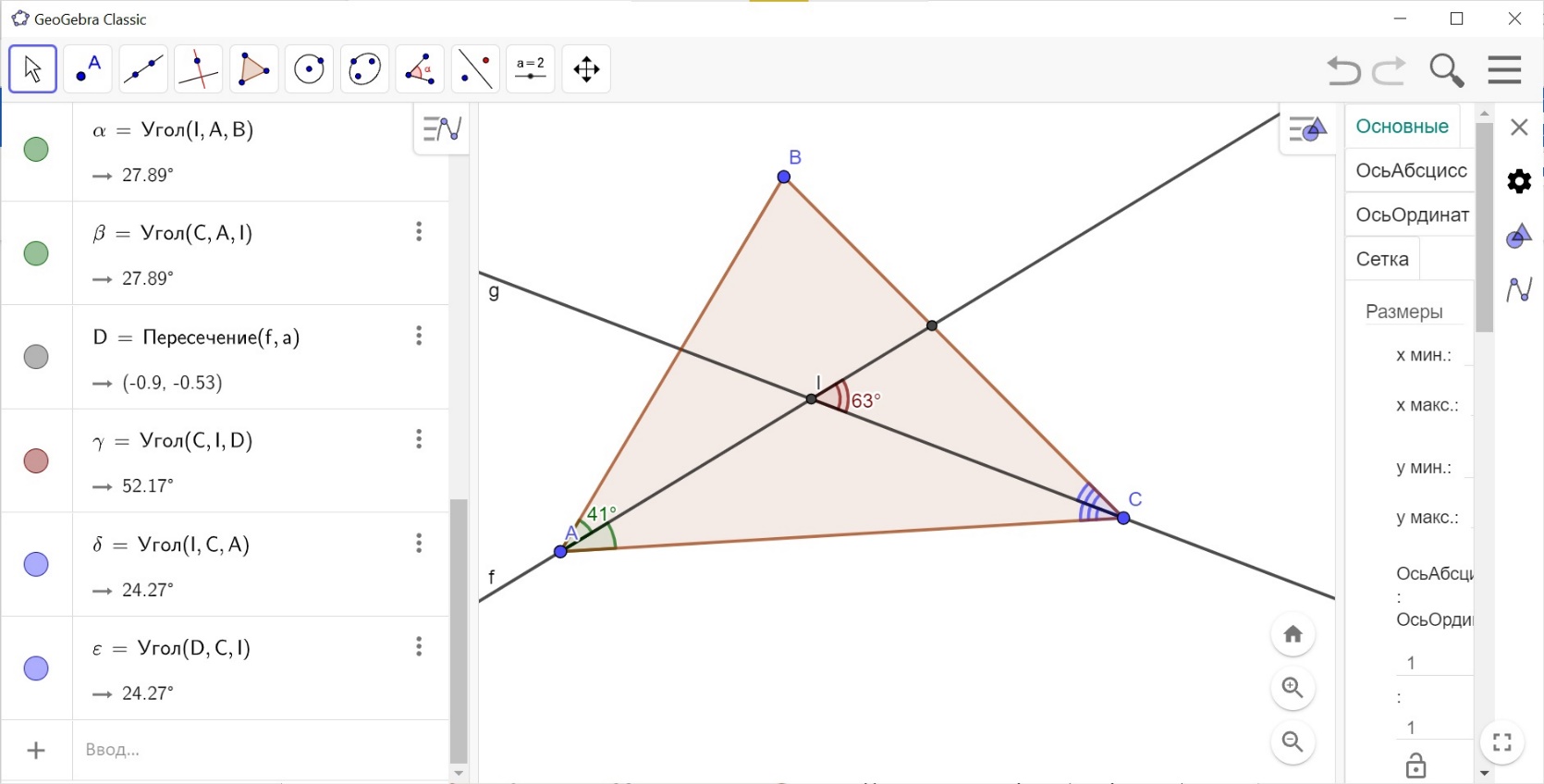
В остроугольном треугольнике АВС проведены биссектрисы из угла А и С, которые пересекаются в I. Найдите угол BIC, если внешний угол для угла А равен 124°, а угол ICB равен 21°. (ответ 124).
В треугольнике АВС проведены высоты АА1 и ВВ1, пересекающиеся в Н. Найти углы НВВ1 и НАА1, если угол С равен 38°. (52°)
Найти площадь треугольника АВС (ответ 2 )
)

Найдите длину отрезка, соединяющего центр описанной окружности и ортоцентром треугольника, если длина отрезка, соединяющего центроид с центром описанной окружности, равна 13. (ответ 39)
Найти угол В (ответ 54°)







 Задача Эйлера
Задача Эйлера  Доказательство:
Доказательство: 



 ано: Треугольник АВС; А1, В1, С1 – середины сторон ВС, СА, АВ; А2, В2, С2 – основания высот, проведенных к этим сторонам; А3, В3, С3 - середины отрезков АН, ВН, СН; А4, В4, С4 – точки, симметричные точке Н относительно сторон треугольника; А5, В5, С5 – точки, симметричные точке Н относительно середин этих сторон; А6, В6, С6 – точки, симметричные точке О относительно прямых В1С1, А1С1, А1В1; Н – точка пересечения высот, О – центр описанной окружности.
ано: Треугольник АВС; А1, В1, С1 – середины сторон ВС, СА, АВ; А2, В2, С2 – основания высот, проведенных к этим сторонам; А3, В3, С3 - середины отрезков АН, ВН, СН; А4, В4, С4 – точки, симметричные точке Н относительно сторон треугольника; А5, В5, С5 – точки, симметричные точке Н относительно середин этих сторон; А6, В6, С6 – точки, симметричные точке О относительно прямых В1С1, А1С1, А1В1; Н – точка пересечения высот, О – центр описанной окружности. 



 Дано: Треугольник АВС, окружность, описанная около АВС, ВМ – биссектриса ∠В, BIB пересекает окружность в точке L, I – центр вписанной окружности, а Iв – центр вневписанной окружности.
Дано: Треугольник АВС, окружность, описанная около АВС, ВМ – биссектриса ∠В, BIB пересекает окружность в точке L, I – центр вписанной окружности, а Iв – центр вневписанной окружности. 








 Дано: треугольник АВС, ОМ1 перпендикулярен ВС
Дано: треугольник АВС, ОМ1 перпендикулярен ВС Следовательно, было доказано, что три точки – середина М1 стороны СВ, основание А1 высоты АА1 и середина К1 отрезка НА – лежат на окружности с центром в середине F отрезка НО и радиусом равным ½R.
Следовательно, было доказано, что три точки – середина М1 стороны СВ, основание А1 высоты АА1 и середина К1 отрезка НА – лежат на окружности с центром в середине F отрезка НО и радиусом равным ½R. соответственно, - лежат на окружности радиуса ½R с центром в точке F. (см. рис. 7)
соответственно, - лежат на окружности радиуса ½R с центром в точке F. (см. рис. 7)  Доказать: О, Н, М лежат на одной прямой
Доказать: О, Н, М лежат на одной прямой
 =
=  = 2.
= 2. 

 Пусть D, E, F — точки пересечения вписанной окружности и сторон треугольника BC, AC и AB соответственно.
Пусть D, E, F — точки пересечения вписанной окружности и сторон треугольника BC, AC и AB соответственно.


 доказывается, что ∠B2A1C2 = ∠BAC, ∠C2B1A2 = ∠ABC.
доказывается, что ∠B2A1C2 = ∠BAC, ∠C2B1A2 = ∠ABC.

 Задача 4. B остроугольном треугольнике ровно один из углов равен 60°. Докажите, что прямая, проходящая через центр описанной окружности и точку пересечения медиан треугольника, отсекает от него равносторонний треугольник. (Московская устная олимпиада по геометрии, 2006)
Задача 4. B остроугольном треугольнике ровно один из углов равен 60°. Докажите, что прямая, проходящая через центр описанной окружности и точку пересечения медиан треугольника, отсекает от него равносторонний треугольник. (Московская устная олимпиада по геометрии, 2006)

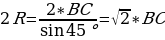 , значит, диаметр окружности девяти точек равен
, значит, диаметр окружности девяти точек равен  , по теореме об окружности Эйлера. Треугольник AC1B1 подобен треугольнику ABC по двум углам. Так как отрезок ВС виден из ∠ВС1С и ∠С1В1С под прямым углом, то около С1В1СВ можно описать окружность, ∠В1С1В + ∠В1СВ = 180°, при этом ∠В1С1В + ∠В1С1А = 180°, следовательно, ∠В1СВ = ∠В1С1А, ∠А=45° – общий. Коэффициент подобия:
, по теореме об окружности Эйлера. Треугольник AC1B1 подобен треугольнику ABC по двум углам. Так как отрезок ВС виден из ∠ВС1С и ∠С1В1С под прямым углом, то около С1В1СВ можно описать окружность, ∠В1С1В + ∠В1СВ = 180°, при этом ∠В1С1В + ∠В1С1А = 180°, следовательно, ∠В1СВ = ∠В1С1А, ∠А=45° – общий. Коэффициент подобия:  , из прямоугольного треугольника АСС1 данное отношение – cos 45°. Значит, В1С1 =
, из прямоугольного треугольника АСС1 данное отношение – cos 45°. Значит, В1С1 =  Решение: Пусть M – точка пересечения отрезков B1C1 и A2C2, а N – отрезков A1C1 и B2C2. (см. рис. 17) Необходимо доказать, что ∠MHB1 = NHB2, это будет означать, что диагональ MN указанного шестиугольника проходит через точку H.
Решение: Пусть M – точка пересечения отрезков B1C1 и A2C2, а N – отрезков A1C1 и B2C2. (см. рис. 17) Необходимо доказать, что ∠MHB1 = NHB2, это будет означать, что диагональ MN указанного шестиугольника проходит через точку H. прямых AB, BC и AC. Докажите, что середины сторон треугольника O1O2O3 лежат на окружности девяти точек треугольника ABC.
прямых AB, BC и AC. Докажите, что середины сторон треугольника O1O2O3 лежат на окружности девяти точек треугольника ABC.  Задача 8. В треугольнике АВС проведены высота BH и биссектриса BL. Точки Р и Q – основания перпендикуляров, опущенных из А на BL и из L на ВС соответственно. Докажите, что точки Н, Р и Q лежат на одной прямой. (Окружная олимпиада, Москва, 2006)
Задача 8. В треугольнике АВС проведены высота BH и биссектриса BL. Точки Р и Q – основания перпендикуляров, опущенных из А на BL и из L на ВС соответственно. Докажите, что точки Н, Р и Q лежат на одной прямой. (Окружная олимпиада, Москва, 2006)

 Задача 10. Пусть M и N – середины гипотенузы AB и катета BC прямоугольного треугольника ABC соответственно. Вневписанная окружность треугольника ACM касается стороны AM в точке Q, а прямой AC – в точке P. (см. рис. 21) Докажите, что точки P, Q и N лежат на одной прямой.
Задача 10. Пусть M и N – середины гипотенузы AB и катета BC прямоугольного треугольника ABC соответственно. Вневписанная окружность треугольника ACM касается стороны AM в точке Q, а прямой AC – в точке P. (см. рис. 21) Докажите, что точки P, Q и N лежат на одной прямой. Задача 11. Окружность с центром I, вписанная в треугольник АВС, касается сторон АВ и ВС в точках С0 и А0 соответственно. Окружность, проходящая через точки В и I, пересекает стороны АВ и ВС в точках X и Y. (см. рис. 22) Докажите, что середина отрезка XY лежит на прямой А0С0.
Задача 11. Окружность с центром I, вписанная в треугольник АВС, касается сторон АВ и ВС в точках С0 и А0 соответственно. Окружность, проходящая через точки В и I, пересекает стороны АВ и ВС в точках X и Y. (см. рис. 22) Докажите, что середина отрезка XY лежит на прямой А0С0. окружность касается сторон АС и ВС в точках А2 и В2. Докажите, что А1В1 || А2В2. (см. рис. 23)
окружность касается сторон АС и ВС в точках А2 и В2. Докажите, что А1В1 || А2В2. (см. рис. 23)
 Задача 13. Пусть А0 и С0 – середины дуг ВС и АВ описанной окружности треугольника АВС, не содержащих третьей вершины треугольника. Найдите угол В треугольника, у которого отрезок А0С0 касается вписанной окружности треугольника АВС. (Региональный этап 2007). (см. рис. 24)
Задача 13. Пусть А0 и С0 – середины дуг ВС и АВ описанной окружности треугольника АВС, не содержащих третьей вершины треугольника. Найдите угол В треугольника, у которого отрезок А0С0 касается вписанной окружности треугольника АВС. (Региональный этап 2007). (см. рис. 24) )
) )
) )
)




















