Проект по математике "О секрете происхождения арабских цифр"

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ "ШКОЛА № 12" ГОРОДА САРОВА

ПРОЕКТНАЯ РАБОТА

по математике

О СЕКРЕТЕ ПРОИСХОЖДЕНИЯ АРАБСКИХ ЦИФР

Выполнил:
учащийся 5 класса А
Иванов Иван Иванович
Руководитель:

учитель географии

Никифорова Екатерина Николаевна

Выполнили:
учащиеся 5 класса А
Забродин Александр,

Коннов Максим
Руководитель:

учитель математики

Голяева Елена Ивановна

Саров - 2019

Оглавлени

Введение 0

Глава 1. Понятие числа 0

Глава 2. Цифры древних народов 0

2.1 Цифры в Древнем Египте 0

2.2 Цифры в Вавилоне 1

2.3 Цифры в Древней Греции 2

2.4 Римская нумерация 4

2.5 Славянская кириллическая нумерация 5

Глава 3. Секрет происхождения арабских цифр 0

Глава 4. Организация и проведение исследования 0

Заключение 0

Список использованной литературы 0

Введение

«Всё есть число»- говорили пифагорейцы. Мы согласны с этим высказыванием. И раньше и сейчас человека окружают числа: стоимость покупки, номер телефона, дата рождения, отметки в школе и т.п. Числа составляются из цифр. Как возникли цифры, каковы были варианты написания цифр у разных народов, что общего в их написании, каковы правила составления чисел из цифр?

Эти вопросы всегда нас интересовали. Однажды мы задумались над следующей проблемой: почему люди, живущие в России, пользуемся арабскими цифрами? И насколько «арабскими» являются арабские цифры? Так как мы любим и математику, и историю, то решили посвятить наш проект ответам на эти вопросы.

Итак, цель нашего проекта – выяснить секрет происхождения арабских цифр и причину их долгожительства.

Для достижения цели нам необходимо решить следующие задачи:

1. С помощью литературных источников и Интернета познакомиться с цифрами разных народов.

2. Найти информацию о происхождении арабских цифр.

3. Сравнить различные системы счисления, чтобы разобраться, почему современные люди пользуются именно арабскими цифрами.

4. Исследовать уровень знаний окружающих нас людей о цифрах, которыми все они пользуются.

5. Создать брошюру, в которой отразить результаты нашей работы.

Таким образом, объектом нашего исследования стали цифры разных народов, древние цифры, современные цифры.

Основные методы исследования: анализ литературы, сравнение, опрос учащихся, ресурсы из интернета, анализ и обобщение полученных в ходе исследования данных.

Глава 1. Понятие числа

Число — это основное понятие математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей. Письменными знаками для обозначения чисел служат цифры, а также символы математических операций. Возникнув ещё в первобытном обществе из потребностей счёта, понятие числа с развитием науки значительно расширилось.

Понятие числа возникло в глубокой древности, примерно 4 -5 тысяч лет тому назад. Из практической потребности людей и развивалось в процессе развития человечества. Область человеческой деятельности расширялась и соответственно, возрастала потребность в количественном описании и исследовании. Сначала понятие числа определялось теми потребностями счёта и измерения, которые возникали в практической деятельности человека, всё более усложняясь. Позже число становится основным понятием математики, и потребности этой науки определяют дальнейшее развитие этого понятия.

Считать предметы человек умел ещё в глубокой древности, тогда и возникло понятие натурального числа. В те времена человек мог оценивать количества однородных предметов, называемых одним словом, например "три человека", "три топора". При этом использовались разные слова "один" "два", "три" для понятий "один человек", "два человека", "три человека" и "один топор", "два топора", "три топора". Это показывает анализ языков первобытных народностей. Такие именованные числовые ряды были очень короткими и завершались неиндивидуализированным понятием "много". Разные слова для большого количества предметов разного рода существуют и сейчас, такие, как "толпа", "стадо", "куча". Примитивный счёт предметов заключался «в сопоставлении предметов данной конкретной совокупности с предметами некоторой определённой совокупности, играющей как бы роль эталона», которым у большинства народов являлись пальцы ("счёт на пальцах").

Глава 2. Цифры древних народов 2.1 Цифры в Древнем Египте

Первые написанные цифры, о которых мы имеем достоверные свидетельства, появились в Египте и Месопотамии около 5000 лет назад.

В Древнем Египте сформировалось скорописное иероглифическое письмо, месопотамские писцы использовали клинопись. Поэтому египетские первые цифры своей формой передавали природу всех окружающих предметов: животные, растения, предметы быта и т.д. Папирус Ринда (1650 г. до н.э.) и папирус Голенищева (1850 г. до н.э.) – числовые древнеегипетские документы — свидетельствуют о высоком культурном развитии народа. Месопотамская клинопись запечатлена на глиняных табличках, на которых цифры представлены небольшими клиньями, повернутыми в разные стороны соответственно своему значению. И в египетских, и в месопотамских системах счисления есть цифры от 1 до 10, особые метки для обозначения десятков, сотен и тысяч, и ноль, который обозначали выделенным пустым местом. Числа древнего Египта построены грамотно и логично. Рационализм и четкость отличают эти системы счисления от аналогичных попыток других народов. Цифры значением меньше десяти обозначались ׀ (рис. 1).

Рисунок 1 – Египетские обозначения цифр

Например, цифра 6 выглядела как ׀׀׀׀׀׀. Число 10 обозначалось перевернутой подковой в иероглифической системе и особым символом – в иератической. Сколько десятков в числе, столько и «подков». Иератическая система письменности предполагала для каждого числа, на десяток выше предыдущего, отдельный символ. Начиная от 100, это была стилизованная клюшка, над которой с каждой новой сотней ставили крохотную пометку.

В иероглифах все проще. Число 100 выглядело почти как арабская цифра 9, но египтяне назвали ее лотосом. Далее все аналогично: «лотоса», 300 – 3 и т.д.

2.2 Цифры в Вавилоне

Числа древнего Вавилона мало отличались от месопотамских: те же клиновидные знаки служили для обозначения единиц — ˅ (рис. 2) , и десятков — ˃. Комбинация этих знаков применялась для обозначения чисел 11-59. Число 60 в письме выглядело как зеркальное отражение буквы «Г». 70 – Г˃, 80 — Г˃˃ и так далее, принцип ясен, клинопись не отличается гениальностью.

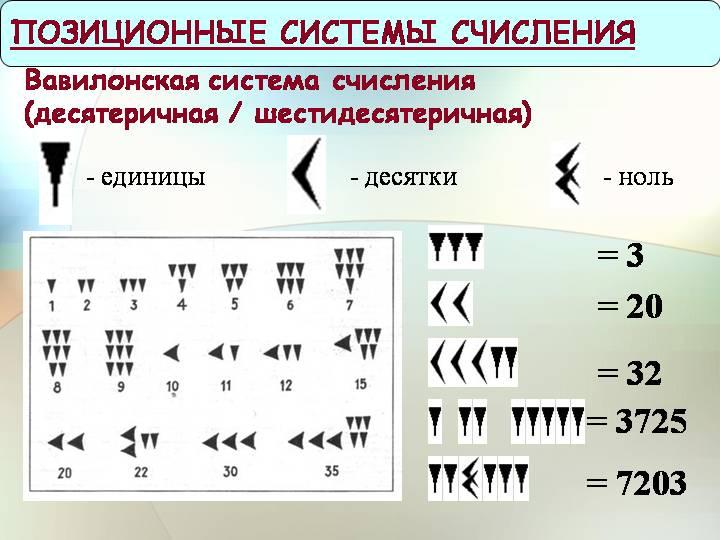
Рисунок 2 – Вавилонская система счисления

Основная ценность заключается в том, что один и тот же знак – обратите внимание – в зависимости от того, где он расположен в записи числа, имеет разное значение. Речь идет о поместном размещении знаков в системе счисления. Те же клиновидные знаки, указанные в разных разрядах, обладают разной значимостью. Поэтому Вавилонскую систему счисления с нулем принято называть позиционной. Математики могут с этим поспорить, потому что не найдено ни одного источника, в которой ноль располагался бы в конце числовой записи, что говорит об относительной позиционности.

Вавилонская система стала своеобразным трамплином, с которого человечество совершило прыжок на новый этап своего развития. Идея со временем попала в руки индусов. Они внесли свои коррективы, усовершенствовав систему счисления. Переняли идею итальянские торговцы, которые привезли ее в Европу вместе с товаром. Позиционная система счисления облетела весь мир, обогатив своим появлением не только математические науки, но и современный счет.

2.3 Цифры в Древней Греции

Греки применяли несколько способов записи чисел. В Древней Греции имели хождение две основных системы счисления - аттическая (или геродианова ) и ионическая (она же александрийская или алфавитная). При использовании ионической нумерации числа выражались буквами алфавита. Чтобы отличить число от слова, над буквами числа ставился специальный значок   -титло. Этот способ записи чисел применялся жителями Милета и Александрии. Афиняне для обозначения чисел пользовались первыми буквами слов-числительных:

    Г (Γέύτέ) - пять,

    Δ(Δέκά)- десять,

   Χ(Χιλιάό) - тысяча,

  Μ(Mυριάό) - десять тысяч,

  I, II, III, IIII -соответственно 1, 2 , 3, 4 

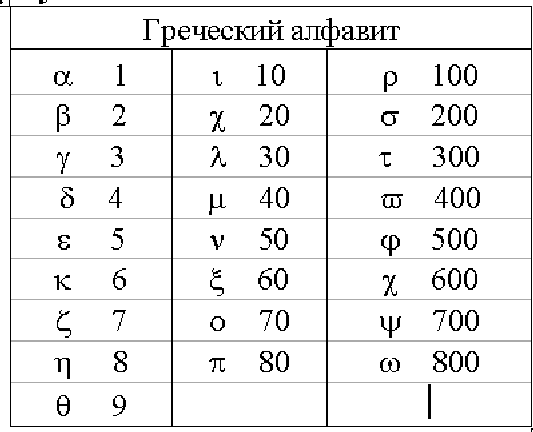
Рисунок 3 – Греческий алфавит

С помощью этих цифр житель Древней Греции мог записывать любое, не очень большое, число. Великий греческий математик Диофант Александрийский записывал дроби примерно так, как приятно сейчас: числитель над знаменателем , но без черты. Это был один из способов записи дробей в Древней Греции.

Вторая принятая в Древней Греции ионическая система счисления - алфавитная. Она получила широкое распространение в начале Александрийской эпохи, хотя возникнуть она могла несколькими столетиями раньше, по всей видимости, уже у пифагорейцев. Чтобы отличить числа от слов, греки над соответствующей буквой ставили горизонтальную черту. Сходство греческой буквы О с современным обозначением нуля может быть чем-то большим, чем случайное совпадение, но у нас нет точных данных, позволяющих утверждать это со всей определенностью. Запись алфавитными символами могла делаться в любом порядке, так как число получалось как сумма значений отдельных букв.

Вплоть до VI века до н. э. греческая математика ничем не выделялась. Были, как обычно, освоены счёт и измерение. Греческая нумерация (запись чисел), как позже римская, была аддитивной, то есть числовые значения цифр складывались. Соответственно была устроена и счётная доска (абак) с камешками (рис. 4).

Рисунок 4 – абак

Кстати, термин калькуляция(вычисление) происходит от calculus  — камешек. Особый дырявый камешек обозначал нуль.

В VI веке до н. э. начинается «греческое чудо»: появляются сразу две научные школы — ионийцы (Фалес Милетский, Анаксимен, Анаксимандр) и пифагорейцы. О достижениях ранних греческих математиков мы знаем в основном по упоминаниям позднейших авторов, преимущественно комментаторов Евклида, Платона и Аристотеля.

2.4 Римская нумерация

Римская система нумерации с помощью букв была распространена в Европе на протяжении двух тысяч лет. Только в позднем средневековье ее сменила более удобная для вычислений десятичная система цифр, заимствованная у арабов. Но, до сих пор римскими цифрами обозначаются даты на монументах, время на часах и (в англо-американской типографической традиции) страницы книжных предисловий. Кроме того, в русском языке римскими цифрами принято обозначать порядковые числительные.

Для обозначения чисел применялось 7 букв латинского алфавита: I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000. Промежуточные числа образовывались путем прибавления нескольких букв справа или слева. Сначала писались тысячи и сотни, затем десятки и единицы. Таким образом, число 24 изображалось как XXIV. Горизонтальная линия над символом означала умножение на тысячу.

Натуральные числа записываются при помощи повторения этих цифр. При этом, если большая цифра стоит перед меньшей, то они складываются (принцип сложения), если же меньшая - перед большей, то меньшая вычитается из большей (принцип вычитания). Последнее правило применяется только во избежание четырёхкратного повторения одной и той же цифры. Например, I, Х, С ставятся соответственно перед Х, С, М для обозначения 9, 90, 900 или перед V, L, D для обозначения 4, 40, 400. Например, VI = 5+1 = 6, IV = 5 - 1 = 4 (вместо IIII). XIX = 10 + 10 - 1 = 19 (вместо XVIIII), XL = 50 - 10 =40 (вместо XXXX), XXXIII = 10 + 10 + 10 + 1 + 1 + 1 = 33 и т.д.

Выполнение арифметических действий над многозначными числами в этой записи весьма неудобно. Система Римских цифр настоящее время не применяется, за исключением, в отдельных случаях, обозначения веков (XV век и т.д.), годов н. э. (MCMLXXVII т. д.) и месяцев при указании дат, порядковых числительных, а также иногда производных небольших порядков.

2.5 Славянская кириллическая нумерация

Эта нумерация была создана вместе со славянской алфавитной системой для перевода священных библейских книг для славян греческими монахами братьями Кириллом и Мефодием в IX веке. Эта форма записи чисел получила большое распространение в связи с тем, что имела полное сходство с греческой записью чисел (рис. 5). До XVII века эта форма записи чисел была официальной на территории современной России, Республики Беларусь, Украины, Болгарии, Венгрии, Сербии и Хорватии. До сих пор православные церковные книги используют эту нумерацию.

Рисунок 5 – Славянская кириллическая нумерация

Числа записывали из цифр так же слева направо, от больших к меньшим. Числа от 11 до 19 записывались двумя цифрами, причем единица шла перед десятком.

Читаем дословно "четырнадцать" - "четыре и десять". Как слышим, так и пишем: не 10+4, а 4+10, - четыре и десять (или, например, 17 — сем-на-дцать). Числа от 21 и выше записывались наоборот, сначала писали знак полных десятков. Запись числа, использованная славянами аддитивная, то есть в ней используется только сложение.

Для того чтобы не перепутать буквы и цифры, использовались титла - горизонтальные черточки над числами, что мы видим на рисунке 6. Для обозначения чисел больших, чем 900 использовались специальные значки, которые дорисовывались вокруг буквы. Так образовывались следующие большие числа:

Обозначение	Название	Значение
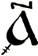
	Тысяча	1000
	Тьма	10 000
	Легион	100 000
	Леодр	1 000 000
	Ворон	10 000 000
	Колода	100 000 000

Рисунок 6

Славянская нумерация просуществовала до конца XVII столетия, пока с реформами Петра I в Россию из Европы не пришла позиционная десятичная система счисления - арабские числа.

Интересный факт, что почти та же система использовалась и у греков. Именно этим объясняется то, что для буквы б не было цифрового значения. Хотя, ничего особенно удивительного здесь нет: кириллическая нумерация полностью скопирована с греческой. Близкие цифры были и у готов.

Глава 3. Секрет происхождения арабских цифр

История наших привычных «арабских» чисел очень запутана. Нельзя сказать точно и достоверно как они произошли. Одно точно известно, что именно благодаря древним астрономам, а именно их точным расчетам мы и имеем наши числа. Между II и VI веками н.э. индийские астрономы познакомились с греческой астрономией. Они переняли шестидесятеричную систему и круглый греческий нуль. Индийцы соединили принципы греческой нумерации с десятичной мультипликативной системой, взятой из Китая. Так же они стали обозначать цифры одним знаком, как было принято в древнеиндийской нумерации брахми. Блестящая Севильи перевел на латынь эту книгу, и индийская система счета широко распространилась по всей Европе.

Индийские цифры возникли в Индии не позднее V века. Тогда же было открыто и формализовано понятие нуля (шунья), которое позволило перейти к позиционной записи чисел.

Арабские и индо-арабские цифры являются видоизменёнными начертаниями индийских цифр, приспособленными к арабскому письму.

Индийскую систему записи широко популяризировал учёный Аль-Хорезми, автор знаменитой работы «Китаб аль-джебр ва-ль-мукабала», от названия которой произошёл термин «алгебра». Аль-Хорезми написал книгу «Об индийском счёте», способствовавшую популяризации десятичной позиционной системы записи чисел во всём Халифате, вплоть до Мусульманской Испании. 

Арабские цифры стали известны европейцам в X веке. Благодаря тесным связям христианской Барселоны и мусульманской Кóрдовы , Сильвестр II (папа римский с 999 по 1003 годы) имел возможность доступа к научной информации, которой не имел никто в тогдашней Европе. В частности, он одним из первых среди европейцев познакомился с арабскими цифрами, понял удобство их употребления по сравнению с римскими цифрами и начал пропагандировать их внедрение в европейскую науку. В XII веке книга Аль-Хорезми «Об индийском счёте» была переведена на латинский язык и сыграла очень большую роль в развитии европейской арифметики и внедрении индо-арабских цифр. Название «арабские цифры» образовалось исторически, из-за того, что именно арабы распространяли десятичную позиционную систему счисления. Цифры, которые используют в арабских странах, по начертанию сильно отличаются от используемых в европейских странах.

В старых вавилонских текстах, датируемых 1700 годом до нашей эры, не встречается специального знака, обозначающего нуль, для его обозначения просто оставляли пустое место, более или менее выделенное.

Написание арабских цифр состояло из отрезков прямых линий, где количество углов соответствовало величине знака. Вероятно, кто-то из арабских математиков когда-то предложил идею - связать числовое значение цифры с количеством углов в ее написании (рис. 7).

Посмотрим на арабские цифры и видим, что:

Рисунок 7

0 - цифра без единого угла в начертании.

1 - содержит один острый угол.

2 - содержит два острых угла.

3 - содержит три острых угла (правильное, арабское, начертание цифры получается при написании цифры 3 при заполнении почтового индекса на конверте)

4 - содержит 4 прямых угла (именно этим объясняется наличие «хвостика» внизу цифры, никак не влияющего на ее узнаваемость и идентификацию)

5 - содержит 5 прямых углов (назначение нижнего хвостика - то же самое, что у цифры 4 - достройка последнего угла)

6 - содержит 6 прямых углов.

7 - содержит 7 прямых и острых углов (правильное, арабское, написание цифры 7 отличается от приведенного на рисунке наличием дефиса, пересекающего под прямым углом вертикальную линию посередине (вспомним, как мы пишем цифру 7), что дает 4 прямых угла и 3 угла дает еще верхняя ломаная линия)

8 - содержит 8 прямых углов.

9 - содержит 9 прямых углов (именно этим объясняется столь замысловатый нижний хвостик у девятки, который должен был достроить 3 угла, чтобы общее их число стало равно 9.

В современном мире мы пользуемся арабскими цифрами. Так как они более удобные по написанию. Их система называется десятеричной, для того чтобы написать число нам нужно всего лишь 10 цифр: 0 1 2 3 4 5 6 7 8 9. А не как у славян более 50. И с помощью этих цифр мы можем написать любое число без ограничения. Также благодаря нулю, придуманными мусульманами, написание стало намного легче. Поэтому в наши дни арабские цифры считаются самыми удобными и простейшими.

Глава 4. Организация и проведение исследования

Наше исследование проводилось среди учащихся 5 классов и в интернет – опросе. Всего было опрошено 30 человек.

Учащимся и интернет - пользователям было предложено 3 вопроса:

1. Какими цифрами мы пользуемся в современном мире?

2. Откуда к нам пришли цифры?

3. Где зародилось понятие ноль?

Результаты исследования:

Вопрос 1: Какими цифрами мы пользуемся в современном мире (рис. 8).

Рисунок 8 – Результат вопроса 1 Рисунок 9 – Результат вопроса 2

Глядя на диаграмму (рисунок 1), мы видим, что большинство опрошенных не ошиблись и выбрали правильный ответ. В современном мире мы пользуемся арабскими цифрами.

Вопрос 2: Откуда к нам пришли цифры.

Со вторым вопросом опрошенные не справились. Большинство ответили, что цифры пришли к нам из Арабии (Рисунок 2). И только 10 человек выбрали правильный ответ: цифры пришли к нам из Индии.

Вопрос 3: Где зародилось понятие ноль.

Рисунок 10 – Результат вопроса 3

Заключение

Целью нашего проекта было выяснить секрет происхождения арабских цифр и причину их долгожительства. Для её достижения нам пришлось решать поставленные задачи. Вот что из этого получилось:

1. С помощью литературных источников и Интернета познакомиться с цифрами разных народов. В ходе решения данной задачи мы познакомились с цифрами Древнего Египта, Вавилона, древней Греции и Рима, не обошли вниманием славянскую кириллическую нумерацию и, разумеется, арабские цифры. На наш взгляд, в рамках данного проекта, задача решена на 100%. И очень здорово, что работу в данном направлении можно продолжать, ведь существует ещё множество различных нумераций, как изученных, так и не изученных.

2. Найти информацию о происхождении арабских цифр. С этой задачей мы также полностью справился благодаря сети Интернет. Действительно, история происхождения арабских цифр оказалась очень запутанной. Нам стало понятно, что не совсем правильно называть наши цифры арабскими. В них сконцентрировался опыт многих цивилизаций: и египетской, и вавилонской, и греческой, и, конечно, индийской. Да, арабы добавили в индийскую систему счисления много своего, и именно арабы распространили эти цифры по Европе, но считать их только арабским достижением было бы несправедливо.

3. Сравнить различные системы счисления, чтобы разобраться, почему современные люди пользуются именно арабскими цифрами. Полагае, что и с этой задачей нам удалось разобраться. К сожалению, пришлось признать, что наши славянские цифры крайне неудобны в использовании. Удобство арабской нумерации очевидно: арабская система счисления позиционная, т.е. значение цифры зависит от её места в записи числа, в ней присутствует понятие «нуль» и именно поэтому с помощью всего десяти цифр мы имеем возможность записать абсолютно любое число!

4. Исследовать уровень знаний окружающих нас людей о цифрах, которыми все они пользуются. Данная задача была решена с помощью опроса учащихся школы и Интернет – опроса. Мы выяснили, что большинство опрошенных знает, что мы пользуемся арабской системой счисления, однако очень мало людей имеют представление о том, откуда пришли к нам наши цифры, и где зародилось понятие нуля.

5. Создание буклета, в которой отразились бы результаты нашей работы – так же решена.

Мы считаем, что достигли цели и выполнил все задачи. Нам очень понравилась работать с проектом. В дальнейшем мы хотим продолжить работу в этом направлении, так как ещё осталось много интересных вопросов о числах.

Список использованной литературы

1. www.437000.ru

2. www.collectionstudio.com

3. comp-science.narod.ru

4. info-7.ru

5. festival.1september.ru

6. www.wikipedia.org

Приложение 1

Цифры разных народов: