Проект по математике
«Способы решения уравнений различных видов»

Подготовили учащиеся 8 класса
Руководитель:
Учитель математики - Некрасова Тамара Ивановна
«Уравнение представляет собой наиболее серьёзную и важную вещь в математике».
Лодж О.
«Посредством уравнений, теорем
Он уйму всяких разрешал проблем:
И засуху предсказывал, и ливни.
Поистине его познанья дивны»
Чосер Д
Тема проекта «Способы решения уравнений различных видов»
Тип проекта: групповой, краткосрочный, творческо-исследовательский
Участники проекта: ученики 8 класса.
Сроки реализации проекта: три недели.
Результат: защита проектов, создание презентации, а затем оказание помощи одноклассникам, испытывающим затруднения по данному учебному материалу.
Целью работы является комплектовать все виды уравнений по видам и разобрать основные способы решения данных уравнений.
Задания для групп (в каждой группе 2 человека)
Основополагающий вопрос
Зачем нужно уметь решать уравнения?
Проблемные вопросы
Какими методами решаются уравнения?
1. Обсуждение и утверждение плана работы. Распределение учащихся на группы, выбор каждой группой вопросов-заданий и форм (проектных продуктов) представления результатов работы (первая неделя).
2. Изучение и анализ источников и литературы.(вторая неделя)
3. Оформление результатов работы над проектом.(вторая неделя)
4. Представление проектных продуктов.(третья неделя)
Работа над проектом
Подбор исторических сведений об уравнениях (1 учащийся)
Задание для группы 1.
Собрать информацию по теме «Линейные уравнения, методы их решения» (источники: материалы учебников алгебры 7-8, справочники, Интернет).
Подобрать 10 – 15 уравнений по данной теме (вместе с решением).
Оформить отчёт о проделанной работе: теория + практические задания («бумажный» вариант).
Подготовиться к защите проекта.
Задание для группы 2.
Собрать информации по теме «Квадратные уравнения и уравнения, приводимые к квадратным, методы их решения» (источники: материалы учебников алгебры 7-8, справочники, Интернет).
Подобрать 10 – 15 уравнений по данной теме (вместе с решением).
Оформить отчёт о проделанной работе: теория + практические задания («бумажный» вариант).
Подготовиться к защите проекта.
Задание для группы 3.
Собрать информации по теме «Дробно-рациональные уравнения, методы их решения» (источники: материалы учебников алгебры 7-8, справочники, Интернет).
Подобрать10 – 15 уравнений по данной теме (вместе с решением).
Оформить отчёт о проделанной работе: теория + практические задания («бумажный» вариант).
Подготовиться к защите проекта.
Создание презентации (коллективная работа)
Приложение 1
Историческая справка
В те далекие времена, когда мудрецы впервые стали задумываться о равенствах содержащих неизвестные величины, наверное, еще не было нимонет, ни кошельков. Но зато были кучи, а также горшки, корзины, которыепрекрасно подходили на роль тайников-хранилищ, вмещающих неизвестное количество предметов. "Ищется куча, которая вместе с двумя третями ее, половиной и одной седьмой составляет 37...", - поучал во II тысячелетии до новой эры египетский писец Ахмес. В древних математических задачах Междуречья, Индии, Китая, Греции неизвестные величины выражали число
павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущества. Хорошо обученные науке счета писцы, чиновники и посвященные в тайные знания жрецы довольно успешно справлялись с такими задачами.
Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Однако ни в одном папирусе, ни в одной глиняной табличке не дано описания этих приемов. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: "Смотри!", "Делай так!", "Ты правильно нашел". В этом смысле исключением является "Арифметика"
греческого математика Диофанта Александрийского (III в.) – собрание задач на составление уравнений с систематическим изложением их решений.
Однако первым руководством по решению задач, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда бен Мусы аль-Хорезми. Слово "аль-джебр" из арабского названия этого трактата – "Китаб аль-джебер валь-мукабала" ("Книга о восстановлении и противопоставлении") – со временем превратилось в хорошо знакомое всем слово "алгебра", а само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений.
Приложение 2
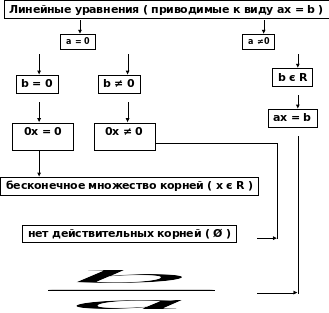
Линейные уравнения.
1) Сейчас мы с вами рассмотрим решения линейных уравнений.
Вспомним, что уравнение вида ax+b=0 называется линейным уравнением или
уравнением первой степени так как при переменной «х» старшая степень
находится в первой степени.
Решение линейного уравнения очень простое:
ax+b=0 ;
аx=−b .
х = -b : а
Пример 1 Решите уравнение 3x+3=5x
Линейное уравнение решается методом переноса членов содержащих
неизвестные в левую часть от знака равенства, свободные коэффициенты в
правую часть от знака равенства:
3x – 5x = – 3
- 2x = - 3
х = −3 : (−2)
x = 1,5
Значение переменной, обращающее уравнение в верное равенство
называется корнем уравнения.
Выполнив проверку получим:
3 ∙1,5+3=5∙ 1,5
4,5+3=7,5
7,5=7,5
Значит 1,5 – корень уравнения.
Ответ: 1,5.
Решения уравнений методом переноса слагаемых из одной части
уравнения в другую, при этом знак слагаемых меняется на противоположный
и применяют свойства уравнений – обе части уравнения можно умножить
(разделить) на одно и то же отличное от нуля число или выражение, можно
рассмотреть при решении следующих уравнений.
Пример 2 Решите уравнения:
а) 6x+1=− 4x; б) 8+7x=9x+4; в) 4(x−8)=− 5
Решение.
а) Методом переноса решаем
6x + 4 x = ─1;
10x = ─1;
х = ─1 : 10;
x = ─ 0,1.
Проверка:
6 ∙ (−0,1 )+1=−4 ∙ (−0,1 ) ;
−0,6+1=0,4 ;
0,4=0,4.
Ответ: –0,1
б) Аналогично предыдущему примеру решаем методом переноса:
9 x−7 x=8−4 ;
2 x=4 ;
х = 4 :2 ;
x = 2.
Проверка :
8+7 ∙ 2=9∙ 2+4 ;
8+14=18+4 ;
22=22.
Ответ: 2
в) В данном уравнении необходимо раскрыть скобки, применяя
распределительное свойство умножения относительно операции сложения.
4 ( x−8 )=−5 ;
4 x−32=−5 ;
4 x=−5+32 ;
x=27 :4 ;
x=6,75.
Проверка :
4 (6,75−8 )=−5 ;
4∙ (−1,25 )=−5 ;
−5=−5.
Ответ: 6,75.
2)
| 1 Найдите корень уравнения 6 x + 1 = − 4x 6х + 4х = -1 10х = -1 х = - 1 : 10 х = - 0,1 Ответ: - 0,1 | 2 Найдите корень уравнения −2 x−4 = 3x - 2х – 3х = 4 -5х= 4 х = 4 : (- 5) х = - 0,8 Ответ: - 0,8 |
| 3. 7m + 1 = 8m + 9 7m – 8m = 9 – 1 -1m = 8 m = 8 : (-1) m = -8 Ответ: -8 | 4. 4 + 25y = 6 + 24y 25y – 24y = 6 - 4 1y = 2 у = 2 : 1 у = 2 Ответ: 2 |
| 5. 2,1 · ( 4 – 6y ) = - 42 8,4 – 12,6y = -42 -12.6 = -42 – 8.4 -12.6 = -50.4 y = -50.4 : ( -12.6 ) y = 4 Ответ: 4 | 6. -3 · ( 2 – 15x ) = -6 - 6 + 45х = - 6 45x = -6 + 6 45x = 0 х = 0 : 45 х = 0 Ответ: 0 |
| 7. 4y + 15 = 6y + 17 4y – 6y = 17 – 15 -2y = 2 y = 2 : ( -2 ) y = -1 Ответ: -1 | 8. 3y – (5 – y) = 11 3у – 5 + у = 11 4у = 11 + 5 4у = 16 у = 16 : 4 у = 4 Ответ: 4 |
| 9. -27x + 220 = 5x -27x + 5x = - 220 -22x = -220 x = -220 : ( -22 ) х = 10 Ответ: 10 | 10. -5( 5 – x ) – 4x = 18 -25 + 5x – 4x = 18 5x – 4x = 18 + 25 1x = 43 x = 43 : 1 x = 1 Ответ: 1 |
| 11. 3( y – 5 ) – 2( y – 4 ) = 8 3y – 15 – 2y – 8 = 8 3y – 2y = 8 + 8 + 15 1y = 31 y = 31 : 1 y = 31 Ответ: 31 | 12.( 3x – 1.2 ) * 7 = 10.5 21x – 8.4 = 10.5 21x = 18.9 x = 18.9 : 21 x = 0.9 Ответ: 0.9 |
Приложение 3
Квадратные уравнения
Уравнение вида a x2 + bx + c = 0 называют квадратным уравнением, где a –
старший коэффициент, b – средний коэффициент, с – свободный член.
В зависимости от коэффициентов а, b и с – уравнение может быть,
полным или не полным, приведенным или не приведенным.
Неполные квадратные уравнения
Рассмотрим способы решения неполных квадратных уравнений:
1) ax2 + bx = 0 (c=0) ;
Начнем разбираться с решением первого вида неполных квадратных уравнений при c=0. Неполные квадратные уравнения вида a∙x2+b∙x=0 позволяет решить метод разложения на множители. В частности метод вынесения за скобки.
Мы можем , находящийся в левой части уравнения общий множитель x, вынести за скобки . Это позволяет перейти от исходного неполного квадратного уравнения к равносильному уравнению вида: x∙(a ∙ x + b) = 0.
А это уравнение равносильно совокупности двух уравнений x=0 или
a∙x + b = 0, последнее из которых является линейным и имеет корень x = −ba .
Итак, неполное квадратное уравнение a∙x2+b∙x=0 имеет два корня
x=0 и x=−ba .
2) ax2 + c = 0 (b = 0) ;
Теперь рассмотрим, как решаются неполные квадратные уравнения, в которых коэффициент b равен нулю, а c≠0, то есть, уравнения вида a∙x2 + c=0. Мы знаем, что перенос слагаемого из одной части уравнения в другую с противоположным знаком, а также деление обеих частей уравнения на отличное от нуля число дают равносильное уравнение.
Поэтому можно провести следующие равносильные преобразования
неполного квадратного уравнения a∙x2 + c=0:
перенести c в правую часть, что дает уравнение a∙x2=−c,
и разделить обе его части на a, получаем х2 =  .
.
Полученное уравнение позволяет сделать выводы о его корнях.
Если число − – отрицательное, то уравнение не имеет корней. Это
– отрицательное, то уравнение не имеет корней. Это
утверждение следует из того, что квадрат любого числа есть число
неотрицательное.
Если же −  – положительное число, то дело с корнями уравнения обстоит
– положительное число, то дело с корнями уравнения обстоит
иначе. В этом случае, нужно вспомнить, что корень уравнения есть, им
является число. Корень уравнения вычисляется по схеме: x = ± √ 
Известно, что подстановка в уравнение вместо x его корней обращает
уравнение в верное равенство.
3) ax2=0 (b , c=0 ).
Решения неполных квадратных уравнений, в которых коэффициенты b и cравны нулю, то есть, с уравнений вида a∙x2=0.
Уравнению a∙x2=0 следует x2=0, которое получается из исходного делением
его обеих частей на отличное от нуля число a. Очевидно, корнем
уравнения x2=0 является нуль, так как02=0. Других корней это уравнение не
имеет.
Итак, неполное квадратное уравнение a∙x2=0 имеет единственный
корень x=0.
Пример 3 Решите уравнения: а) x2=5x, если уравнение имеет несколько корней, то в ответе укажите меньший из них;
б) 5 x2−10 x=0, если уравнение имеет несколько корней, то в ответе укажите
больший из них;
в) x2 −9=0, если уравнение имеет несколько корней, то в ответе укажите
меньший из них.
Решение.
a) x2=5 x ; Переносим всечлены уравнения водну сторону
x2−5 x=0 ; получили неполное квадратное уравнение к котором отсутствует
свободный член. Решаем методом вынесения за скобки.
x ( x−5 )=0 ;
x1=0 или x2=5.
Уравнение умеет два корня, меньшее из которых является 0
Ответ: 0
б) 5 x2−10 x=0. Аналогично предыдущему примеру применяем метод
вынесения за скобки
5x ( x − 2 ) = 0 ;
5x = 0 или x−2=0 ;
х = 0 или x = 2.
В ответе необходимо указать больший из корней. Таковым является число 2
Ответ: 2
в) x2−9=0. Данное уравнение является неполным квадратным уравнением, у
которого отсутствует средний коэффициент.
x2=9 ;
x=±√9 ;
x1,2=± 3
Меньшим из данных корней является число – 3
Ответ: –3.
Полные квадратные уравнения.
1 основная формула корней квадратного уравнения
Для решения квадратных уравнений вида a x2+bx+c=0 существуют формула
корней.
Запишем формулу корней квадратного уравнения пошагово:
1) D=b2−4·a·c – так называемый дискриминант квадратного уравнения.
а) если D2+bx+c=0не имеет действительных корней;
б) если D0, то уравнение a x2+bx+c=0не имеет один корень: x=−b:2a
в) если D2+bx+c=0не имеет два корня:
x = (−b±√D) / 2a
Алгоритм решения квадратных уравнений по формулам корней
На практике при решении квадратных уравнения можно сразу
использовать формулу корней, с помощью которой вычислить их значения.
Но это больше относиться к нахождению комплексных корней.
Однако в школьном курсе алгебры обычно речь идет не о
комплексных, а о действительных корнях квадратного уравнения. В этом
случае целесообразно перед использованием формул корней квадратного
уравнения предварительно найти дискриминант, убедиться, что он
неотрицательный (в противном случае можно делать вывод, что уравнение не
имеет действительных корней), и уже после этого вычислять значения
корней.
Приведенные рассуждения позволяют записать алгоритм решения
квадратного уравнения. Чтобы решить квадратное уравнение a∙x2+b∙x+c=0,
надо:
по формуле дискриминанта D=b2−4∙a∙c вычислить его значение;
заключить, что квадратное уравнение не имеет действительных корней, если дискриминант отрицательный;
вычислить единственный корень уравнения по формуле , если D=0;
найти два действительных корня квадратного уравнения по формуле корней, если дискриминант положительный.
2 вторая формула корней квадратного уравнения
(при четном втором коэффициенте).
Для решения квадратных уравнений вида a x2+bx+c=0, при четном
коэффициенте b=2k существуют другая формула.
Запишем новую формулу корней квадратного уравнения при k=b2:
1) D=k2−a·c – так называемый дискриминант квадратного уравнения.
а) если D 2 + 2k + c = 0 не имеет действительных
корней;
б) если D = 0, то уравнение ax2 + 2kx + c = 0 имеет один корень: x=−k/a
в) если D ˃ 0, то уравнение a x2+2 kx+c=0 имеет два корня:
x = (−k ±√D) / а
Пример 4 Решите уравнение 2x2 −3x+1=0
Решение. В первом случае имеем следующие коэффициенты
квадратного уравнения: a=2,b=-3 и c=1. Согласно алгоритму, сначала надо
вычислить дискриминант D=b2−4∙a∙c=(-3)2−4∙2∙1=9-8=1. Так как 10, то
есть, дискриминант больше нуля, то квадратное уравнение имеет два
действительных корня. Найдем их по формуле корней
х1 =  и х2 =
и х2 =  ; D = 9 – 8 = 1 х1 =
; D = 9 – 8 = 1 х1 =  = 1;
= 1;
х2 =  =
= 
Ответ: 1; 
| 5х2=125 2х2-3х+1=0 3х2+4х+3=0 9х2=81 2х2+3х+1=0 х2-4х-5=0 | 2х2-7х-4=0 х2-5х-6=0 4х2-11х+6=0 х2+6х-40=0 6х2+х-1=0 х2+5х+6=0 |
Приложение 4
Рациональные уравнения
Дробно-рациональные уравнения.
Если равенство, содержащее переменную величину, (которую обычно обозначают одной из последних букв латинского алфавита, например x) является истинным не при всех допустимых значениях этой переменной, оно называется уравнением (с одним неизвестным).
Решение дробно-рационального уравнения сводится в конечном итоге к замене исходного уравнения целым уравнением, которое равносильно исходному уравнению или является его следствием.
Определение. Уравнение f (x) = g (x) называется дробно-рациональным, если f (x) и g(x) являются дробно-рациональными функциями.
1. 2.
2.



Алгоритм решения дробно-рациональных уравнений:
При решении дробных рациональных уравнений поступают следующим образом:
1.находят общий знаменатель дробей, входящих в уравнение; общий знаменатель(x+5)(3-x)
общий знаменатель(x+5)(3-x)



3.решают получившееся целое уравнение;

4.исключают из его корней те, которые обращают в ноль общий знаменатель.

 или
или 
Умножение крест-накрест. При необходимости перепишите данное
вам уравнение так, чтобы на каждой его стороне находилась одна дробь
(одно рациональное выражение); только в этом случае вы сможете
воспользоваться методом умножения крест-накрест.
Умножьте числитель левой дроби на знаменатель правой.
Повторите это с числителем правой дроби и знаменателем левой.
Умножение крест-накрест основано на основных алгебраических
принципах. В рациональных выражениях и других дробях можно избавиться
от числителя, соответственно перемножив числители и знаменатели двух
дробей.
Приравняйте полученные выражения и упростите их.
Решите полученное уравнение, то есть найдите «х». Если «х»
находится с обеих сторон уравнения, обособьте его на одной стороне
уравнения.
| 1.  ОДЗ: х ≠ − 2, х ≠ 4 ОДЗ: х ≠ − 2, х ≠ 4 (х – 2)(х – 4) = (х + 2)(х + 3) х2 – 4х – 2х + 8 = х2 + 3х + 2х + 6 х2 – 6х – х2 – 5х = 6 – 8 -11х = -2 х = -2 : (-11)  Ответ: 
| 2. 2. Решение: | ∙ 6 3х – 3 + 4х = 5х 7х – 5х = 3 2х = 3 х = 3 : 2 х = 1,5 Ответ: 1,5
|
| 3.  Решение:  | ∙ (7 – х) | ∙ (7 – х) 12 = х(7 – х) 12 = 7х – х2 х2 – 7х + 12 = 0 D = 1 0, х1 = 3, х2 = 4. Ответ: 3; 4 | 4. Решение: ОДЗ: х ≠ 0, х ≠ 5 Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю. х² − 3 х + х – 5 – х – 5 = 0 х² − 3 х – 10 = 0 D = 49 0, х1 = 5, х2 = − 2 х = 5 не удовлетворяет ОДЗ. Говорят, 5 – посторонний корень. Ответ: − 2 |
| Общий знаменатель дробей x(x - 2)(х + 2). Умножив обе части уравнения на общий знаменатель дробей, получим 2х - (х + 2) = (4 - х)(х - 2). Отсюда Если x = 2, то х(х - 2)(х + 2) = 0; если х = 3, то х(х - 2)(х + 2) ≠ 0. Значит, корнем исходного уравнения является число 3. Ответ: 3.
|









 .
.
 и х2 =
и х2 =  ; D = 9 – 8 = 1 х1 =
; D = 9 – 8 = 1 х1 =  = 1;
= 1;  =
= 
 2.
2.



 общий знаменатель(x+5)(3-x)
общий знаменатель(x+5)(3-x)



 или
или 










