ОКОУ «Льговская школа-интернат для детей с ОВЗ»
Проект по геометрии для учащихся 7 классов: «Геометрия вокруг нас»
Подготовила:
учитель математики
Максакова Наталья Андреевна
г. Льгов
2020
СОДЕРЖАНИЕ
| ВВЕДЕНИЕ…………………………………………………………………………. | 3 |
| 1. ГЕОМЕТРИЧЕСКИЕ СВЕДЕНИЯ…………………………………………… | 4 |
| 2. ПРИМЕНЕНИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР |
|
| 2.1. Геометрические фигуры в быту………………………………………………… | 4 |
| 2.2 Геометрические фигуры в архитектуре………………………………………… | 6 |
| 2.3. Геометрические фигуры в природе……………………………………………. | 6 |
| 2.4. Геометрические фигуры в искусстве …………………………………………. | 7 |
| 4. СОЦИОЛОГИЧЕСКИЙ ОПРОС……………………………………………… | 8 |
| 5. ПРАКТИЧЕСКАЯ ЧАСТЬ……………………………………………………… | 10 |
| ЗАКЛЮЧЕНИЕ……………………………………………………………………… | 12 |
| СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ………………………………… | 11 |
ВВЕДЕНИЕ
«Окружающий нас мир – это мир геометрии»
А.Д. Александров
Геометрия зародилась в глубокой древности. Строя жилища и храмы, украшая их орнаментами, размечая землю, измеряя расстояния и площади, человек применял свои знания о форме, размерах и взаимном расположении предметов, он использовал свои геометрические знания, полученные из наблюдений и опытов. Почти все великие ученые древности и средних веков были выдающим геометрами.
Геометрия – это не только раздел математики, школьный предмет, это, прежде всего феномен общечеловеческой культуры, являющийся носителем собственного метода познания мира.
Она тесно связана с окружающим нас миром. Ведь все, что мы видим вокруг (окна, загадочный узор снежинки, дома, капля воды), так или иначе относится к геометрии, ничто не ускользает от ее внимательного взгляда. Изучая геометрию можно узнать много об окружающих нас предметах, увидеть красоту обычных вещей, смотреть, думать и делать выводы. “Окружающий нас мир – это мир геометрии”. Так сказал выдающийся российский математик, физик и философ XX века Александр Данилович Александров, намекая на тесные и многообразные связи геометрии с окружающей нас действительностью. Нам захотелось изучить, как геометрия связана с жизнью, на примере геометрических фигур.
Актуальность исследования в том, что геометрические фигуры являются неотъемлемой частью нашей жизни. Если будем изучать выбранную нами тему, то докажем что почти все, что нас окружает – это геометрические фигуры.
Цели и задачи исследовательской работы.
Цель: найти связь геометрических фигур с предметами окружающего мира.
Задачи:
изучить литературу, СМИ и интернет-ресурсы;
исследовать применение геометрических фигур в быту, архитектуре, их нахождение в природе и других местах;
провести социологический опрос;
показать применение геометрических фигур на практике.
Объект исследования: предметы окружающего мира.
Предмет исследования: взаимосвязь предметов окружающего мира и геометрических фигур.
Методы исследования: изучение и анализ теоретических сведений по данной теме,
социологический опрос, практическая деятельность, наблюдение.
1. ГЕОМЕТРИЧЕСКИЕ СВЕДЕНИЯ
Геометрические фигуры весьма разнообразны. Мы знаем, что такое точка, прямая, отрезок, луч, угол. Знакомы с треугольником, прямоугольником, кругом и другими фигурами, рассматриваемыми в планиметрии за курс основной школы.
Теперь рассмотрим геометрические фигуры, которые изучаются в стереометрии и пригодятся в нашем дальнейшем исследовании.
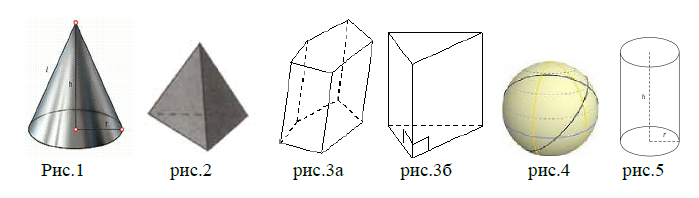
Конус – от греческого слова «конос» (сосновая шишка, остроконечная верхушка шлема). Определение. Конусом называется тело. Которое состоит из круга – основание конуса, точки, не лежащей в плоскости этого круга – вершины конуса, и всех отрезков, соединяющих вершину конуса с точками основания. Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса (рис.1).
Пирамида – от греческого слова «пюрамис», которым греки называли египетские пирамиды. А это слово происходит от древнеегипетского слова «пурама», которым эти пирамиды называли сами египтяне. Определение. Многогранник, у которого одна грань, называемая основанием, – многоугольник, а другие грани – треугольники с общей вершиной, называется пирамидой (рис.2).
Призма – от слова «присма» («опиленная», «отпиленная часть»). Определение. Призмой называется многогранник, у которого две грани (основания) лежат в параллельных плоскостях, а все ребра вне этих граней параллельны между собой (рис.3а,б).
Сфера – от греческого слова «сфайра» – «шар», «мяч». Термин этот встречается у
древнегреческих математиков еще до Евклида. Определение: Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки (рис.4).
Цилиндр (греч. Kэlindros, валик, каток. Определение: Цилиндром называется тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов (рис.5).
2. ПРИМЕНЕНИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР
2.1. Геометрические фигуры в быту.
Все предметы в нашей квартире напоминают различные геометрические фигуры. Рассмотрим и опишем некоторые из них.
Толстая книга похожа на параллелепипед (рис.6). Потому, что как и у параллелепипеда все противолежащие грани и стороны у неё параллельны. Шкафы, полки и тумбочки это те же параллелепипеды. Двери имеют форму прямоугольников. Стены, потолок, окна так же напоминают прямоугольники.
В быту мы часто используем вёдра, имеющие форму усечённого конуса, служащие нам ёмкостью для различных жидкостей и сыпучих веществ (рис.7). Наши растения, благоприятно развиваются в цветочных горшках. А эти предметы чаще всего имеют форму либо прямого кругового конуса, либо форму усечённого конуса (рис.8).

Люстры, торшеры, светильники имеют геометрические формы или состоят из них (рис. 9-11). Зайдя в ювелирный магазин, перед нашими глазами предстает огромный выбор из миллиона украшений, сделанных в виде пирамиды. Многочисленные статуэтки, разнообразные подставки, необыкновенной красоты скульптуры – все это пирамиды. Вытяжка для угловой стены, сувениры из драгоценных камней, бижутерия, разнообразные упаковки для пищевых продуктов имеют форму геометрических фигур (рис12-17).

Игрушки и игры – и здесь многое подчинено геометрическим формам: кубики, шахматная доска, домино, игральные кости. Форму цилиндра, шара, а также их элементов можно также увидеть в быту: мячи, воздушные шары, свечи и подсвечники, ювелирные украшения и многое другое (рис.18, 19)
Цветочная клумба – это цветник различной геометрической формы: в виде круга, овала, прямоугольника, треугольника, многогранника (рис.20, 21).

Орнамент (лат. Ornamentum — украшение) — узор, основанный на повторе и чередовании составляющих его элементов. Орнамент предназначен: для украшения различных предметов (утварь, орудия и оружие, текстильные изделия, мебель, книги и т. д.), архитектурных сооружений (как извне, так и в интерьере), произведений пластических искусств (главным образом прикладных). Связанный с поверхностью, которую он украшает и зрительно организует, орнамент, как правило, выявляет, или акцентирует архитектонику предмета, на который он нанесён. Орнамент либо оперирует отвлечёнными формами, либо стилизует реальные мотивы, зачастую схематизируя их до неузнаваемости (рис.22-25). Неограниченный выбор цветов, оттенков, индивидуальных особенностей фактуры камня, возможность изготовить самый причудливый орнамент, мозаику — открывают перед дизайнерами просто неограниченные возможности (рис. 26-29).

2.2. Геометрические фигуры в архитектуре
Архитектурные произведения живут в пространстве, являются его частью, вписываясь в определенные геометрические формы. Кроме того, они состоят из отдельных деталей, каждая из которых строится на базе определенного геометрического тела. Часто геометрические формы являются комбинациями различных геометрических тел. В элементах архитектуры мы чаще встречаем конус, пирамиду, цилиндр, призму. Базовая часть зданий представляет собой прямую призму (реже цилиндр), а в основании крыш домов, церквей лежат конус, пирамида, полусфера (рис. 30 – 34).

Конус, пирамиду можно встретить не только в виде элементов зданий, но и в виде
индивидуальных построек (рис.35 – 37).

Хочется сказать несколько слов об египетских пирамидах. Арабская пословица гласит «Всё на свете страшится времени, а время страшится пирамид». Действительно, египетские пирамиды – это величайшие творения древнего архитектурного искусства. Среди грандиозных пирамид Египта особое место занимает великая пирамида фараона Хеопса. Она самая крупная и наиболее хорошо изученная. Правильная четырехгранная пирамида является одной из хорошо изученных геометрических фигур, символизирующих простоту и гармонию формы, олицетворяющую устойчивость, надежность, устремление вверх (рис. 38). Плоские геометрические фигуры можно также встретить на фасадах зданий виде орнамента или отдельных элементов (рис. 39, 40). Таким образом, мы можем говорить о пространственных геометрических фигурах, которые служат основой сооружения в целом или отдельных его частей, а также плоских фигурах, которые обнаруживаются на фасадах зданий.
2.3. Геометрические фигуры в природе
И в природе мы встречаем геометрические фигуры. В песчаной пустыне Сахаре, холмы представляют собой конус (рис.41).
Эту же фигуру мы видим в терриконах вулканов и в виде сосульки (рис.42,43). Многие растения также имеют форму геометрических фигур, в основном конус и шар (рис. 44-48).

Большая часть земной поверхности занята горными образованиями. Часто можно видеть, что скальные породы при разрушении дают каменные глыбы, имеющие формы параллелепипедов. Многие материалы имеют кристаллическую структуру. Госпожа природа, создает великолепные шедевры, не доступные мастерам культуры. Разве не впечатляют драгоценные произведения природы, достигаемые из ее кладовых (рис.49-52).
Прообразы колонн и цилиндров человек видел в стволах деревьев и карстовых пещерах.

2.4. Геометрические фигуры в искусстве
В искусстве существует такой вид, как абстракционизм (лат. Abstractio – удаление, отвлечение) – форма изобразительной деятельности, не ставящая своей целью имитацию или отображение визуально воспринимаемой реальности. Абстракция вопреки бытующим представлениям не является стилистической категорией. Эта специфическая форма изобразительного творчества распадается на несколько направлений. Нас интересует геометрическая абстракция (рис.53,54)
В космическом пространстве Земля, как и Луна и другие планеты имеет форму шара (рис.55). Также известно, что на Марсе были найдены пирамиды, полностью копирующие всем известные египетские пирамиды, а также изваяние Сфинкса (рис.56,57).

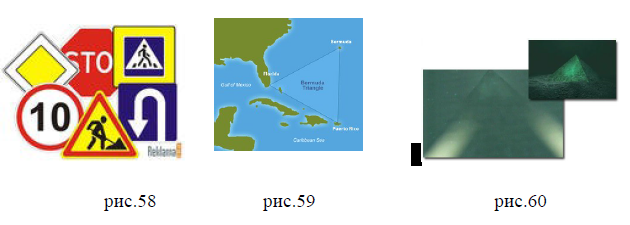
Форму геометрических фигур имеют дорожные знаки и указатели (рис.58). Одним из самых загадочных и таинственных мест на нашей планете является Бермудский треугольник. Это место, где по уверениям большинства очевидцев, происходит множество необъяснимых явлений (рис.59). В самом центре Бермудского треугольника обнаружена подводная пирамида. Обработав данные, ученые пришли к выводу, что поверхность сооружения пирамидальной формы идеально гладкая. По размерам она почти в три раза больше пирамиды Хеопса! Согласно характеристикам эхо-сигналов, грани пирамиды сложены из некоего таинственного материала, похожего на отполированную керамику или стекло (рис.60).
В народной медицине нашло применение целебных камней в форме пирамиды. Такие камни как аметист, змеевик, оникс, малахит и хрусталь обладают целебными свойствами (рис.61-65 соответственно). Получить такой подарок – большая удача так, как сувениры доставляют эстетическое удовольствие и украшают интерьер.

3. СОЦИОЛОГИЧЕСКИЙ ОПРОС
Учащиеся 7 «А» класса изучают геометрические фигуры в планиметрии, а 9 «Б» класса – в стереометрии. Среди них был проведен социологический опрос по теме «Геометрические фигуры вокруг нас». Всего в опросе приняли участие 17 человек. Учащимся были предложены следующие вопросы:
1. С какими профессиями связана геометрия?
2. Какие геометрические фигуры (объемные, необъемные) вы встречаете в обыденной
жизни чаще?
3. Встречали вы геометрические фигуры:
| - в природе |
| - в архитектуре |
| - в технике |
| - в быту |
| - (свой вариант) |
|
|
4. Можно ли из геометрических фигур сделать игры или игрушки?
5. Дорисуйте, какие-нибудь элементы к геометрическим фигурам.
Результаты социологического опроса
На вопрос: «С какими профессиями связана геометрия?», учащиеся ответили: архитектор, инженер, чертежник, строитель, художник, учитель геометрии, дизайнер, программист, конструктор.
На второй вопрос дети ответили, что чаще всего встречают в обыденной жизни квадрат, круг, овал, прямоугольник, треугольник, конус, шар, куб.
Ответы на третий вопрос опросника представлены в виде таблицы и в виде диаграммы:
| Встречали вы геометрические фигуры: | Да | Нет | Не знаю |
| в природе | 14 | 2 | 1 |
| в архитектуре | 17 | 0 | 0 |
| в технике | 13 | 2 | 2 |
| в быту | 16 | 1 | 0 |
| прочее | 9 | 0 | 8 |
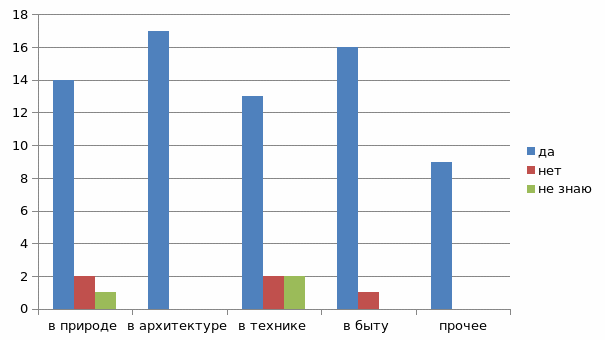
Таким образом, все учащиеся сходятся во мнении, что геометрические фигуры можно встретить повсюду: в повседневной быте человека, в технике, природе и архитектуре. Однако некоторые учащиеся еще в этом сомневаются.
На четвертый вопрос «Можно ли из геометрических фигур сделать игры или игрушки?» все классы ответили «да». А некоторые учащиеся после прохождения опроса нашли в библиотеке и интернете иллюстрации игры конструктор из геометрических фигур.
В пятом задании, где нужно было дорисовать, какие-нибудь элементы к геометрическим фигурам, учащиеся сделали следующие рисунки:

4. ПРАКТИЧЕСКАЯ ЧАСТЬ
Изготовление из геометрических фигур игрушек, игр, полезных вещей.
В социологическом опросе был вопрос: «Можно ли из геометрических фигур сделать аппликации, детские игры или игрушки?». Учащиеся со 100%-ой уверенностью отвечали – да и даже делали рисунки.
А вот какие забавные и весьма интересные игрушки мы нашли в интернете и книгах (рис.66- 70).

Оригами. Вряд ли кто не умеет сам из квадратного куска бумаги сделать «петушка», лодочку, кораблик, коробочку и т. д. Достигается это путем разнообразного перегибания и складывания бумажного квадрата. Полученные при этом сгибы (складки) позволяют придавать взятому куску бумаги ту или иную желаемую форму.

Игрушки из геометрических фигур. Можно изготавливать игрушки из геометрических фигур или их отдельных элементов. Нами был изготовлен тигр и два шарика.

Игра. Даны 6 кубиков. Из них нужно сложить 6 картинок. В изготовлении она представляет небольшие сложности, но зато интересная. Особенно для детей дошкольного возраста.


Полезные вещи. Изготовленные ознакомительного плаката о геометрических фигурах, встречающихся в повседневной жизни человека.
А вот те, которые сделаны своими руками (рис 71-74.).

ЗАКЛЮЧЕНИЕ
«Глядя на мир, нельзя не удивляться!» писал Козьма Прудков. Действительно, изучив литературу по данной теме, исследовав применение геометрических фигур в быту, архитектуре и их нахождение в природе и других местах, можно с уверенностью сказать, что цель нашего исследования достигнута, между геометрическими фигурами и предметами окружающего мира существует связь и, причем очень тесная. Это подтверждают и проведенный нами социологический опрос и практическая деятельность, с помощью которых мы еще раз доказали, что почти все, что нас окружает – это геометрические фигуры. Думаем, что описанный опыт данного исследования и его результаты представляют интерес для учащихся и людей, интересующихся геометрией, ведь их немало. И причем данная тема хорошее подспорье для дальнейших исследований.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. Алышева Т.В. «Математика: 7 класс: учебник для специальных (коррекционных) образовательных учреждений VIII вида»: М., «Просвещение», 2008г.
2. Перова М.Н. «Математика: 9 класс: учебник для специальных (коррекционных) образовательных учреждений VIII вида»: М., «Просвещение», 2008г.
3. Черчение: Учеб. Для 9 кл. общеобразоват. Учреждений /Н.А. Гордеенко, В.В. Степакова. – М. : ОООИ «Издательство Астрель», 2004. – 262 с.:ил.
4. 100 чуде вета. Величайшие окровища человечества на пяти континентах – Перевод с немецкого языка. – М.: ООО ТД Издательство «Мир книги», 2006. – 208с. С цвет. Ил.
5. http://piramidainfo.net
6. http://ru.wikipedia.org/wiki/Бермудский_треугольник
7. http://rusmineral.ru
8. http://www.youryoga.org/article/old/chudesa6.htm
9. http://www.stimex-trade.ru
10. http://sferica.by.ru/appendix/termin.html
11. http://www.uztest.ru/abstracts/?idabstract=803721
12. http://school21.m-sk.ru/npk_d_mat/karpovich.htm
13. http://www.likt590.ru/project/matematika/1/01.html
14. http://www.landmoney.ru/otzivi.html
15. http://www.goodgoods.ru/pages/content/1093427197.html
16. http://www.uztest.ru/abstracts
17. http://aibolit.givitca.ru/2009/05/12/neproizvolnye-dvizheniya.__
10