Россия, д. Хвощеватое, Новодугинского района, Смоленской области
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 20.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 21.04.2020 11:52
Огурцова Наталья Борисовна
учитель физики и математики.
68 лет
1 291
46 291 
Местоположение
Специализация
Проект «Зависимость расположения графика функции у=ах2+bх+с от значения коэффициентов».
Категория:
Математика
25.10.2019 14:07
Просмотр содержимого документа
«Проект «Зависимость расположения графика функции у=ах2+bх+с от значения коэффициентов».»
МКОУ «Хвощеватовская ОШ»
Исследовательский проект
«Зависимость расположения графика квадратичной функции от значения коэффициентов и дискриминанта»
Автор: ученица 9 класса
Савельева Анастасия
Руководитель: Огурцова Н.Б.
2017 г.
Функция у=ах2 +вх +с, (где а,в,с – числа и а≠0) - называется квадратичной.
Графиком квадратичной функции является парабола.
На графике парабола может располагаться по-разному.
Зависимость расположение графика квадратичной функции от дискриминанта.
D = b² - 4ac.
По графику легко определяются знаки корней (корни квадратного трехчлена ax2+bx+c - это абсциссы точек пересечения графика функции y=ax2+bx+c с осью абсцисс).
1)a0,D = 0 1 корень
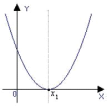
2)a0, D0 2 корня
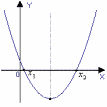
3)a
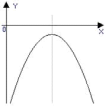
Зависимость расположение графика квадратичной функции от коэффициента а.
По графику квадратичной функции мы легко можем определить знак коэффициента a:
Если ветви параболы направлены вверх вдоль оси ординат-Оу, то a0.
(Парабола улыбается, когда a0)
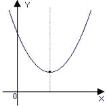
Если a
(Парабола грустит, когда a
Зависимость расположение графика квадратичной функции от коэффициента С.
Коэффициент с показывает ординату точки пересечения графика с осью ординат- Оу.
Если ветвь параболы и ось ординат- Оу пересекаются в точке выше нуля,
то коэффициент +С (с0)
Если ветвь параболы и ось ординат- Оу пересекаются в точке ниже нуля,
т
о коэффициент –С (с
Зависимость расположение графика квадратичной функции от коэффициента b.
Знак коэффициента b можно узнать из формулы, определяющей абсциссу вершины параболы: x0=-b/2a, отсюда b=-2ax0.
Зная значение а,x0 можно определить знак и числовое значение коэффициента b.
Рассмотрим примеры.
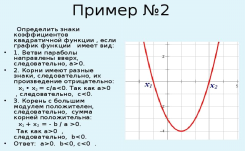
Замечание: c - ордината точки пересечения параболы с осью OY, поэтому знак c можно определить сразу.
Выводы, выделив «основную» роль каждого из коэффициентов, имеем:
1) Коэффициент а влияет на направление ветвей параболы: при а 0 – ветви направлены вверх, при а
2) Коэффициент b влияет на расположение вершины параболы. При b = 0 вершина лежит на оси оу.
3) Коэффициент с показывает точку пересечения параболы с осью ординат- ОУ.
Зависимость расположения параболы от знака коэффициентов a, b, c.
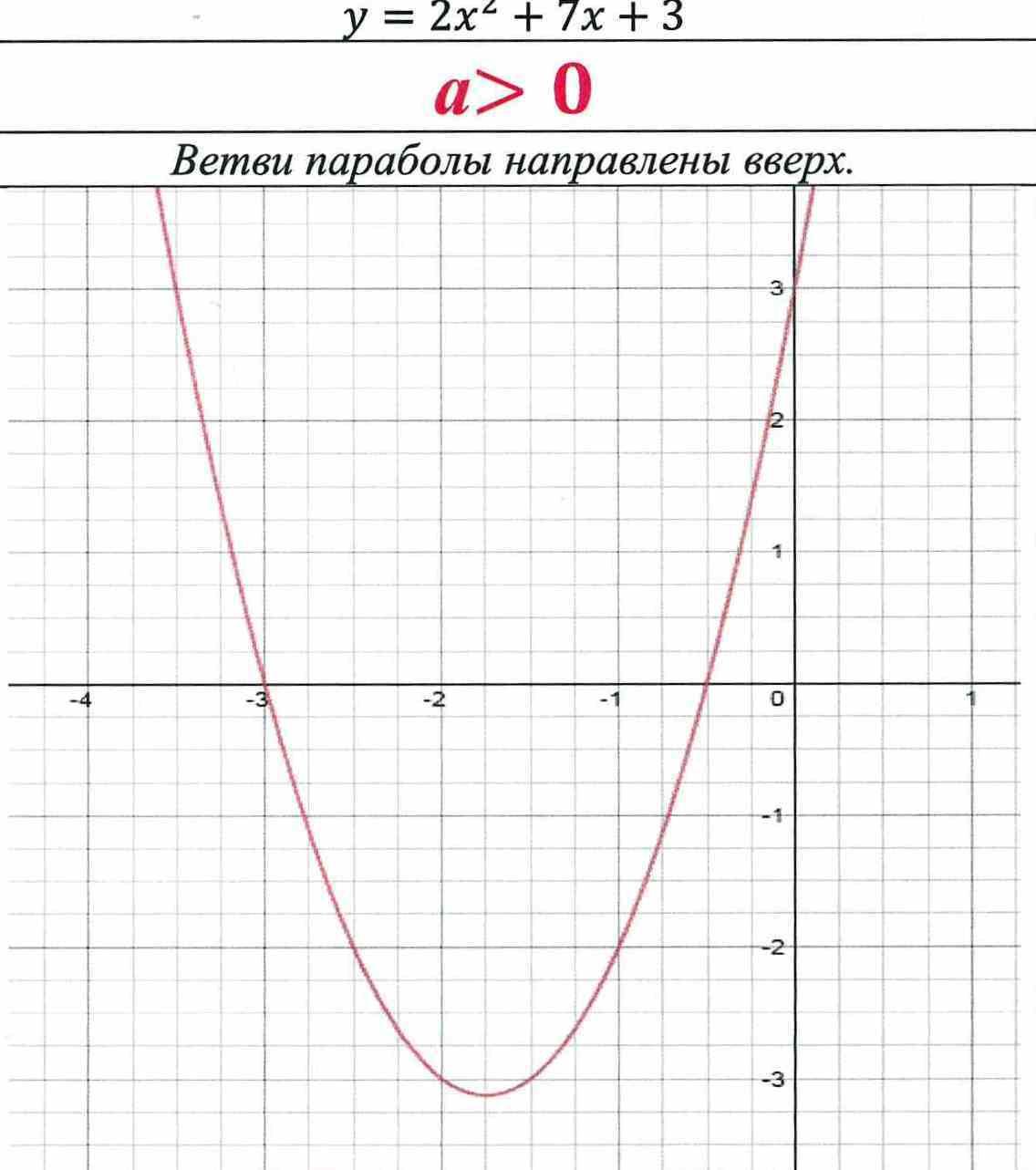
y = 2x2 + 7х + 3
a 0
Ветви параболы направлены вверх.
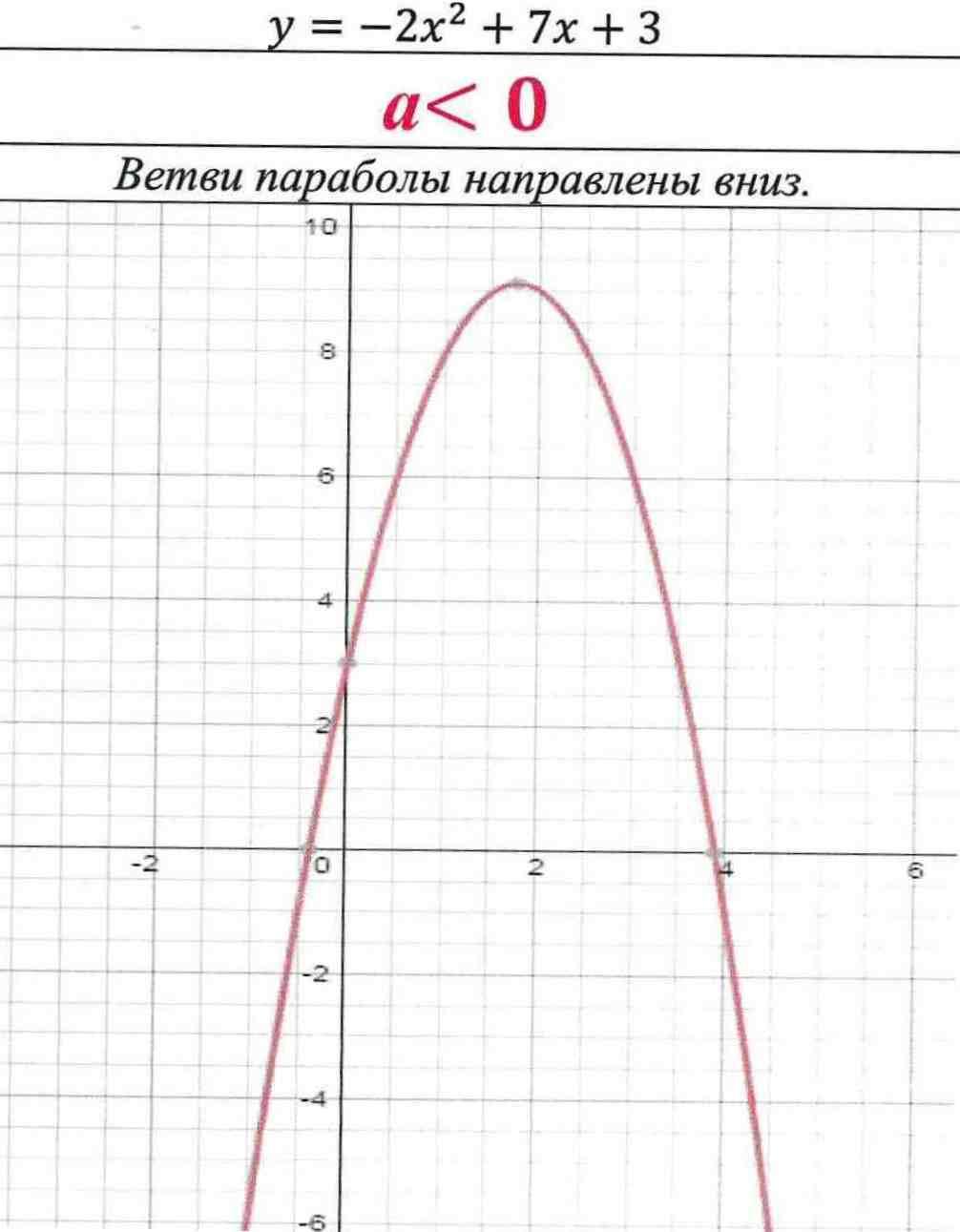
y = -2x2 + 7х + 3
a
Ветви параболы направлены вниз.
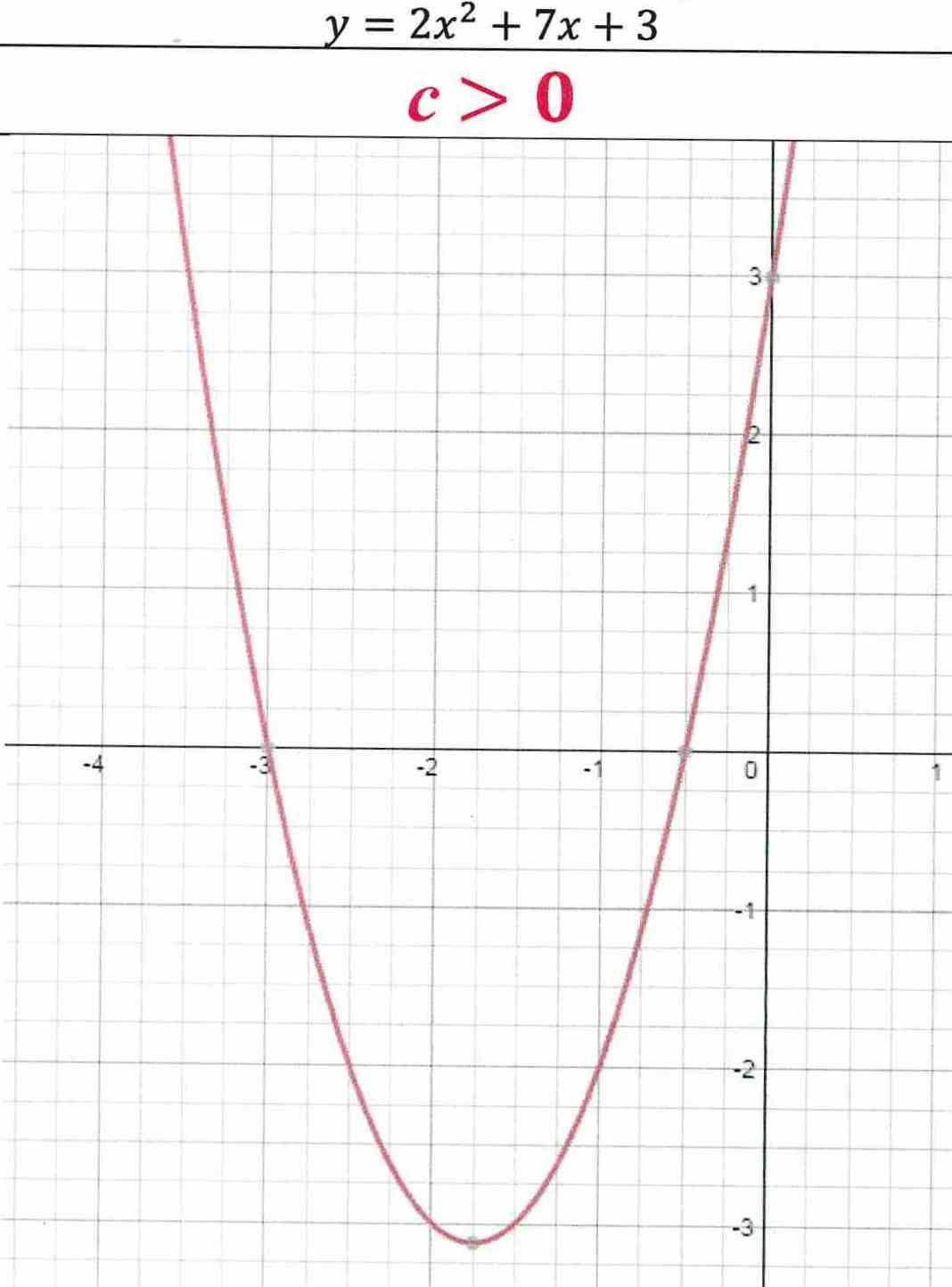
y = 2x2 + 7х + 3
c 0
Парабола пересекает
ось ординат в точке (0;с).
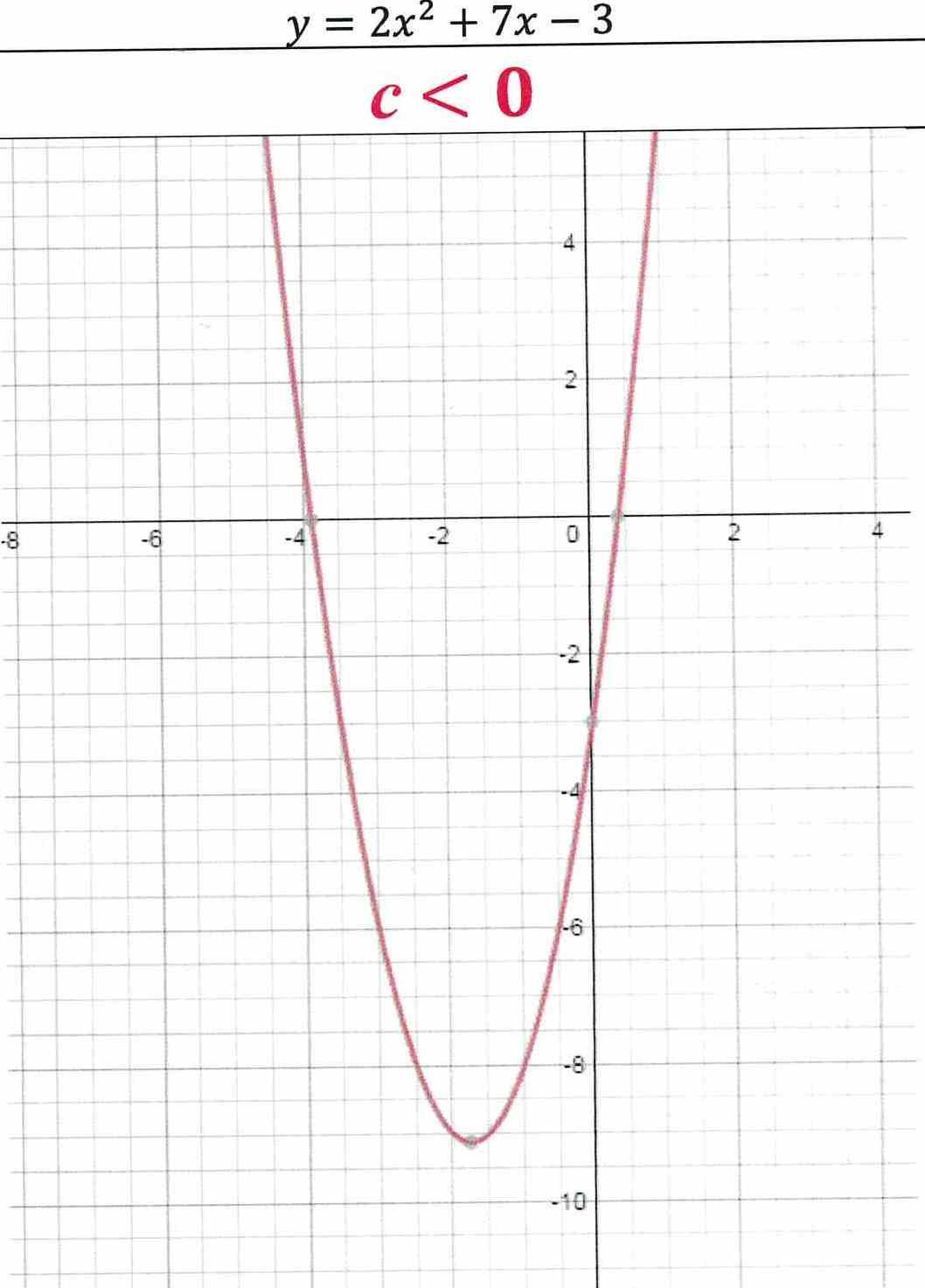
y = 2x2 + 7х - 3
c
Парабола пересекает
ось ординат в точке (0;с).
y = 2x2 + 7х + 3
a 0 b 0
Коэффициенты а и b имеют одинаковый знак.
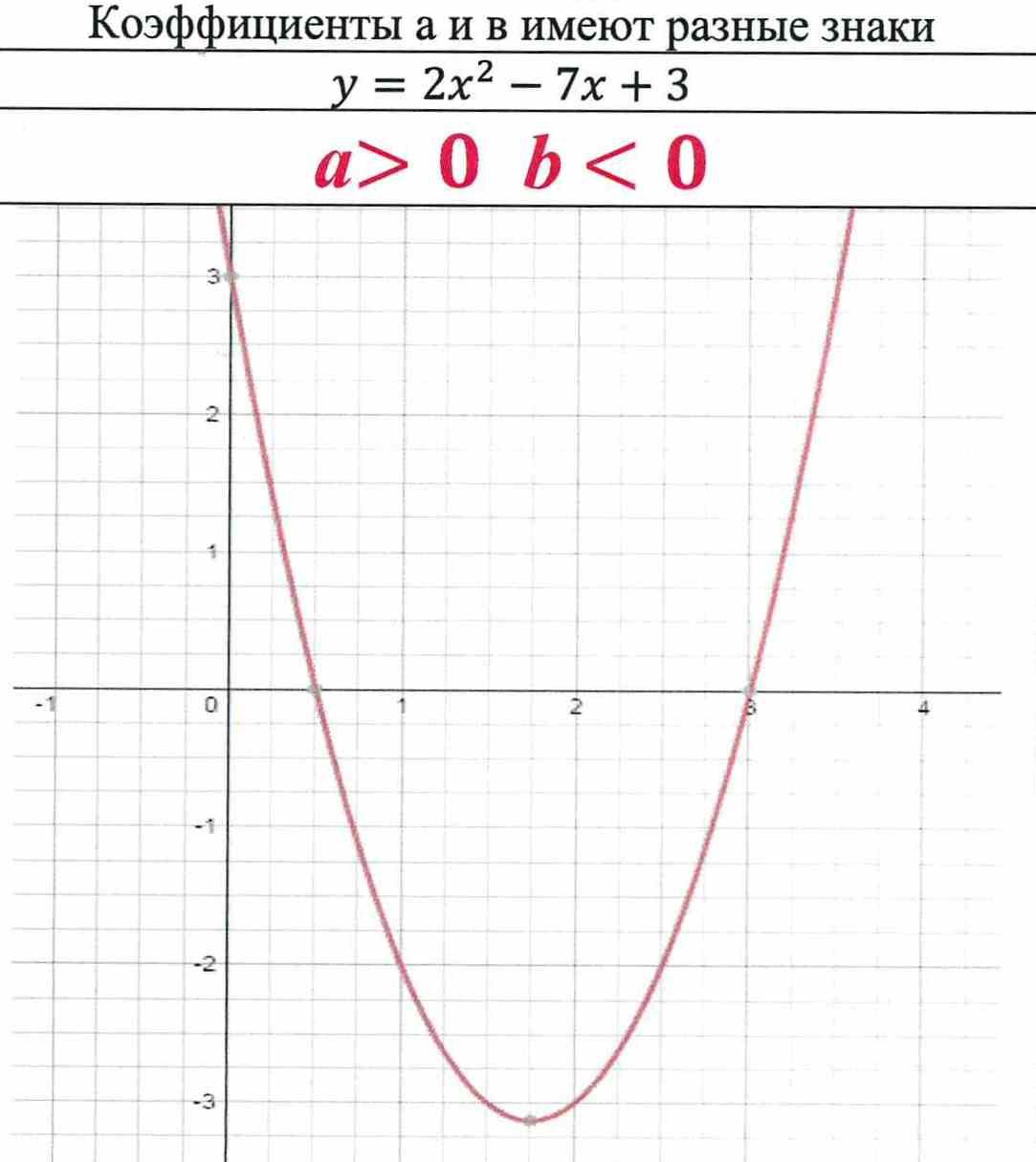
y = 2x2 - 7х + 3
a 0 b
Коэффициенты а и b имеют одинаковый знак.
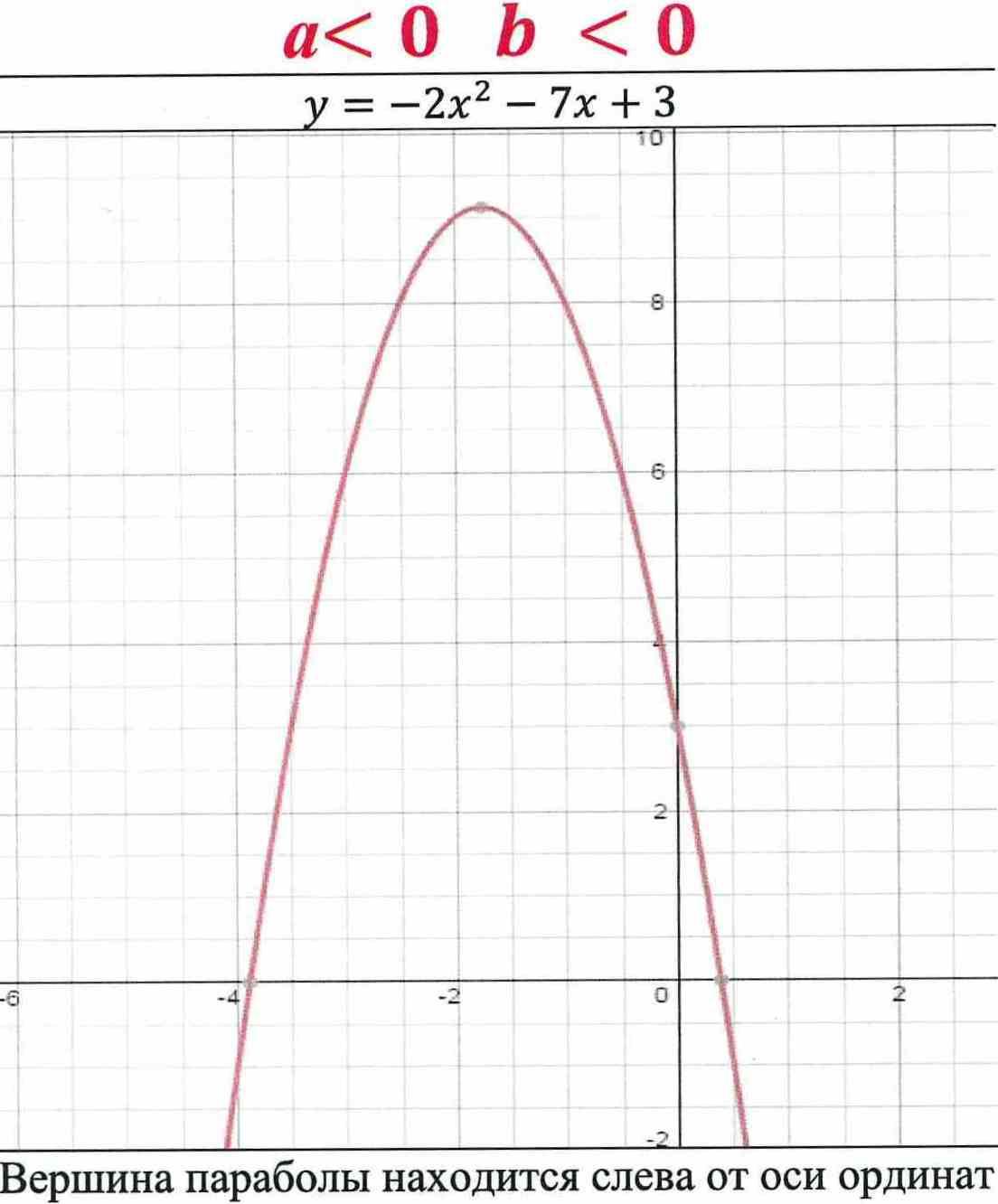
y = - 2x2 - 7х + 3
a b
Вершина параболы находится слева от оси ординат.
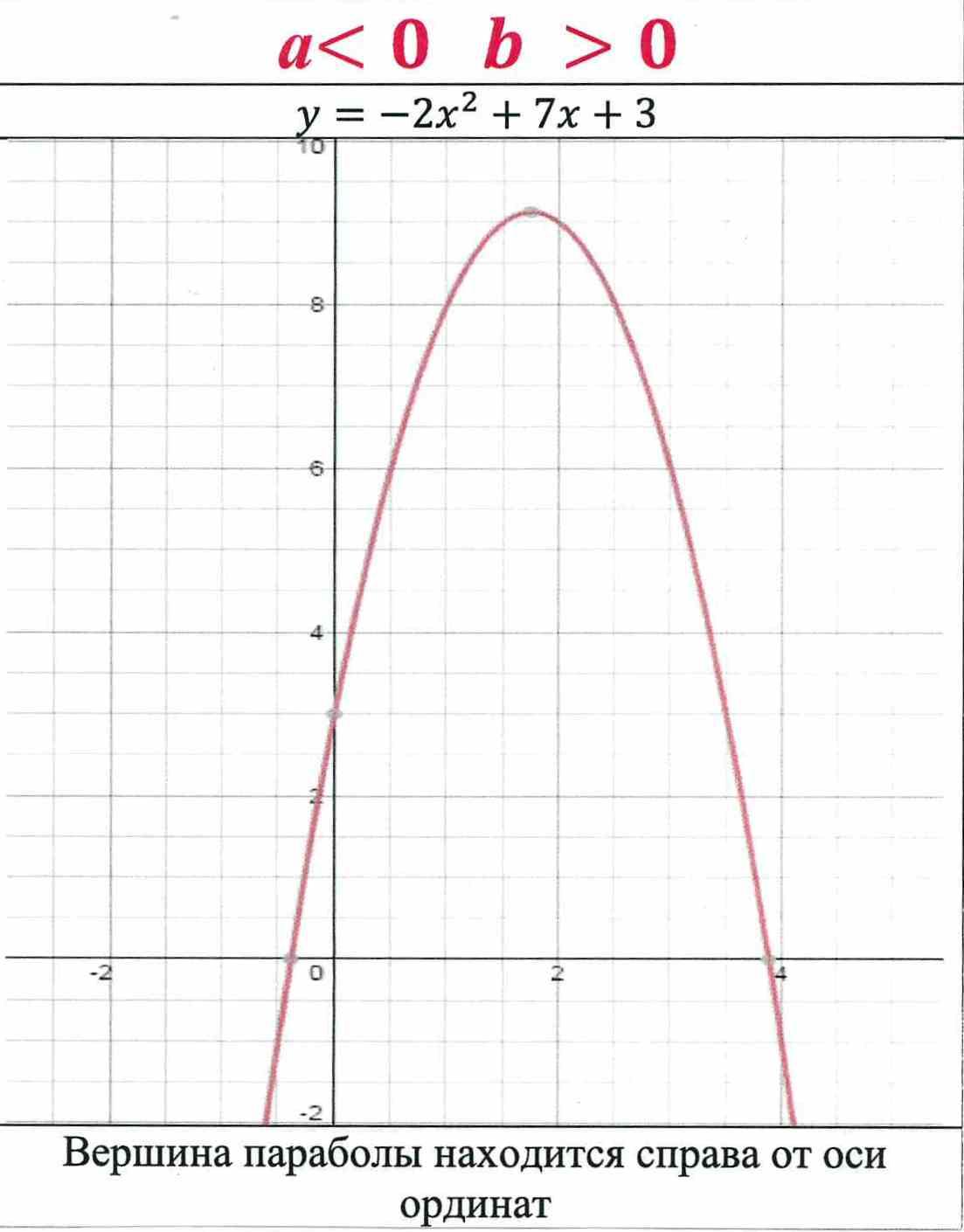
y = - 2x2 + 7х + 3
a b 0
Вершина параболы находится справа от оси ординат.
Примеры из заданий ОГЭ:
КОЭФФИЦИЕНТЫ
А) а 0, с
Б) a
В) а 0, с 0
ГРАФИКИ
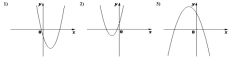
Установите соответствие между графиками и коэффициентами:
| А | Б | С |
|
|
|
|
2.
ГРАФИКИ
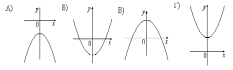
КОЭФФИЦИЕНТЫ
1) а 0, с
2) a 0
3) а 0, с 0
4) a
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В | Г |
|
|
|
|
|
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
