

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока


Проектирование обучающего курса «Теория вероятностей в ЕГЭ по математике»
Решение различных задач в школьном курсе математики занимают одно из важнейших мест. В том числе, важное значение отводится изучению задач, связанных с вычислением вероятности какого-либо события. Понимание основ теории вероятностей необходимо в самых разнообразных видах человеческой деятельности, как в прикладной, так и в повседневной, так как люди должны осознавать, что наш мир состоит из случайных событий, через которые пробиваются закономерности. Знакомство с теорией вероятностей происходит в школьном курсе математики.
Просмотр содержимого документа
«Проектирование обучающего курса «Теория вероятностей в ЕГЭ по математике»»
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Кузбасский гуманитарно-педагогический институт
федерального государственного бюджетного образовательного учреждения
высшего образования
«Кемеровский государственный университет»
Факультет информатики, математики и экономики
Кафедра математики, физики и математического моделирования
Воронцова Кристина Игоревна
гр. Ми-20-1
Проектирование обучающего курса «Теория вероятностей в ЕГЭ по математике»
Курсовая работа
по дисциплине «Методика обучения и воспитания по профилю «Математика»
по направлению подготовки 44.03.05 - Педагогическое образование
(с двумя профилями подготовки)
направленность (профиль) «Математика и Информатика»
Проверил:
Руководитель
канд. физ. - мат. наук,
доцент Фомина А.В.
Общий балл: _____________
Оценка: _________________
______________
подпись
«____» ___________ 2023 г.
Новокузнецк, 2023
ОГЛАВЛЕНИЕ
Введение 4
1. Теоретические основы обучения решению задач по теме «Теория вероятностей».........................................................................................................7
1.1. Основные правила и формулы комбинаторики...........................................7
1.2. Теоремы о вероятностях событий...............................................................12
1.3. Формулы для решения «сложных» задач теории вероятностей. 15
2. Проектирование обучающего курса по теории вероятностей для подготовки к ЕГЭ по математике 23
2.1. Программа обучающего курса "Теория вероятностей в ЕГЭ по математике"..........................................................................................................23
2.2. Дидактические материалы обучающего курса..........................................28
2.3. Применение интерактивных платформ и онлайн-сервисов при проведе-нии уроков в рамках обучающего курса............................................................51
Заключение 62
Список использованных источников 63
Приложение..........................................................................................................65
Решение различных задач в школьном курсе математики занимают одно из важнейших мест. В том числе, важное значение отводится изучению задач, связанных с вычислением вероятности какого-либо события. Понимание основ теории вероятностей необходимо в самых разнообразных видах человеческой деятельности, как в прикладной, так и в повседневной, так как люди должны осознавать, что наш мир состоит из случайных событий, через которые пробиваются закономерности. Знакомство с теорией вероятностей происходит в школьном курсе математики. Несмотря на то, что это направление является одним из важных разделов математики, доступной литературы по данному направлению недостаточно, это является неблагоприятным фактором на пути изучения теории вероятностей. Именно поэтому остро встает вопрос о включении методически грамотно выстроенного курса элементов теории вероятностей в школьный курс математики [4]. В большинстве УМК знакомство с теорией вероятностей начинается ещё в 5 классе. Более глубже изучать данную тему обучающиеся начинают уже в курсе алгебры за 8-9 классы. Задания же на проверку знаний по этой теме присутствуют не только в ОГЭ, но и в ЕГЭ по математике как базового, так и профильного уровня. Однако не все ученики справляются с этими заданиями. Простые задачи по теории вероятностей включены в ОГЭ, ученики привыкли и не боятся, как правило, этих задач. Однако, сложность задач, представленных в базе данных ЕГЭ растёт. Иногда встречаются задачи, вызывающие затруднение и у учителей. В тексте задачи встречаются лишние условия, которые запутывают ученика. Также могут встретиться завуалированные условия, увидеть которые учащиеся могут не сразу.
Так как в процессе обучения основного курса математики особо глубоко не затрагивается тема «Теория вероятностей», актуальность выбранной темы обуславливается возможностью расширить у учащихся базовых знаний, удовлетворить интерес в выбранном виде деятельности, подготовить к успешному решению задачи на вероятность при сдаче ЕГЭ.
Цель исследования: проектирование обучающего курса «Теория вероятностей в ЕГЭ по математике»
Объект исследования: задачи ЕГЭ по теме «Теория вероятностей»
Предмет исследования: процесс обучения решению задач ЕГЭ по теме «Теория вероятностей» в рамках обучающего курса.
В соответствии с целью, объектом и предметом курсовой работы поставлены следующие задачи исследования:
- Рассмотреть основные правила и формулы комбинаторики.
- Рассмотреть теоремы о вероятностях событий.
- Рассмотреть формулы для решения «сложных» задач по теории вероятностей.
- Спроектировать обучающий курс «Теория вероятностей в ЕГЭ по математике»;
- Разработать технологическую карту одного из уроков обучающего курса «Теория вероятностей в ЕГЭ по математике»;
- Рассмотреть интерактивные онлайн-сервисы и платформы, которые используются на уроках данного курса;
- Разработать интерактивный веб-квест по теории вероятностей для подготовки к ЕГЭ по математике.
Методы и инструменты исследования: поиск и изучение специальной, методической и справочной литературы; анализ и синтез полученной информации.
Теоретическая значимость: систематизация теоретического материала для проектирования обучающего курса ««Теория вероятностей в ЕГЭ по математике».
Практическая значимость: разработан обучающий курс по теме «Теория вероятностей» в ЕГЭ по математике.
Структура курсовой работы: работа состоит из введения, двух глав, заключения и списка литературы.
Первая глава содержит в себе теоретические сведения о теории вероятностей, которая включает в себя теоретическую информацию о различных типах задач по данной теме.
Во второй главе разработан обучающий курс на конкретную тему «Теория вероятностей в ЕГЭ по математике», который содержит пояснительную записку, учебно-тематический план, содержание изучаемого курса, методические рекомендации, технологическую карту одного из уроков изучаемого курса, а также список используемых при изучении курса интерактивных онлайн-сервисов, онлайн-платформ и список литературы.
1. Теоретические основы обучения решению задач из раздела «Теория вероятностей»
Основные правила и формулы комбинаторики
Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами [12].
Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин [16].
Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.
Теперь разберём основные правила и формулы комбинаторики, а также рассмотрим примеры решения задач по данным правилам.
Правило сложения (правило «или»)
Если два действия А и В не имеют общих элементов, причём действие А можно выполнить m способами, а В - n способами, то выполнить одно любое из этих действий (либо А, либо В) можно  способами [12].
способами [12].
Пример 1. На тарелке лежит 5 яблок и 7 слив. Сколькими способами можно взять фрукт с тарелки?
Решение: Сложим количество яблок и слив 5+7 = 12.
Ответ: 12 способов.
Если один из способов выбора действия А совпал с каким - либо способом выбора действия В, то правило сложения имеет вид:
 , где k - число совпадений.
, где k - число совпадений.
Пример 2. В группе 7 человек имеют «5» по математике, 9 человек - «5» по философии. В сессии 2 экзамена. Известно, что 4 человека сдали сессию отлично. Сколько человек имеет хотя бы одну пятёрку в сессии?
Решение: 7 + 9 - 4 = 12
Ответ:12 способов.
Правило умножения (правило «и»)
Если действие А можно выполнить m способами, а В - n способами, то упорядоченная пара (А и В) может быть составлена  способами[12].
способами[12].
Пример 3. В меню столовой указано 4 закусок, 7 первых блюда, 4 вторых и 5 десерта. Каким числом способов можно заказать обед из четырёх блюд?
Решение: Перемножим все имеющиеся числа 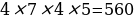
Ответ: 560 способов.
Пример 4. Марина купила 3-х кроликов: серого, белого и рябого. Сколько существует различных способов посадить этих кроликов в 3 клетки, если в одной клетке может находиться только 1 кролик?
Решение:
В первую клетку можно посадить одного из 3 кроликов - 3 возможности.
Во вторую клетку можно посадить одного из 2 оставшихся кроликов - 2 возможности.
В третьей клетке остаётся последний кролик - 1 возможность. Вместе 
Ответ: 6 способами.
Формулы комбинаторики
1. Сочетания без повторений .
Классической задачей комбинаторики является формула о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов [6]?

Пример 5. Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?
Решение: Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:
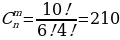
Ответ: 210 способами.
2. Сочетания с повторениями.
Данную формулу применяю при решении задач, в которых имеются по r одинаковых предметов каждого из n различных типов; сколькими способа-ми можно выбрать m (![]() ) из этих (
) из этих ( ) предметов?
) предметов?

Пример 6. В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
Решение: Так как среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.

Ответ: 120 способами.
3. Размещения без повторений.
Такая формула нужна при решении таких задач, условие которой можно выразить следующим вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов? Решается такая задача с помощью следующей формулы[6]:

Пример 7. В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?
Решение: В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:

Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.
Ответ: 11880.
4. Размещения с повторениями.
Формула, которая применяется при решении задач о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые? При решении задачи с повторениями используют следующую формулу [6]:
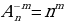
Пример 8. У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик?
Решение: Можно считать, что опыт состоит в 5-кратном выборе с возвращением одной из 3 цифр (1, 3, 7). Таким образом, число пятизначных номеров определяется числом размещений с повторениями из 3 элементов по 5:

Ответ: 243.
5. Перестановки без повторений.
Перестановкой из n называют комбинацию, имеющую n элементов, взятых из наперед заданных n элементов без повторений. Данная формула применяется при решении таких задач, содержание которых можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах [6]?
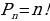
Пример 9. Сколькими различными способами можно составить список учеников из 5 человек?
Решение: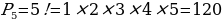
Ответ: 120 способов.
Пример 10. Сколько можно составить четырехбуквенных «слов» из букв слова «брак»?
Решение:
Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.
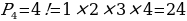
Ответ: 24 слова.
6. Перестановки с повторениями.
Для случая, когда среди выбираемых n элементов есть одинаковые (так называемая, выборка с возвращением), формулу применяемую при решении задач о числе перестановок с повторениями (такую задачу можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (kn), т.е. есть одинаковые предметы [6].
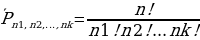
Пример 11. Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?
Решение: Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно

Ответ: 2520 буквосочетаний.
- Теоремы о вероятностях событий.
Теория вероятностей - это раздел математики, который изучает закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.
Вероятностью события A называется отношение числа m благоприятствующих этому событию исходов к общему числу n всех равновозможных несовместных элементарных исходов, образующих полную группу [12].
Вероятность события A обозначается p(A).
Определение, приведенное выше, является классическим определением вероятности, согласно которому
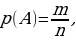
где m - количество благоприятных исходов,
n - количество всех исходов.
В теории вероятностей также имеются и другие формулы для решения различных типов задач по данной теме.
Перед тем, как рассмотреть эти формулы, выведем понятие о частоте случайного события, а также рассмотрим понятия независимых, совместных, несовместных и объединения событий.
Частота случайного события - это отношение числа испытаний, в которых появилось данное событие к общему числу испытаний.
Также здесь стоит отметить, про такие события, как совместные и несовместные.
Два события А и В называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию А, так и событию В.
События называются совместными, если наступление одного из них не исключает наступления других событий в одном и том же опыте.
Например, при бросании кубика события «выпало число 3» и «выпало чётное число» несовместны. При этом события «выпало число больше 3» и «выпало чётное число» совместны.
Два события А и В называют независимыми, если вероятность каждого из них не зависит от появления или не появления другого события. Например, выполним последовательно два подбрасывания монеты. Тогда события «при первом подбрасывании выпала решка» и при «втором подбрасывании выпал орёл» являются независимыми: вероятность каждого из них равна 0,5 независимо от того, что произошло при другом подбрасывании.
Пусть событие С означает, что произошло хотя бы одно из событий А и В. Тогда С называют объединением событий А и В, пишут С = 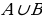 . Также объединение событий иногда называют суммой событий и обозначают
. Также объединение событий иногда называют суммой событий и обозначают  .
.
Пусть событие С означает , что произошло как событие А, так и В. Тогда С называют пересечением событий А и В, пишут 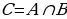 . Также пересечение событий иногда называют произведением событий и обозначают
. Также пересечение событий иногда называют произведением событий и обозначают  .
.
1. Теорема об объединении событий.
Если события А и В несовместны, то вероятность их объединения равна сумме вероятностей А и В: 
2. Теорема о пересечении событий.
Если события А и В независимы, то вероятность их пересечения равна произведению событий А и В: 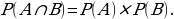
3. Теорема об объединении пересечений событий.
Если события А и В пересекаются, т.е. совместны, то вероятность их объединения можно найти по формуле: 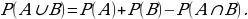
Подводя итоги данного параграфа, разберём примерные задачи по изученным событиям.
Задача о пересечении независимых событий. По отзывам покупателей Пётр Петрович оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,85. Вероятность того, что этот товар доставят из магазина Б, равна 0,96. Пётр Петрович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.
Решение. 1-й способ: Обозначим через А - событие «товар доставили из магазина А», через В - «товар доставили из магазина Б». Тогда  - искомая величина. По условию, Р(А)=0,85; Р(В)=0,96. Поэтому Р(
- искомая величина. По условию, Р(А)=0,85; Р(В)=0,96. Поэтому Р(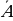 ) = 1-0,85=0,15; Р(
) = 1-0,85=0,15; Р( ) = 1-0,96=0,04. События А и В по условию независимы, поэтому события
) = 1-0,96=0,04. События А и В по условию независимы, поэтому события 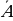 и
и  . По формуле вероятности пересечения независимых событий находим
. По формуле вероятности пересечения независимых событий находим 
2-й способ: Вероятность того, что из магазина А не доставят товар, равна 1-0,85=0,15. Вероятность того, что из магазина Б не доставят товар, равна 1-0,96=0,04. Так как магазины работают независимо, то вероятность отсутствия доставки из обоих магазинов сразу (то есть, пересечение вероятностей отсутствия доставки из каждого магазина) равна 0,15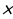 0,04=0,006.
0,04=0,006.
Ответ: 0,006.
Задача об объединении несовместных событий. На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Ромб», равна 0,1. Вероятность того, что это вопрос на тему «Описанная окружность», равна 0,15. Вопросов, относящихся одновременно к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение: Пусть событие А означает, что школьнику достался вопрос по теме «Ромб», событие В - вопрос по теме «Описанная окружность». По условию Р(А) = 0,1; Р(В) = 0,15. По условию события А и В несовместны. Искомая вероятность равна 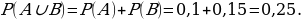
Ответ: 0,25.
Задача об объединении пересечений событий.
Бросают два кубика. С какой вероятностью будет выброшена хотя бы одна шестёрка?
Решение:
Событие А: шестёрка выпала на первом кубике.
Событие В: шестёрка выпала на втором кубике.
Событие 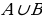 : шестёрка выпала хотя бы на одном кубике.
: шестёрка выпала хотя бы на одном кубике.
Событие А∩В: выпали две шестёрки.
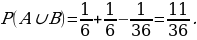
Ответ: 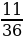 .
.
Задача о частоте. Вероятность того, что новый DVD-проигрыватель в течение года поступит в гарантийный ремонт, равна 0,05. В некотором городе из 2000 проданных DVD-проигрывателей в течение года в гарантийную мастерскую поступили 130 штук. Настолько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
Решение: Частота события «гарантийный ремонт» равна:
 От вероятности она отличается на 0,065 - 0,05 = 0,015.
От вероятности она отличается на 0,065 - 0,05 = 0,015.
Ответ: 0,015.
- Формулы для решения «сложных» задач теории вероятностей
1. Теорема сложения вероятностей двух совместных событий [15].
Вероятность суммы двух совместных событий равна сумме вероятностей этих событий минус вероятность их совместного появления:
p(A + B) = p(A)+ p(B)− p(A⋅ B).
Пример задачи ЕГЭ. В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен [13].
Решение:
Вероятность того, что исправен первый автомат (событие А) равна 0,95. Вероятность того, что исправен второй автомат (событие В) равна 0,95. Это совместные независимые события. Вероятность их произведения равна произведению вероятностей этих событий, а вероятность их суммы равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения.
Имеем: P(A + B) = P(A) + P(B) − P(A·B) = P(A) + P(B) − P(A)P(B) = 0,95 + 0,95 − 0,95·0,95 = 0,9975.
Ответ: 0,65.
2. Теорема сложения вероятностей несовместных событий [15].
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:
p(A + B) = p(A)+ p(B).
Вероятность появления хотя бы одного из нескольких попарно несовместных событий A1 , A2 , …, An равна сумме вероятностей этих событий:
p (A1 + A2 +…+ An) = p (A1) + p (A2) +…+ p (An).
Пример задачи ЕГЭ (два несовместных события). Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 18 пассажиров, равна 0,82. Вероятность того, что окажется меньше 10 пассажиров, равна 0,51. Найдите вероятность того, что число пассажиров будет от 10 до 17 [5].
Решение: Рассмотрим события A = «в автобусе меньше 10 пассажиров» и В = «в автобусе от 10 до 17 пассажиров». Их сумма — событие A + B = «в автобусе меньше 18 пассажиров». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий:
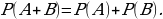
Тогда, используя данные задачи, получаем: 0,82 = 0,51 + P(В), откуда P(В) = 0,82 − 0,51 = 0,31.
Ответ: 0,31.
Пример задачи ЕГЭ (несколько несовместных событий). Вероятность того, что новый электрический чайник прослужит больше года, равна 0,93. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года [5].
Решение: Пусть A = «чайник прослужит больше года, но меньше двух лет», В = «чайник прослужит больше двух лет», С = «чайник прослужит ровно два года», тогда A + B + С = «чайник прослужит больше года».
События A, В и С несовместные, вероятность их суммы равна сумме вероятностей этих событий. Вероятность события С, состоящего в том, что чайник выйдет из строя ровно через два года — строго в тот же день, час и секунду - равна нулю. Тогда: P(A + B+ С) = P(A) + P(B)+ P(С)= P(A) + P(B), откуда, используя данные из условия, получаем 0,93 = P(A) + 0,87.
Тем самым, для искомой вероятности имеем: P(A) = 0,93 − 0,87 = 0,06.
Ответ: 0,06.
Сумма вероятностей попарно несовместных событий A1, A2,…, An, образующих полную группу, равна единице: p(A1)+ p(A2)+…+ p(An)=1.
Для более полного понимания формулы рассмотрим ещё одно понятие – полная группа. Полная группа событий – это совокупность единственно возможных событий при данном испытании [3].
Пример. Студент может сдать экзамен на любую оценку. В данном случае возможны следующие события: студент может сдать экзамен на 5, студент может сдать экзамен на 4, студент может сдать экзамен на 3. Эти события образуют полную группу.
Противоположные события. Два случайные события А и В называются противоположными, если они несовместны и образуют полную группу событий. Примеры: студент может сдать или не сдать экзамен, день и ночь.
Конкретный результат испытания называется элементарным событием. Совокупность всех возможных, различных, конкретных исходов испытаний называется множеством элементарных событий [3].
3. Теорема о сумме вероятностей противоположных событий [5].
Сумма вероятностей противоположных событий равна единице: p(A)+ p(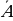 ) =1.
) =1.
Пример задачи ЕГЭ. Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36,8 °С, равна 0,81. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8 °С или выше [5].
Решение: Указанные события противоположны, поэтому искомая вероятность равна 1 − 0,81 = 0,19.
Ответ: 0,19.
4. Теорема умножения двух зависимых событий [15].
Вероятность произведения двух зависимых событий равна произведению вероятности одного из этих событий на условную вероятность другого при условии, что первое событие произошло:
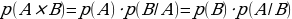
5. Теорема умножения нескольких зависимых случайных событий [15].
Вероятность произведения зависимых случайных событий A1, A2,…,An равна произведению одного из них на условные вероятности всех остальных, вычисленные в предположении, что все предыдущие события наступили. 
Далее приведем пример, в котором применяется теорема умножения и теорема сложения вероятностей одновременно.
Пример задачи ЕГЭ. Студент выучил 8 вопросов из 10. Найти вероятность того, что он ответит только на один вопрос из двух ему заданных [16].
Решение: Опыт – ответ на вопросы.
Введем события:
Ai – «студент ответит на i – ый вопрос», i = 1, 2 ;
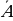 i – «студент не ответит на i – ый вопрос», i = 1, 2 ;
i – «студент не ответит на i – ый вопрос», i = 1, 2 ;
A –«студент ответит только на один вопрос из двух ему заданных». Тогда событие A произойдет когда, произойдет событие: 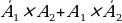 , то есть
, то есть 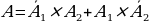 .
.
Так как, событие  и
и 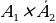 несовместны, то по теореме сложения для несовместных событий имеем:
несовместны, то по теореме сложения для несовместных событий имеем:
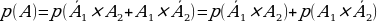
Так как события 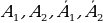 попарно зависимые, то по теореме умножения для зависимых событий имеем:
попарно зависимые, то по теореме умножения для зависимых событий имеем:
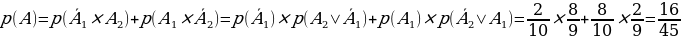 .
.
Ответ: 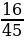
6. Теорема умножения двух независимых случайных событий [15].
Вероятность произведения двух независимых событий равна произведению вероятностей этих событий: 
Пример задачи ЕГЭ. Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза [5].
Решение: Возможность выиграть первую и вторую партию не зависят друг от друга. Вероятность произведения независимых событий равна произведению их вероятностей: 0,52 · 0,3 = 0,156.
Ответ: 0,156.
7. Теорема умножения нескольких независимых случайных событий [15].
Чтобы получить формулу для произведения событий больше двух, придется ввести понятие событий независимых в совокупности. Это более сильное требование, предъявляемое к событиям, чем попарная независимость.
События называются независимыми в совокупности, если они попарно независимы и независимы любые комбинации этих событий относительно умножения.
Вероятность произведения независимых случайных событий A1, A2,…, An равна произведению вероятностей этих событий, то есть

Пример задачи ЕГЭ.
Три стрелка стреляют по цели. Вероятность попадания в цель первым стрелком равна 0,3, вторым – 0,4, третьим – 0,5. Определить вероятность того, что все три стрелка одновременно попадут в цель при одном выстреле [15].
Решение: Опыт – выстрел по цели тремя стрелками. Введем обозначение событий:
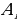 - «i – ый стрелок попадет в цель», i =1, 2,3;
- «i – ый стрелок попадет в цель», i =1, 2,3;
A - «три стрелка одновременно попадут в цель при одном выстреле». Событие A произойдет, если произойдет событие  . По условию задачи p(A1 ) = 3,0; p(A2 ) = 4,0; p(A3 ) = 5,0. Так как события A1 , A2 , A3 независимые, то искомая вероятность будет равна
. По условию задачи p(A1 ) = 3,0; p(A2 ) = 4,0; p(A3 ) = 5,0. Так как события A1 , A2 , A3 независимые, то искомая вероятность будет равна
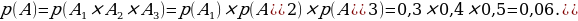
Ответ: 0,06.
8. Формула условной вероятности [16].
Вероятность того, что произошло событие A при условии, что произошло событие B, называют условной вероятностью события A при условии B и обозначают  .
.
Пример задачи ЕГЭ. В плейлисте Савелия 50 песен: 18 в стиле хардбоп, 25 - в стиле джаз-рок и 7 - в стиле фри-джаз. Песни воспроизводятся в случайном порядке, не повторяясь. Какова вероятность того, что в первый раз песня в стиле фри-джаз прозвучит третьей по счёту [13]?
Решение: Вероятность того, что первой прозвучит песня, не относящаяся к фри-джазу, равна 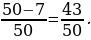 Если это событие наступит, то вероятность прозвучать снова песне не в стиле фри-джаз станет равна
Если это событие наступит, то вероятность прозвучать снова песне не в стиле фри-джаз станет равна 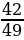 (так как останется 42 песни не в стиле фри-джаз из 49). Таким образом, вероятность того, что первые две песни не относятся к фри-джазу, равна
(так как останется 42 песни не в стиле фри-джаз из 49). Таким образом, вероятность того, что первые две песни не относятся к фри-джазу, равна  Вероятность того, что следующая после них песня окажется в стиле фри-джаз, равна
Вероятность того, что следующая после них песня окажется в стиле фри-джаз, равна  Тогда искомая вероятность равна
Тогда искомая вероятность равна 
Ответ: 0,1075.
9. Формула полной вероятности [16].
Пусть требуется найти вероятность события A, которое происходит вместе с одним из несовместных событий H1, H2,..., Hn, образующих полную группу попарно - несовместных событий, называемых гипотезами.
Тогда вероятность события A вычисляется по формуле, которая называется формулой полной вероятности:
Р(А)=Р(А/Н1)Р(Н1)+Р(А/Н2)Р(Н2)+...+ Р(А/Нm)Р(Нm).
Пример задачи ЕГЭ. Телефон передаёт SMS-сообщение. В случае неудачи он делает следующую попытку. Вероятность того, что SMS-сообщение удастся передать без ошибок, в каждой отдельной попытке равна 0,95. Найдите вероятность того, что для передачи сообщения потребуется не больше двух попыток [13].
Решение: Вероятность неудачи в случае каждой отдельно взятой попытки равна 1-0,95=0,05. По условию должна потребоваться одна или две попытки. Пусть событие А1 - «потребовалась ровно одна попытка». По условию Р(А1) = 0,95.
Пусть событие А2 - «потребовалось ровно две попытки». Это означает, что первая попытка должна была быть неудачной, а вторая - удачной. Тогда Р(А2) = 0,05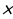 0,95 = 0,0475.
0,95 = 0,0475.
Так как события А1 и А2 несовместны, то искомая вероятность Р(А1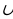 А2) = Р(А1) + Р(А2) = 0,9975.
А2) = Р(А1) + Р(А2) = 0,9975.
Ответ: 0,9975.
10. Формула Байеса [3].
Пусть событие A происходит вместе с одним из несовместных событий H1, H2,..., Hk, образующих полную группу попарно - несовместных событий (гипотез). Произведен опыт, в результате которого появилось событие A. Условные вероятности гипотез H1, H2,..., Hk относительно события A определяется формулой, которая называется формулой Байеса:
 , где Р(А) ≠ 0.
, где Р(А) ≠ 0.
Пример задачи ЕГЭ. При подозрении на наличие некоторого заболевания пациента отправляют на ПЦР-тест. Если заболевание действительно есть, то тест подтверждает его в 88% случаев. Если заболевания нет, то тест выявляет отсутствие заболевания в среднем в 92% случаев. Известно, что в среднем тест оказывается положительным у 11% пациентов некоторой поликлиники, направленных на тестирование. При обследовании пациента А. врач направил его на ПЦР-тест, который оказался положительным. Какова вероятность того, что пациент А. действительно имеет это заболевание [13]?
Решение: Пусть эксперимент заключается в выборе одного случайного пациента, направленного на анализ. Рассмотрим две гипотезы, являющиеся противоположными событиями: Н1 - «этот пациент болен», Н2 - «этот пациент не болен». Событие А - «у наудачу взятого пациента тест дал положительный результат». По условию Р(А) = 0,11. Вероятность положительного теста у больного пациента равна Р(А/H1) = 0,88, а у здорового - P(A/H2) = 1-0,92 = 0,08.
Пусть х - это Р(Н1), то есть х - это вероятность того, что наудачу взятый пациент болен (тогда Р(Н2) =1-х - это вероятность того, что наудачу взятый пациент здоров).
По формуле полной вероятности получим, что
Р(А) = Р(А/Н1)Р(Н1) + Р(А/Н2)Р(Н2) = 0,88х + 0,08(1-х).
Получим уравнение: 0,88х + 0,08(1-х) = 0,11.
0,8х = 0,03, х = 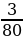 .
.
Искомая вероятность  = 0,3.
= 0,3.
Ответ: 0,3.
- Проектирование обучающего курса «Теория вероятнос-тей в ЕГЭ по математике»
- Программа обучающего курса "Теория вероятностей в ЕГЭ по математике"
Обучающий курс "Теория вероятностей в ЕГЭ по математике" предназначен для подготовки учащихся к единому государственному экзамену в 10-11 классах, а также может быть использован для предпрофильной подготовки в 9 классе.
Актуальность этого курса состоит в том, что он является средством для выполнения одной из главных функций современного образования: показывает связь теоретической математики с жизнью. Учащиеся узнают об универсальности вероятностных законов, которые широко применяются в современной химии, физике, биологии, социально-экономических науках, военном деле и т.д.
Курс ориентирован на развитие у школьника умений решать жизненные задачи: выбор наилучшего из возможных вариантов, оценка степени риска, шансов на успех и другое.
Данный обучающий курс предназначен для широкого круга учащихся вне зависимости от выбранного профиля обучения, так как в процессе его изучения появляется возможность формирования навыков соотнесения вероятного и достоверного, справедливости и несправедливости в играх и других реальных жизненных ситуациях.
В школьном курсе математики разделы теории вероятности и статистики являются новыми, поэтому разработка данного обучающего курса очень актуальна. Интеграция этого курса с другими предметами на этапе выполнения завершающего проекта по теме позволит учащимся определить ту область, которая их интересует и даст возможность продолжать исследования в данной области. Применение компьютерных технологий в процессе изучения курса поможет определиться с выбором профессии в этом направлении.
Цели обучающего курса: овладение языком теории, знаниями и умениями, необходимыми для решения вероятностных задач; а также способствовать развитию у учащихся первоначальных навыков решения задач, связанных, в том числе, с жизненными ситуациями.
Задачи:
· расширить кругозор учащихся;
· расширить знания о комбинаторике;
·сформировать у учащихся представления о комбинаторике и основных элементах теории вероятностей;
·сформировать первоначальный навык решения задач, связанных, в том числе, с конкретными жизненными ситуациями;
·способствовать формированию у школьников интереса к изучению математики.
Ожидаемые результаты:
В результате изучения основ теории вероятности ученик должен:
знать/понимать
· значение основ теории для решения задач, возникающих в теории и практике;
· основные понятия стохастики: понятие вероятности случайного события, теорем сложения и умножения вероятности, формулы полной вероятности, понятия независимости событий;
· обладать знаниями, необходимыми для применения перечисленных ниже умений;
Уметь
· группировать данные по определенному признаку;
· осуществлять целенаправленный и организованный перебор вариантов;
· ощущать степень случайности в явлениях окружающей действительности и использование для ее оценки адекватных вероятностных терминов («достоверно», «маловероятно» и т.д.);
·узнавать равновозможные исходы испытания, основываясь на «соображениях симметрии»;
·оценивать и сравнивать шансы (вероятности) событий в испытаниях с очевидным числом равновозможных исходов;
Основные методические особенности курса:
1. Подготовка по тематическому принципу, соблюдая «правила спирали» от простых типов заданий к более сложным;
2. Работа с тематическими тестами, выстроенными в виде совокупности заданий;
4. Работа с тренировочными тестами в режиме максимальной нагрузки, как по содержанию, так и по времени для всех школьников в равной мере.
Структура курса
Программа включает следующие разделы: пояснительную записку, учебно-тематическое планирование с указанием минимального числа проведенных часов, которые отводятся на изучение каждой темы, а также дидактический материал курса, который включает в себя содержание курса, методические рекомендации и литературу.
Методы преподавания.
Основные методы преподавания – это использование метода проектов, технологии проблемного обучения, информационных технологий, технологии развития логического мышления.
Формы организации учебных занятий
Формы проведения занятий включают в себя лекции, практические работы, тренинги по использованию методов поиска решений.
Основной тип занятий комбинированный урок. Каждая тема курса начинается с постановки задачи. Теоретический материал излагается в форме мини-лекции, сопровождающиеся презентацией, опрос, также при объяснении некоторых тем, а также при их закреплении предполагается использовать различные онлайн-сервисы. После изучения теоретического материала выполняются практические задания для его закрепления. Занятия строятся с учётом индивидуальных особенностей обучающихся, их темпа восприятия и уровня усвоения материала. В ходе обучения периодически проводятся непродолжительные, рассчитанные на 5-10 минут, контрольные работы и тестовые испытания для определения глубины знаний и скорости выполнения заданий. Контрольные замеры обеспечивают эффективную обратную связь, позволяющую учащимся корректировать свою деятельность. Систематическое повторение способствует более целостному осмыслению изученного материала, поскольку целенаправленное обращение к изученным ранее темам позволяет учащимся встраивать новые понятия в систему уже освоенных знаний.
Контроль и система оценивания
Предполагается использование текущего, тематического и итогового контроля.
Текущий контроль проводится в форме собеседования с учащимися по решению практических задач.
Тематический контроль предполагает проверку выполнения тестовых заданий.
Итоговый контроль происходит в форме контрольной работы по всему пройденному материалу.
Учебно-тематический планОбучающий курс «Теория вероятностей в ЕГЭ по математике» предназначенный для подготовки учащихся к единому государственному экзамену проводится в рамках факультативных занятий в течение трёх-четырёх недель и рассчитан на 18 учебных часов из расчёта 4-5 часов в неделю.
| Тема | Количество часов | Тип занятия | ||
| Всего, ч. | Количество часов на усвоение материала, ч.
| Количество часов для самостоятельных работ, ч. | ||
| Понятие теории вероятностей. Формула классической вероятности. | 1 | 1 | - | Комбинированный |
| Случайные опыты и события. Элементарные события. | 2 | 1 | 1 | Комбинированный Тест |
| Правило умножения и сложения. | 1 | 1 | - | Комбинированный |
| Перестановки. Размещения. Сочетания. | 3 | 2 | 1 | Комбинированный Тест |
| Несовместные события. Теорема сложения. | 1 | 1 | - | Комбинированный |
| Совместные события. Теорема сложения. Теорема умножения. Полная вероятность. | 3 | 2 | 1 | Комбинированный Самостоятельная работа. |
| Условная вероятность. Независимые события. Теорема умножения. | 3 | 2 | 1 | Комбинированный Самостоятельная работа |
| Зависимые события. | 1 | 1 | - | Комбинированный |
| Задачи на применение теорем сложения и умножения вероятностей. | 1 | 1 | - | Комбинированный |
| Формула Байеса. | 1 | 1 | - | Комбинированный |
| Контрольная работа по пройденному материалу. | 1 | 1 |
| Контрольная работа |
| Итого: | 18 | 14 | 4 |
|
Дидактические материалы обучающего курса
Содержание программы
Тема 1. Понятие теории вероятностей. Формула классической вероятности. (1 час)
Тема 2. Случайные опыты и события. Элементарные события. Тест. (2 часа)
Тема 3. Правило умножения и сложения. (1 час)
Тема 4. Перестановки. Размещения. Сочетания. Тест. (3 часа)
Тема 5. Несовместные события. Теорема сложения. (1 час)
Тема 6. Совместные события. Теорема сложения. Теорема умножения. Полная вероятность. Самостоятельная работа. (3 часа)
Тема 7. Условная вероятность. Независимые события. Теорема умножения. Самостоятельная работа. (3 часа)
Тема 8. Зависимые события. (1 час)
Тема 9. Задачи на применение теорем сложения и умножения вероятностей. (1 час)
Тема 10. Формула Байеса. (1 час)
Тема 11. Контрольная работа по пройденному материалу. (1 час)
Методические рекомендации
Данный обучающий курс необходимо базировать на новом для учащихся теоретическом материале по математике и формировать межпредметные связи с профильными дисциплинами данного класса. Кроме того, нужно использовать взаимопроверку, взаимообучение, взаимоконтроль, уроки - консультации, проблемное обучение, исследовательскую или проектную деятельность. Так как на занятиях чаще всего будет даваться теоретический и практический материал, то самостоятельная деятельность обучающихся должна быть в равной степени с деятельностью учителя. Для объяснения теоретического материала лучше всего использовать приёмы деятельностного или проблемного метода, а для отработки практической части можно использовать групповые и парные работы. Каждое занятие сопровождается не только объяснением теоретического материала, но и самостоятельным решением заданий, получением домашней работы. После изучения каждой темы проводится небольшая контрольная работа, с помощью которой выявляются:
· знания обучающихся определений и формул;
· умения делать выводы, находить нужное решение;
· умения работать со справочной литературой;
· умения решать нестандартные задачи.
Система задач по темам, входящим в учебно-тематический план обучающего курса.
Тема 1. Понятие теории вероятностей. Формула классической вероятности. (1 час)
Задача 1. Абонент забыл последние 2 цифры телефонного номера, но помнит, что они различны и образуют двузначное число, меньшее 30. С учетом этого он набирает наугад 2 цифры. Найти вероятность того, что это будут нужные цифры[13].
Ответ: 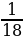
Задача 2. В лотерее разыгрывается 3 книги. Всего в урне 50 билетов. Первый подошедший к урне вынимает билет. Найти вероятность того, что билет окажется выигрышным[13].
Ответ: 0,06
Задача 3. Абонент забыл последнюю цифру номера телефона и поэтому набирает её наугад. Определить вероятность того, что ему придётся звонить не более чем в 3 места[13].
Ответ: 0,3
Задача 4. На экзамен вынесено 60 вопросов, Андрей не выучил 3 из них. Найдите вероятность того, что ему попадется выученный вопрос[13].
Ответ: 0,95
Задача 5. Родительский комитет закупил 30 пазлов для подарков детям на окончание учебного года, из них 12 с картинками известных художников и 18 с изображениями животных. Подарки распределяются случайным образом. Найдите вероятность того, что Вове достанется пазл с животным[13].
Ответ: 0,6
Тема 2. Случайные опыты и события. Элементарные события. Тест. (2 часа)
Задача 1. Являются ли случайными следующие события?
Ученицу школы бельчонка Беллу завтра спросят на уроке.
Летом у школьников будут каникулы.
Мистеру Фоксу сегодня дорогу перейдёт чёрная кошка.
Ответ: 1) да; 2) нет; 3) да.
Задача 2. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых[1].
Ответ: 0,14
Задача 3. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз[1].
Ответ: 0,5
Задача 4. В сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос по ботанике. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике[13].
Ответ: 0,2
Задача 5. В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по неравенствам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам[13].
Ответ: 0,6
Задача 6. На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной[1]?
Ответ: 0,5
Задача 7. Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на три[1]?
Ответ: 0,3
Тема 3. Правило умножения и сложения. (1 час)
Задача 1. В первом ящике 2 белых и 10 черных шаров. Во втором ящике 8 белых и 4 черных шаров. Из каждого ящика вынули по шару. Определить вероятность того, что один из вынутых шаров белый, а другой — черный[13].
Ответ: 
Задача 2. Опыт состоит в случайном извлечении карты из колоды в 36 листов. Чему равна вероятность того, что извлеченная карта – туз или имеет бубновую масть[13]?
Ответ: 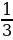
Задача 3. Компания, занимающаяся разработкой программного обеспечения, претендует на получение заказов от двух фирм «Аврора» и «Bенера».. Эксперты компании считают, что вероятность получения заказа от «Авроры» равна 0.45. Эксперты также полагают, что если компания получит заказ от фирмы «Аврора», то вероятность того, что и фирма «Bенера» обратится к ним, равна 0.9. Какова вероятность того, что компания получит оба заказа[2]?
Ответ: 0,405
Задача 4. Студент пришел на экзамен, изучив только 20 вопросов из 25 предложенных. Экзаменатор задает студенту поочередно три вопроса. Найти вероятность того, что студент ответит а) на все три вопроса, б) хотя бы на один вопрос[1].
Ответ: а) 0,496; б) 0,996
Задача 5. Вероятность того, что потребитель увидит рекламу дезодоранта «Скунс» по телевидению, равна 0.06. Вероятность того, что потребитель увидит рекламу этого дезодоранта на рекламном стенде, равна 0.04. Предполагается, что оба события – независимы. Чему равна вероятность того, что покупатель увидит а) обе рекламы; б) хотя бы одну рекламу[1]?
Ответ: а) 0,0024; б) 0,0976
Тема 4. Перестановки. Размещения. Сочетания. Тест. (3 часа)
Задача 1. При окончании деловой встречи специалисты обменялись визитными карточками. Сколько всего визитных карточек перешло из рук в руки, если во встрече участвовали 6 специалистов[13]?
Ответ: 30
Задача 2. При встрече каждый из друзей пожал другому руку. Сколько всего было рукопожатий, если встретились 6 друзей[13]?
Ответ: 15
Задача 3. В хоровом кружке занимаются 9 человек. Необходимо выбрать двух солистов. Сколькими способами это можно сделать[13]?
Ответ: 36
Задача 4. В спортивной команде 9 человек. Необходимо выбрать капитана и его заместителя. Сколькими способами это можно сделать[13]?
Ответ: 72
Задача 5. В понедельник в пятом классе 5 уроков: музыка, математика, русский язык, литература и история. Сколько различных способов составления расписания на понедельник существует[13]?
Ответ: 120
Задача 6. Сколько существует вариантов рассаживания вокруг стола 6 гостей на 6 стульях[13]?
Ответ: 720
Задача 7. Сколькими способами 10 футбольных команд могут разыграть между собой золотые, бронзовые и серебряные медали[13]?
Ответ: 720
Задача 8. Пятеро друзей сыграли между собой по одной партии в шахматы. Сколько всего партий было сыграно[13]?
Ответ: 10
Задача 9. Имеется 6 видов овощей. Решено готовить салаты из трёх видов овощей. Сколько различных вариантов салатов можно приготовить[1]?
Ответ: 20
Задача 10. В меню столовой предложено на выбор 2 первых блюда, 6 вторых и 4 третьих блюда. Сколько различных вариантов обеда, состоящего из первого, второго и третьего блюда, можно составить[1]?
Ответ: 48
Задача 11. В магазине продаются блокноты 7 разных видов и ручки 4 разных видов. Сколькими разными способами можно выбрать покупку из одного блокнота и одной ручки[13]?
Ответ: 28
Задача 12. В магазине продаются блокноты 7 разных видов и ручки 4 разных видов. Сколькими способами можно выбрать покупку из двух разных блокнотов и одной ручки[13]?
Ответ: 84
Задача 13. На прививку в медпункт отправились 7 друзей. Сколькими разными способами они могут встать в очередь у медицинского кабинета[1]?
Ответ: 5040
Задача 14. Секретный замок состоит из 4 барабанов, на каждом из которых можно выбрать цифры от 0 до 9. Сколько различных вариантов выбора шифра существует[1]?
Ответ: 10000
Задача 15. Сколько различных трёхзначных чисел можно составить при помощи цифр 4, 7, 9 [1]? (Цифры в записи числа не повторяются).
Ответ: 6
Задача 16. Сколько различных трёхзначных чисел можно составить с помощью цифр 1, 3, 7[1]? (Цифры могут повторяться).
Ответ: 27
Задача 17. Сколько различных трёхзначных чисел можно составить с помощью цифр 7 и 3[1]?
Ответ: 8
Задача 18. Сколько различных трёхзначных чисел можно составить из цифр 7, 6, 5, 0, если цифры в записи числа не могут повторяться[1]?
Ответ: 18
Задача 19. Сколько различных дробей можно составить с использованием цифр 2, 3, 4[2]? (В числителе и знаменателе не может быть одна и та же цифра.)
Ответ: 18
Задача 20. Сколько различных двузначных чисел можно составить при помощи цифр 4, 7, 9[2]? (Цифры в записи числа не повторяются).
Ответ: 6
Задача 21. Сколько четных трёхзначных чисел можно составить из цифр 3, 4, 5, 6[2]? (Цифры в записи числа могут повторяться).
Ответ: 12
Тема 5. Несовместные события. Теорема сложения. (1 час)
Задача 1. Игральную кость (кубик) бросили один раз. Какова вероятность того, что выпало очков, не меньшее, чем 3[13]?
Ответ:
Задача 2. В соревнованиях по плаванию участвуют 4 спортсмена из Германии, 6 спортсменов из Италии, 7 спортсменов из России и 5 из Китая. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что спортсмен из Италии Джованни Лучио будет выступать первым, вторым или третьим[13].
Ответ:
Задача 3. Вероятность того, что новый сканер прослужит больше года, равна 0,96. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года[5].
Ответ: 0,09
Задача 4. На экзамене по геометрии школьнику достается один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Внешние углы», равна 0,1. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,35. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем[13].
Ответ: 0,45
Задача 5. В магазине канцтоваров продается 120 ручек, из них 15 – красных, 22 – зеленых, 27 – фиолетовых, еще есть синие и черные, их поровну. Найдите вероятность того, что Алиса наугад вытащит синюю или зеленую ручку[13].
Ответ: 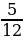
Задача 6. Стрелок стреляет по мишени, разделенной на 4 концентрические зоны. Вероятности попадания в эти зоны соответственно равны 0,4; 0,3; 0,2 и 0,1. Найти вероятность попадания либо в первую, либо во вторую зону[13].
Ответ: 0,7
Задача 7. На складе готовой продукции находятся изделия, среди которых 5% нестандартных. Найти вероятность того, что при выдаче изделия со склада оно будет стандартным[5].
Ответ: 0,95
Задача 8. В магазине имеется 10 телевизоров, из которых 2 неисправных. Найти вероятность того, что среди наугад взятых трех телевизоров будет хотя бы один неисправный[1].
Ответ: 0,53
Тема 6. Совместные события. Теорема сложения. Полная вероятность. Самостоятельная работа. (3 часа)
Задача 1. Какова вероятность того, что число, выбранное наугад из всех двузначных чисел, делится хотя бы на одно из чисел 3 и 5[5]?
Ответ: 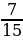
Задача 2. Ведется стрельба по мишени двумя стрелками. Вероятность поражения мишени первым стрелком равна 0,8, а вероятность поражения мишени вторым – 0,7. Какова вероятность поражения мишени[13]?
Ответ: 0,94
Задача 3. В соревнованиях по плаванию участвуют 4 спортсмена из Германии, 6 спортсменов из Италии, 7 спортсменов из России и 5 из Китая. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что хотя бы один из спортсменов из Италии будет выступать первым, вторым или третьим[13].
Ответ: 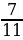
Задача 4. Помещение освещается фонарем с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,2. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит[13].
Ответ: 0,96
Задача 5. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах[13].
Ответ: 0,52
Задача 6. В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен[13].
Ответ: 0,9975
Задача 7. Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание. Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5. Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей[2].
Ответ: 0,408
Задача 8. У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероятность того, что первый из взятых валиков — конусный, а второй — эллиптический[2].
Ответ: 0,21
Задача 9. В урне 5 белых, 4 черных и 3 синих шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его обратно. Найти вероятность того, что при первом испытании появится белый шар (событие А), при втором — черный (событие В) и при третьем—синий (событие С)[1].
Ответ: 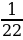
Задача 10. В эксперименте используются карточки белого и зеленого цветов, на которых изображены геометрические фигуры: квадрат или треугольник. Вероятность того, что на зеленой карточке изображен треугольник, равна 0,85. Для белой карточки эта вероятность равна 0,9. Найдите вероятность того, что наудачу взятая карточка будет содержать треугольник, если в эксперименте используется одинаковое количество карточек зеленого и белого цветов[2].
Ответ: 0,875
Задача 11. Прибор, установленный на борту самолета, может работать в двух режимах: в условиях нормального крейсеровского полѐта и в условиях перегрузки при взлете и посадке. Крейсерский режим полета составляет 80% всего времени полѐта, условия перегрузки – 20%. Вероятность выхода прибора из строя за время полета в нормальном режиме равна 0,1, в условиях перегрузки – 0,4. Найти вероятность того, что прибор не откажет в течение всего полѐта[2].
Ответ: 0,84
Задача 12. Имеются три урны с шарами. В первой урне 4 белых и 5 черных, во второй – 5 белых и 4 черных, в третьей – 6 белых шаров. Некто выбирает наугад одну из урн и вынимает из нее шар. Найти вероятность того, что, этот шар окажется белым[1].
Ответ:
Задача 13. На двух станках обрабатываются однотипные детали. Вероятность брака для станка № 1 составляет 0,03, для станка № 2 – 0,02. Обработанные детали складываются в одном месте, причем деталей, обработанных на станке № 1, вдвое больше, чем деталей, обработанных на станке № 2. Найти вероятность того, что, взятая наугад деталь будет стандартной[1].
Ответ: 
Задача 14. В пирамиде стоят 19 винтовок, из них 3 с оптическим прицелом. Стрелок, стреляя из винтовки с оптическим прицелом, может поразить мишень с вероятностью 0,81, а стреляя из винтовки без оптического прицела, - с вероятностью 0,46. Найдите вероятность того, что стрелок поразит мишень, стреляя из случайно взятой винтовки[2].
Ответ: 0,515
Задача 15. Из урны, содержащей 2 белых и 3 черных шара, наудачу извлекаются два шара и добавляется в урну 1 белый шар. Найдите вероятность того, что наудачу взятый шар окажется белым [2].
Ответ: 0,55
Тема 7. Условная вероятность. Независимые события. Теорема умножения. Самостоятельная работа. (3 часа)
Задача 1. Производится два выстрела по цели. Вероятность попадания при первом выстреле 0,2, при втором — 0,6. Вероятность разрушения цели при одном попадании 0,3, при двух — 0,9. Найдите вероятность того, что цель будет разрушена[1].
Ответ: 0,276
Задача 2. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероятность появления белого шара при втором испытании (событие В), если при первом испытании был извлечен черный шар (событие А)[1].
Ответ: 0,6
Задача 3. В трамвайном парке имеются 15 трамваев маршрута №1 и 10 трамваев маршрута №2. Какова вероятность того, что вторым по счету на линию выйдет трамвай маршрута №1[1]?
Ответ: 0,6
Задача 4. В урне находятся 3 белых шара и 2 черных. Из урны вынимается один шар, а затем второй. Событие В – появление белого шара при первом вынимании. Событие А – появление белого шара при втором вынимании[1].
Ответ: 0,75
Задача 5. Какова вероятность того, что 2 карты, вынутые из колоды в 36 карт, окажутся одной масти[2]?
Ответ: 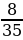
Задача 6. Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза[2].
Ответ: 0,15
Задача 7. Вероятность того, что батарейка бракованная, равна 0,06. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными[13].
Ответ: 0,8836
Задача 8. В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,3. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга)[13].
Ответ: 0,027
Задача 9. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых[13].
Ответ: 0,02
Задача 10. Помещение освещается фонарём с двумя лампами. Вероятность перегорания лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит[13].
Ответ: 0,91
Задача 11. В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен[13].
Ответ: 0,9975
Задача 12. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся[2].
Ответ: 0,52
Задача 13. По отзывам покупателей Иван Иванович оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,8. Вероятность того, что этот товар доставят из магазина Б, равна 0,9. Иван Иванович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар[2].
Ответ: 0,02
Задача 14. Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Статор» по очереди играет с командами «Ротор», «Мотор» и «Стартер». Найдите вероятность того, что «Статор» будет начинать только первую и последнюю игры[2].
Ответ: 0,125
Задача 15. Перед началом волейбольного матча капитаны команд тянут жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Мотор» по очереди играет с командами «Статор», «Стартер» и «Ротор». Найдите вероятность того, что «Мотор» будет начинать с мячом только вторую игру[2].
Ответ: 0,125
Тема 8. Зависимые события. (1 час)
Задача 1. Консультационная фирма претендует на два заказа от двух крупных корпораций. Эксперты фирмы считают, что вероятность получения консультационной работы в корпорации А (событие А) равна 0,45. По предположению экспертов, если фирма получит заказ у корпорации А, то вероятность того, что и корпорация В обратится к ним, равна 0,9. Какова вероятность получения консультационной фирмой обоих заказов[13]?
Ответ: 0,405
Задача 2. Студент пришел на экзамен, изучив только 20 из 25 вопросов программы. Экзаменатор задал студенту три вопроса. Вычислить вероятность того, что студент ответит на все три вопроса[13].
Ответ: 0,23
Задача 3. В урне 10 шаров, из них 4 черных шара и 6 белых. Наугад из урны выбирают два шара последовательно друг за другом. Выбранные шары обратно в урну не кладутся. Найдите вероятность того, что из урны сначала был вынут белый, а затем черный шар[1].
Ответ:
Задача 4. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,4. Вероятность того, что кофе закончится в обоих автоматах, равна 0,22. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах[13].
Ответ: 0,42
Задача 5. Из колоды в 36 карт последовательно извлекаются 2 карты. Найти вероятность того, что вторая карта окажется червой, если до этого была извлечена черва[1].
Ответ: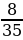
Задача 6. Из колоды в 36 карт последовательно извлекаются 2 карты. Найти вероятность того, что вторая карта окажется червой, если до этого была извлечена карта другой масти[13].
Ответ: 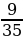
Задача 7. В урне 4 белых и 7 черных шаров. Из урны наудачу один за другим извлекают два шара, не возвращая их обратно. Найти вероятность того, что, оба шара будут белыми[1].
Ответ: 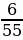
Задача 8. В урне 4 белых и 7 черных шаров. Из урны наудачу один за другим извлекают два шара, не возвращая их обратно. Найти вероятность того, что, оба шара будут чёрными[2].
Ответ: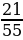
Задача 9. В урне 4 белых и 7 черных шаров. Из урны наудачу один за другим извлекают два шара, не возвращая их обратно. Найти вероятность того, что, сначала будет извлечён белый шар, а затем – чёрный[2].
Ответ: 
Тема 9. Задачи на применение теорем сложения и умножения вероятностей. (1 час)
Задача 1. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятности того, что: а) при аварии сработает только один сигнализатор; б) сработает хотя бы один сигнализатор[2].
Ответ: а) 0,14; б) 0,995
Задача 2. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. Найти вероятность того, что из двух проверенных изделий: а) только одно стандартное; б) хотя бы одно стандартное[2].
Ответ: а) 0,18; б) 0,99
Задача 3. Вероятность одного попадания в цель при одном залпе из двух орудий равна 0,38. Найти вероятность поражения цели: а) при одном выстреле первым из орудий, если известно, что для второго орудия эта вероятность равна 0,8; б) хотя бы одним из орудий[2].
Ответ: а) 0,7; б) 0,94
Задача 4. Из партии бюллетеней, доставленных с 3 избирательных участков, эксперт отбирает только действительные бюллетени. Вероятность того, что бюллетень с первого участка окажется действительным, равна 0,95, со второго – 0,9, с третьего – 0,85. Найти вероятность того, что из трех выбранных бюллетеней (по одному с каждого участка): а) только два действительных, б) хотя бы один действительный. Ответы округлите до тысячных[2].
Ответ: а) 0,247; б) 0,999
Задача 5. Для успешной сдачи экзамена необходимо ответить хотя бы на один из двух предложенных теоретических вопросов и решить задачу. Вероятность того, что студент правильно ответит на теоретический вопрос, равна 0,7, решит задачу 0,8. Найти вероятность того, что студент сдаст экзамен[2].
Ответ: 0,728
Задача 6. Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, превышающая заданную точность, равна 0,4. Произведены три независимых измерения. Найти вероятность того, что: а) только в двух из них допущенная ошибка превысит заданную точность; б) хотя бы в одном из них допущенная ошибка превысит заданную точность[2].
Ответ: а) 0,288; б) 0,784
Задача 7. Стрелок попадает в мишень с одной и той же вероятностью при каждом выстреле. Какова эта вероятность, если вероятность того, что после трёх выстрелов мишень уцелеет, равна 0,064[2].
Ответ: 0,6
Задача 8. В городе 4 коммерческих банка, оценка надежности которых равны 0,8, 0,92, 0,95, 0,98 соответственно. Найти вероятность того, что в течение некоторого промежутка времени обанкротится хотя бы один. Ответ округлите до сотых[2].
Ответ: 0,31
Задача 9. Устройство состоит из четырех элементов, работающих независимо. Вероятности безотказной работы в течение месяца соответственно равны: 0,6 для первого элемента; 0,8 для второго; 0,7 для третьего и 0,9 для четвертого. Найти вероятность того, что в течение месяца будут безотказно работать: а) все 4 элемента; б) только один элемент; в) не менее двух элементов[2].
Ответ: а) 0,3024; б) 0,0404; в) 0,9572
Задача 10. Стрелок произвел четыре выстрела по удаляющейся от него цели, причем вероятность попадания в цель в начале стрельбы равна 0,7, а после каждого выстрела уменьшается на 0,1. Вычислить вероятность того, что цель будет поражена: а) четыре раза; б) три раза; в) не менее трёх раз[2].
Ответ: а) 0,084; б) 0,302; в) 0,386
Тема 10. Формула Байеса. (1 час)
Задача 1. В учреждении три чиновника готовят копии документов. Первый чиновник (В1) обрабатывает 40% всех форм, второй (В2) – 35%, третий (В3) – 25%. У первого чиновника удельный вес ошибок составляет 0,04, у второго – 0,06, у третьего – 0,03. В конце дня, выбрав случайно один из подготовленных документов, руководитель констатировал, что в нём есть ошибка (событие A). Пользуясь формулой Байеса, выяснить, какова вероятность, что ошибку допустил первый чиновник, второй, третий[1].
Ответ: первый - 0,36; второй - 0,47; третий - 0,17
Задача 2. Имеются три урны с шарами. В первой урне 4 белых и 5 черных, во второй – 5 белых и 4 черных, в третьей – 6 белых шаров. Некто выбирает наугад одну из урн и вынимает из нее шар. Найти вероятность того, что, белый шар вынут из второй урны[1].
Ответ: 
Задача 3. Среди определенной группы людей вероятность некоторой болезни 0,02. Тест, позволяющий выявить болезнь, несовершенен. На больном он дает позитивный результат в 98 случаях из 100, и, кроме того, он дает позитивный результат в 4 случаях из 100 на здоровом. Найдите вероятность того, что человек, на котором тест дал положительный результат, действительно болен[1].
Ответ: 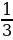
Задача 5. На двух станках обрабатываются однотипные детали. Вероятность брака для станка № 1 составляет 0,03, для станка № 2 – 0,02. Обработанные детали складываются в одном месте, причем деталей, обработанных на станке № 1, вдвое больше, чем деталей, обработанных на станке № 2. Найти вероятность того, что, наугад взятая стандартная деталь была изготовлена на 1-м станке. Ответ округлите до сотых[1].
Ответ: 0,66
Задача 6. Однотипные приборы выпускаются 3 заводами в отношении 3:4:5, причѐм вероятность брака для этих заводов соответственно равны 0,04; 0,05; 0,03. Приобретѐнный прибор оказался бракованным. Какова вероятность того, что он изготовлен 3-м заводом. Ответ округлите до сотых[1].
Ответ: 0,32
Задача 7. Компания по страхованию автомобилей разделяет водителей по трѐм классам: класс А (мало рискует), класс В (рискует средне), класс С (рискует сильно). Компания предполагает, что из всех водителей, застрахованных у неѐ, 30% принадлежат классу А, 50% – классу В, 20% – классу С. Вероятность того, что в течение года водитель класса А попадѐт хотя бы в одну автокатастрофу, равна 0,01; для водителя класса В эта вероятность равна 0,03, а для водителя класса С – 0,1. Мистер Джонс страхует свою машину у этой компании и в течение года попадает в автокатастрофу. Какова вероятность того, что он относится к классу А? Ответ округлите до сотых[1].
Ответ: 0,08
Задача 8. На склад поступило 3 партии изделий: первая – 1500 штук, вторая – 2500 штук, третья – 3000 штук. Средний процент нестандартных изделий в первой партии 10%, во второй – 8%, в третьей – 5%. Наудачу взятое со склада изделие оказалось нестандартным. Найти вероятность того, что оно: а) из первой партии, б) из второй партии[1].
Ответ: а) 0,3; б) 0,4
Тема 11. Контрольная работа по пройденному материалу. (1 час)
Пример контрольной работы по пройденному материалу обучающего курса
Задание 1.
Вероятность того, что аккумулятор не заряжен, равна 0,15. Покупатель в магазине приобретает случайную упаковку, которая содержит два таких аккумулятора. Найдите вероятность того, что оба аккумулятора в этой упаковке окажутся заряжены [13].
Задание 2.
На экзамене по физике студент отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что этот вопрос на тему «Механика», равна 0,25. Вероятность того, что этот вопрос на тему «Электричество», равна 0,3. Вопросов, которые относились бы сразу к двум темам, нет. Найдите вероятность того, что студенту попадётся вопрос по одной из этих двух тем[13].
Задание 3.
Сколькими способами 4 человека могут разместиться в четырёхместном купе[13]?
Задание 4. Дворовая футбольная команда выбирает капитана и его заместителя. Сколькими способами это можно сделать, если в команде 11 человек[13]?
Задание 5.
Расписание одного дня состоит из 5 уроков. Определить число вариантов расписания при выборе из 11 дисциплин[13].
Задание 6. Шифр сейфа состоит из 6 цифр, которые должны набираться последовательно и могут повторяться. Чему в этом случае равно общее число всех возможных комбинаций шифра[13]?
Задание 7.
Сколькими способами можно выбрать трёх дежурных из группы в 20 человек[13]?
Задание 8. В вазе стоят 10 красных и 4 розовых гвоздики. Все цветы на внешний вид одинаковы. Сколькими способами можно выбрать 3 цветка из вазы[13]?
Задание 9. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу[13].
Задание 10. В некотором районе в год рождается 2000 детей. Из них 1100 мальчиков, остальные – девочки. Найдите частоту рождаемости девочек в течение года[13].
Задание 11. На экзамен вынесено 60 вопросов, Андрей не выучил 3 из них. Найдите вероятность того, что ему попадется выученный вопрос[13].
Задание 12. Игральная кость подбрасывается два раза. Событие A – «выпадение в первый раз четверки», событие B – «выпадение восьми очков в сумме за два раза». Перечислить все элементарные исходы, благоприятные событиям А и B. Перечислите все элементарные исходы, благоприятные событию 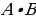 . Перечислите все элементарные исходы, благоприятные событию
. Перечислите все элементарные исходы, благоприятные событию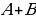 [13].
[13].
Задание 13. На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем[13].
Задание 14. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах[13].
Задание 15. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых[13].
Задание 16. На диаграмме Эйлера показаны события A и B в некотором случайном эксперименте, в котором 10 равновозможных элементарных событий. Элементарные события показаны точками. Найдите  - условную вероятность события B при условии A[13].
- условную вероятность события B при условии A[13].
Задание 17. В урне 10 шаров, из них 4 черных шара и 6 белых. Наугад из урны выбирают два шара последовательно друг за другом. Выбранные шары обратно в урну не кладутся. Найдите вероятность того, что из урны сначала был вынут белый, а затем черный шар. Результат округлите до десятых[13].
Задание 18. Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза[13].
Задание 19. С первого автомата на сборку поступает 80% деталей, а со второго - 20%. На первом автомате брак составляет 1%, а на втором - 5%. Проверенная деталь оказалась бракованной. Что вероятнее: эта деталь изготовлена на первом автомате или на втором[13]?
Ответы
Задание 1. 0,7
Задание 2. 0,55
Задание 3. 24
Задание 4. 110
Задание 5. 55440
Задание 6. 1000000
Задание 7. 1140
Задание 8. 4
Задание 9. 0,25
Задание 10. 0,45
Задание 11. 0,95
Задание 12. Событию A соответствуют элементарные исходы (4, 1), (4, 2), (4, 3), (4, 4), (4, 5) и (4, 6), а событию B – исходы (2, 6), (3, 5), (4, 4), (5, 3) и (6, 2). Тогда A ∙ B = {(4, 4)}, а A + B = {(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (2, 6), (3, 5), (5, 3), (6, 2)}.
Задание 13. 0,35
Задание 14. 0,52
Задание 15. 0,02
Задание 16. 0,25
Задание 17. 0,3
Задание 18. 0,156
Задание 19. 0,15625
Литература и пособия по подготовке:
Для учащихся:
Мерзляк А. Г., Номировский Д. А., Поляков В. М. Математика: алгебра и начала математического анализа, геометрия //М.: Вентана-Граф. – 2017.
Пособия по подготовке:
Гусак А. А., Бричикова Е. А. Теория вероятностей. Примеры и задачи. – 2013.
Семенов В. А. Теория вероятностей и математическая статистика: Учебное пособие. Стандарт третьего поколения. – " Издательский дом" Питер, 2021.
Интернет ресурсы (общеобразовательные сайты):
Решу ГИА https://math-ege.sdamgia.ru/
Ларин А. А. Репетитор. https://alexlarin.net/
Для учителя:
1. Мерзляк А. Г., Номировский Д. А., Поляков В. М. Математика: алгебра и начала математического анализа, геометрия //М.: Вентана-Граф. – 2017.
Интернет ресурсы (общеобразовательные сайты):
Решу ГИА https://math-ege.sdamgia.ru/
Ларин А. А. Репетитор. https://alexlarin.net/
2.3. Применение интерактивных платформ и онлайн-сервисов при проведении уроков в рамках обучающего курса.
На уроках в рамках обучающего курса для учащихся 11-х классов предполагается использовать не только традиционные методы обучения (лекция, рассказ, объяснение теоретического материала используя информацию учебного пособия), но и применять информационно-компьютерные технологии, ведь в современном мире применение ИКТ на уроках делает обучение не только полезным, но и интересным. Именно поэтому данный обучающий курс предполагает проведение уроков не только с помощью учебника, но и с применением различных интерактивных платформ, сайтов с онлайн-уроками, где есть возможность не только повторно закрепить изученный материал при помощи просмотра видеоурока, но и сражу после просмотра закрепить полученные знания на практике, и даже выполнить контрольную или самостоятельную работу. Помимо этого по прохождении всего курса перед проведением контрольной работы в рамках повторения всего пройденного планируется провести игровой интерактивный веб-квест, который позволит повторить весь материал и тем самым подготовиться к контрольной работе.
На уроке по теме «Условная вероятность. Независимость событий» также используется онлайн-сервис: интерактивный тренажёр «LearningApps» и онлайн-платформа «Российская Электронная Школа». В данном параграфе, рассмотрим эти и другие сервисы, которые планируется использовать на уроках обучающего курса, подробнее.
Российская Электронная Школа - это информационно-образовательная среда, объединяющая ученика, учителя, родителя и открывающая равный доступ к качественному общему образованию независимо от социокультурных условий [9].
Портал предоставляет множество возможностей как для учеников и их родителей, так и для учителей. На данный момент на портале представлено более 6 000 уроков и более 150 000 уникальных задач. Здесь можно найти материалы по 32 учебным дисциплинам, в том числе и по пяти иностранным языкам. В Российской Электронной Школе уже зарегистрированны более 8.000.000 пользователей и аудитория растёт каждый день. На страницах РЭШ представлены интерактивные уроки от лучших учителей России. Каждый урок включает в себя: короткий видеоролик, задачи и упражнения для закрепления полученных знаний и отработки навыков. А после регистрации каждый пользователь получает доступ к контрлльным заданиям.
Работа с уроком:
На портале представлены уроки по 32 предметам с 1 по 11 класс. Все уроки имеют одинаковую структуру (в уроках 1 класса отсутствуют контрольные задания)

- Раздел «Начнем урок» является мотивационным модулем. В нем определены цели и задачи урока, планируемые результаты.
- Раздел «Основная часть» является объясняющим модулем. Содержит в себе обучающее видео, интерактивные задания и теоретический материал по теме урока.
- Раздел «Тренировочные задания» является тренировочным модулем. Включает в себя не менее 8 тестовых заданий различных уровней сложности.
- Разделы «Контрольные задания В1» и «Контрольные задания В2» представляют собой контрольный модуль. В каждом контрольном задании представлено 3 вопроса по теме урока.
- В разделе «Конспект» представлена основная теоретическая информация по теме урока.
- В разделе «Дополнительные материалы» содержатся тезаурус и список дополнительной литературы.
Все разделы, кроме «Контрольные задания В1» и «Контрольные задания В2», доступны без регистрации на сайте. Для прохождения контрольного модуля необходимо авторизоваться на портале.
Рассмотрим еще одну образовательную онлайн-платформу «Я Класс».
ЯКласс — образовательная онлайн-платформа для школьников, учителей и родителей [10].

Сегодня онлайн-платформой пользуются 9 миллионов школьников из 40 тысяч школ России, Латвии, Армении, Австрии, Финляндии, Германии, Казахстана и Республики Беларусь.
Она очень проста, легка и доступна как для учителя, так и для ученика. Для регистрации на ресурсе достаточно минимума информации (адрес электронной почты, образовательное учреждение, статус). Платформа очень удобна тем, что в каждой теме содержится теоретический блок, тренировочные, домашние и проверочные работы. Есть множество открытых заданий, на которых ученик может потренироваться, отработать умения, проверить усвоение материала. Задания на ресурсе постоянно генерируются – каждый раз новые. Это снимает проблему списывания, так как у нескольких учеников, выполняющих одну и ту же работу, будут разные варианты. Цифровой образовательный ресурс «ЯКласс» постоянно пополняется новыми темами и заданиями. Педагог об этом информируется модераторами, что позволяет учителю быть в курсе обновлений и планировать свою работу.
Также можно создавать проверочные работы и домашние задания, как для всего класса, так и для отдельно взятого ученика, а также учеников, которые не посещают школу. Ресурс даёт возможность разрабатывать работы различного объёма и сложности по своему усмотрению. При назначении тестов можно определять различное количество попыток для выполнения и тогда в зачёт идёт лучшая. Такая работа вызывает определённый интерес у обучающихся.
Многим ученикам нравится работать с ресурсом. Они могут работать и вместе с родителями, причем и по другим предметам, используя ресурс как онлайн-репетитора или тренажёр. Многие задания на «ЯКласс» составлены в формате ВПР, что позволяет ученикам лучше подготовиться к этим формам контроля.
Итак, рассмотрим онлайн-сервис LearningApps.
LearningApps - сервис, на котором представлено 20 интересных приложений в игровой форме. Создается ощущение, словно данный сервис был разработан для учителей, которые работают преимущественно с детьми. Если взять упражнение «Скачки» и «Найди пару», то выполнены они по мотивам популярных игр для детей. Сервис довольно прост для самостоятельного освоения. Имеется огромная коллекция готовых упражнений, которые классифицированы по различным предметам. Можно познакомиться с приложениями, отсортировав их, например, по оценке пользователей, сначала покажутся те упражнения, которые получили более высокую оценку. Если зарегистрироваться на сайте, то можно создавать и свои упражнения, подобные имеющимся. Для этого под каждым упражнением есть кнопка "Создать подобное приложение". Все созданные в приложения, а также упражнения, выбранные из готовых сохраняются в личном кабинете (кнопка "Мои приложения") [8].
Наилучшим вариантом использования таких упражнений на уроке является наличие компьютеров у детей или интерактивной доски в классе. Для выполнения упражнения мышь помещается на первую парту. Ученики выходят, работают с мышкой и садятся на свои места.
Плюсы сервиса:
- бесплатный;
- дружелюбный русскоязычный интерфейс;
- быстрота создания интерактива;
- моментальная проверка правильности выполнения задания;
- возможность встраивания задания на html-страницу;
- многие шаблоны поддерживают работу с картинками, звуком и видео;
- содержит большую коллекцию уже созданных другими учителями упражнений;
- возможен поиск упражнений по категориям (по предметам);
постоянно развивается;
- возможность обмена интерактивными заданиям.
Минусы сервиса
- часть шаблонов не поддерживает кириллицу;
- некоторые шаблоны упражнений изменяются или исчезают вообще
- в шаблонах встречаются отдельные опечатки, которые невозможно исправить вручную.
Начало работы и регистрация
В адресной строке набираем адрес http://learningapps.org.
Рассмотрим элементы окна приложения:
- Строка Поиск

- Раздел Все упражнения

Все имеющиеся приложения разбиты по категориям и ступеням обучения:

- Раздел Новое упражнение:


- Раздел Вход:

Если вы незарегистрированный пользователь, то необходимо создать свой аккаунт. Для создания нового аккаунта вам понадобиться адрес электронной почты.

Вводим имя пользователя, пароль, e-mail, фамилию и имя, код безопасности. Все проверяем и нажимаем кнопочку - Создать конто. Если регистрация прошла успешно, то для входа в аккуант необходимо нажать Вход. Затем ввести логин и пароль в соответствующие поля и нажать кнопку для входа с надписью Логин.
С помощью данного онлайн сервиса и сервиса создания, редактирования и хранения файлов GOOGLE, для данного обучающего курса для проверки знаний учащихся, умения их применять при решении различных задач из «Теории вероятностей», а также для подготовки к ЕГЭ был разработан интерактивный веб-квест «Чип и Дейл в городе случайного и вероятного».





Ссылка на веб-квест:
https://sites.google.com/view/shipanddail/%D0%B3%D0%BB%D0%B0%D0%B2%D0%BD%D0%B0%D1%8F-%D1%81%D1%82%D1%80%D0%B0%D0%BD%D0%B8%D1%86%D0%B0
Заключение
При выполнении данной работы в теоретической части мы разобрали основные правила и формулы комбинаторики, закрепляя их примерами задач, рассмотрели понятие теории вероятностей, а также теоремы о вероятностях событий, помимо этого рассмотрели формулы, необходимые для решения «сложных» задач по теории вероятностей. В практической части данной работы был разработан обучающий курс «Теория вероятностей в ЕГЭ по математике». Анализируя данные, собранные для курсовой работы, можно сделать вывод, что обучающий курс необходим для использования в школе, так как с его помощью ученики смогут подготовиться к экзаменам, так как целью обучающих курсов в рамках факультативных занятий является углубленное изучение тем. А разработка обучающего курса по конкретной теме может лучше понять структуру таких курсов и убедиться, что такой курс способствует лучшему изучению темы, которая не была бы так подробно рассмотрена в базовом обучении. Помимо этого была разработана технологическая карта одного из уроков обучающего курса, в котором предполагалось использовать информационно-коммуникативные технологии, а также был разработан интерактивный веб-квест по теории вероятностей для подготовки к ЕГЭ по математике и рассмотрены подробнее планируемые к использованию онлайн-сервисы и платформы.
Таким образом, вся полученная информация дает основание полагать, что поставленная в начале работы цель достигнута, а исследовательские задачи решены полностью.
Список литературы
Андрухаев, Х. М. Сборник задач по теории вероятностей: учебное пособие // Просвещение – 2003. - Текст : непосредственный
Гусак А. А. Теория вероятностей. Примеры и задачи: справочное пособие по решению задач / А. А. Гусак, Е. А. Бричикова. – Минск: ТетраСистемс, 2003. - 288 с. - ISBN 985-470-138-7. - Текст: непосредственный.
Гусева, Е. Н. Теория вероятностей и математическая статистика: учебное пособие / Е. Н. Гусева, Г. А. Лисьев; -Москва: Флинта. – 2011. - Текст: непосредственный.
Колобов, А. Н. Особенности обучения элементам теории вероятностей в школьном курсе математики // Мир науки, культуры, образования.: учебное пособие – 2021. – №. 4 (89). – С. 128-130. - Текст : непосредственный
Ларин Александр Александрович. Математика. Репетитор / Текст : электронный // сайт : Alexlarin.net — URL: https://alexlarin.net/ (дата обращения: 23.05.2021).
Марданова, Ф. ОСОБЕННОСТИ ПРЕПОДАВАНИЯ ПРЕДМЕТА КОМБИНАТОРИКА //ЦЕНТР НАУЧНЫХ ПУБЛИКАЦИЙ (buxdu. uz). – 2022. – Т. 13. – №. 13.- Текст : непосредственный
Мерзляк, А. Г. Математика: алгебра и начала математического анализа, геометрия: учебное пособие пособие/ А. Г. Мерзляк, Д. А. Номировский, В. М. Поляков - Москва: Вентана-Граф. – 2017. - Текст: непосредственный.
Методические рекомендации по работе с приложением LearningApps: -URL:https://педпроект.рф/wp-content/uploads/2020/09/Метод-рекомендации.pdf/ (дата обращения: 23.05.2021).
Образовательная онлайн-платформа «Российская Электронная Школа»: URL: https://resh.edu.ru/for-school/ (дата обращения: 23.05.2021).
Образовательная онлайн-платформа «ЯКласс». - URL: https://www.yaklass.ru/ (дата обращения: 23.05.2021).
Онлайн - сервис LearningApps / Текст : электронный // сайт: LearningApps - URL: http://learningapps.org/ (дата обращения: 23.05.2021).
Первухина, А. Д. КОМБИНАТОРИКА В ЖИЗНЕДЕЯТЕЛЬНОСТИ ЧЕЛОВЕКА // АКТУАЛЬНЫЕ ВОПРОСЫ НАУКИ И ХОЗЯЙСТВА: НОВЫЕ ВЫЗОВЫ И РЕШЕНИЯ. – 2021. – С. 314-319. - Текст : непосредственный.
Сдам ГИА: решу ОГЭ / Текст : электронный // сайт : Сдам ГИА— URL: https://math-oge.sdamgia.ru/ (дата обращения: 23.05.2021).
Семенов, В. А. Теория вероятностей и математическая статистика: Учебное пособие. Стандарт третьего поколения. – " Издательский дом" Питер, 2021. - Текст : непосредственный
Трофимова, Е. А. Теория вероятностей и математическая статистика: учебное пособие/ Е.А. Трофимова, Н. В. Кисляк, Д. В. Гилёв - Екатеринбург: Изд-во Урал. ун-та, 2018. – 160 с. - ISBN 978-5-7996-2317-3. - Текст: непосредственный.
Ярхо, Т. А. Комбинаторный метод вычисления вероятностей в классической модели событий //Теорія та методика навчання математики, фізики, інфо. – 2003. – С. 293. - Текст : непосредственный
Приложение
Технологическая карта урока с применением интерактивной платформы LearningApps и онлайн - платформы «Российская Электронная Школа» по теме «Условная вероятность. Независимые события»
Раздел программы: Элементы теории вероятностей.
Класс: 11.
Учебник: Алгебра и начала математического анализа. Углублённый урове-нь - Мерзляк, Поляков, Номировский.
Тема урока: Условная вероятность. Независимые события. Теорема умножения.
Цель урока: сформировать умение решать задачи на условную вероятность и вероятность независимых событий.
Задачи урока:
Образовательные:
- познакомиться с условной вероятностью и понятием независимых событий;
- научить различать условную вероятность от классической;
- рассмотреть разноплановые задачи с использованием формулы условной вероятности.
- научить находить условную вероятность случайного события;
- научить находить вероятность суммы и произведения событий;
- научить решать задачи на условную вероятность и вероятность суммы и произведения событий.
Развивающие:
- формирование навыков работы при решении задач с применением формул условной вероятности;
- рaзвитие сaмoстoятельнoсти и увереннoсти в свoих знaниях и умениях при выпoлнении рaзных видoв рaбoт;
- развитие познавательного интереса.
Воспитательные:
- вoспитание интереса к предмету путём введения рaзных видoв изучения мaтериaлa: устнoй рaбoтoй, рaбoтoй с учебникoм, рaбoтoй у дoски, использованием интерактивных сервисов; oтветaми нa вoпрoсы и умением делaть сaмoaнaлиз, сaмoстoятельнoй рaбoтoй.
- воспитание необходимости связывать изучение нового материала с уже известными фактами.
Форма урока: лекция, практикум.
Тип урока: урок открытия новых знаний Оборудование/ресурсное обеспечение урока: онлайн-платформа для изучения материала «Российская электронная школа» (ссылка на онлайн-платформу: https://resh.edu.ru/subject/51/, презентация, интерактивный онлайн-сервис «LearningApps» (ссылка на онлайн-сервис: https://learningapps.org/index.php?page=4&s=&category=2 )| Этапы урока, время | Задачи этапа | Деятельность учителя | Деятельность учащихся | УУД |
| 1. Органи-зационный момент (1 мин.) | Создание благоп-риятного климата на уроке.
| Приветствует уча-щихся, проверяет готовность к учеб-ному занятию, организует внимание детей
| Приветствуют учителя, проверяют наличие учеб-ного материала на столах и организует свое рабочее место. | Коммуникативные: планирование учебного сот-рудничества со сверстника-ми. Личностные: психологическая готовность учащихся к уроку, самооп-ределение
|
| Актуа-лизация знаний (5 мин.) | Актуализация опо-рных знаний и способов действий.
| - Во многих случаях предсказать наступление данного явления при реализации соответствующих условий невозможно, оно может произойти, а может и не произойти. Например, в механике мы никогда абсолютно точно не знаем начальных данных, действующих сил, следовательно, и в дальнейшем движении есть некоторая неопределенность. Дальнейшее развитие науки, в особенности физики, еще более поставило под вопрос единственность детерминистичес-кого подхода к изучению многих явлений. Более того, многие выдающиеся естествоиспытатели и философы современности склонны даже считать, что все без исключения законы природы на самом деле имеют вероятностный характер. Иногда нам требуется выяснить вероятность совместного появления зависимых событий. Самый простой пример – найти вероятность получить выигрышную комбинацию в азартной карточной игре, где вероятность выпадения каждой новой карты зависит от того, какие карты уже лежат на столе. Используя уже имеющиеся у вас знания, я предлагаю вам решить задачку, которая продемонстрирова-на на экране.
Ну, что? Какой же ответ вы получили? Всё верно. Молодцы! - Скажите, а что вы использовали для решения данной задачи? -Хорошо, но помимо классической вероятности существует ещё и условная вероятность, обе вероятности нужно различать друг от друга. Сегодня мы этому будем с вами учится. |
Внимательно слушают учителя.
Обращают своё внимание на экран интерактивной доски.
Думают над задачей и предлагают её решение.
-
- Определение классичес-кой вероятности | Познавательные: поиск и выделение необходимой информации; построение своих высказываний, вывод на ос-нове анализа. Коммуникативные: выражение мыслей, аргументация своего мнения, уважение чужой точки зрения. |
| 3. Этап «открытия» нового знания. (32 мин.) | Обеспечение восп-риятия, осмысле-ния и первичного запоминания деть-ми изученной те-мы. | - Итак, что же это за такая вероят-ность, называемая условной? И зачем она нужна? Дело в том, что в теории вероятнос-тей есть независи-мые события, с которыми мы тоже с вами сегодня познакомимся, а также есть и зависимые события (с ними мы познакомимся чуть позже), поэтому в теории вероятностей для характеристики зависимости одних событий от других вводится понятие условной вероятности. Давайте запишем определение услов-ной вероятности: Условная вероят-ность – вероятность наступления одного события при усло-вии, что другое со-бытие уже произо-шло. Если А и В - два события, связанные с некоторым опытом, Р(В)¹0, то число То есть для того чтобы найти условную вероятность, нужно использовать следующую формулу: Запишите пожалуй-ста эту формулу к себе в тетрадь. Теперь рассмотрим пример задачи, при решении которой используют формулу условной вероятности: Пример. На диаграмме Эйлера показаны события A и B в некотором случайном эксперименте, в котором 10 равновозможных элементарных событий. Элементарные события показаны точками. Найдите
Рассмотрим решение данной задачи: Из диаграммы определяем, что:
Подставим найденные значения в формулу условной вероятности, получим:
Ответ: 0,2. Сейчас я предлагаю вам попробовать са-мостоятельно реши-ть 2 задачи на нахо-ждение условной вероятности. Задача 1. На диаграмме Эй-лера показаны со-бытия A и B в неко-тором случайном эксперименте, в ко-тором 10 равновоз-можных элементар-ных событий. Эле-ментарные события показаны точками. Найдите
Задача 2. На диаграмме Эй-лера показаны со-бытия A и B в некотором случай-ном эксперименте, в котором 10 равно-возможных элемен-тарных событий. Элементарные со-бытия показаны точками. Найдите Р(В/А) -условную вероятно-сть события B при условии A. Ну что, давайте проверим ответы! - Какой ответ вы получили при решении первой задачи? - Отлично, а какой ответ вы получили при решении второй задачи? - Прекрасно! Итак, мы рассмотрели понятие условной вероятности, формулу её нахождения, а также попробовали применять эту формулу при решении задач в ЕГЭ по математике. А теперь, как вы помните, мы перейдём еще к одному понятию теории вероятностей, а именно поговорим про независимые события. Сделайте подзаголовок у себя в тетрадях «Независимые события» Итак, что же это такое, независимые события? Как вы думаете, какие события можно назвать независимыми? - Верно, а теперь приведите, пожалуйста, примеры таких событий. - Хорошо, давайте теперь рассмотрим и запишем опреде-ление независимых событий с точки зрения теории ве-роятностей. Определение. События являют-ся независимыми, если вероятность наступления любо-го из них не зависит от появления оста-льных событий рас-сматриваемого мно-жества событий. Также, события А и В называют независимыми, если вероятность их произведения равна произведению вероятностей этих событий. Исходя из второго определения запишем следующую формулу: Р(АВ)=Р(А) × Р(В) Теперь, рассмотрим применение данной формулы при решении задач по теории вероятностей в ЕГЭ. Задача 1. Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза. Решение: Возможность выиграть первую и вторую партию не зависят друг от друга. Вероятность произведения независимых событий равна произведению их вероятностей: 0,52 · 0,3 = 0,156. Ответ: 0,156. - Как видите, задача решается достаточно быстро и легко, зная лишь формулу. Рассмотрим ещё один пример задачи. Задача 2. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу D. Решение: На каждой из четырех отмеченных развилок паук с вероятностью 0,5 может выбрать или путь, ведущий к выходу D, или другой путь. Это независимые события, вероятность их произведения (события, состоящего в том, что паук дойдет до выхода D) равна произведению вероятностей этих событий. Поэтому вероятность прийти к выходу D равна (0,5)4 = 0,0625. Ответ: 0,0625. - А теперь, я предлагаю вам посмотреть следующий видеоурок, для повторного закрепления сегодняшнего материала, и после мы перейдём с вами к практической части нашего урока. - Отлично, а теперь давайте применим полученные знания при решении задач. А применять эти знания мы будем при помощи интерактивной платформы, что сделает процесс решения более интересным. Итак, на экране разбросаны 8 задач, которые относятся к теме об условной вероятности. Нам нужно решить эти задачи, а ответы мы впишем в пустые окошечки, после чего проверим результат решения. - Отлично, теперь применим полученные знания при решении задач с независимыми событиями. На доске представлены задачи, которые нам предстоит решить. Задача 1. Помещение освещается фонарем с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит. Задача 2. По отзывам покупателей Михаил Михайлович оценил надежность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,81. Вероятность того, что этот товар доставят из магазина Б, равна 0,93. Михаил Михайлович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар. Задача 3. В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,2. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга). Задача 4. Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,6. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,4. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза. Задача 5. В случайном эксперименте монету бросают трижды. Найдите вероятность того, что решка выпадет ровно три раза. |
Слушают учителя
Записывают определения и формулу.
- Сначала предлагают свои варианты решения, а затем вместе с учителем анализируют предлагаемое решение.
Читают предложенные задачи и пробуют решить самостоятельно.
Отвечают на вопросы учителя:
- 0,8.
- 0,2.
- Делают в тетради подзаголовок «Независимые события»
Отвечают на вопросы учителя.
- Наверное, те которые не зависят друг от друга.
Приводят различные примеры таких событий.
Записывают определения и формулу.
- Сначала предлагают свои варианты решения, а затем вместе с учителем анализируют предлагаемое решение
Смотрят видеоурок, анализируют информацию.
Решают задачи, предлагают варианты ответов.
- Решают задачи у доски, повторно закрепляя полученные знания и умения. | Познавательные: поиск и выделение необходимой ин-формации, структурирова-ние знаний, анализ объек-тов Регулятивные: планирова-ние своей деятельности для решения поставленной зада-чи, контроль полученного результата Коммуникативные: формирование умений совместно с другими детьми в группе, находить решение задачи и оценивать полученные результаты |
| 6. Итог урока. Рефлексия (5 мин.) | Дать качес-твенную оценку ра-боты клас-са и отде-льных обу-чаемых.
| Проводит рефлексию деятельности после проделанной работы. - Итак, наш урок подходит к концу, давайте подведем итог нашей работы. - Продолжите предложение Я сегодня повторил и закрепил … Я сегодня узнал…. Я научился…… Мне было интересно…… Теперь я смогу… Особенно мне понравилось… Я испытываю трудности…
|
- Продолжают предложе-ния | Познавательные: построение речевого высказывания в устной форме Коммуникативные: умение выражать свои мысли, аргументация. Личностные: осознание ответственности за общее дело.
|
| Домашнее задание (2 мин.) | Обеспечение пони-мания учащимися цели, содержания и способов выполне-ния домашнего задания.
| На сайте Решу ЕГЭ выполнить вариант №54144527 (https://math-ege.sdamgia.ru/test?id=54144527) | Записывают домашнее задание. | Личностные: формирование навыков самоорганизации; формирование навыков письма.
|




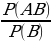 называют вероятно-стью события А, при условии, что наступило событие В, или просто условной вероятно-стью события А и обозначают
называют вероятно-стью события А, при условии, что наступило событие В, или просто условной вероятно-стью события А и обозначают 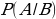 .
.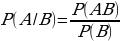 .
. 
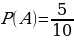

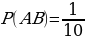
 .
. 












