Проект "Теория вероятности и её применение"

Тематика:
Математика
Автор работы:
Магомедова Халимат
Руководитель проекта:
Ильясова Зарият Хангишиевна
Учреждение:
МКОУ «Султанянгиюртовская СОШ им.Ю.А.Акаева»
Класс:
9
В процессе исследовательской работы по математике "Теория вероятности и её применение" ученицей 9 класса была поставлена цель изучить данную тему, пополнить личный опыт и посмотреть применение теории вероятности в жизни. В проекте изучаются теоретические сведения о теории вероятностей, проводится практическое исследование данной теории.
В исследовательской работе по математике "Теория вероятности и её применение" автор выдвигает гипотезу, что если ездить 2 месяца на некотором автобусе и собирать автобусные билеты, приобретенные в нем ежедневно, то можно вычислить вероятность выпадения счастливого билета в данном транспорте за определенный период времени.
В предложенном проекте по математике "Теория вероятности и её применение" автором предложены результаты практического применения теории вероятности на примере покупки билетов в автобусе.
Оглавление
Введение
1.Теоретические сведения о теории вероятности.
2.Практическое исследование теории вероятности.
Заключение
Источники информации
Приложения
Введение
«Есть в математике нечто, вызывающее человеческий восторг» - говорил Хаусдорф. Действительно, есть в этой науке темы, о которых хочется говорить бесконечно. Они завораживают своей загадочностью или наоборот простотой, над которой стоит задуматься.
Таких тем бесконечное множество: «Равенство классов P и NP», «Гипотеза Ходжа», «Гипотеза Пуанкаре», «Квантовая теория Янга — Миллса» и др.
Одна из них – теория вероятностей. Достаточно обширная тема для размышлений. Хотелось ли вам когда-нибудь узнать, какой из билетов в общественном транспорте вам попадется: «счастливый» или «несчастливый»? А сможете ли вы выиграть лотерею, купив определенный билет? Заманчивые вопросы, не так ли? Человек всегда стремился предугадать будущее, изменить его. Воспользовавшись теорией вероятностей это возможно! Взяв формулу и подставив в нее числа, получим процент вероятности события.
«Метод решения хорош, если с самого начала мы можем предвидеть - и далее подтвердить это, - что, следуя этому методу, мы достигнем цели» - Г. Лейбниц. Это высказывание полностью описывает данную теорию.
Теория вероятностей доказывает, казалось бы, невероятные вещи: машина опасней самолета; кокосы убивают больше человек, чем акулы и др.
Цель: изучить данную тему, пополнить личный опыт и посмотреть применение теории вероятности в жизни.
Актуальность: тема актуальна в связи с малым интересом к математике, потому как многие школьники считают данный предмет малополезным в жизни.
Теоретическая значимость этого исследования заключается в доказательстве возможности использовать математику в повседневной жизни.
Практическая значимость моего исследования заключается в том, чтобы показать применение теории вероятностей в повседневной жизни и подтолкнуть учащихся на поиск использования математики не только в подсчётах, но и для общего развития.
Метод исследования: наблюдение, счет, построение таблиц и диаграмм.
Объект исследования: автобусные билеты.
Перед написанием работы мною была выдвинута гипотеза: если я буду ездить 2 месяца на некотором автобусе и собирать автобусные билеты, приобретенные в нем ежедневно, то смогу вычислить вероятность выпадения счастливого билета в данном транспорте за определенный период времени.
Для достижения данной цели были поставлены следующие задачи:
Накопить автобусные билеты.
Вычислить по формуле вероятность выпадения счастливого билета в данном автобусе.
Провести анализ результатов.
Оформить результаты исследования.
Теоретические сведения о теории вероятности
Проект "Теория вероятности и её применение"
1. О теории вероятности
Теория вероятностей — раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними.
Теория вероятностей – важнейший раздел математики, который изучают в подавляющем большинстве ВУЗов, а сейчас и в школах. В нем есть определенные формулы, каждая из которых используется для вычисления различных вероятностей. Вот пара самых распространенных из них.
1. Классическая вероятность (основная, взятая в исследование)
Классическая вероятность события находится как отношение числа благоприятных исходов m к общему числу всех элементарных исходов n.


Понять формулу проще всего на примерах.
Задача: В коробке было 5 синих и 14 красных карандашей. Наугад (не глядя) достаём один из них. Какова вероятность того, что выбранный таким образом карандаш окажется синим?
Решение. Вычислим вероятность выбора синего карандаша с помощью формулы.
Событие А: "выбранный шар оказался синего цвета".
Общее число всех возможных исходов: 5+14=20 (количество всех шаров, которые мы могли бы вытащить).
Число благоприятных для события «А» исходов: 5 (количество таких исходов, при которых событие «А» произошло, - то есть, количество синих шаров).
P(A)=5/20=0,25
Ответ: 0,25
Стоит отметить, что вероятность того или иного события лежит в пределах от 0 до 1 и не может быть меньше 0, либо больше 1: 0
При этом вероятность равна нулю у событий, которые не могут произойти. В нашем примере это была бы вероятность вытащить из коробки зелёный карандаш. Число благоприятных исходов равно 0, Р(А)=0/20=0, если считать по формуле.
Вероятность равно единице, если имеет события, которые абсолютно точно произойдут, в частности, вероятность того, что «выбранный карандаш окажется или красным или синим» - для нашей задачи. Число благоприятных исходов: 20, Р(А)=20/20=1.
2. Статистическая вероятность
При статистическом определении в качестве вероятности события принимают его относительную частоту.

где m - число испытаний, в которых событие A наступило, n - общее число произведённых испытаний.
Задача: В некотором подъезде родилось с начала года 71 младенец, из них 32 девочки. Какова вероятность рождения девочки в данном подъезде?
Общее число произведённых испытаний – 71, а число испытаний – 32.
Подставим в формулу числа: W(A)=32/71≈0,45
Ответ: ≈0,45
Практическое исследование теории вероятности 2. Применение теории вероятности на практике
На протяжении первого месяца я ежедневно сохраняла билеты с одного и того же автобуса. В итоге за этот промежуток времени накопила 30 билетов. Счастливым считается полученный в общественном транспорте билет, в шестизначном номере которого сумма первых трёх цифр совпадает с суммой трёх последних.
Первый месяц
| Номер билета | Вид |
| 193833 | Несчастливый |
| 033282 | Несчастливый |
| 156445 | Несчастливый |
| 174724 | Несчастливый |
| 084850 | Несчастливый |
| 081514 | Несчастливый |
| 191811 | Несчастливый |
| 105759 | Несчастливый |
| 081006 | Несчастливый |
| 105247 | Несчастливый |
| 081610 | Несчастливый |
| 163359 | Несчастливый |
| 162391 | Несчастливый |
| 133597 | Несчастливый |
| 159926 | Несчастливый |
| 175235 | Несчастливый |
| 166127 | Несчастливый |
| 164628 | Несчастливый |
| 142429 | Несчастливый |
| 148937 | Несчастливый |
| 199334 | Несчастливый |
| 196765 | Несчастливый |
| 159003 | Несчастливый |
| 154224 | Несчастливый |
| 154511 | Несчастливый |
| 136023 | Несчастливый |
| 287359 | Счастливый |
| 196565 | Счастливый |
| 165543 | Счастливый |
| 128731 | Счастливый |
Второй месяц
| Номер билета | Вид |
| 122409 | Несчастливый |
| 172754 | Несчастливый |
| 147331 | Несчастливый |
| 193215 | Несчастливый |
| 188446 | Несчастливый |
| 102881 | Несчастливый |
| 189697 | Несчастливый |
| 033833 | Несчастливый |
| 194502 | Несчастливый |
| 198664 | Несчастливый |
| 265554 | Несчастливый |
| 185270 | Несчастливый |
| 231305 | Несчастливый |
| 158324 | Несчастливый |
| 353912 | Несчастливый |
| 055344 | Несчастливый |
| 448110 | Несчастливый |
| 366023 | Несчастливый |
| 191961 | Несчастливый |
| 023930 | Несчастливый |
| 085552 | Несчастливый |
| 213498 | Несчастливый |
| 509087 | Несчастливый |
| 086680 | Счастливый |
| 139391 | Счастливый |
| 082307 | Счастливый |
| 194617 | Счастливый |
| 095086 | Счастливый |
| 165192 | Счастливый |
| 093651 | Счастливый |
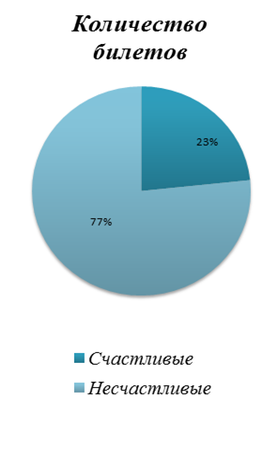
Результаты исследования
Вычислим вероятность выпадения счастливого билета для первого и второго месяцев.
Первый месяц: P(A)=4/30≈0,13
Второй месяц: P(A)=7/30≈0,23
Вероятность выпадения счастливого билета и в том, и в другом случае относительно не велика. Неудивительно, так как согласно статистике в среднем на 18 проездных билетов приходится 1 счастливый. В нашем же случае вероятность выпадения счастливого билета оказалась в разы выше.
Вывод исследования
Из полученных значений вероятности выпадения счастливого билета за каждый из двух месяцев можно сделать следующий вывод: вероятность того, что попадется счастливый билет, непостоянна.
Заключение
Непостоянность вероятности обуславливается различными факторами: время года, количество праздников и рабочих дней за месяц, погода. От этого зависит количество пассажиров в автобусе, а значит и вероятность выпадения счастливого билета.
Кроме того, данный шанс относителен и непостоянен, поэтому нельзя сказать наверняка выпадет ли Вам в тот или иной месяц заветный счастливый билет.
Я нашла один из способов применения теории вероятностей в жизни, посчитала вероятность выпадения счастливого билета, а так же исследовала её зависимость от внешних факторов. Цель достигнута. Результатом довольна.
Источники информации
1. Википедия. Теория вероятности
2. Википедия. Счастливый билет



















