Проектная работа ученицы 9 “Б” класса Барбенковой Дарьи "“Математика в распространённых профессиях”

Муниципальное бюджетное общеобразовательное учреждение

«Средняя образовательная школа №7»

г. Сафоново Смоленской области

Тема проекта

“Математика в распространённых профессиях”

Работа ученицы 9 “Б” класса

Барбенковой Дарьи Александровны.

Руководитель проекта

Архипова Елена Сергеевна.

Сафоново
2022

Содержание проекта.

1. Паспорт проекта.

2. Содержание работы:

А) Вступление.

Б) Бухгалтер.

В) Инженер.

Г) Врач.
Д) Кассир.

1. Ответ на основной вопрос (заключение).

2. Источники.

1. Паспорт проекта.

Название проекта:Математика в распространённых профессиях.

Руководитель проекта: Архипова Елена Сергеевна.

Автор проекта:Барбенкова Дарья Александровна.

Учебная дисциплина: математика.

Тип проекта: реферативный, практико-ориентированный.

Цель работы: узнать профессии, где используется математика.

Задачи работы: 1. Доказательство потребности изучения математики. 2. Изучение профессий, где используется эта наука. 3. Изучение математический решений в той или иной профессии. 4. Сбор материала и его подготовка.

Вопрос проекта: Какие есть распространенные профессии, связанные с математикой?

Актуальность проекта: Практическая ценность работы заключается в том, что она показывает необходимость изучения математики в школе для овладения будущей профессией, и она дает возможность привить интерес учеников к предмету «Математика».

Краткое содержание проекта: Творческая работа показывает необходимость изучения математики в школе для овладения будущей профессией, и дает возможность привить интерес учеников к предмету «Математика». Также в проекте рассказывается о профессиях: бухгалтер, инженер, врач,кассир более подробно, что возможно поможет с выбором будущей работы.

2. Содержание работы.

Вступление.

Матема́тика (др.-греч. μᾰθημᾰτικά

Без знания основных математических законов и умения ими пользоваться в современном мире становится очень трудно обучаться практически любым профессиям. С цифрами и операциями с ними имеют дело не только финансисты и бухгалтера. Астроном не сможет определить без таких знаний расстояние до звезды и наилучшее время наблюдения за ней, а молекулярный биолог — понять, как бороться с генной мутацией. Инженер не сконструирует рабочую систему сигнализации или видеонаблюдения, а программист не найдет подход к операционной системе. Многие из этих и других профессий без математики просто не существуют.

Математика в настоящее время перестала быть предметом занятий только научной элиты; теперь занятия математикой привлекают к себе всё большее число одарённых людей. Значительно расширились область математических исследований и применения математического аппарата. Приложения математических методов проникают далеко за пределы собственно математики: в физику, новые отрасли техники, биологию, в экономику и другие социальные науки; без строгой математической логики невозможна работа юриста или менеджера. Информационно – компьютерные технологии способствовали появлению новых областей научных исследований, имеющих, несомненно, чрезвычайно огромное значение как для самой математики, так и для всех наук, непосредственно связанных с ней.

Математика в нашей жизни присутствует не только в процессе освоения профессии и реализации полученных знаний. Так или иначе мы используем царицу наук практически в каждый момент времени. Именно поэтому математике начинают обучать достаточно рано. Решая простые и сложные задачи, ребенок не просто учится складывать, вычитать и умножать. Он медленно, с азов постигает устройство современного мира. Для жизни в нынешнем информационном обществе важным является формирование математического стиля мышления, проявляющегося в умении применять индукцию и дедукцию, обобщение и конкретизацию, анализ и синтез, классификацию и систематизацию, абстрагирование и аналогию. Для того чтобы уверенно чувствовать себя в современном мире, человек должен уметь проанализировать возникающую проблему, учесть все ее аспекты и сделать правильный выбор. Занятия математикой не столько самоцель, сколько средство к углублённому изучению теории и вместе с тем средство развития мышления, путь к осознанию окружающей действительности, тропинка к пониманию мира.

Математика играет важную роль в естественнонаучных, инженерно-технических и гуманитарных исследованиях. Причина проникновения математики в различные отрасли знаний заключается в том, что она предлагает весьма четкие модели для изучения окружающей действительности в отличие от менее общих и более расплывчатых моделей, предлагаемых другими науками. Без современной математики с ее развитым логическим и вычислительным аппаратом был бы невозможен прогресс в различных областях человеческой деятельности.

В биологических науках математический метод играет более подчинённую роль. В ещё большей степени, чем в биологии, математический метод уступает своё место непосредственному анализу явлений во всей их конкретной сложности в социальных и гуманитарных науках. Применение математического метода в биологических, социальных и гуманитарных науках осуществляется главным образом через информационно-компьютерные технологии. Существенным остаётся значение математики для социальных дисциплин в форме подсобной науки — математической статистики.

На примере ряда физических теорий можно наблюдать способность математического метода охватывать и самый процесс перехода познания действительности с одной ступени на следующую. Почти не существует области физики, не требующей употребления весьма развитого математического аппарата, но часто основная трудность исследования заключается не в развитии математической теории, а в выборе предпосылок для математической обработки и в истолковании результатов, полученных математическим путём. Американский исследователь Ф. Дайсон пишет: "Математика для физики - это не только инструмент, с помощью которого она может количественно описать явление, но и главный источник представлений и принципов, на основе которых зарождаются новые теории".

Прямые связи математики с техникой имеют характер применения уже созданных математических теорий к техническим проблемам. Создание метода наименьших квадратов связано с геодезическими работами; изучение многих новых типов дифференциальных уравнений в частных производных было начато с решения технических проблем; операторные методы решения дифференциальных уравнений были развиты в связи с электротехникой. Из запросов связи возник новый раздел теории вероятностей — теория информации. Задачи синтеза управляющих систем привели к развитию новых разделов математической логики. Наряду с нуждами астрономии решающую роль в развитии методов приближённого решения дифференциальных уравнений играли технические задачи. Целиком на технической почве были созданы многие методы приближённого решения дифференциальных уравнений в частных производных и интегральных уравнений. Задача быстрого фактического получения численных решений приобретает большую остроту с усложнением технических проблем. В связи с возможностями, которые открыли компьютеры для решения практических задач, всё большее значение приобретают численные методы. Высокий уровень теоретической математики дал возможность быстро развить методы вычислительной математики. Вычислительная математика сыграла большую роль в решении ряда крупнейших практических проблем, включая проблему использования атомной энергии и космические исследования.

Выдающийся учёный Н. Винер – в 1945–1947 заинтересовался системами с обратной связью и проблемами передачи, хранения и переработки информации. Новую науку – общую теорию управления и связи – он назвал кибернетикой. В своей книге, подводившей итог жизни, и названной «Я – математик» Винер сказал: «Высшее назначение математики состоит в том, чтобы находить скрытый порядок в хаосе, который нас окружает». Современные создатели компьютерных программ отчётливо осознают, что без знания математического аппарата их работа невозможна. Опрос программистов, проведённый на сайте CyberForum.ruпоказал, что подавляющее большинство (91 %) программистов применяют или применяли математику в программировании.

Из этого следует, что математика - удивительная наука. При всей своей искусственности она умудряется описывать каждый процесс, происходящий с нами и вокруг нас. При помощи математики можно вывести правила, по которым происходят обменные процессы в нашем организме, описать сокращение мышц и многое, многое другое. Также она всегда направлена на некий результат или же на доказательство того, что результата добиться невозможно. Иными словами, все в математике подчинено алгоритмам. Алгоритм - это заданная последовательность действий, направленная на достижение определенной цели. Похоже на работу, не так ли? Цели одни и те же. Конечно, напрямую сложно найти области, в которых используется чистая, не прикладная физика и математика. Профессии такие очень узки по специфике, мы же рассмотрим ниже общие варианты. Необходимо понимать, что перечень не ограничивается тем, что мы расскажем, так как любая человеческая деятельность, какой бы творческой и абстрактной она ни была, в основе своей содержит самое простое - механизм действия. То, что можно описать и разложить пошагово на математические формулы. Математика - скелет любого процесса

Я хочу выделить 5 профессий, где встречается математика и подробнее пройтись по ним. Эти профессии – бухгалтер, медик, инженер и кассир.

Бухгалтер.

Так как моя мама работает главным бухгалтером, описать эту профессию будет достаточно просто.

Бухгалтер – это специалист, ведущий финансовый учет в организации в соответствии с действующим законодательством. Работа бухгалтера заключается в выполнении следующих функций: ведение бухгалтерского и налогового учета; подготовка периодической отчетности и ее предоставление в налоговые органы и государственные фонды; начисление заработной платы сотрудникам организации; ведение кассы и сопутствующей документации.

Математика в профессии бухгалтера является неотъемлемой частью бухгалтерского учёта. Бухгалтерский учёт основан на простых и сложных математических и алгебраических вычислениях.

Математика способствует решению бухгалтерских, статистических, общеэкономических задач. Она является совокупным, взаимодействующим звеном в бухгалтерском учёте на каждом историческом этапе развития учёта. Значимость математики связывалась с их природой и функциями и указывала на необходимость понимания и изучения.

Бухгалтерский учёт формулировался в результате дифференциации точных и общественных наук. Экономический анализ комплексно, системно использует фактические данные, прибегая к приему и способам исследования статистики и математики. Бухгалтер при помощи математических данных, составив отчёт, определяет каковосостояние хозяйственных средств и источников их формирования. Использование в аналитических исследованиях математических методов, значительно обогатило бухгалтерский учёт и экономический анализ.

Выделим 3 задачи бухгалтера, где используется математика.

1. Учёт амортизации основных средств.

2. Учёт труда и заработной платы.

3.При учёте товарно-материальных ценностей (ТМЦ).

1. Учёт амортизации основных средств.

При расчёте месячной суммы амортизации используют нормы амортизации основных средств, определённые в процентах от первоначальной стоимости основных средств.

Сумма амортизации за месяц = Первоначальная стоимость основных средств × месячная норма амортизации (в %)

Рассчитанные суммы амортизации по всем объектам основных средств предприятия позволяют правильно рассчитать стоимостной показатель потери объектами основных средств своих физических и технико-экономических качеств.

Первоначальная стоимость объекта основных средств 4000000. Годовая норма амортизации объекта 8,2%.

Сумма амортизации объекта основных средств за месяц = 4000000 × (8,2%:12) = 4000000 × 0,68% = 27200

2. Учёт труда и заработной платы.

При расчёте суммы удержаний по исполнительным листам (алиментов) применяются установленные проценты удержаний:

-25%- на одного ребёнка

-33%- на двоих детей

-50% - на троих и более детей

Для расчёта суммы алиментов из суммы начисленной оплаты труда вычитают сумму налога на доход физических лиц (НДФЛ) и применяют установленный процент.

Производственная ситуация

Оклад работника 19000 (январь 2010 года). В бухгалтерию пришёл исполнительный лист на уплату алиментов на одного ребёнка.

Расчёт суммы алиментов производится следующим образом:

19000 – 400 – 1000 (стандартные налоговые вычеты) × 25% = 4400

Примечание: 400; 1000 - стандартные налоговые вычеты по НДФЛ, установленные налоговым кодексом РФ.

3. При учёте товарно-материальных ценностей (ТМЦ)

При списании транспортно-заготовительных расходов (ТЗР) рассчитывают средний процент ТЗР.

Средний процент ТЗР = (Сумма ТЗР на начало месяца + сумма ТЗР по поступившим материалам: Стоимость материалов на начало месяца + стоимость поступивших материалов) × 100 (Стоимость материалов должна отражаться по учётным ценам)

Полученный расчётным путём средний процент ТЗР умножают на стоимость материалов, отпущенных на производственные цели, что позволяет рассчитать суммы ТЗР и влияет на формирование фактической производственной себестоимости готовой продукции.

Фактическая себестоимость материалов на начало периода 45000, в том числе ТЗР 2450. Стоимость материалов по учётным ценам, поступившим в течение месяца 120000, сумма ТЗР по поступившим материалам 40000.

Средний процент ТЗР = (2450+40000:(45000-2450) + 120000) × 100 = 26%

Инженер.

Математика -основа инженерного дела. Необходимо производить расчеты материалов, расчеты параметров работы, всевозможных инженерных узлов.

Какие разделы математики нужны инженеру?

Инициировали опрос среди заинтересованных специалистов-инженеров, и получили вот такие данные:

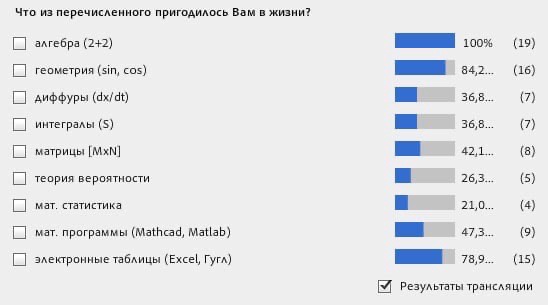
Действительно: далеко не всё, что студенты изучают в рамках вузовской высшей математики, матстатистики, математического моделирования активно используется потом в практической деятельности.

Виталий Артемов, специалист по расчету и моделированию строительных конструкций:

“В своей инженерной работе я, конечно же, регулярно использую алгебру. Именно ту школьную алгебру, с которой всё начинается — дроби, простейшие математические действия. Ну, потому что многое из того, что нужно инженеру для работы, уже доказано, определено, посчитано и представлено в виде таблиц или готовых формул (например, в нормах проектирования). Остается только подставить в эти формулы корректные значения.

Иногда бывает нужно вспомнить что-то из векторной геометрии. Но, по большому счету, с прикладной математикой — как в том фильме: “всё уже украдено до вас.”

Знания, например, по дифференциальному исчислению и интегрированию мне понадобились только в научной деятельности. После завершения работы над диссертацией к этим вопросам больше не возвращался”

Где в инженерии применяется математика?

Понадобится ли специалисту инженерной сферы доказывать теоремы или иметь дело с комплексными числами в своей повседневной работе? Вряд ли…

А вот векторный анализ очень может пригодиться. Силы, действующие в элементах строительных и машиностроительных конструкций, как правило, представляются векторами. Будущему инженеру полезно научиться их складывать, понимать разницу между скалярной величиной и векторной.

Кстати, на курсе теоретической механики этим вопросам уделено несколько занятий в разделе статики:

Занятие 1. Вектора. Сложение и вычитание векторов. Проекция и компоненты вектора. Длина и направление вектора. Единичный вектор направления. Выражение силы в векторной форме

Занятие 2. Скалярное произведение векторов. Пример расчета компонента силы в стержнях пространственной системы. Векторное произведение векторов. Правило правой руки

Инженер должен понимать, что такое максимум и минимум функции. Матричные исчисления также играют немаловажную роль в инженерной деятельности. Собственно, метод конечных элементов и программы, связанные с симуляциями, основаны на матричных вычислениях. Необходимо понимать, как матрицы складывать, преобразовать и т. п.

Специалисту, который плотно работает с расчетами и часто вынужден анализировать полученную модель, может, и придется копнуть глубже, так как результаты, выдаваемые инженерной программой, нередко требуют дальнейшего анализа, обработки. Рядовому инженеру-конструктору эти знания особо не требуются. Теория вероятностей находит свое применение в работе со стандартами (Еврокодами, например).

Также. Базовые дисциплины, которые изучают инженеры-технологи в университетах:

•общая физика и специальные разделы физики, высшая математика, теория вероятности и математическая статистика, теоретические основы электротехники и электроники, теория информации, теория автоматического управления, программирование микропроцессорных устройств, алгоритмические языки высокого уровня.

Все знания, необходимые инженеру-технологу, базируются на математике.

Врач.

Медицина не существовала бы без математики. Базовые математические знания необходимы каждому врачу. Доктору нужно знать и уметь применять на практике такие математические знания как: проценты, анализ статистических данных, графики, таблица умножения, пропорции, уметь работать с различными единицами измерения, осуществлять точные расчеты, производить расчеты по математическим формулам. Математика дает точность медицине, а без точности нельзя ждать благоприятный результат.

Математика применяется в сестринском деле. В этой области врачам необходимо уметь находить цену деления, рассчитывать пропорции, нужно уметь работать с различными единицами измерения. Чтобы сделать укол, нужно правильно выбрать соотношение лекарства, обезболивающего и водного раствора.

В фармакологии важны точные математические расчеты, на основе которых будет создана дозировка лекарства. Фармакологи должны правильно подбирать химические и биологические вещества для лекарства в нужной пропорции.

Огромную роль математика играет в педиатрии. Новорожденные не умеют говорить и, поэтому их состояние здоровья, помогает определить математическая статистика, также педиатры используют для сравнения частных случаев средние показатели, а это есть такие математические понятия как среднее арифметическое и мода.

Терапевты работают с математическими формулами, статистическими данными, с пропорциями. Действия терапевтов координируют процесс лечения больного. Мы хотим разобрать одну терапевтическую формулу, которая напрямую зависит от математики.

ИМТ= вес (измеряется в килограммах) / рост2 (в метрах)

ИМТ - расшифровывается как индекс массы тела. Данный показатель оценивает массу тела, она может быть в недостатке, нормальной или избыточной. При отклонениях массы от нормы, врач может назначить обследование, чтобы выявить заболевание, если оно таковое имеется.

Математические методы в своей работе использует врач - ортопед. Чтобы определить такое заболевание как сколиоз врач должен знать симметрию тела.

В вирусологии учитываются такие показатель как геометрическая прогрессия, статистика, теории вероятности. Очень важно знать, как быстро размножаются те или иные вирусы, уметь прогнозировать возможные эпидемии.

В гастроэнтерологии для диагностики заболеваний выполняют эндоскопические исследования, в настоящее время с помощью высококачественных камер удается получить изображение желудка, кишечника. Проводить данное исследование удается благодаря математической системе координат. Также в гастроэнтерологии важны точные математические данные, ведь любое увеличение органа желудочно-кишечного тракта, может говорить о патологии

Офтальмология - область медицины, изучающая глаз, его анатомию, физиологию и болезни, а также разрабатывающая методы лечения и профилактики глазных болезней.

Офтальмология как наука не может существовать без математики. Большинство офтальмологических исследований базируются на математических измерениях и формулах.

Примеры:

1. В офтальмологии существует формула Снеленна-Дондерса, которая служит для определения остроты зрения. Она выглядит так: V=d/D.

V-острота зрения

d- расстояние, с которого видит больной

D-расстояние, с которого должен видеть глаз с нормальной остротой зрения знаки данного ряда на таблице.

К примеру, если d=3 метрам, а D= 6 метрам, то острота зрения V=3м./6м.=0.5

Эта простая формула помогает определить такие заболевания как близорукость и дальнозоркость.

Другим направлением математики в офтальмологии является микрохирургия глаза. Благодаря точным математическим расчетам удается улучшить и восстановить зрение. Примерами микрохирургических операций глаз являются лазерная коррекция зрения, операция по лечению катаракты, глаукомы, пересадка роговицы.

Разберем лазерную коррекцию зрения. Операция лазерная коррекция направлена на улучшение зрения. Лазер изменяет форму роговицы по заданным параметрам. Здесь и применяются точные математические расчеты.

При изготовлении очков, производятся точные расчеты расстояния между центрами зрачков в миллиметрах. Также важно знать и уметь пользоваться формулой нахождения диоптрии. Диоптрия - оптическая сила линзы.

D=1\F, где D-оптическая сила линзы

Кардиология – обширный раздел медицины, занимающийся изучением сердечно – сосудистой системы человека: строения и развития сердца и сосудов, их функций, а также заболеваний, включая изучение причин их возникновения, механизмов развития, клинических проявлений, вопросов диагностики, а также разработку эффективных методов их лечения и профилактики. Кроме того, в сфере ведения кардиологии лежат проблемы медицинской реабилитации лиц с поражениями сердечно - сосудистой системы, которые занимают второе место по смерти человека.

В кардиологии математика помогает диагностировать патологии сердца. Зачастую своевременная диагностика сердечно – сосудистых заболеваний приводит к благоприятному исходу. Широко использованным методом диагностики является Электрокардиография или в сокращение ЭКГ.

Во время процедуры снятия ЭКГ электроды, устанавливаемые на определенные точки, улавливают возникающие в сердце электроимпульсы и передают их через гальванометр в регистрирующее устройство. Далее самописцы отображают полученную информацию на движущейся с определенной скоростью бумаге в виде графиков, отображающих функционирование разных отделов сердца. Графики ЭКГ записываются на миллиметровой бумаге в виде линий из зубцов разных размеров. Эти размеры зависят от того, какой по силе сигнал подается тем или иным отделом сердца.

После проведения диагностики врач расшифровывает графики ЭКГ, здесь и пригождаются математические знания. При расшифровке графика кардиограммы врачи должны иметь базовые знания о функциях Y=SinXи Y=CosX, так как на этих функциях основаны кардиограммы.

Даже общий анализ крови невозможно сделать без знаний математики. Многие показатели ОАК измеряются в процентах, а также нужно провести точные математические расчеты. Благодаря общему анализу крови можно выявить ряд заболеваний и назначить правильное лечение.

На основе математической системы координат (ось X, Y, Z) удалось создать технику, которая диагностирует различные заболевания. Яркими примерами такой диагностики является рентгенография, компьютерная томография, УЗИ. На примере рентгенографии можно рассмотреть взаимосвязь математической системы координат и этого метода исследования.

Лучи просвечивают тело исследуемого, отображая изображение органов, это изображение проецируется на мониторе, а, как известно проецирование, это и есть математическая система координат. С помощью рентгенографии можно выявить такие заболевания как пневмония, туберкулез, рак легких.

В чём проявляется важность математики в аптеке?

1 . Работа с клиентом:

- суммирование стоимости нескольких товаров

- выдача сдачи

- вычитание % скидки, если таковая имеется.

Да, вы можете сказать, что сейчас все вычислительные операции выполняет компьютер, и будете правы, но что, если он сломался, а работать-то надо.

2. Приём товара, наценка товара.

Иногда требуется проверять данные, занесённые в компьютер, ведь машины тоже ошибаются.

3. Составление отчётов о работе аптеки: кол-во заказанного товара, кол-во реализованного товара, средний чек и т.п.

Мы решили узнать про статистику аптеки в зимней период, нам были рассказаны следующие статистические данные: увеличение спроса на противовирусные препараты, витамины, антибактериальные препараты, лекарства от кашля, насморка. Вся данная статистика, находит себе объяснение в том, что с наступлением зимнего сезона увеличивается количество заболевших.

Решение задач занимает в математическом образовании важное место, так как это один из приемов обучения, посредством которого обеспечивается более глубокое и полное усвоение учебного материала по математике. Умение решать задачи, является одним из показателей уровня развития математического мышления будущего абитуриента, глубины усвоения ими учебного материала.

Процесс постановки врачом правильного диагноза можно сравнить с решением математического уравнения с одним, а часто с несколькими неизвестными. Как и в математике, успех решения этой задачи зависит от знаний врача и умения логически мыслить, применить правила и умения на практике. Каждый человек в своей профессиональной деятельности встречается с разными типами текстовых задач. Приведем для примера некоторые из них.

Примеры задачи на ОГЭ:

Задача 16. Одна таблетка лекарства весит 20 мг и содержит 5% активного вещества. Ребёнку в возрасте до 6 месяцев врач прописывает 1,4 мг активного вещества на каждый килограмм веса в сутки. Сколько таблеток этого лекарства следует дать ребёнку в возрасте четырёх месяцев и весом 5 кг в течение суток?

Решение.В одной таблетке лекарства содержится 20 * 0,05 = 1 мг активного вещества. Суточная норма активного вещества для ребенка весом 5 кг составит: 1,4 * 5 = 7 мг. Тем самым, ребенку следует дать 7 таблеток.

Ответ: 7.

Кассир.

Продавец, контролёр-кассир требует понимания постоянного процентного движения цен на рынке. Тесной связи с покупателями. Поэтому в этой профессии важны задачи на проценты и количества продаваемого продукта или любого другого материала.

В процессе хозяйственной деятельности торговые предприятия используют абсолютные и относительные величины. При определении качественных показателей возникает необходимость вычисления отношения между различными числами для их сравнения. Выполнение плана товарооборота в целом, по товарным группам или товарному ассортименту, подсчет торговой скидки или накидки, снижение розничных цен или уровня издержек обращения. С понятием «проценты» повседневно встречаются все работники торговли, начиная с продавца и контролера-кассира, которые должны четко представлять, как ими оперировать.

Нахождение наращенного числа, т.е. стоимости товара после наценки вычисляется по специальной формуле, которая применяется в торговле.

Примеры задач:

Нахождение наращенного числа по процентной таксе и процентной сумме. Чтобы определить наращенное число по процентной таксе и процентной сумме, нужно процентную сумму разделить на процентную таксу, а полученное частное умножить на сумму процентной таксы и 100%:

Нч =П: Т*(Т + 100).

Сумма наценки на стоимость товара составила 600 рублей, что составляет 5%. Определите стоимость товара после наценки.

Запишем сокращенное условие задачи:

Дано: П = 600 р.,

Т=5%

Найти: Н.=?

Подставим в формулу, приведенную выше, исходные данные:

Нч = 600 : 5% х (5% + 100%) = 12600р.

Также есть формулы для вычисления плана товарооборота, определение процента недовыполнения плана.

Для выполнения операций: приемка товаров, хранение, подготовка к продаже, выкладка, показ, продажа важно расположить товар в определенном наборе мебели, используемых соответственно для торгового зала и подсобных помещений

Рассматривая примеры мебели мы говорим о расположении прямых и плоскостей в пространстве, находим подтверждение аксиом и теорем стереометрии.

Учащиеся выполняют операции приемка товаров, подготовка к продаже, выкладка, показ, продажа в лаборатории школа-магазин и видят, что сам товар или его упаковка имеют определенную геометрическую форму Т.е. предметы для продажи имеет форму различных многогранников или тел вращения, которые мы изучаем на уроках математики. Для практических работ учащиеся сами выбирают некоторый товар или его упаковку и на уроках вычисляем площадь полной поверхности и объем данной геометрической фигуры или тела вращения.

Продавец рекламирует имеющийся товар.

Заключение.

Работая над этим проектом, я поняла, что математика пригодится нам не только в профессии, а практически, во всей нашей будущей жизни.

В современном мире математика нужна, пожалуй, как никогда раньше. Ведь нас со всех сторон окружают компьютеры, цифры. Мир входит в новую эпоху - эпоху цифр. Мы неразрывно связаны с математикой.Без математики не движется прогресс, без неё мы не смогли бы сделать даже маленькое дело. Математика — наука, как прошлого, так и будущего. Не каждый может и должен стать математиком, но математика в жизни нужна будет каждому.

Математические знания и навыки необходимы практически во всех профессиях, прежде всего, конечно, в тех, что связаны с естественными науками, техникой и экономией

Следовательно, математика и математическое образование нужны для подготовки к будущей профессии. Для этого необходимы знания из алгебры, математического анализа, теории вероятности и статистики.

На самом деле математику не зря называют царицей наук. В жизни человека она занимает особое место и важна для всех профессий, ведь существуют многочисленные профессии, связанные с математикой, о которых я получше узнала для этого проекта. Надеюсь, будет полезно кому-то ещё.

Источники:

1. https://fb.ru/article/218171/rol-matematiki-v-jizni-cheloveka-dlya-chego-nujna-matematika

2. https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0

3. https://nsportal.ru/shkola/mezhdistsiplinarnoe-obobshchenie/library/2013/12/12/rol-matematiki-v-sovremennom-mire

4. https://fb.ru/article/189460/matematika-v-professiyah-v-kakih-professiyah-nujna-matematika

5. https://edu.dystlab.com/index.php/ru/blog/260-why-engineer-need-math?ysclid=l12400pyef

6. https://school-science.ru/8/7/43108

7. https://infourok.ru/metodicheskaya-razrabotka-po-matematike-na-temu-matematika-v-professii-prodavec-kontrolerkassir-2251149.html

8. Смирнов А.И. Мир профессий М., 1987г.

9. Сборник задач по финансовой грамотности.

10. Люди, работающие на данных в пример профессиях.

18