МБОУ «СШ №1»
Вписанный четырехугольник с перпендикулярными диагоналями.
Выполнила учащиеся 8 класса :
Лисина Олеся
Проверила учитель математики:
Шаранцова Л.А.
Касимов,2019-2020 уч.год
Четырехугольник с перпендикулярными диагоналями.
Теорема:
Диагонали четырехугольника перпендикулярны тогда и только тогда,когда равны суммы квадратов его противолежащих сторон.
Доказательство:
Пусть точка Р — точка пересечения диагоналей четырехугольника.
Введем обозначения длин сторон(рис 1а)








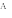
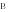
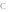
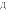

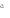
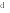

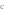 1)Применяя теорему Пифагора в каждом из четырех прямоугольных треугольников (рис 1а),получим,что АР2 + BP2=a2;СР2+ДР2=с2;ВР2+СР2=b2;АР2+ДР2=d2.
1)Применяя теорему Пифагора в каждом из четырех прямоугольных треугольников (рис 1а),получим,что АР2 + BP2=a2;СР2+ДР2=с2;ВР2+СР2=b2;АР2+ДР2=d2.
Следовательно,a2+c2=b2+d2.
2)Признак.Пусть диагонали четырехугольника
не перпендикулярны(см.рис.1б)
Проведем перпендикулярны BK и DM
к диагонали АС.Тогда a2-b2=
AK2-CK2=
(AK+СК)(АК-CК)=АС(AК-CК) и
d2-c2=АМ2-СМ2 =(АМ+СМ)(АМ-СМ)=
АС(АМ-СМ).Так как a2+c2=b2+d 2
a2-b2=d2-c2,то AK-CK=AM-CM
AK+CM=AM+CK.
Это равенство выполняется только
в случае,если точки К и М совпадают,то
есть диагонали АС и ВД этого четырехугольника
также перпендикулярны.
Доказательство аналогично для невыпуклого
 четырехугольника.
четырехугольника.

![]()





![]()
![]()
![]()
![]()








Свойства вписанного в окружность четырехугольника со взаимно перпендикулярными диагоналями.
Вписанный в окружность четырехугольник со взаимно перпендикулярными диагоналями обладает рядом замечательных свойств.
Приведем несколько задач.

-
Суммы градусных мер дуг,стягиваваемых противоположными сторонами четырехугольника,равны и составляют 1800.



 Доказательство.
Доказательство.
 По условию АС ВД,значит, треугольник РДС
По условию АС ВД,значит, треугольник РДС
прямоугольный(рис 2) и РСД+ РДС=90º.


![]()
![]() По свойству вписанных углов получим,что
По свойству вписанных углов получим,что



 дуги АmД + BnC =180º. Аналогично доказываем,
дуги АmД + BnC =180º. Аналогично доказываем,

 что дуги ApB+DkC=180º.
что дуги ApB+DkC=180º.


2)Сумма квадратов противоположных сторон четырехугольника равна квадрату диаметра описанной около четырехугольника окружность.
Доказательство.
Проведем диаметр описанной окружности через одну из вершин четырехугольника,например диаметр DM(рис 3), и соединим точку М с вершинами А и С.Поскольку дуги ͜ DmA+
͜ BnC=180º(см задачу 1) и ͜ DmA + ͜ AlM=180º,то дуги AlM=BnC,а отсюда АМ=ВС.

 Из прямоугольного треугольника МАD(MAD =90º) имеем AD2+AM2=DM2,то есть AD2+BC2=4R2.
Из прямоугольного треугольника МАD(MAD =90º) имеем AD2+AM2=DM2,то есть AD2+BC2=4R2.







![]()











-
Площадь четырехугольника равна полусумме произведений противоположных сторон.
Доказательство(рис 3).
SАВСД =SАМСД=S∆АМД+S∆ДМС=1/2(AD∙AM+DC∙MC)=1/2(AD∙BC+DC∙AB).
К тому же выводу придем,применив теорему Птолемея:
AC∙BD=AD∙BC+AB∙DC.
Поскольку АС ┴ ВD,то S =1/2AC∙BD,а тогда S=1/2(AD∙BC+AB∙DC).
Теорема Птолемея
Если четырехугольникABCD вписан в окружность, то произведение его
диагоналей равно сумме произведений его противоположных сторон:
AC∙ BD = AB ∙CD + AD ∙BC
Проведем из точки B отрезок BE до пересечения с диагональю AC таким образом, чтобы CBE = ABD.  Углы BCЕ и BDA равны как вписанные, опирающиеся на одну и ту же дугу AB. Тогда
Углы BCЕ и BDA равны как вписанные, опирающиеся на одну и ту же дугу AB. Тогда треугольники ABD и СBЕ подобны (по двум углам). Отсюда следует, что и, следовательно, далее имеем:
треугольники ABD и СBЕ подобны (по двум углам). Отсюда следует, что и, следовательно, далее имеем:
AD . BC = BD . CE. (2)
 Подобны также треугольники ABE и DBC, так как ABE = DBC и BAE = BDC.
Подобны также треугольники ABE и DBC, так как ABE = DBC и BAE = BDC.
Отсюда следует, что и затем имеем:
AB . CD = BD .AE. (3)
Сложим соответственно левые и правые части равенств (2) и (3). Получим
AD . BC + AB . CD = BD . CE + BD . AE или
AD . BC + AB . CD = BD . (CE + AE) , то есть
AD . BC + AB . CD = BD . AC, что и требовалось.
Замечание. К этому же можно прийти, введя другие обозначения.
Если АВ = ВС = СD = DА = АС = ВD = , то выберем на диагонали АС точку Е так, чтобы угол СВЕ был равен .
Тогда треугольники СВЕ и DВА подобны.
Поэтому ЕС :
Из подобия треугольников АВЕ и DВС (углы АВЕ и DВС равны как равносоставленные) получаем АЕ :
Значит, ЕС = АЕ = АЕ + ЕС =АС,
отсюда
Теорема Птолемея доказана. ◄
(Справедлива и теорема, обратная теореме Птолемея).
4)Если вписанный четырехугольник имеет перпендикулярные диагонали,пересекающиеся в точке М,то прямая,проходящая через точку М и перпендикулярная одной из его сторон,делит противовоположную ей сторону пополам.






![]()
![]()











Формула Брахмагупты
р=(a+b+c+d)/2


 S= (p-a)(p-b)(p-c)(p-d)
S= (p-a)(p-b)(p-c)(p-d)
Упражнения и задачи для самостоятельного решения
1 Докажите, что если четырехугольник АВСD с перпендикулярным диагоналям вписан в
окружность с центром О, то АОВ + СОD = 180.
2 Докажите, что во вписанном четырехугольнике с перпендикулярными диагоналями
расстояние от центра описанной окружности до стороны равно половине противолежащей
стороны.
3)Диагонали четырехугольника АВСD,вписанного в окружность радиуса R,
перпендикулярны и пересекаются в точке Р. а) Докажите, что AP2 + BP2+ CP2 + DP2 = 4R2.
б) Найдите сумму квадратов сторон четырехугольника АВСD.













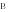
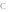
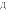


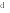

 1)Применяя теорему Пифагора в каждом из четырех прямоугольных треугольников (рис 1а),получим,что АР2 + BP2=a2;СР2+ДР2=с2;ВР2+СР2=b2;АР2+ДР2=d2.
1)Применяя теорему Пифагора в каждом из четырех прямоугольных треугольников (рис 1а),получим,что АР2 + BP2=a2;СР2+ДР2=с2;ВР2+СР2=b2;АР2+ДР2=d2. четырехугольника.
четырехугольника.