Проектно- исследовательская работа Тема «Неевклидова геометрия»

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

КИСЕЛЕВСКОГО ГОРОДСКОГО ОКРУГА

«СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 27»

Проектно- исследовательская работа

Тема «Неевклидова геометрия»

Выполнил:

Демидов Никита Алексеевич,
учащийся 9 «А» класса

МБОУ СОШ № 27

Г. Киселевск

Руководитель: Бельц Марина Николаевна,

учитель математики.

2022 год

Содержание:

Введение………………………………………………………….	3
Происхождение геометрии Лобачевского……………………..	5
Три модели геометрии Лобачевского…………………………..	7
1) Модель Пуанкаре………………………………………..........	7
2) Модель Клейна………………………………………………	8
3) Интерпретация Бельтрами…………………………………...	8
Свойства и понятия……………………………………………...	9
Практическое применение геометрии Лобачевского…………	11
Вывод……………………………………………………………	12
Список источников………………………………………………	13

Цель:

Ознакомление с основным содержанием геометрии Лобачевского

Задачи:

1. изучить аксиому параллельности геометрии Лобачевского

2. рассмотреть три модели геометрии Лобачевского

3. выполнить сравнительный анализ двух геометрий

1. Введение:

Геометрия – это одна из древнейших наук. Исследовать различные пространственные формы издавна побуждало людей их практическая деятельность. Древнегреческий ученый Эдем Родосский в IV веке до нашей эры писал: «Геометрия была открыта египтянами, и возникла при измерении Земли. Это измерение было им необходимо вследствие разлития реки Нил, постоянно смывавшей границы. Нет ничего удивительного, что эта наука, как и другие, возникла из потребности человека».

Многие первоначальные геометрические сведения получили также шумеро-вавилонские, китайские и другие ученые древнейших времен. Устанавливались они сначала только опытным путем, без логических доказательств.

Как наука, геометрия впервые сформировалась в Древней Греции, когда геометрические закономерности и зависимости, найденные ранее опытным путем, были приведены в надлежащую систему и доказаны.

В III веке до нашей эры греческий ученый Евклид привел в систему известные ему геометрические сведения в большом сочинении «Начала». Эта книга более двух тысяч лет служила учебником геометрии во всем мире.

В своём проекте я хочу показать, что кроме геометрии, которую изучают в школе (Геометрии Евклида или употребительной геометрии), существует еще одна геометрия, геометрия Лобачевского. Эта геометрия существенно отличается от евклидовой, например, в ней утверждается, что через данную точку можно провести бесконечно много прямых, параллельных данной прямой, что сумма углов треугольника меньше 180 В геометрии Лобачевского не существует прямоугольников, подобных треугольников и так далее.

Я выбрал данную тему по нескольким причинам: теория геометрии Лобачевского помогает взглянуть по-другому на окружающий нас мир, это интересный, необычный и прогрессивный раздел современной геометрии, она дает материал для размышлений – в ней не все просто, не все ясно с первого взгляда, чтобы ее понять, нужно обладать фантазией и пространственным воображением. Ситуация с геометрией Лобачевского и геометрией Евклида во многом похожа на ситуацию с Теорией относительности Эйнштейна и классической физикой. Геометрия Лобачевского и ОТП Эйнштейна это прогрессивные взаимосвязанные теории, выполняющиеся на огромных величинах и расстояниях, и остающимися верными на приближениях к нулю. В пространственной модели ОТП используется не обычная евклидовая плоскость, а искривленное пространство, на котором верна теория Лобачевского.

Неевклидова геометрия появилась вследствие долгих попыток доказать V постулат Евклида, аксиому параллельности. Эта геометрия во многом удивительна, необычна и во многом не соответствует нашим привычным представлениям о реальном мире. Но в логическом отношении данная геометрия не уступает геометрии Евклида.

2.Происхождение Неевклидовой геометрии.

Среди аксиом Евклида была аксиома о параллельности прямых, а точнее, пятый постулат о параллельных линиях: если две прямые образуют с третьей по одну ее сторону внутренние углы, сумма которых меньше развернутого угла, то такие прямые пересекаются при достаточном продолжении с этой же стороны.

В современной формулировке она говорит о существовании не более одной прямой, проходящей через данную точку вне данной прямой и параллельной этой данной прямой.

Сложность формулировки пятого постулата породила мысль о возможной зависимости его от других постулатов, и потому возникали попытки вывести его из остальных предпосылок геометрии. Все попытки заканчивались неудачей. Были попытки доказательства от противного: прийти к противоречию, предполагая верным отрицание постулата. Однако и этот путь был безуспешным.

Оказалось то, что пятый постулат не зависит от предыдущих, а значит, его можно заменить на ему эквивалентный. И в начале XIX века, почти одновременно сразу у нескольких математиков: у К. Гаусса в Германии, у Я. Больяи в Венгрии и у Н. Лобачевского в России, возникла мысль о существовании геометрии, в которой верна аксиома, заменяющая пятый постулат: на плоскости через точку, не лежащую на данной прямой, проходят, по крайней мере, две прямые, не пересекающие данную.

В силу приоритета Н. Лобачевского, который первым выступил с этой идеей в 1826, и его вклада в развитие новой, отличной от евклидовой геометрии последняя была названа в его честь «геометрией Лобачевского».

Аксиоматика планиметрии Лобачевского отличается от аксиоматики планиметрии Евклида лишь одной аксиомой: аксиома параллельности заменяется на ее отрицание – аксиому параллельности Лобачевского:

Найдутся такая прямая a и такая не лежащая на ней точка A, что через A проходят по крайней мере две прямые, не пересекающие a.

Непротиворечивость системы аксиом доказывается представлением модели, в которой реализуются данные аксиомы.

3. Три модели геометрии Лобачевского.

Выделяют три различные модели геометрии Лобачевского:

1) Модель Пуанкаре

2) Модель Клейна

3) Отображение геометрии Лобачевского на псевдосфере (интерпретация Бельтрами)

Единой основой, прообразом всех трёх моделей плоскости Лобачевского будет служить прозрачная полусфера с нарисованными на ней полуокружностями, перпендикулярными её границе — экватору. Таким образом, если экватор полусферы лежит в горизонтальной плоскости, то окружности следует проводить в вертикальных плоскостях.

1) Модель Пуанкаре в круге

Модель Пуанкаре в круге можно получить, если полусферу поставить на стол полюсом, а точечный источник света поместить в противоположный, северный полюс сферы. Считая, что источник точечный, т. е. лучи от него расходятся по прямым в разные стороны, получается стереографическая проекция сферы (в нашем случае — полусферы) на плоскость. Стереографическая проекция сохраняет углы между линиями, а любые окружности на сфере переводит в окружности на плоскости. (Точнее, окружности, не проходящие через центр проекции, переходят в окружности на плоскости, а проходящие через него — в прямые.)

Э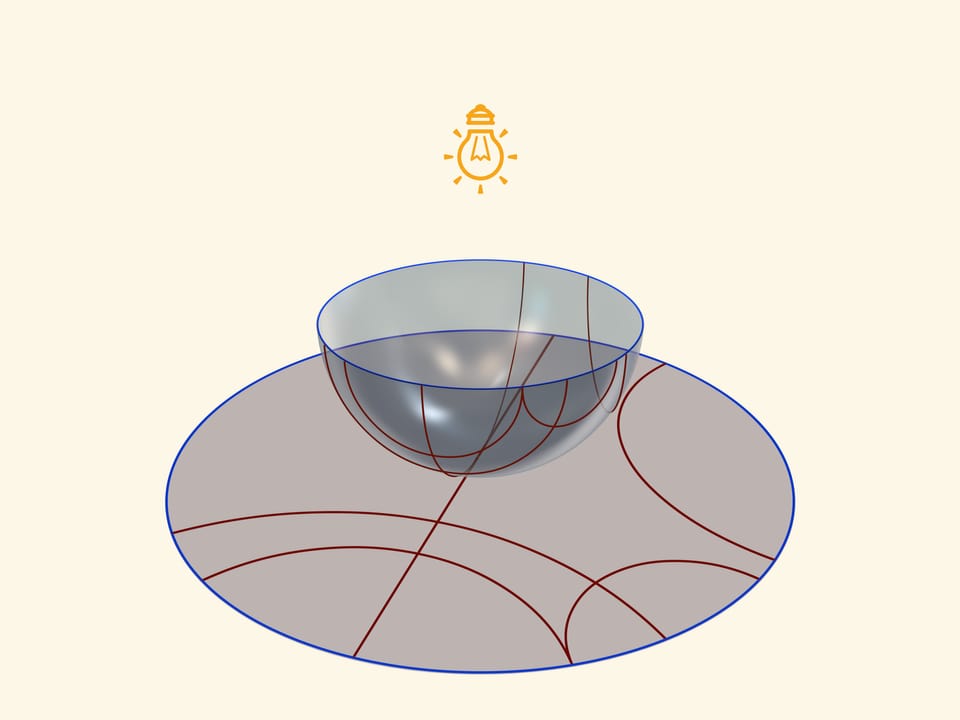 кватор полусферы переходит в абсолют плоскости Лобачевского (его точки не принадлежат ей), который является границей модели Пуанкаре в круге. Окружности на полусфере, перпендикулярные экватору, переходят в окружности на круге, перпендикулярные абсолюту. Это и есть «прямые» на плоскости Лобачевского.

2) Модель Кэли-Клейна в круге

М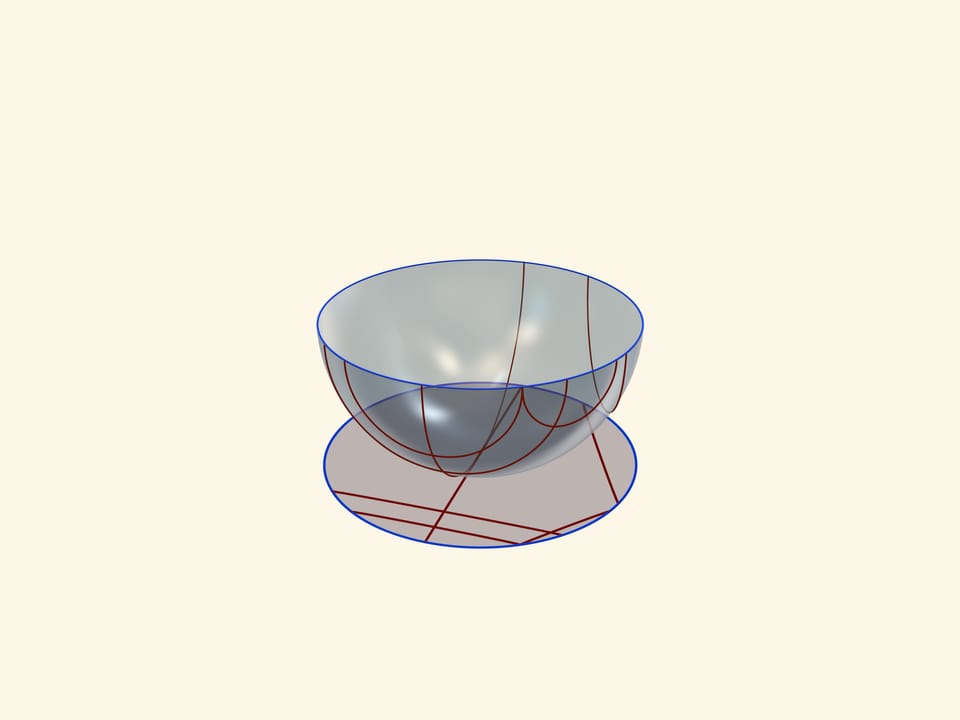 одель Бельтрами—Клейна в круге (проективная модель) получится, если при таком же положении полусферы источник света «угнать на бесконечность», т. е. освещать полусферу вертикальными параллельными лучами. Абсолютом будет проекция экватора, а прямыми плоскости Лобачевского — хорды круга.

3) Отображение геометрии Лобачевского на псевдосфере (интерпретация Бельтрами)

П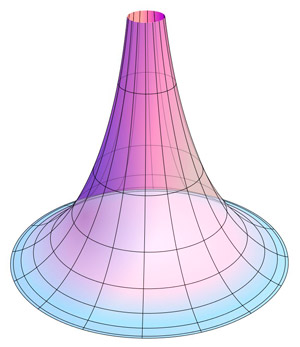 севдосфера — поверхность вращения кривой вокруг оси (нужно лишь представлять, что псевдосфера похожа на граммофонную трубу). Прямыми Лобачевского на этой поверхности являются геодезические, то есть линии кратчайшей длины, соединяющие две точки. Геодезическую можно получить, натянув по поверхности нить. Большая часть геодезических на псевдосфере — это спирали, навивающиеся на граммофонную трубу. Но геодезическими также являются сечения псевдосферы плоскостями, проходящими через ее ось вращения. Расстояния в этой модели — обычные евклидовы длины геодезических (поскольку псевдосфера вложена в обычное трехмерное пространство, то эти длины можно найти).

4. Свойства и понятия.

Рассмотрим некоторые свойства, понятия и факты выполняющиеся в геометрии Лобачевского. В данном случае я рассматривал свойства основываясь на модели Клейна. Большинство из них будут выполнятся и на других моделях неевклидовой геометрии.

1) Параллельность прямых

а 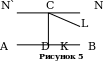) Если прямые CN и CL не встречают прямой АВ, то любая прямая СМ, проходящая через т. C внутри угла NCL также не встретит прямой АВ (рис.5). Отсюда первое следствие аксиомы Лобачевского: через т. С вне прямой АВ плоскости АВС, проходит бесчисленное множество прямых, не пересекающихся с прямой АВ.

б) Если соединить (рис.5) какую-либо точку прямой DB с т. С, получим прямую, допустим, СК, проходящую через т. С и встречающую АВ. Итак, все прямые, проходящие через т. С внутри прямого угла NCD, разбиваются на две категории, на два класса: встречающие прямую АВ (названные Лобачевским «сходящимися» с АВ) и не встречающие прямую АВ (их Лобачевский называет «расходящимися» с АВ). Любая прямая первой категории образует с перпендикуляром CD угол, меньший угла, образованного перпендикуляром CD с любой прямой второй категории. CL - предельная прямая, отделяющая сходящиеся от расходящихся прямых, и названная Лобачевским параллельной к прямой АВ из т. С. Итак, параллельная CL – это не просто расходящаяся прямая, а первая, граничная расходящаяся, т.е. такая, что любая прямая, проходящая через т. С внутри угла, образованного параллельной CL и перпендикуляром CD, является сходящейся прямой, а всякая прямая, проходящая внутри угла LCN будет расходящейся с прямой АВ. Угол DCL, образованный параллельной CL с перпендикуляром CD, называют углом параллельности.

Приведем некоторые другие понятия и факты геометрии Лобачевского:

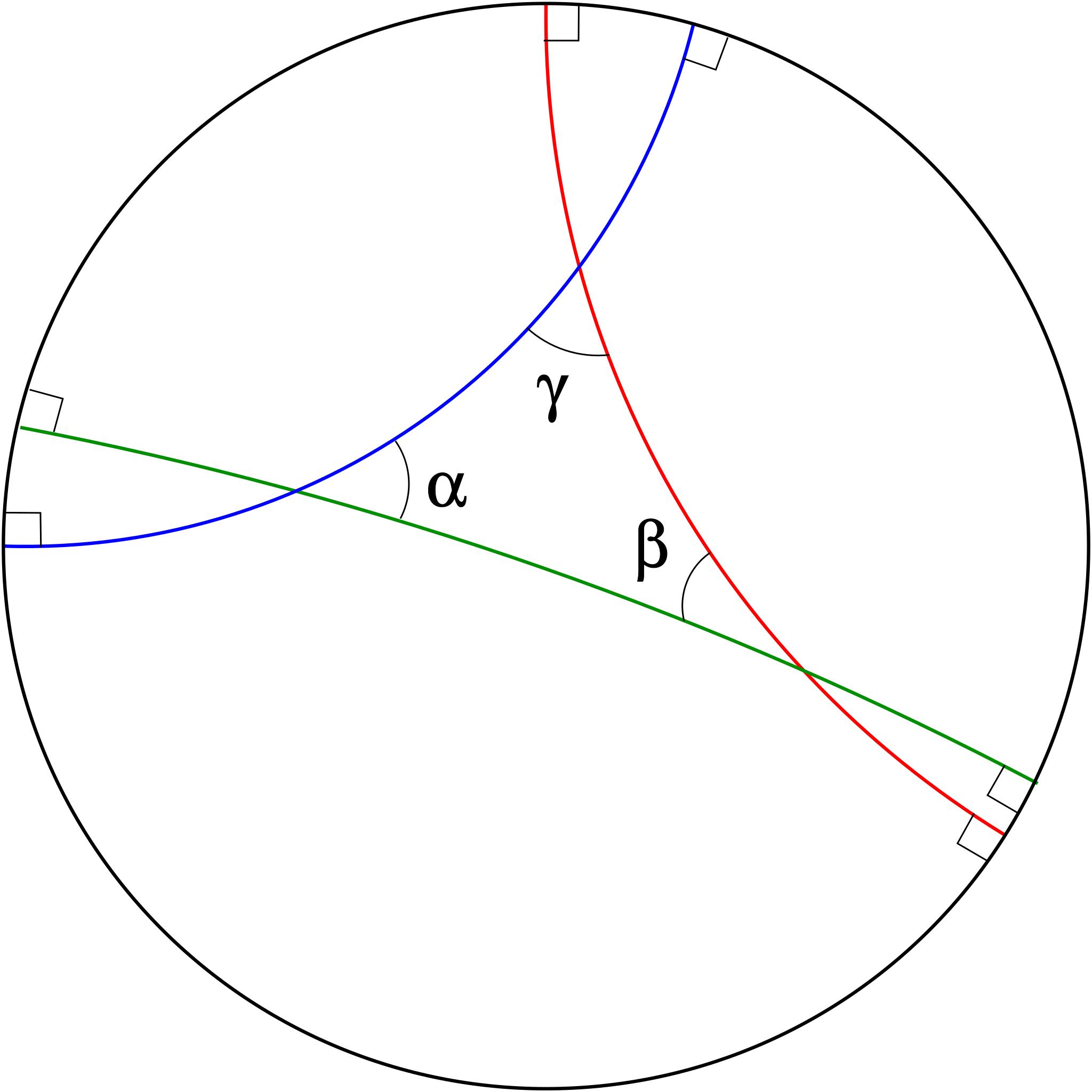
2) Сумма углов треугольника меньше 180°

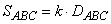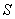Разность между 180° и суммой углов треугольника  в геометрии Лобачевского положительна; она называется дефектом этого треугольника. Оказывается, что в этой геометрии площадь треугольника замечательным образом связана с его дефектом:  , где   и 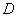  означают площадь и дефект треугольника, а число  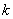 зависит от выбора единиц измерения площадей и углов.

3) Предложение «сумма углов четырехугольника меньше 360» вытекает из предыдущего. Отсюда следует, что в геометрии Лобачевского нет ни прямоугольников, ни квадратов. Вообще сумма углов n – угольника меньше 180(n-2).

4) Внешний угол треугольника больше суммы внутренних, с ним не смежных углов. Действительно, пусть внешний угол треугольника, смежный с внутренним углом треугольника и пусть и  - остальные его внутренние углы, тогда: 180°.

Следует, что  + .

5) Если три угла одного треугольника соответственно равны трем углам другого треугольника, то эти треугольники равны между собой. Это четвертый признак равенства треугольников в геометрии Лобачевского.

Таким образом, в плоскости Лобачевского треугольник вполне определяется своими углами. Стороны и углы зависят друг от друга. Отсюда ясно, что в геометрии Лобачевского нет подобных фигур. Действительно, ведь из существования подобных фигур вытекает евклидова аксиома параллельности.

4. Практическое применение геометрии Лобачевского Спутниковые навигационные системы (GPS и ГЛОНАСС) состоят из двух частей: орбитальная группировка из 24-29 спутников, равномерно расположенных вокруг Земли, и управленческий сегмент на Земле, обеспечивающий синхронизацию времени на спутниках и использование ими единой системы координат. На спутниках установлены очень точные атомные часы, а в приемниках (GPS-навигаторах) обычные, кварцевые. В приемниках также есть информация о координатах всех спутников в любой момент времени. Спутники с маленькими интервалами передают сигнал, содержащий данные о времени начала передачи. Получив сигнал от не менее четырех спутников, приемник может скорректировать свои часы и вычислить расстояния до этих спутников по формуле ((время отправки сигнала спутником) — (время приема сигнала от спутника)) х (скорость света) = (расстояние до спутника). Вычисленные расстояния также корректируются по встроенным в приемник формулам. Далее, приемник находит координаты точки пересечения сфер с центрами в спутниках и радиусами, равными вычисленным расстояниям до них. Очевидно, это будут координаты приемника.

Формулы геометрии Лобачевского также используются в физике высоких энергий, а именно, в расчетах ускорителей заряженных частиц. Гиперболические пространства (т.е. пространства, в которых действуют законы гиперболической геометрии) встречаются и в самой природе.

5. Вывод:

Открытие неевклидовой геометрии, начало которому положил Лобачевский, не только сыграло огромную роль в развитии новых идей и методов в математике естествознании, но имеет и философское значение. Господствовавшее до Лобачевского мнение о незыблемости геометрии Евклида в значительной мере основывалось на учении известного немецкого философа И. Канта (1724-1804), родоначальника немецкого классического идеализма. Кант утверждал, что человек упорядочивает явления реального мира согласно априорным представлениям, а геометрические представления и идеи якобы априорны (латинское слово aprior означает – изначально, заранее), то есть, не отражают явлений действительного мира, не зависят от практики, от опыта, а являются врожденными человеческому миру, раз и навсегда зафиксированными, свойственными человеческому разуму, его духу. Поэтому, Кант считал, что Евклидова геометрия непоколебима, неизменна, и является вечной истиной. Еще до Канта геометрия Евклида считалась незыблемой, как единственно возможное учение о реальном пространстве.

Открытие неевклидовой геометрии доказало, что нельзя абсолютировать представления о пространстве, что «употребительная» (как назвал Лобачевский геометрию Евклида) геометрия не является единственно возможной, однако это не подорвало незыблемость геометрии Евклида. Итак, в основе геометрии Евклида лежат не априорные, врожденные уму понятия и аксиомы, а такие понятия, которые связаны с деятельностью человека, с человеческой практикой. Только практика может решить вопрос о том, какая геометрия вернее излагает свойства физического пространства. Открытие неевклидовой геометрии дало решающий толчок грандиозному развитию науки, способствовало и поныне способствует более глубокому пониманию окружающего нас материального мира.

Список источников:

1. Математика XIX века, «Наука», М., 1981

2. “Квант” №11,№12 Академик АН СССР А.Д. Александров, Интернет-издания.

3. Юшкевич А.П., История математики в России, «Наука», М., 1968

4. Ефимов Н.В., Высшая геометрия, «Наука», М.,1971.

5. Неевклидовы пространства и новые проблемы физики, «Белка», М., 1993

6. Клайн М., Математика. Утрата определенности, «Мир», М., 1984

7. Г.И. Глейзер. История математики в школе IX – X классы. Пособие для учителей. Москва, «Просвещение» 1983г.

8. Даан Дальмедино А., Пейффер И. Пути и лабиринты. Очерки по истории математики. Перевод с французского. М: Мир.1986г.

9. Б.Л. Лаптев. Н.И. Лобачевский и его геометрия. Пособие для учащихся. М. «Просвещение», 1970г.

10. И.М. Яглам. Принцип относительности Галилея и неевклидова геометрия. Серия «Библиотека математического кружка» М: 1963г.

11. http://www.bankreferatov.ru

12. http://www.refportal.ru

13. http://www.edu.ru

14. http://www.allbest.ru

15. http://www.themesoch.narod.ru/t_s

16. http://www.referat.online.ru

17. http://www.pautina.net