П Р О Г Р А М М А
адаптированная на возможность обучающихся 10-х классов участвовать в ЕГЭ по математике (базовый уровень),
составлена на основе программы А.Г.Мордковича «Алгебра и начала анализа 10-11 классы», (учебник А.Г.Мордкович «Алгебра и начала анализа 10 класс,11 класс» профильный уровень),
издательство «Мнемозина», 2012г.
Алгебра и начала математического анализа
10-11 классы
профильный уровень
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Главной целью школьного образования является развитие как компетентной личности путем включения его в различные виды ценностной человеческой деятельности: учеба, познания, коммуникация, профессионально-трудовой выбор, личностное саморазвитие, ценностные ориентации, поиск смыслов жизнедеятельности. С этих позиций обучение рассматривается как процесс овладения не только определенной суммой знаний и системой соответствующих умений и навыков, но и как процесс овладения компетенциями. Это определило цели обучения алгебре и началам анализа:
формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, а также последующего обучения в высшей школе;
овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
воспитание средствами математики культуры личности, понимания значимости математики для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры .
На основании требований Государственного образовательного стандарта в содержании предполагается реализовывать актуальные в настоящее время компетентностный, личностно ориентированный, деятельностный подходы, которые определяют задачи обучения:
преобретение математических знаний и умений;
овладение общественными способами мыслительной, творческой деятельностей;
освоение компетенций (учебно-познавательной, коммуникативной, рефлексивной, личностного саморазвития, ценностно-ориентированной) и профессионально-трудового выбора.
Специфика целей и содержание изучения алгебры и начал анализа на профильном уровне существенно повышает требования к рефлексивной деятельности учащихся; к объективному оцениванию своих учебных достижений, поведения, черт своей личности, способности и готовности учитывать мнения других людей при определении собственной позиции и самооценке, понимать ценность образования как средства развития культуры личности.
СОДЕРЖАНИЕ ПРОГРАММЫ
10 класс (170 ч)
Действительные числа (16 ч)
Натуральные и целые числа. Делимость чисел. Основная теорема арифметики натуральных чисел. Рациональные, иррациональные, действительные числа, числовая прямая. Числовые неравенства. Арифметика действительных чисел. Модуль действительного числа. Метод математической индукции.
Числовые функции (12 ч)
Определение функции, способы ее задания, свойства функций. Обратная функция.
Периодические и обратные функции.
Тригонометрические функции (30 ч)
Числовая окружность. Длина дуги единичной окружности. Числовая окружность на координатной плоскости. Синус и косинус. Тангенс и котангенс. Тригонометрические функции числового аргумента. Тригонометрические функции углового аргумента. Формулы приведения. Функция у=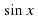 , ее свойства и график. Функция у=
, ее свойства и график. Функция у=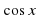 , ее свойства и график. Построение графиков. Функции у=
, ее свойства и график. Построение графиков. Функции у=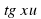 у=ctg х, их свойства и графики. Сжатие и растяжение графиков тригонометрических функций.
у=ctg х, их свойства и графики. Сжатие и растяжение графиков тригонометрических функций.
Тригонометрические уравнения(12ч)
Первые представления о решении тригонометрических уравнений, Арккосинус, арксинус, арктангенс и арккотангенс. Решение простейших тригонометрических уравнений. Методы решения тригонометрических уравнений. Методы решения тригонометрических уравнений: введение новой переменной и разложение на множители, с применением тригонометрических формул. Однородные тригонометрические уравнения.
Преобразование тригонометрических выражений (16 ч)
Синус и косинус суммы и разности аргументов. Формулы двойного аргумента. Формулы понижения степени. Преобразование сумм тригонометрических функций в произведение. Преобразование произведений тригонометрических функций в суммы.
Производная (20 ч)
Определение числовой последовательности и способы ее задания. Свойства числовых последовательностей. Определение предела последовательности. Вычисление пределов последовательностей. Сумма бесконечной геометрической прогрессии. Предел функции на бесконечности, в точке. Приращение аргумента, функции. Задачи, приводящие к понятию производной. Определение производной. Алгоритм отыскания производной. Формулы дифференцирования. Правила дифференцирования. Уравнение касательной к графику функции. Алгоритм составления уравнения касательной к графику функции. Применение производной для исследования функций. Построение графиков функций.
Степени и корни. Степенные функции (12 ч)
Понятие корня 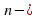 ой степени из действительного числа. Функции у =
ой степени из действительного числа. Функции у = 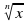 , их свойствах и графики. Свойства корня
, их свойствах и графики. Свойства корня 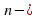 ой степени.
ой степени.
Показательная и логарифмическая функции (23 ч)
Показательная функция, ее свойства и график. Показательные уравнения. Показательные неравенства. Понятие логарифма. Логарифмическая функция, ее свойства и график. Свойства логарифмов. Логарифмические уравнения. Логарифмические неравенства.
Элементы математической статистики, комбинаторики и теории вероятностей (10 ч)
Статистическая обработка данных. Простейшие вероятностные задачи. Случайные события и их вероятности.
Обобщающее повторение (19 ч)
11класс (170 ч)
Многочлены (14)
Многочлены от одной и нескольких переменных. Теорема Безу. Схема Горнера. Симметричные и однородные многочлены. Уравнения высших степеней.
Комплексные числа (12 ч)
Комплексные числа и арифметические операции над ними. Комплексные числа и координатная плоскость. Тригонометрическая форма записи комплексного числа. Возведение комплексного числа в степень. Извлечение корня из комплексного числа.
Преобразование тригонометрических выражений (10 ч)
Формулы понижения степени. Преобразование сумм тригонометрических функций в произведение. Преобразование произведений тригонометрических функций в суммы.
Применение различных комбинаций формул. Методы решения тригонометрических уравнений (продолжение)
Производная (15 ч)
Применение производной для отыскания наибольшего и наименьшего значений непрерывной функции на промежутке. . Чтение графиков функций и графиков производной функции. Дифференцирование сложной функции. Дифференцирование обратной функции. Применение производной к доказательству тождеств и неравенств. Задачи на оптимизацию.
Первообразная и интеграл (11 ч)
Первообразная. Правила отыскания первообразных. Таблица основных неопределенных интегралов. Задачи приводящие к понятию определенного интеграла. Понятие определенного интеграла. Формула Ньютона – Лейбница. Вычисление площадей плоских фигур с помощью определенного интеграла. Применение интеграла в физике.
Степени и корни. Степенные функции (19 ч)
Преобразование выражений, содержащих радикалы. Обобщение понятия о показатели степени. Степенные функции, их свойства и графики. Дифференцирование и интегрирование.
Показательная и логарифмическая функции (15 ч)
Логарифмические уравнения и неравенства. Переход к новому основанию логарифма.
Дифференцирование показательной и логарифмической функций.
Уравнения и неравенства. Системы уравнений и неравенств (40 ч) Равносильность уравнений. Общие методы решения уравнений: замена уравнений равносильными уравнениями, разложение на множители, введение новой
переменной, функционально-графический метод. Решение неравенств с одной переменной. Равносильность неравенств, системы и совокупности неравенств, иррациональные неравенства, неравенства и уравнения с модулями. Системы уравнений. Уравнения и неравенства с параметрами.
Элементы математической статистики, комбинаторики и теории вероятностей (11 ч)
Статистическая обработка данных. Простейшие вероятностные задачи. Случайные события и их вероятности.
Обобщающее повторение (23 ч)
| К составлению программы по алгебре и началам анализа 10-11 класс (профиль)
|
| № п.п. | содержание | 10 кл. | 11кл. | 10-11 кл. |
| 1 | Действительные числа | 16 |
| 16 |
| 2 | Числовые функции | 12 |
| 12 |
| 3 | Тригонометрические функции | 30 |
| 30 |
| 4 | Тригонометрические уравнения и неравенства | 12 |
| 12 |
| 5 | Преобразование тригонометрических выражений | 16 | 10 | 26 |
| 6 | Комплексные числа |
| 12 | 12 |
| 7 | Производная | 20 | 15 | 35 |
| 8 | Комбинаторика и вероятность | 10 |
| 10 |
| 9 | Многочлены |
| 14 | 14 |
| 10 | Степени и корни. Степенные функции | 12 | 19 | 31 |
| 11 | Показательная и логарифмическая функции | 23 | 15 | 38 |
| 12 | Интеграл |
| 11 | 11 |
| 13 | Элементы математической статистики, комбинаторики и теории вероятностей |
| 11 | 11 |
| 14 | Уравнения и неравенства. Системы уравнений и неравенств. |
| 40 | 40 |
| 15 | Обобщающее повторение | 19 | 23 | 42 |
| Итого : | 170 | 170 | 340 |
ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ ВЫПУСКНИКОВ
В результате изучения математики на профильном уровне ученик должен:
знать/понимать
значение математической науки для решения задач, возникающих в теории и практике; широту и ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки;
идеи расширения числовых множеств как способа построения нового математического аппарата для решения практических задач и внутренних задач математики;
значение идей, методов и результатов алгебры и математического анализа для построения моделей реальных процессов и ситуаций;
универсальный характер законов логики математических рассуждений, их применимость в различных областях человеческой деятельности;
различие требований, предъявляемых к доказательствам в математике, естественных, социально-экономических и гуманитарных науках, на практик;
роль аксиоматики в математике; возможность построения математических теорий на аксиоматической основе; значение аксиоматики для других областей знания и для практики;
вероятностный характер различных процессов и закономерностей окружающего мира;
Алгебра.
уметь:
находить значения тригонометрических выражений; пользоваться оценкой и прикидкой при практических расчетах;
проводить по известным формулам и правилам преобразования тригонометрических выражений, буквенных выражений.
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
практических расчетов по формулам, включая формулы, содержащие тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.
Функции и графики.
уметь:
определять значения тригонометрических функций по значению аргумента при различных способах задания функции;
строить графики тригонометрических функций;
строить графики, описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
решать тригонометрические уравнения, используя свойства функций и их графики;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Начала математического анализа.
уметь:
вычислять производные элементарных функций, используя справочные материалы;
исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения прикладных задач, в том числе социально – экономических и физических, на наибольшее и наименьшее значения, на прохождение скорости и ускорения.
Уравнения и неравенства .
уметь:
Элементы комбинаторики, статистики и теории вероятностей:
уметь:
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
вычислять в простейших случаях вероятности событий на основе подсчёта числа исходов.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
анализа реальных числовых данных, представленных в виде диаграмм, графиков;
анализа информации статистического характера.






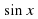 , ее свойства и график. Функция у=
, ее свойства и график. Функция у=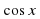 , ее свойства и график. Построение графиков. Функции у=
, ее свойства и график. Построение графиков. Функции у=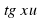 у=
у=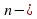 ой степени из действительного числа. Функции у =
ой степени из действительного числа. Функции у = 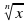 , их свойствах и графики. Свойства корня
, их свойствах и графики. Свойства корня 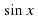 , ее свойства и график. Функция у=
, ее свойства и график. Функция у=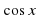 , ее свойства и график. Построение графиков. Функции у=
, ее свойства и график. Построение графиков. Функции у=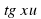 у=
у=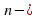 ой степени из действительного числа. Функции у =
ой степени из действительного числа. Функции у = 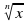 , их свойствах и графики. Свойства корня
, их свойствах и графики. Свойства корня 









