Программа "Генератор сечений"

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ

ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ПЕТРОВСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА

ПРОЕКТ

ГЕНЕРАТОР СЕЧЕНИЙ

Выполнил ученик 11-А класса

Дегтярев Михаил

Учитель математики и информатики

Скорнякова Татьяна Евгеньевна

с. Петровское

2014

Содержание:

Введение	3
Уравнение плоскости	3
Исследование особых случаев расположения плоскости в пространстве относительно системы координат.	3
Векторное произведение векторов	7
Расстояние от точки до плоскости	8
Объем пирамиды	8
Геометрическое моделирование в среде программирования	9
Заключение	11
Литература и источники Интернета	11

1. Введение

Школьный курс геометрии состоит из двух частей: планиметрии и стереометрии. В планиметрии изучаются свойства геометрических фигур на плоскости. Стереометрия – это раздел геометрии, в котором изучаются свойства фигур в пространстве.

При изучении пространственных фигур, в частности геометрических тел, пользуются их изображениями на чертеже. Как правило, изображением пространственной фигуры служит ее проекция на ту или иную плоскость. [1]

В своей работе я решил запрограммировать вывод изображения прямоугольного параллелепипеда на плоскость экрана монитора и построить сечение этого параллелепипеда плоскостью, проходящей через три заданные точки. Координаты точек буду вводить с клавиатуры. Это позволит лучше изучить геометрию и в дальнейшем выполнять проверку при решении задач.

1. Уравнение плоскости.

Если точка 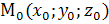_ и отличная от нее точка 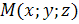_принадлежат плоскости , а вектор 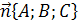_перпендикулярен плоскости  (Рис.1), то скалярное произведение векторов 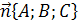_ и 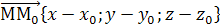_ равно нулю.

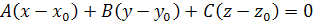
Это уравнение является уравнением плоскости [1]. Если раскрыть скобки и ввести обозначение 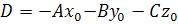_, то уравнение плоскости можно записать в виде_.

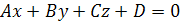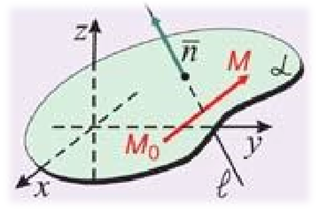Рис.1

1. Исследование особых случаев расположения плоскости в пространстве относительно системы координат.

Компьютерная программа строит прямоугольный параллелепипед по трем его измерениям, а если ввести координаты точек, то строит сечение параллелепипеда плоскостью, проходящей через эти точки, а также составляет уравнение плоскости.

Если один из коэффициентов уравнения равен нулю, то получается неполное уравнение плоскости[3].

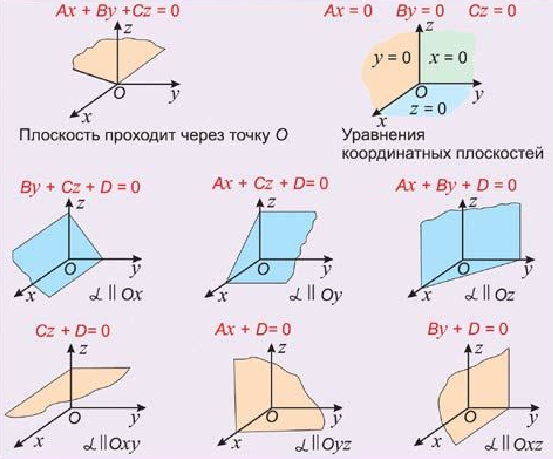Рис.2

Я провел исследование различных способов расположения плоскости в пространстве (Табл.1)[2].

Коэффициенты		Особенности расположения плоскости	Результат выполнения программы
А≠0,В≠0, C≠0, D≠0				Уравнение плоскости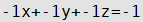
D≠0	А=0,В≠0, C≠0	Плоскость параллельна оси Ох		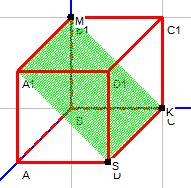Уравнение плоскости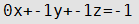
D≠0	В=0,А≠0, C≠0	Плоскость параллельна оси Оу		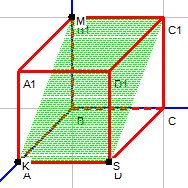Уравнение плоскости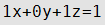
D≠0	С=0,А≠0,В≠0	Плоскость параллельна оси Оz		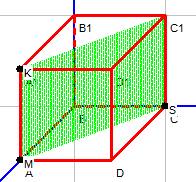Уравнение плоскости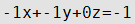
D≠0	B=0, С=0,А≠0	Плоскость параллельна плоскости Оzy		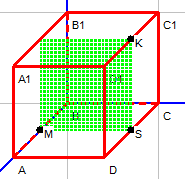Уравнение плоскости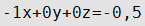
D≠0	A=0, С=0,В≠0	Плоскость параллельна плоскости Оxz		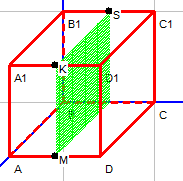Уравнение плоскости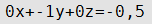
D≠0	B=0, A=0, C≠0	Плоскость параллельна плоскости Охy		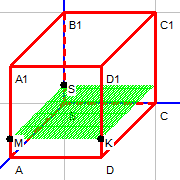Уравнение плоскости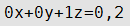
Если D=0, секущая плоскость проходит через начало координат
D=0	A=0, B≠0, C≠0	Плоскость проходит через ось Ох		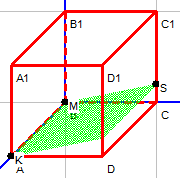Уравнение плоскости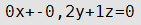
D=0	В=0, А≠0, C≠0	Плоскость проходит через ось Оу		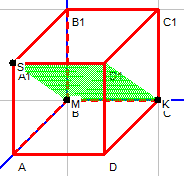Уравнение плоскости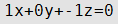
D=0	C=0, А≠0, B≠0	Плоскость проходит через ось Оz		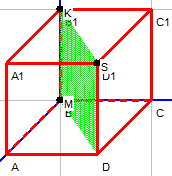Уравнение плоскости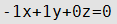
D=0	B=0, С=0,А≠0	Плоскость параллельна плоскости Оzy или совпадает с ней		Уравнение плоскости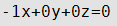
D=0	A=0, С=0,В≠0	Плоскость параллельна плоскости Оxz или совпадает с ней		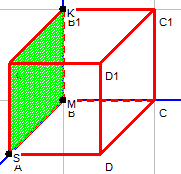Уравнение плоскости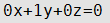
D=0	B=0, A=0, C≠0	Плоскость параллельна плоскости Охy или совпадает с ней		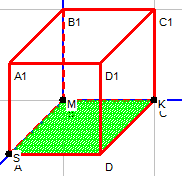Уравнение плоскости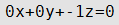

1. Векторное произведение векторов

Ч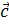

тобы составить уравнение плоскости, проходящей через три точки, я изучил понятие векторного произведения векторов.

В

Рис. 3

екторным произведением вектора_ на вектор _  в пространстве  называется вектор _ (Рис.3), удовлетворяющий следующим требованиям:

• длина вектора _ равна произведению длин векторов _  и _ на синус угла  между ними: _ ;

• вектор _  перпендикулярен каждому из векторов  _  и _;

• вектор _ направлен так, что тройка векторов _ является правой (Рис. 4);[4].

З

Рис..4

начит координаты вектора _, или коэффициенты _в уравнении плоскости, можно найти из векторного произведения _  и _:

_.

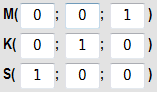
Даны координаты точек _. Считаем _, _

_.

1. Расстояние от точки до плоскости

Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из точки на плоскость (Рис.5).[3]

Рис.5

Программа находит расстояние от секущей плоскости до точки Е. Если задано уравнение плоскости 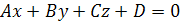_, то расстояние от точки _ до плоскости можно найти, используя следующую формулу [1]:

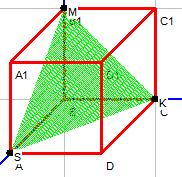
1. Объем пирамиды

Объем пирамиды равен одной трети произведения площади основания на высоту (Рис.6). [3]

Рис.6 Рис.7

Площадь треугольника MKS(Рис.7) равна половине площади параллелограмма, построенного на векторах _ и _ (Рис.3), или половине модуля вектора 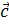_ :_. Расстояние dот точки Е до плоскости MKS является высотой пирамиды, значит объем равен

1. Геометрическое моделирование в среде программирования

1. Каждая вершина параллелепипеда задается 3 координатами. Изображение на плоскости двумерно. Возникает необходимость пересчета пространственных координат в экранные.

   1. _

Тогда _

1. _

Т

Рис.8

очка _ расположена левее и ниже точки _ на величину длины катета прямоугольного треугольника с гипотенузой _.

Тогда _

_, _ - масштаб

1. _

Точка _ правее точки _ на _. Тогда _

1. _

З

Рис.9

аметим, что _

Точка _ расположена правее точки _ на _, тогда_

Подставляя (2), имеем _

Точка _ расположена ниже точки _ на_, тогда

1. Чтобы фигура не выглядела вытянутой, ребра, направленные вдоль оси Ох трехмерной фигуры, уменьшим, для этого подберем подходящий множитель, например _

1. На следующем этапе нужно построить сечение прямоугольного параллелепипеда плоскостью, проходящей через три заданные точки. Для проверки задача была решена в тетради для параллелепипеда с измерениями 3, 5 и 6. Построена секущая плоскость в PascalABC, проходящая через точки (6, 0, 0), (0, 9, 0), (0, 0, 7). По этим данным составлено уравнение плоскости _ и проверена программа построения (Рис.10).

Рис.10

1. В общем случае задача решена в среде программирования Lazarus, проектный продукт – исполняемый файл – Генератор сечений, не требует установки на компьютере.

Выполняет следующие действия:

1. Строит прямоугольный параллелепипед по трем измерениям

2. Строит сечение параллелепипеда по трем точкам

3. Составляет уравнение плоскости сечения

4. Находит расстояние от точки до плоскости

5. Вычисляет объем пирамиды

Программа нахождения объема пирамиды проверена на задачах [5], в которых координаты выражаются целыми числами или десятичными дробями (Рис.11).

Рис. 11

1. Заключение.

Изучая свойства геометрических фигур, мы получаем представление о геометрических свойствах реальных предметов (их форме, взаимном расположении и т.д.) и можем использовать эти свойства в практической деятельности.

1. Литература и источники Интернета:

1. Геометрия 10-11: учебник для общеобразовательных учреждений/Атанасян Л.С., Бутусов В.Ф., Кадомцев и др. - М.: Просвещение, 2007

2. Практикум и индивидуальные задания по векторной алгебре и аналитической геометрии (типовые расчеты): Учебное пособие.- СПб.: Издательство «Лань», 2013

3. http://xn--e1aogju.xn--p1ai/shemy/other/stereometrija-vzaimnoe-raspolozhenie-figur-v-prostranstve-2010-g/page-1

4. http://ru.wikipedia.org/wiki/Векторное_произведение

5. Векторы и координаты в решении задач школьного курса стереометрии: учебное пособие/ П.Ф.Севрюков, А.Н.Смоляков. М.: Илекса: Народное образование; Ставрополь: Сервисшкола, 2010

13