Программа внеурочной деятельности для 8-9 классов "Математика в искусстве, искусство в математике"

Содержание

	Страница
Пояснительная записка	3
Основные цели программы	5
Планируемые результаты	6
Оценивание результатов деятельности обучающихся	7
Тематическое распределение количества часов	9
Содержание курса	12
Методические материалы для подготовки и проведения занятий	15
Информационно-методическое обеспечение для учителя	65
Информационно-методическое обеспечение для обучающихся	67

Пояснительная записка

"Музыка может возвышать или умиротворять душу, живопись - радовать глаз, поэзия - пробуждать чувства, философия - удовлетворять потребности разума, инженерное дело - совершенствовать материальную сторону жизни людей. Но математика способна достичь всех этих целей".

Морис Клайн, американский математик

За долгую историю человеческой культуры накоплена необъятная литература об искусстве и огромная по математике. Но в то время как библиотечные полки прогибаются «под мудрой тяжестью подробнейших сочинений о науке и об искусстве, отдельно – о науке, и отдельно – об искусстве, …о механизме и об истории теснейшего взаимодействия этих органов жизни человечества не написано почти ничего».

Однако с давних пор человек стремится окружать себя красивыми вещами. Уже предметы обихода жителей древности, которые, казалось бы, преследовали чисто утилитарную цель - служить хранилищем воды, оружием на охоте и т.д., демонстрируют стремление человека к красоте. На определенном этапе своего развития человек начал задаваться вопросом: почему тот или иной предмет является красивым и что является основой прекрасного? Уже в Древней Греции родилось представление о том, что основой прекрасного является гармония. Красота и гармония стали важнейшими категориями познания, в определенной степени даже его целью, ибо в конечном итоге художник ищет истину в красоте, а ученый - красоту в истине.

Математику учащиеся нередко воспринимают как предмет обязательный, но жёсткий и сухой, некое нагромождение чисел, формул, расчётов. Формулы ради формул, расчёты ради расчётов не способствуют созданию положительной мотивации для усвоения науки математики. Программа внеурочной деятельности «Математика в искусстве, искусство в математике» помогает посмотреть на эту науку совсем с другой стороны, понять её красоту, её неотъемлемую связь с тем, что мы называем прекрасным, показать, что между словами «математика» и «искусство» действительно должен стоять соединительный союз «и», а не разделительный «или». Он разъясняет учащимся, что человеку любой профессии для создания качественного, удобного, привлекательного изделия, необходим точный математический расчёт. И в природе всё, что радует глаз человека, имеет свои законы, которые можно выразить языком математики. Математика не придумывает формулы, она открывает их как связь, существующую в природе. Все великие художники и зодчие, создавая свои бесценные произведения, опирались на эти математические законы. Преподнося эти факты, данный курс знакомит учащихся со многими нетленными творениями человечества, позволяет посмотреть на них более зрело, развивает эстетически. Кроме того, позволяет взглянуть на самих математиков, как на людей, имеющих нередко разносторонние интересы и таланты.

Представленная программа по составлена в соответствии с требованиями Федерального государственного образовательного стандарта основного общего образования. Программа внеурочной деятельности «Математика в искусстве, искусство в математике» базируется на принципах природосообразности, гуманизма, демократии, творческого развития личности, свободного выбора каждым ребенком вида и объема деятельности, дифференциации образования с учетом реальных возможностей каждого обучающегося. Программа курса сформирована с учётом психолого-педагогических особенностей развития детей 13—16 лет.

Содержание программы, формы и методы ее реализации определяются, исходя из образовательно-воспитательных задач, психолого-педагогической целесообразности, санитарно-гигиенических норм, материально-технических условий.

Данная программа является частью интеллектуально-познавательного направления программы внеурочной деятельности лицея и расширяет содержание программ общего образования. Программа коррелирует с курсом «Искусство». При разработке и реализации программы внеурочной деятельности «Математика в искусстве, искусство в математике» основное внимание уделяется вопросам, не входящим в школьный курс обучения. Именно этот фактор является значимым при дальнейшей работе с одаренными детьми, подготовке их к олимпиадам различного уровня.

Реализация программы осуществляется с использованием различных форм занятий, как традиционных (аудиторные занятии), так и нестандартных (внеаудиторные занятия, мастерская, экскурсии, тематические вечера, концерты, выставки...), и направлена на достижение планируемых результатов освоения основной образовательной программ ООО. Согласно ФГОС внеурочная деятельностью является одним из инструментом достижения планируемых личностных, предметных и метапредметных результатов образования школьников.

Программа внеурочной деятельности «Математика в искусстве, искусство в математике» рассчитана на 34 часа, включает знания многих разделов математики. При этом в ней предусмотрен резерв свободного учебного времени в объеме 4 учебных часов для реализации авторских подходов, использования разнообразных форм организации учебного процесса, внедрения современных методов обучения и педагогических технологий.

Основные цели программы

В связи с тем, что в основе реализации программы лежит системно-деятельностный подход, основными целями являются:

— воспитание и развитие качеств личности, отвечающих требованиям информационного общества, задачам построения российского гражданского общества на основе принципов толерантности, диалога культур и уважения его многонационального, поликультурного и поликонфессионального состава;

— формирование соответствующей целям общего образования социальной среды развития обучающихся в системе образования на основе разработки содержания и технологий образования, определяющих пути и способы достижения желаемого уровня (результата) личностного и познавательного развития обучающихся;

— ориентация на достижение цели и основного результата образования — развитие на основе освоения универсальных учебных действий, познания и освоения мира личности обучающегося, его активной учебно-познавательной деятельности, формирование его готовности к саморазвитию и непрерывному образованию;

— признание решающей роли содержания образования, способов организации образовательной деятельности и учебного сотрудничества в достижении целей личностного и социального развития обучающихся;

— учёт индивидуальных возрастных, психологических и физиологических особенностей обучающихся, роли, значения видов деятельности и форм общения при построении образовательного процесса и определении образовательно-воспитательных целей и путей их достижения;

— разнообразие индивидуальных образовательных траекторий и индивидуального развития каждого обучающегося, в том числе одарённых детей, детей-инвалидов и детей с ограниченными возможностями здоровья.

Задачи реализации программы

– показать учащимся красоту математики, расширить их знания по предмету;

– интегрировать знания, полученные на самых различных уроках, и получить новые знания по математике;

– показать, как взаимодействуют и взаимно обогащаются две великие сферы человеческой культуры – наука и искусство; показать единство науки и красоты, истины и красоты;

– показать, что глубинные фундаментальные закономерности, присущие всем видам искусства, находят адекватное выражение на языке математики, например, геометрические фигуры – это лишь модели реальных объектов природы, а функции, изучаемые в школе – лишь абстрагированные обобщённые закономерности, отражающие множество реальных закономерностей, существующих в природе.

Планируемые результаты

Реализация программы внеурочной деятельности «Математика в искусстве, искусство в математике» в основной школе направлено на достижение следующих результатов:

1) в направлении личностного развития

• развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;

• формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;

• воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;

• формирование качеств мышления, необходимых для адаптации в современном информационном обществе;

• развитие интереса к математическому творчеству и математических способностей;

2) в метапредметном направлении

• формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;

• развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;

• формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;

3) в предметном направлении

• овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни;

• создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.

Оценивание результатов деятельности обучающихся

Реализация программы внеурочной деятельности «Математика в искусстве, искусство в математике» подразумевает выполнение индивидуального (группового) проекта, обязательно для каждого обучающегося. В соответствии с целями подготовки проекта для каждого обучающегося разрабатываются план, программа подготовки проекта, которая включает в себя требования по следующим рубрикам:

• организация проектной деятельности;

• содержание и направленность проекта;

• защита проекта;

• критерии оценки проектной деятельности.

Результатом (продуктом) проектной деятельности может быть любая из следующих работ:

а) письменная работа (эссе, реферат, аналитические материалы, обзорные материалы, отчёты о проведённых исследованиях, стендовый доклад и др.);

б) художественная творческая работа (в области литературы, музыки, изобразительного искусства, экранных искусств), представленная в виде прозаического или стихотворного произведения, инсценировки, художественной декламации, исполнения музыкального произведения, компьютерной анимации и др.;

в) материальный объект, макет, иное конструкторское изделие;

г) отчётные материалы по социальному проекту, которые могут включать как тексты, так и мультимедийные продукты.

Критерии оценки индивидуального проекта:

1. Сформированность познавательных учебных действий: способность к самостоятельному приобретению знаний и решению проблем, проявляющаяся в умении поставить проблему и выбрать адекватные способы её решения, включая поиск и обработку информации, формулировку выводов и/или обоснование и реализацию/апробацию принятого решения, обоснование и создание модели, прогноза, модели, макета, объекта, творческого решения и т. п.

2. Сформированность предметных знаний и способов действий, проявляющаяся в умении раскрыть содержание работы, грамотно и обоснованно в соответствии с рассматриваемой проблемой/темой использовать имеющиеся знания и способы действий.

3. Сформированность регулятивных действий, проявляющаяся в умении самостоятельно планировать и управлять своей познавательной деятельностью во времени, использовать ресурсные возможности для достижения целей, осуществлять выбор конструктивных стратегий в трудных ситуациях.

4. Сформированность коммуникативных действий, проявляющаяся в умении ясно изложить и оформить выполненную работу, представить её результаты, аргументированно ответить на вопросы.

Тематическое распределение количества часов

№	Тема, раздел	Количество часов	Творческая работа, проекты
1	Искусство, наука, красота	4	Создание альбома симметричных фигур (отображение кляксы, ИКТ), подбор иллюстраций.
1.1	Эстетика: наука о прекрасном. Математика: прекрасное в науке	2
1.2	Наука и искусство - грани творчества	1
1.3	Симметрия, пропорция, гармония - слагаемые прекрасного
2	Математика и музыка	4	Музыкальная гостиная (разучивание и исполнение песен, в которых есть математические термины, понятия)
2.1	Пифагор и пифагорейское учение о числе. Пифагорова гамма	1
2.2	"Космическая музыка": от Платона до Кеплера	1
2.3	Математический строй музыки. Пропорции музыкальной гаммы	2
3	Математика и архитектура	5	Творческая работа: «Создание эскиза фантастического здания». Создать выставку «город будущего»
3.1	Архитектура = (наука + техника)*искусство	1
3.2	Тайны золотого сечения.	1
3.3	Пропорции: от Парфенона до Нотр-Дама	1
3.4	Пропорции: от Покрова на Нерли до Модулора ле Корбюзье	1
3.5	Пропорция - математика архитектурной гармонии	1
4	Математика и живопись	5	Рефераты по истории живописи, истории проективной геометрии
4.1	"Законы красоты" человека	2
4.2	Перспектива - геометрия живописи	2	http://www.smekalka.pp.ru/picture задачи по картинкам
4.3	Геометрия и живопись: страницы истории	1
5	Математическое изобразительное искусство	6
5.1	Выдающиеся люди в истории математического изобразительного искусства	2
5.2	Общие темы в математическом искусстве	4
5.2.1	Многогранники	1	Модели правильных многогранников.
5.2.3	Искажённые и необычные перспективы	1	http://www.smekalka.pp.ru/optic.html оптические иллюзии
5.2.4	Лента Мёбиуса	1	Проект «В нём бесконечность свёрнута кольцом…»
5.2.5	Фракталы	1	http://www.evilmadscientist.com/2009/fractal-snowflake-cupcakes/ проект «Печенье-фракталы»
6	Математика и литература	3	http://www.smekalka.pp.ru/word_other.html старинные, сказочные, литературные задачи; задачи со словами
6.1	Математики-поэты (Ломоносов М.В., Ковалевская С.В., Лобачевский Н.И., Омар Хайам,..)	1
6.2	Математика в литературных произведениях	1	http://www.smekalka.pp.ru/old.html
6.3	Вечер поэзии: - стихи, посвящённые великим математикам; - стихи, в которых встречаются математические понятия; - стихи – задачи;	1
7	Математика и театр	3	Подготовка и выступление "Математического театра": странички из жизни древних ученых-математиков; значение и роль некоторых математических кривых ДРАМА + ДРАМА = ТЕАТР Ответ: 18969 + 18969 = 37938
	Резерв	4

Содержание курса

1 Искусство, наука, красота. 4 часа.

Наука и искусство - два основных начала в человеческой культуре, две дополняющие друг друга формы высшей творческой деятельности человека. Красота математики среди наук недосягаема, а красота является одним из связующих звеньев науки и искусства.

1.1 Эстетика: наука о прекрасном. Математика: прекрасное в науке. Раздумья о красоте научного поиска, о величии человеческого духа никогда не переставали волновать мыслящих людей. Математика несет красоту в любую науку. Особая роль математики в науке и ее особая эстетическая ценность.

1.2 Наука и искусство - грани творчества. Что же сближает и что разъединяет науку и искусство? Прежде всего, наука и искусство - две грани одного и того же процесса - творчества. Таким образом, цель и у науки, и у искусства одна - торжество человеческой культуры, хотя достигается она разными путями.

1.3 Симметрия, пропорция, гармония - слагаемые прекрасного. Пифагорейцы пытались математически обосновать идею единства мира, утверждали, что в основе мироздания лежат симметричные геометрические формы. Об использовании пропорции в искусстве Леонардо да Винчи. Таким образом, пропорциональность, соразмерность частей целого является важнейшим условием гармонии целого и может быть выражена математически посредством пропорций.

2 Математика и музыка 4 часа

2.1 Пифагор и пифагорейское учение о числе. Пифагорова гамма. Именно в математике, в познании количественных отношений, видели пифагорейцы ключ к разгадке мировой гармонии, постижение которой и составляло-смысл их жизни. Звездчатый пятиугольник, или пентаграмма,- пифагорейский символ здравия и тайный опознавательный знак. Обет молчания, даваемый пифагорейцами, нашел отражение в символе "бык на языке", что на современный лад означает "держи язык за зубами". Именно в музыке была первые обнаружена таинственная направляющая роль чисел в природе. По преданию, сам Пифагор установил, что приятные слуху созвучия получаются лишь в том случае, когда длины струн, издающих эти звуки, относятся как целые числа первой четверки: 1:2, 2:3, 3:4.

2.2 "Космическая музыка": от Платона до Кеплера. Задолго до нашей эры, во времена, когда человечество "летало" только на восковых крыльях в мифах о Дедале и Икаре, была своя "космическая музыка", многим, возможно, покажется удивительным. По преданию, слово "космос", первоначально означавшее прекрасно устроенный, ввел в обиход Пифагор. Космос для пифагорейцев - это гармоничное, пропорциональное строение мира. Сами же пропорции, как мы уже видели, мыслились греками музыкально" поэтому и весь космос оказывался гармонично устроенным и музыкально звучащим телом. Учение о музыке сфер - самый туманный и вместе с тем поэтичный мотив пифагорейской эстетики. Он имел тысячи вариантов, оттенков и тысячелетнюю традицию, начиная от Пифагора и Платона до "Гармонии мира" Иоганна Кеплера, написанной уже в XVII веке.

2.3 Математический строй музыки. Пропорции музыкальной гаммы. Музыкальная гамма разделена на пропорциональные части; она буквально пронизана пропорциями, а пропорциональность, как мы знаем, является одним из объективных критериев красоты. Пифагорова комма. 12-звуковая равномерная темперация.

3 Математика и архитектура 5 часов

3.1 Архитектура = (наука + техника)*искусство. "Прочность - польза - красота",- говорит формула архитектуры Витрувия. "Прекрасно то, что хорошо служит данной цели",- учит Сократ. "Дома строят для того, чтобы в них жить, а не для того, чтобы ими любоваться",- вторил Сократу через 2000 лет Фрэнсис Бэкон. Англичанина Рескина поддерживал француз Теофил Готье: "По-настоящему прекрасным является только то, что ничему не служит". Вся история архитектуры - это история поисков гармонического единства "функции - конструкции - формы", это история непрерывного восхождения на пути к вершине, имя которой "прочность - польза - красота ". В формуле архитектуры, данной известным советским архитектором, лауреатом Государственных премий Ф. А. Новиковым, искусство стоит не слагаемым, а сомножителем: архитектура = (наука + техника) * искусство.

3.2 Тайны золотого сечения. Геометрия владеет двумя сокровищами: одно из них - это теорема Пифагора, а другое - деление отрезка в среднем и крайнем отношении ... Первое можно сравнить с мерой золота; второе же больше напоминает драгоценный камень (И. Кеплер) Ряд золотого сечения и тесно связанный с ним ряд Фибоначчи обладают массой исключительных математических свойств, которые каким-то поразительным образом сошлись в этих феноменах. Но золотое сечение и числа Фибоначчи имеют не менее удивительные приложения не только в искусстве, но и в живой природе.

3.3 Пропорции: от Парфенона до Нотр-Дама. "Человек - мера всех вещей..." Этот знаменитый афоризм древнегреческого философа-софиста Протагора (ок. 490 - ок. 420 до н. э.) является ключом к разгадке тайны пропорций Парфенона, его поразительной гармонии и спокойствия. Но если греческое сознание всегда было обращено к человеку, если даже в дорических колоннах греки видели торжественное могущество мужского тела, а в изящных завитках ионических волют - женскую грацию и кокетство, то ни о каких реминисценциях с пропорциями человеческого тела в готической архитектуре не могло быть и речи.

3.4 Пропорции: от Покрова на Нерли до Модулора ле Корбюзье. Шедевр древнерусского зодчества церковь Покрова Богородицы на Нерли. Система мер, существовавшая в Древней Руси. Основные древнерусские меры длины и геометрическая взаимосвязь между ними. "Как мера и красота скажет..." - союз математики (мера) и искусства (красота) в создании архитектурных памятников. Система модульной унификации – модулор.

3.5 Пропорция - математика архитектурной гармонии. Пропорции являются важным и надежным средством зодчего для достижения хрупкого и тонко сбалансированного равновесия между целым и его частями, имя которому - гармония. Гармония в природе и гармония в архитектуре - две стороны единого великого процесса созидания.

4 Математика и живопись 5 часов

4.1 "Законы красоты" человека. Во все времена, от наскальной живописи в Сахаре до полотен Сальвадора Дали, человек был и остается главной темой изобразительного искусства. С древнейших времен пропорции человека составляли предмет изучения художника, его "математическую лабораторию". Три древнеегипетских канона. Греческое искусство. Леонардо да Винчи. Труды Дюрера. Да, человек - мера всех вещей - настолько разнообразен, что его нельзя втиснуть в рамки дискретных канонов. Теория пропорций сегодня не умерла, а лишь замерла в ожидании качественно нового скачка, в ожидании перехода от "арифметического" к "аналитическому" и даже "компьютерному" выражению.

4.2 Перспектива - геометрия живописи. Все проблемы Перспективы можно пояснить при помощи пяти терминов Математики: точка, линия, угол, поверхность и тело. (Леонардо да Винчи). Развитие понятия перспективы. Начертательная и проективная геометрия. Важнейшие виды проекций: центральные (а), параллельные (б) и ортогональные (в).

4.3 Геометрия и живопись: страницы истории. Геометрия дарила живописи новые изобразительные возможности, обогащала язык живописи, а живопись эпохи Возрождения стимулировала исследования по геометрии, дала начало проективной геометрии. "Ортогональная" живопись Древнего Египта. "Параллельная" живопись средневекового Китая и Японии. Линейная перспектива Возрождения. Обратная перспектива живописи Древней Руси.

5 Математическое изобразительное искусство 6 часов.

5.1 Выдающиеся люди в истории математического изобразительного искусства.

5.2 Общие темы в математическом искусстве. Многогранники. Искажённые и необычные перспективы. Оптические иллюзии. Лента Мёбиуса. Фракталы . Математические изобразительное искусство процветает сегодня, и многие художники создают картины в стиле Эшера и в своем собственном стиле. Эти художники работают в различных направлениях, включая скульптуру, рисование на плоских и трехмерных поверхностях, литографию и компьютерную графику. А наиболее популярными темами математического искусства остаются многогранники, тесселляции, невозможные фигуры, ленты Мебиуса, искаженные системы перспективы и фракталы.

6 Математика и литература 3 часа

6.1 Математики-поэты. Математика и поэзия. Что роднит их, казалось, на первой взгляд они такие разные… Ученым не чужда поэзия. Как показывает история науки, еще со времен пифагорейцев выдающиеся математики увлекались поэзией и даже сами пробовали писать.Ученые и поэзия. Женщина-математик Софья Васильевна Ковалевская. Великий русский ученый М. В. Н.И. Лобачевский. Пушкин и математика.

6.2 Математика в литературных произведениях. Старинные сказочные литературные задачи. Задачи со словами.

6.3 Вечер поэзии:

- стихи, посвящённые великим математикам;

- стихи, в которых встречаются математические понятия;

- стихи – задачи.

7 Математика и театр 3 часа

Подготовка и выступление "Математического театра": странички из жизни древних ученых-математиков; значение и роль некоторых математических кривых.

Резерв 4 часа

Невозможно навести "математический" порядок в искусстве, а то и вовсе "математизировать" искусство, как это происходит сегодня со многими науками. Английский художник У. Хогарт писал о сущности художественного метода: "Все математические представления следует совершенно устранить из нашего метода, потому что они для него не имеют никакого смысла". А вот французский скульптор Антуан Бурдель (1861-1929) считал: "Искусство - это завуалированная алгебра, отнимающая жизнь у тех, кто стремится приподнять ее покрывало". Однако есть третье мнение, отражающее глубокое понимание диалектики искусства, мнение, которое высказал в дискуссии ученых и художников профессор М. Каган: "... невозможно проверить алгеброй гармонию и невозможно проверить - т. е. познать - гармонию без алгебры". Искусство - это не только "содержание", но и "форма". Последняя, по всей видимости, имеет сходные законы построения (формообразования) как в природе, так и в искусстве. И, как все закономерное форма, должна подчиняться прежде всего математическим законам. Красота не является избранницей только искусства. Красота есть всюду. Есть она и в науке, и в особенности в ее жемчужине - математике. К сожалению, эстетика науки до сих пор живет на положении Золушки и о красоте науки сказано мало. Но те, кто собирается посвятить свою жизнь науке, должны ясно представлять, что наука во главе с "царицей всех наук" - математикой - откроет перед ними сказочные сокровища красоты.

Методические материалы для подготовки и проведения занятий.

1 Искусство, наука, красота.

Наука и искусство - два основных начала в человеческой культуре, две дополняющие друг Друга формы высшей творческой деятельности человека. В истории человечества были периоды, когда эти начала дружно уживались, а были и времена, когда они противоборствовали. Но видимо, высшая их цель - быть взаимодополняющими гранями человеческой культуры, как принципы Ин-Ян в древнекитайском знаке. Более того, как и в этом мудром знаке, даже в самой сердцевине науки есть элемент искусства, а всякое искусство несет в себе частицу научной мудрости. Первоначальное значение слова "математика" (от греч. mathema - знание, наука) не утрачено и сегодня. Математика остается олицетворением науки, символом мудрости, царицей всех наук. Красота математики среди наук недосягаема, а красота является одним из связующих звеньев науки и искусства.

1.1 Эстетика: наука о прекрасном. Математика: прекрасное в науке

Потребность красоты и творчества, воплощающего ее,- неразлучна с человеком, и без нее человек, быть может, не захотел бы жить на свете.

Ф. Достоевский

Добро, Истина, Красота... Еще древние учили о триединстве этих трех ликов культуры. Со временем, увы, это триединство распалось: Истина отошла к науке, Красота - к искусству, Добро вообще повисло в воздухе. Сегодня, как никогда, важно возродить это утраченное триединство. Наука, не освященная гуманистическими идеалами Добра, ведет мир к катастрофе. Искусство, потерявшее луч Истины, погружается в сумерки декаданса. Красота в равной мере должна питать искусство и науку.

Искусство... Мы много спорим об искусстве, хотя и говорим, что о вкусах не спорят. Но раз мы все-таки спорим, значит, возможны какие-то общепринятые точки зрения во вкусах, в оценках произведений искусства, во взглядах на прекрасное. Но есть ли законы красоты и каковы они? Наука... Мы преклоняемся перед ее мудростью, ее успехи окружают нас со всех сторон и кружат нам голову. Но многие ли ощущают, что наука прекрасна, как и искусство? В чем же красота науки?

Но что же такое красота, которая составляет, по его мнению, содержание искусства? Как она определяется и что это такое? Еще на заре цивилизации основатель античной математики Пифагор (VI в. до н. э.) учил: "Все прекрасно благодаря числу". Древнегреческий философ Гераклит (кон. VI в.- нач. V в. до н. э.) указывал на относительность понятия прекрасного: "Самая прекрасная обезьяна безобразна по сравнению с родом людей". Величайший из философов Платон (428-348 гг. до н. э.) писал: "Умеренность и соразмерность всюду становится красотой". Платону вторил его любимый ученик Аристотель (384-322 гг. до н. э.): "Красота состоит в соразмерности и правильном расположении". Средневековые мыслители Аврелий Августин (354-430) и Фома Аквинский (1226-1274) источник прекрасного усматривали в боге. Выдающийся итальянский ученый-гуманист и архитектор Леон Баттиста Альберти (1404-1472) как. истинный представитель эпохи Возрождения свои идеалы и убеждения черпал из греческой классики: "Что такое красота и украшение и чем они между собой разнятся, мы, пожалуй, отчетливее поймем чувством, чем я могу изъяснить это словами. Тем не менее совсем кратко мы скажем так: красота есть строгая соразмерная гармония всех частей, объединяемых тем, чему они принадлежат,- такая, что ни прибавить, ни убавить, ни изменить ничего нельзя, не сделав хуже" (легко Заметить, что определение Альберти перекликается с высказываниями Платона и Аристотеля). В эпоху Просвещения прекрасное рассматривалось как связующее звено между разумом и чувствами, между долгом (разум) и увлечениями (чувства). Широко известна формула Н. Г. Чернышевского (1828-1889): "Прекрасное есть жизнь".

Но пожалуй, наибольшую мудрость в определении формулы прекрасного проявил человек, всю свою жизнь посвятивший служению красоте,- выдающийся немецкий художник эпохи Возрождения Альбрехт Дюрер (1471 -1528): "Что такое красота - этого я не знаю. Но для себя здесь понимаю красоту таким образом: что разные человеческие времена большинством почитать прекрасным, то мы и должны усердно стремиться создавать".

В древнегреческой философии - науке наук - берут начало все будущие философские течения, многие теории и науки. Древними было замечено, что люди познают мир с помощью органов чувств и осмысливают познанное разумом. Чувство и мышление не только два уровня, но и два звена в цепи познания. И как нужна наука о законах мышления - логика, столь же необходима и наука о чувственном восприятии - эстетика. Обе эти науки зарождаются одновременно в Древней Греции.

Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства. Б. Рассел

Раздумья о красоте научного поиска, о величии человеческого духа никогда не переставали волновать мыслящих людей. В чем же заключается красота науки?

Итак, стремясь дать новое определение прекрасного, ученые сформулировали признаки красоты в науке: 1) эстетическое впечатление "возникает только в связи с целесообразным, сложным (трудным) преодолением"; 2) "красиво сведение сложности к простоте"; 3) "всякое математическое оформление научных достижений, если оно наглядно и гармонично, вызывает эстетическое впечатление".

Легко видеть, что формула "красота есть целесообразное, трудное преодоление" перекликается с формулой "красота есть обретение неочевидной истины". Да, Природа прячет свои законы в сокровенных тайниках и открываются они только тому, у когс хватает сил на трудное преодоление. И как вознаграждение в конце пути ожидает ученого красота открывающейся истины. Альберт Эйнштейн (1879-1955) любил повторять, что Бог (т. е. Природа) изощрен но не злонамерен (эта надпись была сделана у Эйнштейна на камине). Изощренность Природы состоит в том что она ловко скрывает от человека свои законы, а ю внешнее проявление выглядит поначалу как полный хаос. Не злонамеренность же Природы означает существование у нее законов и принципиальную возможность их обнаружения в конце целесообразного и трудное преодоления. Познание гармонии Природы, когда лишь нее и кажущееся отпадает, когда истина обретает вели чавую простоту и ясность, и есть высшая красота научного поиска.

Математика несет красоту в любую науку. Строго говоря, этот тезис является следствием предыдущего: красиво сведение сложности к простоте, ибо математика и есть тот инструмент науки, который позволяет, говоря словами основоположника кибернетики Норберта Винера (1894-1964), "находить порядок в хаосе, который нас окружает". Волькенштейн отмечает эту особую роль математики в науке и, следовательно, ее особую эстетическую ценность: "Математика есть область утонченной красоты. Ее формулы выражают сложные соотношение чисел в определенной форме. Поэтому они могут быть красивы, или, как говорят математики, "изящны".

Ни одно человеческое исследование не может называться истинной наукой, если оно не прошло через математические доказательства. Леонардо да Винчи

Среди всех наук Математика пользуется особенным уважением; основанием этому служит то единственное обстоятельство, что ее положения абсолютно верны и неоспоримы, в то время как положения других наук до известной степени спорны, и всегда существует опасность их опровержения новыми открытиями. А. Эйнштейн

Математика раскрывает перед человеком красоту внутренних связей, существующих в природе, и указывает на внутреннее единство мира.

1.2 Наука и искусство - грани творчества

И мы вновь возвращаемся в Древнюю Грецию... Из всех народов античности греки оказали самое сильное влияние на развитие европейской цивилизации. Вероятно, источник греческого гения и в том, что, входя в контакты с великими и более древними восточными цивилизациями, греки сумели не отвергать, а усваивать их уроки, дабы извлечь из них оригинальную культуру, ставшую основой и непревзойденным образцом для дальнейшего развития человечества. Примечательно, что именно восточные греки заложили фундамент философии (Фалес из Милета), математики (Пифагор с острова Самос) и лирической поэзии (Сапфо с острова Лесбос). Своего апогея греческая цивилизация достигает в V веке до н. э. В это время стратег Перикл возводит грандиозные монументы Акрополя, скульпторы Фидий и Поликлет высекают свои бессмертные шедевры, Эсхил, Софокл и Еврипид пишут трагедии, Геродот и Фукидид составляют бесценную хронику древней истории, философы и ученые Зенон, Демокрит, Сократ прославляют торжество человеческого разума. Затем Греция дарит миру РЛЙКИХ философов Платона и Аристотеля, чьи бессмертные идеи третье тысячелетие питают философов его мира, основоположника геометрии, автора знаменитых "Начал" Евклида, величайшего математика древнего мира Архимеда. Была и другая эпоха единого взлета науки и искусства - эпоха Возрождения. Человечество вновь, через тысячу лет, открывало для себя забытые сокровища античной культуры, утверждало идеалы гуманизма, возрождало великую любовь к красоте мира и непреклонную волю познать этот мир. Олицетворением многосторонних интересов человека эпохи Возрождения, символом слияния науки и искусства является гениальная фигура Леонардо да Винчи (1452-1519), итальянского живописца, скульптора, архитектора, теоретика искусств, математика, механика, гидротехника, инженера, изобретателя, анатома, биолога. Леонардо да Винчи - одна из загадок в истории человечества.

Перенесемся же во вторую половину XX века, когда споры о науке и искусстве достигли наивысшего накала. Главная причина, вызвавшая вспышку таких споров, заключается в том, что в условиях современной научно-технической революции наука стала непосредственной производительной силой, охватившей значительную часть общества. Только в нашей стране армия научных работников превышает один миллион человек, что почти в два раза больше армии Наполеона в Отечественной войне 1812 г. Овладение энергией атома и освоение человеком новой стихии - космического пространства - обеспечили современной науке небывалый престиж. Сложилось убеждение, что основная сила человеческого разума должна концентрироваться именно в науке, и прежде всего в математике и физике - столпах всей научно-технической революции. Искусству же отводилась роль падчерицы, и то, что эта падчерица вопреки прогнозам столетней давности всегда мешалась под ногами, только раззадоривало технократов.

Что-то физики в почете,

Что-то лирики в загоне.

Дело не в сухом расчете,

Дело в мировом законе.

Значит, что-то не раскрыли

Мы, что следовало нам бы!

Значит, слабенькие крылья -

Наши сладенькие ямбы... (Б. Слуцкий)

Что же сближает и что разъединяет науку и искусство? Прежде всего, наука и искусство - две грани одного и того же процесса - творчества. Наука и искусство - это дороги, а часто и крутые нехоженые тропы к вершинам человеческой культуры. Таким образом, цель и у науки, и у искусства одна - торжество человеческой культуры, хотя достигается она разными путями.

1.3 Симметрия, пропорция, гармония - слагаемые прекрасного

Еще в глубокой древности человеком было обнаружено, что все явления в природе связаны друг с другом, что все пребывает в непрерывном движении, изменении, и, будучи выражено числом, обнаруживает удивительные закономерности. Пифагорейцы и их последователи всему сущему в мире искали числовое выражение. Ими было обнаружено; что математические пропорции лежат в основе музыки (отношение длины струны к высоте тона, отношения между интервалами, соотношение звуков в аккордах, дающих гармоническое звучание) . Пифагорейцы пытались математически обосновать идею единства мира, утверждали, что а основе мироздания лежат симметричные геометрические формы. Пифагорейцы искали математическое обоснование красоте. Они исследовали пропорции человеческого тела и утвердили математический канон красоты, по которому скульптор Поликлет создал статую "Канон". Вслед за пифагорейцами средневековый ученый Августин назвал красоту "числовым равенством". Философ-схоласт Бонавентура писал: "Красоты и наслаждения нет без пропорциональности, пропорциональность же прежде всего существует в числах. Необходимо, чтобы все поддавалось счислению". Об использовании пропорции в искусстве Леонардо да Винчи писал в своем трактате о живописи: "Живописец воплощает в форме пропорции те же таящиеся в природе закономерности, которые в форме числового закона по знает ученый". Таким образом, пропорциональность, соразмерность частей целого является важнейшим условием гармонии целого и может быть выражена математически посредством пропорций.

"Раз, стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия приятна для глаз? что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно основано? Разве во всем в жизни симметрия?" (Л. Толстой. "Отрочество").

Вместе с Николенькой Иртеньевым из трилогии Льва Толстого задумаемся и мы над тем, почему в природе царит симметрия. Почему симметрично все Живое от микроорганизмов до человека? Наконец, почему симметричное часто ассоциируется с прекрасным? Бабочка парусник махаон - прекрасный пример билатеральной симметрии в природе. На первые два вопроса ответ существует: господство симметрии в природе прежде всего объясняется силой Тяготения, действующей во всей Вселенной. Действием Тяготения или отсутствием такового объясняется то, что и Космические тела, плывущие во Вселенной, и Микроорганизмы, взвешенные в воде, обладают высшей Формой симметрии - сферической (при любом повороте относительно центра фигура совпадает сама с собой). Все организмы, растущие в прикрепленном состоянии (деревья) или живущие на дне океана (морские звезды), т. е. организмы, для которых направление силы тяжести является решающим, имеют ось симметрии (множество всевозможных поворотов вокруг центра сужается д0 множества всех поворотов вокруг вертикальной оси). Наконец, для животных, способных передвигаться в воде, воздухе или по земле, кроме направления силы тяжести, важным оказывается и направление движения животного. Такие животные могут обладать только плоскостью симметрии, которая определяется векторами силы тяжести и направления движения. Биологи эту плоскость симметрии называют билатеральной, а тип симметрии - зеркальным. Ясно, что в случае асимметричного развития животного поворот в одну из сторон был бы для него затруднен и естественным для животного стало бы не прямолинейное, а круговое движение. Хождение же по кругу рано или поздно закончится трагически для животного. Билатеральной симметрией обладает, например, автомобиль, одинаково хорошо поворачивающий и вправо, и влево, чего нельзя сказать о мотоцикле с коляской, который такой симметрией не обладает и постепенно вытесняется автомобилем и своим двухколесным (зеркально-симметричным) собратом.

Любопытно, что переход от сферической симметрии у низших животных к зеркальной у высших (в частности, у человека) пытались объяснить еще древние греки.

Так, в диалоге Платона "Пир" Аристофан рассказывает о том, что первоначально люди были круглыми, "спина не отличалась от груди, рук было четыре, ног столько же, сколько и рук, и у каждого на круглой шее два лица, совершенно одинаковых... Страшные своей силой и мощью, они питали великие замыслы и посягали даже на власть богов... И вот Зевс и прочие боги стали совещаться, как поступить с ними... Наконец, Зевс, насилу кое-что придумав, говорит:

- Кажется, я нашел способ и сохранить людей, и положить конец их буйству, уменьшив их силу. Я разрежу каждого из них пополам, и тогда они, во-первых, станут слабее, а во-вторых, полезней для нас, потому что число их увеличится. И ходить они будут прямо, на двух ногах. А если они и после этого не угомонятся и начнут буйствовать, я, сказал он, рассеку их пополам снова, и они запрыгают у меня на одной ножке".

Симметрия господствует на Земле благодаря силе тяготения. Более того, поскольку эта сила действует повсюду во Вселенной, то и предполагаемые космические пришельцы не могут быть безудержно чудовищами, как их порой изображают, а обязательно должны быть симметричными.

Природа почти симметрична, но не абсолютно симметрична! Так, планетные орбиты, которые еще Пифагором мыслились в виде совершенных окружностей, на самом деле оказались почти окружностями, но все-таки не окружностями, а эллипсами. Нарушение симметрии обнаружено во многих явлениях ядерной физики. Приблизительная симметрия является сегодня одной из научных загадок. Вот что по этому поводу пишет современный американский физик, лауреат Нобелевской премии Ричард Фейнман: "Почему природа столь близка к симметрии? По этому вопросу ни у кого нет никакой разумной мысли. Единственное, что я могу предложить вам,- это старое японское предание. В японском городе Никко есть ворота, которые японцы называют самыми красивыми воротами страны. Они были построены в период большого влияния китайского искусства. Это необычайно сложные ворота, со множеством фронтонов, изумительной резьбой и большим количеством колонн, на основании которых вырезаны драконьи головы, божества и т. п. Но, приглядевшись, можно заметить, что в сложном и искусном рисунке на одной из колонн некоторые из его мелких деталей вырезаны вверх ногами. В остальном рисунок полностью симметричен. Спрашивается: для чего это было нужно? Как говорит предание, это было сделано для того, чтобы боги не заподозрили человека в совершенстве. Ошибка была сделана намеренно, дабы не вызвать зависти и гнева богов.

Перейдем, наконец, к эстетическому содержанию симметрии, к ответу на толстовский вопрос: "почему симметрия приятна для глаз?" Видимо, господством симметрии в природе, о котором мы не случайно так много говорили, и объясняется прежде всего эстетическая ценность симметрии для человека. С детства человек привыкает к билатерально симметричным родителям, затем у него появляются билатерально симметричные друзья; он видит зеркальную симметрию в бабочках, птицах, рыбах, животных, поворотную - в стройных елях и волшебных узорах снежинок, переносную - в оградах парков, решетках мостов, лестничных маршах, бордюрах, которые издревле были любимым декоративным элементом. Человек привыкает видеть в природе вертикальные оси и плоскости симметрии, и вертикальная симметрия воспринимается нами гораздо охотнее. Мы нигде не увидим обои с горизонтальными осями симметрии, ибо это вызвало бы неприятный контраст с вертикальной симметрией растущих за окном деревьев.

Единственная горизонтальная симметрия, которую мы встречаем в природе,- это отражения в зеркале воды. Возможно, в необычности такой симметрии и заключается ее завораживающая сила.

Таким образом, симметрия воспринимается человеком как проявление закономерности, порядка, царящего в природе. Восприятие же закономерного всегда доставляет нам удовольствие, сообщает некоторую уверенность и даже бодрость. "Порядок освобождает мысль",- любил повторять великий французский математик, философ и храбрый воин Рене Декарт (1596-- 1650). Его соотечественник, выдающийся зодчий XX века, авторитет, равного которому в архитектуре не было со времен Микеланджело, Ле Корбюзье (1887-1965) писал: "Человеку необходим порядок; без него все его действия теряют согласованность, логическую взаимосвязь. Чем совершеннее порядок, тем спокойнее и увереннее чувствует себя человек. Он делает умозрительные построения, основываясь на порядке, который продиктован ему потребностями его психики,- это творческий процесс. Творчество есть акт упорядочения".

Итак, симметрия, воспринимаемая человеком как закономерность структуры, как внешнее проявление внутреннего порядка, начинает обладать эстетической ценностью, т. е. воспринимается как красота. Простой пример убеждает в этом. Чернильная клякса сама по себе некрасива. Но стоит перегнуть лист бумаги с невысохшей кляксой пополам, и мы получим кляксу, которая уже производит приятное впечатление. Зеркальная симметрия новой кляксы, т. е. закономерное расположение ее частей, и определяет красоту нашей "рукотворной" кляксы. Знание законов геометрической симметрии сделает такие поиски быстрыми и плодотворными.

Чувство глубочайшего уважения к мощи законов симметрии никогда не ослабевает у того, кто обдумывал изящество и красоту безупречных математических доказательств и сопоставлял это со сложными и далеко идущими физическими и философскими следствиями. Чжень-нин Янг Нобелевская лекция

Примером удивительного сочетания симметрии и Симметрии является Покровский собор (храм Василия блаженного) на Красной площади в Москве. Эта причудливая композиция из десяти храмов, каждый из которых обладает центральной симметрией, в целом Не имеет ни зеркальной, ни поворотной симметрии. Симметричные архитектурные детали собора кружатся в своем асимметричном, беспорядочном танце вокруг его центрального шатра: они то поднимаются, то опускаются, то как бы набегают друг на друга, то отстают, создавая впечатление радости и праздника. Без своей удивительной асимметрии храм Василия Блаженного просто немыслим!

Итак, "сфера влияния" симметрии (а значит, и ее антипода - асимметрии) поистине безгранична. Природа - наука - искусство. Всюду мы видим противоборство, а часто и единство двух великих начал - симметрии и асимметрии, которые во многом и определяют гармонию природы, мудрость науки и красоту искусства.

Пропорция. Слово "пропорция" ввел в употребление Цицерон в I веке до н. э., переведя им на латынь платоновский термин "аналогия", который буквально означал "вновь-отношение", или, как мы говорим, "соотношение". С тех пор вот уже 2000 лет пропорцией в математике называют равенство между отношениями четырех величин а, b, с, d. Пропорция в искусстве также определяет соотношение величин элементов художественного произведения либо соотношение отдельных элементов и всего произведения в целом. В эстетике пропорция, как и симметрия, является составным элементом категории меры и выражает закономерность структуры эстетического образа.

Симметрия воспринимается слишком статично, скованно и только единство симметрии и асимметрии создает подлинную гармонию красоты. Так вот, в качестве меры соотношения симметричного и асимметричного часто и выступает пропорция. Возьмем простой пример: деление отрезка прямой. Если отрезок разделить пополам, зеркально-симметрично, то такое деление выглядит уравновешенным, мертвым. Если же точку деления взять слишком близко к одному из концов отрезка, то новая конфигурация будет чересчур неуравновешенной и беспокойной. Только некоторая "золотая середина", которая в данном случае отнюдь не является геометрической серединой, обеспечит желаемое единство симметрии и асимметрии.

Такое "радующее глаз" деление отрезка, по преданию, было известно еще Пифагору и называлось им золотой пропорцией. Впрочем, скорее всего золотая пропорция была заимствована Пифагором у древних египтян, которые знали ее задолго до Пифагора и которых он посетил в своих странствиях по свету. Золотая пропорция определяется как деление отрезка на две неравные части, при котором меньшая из них так относится к большей, как последняя ко всей длине отрезка. С тех пор золотая пропорция становится общепризнанным каноном искусства. Художник и инженер Леонардо да Винчи, изучавший и восхвалявший золотую пропорцию на протяжении всей своей жизни, называет ее "Sectio aurea" (золотое сечение), а математик и астроном Иоганн Кеплер, обнаруживший золотую пропорцию в ботанике, говорит о ней как о бесценном сокровище, как об одном из двух сокровищ геометрии* и именует ее "Sectio divina" (божественное сечение). Название Леонардо да Винчи сохранилось и сегодня.

Идея Гармонии, как антитеза идеи Хаоса, имеет тысячелетнюю традицию: Хепри и Нун в космологических мифах Древнего Египта, Сат и Асат в гимнах Ригведы, Ин-Ян и Дао в книгах даосских мудрецов, Свет и Тьма в Библии, Космос и Хаос в поэмах Гесиода и Гомера. Несмотря на множество вариантов и оттенков, а порой и отличий между этими двумя величайшими смыслообразами двух великих культур - Востока и Запада, их объединяла единая йдеЯ - идея безмерной пучины первобытия, рождающей в своих клокочущих недрах светлый луч гармония жизни. Эту древнейшую в истории мировой культуры идею не поглотили тысячелетия, и сегодня она ясно видна - будь то в последней мандале Ригведы:

Мрак был сокрыт мраком вначале.

Неразличимая пучина - все это.

То жизнедеятельное, что было заключено в пустоту,

Оно одно было порождено силой жара.

или в первых строках Библии:

В начале сотворил Бог небо и землю. Земля же

была безвидна и пустота, и тьма над бездною,

и Дух Божий носился над водою.

Но истинная древность всегда современна. И удивившись единожды почтенному возрасту древней идеи, сохраненной, словно засушенный цветок, в хрупких фолиантах мировых религий, мы удивляемся дважды, встречая ее расцветшей в самых современных научных теориях. Конец XX века знаменуется бурным развитием статистической теории неравновесных процессов в физических, химических и биологических системах, созданной прежде всего благодаря усилиям нашего соотечественника Нобелевского лауреата Ильи Пригожина и его Брюссельской школы. На наших глазах теория неравновесных процессов перерастает во всеобъемлющую теорию изменения, имеющую самые широкие мировоззренческие следствия. Суть этой теории в сильно упрощенном виде состоит в том, что в открытых системах, т. е. системах, обменивающихся с окружающей средой энергией и веществом и составляющих основу всего мироздания, возникают процессы самоогранизации, т. е. процессы, в ходе которых из физического хаоса рождаются некоторые структуры.

Отметим три важных аспекта, которые выделяют в современных воззрениях на гармонию,- математический, эстетический и художественный. На ранних этапах развития учения о гармонии господствовало ее математическое понимание. Гармония трактовалась как соразмерность, пропорциональность отдельных частей, а также частей и целого. Такое внешнее, формальное толкование гармонии, выделяющее прежде всего количественную математическую сторону, было характерно Для пифагорейцев и мыслителей средневековья. В XVII веке пифагорейские "математические" взгляды на гармонию поднял на щит Иоганн Кеплер. В эпоху Возрождения математическое понимание гармонии постепенно вытесняется эстетическим. В отличие от математического эстетическое понимание гармонии является не просто количественным, а качественным, выражающим внутреннюю природу объекта. В эстетическом понимании гармонии получает развитие мысль Платона о связи гармонии с прекрасным. Поэтому эстетическая гармония связывалась с эстетическим еРезкиванием, с чувством прекрасного. В европейской этике красота природы становится неотделимой от РеДставления о ее гармонии. Более глубокое и диалектическое - художественное понимание гармонии вырабатывается в эстетике нового времени. Художественная гармония - это гармония искусства, это не только математическое соответствие между однородными элементами, но и единство противоположных эстетических категорий: прекрасного и безобразного, трагического и комического, возвышеного и низменного. Благодаря единству и борьбе этих противоречивых категорий художественная гармония приобретает движение и наполняется жизнью.

Итак, гармония - это сложное и многозначное понятие; поэтому гармония так близка и естествоиспытателю, и философу, и художнику. Вот почему современные физики так часто говорят о гармонии природы, искренне веря, что сердцевину мироздания составляют простые и красивые математические закономерности и формулы. "Восприняв от античности идею о математическом истолковании порядка в природе,- пишет В. Гейзенберг,- современное естествознание осуществляет ее, однако, другим... способом... Наука нового времени показала, что в окружающем нас реальном мире неизменными являются не геометрические формы, а динамические законы... Гармонию пифагорейцев, которую еще Кеплер надеялся найти в орбитах небесных светил, естествознание со времен Ньютона ищет в математической структуре законов динамики, в уравнениях, формулирующих эти законы".

Вот почему художники так боготворят гармонию. "Поэт - сын гармонии,- говорил в своей речи "О назначении поэта" А. Блок,- и ему дана какая-то роль в мировой культуре. Три дела возложены на него: во-первых, освободить звуки из родной безначальной стихии, в которой они пребывают; во-вторых, привести эти звуки в гармонию, дать им форму; в-третьих, внести эту гармонию во внешний мир".

Поиски скрытой гармонии - высший удел и ученых, и художников. Это вечный путь человеческой культуры, путь, приносящий и ученым, и художникам муки и радости. А в конце пути, когда "ни прибавить, ни убавить, ни изменить ничего нельзя, не сделав хуже", сияет недосягаемая вершина - Гармония. О трудном пути к этой вершине писано немало. Писал о нем и русский художник В. И. Суриков: "А какое время надо, чтобы картина утряслась так, чтобы переменить ничего нельзя было. Действительные размера каждого предмета найти нужно. Важно найти замок" чтобы все части соединить. Это - математика".

2 Математика и музыка 4 часа

2.1 Пифагор и пифагорейское учение о числе. Пифагорова гамма

Греки совершили открытие, величайшее из когда-либо совершенных человеком: они открыли могущество разума.

М. Клайн

С берегов Средиземноморья - "колыбели европейской цивилизации", с тех давних времен, названных через много веков "весною человечества", дошло до нас имя Пифагора - математика, философа, мистика. Мы не знаем доподлинно портрета Пифагора, не сохранилось ни одной строки из его сочинений; его биография стала легендой, полной невероятных преувеличений, а самого Пифагора назвали "на одну десятую гением, на девять десятых выдумкой". По преданию, вид его был так величествен, что ученикам часто казалось, будто это сам бог Аполлон говорит с ними.

Пифагор - едва ли не самый популярный ученый не только в античности, но и в наши дни. И дело, конечно, не в том, что "таблица Пифагора" смотрит на нас с любой тетрадки в клеточку. Дело в том, что "то ли по счастливому стечению обстоятельств, то ли благодаря гениальной интуиции пифагорейцам удалось сформулировать два тезиса, общезначимость которых подтвердило все последующее развитие науки: во-первых, что основополагающие принципы, на которых зиждется мироздание, можно выразить на языке математики; во-вторых, что объединяющим началом всех вещей служат числовые отношения, которые выражают гармонию и порядок природы". Так определяет роль Пифагора в современной науке американский математик М. Клайн. В Кротоне Пифагор учредил нечто вроде религиозно-этического братства или тайного монашеского ордена, члены которого обязывались вести так называемый пифагорейский образ жизни. Это был одновременно и религиозный союз, и политический клуб, и научное общество. Система жизненных принципов и правил, проповедуемая Пифагором, и сейчас достойна подражания. Так, Пифагор учил: "беги от всякой хитрости, любым орудием отсекай от тела болезнь, от души - невежество, от утробы - роскошество, от семьи - ссору, от всего, что есть - неумеренность". День пифагорейцу надлежало заканчивать вопросом:

"Не допускай ленивого сна на усталые очи,

Прежде чем на три вопроса о деле дневном не ответишь:

Что я сделал? чего не сделал? и что мне осталось сделать?"

и начинать с вопроса:

"Прежде чем встать от сладостных снов, навеваемых ночью,

Думой раскинь, какие дела тебе день приготовил".

Сам Пифагор начинал занятия ранним утром, успокоив душу игрою на лире и пением стихов Гомера, предпочитал уединенные прогулки, замечая при этом, что "где тише всего, там и краше всего". Система этических правил Пифагора была собрана в своеобразный моральный кодекс пифагорейцев - "Золотые стихи". Пифагор предписывал чтить старейших, "ибо всюду предшествующее почетнее последующего". Пифагор высоко ценил дружбу, считая, что у друзей все общее и что друг - это второе я. Скромность и пристойность он видел в том, чтобы не хохотать и не хмуриться, избегать издевок и пошлых рассказов. В еде он довольствовался хлебом, медом и овощами и воздерживался от животной пищи^*. Носил Пифагор ослепительно белые одежды. К сожалению, реальные и вызывающе глубокое уважение к личности Пифагора сведения были перемешаны со множеством сказок и легенд, которые со врежем породили несерьезное отношение Пифагору как исторической личности. Легенды наперебой объявляли Пифагора чудотворцем: сообщали, что у него было золотое бедро; что люди видели его одновременно в двух разных местах говорящим со своими учениками; что однажды, когда он с многочисленными спутниками переходил реку и заговорил с ней, река вышла из берегов и воскликнула: "Да здравствует Пифагор!"; что он предсказывал землетрясения, останавливал повальные болезни, отвращал ураганы, укрощал морские волны и т. д.

Ритуал посвящения в члены пифагорейского братства был окружен множеством таинств, разглашение которых сурово каралось. Но и попав в орден после строгого отбора и испытательного периода, новички могли только из-за занавеса слушать голос Учителя, видеть же его самого разрешалось только после нескольких лет аскетической жизни. "Стремление уйти от мира, замкнутая монашеская жизнь, вегетарианство и общность имущества встречались у многих сект. Но что отличало пифагорейцев от всех других - это способ, при помощи которого они считали возможным достигнуть очищения души и соединения с божеством; это делалось именно при помощи математики. Математика была одной из составных частей их религии". Эта меткая характеристика пифагорейского братства принадлежит известному голландскому математику и историку науки Б. Л. ван дер Вардену.

Итак, именно в математике, в познании количественных отношений, видели пифагорейцы ключ к разгадке мировой гармонии, постижение которой и составляло-смысл их жизни. Но почему постижение всеобщей гармонии ставилось высшей жизненной целью? Дело в том, что пифагорейцы верили в бессмертие души и переселение души человека в животных^**. Поэтому они полагали, что посвящение в тайны всеобщей гармонии, т. е. стремление к истине, приближает душу человека к божеству, создавшему эту гармонию, вследствие чего душа сможет освободиться от дальнейших перевоплощений. Известна легенда, рассказывающая, что однажды, увидев, как били собаку, Пифагор сказал: "Перестаньте ее бить, в этой собаке живет душа моего друга: я узнал его по голосу".Учение Пифагора носило эзотерический, т. е. тайный, характер и не излагалось письменно, почему и не сохранилось никаких письменных трудов самого Пифагора. В силу этого, а также в силу существовавшей в античности традиции приписывать результаты открытий учеников своему учителю практически невозможно определить, что сделал в науке сам Пифагор, а что - его ученики и представители пифагорейской школы. Споры вокруг "пифагорейского вопроса" ведутся третье тысячелетие, однако общего мнения не существует и поныне. Вот почему принято осторожно говорить "пифагорейское учение", а не "учение Пифагора".

Звездчатый пятиугольник, или пентаграмма,- пифагорейский символ здравия и тайный опознавательный знак. Обет молчания, даваемый пифагорейцами, нашел отражение в символе "бык на языке", что на современный лад означает "держи язык за зубами". Вообще, пифагорейцы имели множество знаков и символов, которые были своего рода заповедями, например: "через весы не шагай", т. е. не нарушай справедливости; "огня ножом не вороши", т. е. не задевай гневных людей обидными словами; "не ешь сердца", т. е. не подтачивай душу страстями или горем. Но главным пифагорейским символом - символом здоровья и опознавательным знаком - была пентаграмма или пифагорейская звезда - звездчатый пятиугольник, образованный диагоналями правильного пятиугольника. Звездчатый пятиугольник обладает замечательными математическими свойствами, которые мы рассмотрим в главе 15. Он содержит все пропорции, известные пифагорейцам: арифметическую, геометрическую, гармоническую и так называемую золотую. Видимо, поэтому пентаграмма и была выбрана в качестве пифагорейского символа. Нарисованная пентаграмма была тайным знаком, по которому пифагорейцы узнавали друг друга. Согласно легенде, когда один пифагореец умирал на чужбине и не мог расплатиться с гостеприимным хозяином дома, ухаживавшим за ним, он велел хозяину нарисовать на стене своего дома пентаграмму. "Если когда-нибудь мимо пройдет пифагореец, он обязательно сюда заглянет",- сказал умиравший. Действительно, через несколько лет другой странствующий пифа гореец увидел знак, расспросил о случившемся хозяина и щедро вознагради его. Однако в первоначальном виде пифагорейский союз просуществовал недолго и к концу VI века (ок. 510 г. до н. э.) подвергся кровавой расправе. Пифагорейцы бежали из Кротона в другие города, что во многом способствовало распространению учения Пифагора по всей Греции и даже за ее пределы. Сам Пифагор удалился в город Метапонт, расположенный неподалеку от Кротона, где и провел остаток своей жизни. Примечательно, что отправным пунктом в пифагорейском учении о числе была музыка. Именно в музыке была первые обнаружена таинственная направляющая роль чисел в природе. По преданию, сам Пифагор установил, что приятные слуху созвучия получаются лишь в том случае, когда длины струн, издающих эти звуки, относятся как целые числа первой четверки: 1:2, 2:3, 3:4 (см. гл. 6). Это открытие потрясло Пифагора и долго вдохновляло его учеников на поиски новых числовых закономерностей в природе. Открытие математических закономерностей в музыкальных созвучиях послужило первым "экспериментальным" подтверждением пифагорейской философии числа. "Открытие Пифагора... было первым примером установления числовых связей в природе,- читаем мы в "Фейнмановских лекциях по физике".- Поистине должно быть было удивительно вдруг неожиданно обнаружить, что в природе есть факты, которые описываются простыми числовыми отношениями". С этого времени музыка, точнее теория Музыки или учение о гармонии, занимает Почетное место в пифагорейской системе Знаний. "Музыкантов"-пифагорейцев интересует не столько музыкальное искусство, реальная музыка звуков, сколько е математические пропорции и соотношения, которые, как считалось, лежат в основе музыки. Многие греческие математики, в том числе Евклид (III в. до н. э.) и Клавдий Птолемей (85? -165?), посвятили музыкальным созвучиям и построению музыкальной шкалы специальные сочинения. Впрочем, поиски математических закономерностей в музыкальных созвучиях вели и через два тысячелетия такие великие математики, как Иоганн Кеплер, Готфрид Лейбниц, Леонард Эйлер. Идея музыкальных соотношений настолько увлекла пифагорейцев, что они пытались обнаружить их всюду. В конце концов эта идея приняла "космические масштабы" и переросла в идею "всеобщей гармонии". Пифагорейцы утвердились в том, что вся Вселенная устроена на основе музыкальных, т. е. простых числовых, соотношений, что движущиеся планеты издают "музыку небесных сфер", а обычная музыка является лишь "отзвуком" царящей всюду "всеобщей гармонии".

Таким образом, музыка и астрономия были сведены пифагорейцами к анализу числовых закономерностей, т. е. к арифметике и геометрии. Все четыре дисциплины стали считаться математическими и называться одним словом - "математа". Пифагорейское отношение к музыке как точной науке сохранилось и в средние века. Так, квадривиум (буквально - пересечение четырех дорог) - повышенный курс светского образования в средневековых университетах - состоял из четырех предметов: музыки, арифметики, геометрии и астрономии. "Высшая наука - математика - подразделяется на следующие искусства: арифметику, музыку, геометрию и астрономию - это определение римского писателя VI века Кассиодора (ок. 487- ок. 578).- Арифметика - учение о количестве, выражаемом числом, музыка же - учение, которое рассматривает числа по отношению к явлениям наблюдаемым в звуке". Вместе с тривииумом, содержавшим грамматику, риторику и диалектику, квадривиум составлял так называемые "семь свободных искусств" Это был, по мнению Кассиодора, своп элементарных знаний, необходимых монахам для понимания Библии, которму суждено было на протяжении целого тысячелетия представлять систему средневекового образования.

Как видим, термины "наука" и "искусство" в далекие времена античности практически не различались. Пифагорейцы называли математику и музыку родными сестрами. С тех пор дороги математики и музыки разошлись настолько, что их сопоставление сейчас многим покажется просто недоразумением. А ведь музыка пронизана математикой, как и математика полна поэзии и музыки! Это прекрасно чувствовали древние греки, и доказательство тому - содержание следующей главы.

2.2 "Космическая музыка": от Платона до Кеплера

В наш бурный век космической тематикой вряд ли кого удивишь. "Космическая музыка" - это нечто вибрирующее, электронное из фильмов о летающих тарелках и инопланетянах - тоже стала привычной. Но вот то, что задолго до нашей эры, во времена, когда человечество "летало" только на восковых крыльях в мифах о Дедале и Икаре, была своя "космическая музыка", многим, возможно, покажется удивительным. По преданию, слово "космос", первоначально означавшее прекрасно устроенный, ввел в обиход Пифагор. "Скажи мне, ...разве есть что-либо стройное и прекрасное, что не было бы подражанием миру. Отсюда имя "Космос", которое греки дали ему",- вторил Пифагору через полтысячелетия Апулей. Из античности термин "космос" перешел в современную науку как синоним слова "вселенная". Итак, космос для пифагорейцев - это гармоничное, пропорциональное строение мира. Сами же пропорции, как мы уже видели, мыслились греками музыкально" поэтому и весь космос оказывался гармонично устроенным и музыкально звучащим телом. Согласно пифагорейским представлениям, планеты располагались на небесных сферах и совершали вместе с ними круговое вращение. Тогда, как и все движущиеся тела, вследствие трения об эфир они издавали звуки, которые соединялись в музыкальные созвучия. Так рождалась чудесная музыка - "мировая Музыка", или "гармония сфер", без коброй мир бы распался. Сама же музыка - это первое из искусств, доставляющих людям радость,- являлась, по их мнению, отражением гармонии, царящей среди небесных сфер.

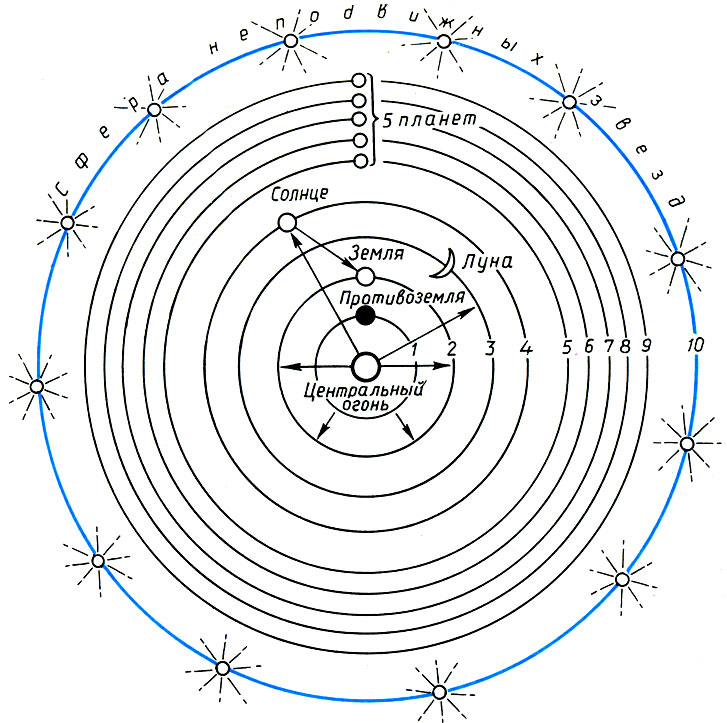
Система мира по Филолаю

Учение о музыке сфер - самый туманный и вместе с тем поэтичный мотив пифагорейской эстетики. Он имел тысячи вариантов, оттенков и тысячелетнюю традицию, начиная от Пифагора и Платона до "Гармонии мира" Иоганна Кеплера, написанной уже в XVII веке. Разумеется, учение о "космической музыке" для нас, современников космических полетов, не более как красивая сказка, и расскажем мы эту сказку, чтобы показать, насколько сильным было музыкальное начало во всем античном мировоззрении. Кроме того, как и во всякой сказке, в этом учении рассыпаны зерна истины, позволяющие увидеть глубокие параллели в развитии человеческой мысли. Внутреннее устройство пифагорейского космоса напоминало своеобразную музыкальную шкатулку: каждая из десяти движущихся сфер издавала некоторый звук. "Когда несутся Солнце, Луна и еще столь великое множество таких огромных светил со столь великой быстротою, невозможно, чтобы не возникал некоторый необыкновенный по силе звук",- утверждает неизвестный пифагорейский автор возможно Филолай. Высота звука определялась скоростью движения сферы, зависящей от расстояний между сферами, а последние находились в той же пропорции, что и интервалы музыкальной гаммы. Таким образом, колеблемый движением сфер эфир издает чудесную мировую музыку. Однако человеческое ухо не слышит этой ни с чем не сравнимой музыки. Как рожденный на берегу моря человек перестает в конце концов различать беспрестанный рокот волн, так и слух человека привык и не замечает гармонического звучания небесных сфер. Итак, согласно пифагорейцам, небесная музыка изначально незримо живет в человеке. Вот почему человеческая душа охотно откликается на обычную земную музыку, которая является лишь подражанием небесной; вот почему из всех искусств музыке в античности отводилась исключительная роль.

Дальнейшее развитие пифагорейское учение о гармонии сфер получило в трудах Платона. Платон исходит из геоцентрической системы космоса: центром мироздания. Для него является неподвижная Земля, вокруг которой на семи сферах^* вращаются Луна, Солнце, Венера, Меркурий, Марс, Юпитер, Сатурн. Далее следует сфера неподвижных звезд. Несостоятельность Центрального Огня и Противоземли ко времени Платона была уже осознана.

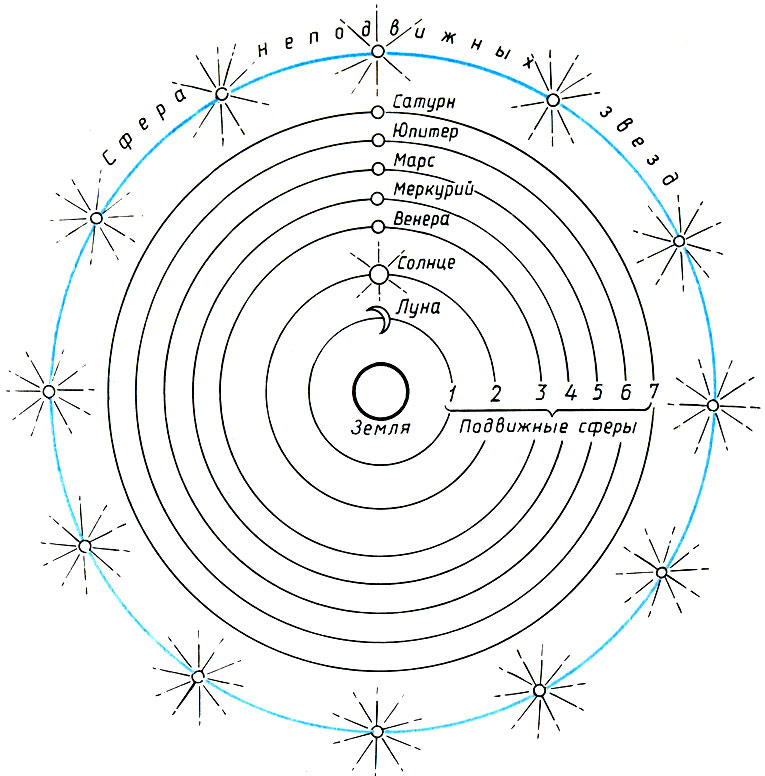
Заключительные аккорды "космической музыки" прозвучали в работах Иоганна Кеплера (1571 -1630) - выдающегося немецкого математика, физика, астронома. Следуя пифагорейско-платоновской традиции, Кеплер верил, что в основе мироздания лежат простые числовые соотношения и совершенные геометрические формы.

Не следует спешить обвинять Кеплера в мистицизме, богоискательстве, числовых спекуляциях и увлечении отжившими античными теориями. Правильнее видимо, вспомнить о времени, в которое он жил и творил: XVI век закончился костром на площади Цветов в Риме, где 17 февраля 1600 Г. был сожжен Джордано Бруно. Следует вспомнить трагическую историю матери Кеплера, Катерины Кеплер, которую публично объявил ведьмой и процесс над которой тянулся долгие 6 лет. Обвиняемую заковывали в цепи, ставили перед палачом с орудиями пыток, и только искусные действия ее сына Иоганна, который сам вел защиту, позволили выиграть процесс у церковных мракобесов. "Арестованную, к сожалению, защищает ее сын, господин Иоганн Кеплер, математик",- свидетельствовал судебный писец. Только в родном городе Кеплера Вейле с 1615 по 1629 г. ужасная смерть постигла 38 "колдуний". Вот в какое время рождалось современное естествознание!

Поискам гармонических соотношений посвящена одна из глав книги "Гармония мира" (1619), которую он считал своей вершиной: "жребий брошен. Я написал книгу либо для современников, либо для потомков..." Кеплер установил семь основных гармонических интервалов (консонансов): октаву (2/1), большую сексту (5/3), малую сексту (8/5), чистую квинту (3/2), чистую кварту (4/3), большую терцию (5/4) и малую терцию (6/5), из которых он выводит весь звукоряд как мажорного, так и минорного наклонения. После долгих поисков гармонических соотношений "на небе", проделав огромную вычислительную работу, Кеплер наконец установил, что отношения экстремальных (наибольших и наименьших) угловых скоростей^* для некоторых планет близки к гармоническим: Марс - 3/2, Юпитер - 6/5, Сатурн - 5/4. "Солнце гармонии засияло во всем блеске... Небесные движения есть не что иное, как ни на миг не прекращающаяся многоголосая музыка". И здесь Кеплера не оставляет буйная фантазия. Небольшие расхождения теории и эксперимента он объясняет тем, что небесный секстет должен звучать одинаково согласованно и в миноре, и в мажоре, а для этого ему необходимо иметь возможность перестраивать свои инструменты. Далее Кеплер утверждает, что Сатурн и Юпитер "поют" басом, Марс - тенором, Земля и Венера - альтом, а Меркурий - дискантом. Никаких математических "доказательств" здесь он не приводит. Да и сам Кеплер устал в поисках всеобщей гармонии: "Мой мозг устает, когда я пытаюсь понять, что я написал, и мне уже трудно восстановить связь между рисунками и текстом, которую я сам когда-то нашел..." Занималась заря нового естествознания: на смену фантазиям Кеплера шли уравнения Ньютона. Красивая сказка о музыке сфер доживала свой век, и работы Кеплера были ее лебединой песней.

Я, как древний Коперник, разрушил

Пифагорово пенье светил

И в основе его обнаружил

Только лепет и музыку крыл.

(Н. Заболоцкий)

2.3 Математический строй музыки. Пропорции музыкальной гаммы

Настоящая наука и настоящая музыка требуют однородного мыслительного процесса.

А. Эйнштейн

Музыкальная гамма разделена на пропорциональные части; она буквально пронизана пропорциями, а пропорциональность, как мы знаем, является одним из объективных критериев красоты.

Чтобы иметь возможность переходить из лада в лад и из тональности в тональность, строй должен быть равномерным, т. е. иметь одинаковые высотные расстояния (интервальные коэффициенты) между звуками. Казалось бы, что проще: нужно разделить каждый тон-интервал пополам на два полутона, т. е. получить еще пять дополнительных звуков, и шкала пифагорова строя станет равномерной. Но вот тут-то и таилась основная трудность. Дело в том, что половина тона в точности не равна полутону (256/243≈1,0545) (см. с. 105). Поэтому если в качестве единого масштаба строя взять полутон т е заменить на него имеющиеся в (8.1) два полутона 256/243, то эти 12 новых полутонов приведут нас не точно в октаву (2), а чуточку выше: Интервал между октавой, полученной шагами по 12-равномерным полутонам и чистой октавой равен (9/8)⁶:2 ≈ 1,0136 и называется пифагоровой коммой^*.

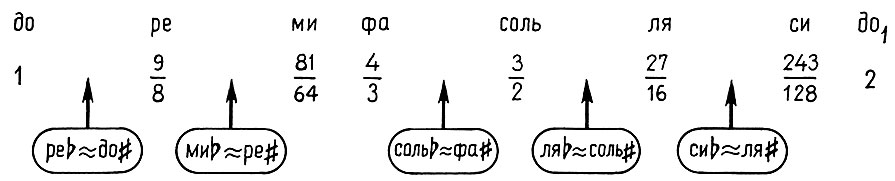
Какие из этих дополнительных звуков взять: с бемолями или диезами? Для музыкантов, играющих на инструментах с нефиксированной высотой звуков (скрипачей, например), эта проблема не стоит. Они берут и те и другие. В результате звучание скрипки становится более выразительным и контрастным, так как в ладе обостряются тяготения неустойчивых звуков к устойчивым. Этим во многом объясняется то "волшебное пение" скрипки, которое доступно только ей одной. (Каким тонким является инструмент скрипка, убеждает простой пример из книги известного венгерского скрипача Карла Флеша "Искусство скрипичной игры": "Пусть на струне ля необходимо сыграть два звука ля и си-бемоль второй октавы. Разница между этими звуками равна 60 Гц. Расстояние на грифе - 2 мм, следовательно, на одно колебание струны приходится 1/30 мм. Предполагая, что ля взято чисто, и желая сыграть математически чисто си-бемоль, мы должны поставить палец в нужное место струны с точностью до 1/30 мм". Насколько же чувствительными должны быть слух и пальцы скрипача, чтобы отмерить расстояние с точностью до 1/30 мм (это 33 микрона)! )

Что касается инструментов с фиксированной высотой звуков, то введение десяти дополнительных звуков на семь основных слишком усложнило бы и сами инструменты, и игру на них. Тем более что и это не решало окончательно проблему и более тонкие построения требовали все новых и новых звуков. На сегодня в теории музыки известна масса строев с числом ступеней от 17 до 84! Но все они так и остались в кабинетах теоретиков. Практика же, руководствуясь мудрым критерием простоты (и красоты), оставила только пять дополнительных звуков: по одному в каждом из целых тонов. Они и стали черными (дополнительными) клавишами фортепиано. Так в октаве стало 12 звуков. Поскольку каждая пара дополнительных звуков отличалась лишь на пифагорову комму (это легко проверить самостоятельно), то их попросту приравняли между собой (до-диез стал равен ре-бемолю и т. д.).

Есть и второй существенный недостаток пифагорова строя. Его заметил еще во II веке древнегреческий ученый пифагореец Дидим. Дело в том, что пифагорова терция (81/64) при гармоническом, т. е. одновременном, исполнении обоих тонов, образующих терцию, звучит слишком напряженно. Дидим предложил заменить пифагорову терцию (81/64) так называемой "чистой терцией" (5/4 = 80/64), которая гармонически звучит значительно приятнее, хотя, как видим, лишь чуть-чуть отличается от пифагоровой терции. Разность пифагоровой и чистой терций (81/64:80/64 = 81/80≈1,0125) называется ди-димовой коммой и приблизительно равна 1/10 целого тона.

...В XIV веке в Европе получает широкое распространение орган, ставший официальным инструментом католической церкви. С развитием органа развивается и многоголосие, которого не знала ни Древняя Греция, ни раннее средневековье. В течение столетий орган настраивался в пифагоровом строе. Никакого другого строя средневековье не знало. Но пифагоровы терции звучали на органе особенно жестко и не давали покоя музыкантам.

Вначале, разумеется, были попытки улучшить чистый строй, который сохранял главный недостаток пифагорова строя: невозможность безболезненного перехода из тональности в тональность. Естественным желанием при решении этой проблемы было увеличить количество звуков в октаве. Сейчас трудно сказать, кому первому пришла идея равномерно разделить октаву (а вместе с ней и пифагорову комму) на 12 равных частей. Идея эта была подготовлена самой логикой развития музыкального строя и, как говорят в таких случаях, носилась в воздухе. Но изложение этой идеи мы находим опять-таки в энциклопедическом труде Мерсенна "Универсальная гармония". Здесь Мерсенн дал математическое описание нового строя и рассчитал его интервальные коэффициенты. Суть нового метода заключалась в следующем. И пифагоров, и чистый строй не замкнуты, т. е. звук, полученный в результате 12 ходов по квинтам вверх или вниз, не является точным октавным повторением исходного звука, а отличается от него на пифагорову комму. На протяжении столетий наибольшее, что позволяли себе теоретики музыки,- это перегонять комму по гамме с места на место. Комма нетронутой блуждала по гамме и время от времени заявляла о себе в завывании "волков". Так вот, Мерсенн предложил сузить полутона так, чтобы они точно укладывались в октаву. Тем самым он равномерно распределил пифагорову комму по всем 12 полутонам, и она как бы "растворилась" в гамме: стала незаметной.

Однако новая система Мерсенна была принята в штыки. Даже приятель Мерсенна по иезуитскому коллежу математик Декарт был возмущен надругательством над чистотой консонансов, а музыкантов, которые рискнут воспользоваться новой темперацией, назвал невеждами, не имеющими никакого представления о законах музыкальной науки. "Что касается Ваших музыкантов,- писал Мерсенну Декарт,- то какими умелыми Вы бы их ни делали, я должен сказать, что они или издеваются, или насмехаются, или никогда ничего не понимали в теории музыки". Чистота звучания и простота целочисленных отношений для консонансов, идущие от родоначальника европейской науки Пифагора, представлялись Декарту нерушимыми. Таким образом, потребовалось еще более полувека, чтобы новая система завоевала себе право на жизнь.

Выдающийся немецкий композитор Георг Фридрих Гендель (1685-1759) не принял новшества. Отказ от совершенных консонансов возмущал его. К счастью, равномерная темперация нашла сторонника в лице сверстника Генделя, великого немецкого композитора и органиста Иоганна Себастьяна Баха (1685-1750). В простоте и математической строгости равномерной темперации Бах гениально предвидел подлинный путь развития музыки. Предвидения Баха сбылись: равномерная темперация сегодня лежит в основе всей мировой музыки. Для демонстрации возможностей нового строя Бах написал свое бессмертное произведение "Хорошо темперированный клавир", основной целью которого было ознакомить играющих на клавире со всеми двадцатью четырьмя (12-мажорными и 12-минорными) тональностями хроматической гаммы нового "хорошо согласованного" строя. Бах хотел показать равноценность всех тональностей при новой системе настройки клавира и вместе с тем выявить характерную окраску каждой тональности. На титульном листе "Хорошо темперированного клавира" значилось: "Для пользы и употребления жадного до учения музыкального юношества, как и для особого времяпрепровождения тех, кто уже преуспел в этом учении, составлено и изготовлено Иоганном Себастьяном Бахом - в настоящее время великокняжеским Ангальт-Кетенским капельмейстером и директором камерной музыки. В году 1722".

И все-таки является ли 12-звуковая равномерная темперация "абсолютной истиной" в музыке? Разумеется, нет! Спор Баха и Генделя продолжается. Музыкантов с особо тонким слухом раздражают "тупые" консонансы темперированного строя. Чайковский после отдыха на природе болезненно ощущал недостатки темперированной музыки, и прежде всего собственной. Известно, как мучился Скрябин, не находя в рояле чистых интервалов. В последние годы жизни Скрябин пытался сконструировать рояль с дополнительными тонами, но неожиданная смерть не позволила осуществить задуманное. Наш соотечественник и современник, крупнейший пианист XX века Святослав Рихтер признается, что он физически старается преодолеть темперацию рояля при помощи звукоизвлечения, придавая диезным и бемольным звукам, когда это нужно, различную тембровую окраску. Поиски новых равномерных темперации продолжаются. Разработаны 24-, 48- и 53-зву-ковые равномерные темперации. На каждую из них специально написана музыка и сконструированы музыкальные инструменты. Но все они практического распространения не получили. Возможно, новые темперации ждут еще нового Веркмейстера и нового Баха...

Музыкальная гостиная (разучивание и исполнение песен, в которых есть математические термины, понятия)

3 Математика и архитектура 5 часов

3.1 Архитектура = (наука + техника)*искусство

"Прочность - польза - красота",- говорит формула архитектуры Витрувия. Прочность не случайно стоит в ней на первом месте. Вся история архитектуры есть история созидания прочности, история борьбы с действием всемогущей силы тяготения. Недаром самый первый строительный кодекс, составленный в царствование вавилонского царя Хаммурапи за 1800 лет до нашей эры, гласит: "Если строитель построил дом для человека, и работа его не крепка, и дом, построенный им, обвалился и убил владельца, то строитель сей должен быть казнен". (Эта запись вытесана на колонне, ныне хранящейся в парижском Лувре.)

Но если относительно "прочности" у архитекторов никогда сомнений не возникало, то "польза" и "красота" являются предметом постоянных дискуссий. Впрочем, дискуссии о красоте и целесообразности (пользе) не являются привилегией одних только архитекторов. Это общеэстетическая проблема, уходящая корнями в седую древность. "Прекрасно то, что хорошо служит данной цели",- учит Сократ. "Дома строят для того, чтобы в них жить, а не для того, чтобы ими любоваться",- вторил Сократу через 2000 лет Фрэнсис Бэкон. Увлечение формулой Бэкона еще через 300 лет привело к тому, что безликие фасады со скоростью произрастания сорняков расплодились по всему земному шару. Невозможно стало отличить не только два новых дома, но и два новых района и даже два новых города. Архитектурная безликость стала притчей во языцех, сделав возможными смешные коллизии типа той, что произошла в пьесе Э. Брагинского и Э. Рязанова "С легким паром!". Надо сказать, что на сегодняшний день ошибочность увлечения одной только пользой в архитектуре осознана всеми и делаются серьезные шаги по преодолению этого заблуждения.

Есть и другая крайность во взглядах На соотношение пользы и красоты. Известный нам Джон Рескин говорил: "Искусство - это то, что бесполезно. Как только вещь становится полезной, она более не может быть красивой". Англичанина Рескина поддерживал француз Теофил Готье: "По-настоящему прекрасным является только то, что ничему не служит". По-видимому, те же взгляды на соотношение пользы и красоты имели и фараоны Древнего царства, жившие за ,4500 лет до Рескина и Готье. Во всяком случае, построенные ими пирамиды останутся в истории человечества непревзойденным образцом самого грандиозного и самого бесполезного сооружения. Только в условиях рабовладельческого строя возможна была такая бессмысленная трата человеческой энергии, когда сто тысяч рабов в течение двадцати лет возводили гробницу для одного из смертных - фараона Хеопса. Внутренний, полезный объем пирамиды настолько ничтожен, что ее вообще с трудом можно отнести к архитектурному сооружению. Зато прочность пирамид недосягаема. Желая прославить своего фараона в веках, древнеегипетские зодчие из всех геометрических тел выбрали именно пирамиду. Выбор этот не случаен, ибо в условиях земного тяготения пирамида является наиболее устойчивой конструкцией, способной существовать в веках без риска обвалиться или рассыпаться. Главное правило устойчивости конструкции - уменьшение ее массы по мере увеличения высоты над землей - выражено в пирамиде с предельной ясностью и симметрией. Рациональность, "полезность" геометрической формы пирамиды заставляют забыть о ее утилитарной бесполезности. Именно эта геометрически оправданная форма пирамиды, подчеркнутая ее циклопическими размерами и точной системой пропорций, придает пирамиде ни с чем не сравнимую выразительность, особую красоту и величие, вызывает ощущение вечности, бессмертия, мудрости и покоя.

Все минет. Как льется вода,

Исчезнут в веках города,

Разрушатся стены и своды,

Пройдут племена и народы;

Но будет звучать наш завет

Сквозь сонмы мятущихся лет!

Что в нас, то навек неизменно.

Всё призрачно, бренно и тленно,-

Песнь лиры, созданье резца.

Но будем стоять до конца.

Как истина под покрывалом

Изиды, Лишь, мы, Пирамиды!

(В. Брюсов)

Простейшей и древнейшей архитектурной конструкцией является стоечно-балочная система. Ее прототипом был дольмен - культовое сооружение, состоящее из двух вертикально поставленных камней, на которые наши предки водрузили третий горизонтальный камень. Назначение дольмена до конца не выяснено. Но ясно одно: дольмен - это гимн челочка о преодолении силы тяжести, это Вступление к грандиозной архитектурной симфонии будущего.

Разумеется, стоечно-балочная конструкция проигрывала пирамиде в устойчивости и распределении веса, но она позволяла создавать внутренние объемы и, безусловно, явилась выдающимся завоеванием человеческой мысли. Главным же недостатком такой конструкции было то, что камень плохо работает на изгиб. Каменный брус сечением 10 X10 см и длиной 1 м 34 см обламывается под действием собственного веса. Вот почему в храме Амона в Карнаке мы видим такой лес колонн. Зато камень прекрасно работает на сжатие. Это свойство камня и дало жизнь новой архитектурной конструкции - арке, а затем и своду.

Родившись в Месопотамии и Персии, арочно-сводчатая конструкция была доведена римлянами до совершенства и стала основой древнеримской архитектуры. Арочно-сводчатая конструкция позволяла римлянам возводить гигантские сооружения. Это амфитеатр Флавиев (Колизей - от лат. colosseus - колоссальный; 75-80 гг.) - самое высокое (48 м) из сохранившихся сооружений античного Рима, вмещавшее 56 тысяч зрителей. Три яруса арок Колизея являются необходимым элементом его конструкции и неотъемлемой частью его архитектурной формы. Построенный за 10 лет, впоследствии Колизей в течение многих веков использовался как каменоломня. Это гигантские термы (бани) Каракаллы (нач. III в.) и Диоклетиана (нач. IV в.) в Риме, вмещавшие одновременно до 3 тысяч посетителей. Римские термы имели мощные цилиндрические и крестовые своды огромной высоты, были пышно украшены мозаикой, скульптурой, росписями, имели залы для омовения, массажа, сухого потения, гимнастических упражнений и даже библиотеки и походили скорее на дворцы. Это система арочных водоводов-акведуков (пролет арок - от 5 до 25 м, высота - более 40 м, общая протяженность - до 60 км), которые стали неотъемлемой частью римского пейзажа. И наконец, вершина древнеримского строительного искусства - Пантеон - храм всех богов. Мы уже отмечали, что в "классе каменных куполов" 43-метровый купол Пантеона в истории зодчества остался недосягаемым. Но Пантеон не только вершина научных и технических достижений древнеримских строителей, а и шедевр архитектурного искусства. В интерьере Пантеона достигнута завораживающая гармония между высотой и диаметром сооружения, которая имеет простое математическое выражение: высота стен Пантеона равна радиусу полусферы его купола, т. е. весь Пантеон как бы наброшен на 43-метровый шар. Цельность и величественность Пантеона оказали огромное влияние на многие поколения архитекторов.

Стрельчатая арка по сравнению с полуциркульной является более совершенной конструкцией: она вызывает меньший боковой распор, а следовательно, и меньший расход камня. Очевидно также, что стрельчатая арка имеет более сложную геометрическую форму по сравнению с полуциркульной, которая строится одним движением циркуля. Таким образом, на примере трех конструкций - стоечно-балочной, арочной и стрельчатой - мы видим, что по мере совершенствования конструкции усложняется и ее геометрия. Современная архитектура подтверждает эту закономерность. Стрельчатая арка привнесла в готическую архитектуру два конструктивных новшества. Во-первых, стрельчатые своды стали выполнять на нервюрах - каменных ребрах, несущих независимые друг от друга части свода - распалубки. Нервюры служат как бы скелетом свода, они воспринимают на себя основную нагрузку. В результате конструкция свода становится более гибкой: она может выдерживать те деформации, которые для монолитного свода окажутся губительными. Таким образом, нервюры явились прототипом современной каркасной конструкции. Во-вторых, боковой распор от стрельчатого свода средневековые зодчие решили гасить не в самих стенах, несущих этот свод, а вне их. Для этого за пределами внутреннего пространства готического собора ставились специальные опоры - контрфорсы, нагрузка на которые передавалась с помощью арочных конструкций - аркбутанов. Аркбутаны, словно растопырившиеся ребра рыбьего скелета, окружали снаружи готический собор.

XIX век можно назвать "железным веком" в истории человечества: железные дороги и паровые машины, первый железный мост через Темзу (1816), первые застекленные металлические крыши (типа крыши московского ГУМа), металлические купола, быстро побившие недосягаемые древнеримские рекорды, и металлические пролеты, превысившие к концу века 100-метровый рубеж. В 1889 г. к открытию Всемирной выставки в Париже как символ победоносного шествия металла в технике и архитектуре была построена знаменитая Эйфелева башня по проекту французского инженера Гюстава Эйфеля (1832-1923). Она сразу вдвое перекрыла все рекорды по преодолению высоты, взметнувшись вверх на 312,6 метра! Так был побит самый долговечный рекорд в истории человечества: ведь пирамида Хеопса в течение 45 веков оставалась самым высоким творением рук человека. Однако объявлять Эйфелеву башню произведением искусства парижане не спешили. "Здесь нет искусства, один металл!" - возмущались они. "Я бежал из Парижа, а затем покинул Францию, потому что меня навязчиво преследовал вид Эйфелевой башни,- писал Ги де Мопассан.- Вообразите же, что скажут отдаленные потомки о нашем поколении, если только вспышка народного гнева не повалит эту высоченную и тощую пирамиду железных лестниц". Но не отдаленные потомки, а уже следующее поколение Парижан не мыслило себе родного города без Эйфелевой башни. И конечно же, бессмертие принесла Эйфелевой башне не ее конструкция, которая сегодня кажется архаичной, а пропорциональность и гармоническое единство ее форм, т. е. как раз то, что и делает строительную конструкцию произведением архитектурного искусства. С новым XX веком пришел и новый необычный материал - железобетон, совершивший подлинную революцию в зодчестве.

Современное зодчество бросило вызов классической тектонике. Получив в свое распоряжение особо прочные материалы и конструкции, оно стремится перевернуть вверх ногами "пирамиду архитектоники". Современная архитектура, будто преодолев силы тяготения, парит в воздухе. Человечество всегда мечтало о легкой и воздушной архитектуре, и вот в XX веке эти мечты обретают плоть. Горизонтальные плоскости, будто летящие в пространстве ("Дом над водопадом" в Бер-Ране, США, арх. Ф. Райт, 1936 г.); гигантские нависающие объемы (Клуб им. И. В. Русакова в Москве, арх. К. Мельников, 1929 г.); V-образные опоры, оторвавшие здание от земли ("Лучезарный дом" в Марселе, арх. Ле Корбюзье, 1952 г.); стены, превращенные в витражи, в которые любуются золотые купола Кремлевских соборов (Кремлевский Дворец съездов, арх. М. Посохин и др., 1961 г.); причудливые линии козырьков и сводов-оболочек в форме гипаров (церковь де ла Виргин Милагроза в Мехико, инж. Ф. Кандела, 1955 г.)- все это приметы современной архитектоники и ставшие классикой примеры современной архитектуры. Все эти приметы, собранные вместе, легко обнаружить в здании Штаб-квартиры ЮНЕСКО в Париже (арх. П. Нерви и др., 1957 г.), которое и было задумано как символ современной архитектуры.

Вся история архитектуры - это история поисков гармонического единства "функции - конструкции - формы", это история непрерывного восхождения на пути к вершине, имя которой "прочность - польза - красота ". И все-таки одному из начал - красоте - зодчие придают особое значение, ибо без красоты, без искусства архитектуры вообще нет, остаются только серые безликие строения. Памятник архитектуры может стать непрочным и бесполезным (таковым сейчас стал двадцатидвухглавый красавец Преображенский собор на острове Кижи - жемчужина древнерусского деревянного зодчества), но памятник архитектуры не может быть некрасивым, ибо в таком случае он из памятника превращается в строение. Вот почему в формуле архитектуры, данной известным советским архитектором, лауреатом Государственных премий Ф. А. Новиковым, искусство стоит не слагаемым, а сомножителем: архитектура = (наука + техника) * искусство. Если множитель "искусство" окажется равным нулю, то и весь результат - "архитектура" - будет равен нулю. И сколько бы мы ни увеличивали стоящие в скобках слагаемые, как бы ни были глубоки научные изыскания и сколь современна ни была бы строительная техника, их детище окажется мертвым, равным нулю, пока его не оживит волшебный сомножитель искусства.

3.2 Тайны золотого сечения.

Геометрия владеет двумя сокровищами: одно из них - это теорема Пифагора, а другое - деление отрезка в среднем и крайнем отношении ... Первое можно сравнить с мерой золота; второе же больше напоминает драгоценный камень.

И. Кеплер

Пятиконечной звезде - около 3000 лет. Ее первые изображения донесли до нас вавилонские глиняные таблички. Из Древней Вавилонии в Средиземноморье, как полагают, звездчатый пятиугольник перевез Пифагор и сделал его символом жизни и здоровья, а также тайным опознавательным знаком. В средние века пентаграмма "предохраняла" от "нечистой силы", что, впрочем, не мешало называть ее "лапой ведьмы". Вспомним гётевского "Фауста":

Мефистофель.

Нет, трудновато выйти мне теперь.

Тут кое-что мешает мне немного:

Волшебный знак у вашего порога.

Фауст.

Не пентаграмма-ль этому виной?

Но бес, пробрался ты за мной?

Каким путем впросак попался?

Сегодня пятиконечная звезда реет на флагах едва ли не половины стран мира.

Чем же объясняется такая популярность звездчатого пятиугольника? Тем, что совершенная форма этой геометрической фигуры радует глаз и разум. Звездчатый пятиугольник буквально соткан из пропорций, и прежде всего золотой пропорции. Красота формы пентаграммы, вытекающая из внутренней красоты ее математического строения, была замечена еще Пифагором и с тех пор не устает радовать глаз художника и разум математика.

Итак, правильный пятиугольник и пятиконечная звезда, образованная его диагоналями, обладают массой интересных свойств:

1. Пересекающиеся диагонали правильного пятиугольника делят друг друга в золотой пропорции

2. Сторона правильного пятиугольника, сторона вписанной в него пятиконечной звезды и сторона образованного звездой внутреннего пятиугольника также относятся в золотой пропорции

3. Стороны правильных пятиугольников и вписанных в них звезд образуют ряд золотого сечения (15.5), который является бесконечно убывающей геометрической прогрессией со знаменателем ф и обладает аддитивным свойством (φⁿ = φⁿ⁺¹ + φⁿ⁺², n = 0, 1, 2, ...).

4. Отрезки пятиконечной звезды АВ = Φ, AD = 1, АЕ = φ и ED = φ² связаны между собой всеми видами "древних" средних (5.1), а именно:

- арифметическое среднее;

- геометрическое среднее;

- гармоническое среднее.

В общем случае для четырех последовательных членов ряда (15.5) φⁿ, φⁿ⁺¹, φⁿ⁺², φⁿ⁺³ нетрудно доказать справедливость соотношения

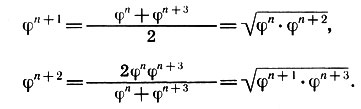
5. Из всех равнобедренных треугольников только треугольник, у которого углы при основании (72°) вдвое больше угла при вершине (36°), обладает особым свойством: биссектриса угла при основании делит противоположную сторону в золотом сечении. Такой треугольник получил название "возвышенного".

Рассмотренные нами геометрические свойства золотого сечения в числе других были с восторгом описаны в 1509 г. в книге монаха ордена францисканцев Луки Пачоли (ок. 1445 - ок. 1514) "О божественной пропорции". Пачоли приводит лишь тринадцать свойств золотого сечения (дабы почтить двенадцать апостолов и их учителя Христа), отмечая, что для перечисления всех свойств золотого сечения не хватило бы чернил и бумаги. Каждому свойству золотого сечения Пачоли ставит особый эпитет, говоря "...о его третьем исключительном свойстве... о его четвертом невыразимом свойстве... о его десятом возвышенном свойстве... о его двенадцатом почти сверхъестественном свойстве...". Пачоли преподавал в различных университетах Италии и был талантливым педагогом. Любопытно, что хорошо известная каждому современному школьнику задача о трубах, наполняющих бассейн, описана в книге Пачоли "Сумма арифметики, геометрии, учения о пропорциях и отношениях", изданной в 1494 г.

Боттичелли. Рождение Венеры. Ок. 1483-1484. Нет живописи более поэтичной, чем живопись Боттичелли, и нет у великого Сандро картины более знаменитой, чем его 'Венера'. Неповторимо нервное изящество боттичеллиевских линий и болезненная хрупкость его вытянутых фигур. Неповторима младенческая чистота Венеры и кроткая печаль ее взора. Неповторим льнущий к телу клубок золотых волос Венеры, в котором, как в клубке змей, таится роковое коварство этого безгрешного существа. Но для неоплатоника Боттичелли его Венера, так же как и для неопифагорейца Поликлета его Дорифор,- это воплощение идеи универсальной гармонии золотого сечения, господствующего в природе.

Итак, ряд золотого сечения (15.4), (15.5) и тесно связанный с ним ряд Фибоначчи (15.6) обладают массой исключительных математических свойств, которые каким-то поразительным образом сошлись в этих феноменах. Но золотое сечение и числа Фибоначчи имеют не менее удивительные приложения не только в искусстве (с чем мы немного познакомились в гл. 4 и гл. 12), но и в живой природе. К настоящему времени накоплено множество фактов, показывающих, что ряд Фибоначчи проявляется в формах живой природы как закон единообразного роста. Ряд Фибоначчи обнаружен и в расположении семян подсолнечника или сосновой шишки, и в распределении листьев и хвои на деревьях, и в расположении стеблей. Возьмите линейку и измерьте длину трех фаланг среднего пальца и пясти. Поделив эти числа на длину первой фаланги, вы с поразительной точностью обнаружите 4 члена ряда золотого сечения (15.4):

Но самым удивительным, пожалуй, является то, что точка, питающая новую жизнь,- пуп человека - делит тело человека в золотом сечении.

Что стоит за этими и многими другими фактами - игра чисел или некоторый универсальный закон природы? Хочется верить, во второе, ибо жизнь - это не хаос случайностей, а претворение генетически определенных законов. Видимо, действием закона золотого сечения в природе и объясняются интригующие проявления этого закона в искусстве. Почему же закон золотого сечения так часто проявляется в архитектуре? Этому есть, на наш взгляд, вполне рациональное, математическое объяснение. Мы знаем, что для достижения гармонии в произведении искусства (в том числе и в архитектурном произведении) должен выполняться принцип Гераклита: "из всего - единое, из единого - все". В самом деле, гармония в архитектурном произведении зависит не столько от размеров самого сооружения, сколько от соотношений между размерами составляющих его частей. Для того чтобы выполнялся основной принцип гармонии "все во всем", взаимосвязь частей и целого в архитектурном произведении должна иметь единое математическое выражение, т. е. архитектурное "целое" а и его части а₁, а₂, а₃, а₄, ... должны находиться в одинаковых отношениях

Итак, из всех геометрических прогрессий (15.13) только ряд золотого сечения обладает аддитивным свойством (15.14), поэтому только при делении "целого" a на части а1 и а2 в золотой пропорции выполняется принцип "все во всем" и одновременно части "сходятся" в целое.

3.3 Пропорции: от Парфенона до Нотр-Дама

"Человек - мера всех вещей..." Этот знаменитый афоризм древнегреческого философа-софиста Протагора (ок. 490 - ок. 420 до н. э.) является ключом к разгадке тайны пропорций Парфенона, его поразительной гармонии и спокойствия. Как это ни парадоксально, но между живыми линиями человеческого тела и застывшими на тысячелетия каменными очертаниями древнего сооружения существует глубокая связь, выраженная в математических законах пропорциональности. Но какой именно математической зависимостью связаны пропорции дорической колонны и человеческого тела? В поисках ответа на этот вопрос роковую роль сыграло следующее высказывание Витрувия: "Желая сделать так, чтобы они (колонны.- А. В.) были пригодны к поддержанию тяжести и обладали правильным и красивым обличьем, они измерили след мужской ступни по отношению к человеческому росту, и, найдя, что ступня составляет шестую его долю, применили это соотношение к колоннаде, и, сообразно с толщиной основания ее ствола, вывели ее высоту в 6 раз больше, включая сюда и капитель. Таким образом, дорийская колонна стала воспроизводить в зданиях пропорции, крепость и красоту мужского тела". Итак, по Витрувию, справедливы отношения: (стопа человека): (высота его тела) = (диаметр колонны): (общая высота колонны) = 1:6. Между тем обмеры дорических колонн упрямо противоречили Витрувию. Неумолимые цифры заставили Брунова отказаться от своих прежних воззрений: "Нельзя утверждать, что дорическая колонна повторяет пропорции тела человека, потому что людей таких пропорций, как колонны Парфенона, не существует". Разгадка была где-то рядом, но ее нашел только в 60-е годы архитектор Шевелев. Вот его решение. Отношение длины стопы человека к длине его тела от основания шеи до стопы 1:5 - ключ к пропорциональному строю Парфенона (по Шевелеву). Со времен Поликлета установлено, что если стопу человека принять за единицу измерения - фут (греческий фут = 30,89 см), то рост человека составит 6 футов, а голова вместе с шеей - 1 фут. В этом можно убедиться, глядя на рисунок на следующей странице. Следовательно, на оставшуюся часть тела приходится 5 футов. Именно эта часть и олицетворяет "крепость и красоту мужского тела". В самом деле, в "человеческой колонне" шея - самое слабое место. Груз взваливают на плечи, и даже атланты сгибают шеи и принимают тяжесть на поднятые к голове руки. Эта простая мысль и привела Шевелева к тому, что ствол колонны, несущий тяжесть, должен ассоциироваться не с полным ростом человека, а с его наиболее крепкой частью от стоп до основания шеи. Все сразу стало на свои места. Возникла цепочка пропорций, выполнявшихся с прекрасной точностью: (нижний диаметр колонны):(высота ствола колонны)=(ширина капители по абаке):(высота колонны с капителью) = (стопа человека):(высота человека от стоп до основания шеи)=1:5. Далее, поскольку "подобное в мириады раз прекраснее того, что неподобно" (Витрувий), отношение 1:5 было распространено на всю соразмерность колоннады в целом: (высота колоннады = колонна + антаблемент):(длина храма по стилобату)=1:5.

А более пытливому исследователю Парфенон открывает и свои более сокровенные тайны. Оказывается, что угловые колонны в Парфеноне толще остальных, рядовых, и сближены с ними. Отношение верхнего диаметра к нижнему в угловых колоннах менее контрастно, чем в рядовых. Такая расстановка колонн логична: ведь и в жизни сильных людей ставят на флангах. Но дело не столько в этом. Дело в том, что угловые колонны смотрятся на фоне яркого неба Эллады. Солнечные лучи дифрагируют, огибают угловые колонны. Поэтому если их сделать одинаковыми с рядовыми колоннами, которые смотрятся на темном фоне целлы - святилища храма, то угловые колонны будут казаться тоньше. Итак, в конструкцию Парфенона введены так называемые оптические поправки. Древние греки прекрасно знали особенности оптического восприятия человеческого глаза: строго вертикальные и параллельные колонны кажутся распадающимися, а горизонтальная балка - прогнувшейся книзу.

Но если греческое сознание всегда было обращено к человеку, если даже в дорических колоннах греки видели торжественное могущество мужского тела, а в изящных завитках ионических волют - женскую грацию и кокетство, то ни о каких реминисценциях с пропорциями человеческого тела в готической архитектуре не могло быть и речи. Человеческая плоть презиралась христианской религией, и в пропорциях готики господствует холодная геометрия. Треугольники и квадраты - простейшие геометрические фигуры - вот основа готических пропорций; триангулирование и квадрирование^* - вот методы достижения гармонии в готике. Но ведь и чистая геометрия прекрасна, и она смогла стать теоретической базой готической архитектуры, которая, по словам Гоголя, "есть явление такое, какого еще никогда не производил вкус и воображение человека".

Но истину нельзя удержать в узде: стало достоянием человечества учение Пифагора, обрели жизнь и теоретические изыскания мастеров-каменотесов. Наиболее ранние из них мы находим в альбоме французского зодчего XIII века Вил л ара де Оннекура. Альбом содержит ряд геометрических конструкций, позволявших моделировать архитектурные формы, а также размышления автора о пропорциях человеческого тела. Сколь отличны эти рисунки от работ античных мастеров! Если древние греки пытались постичь законы пропорционального строения человеческого тела, а затем перенести эти законы на архитектурные сооружения, то средневековые мастера, наоборот, пытаются втиснуть живые линии в рамки простейших геометрических фигур, полностью игнорируя естественные пропорции. Вот голова мужчины, вписанная в сетку квадратов и их диагоналей (см. рис.). Это отнюдь не шарж или шутка, а прорисовка с витражей знаменитого Реймского собора. Человеческое тело не является более "мерой всех вещей". Такой мерой становится система геометрических фигур. Именно сетка геометрических линий является тем скелетом, на котором строится тело здания.

Капелла Сен Шапель - вершина высокой готики, образец совершенной гармонии и безукоризненной формы. Интерьер капеллы ошеломляет даже знатоков готического искусства: потоки теплого света, струящиеся из ее витражей, мощным аккордом вливаются в застывшую симфонию изысканных архитектурных форм капеллы. Согласно исследованиям Виолле-ле-Дюка, пропорциональная сетка капеллы построена на равносторонних треугольниках.

Собор Парижской Богоматери - самый величественный и самый популярный памятник ранней готики. В гордой размеренности западного фасада собора горизонтальные линии еще соперничают с вертикальными. Еще не исчезла стена фасада (ведь это только начало готики), но она уже приобрела легкость и даже прозрачность. Как показал французский историк архитектуры Огюст Шуази, пропорциональную основу западного фасада собора Нотр-Дам составляет квадрат, а высота башен фасада равна половине стороны этого квадрата...

Но чем внимательней, твердыня

Notre-Dame,

Я изучал твои чудовищные ребра,

Тем чаще думал я: "Из тяжести

недоброй

И я когда-нибудь прекрасное

создам..."

(О. Мандельштам)

3.4 Пропорции: от Покрова на Нерли до Модулора ле Корбюзье

И однажды возникло из грезы,

Из молящейся этой души,

Как трава, как вода, как березы,

Диво дивное в русской глуши.

Н. Рубцов

В 1784 г. смиренный отец боголюбовской монашеской братии испросил разрешения у преосвященнейшего Виктора, архипастыря владимирского, благословления на разборку для монастырских потреб обветшавшей и полузаброшенной церковки. Разрешение было милостиво жаловано, но, как говорится, жизнь распорядилась по-своему: заказчики и подрядчики не сошлись в цене. Работы не начались, а там о них и вовсе забыли. Так волею судьбы остался жив памятник, который обошли стороной полчища Батыя и Мамая, пощадили столетия и пожарища бесконечных войн, шедевр древнерусского зодчества церковь Покрова Богородицы на Нерли. В ясные летние дни среди зелени заливных лугов ее стройная белизна, отраженная гладью старицы Клязьмы, дышит поэзией сказки. Лишь в короткие минуты заката белая свеча церкви загорается тревожно-багряным пламенем. В суровые зимы бескрайняя снежная пелена, будто заботливая мать, укутывает и прячет свое замерзшее дитя. "Во всей русской поэзии, давшей миру столько непревзойденных шедевров, нет, быть может, памятника более лирического, чем церковь Покрова на Нерли, ибо этот архитектурный памятник воспринимается как поэма, запечатленная в камне. Поэма русской природы, тихой грусти и созерцания" (Л. Любимов).

Прежде чем приблизиться к тайне очарования древнерусской архитектуры, нам необходимо познакомиться с системой мер, существовавшей в Древней Руси. В разные времена и у разных народов эталоны длины были в принципе одинаковыми: они так или иначе происходили от человеческого тела. Эти так называемые антропометрические меры обладали ценнейшим для архитектуры качеством, о котором с введением метрической системы мер забыли, но к которому в XX веке вернулся Ле Корбюзье. Дело в том, что антропометрические меры в силу своего происхождения соразмерны человеку и поэтому удобны для конструирования искусственной среды обитания людей - архитектурных сооружений. Более того, в "человечьих" мерах заложены пропорции, отобранные самой природой, такие, как деление пополам, золотое сечение, функция золотого сечения. Следовательно, в антропометрических мерах естественным образом заложена гармония природы. Основной строительной мерой в Древней Руси была сажень, равная размаху рук в стороны. Сажень делилась на 2 полусажени, полусажень - на 2 локтя - расстояние от кончиков пальцев до локтя, локоть - на 2 пяди - расстояние между вытянутыми в противоположные стороны большим пальцем и мизинцем. Все четко и логично. Однако чем пристальнее историки изучали древнерусские летописи, тем больше становилось саженей, а когда их число перевалило за десять, голова у историков пошла кругом. Необходимо стало навести математический порядок в древнерусской системе мер. Это сделали историк, академик Б. А. Рыбаков и архитектор И. Ш. Шевелев. Начало антропометрическим мерам дает рост человека а. Главной из всех видов саженей является мерная, или маховая, сажень С_м, которая равна размаху рук человека в стороны. Изучение пропорций человеческого тела показывает, что С_м = 1,03а. Другой важной мерой у всех народов являлся двойной шаг, который равен высоте туловища от стоп до основания шеи. Последнее расстояние, как мы знаем (с. 220), равно ⁵/₆а. Таким образом, двойной шаг, или малая (тмутараканская) сажень, С_т = ⁵/₆а = 0,833а. Но главный сюрприз кроется в отношении этих двух основных размеров:

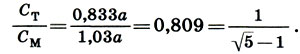
Следовательно, малая сажень С_т относится к мерной С_м как сторона двойного квадрата к его диагонали без малой стороны:

Из (17.1) ясно, что отношение мерной полусажени С_м/2 к малой сажени С_т равно золотому сечению:

Итак, в установленном самой природой отношении полуразмаха рук (RS) к высоте туловища (LQ), т. е. в отношении двух основных мер Древней Руси, заключено золотое сечение, столь распространенное в древнерусской архитектуре.

Рост человека: а = АВ

Мерная сажень: С_н = AC = CN = 1,03a

Малая (тмутараканская) сажень:

Сажень без чети:

Косая новгородская сажень:

Косая великая сажень:

Соотношения между саженями:

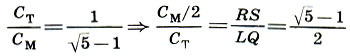
- золотое сечение

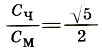
- функция золотого сечения

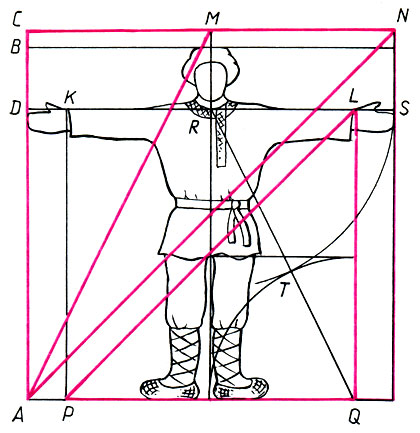
Основные древнерусские меры длины и геометрическая взаимосвязь между ними

Построив квадраты на малой С_т и мерной С_м саженях и проведя в них диагонали, мы получаем еще два типа саженей: косую новгородскую сажень и великую косую сажень . В отличие от первых двух саженей (малой и мерной), выражающих природные меры, косые сажени получены чисто геометрическим путем. Ясно, что

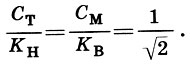
Наконец, существовала еще одна сажень, получаемая геометрическим путем. Это так называемая сажень без чети С_ч, равная диагонали AM половины квадрата, построенного на мерной сажени С_м. У этой сажени не было соответствующей косой пары, и поэтому ее называли саженью без пары, без четы, или без чети. Из треугольника АСМ следует, что , откуда

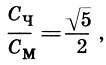
т. е. отношение сажени без чети С_ч к мерной сажени С_м равно функции золотого сечения. Таковы лишь основные типы саженей, существовавших в древнерусской метрологии. Новгородская мерная трость, найденная в 1970 г. (см. с. 219), позволила уточнить их размеры. Новгородские меры XII века соответствуют росту человека: а = 170,5 см. Тогда С_м = 175,6 см, С_т = 142,1 см, К_н= 200,9 см, К_в= 248,3 см, С_ч= 196,3 см. Если же рост человека принять равным 6 греческим футам: а = 6*30,87 = 185,22 см, то для основных саженей (мерной и малой) получим значения: С_м = 190,8 см и С_т = 154,3 см. Именно эти меры наиболее часто встречаются в древнерусских храмах XI века, строительство которых, по-видимому, велось византийскими мастерами. Так, вместе с христианством Русь наследовала византийскую систему мер, которая в свою очередь взросла на античной средиземноморской культуре. Абсолютные размеры саженей в России с течением времени сильно колебались вплоть до введения метрической системы мер в 1918 г. Но важно то, что пропорциональные отношения между парными саженями сохранялись. Эти пропорции становились пропорциями архитектурных сооружений.

Но помимо всех этих пропорций, которые от самой природы перешли в систему мер, а затем и в архитектурные памятники, был у древнерусских мастеров и еще один секрет. Именно этот секрет позволял придавать каждому древнему сооружению неповторимую прелесть, "нюанс", как говорят архитекторы. Секрет этот раскрыт в рядной записи плотника Федора на постройку деревянной церкви Усть-Кулуйского погоста (кон. XVII в.), где сказано: "А рубить мне, Федору, в высоту до порога 9 рядов, а от полу до поволоки - как мера и красота скажет..."

"Как мера и красота скажет..." Эта замечательная формула безвестного русского плотника выражает суть диалектики взаимодействия рационального (мера) и чувственного (красота) начал в достижении прекрасного, союз математики (мера) и искусства (красота) в создании архитектурных памятников.

Непостижимая, казалось бы, гармония храма Покрова подчинена математически строгим законам пропорциональности. План церкви построен на пропорциях функции золотого сечения - "живых квадратах", а ее силуэт определяется рядом золотого сечения. Эта цепь математических закономерностей и становится волшебной мелодией взаимосвязанных архитектурных форм. Конечно, законы пропорциональности определяют только "скелет" сооружения, который должен быть правильным и соразмерным, как скелет здорового человека. Но помимо математических законов меры в недрах архитектурного шедевра непременно заложены и непознанные законы красоты: "как мера и красота скажет..."! Именно диалектика взаимодействия законов меры и законов красоты, которые часто проявляются в отклонениях от законов меры, и создает неповторимый образ архитектурного шедевра.

В 1530 г. в царской усадьбе - селе Коломенском под Москвой - родился будущий царь пробуждающейся России Иван Грозный. А через два года здесь же, в Коломенском, на крутом берегу Москвы-реки, было завершено строительство церкви, поставленной в память об этом событии. Зодчие будто предвидели рождение небывало грозного царя: церковь тоже была небывалой. В ней все", и высота (почти 62 м), и каменный шатер, и устремленная ввысь форма - было невиданным. Новый храм словно символизировал прорыв России в свободное от татарского ига будущее. "...Бе же церковь та велми чюдна высотою и красотою и светлостию, такова не бывала прежде на Руси",- писал о ней летописец. Весь пропорциональный строй церкви, все ее безудержное стремление ввысь как нельзя более соответствовали названию - храм Вознесения. Но для нас храм Вознесения интересен еще и тем, что он является не только гимном расправляющей крылья России, но и архитектурным гимном геометрии. Ни один из рассмотренных архитектурных шедевров, в том числе и Парфенон, не настолько пронизан геометрией, не настолько прост и лаконичен в своей размерной структуре, как храм Вознесения в Коломенском.

Но пропорции храма Вознесения определены не одной, а двумя математическими закономерностями. Помимо пропорции С_т:К_н= 1:√2, определяющей основание, статическое начало храма, есть в нем и другая тема - тема развития вверх, вознесения, которая определена пропорциональной цепью: С_т:С_м = 1:(√5 - 1), а также пропорцией золотого сечения: С_м:2С_т=φ. В проведении этой темы соблюден знакомый нам по Парфенону принцип встречного движения пропорций. Две разные пропорциональные цепи накладываются друг на друга, сталкиваются и противоборствуют. В этом столкновении двух противоборствующих начал - горизонтального и вертикального - и заключается архитектурный образ церкви Вознесения. Не останавливаясь на математическом анализе этих двух систем, предоставим слово автору прекрасного эстетического анализа церкви Вознесения, искусствоведу А. Циресу. "В образе этой церкви,- пишет Цирес,- сплетаются два основных лейтмотива: мотив острого, полного столкновений и диссонансов динамизма и мотив гармонически спокойной красоты... Сложный ритм арок нижних галерей... идет, учащаясь от краев к центру,... теснит арки от краев к углам основного массива церкви и к ее середине,... подсказывает смену горизонтального движения движением, направленным ввысь... Так снизу вверх идет последовательное смягчение кристаллизма и нарастание компактности объема, вплоть до его стянутости в крепкий узел, венчающий всю объемную композицию главкой". Слова автора математического анализа ее пропорций, Шевелева. "Подчеркнем выразительнейшую деталь размерной структуры, наиболее ярко показывающую особенность логики древнего мастера, стремящегося особенно точно выразить в метрологии главное. Так же как 10 саженей определили, по существу, весь храм, его ядро, так же и 10 локтей определили символ и венчание церкви - крест (10С_тХ10С_тХ10С_т - четверик; 10С_тХ10С_тХ10К_н - призма четверика; 10Л_тХ10Л_т - соразмерность креста, ибо в нем заключен для зодчего и смысловой символ соединения, и символ торжества вертикали, и символ храма, и символ пропорции, построившей этот образ)".

Антропометрические меры благодаря своему происхождению оказались как нельзя лучше приспособлены для конструирования архитектурной среды. Они содержали в себе замечательные пропорции, позволявшие древним мастерам создавать прекрасные памятники архитектуры.

7 апреля 1795 г. во Франции была введена метрическая система мер, в разработке которой участвовали такие крупнейшие ученые, как Лаплас, Монж, Кондорсе. За единицу длины - метр - была принята 1/10 000 000 часть 1/4 длины парижского географического меридиана. Метрическая система обладала бесспорными преимуществами и все шире раздвигала границы своего существования. Однако, метр никоим образом не был связан с человеком, и, по мнению Ле Корбюзье, для архитектуре это имело самые серьезные последствия. "Принимая участие в постройке хижин, жилых домов, храмов, предназначенных для потребностей человека, метр, по-видимому, ввел в них чужие и чуждые единицы измерения, и если мы присмотримся к нему ближе, может быть обвинен в дезориентации современной архитектуры и ее искажении... Архитектура, построенная на метрических измерениях, сбилась с правильного пути". Но главная причина, толкавшая зодчих XX века на поиски новых систем измерений в архитектуре, была все-таки не в недостатках метрической системы мер. Английская архитектура с постоянством продолжала пользоваться футами и дюймами, но и у нее возникли те же проблемы. Дело было в том, что вместе с XX веком в архитектуру пришли невиданные объемы и темпы строительства. Проектирование архитектурной среды стало преимущественно типовым, а сама архитектура - индустриальной. В этих условиях строительные элементы необходимо было стандартизировать и унифицировать. Кроме того, архитекторам хотелось бы примирить непримиримое: красоту и стандарт. Требовалось найти такие методы пропорционирования, которые обладали бы максимальной гибкостью, простотой и универсальностью. "Если бы появился какой-нибудь линейный измеритель, подобный системам музыкальной записи, не облегчился бы ряд проблем, связанных со строительством?" - спрашивал Ле Корбюзье. И в 1949 г. он сам отвечает на этот вопрос, предложив в качестве такого измерителя систему модульной унификации – модулор, который вносит порядок, стандарт в производство и в то же время связывает все его элементы законами гармонии.

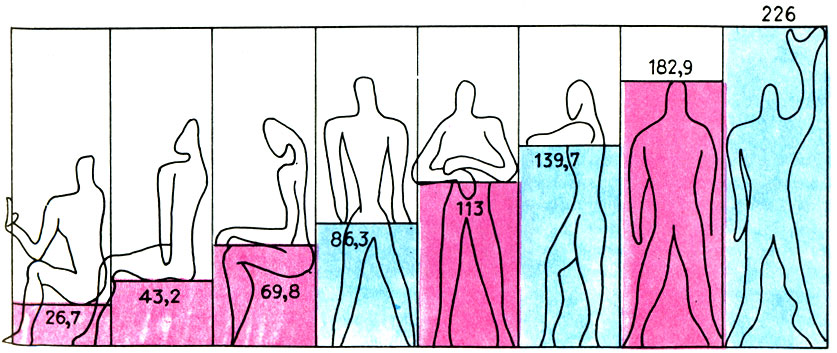
Числа красной и синей шкал модулора - действительные размеры, соответствующие определенным положениям тела человека. (Рисунок Ле Корбюзье)

Что же объединяет все системы пропорциональности? Дело в том, что любая пропорциональная система - это основа, скелет архитектурного сооружения, это та гамма, а точнее, тот лад, в котором будет звучать архитектурная музыка. Именно это свойство модулора Ле Корбюзье имел в виду Альберт Эйнштейн, давая ему восторженную оценку: "Модулор - это гамма пропорций, которая делает плохое трудным, а хорошее - легким". Но гамма - это еще не мелодия, не музыка. Это хорошо осознавал и сам Корбюзье: "Модулор - это гамма. Музыкант располагает гаммой и создает музыку по своим способностям - банальную или прекрасную". В самом деле, как гамма уже третье тысячелетие дает возможность композитору создавать бесконечное разнообразие мелодий, так и система пропорционирования - модулор - нисколько не стесняет в творчестве архитектора. Сам

Корбюзье блестяще доказал это, построив с помощью своего модулора и знаменитый "Лучезарный дом" в Марселе, и не менее знаменитую капеллу в Роншане. Эти два произведения великого зодчего - два антипода, две разные философии в архитектуре. С одной стороны, воплощение здравого смысла, ясного, прямолинейного и рационального. С другой - нечто иррациональное, пластическое, скульптурное, сказочное. Единственное, что объединяет эти два выдающихся памятника зодчества - это модулор, архитектурная гамма пропорций, общая для обоих произведений Ле Корбюзье.

3.5 Пропорция - математика архитектурной гармонии

Пропорции являются важным и надежным средством зодчего для достижения хрупкого и тонко сбалансированного равновесия между целым и его частями, имя которому - гармония. Напомним, что по сравнению с композитором или скульптором архитектор находится в более сложном положении, ибо на пути к гармонии он должен заботиться не только о "красоте", но также и о "пользе", и "прочности". Еще Гораций в послании к братьям Пизонам "Наука поэзии" в образной форме говорил о том, как непросто красиво и целесообразно соединять части в единое целое, что взятые вместе "части": лицо женщины, грива льва, тигровая шкура или павлиний хвост, которые сами по себе являются своеобразными эталонами красоты,- не только не дают нам прекрасного "целого"- гармонии, но представляют, по крайней мере, странное зрелище.

Если художник решит приписать к голове человечьей

Шею коня, а потом облечет в разноцветные перья

Тело, которое он соберет по куску отовсюду -

Лик от красавицы девы, а хвост от чешуйчатой рыбы, -

Кто бы, по-вашему, мог, поглядев, удержаться от смеха?

Гармония в природе и гармония в архитектуре - две стороны единого великого процесса созидания. Замечательный советский зодчий и теоретик И. В. Жолтовский (1867-1959) считал творчество архитектора частью творчества природы. Широко известно высказывание Жолтовского о том, что архитектор - "дитя природы", что архитектурные формы должны члениться, следовать одна за другой, вырастать друг из друга, как ветви древесного ствола.

Вообще архитектура есть застывшая музыка.

Ф. Шеллинг

Один благородный философ говорил о зодчестве как о застывшей музыке и за то не раз подвергался насмешкам. Мы думаем, что мы лучше всего передадим эту прекрасную мысль, назвав архитектуру отзвучавшей мелодией.

И. В. Гёте

С легкой руки великого Гёте афоризм об архитектуре и музыке немецкого философа, идейного вождя немецкого романтизма Фридриха Шеллинга (1775-1854) стал настолько популярным, что сегодня, забыв имя настоящего автора, его настойчиво вкладывают в уста создателя "Фауста". Парадоксальность высказывания Шеллинга, соединившего в себе две столь далекие друг от друга области искусства - архитектуру и музыку, делает его еще более привлекательным. А ведь сопоставление архитектуры и музыки в большей степени закономерно, чем парадоксально, и поистине замечательно, что связующим звеном между архитектурой и музыкой выступает математика.

В чем же проявляется общность архитектуры, музыки и математики? Прежде всего - в максимальной абстрактности этих форм человеческой деятельности. Архитектура является наиболее абстрактным из пластических искусств, т. е. искусств, существующих в пространстве и воспринимаемых зрением. Назначение зрения - воспринимать предметы внешнего мира, а назначение пластических искусств - воспроизводить с той или иной мерой чувственной достоверности эти предметы. Однако архитектура не отображает реально существующие объекты, а создает некоторые абстрактные формы, которые являются плодом фантазии ее творца. Конечно, нам известны колонны в форме лотоса в древнеегипетской архитектуре или древнегреческие атланты и кариатиды, растительные мотивы коринфских капителей или звериные маски во владимиро-суздальском зодчестве. Но все это лишь элементы, украшения, архитектурная скульптура, но не сама архитектура в целом.

Музыка на первый взгляд является антиподом архитектуры. В противоположность архитектуре музыка развивается во времени, а не в пространстве; музыка обращена к слуху. Однако роднит эти два искусства та же абстрактность формы. В самом деле, на слух мы воспринимаем звуковую информацию из внешнего мира. Но музыка не воспроизводит словесную речь, она ничего не описывает и обычно не изображает природные звуки и звукосочетания. Музыкальная форма абстрактна, она рождается в голове ее создателя и практически не имеет аналогов во внешнем мире.

Так же и математика. Будучи наукой, целью которой является выработка и систематизация объективных знаний о действительности, математика не имеет' материального предмета изучения во внешнем мире. Математика - предельно абстрактная наука, но именно это качество наделяет ее силой, позволяет математике стать универсальным языком науки.

Творческая работа: «Создание эскиза фантастического здания». Создать выставку «город будущего»

4 Математика и живопись 5 часов

4.1 "Законы красоты" человека

Человек - мера всех вещей.

Протагор

Во все времена, от наскальной живописи в Сахаре до полотен Сальвадора Дали, человек был и остается главной темой изобразительного искусства. "Виллендорфская Венера" или Венера Милосская, царь Хаммурапи или бог Аполлон, Сикстинская мадонна или девушка с персиками - для художника все они прежде всего были образами человека. Более того, в предыдущей части мы увидели, что образ человека, его пропорции нашли воплощение и в архитектурных произведениях от античных й древнерусских храмов до ультрасовременных сооружений Ле Корбюзье. С древнейших времен пропорции человека составляли предмет изучения художника, его "математическую лабораторию". На первых порах художником руководило, быть может, не столько стремление "дойти до самой сути", сколько необходимость в каких-то объективных - числовых или геометрических - формах передать свой опыт и свое мировоззрение преемникам. Так в искусстве возникали каноны.

Известны три древнеегипетских канона : первый канон эпохи Древнего царства, приписываемый Имхотепу (XXVIII в. до н. э.), слагает рост человека из 6 ступеней ноги; второй - эпохи Среднего и Нового царства (XXI-XII вв. до н. э.) разбивает каждую ступню еще на три части и таким образом составляет рост человека из 18 единиц; третий канон позднего периода^** (XI-IV вв. до н. э.) складывает рост человека из 21 части с четвертью. Текст египетских канонов не сохранился, хотя в дошедшем до нас каталоге храмовой библиотеки в Эдфу под шестым номером значится трактат "Предписание для стенной живописи и канон пропорций". Легко видеть, как с течением времени усложнялся древнеегипетский канон, хотя и на такие ничтожные для современника "уточнения" потребовалось ни много ни мало 2500 лет!

Греческое искусство развивалось очень динамично. Уже через 100 лет после Аполлона Тенейского, в середине V века до н. э., греческая цивилизация достигает своего апогея. Наступает период наивысшего расцвета искусства Древней Греции, именуемый периодом высокой классики. Возвышенные идеалы классики, вера в духовное, нравственное и физическое совершенство свободного эллина нашли отражение в скульптурах Поликлета, творившего во второй половине V века. Поликлет был не только гениальным скульптором, автором "Дорифора", "Дуадумена" и "Раненой амазонки", но и выдающимся теоретиком искусства.

Свои теоретические воззрения о пропорциях человека Поликлет изложил в трактате "Канон". Трактат этот, увы, не сохранился. Но как бы предчувствуя бренность написанного и бессмертие изваянного, Поликлет создает статую, в которой в бронзе воплощает свои теоретические воззрения. (Статуя эта также не сохранилась, но, к счастью, сохранилась ее римская мраморная копия.) Вот почему прославленная статуя юноши-копьеносца "Дорифор" имеет также и другое название - "Канон".

К сожалению, мы опять-таки не знаем, в каких конкретных математических отношениях выражался канон Поликлета. Но знание философских воззрений Поликлета, а главное - его скульптура помогают восстановить эти отношения. Поликлет был пифагорейцем, следовательно, он был неплохим математиком и, безусловно, был знаком с золотой пропорцией, которую пифагорейцы считали верхом совершенства. Можно только догадываться, какое изумление и радость испытал пифагореец Поликлет, когда обнаружил, что золотая пропорция присуща не только абстрактной геометрической фигуре, главному пифагорейскому символу - пятиконечной звезде, но и естественным образом входит в пропорции человека. Человеческое тело оказалось благодатным материалом для философа-пифагорейца: как нам известно, золотая пропорция пронизывает тело человека от малых размеров (три фаланги среднего пальца) до самых больших. Таким образом, открытие золотой пропорции в строении человека, которое, по-видимому, принадлежит Поликлету, можно считать вслед за открытием закона целочисленных отношений в музыке вторым важнейшим событием в "математической теории искусств".

В построении пропорций человека Леонардо да Винчи исходит прежде всего из анализа многочисленных измерений самого человека, из его анатомии, а не из каких-то "высших" соображений, как это делали средневековые художники. Жажда научного знания, основанного на опыте и только опыте, отражает переворот в мышлении эпохи Возрождения, знаменует начало экспериментального естествознания. Стремление как можно глубже изучить пропорции и вообще строение человека, столь необходимые Леонардо-художнику, переросло в страсть к науке анатомии Леонардо-ученого, Составленные им анатомические тетради явились вершиной анатомии того времени и по сей день остаются непревзойденным образцом синтеза науки и искусства.

Свои исследования Леонардо не успел (а может, и не хотел) систематизировать, и они остались рассыпанными в виде рукописных набросков, в которых говорится буквально обо всем на свете, а текст перемежается великолепными рисунками. Мы остановимся лишь на одном наиболее популярном рисунке Леонардо на тему о пропорциях. Вот отрывок текста, которым Леонардо сопровождает рисунок: "Если ты раздвинешь ноги настолько, что убавишься в росте на ¹/₁₄, и если ты тогда разведешь руки и поднимешь их так, что коснешься средними пальцами макушки головы, то должен ты знать, что центром круга, описанного концами вытянутых членов, будет пупок и что пространство между ногами образует равносторонний треугольник. А пролет распростертых рук человека равен его росту". Заметим, что идея этого рисунка восходит к известному нам сочинению Витрувия.

Свое высшее развитие учение о пропорциях человека получило в трудах Дюрера. С немецкой скрупулезностью проводит Дюрер свои измерения и в конце концов доводит разбиение человеческого тела до 1/1800 части его длины, т. е. до величины, не превышающей одного миллиметра! По мнению А. Лосева, столь тщательное измерение "стало самоцелью и каким-то измерительным спортом!". Ни до, ни после Дюрера учение о пропорциях не доводилось до такой степени точности. Но главное, пожалуй, было в другом: Дюрер отказался от создания какого-либо "идеального" канона, а разработал не менее 26 различных типов пропорций человека. Но если пропорции человеческой фигуры еще можно как-то классифицировать, то лицо человека никак не укладывалось у Дюрера в жесткие рамки пропорциональной сетки. Дюрер изобретает массу геометрических способов, которыми можно до неузнаваемости трансформировать изображение лица. Однако чем большим становится набор таких способов, тем яснее видно, что их число уходит в бесконечность.

Глядя по прошествии 500 лет на геометрические построения Дюрера, хорошо видно, как в его исследованиях назрела потребность в точной науке о непрерывных процессах, науке о проявлении прерывного в непрерывном, науке о бесконечно большом числе бесконечно малых изменений. Такая наука родилась лишь через полтора века после Дюрера в трудах Ньютона и Лейбница, когда вместе с понятием производной "в математику вошли движение и диалектика" (Ф. Энгельс, т. 20, с. 573). Таким образом, творчество Дюрера еще раз убеждает нас в том, что пути науки и искусства связаны тысячами нитей. В геометрических поисках Дюрера мы видим, как одно из величайших завоеваний человеческой мысли - дифференциальное исчисление - зрело не только в лоне науки, но и в недрах искусства.

А как развивалась теория пропорций человека после Дюрера? В XVII веке движение вошло не только в науку, но и в искусство. На смену застывшим формам объекта, где царствовали покой и пропорция, в искусстве пробуждается интерес к изменчивому, как солнечный луч, субъекту, его настроению и мироощущению. Голландским люминаристам XVII века и французским импрессионистам XIX века уже не нужны были пропорции, ибо форма, объект растворялись в их полотнах в потоках воздуха, цвета и света. Искусство XX века еще более динамично: оно разрушает все каноны, часто не успевая провозгласить свои. Сегодня каждый художник стремится создать свой собственный канон, что порождает бесконечные споры об искусстве. Тот же "канон Ильи Глазунова" расколол наших современников на сторонников и противников, что, впрочем, не мешает и тем и другим в едином строю опоясывать Манеж с выставками художника.

Да, человек - мера всех вещей - настолько разнообразен, что его нельзя втиснуть в рамки дискретных канонов. Но пропорции живы, как жив и сам человек.Теория пропорций сегодня не умерла, а лишь замерла в ожидании качественно нового скачка, в ожидании перехода от "арифметического" к "аналитическому" и даже "компьютерному" выражению.

4.2 Перспектива - геометрия живописи

Все проблемы Перспективы можно пояснить при помощи пяти терминов Математики: точка, линия, угол, поверхность и тело.

Леонардо да Винчи

В первом наскальном изображении первый первобытный художник столкнулся с непростой математической задачей: отобразить трехмерный оригинал на двумерную плоскость "картины". Сама природа помогла ему в решении этой задачи, ибо, как заметил Леонардо да Винчи, "первая картина состояла из одной-единственной линии, которая окружала тень человека, отброшенную солнцем на стену".

Люди издревле научились отображать всевозможные объекты окружающего их трехмерного мира на двумерную плоскость картины. Однако по мере развития такого искусства отображения все чаще возникал вопрос: насколько точно и насколько убедительно эти плоские образы отражают реальные трехмерные прообразы? На эти вопросы призвана была ответить наука, и прежде всего геометрия. И она по мере сил отвечала на них, хотя решение столь простой на первый взгляд задачи растянулось на тысячелетия. Раздел геометрии, в котором изучаются различные методы изображения пространственных форм на плоскости, называется начертательной геометрией. В основе начертательной геометрии лежит метод проекций, сущность которого такова. В пространстве выбирают фиксированную точку S - центр проектирования и плоскость проекций К (картинную плоскость), не проходящую через S. Для получения изображения - проекции^* - объекта на плоскость К через центр проекций S и каждую точку А, В, С,... объекта проводят проектирующие лучи до пересечения с плоскостью К. Совокупность точек пересечения проектирующих лучей с картинной плоскостью и даст изображение (проекцию) объекта, которое называют центральной проекцией.

Обратим внимание на то, что свойство параллельности прямых при центральном проектировании не сохраняется.

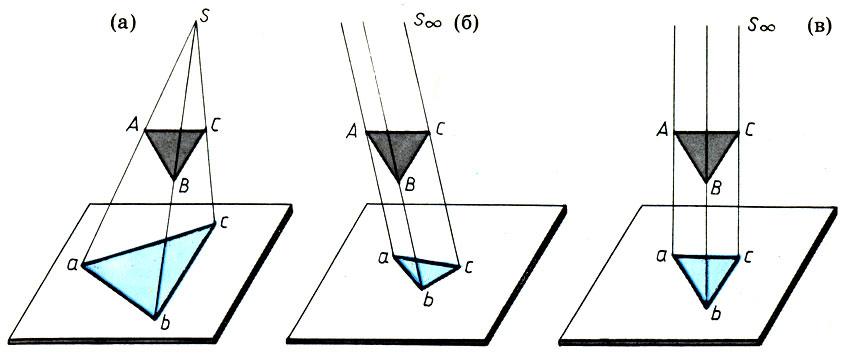
Важнейшие виды проекций: центральные (а), параллельные (б) и ортогональные (в)

Однако ортогональные проекции не дают целостного впечатления о форме пространственного объекта. Более наглядное представление о форме тела дают аксонометрические проекции - частный вид параллельных проекций, отображающих на плоскость.

Сопоставляя все три проекции, мы видим, что перспектива наиболее адекватно, т. е. "похоже", передает видимый нами объект. Это замечательное свойство центральной проекции и снискало ей славу в искусстве живописи, где она получила особое название - перспектива (от лат. perspicio - ясно вижу). Надо заметить, что реально существующий мир и видимый нами мир - не одно и то же. В самом деле, вспомним всем хорошо знакомый пример: рельсы железной дороги кажутся нам сходящимися на горизонте, хотя мы прекрасно знаем, что это не так и ни один машинист, увидев такую картину, не бросится останавливать поезд.

Объяснение этому "парадоксу" было известно еще до нашей эры. В своем сочинении "Оптика" Евклид постулировал, что мы воспринимаем предметы, когда исходящие от них прямолинейные лучи света сходятся в нашем глазу. Таким образом, всю систему лучей зрения можно представить в виде "пирамиды зрения", вершина которой находится в глазу, а основанием служит рассматриваемый объект. В предложении 4 "Оптики" Евклид доказал, что из двух предметов одинакового размера более удаленный, т. е. видимый под меньшим углом зрения, кажется меньшим. Итак, почему дальние предметы кажутся меньшими, было понятно. Оставалось сделать еще один шаг - рассмотреть картину как сечение пирамиды зрения картинной плоскостью. Однако на этот шаг человечеству потребовалось более 1500 лет.

Перспектива открыла перед живописцами небывалые возможности. Впервые у художников появился геометрический метод изображения не отдельного предмета, а всего видимого трехмерного пространства, всего окружающего мира. Невиданные возможности перспективы наиболее ярко раскрывались в изображении интерьера. Вот почему художники Возрождения так любили изображать интерьер (вспомним "Афинскую школу" Рафаэля и "Тайную вечерю" Леонардо да Винчи). Заметим, что проблема правильного построения перспективы "клетчатого" пола долго не давалась художникам Возрождения. Вот почему, решив эту геометрическую задачу, мастера Возрождения так любили изображать квадраты пола на своих полотнах (см. например, "Афинскую школу" и "Обручение Марии" Рафаэля). Квадратные плиты были своеобразной координатной сеткой на плоскости пола и придавали глубине картины особую выразительность.

Вообразим теперь, что, проводя линию горизонта, мы ошиблись и она оказалась у нас не выше, а ниже основания картины. В точности повторяя все предыдущие построения, мы получим обратную перспективу. Вместо привычного в прямой перспективе сокращения видимых размеров предмета по мере удаления его от наблюдателя в обратной перспективе происходит увеличение этих размеров. Заметим, что обратную перспективу прямоугольника можно увидеть, если посмотреть на прямую перспективу этого прямоугольника из-за картины, да еще и "вверх ногами".

Если далее повторить все те же построения с высотами параллелепипеда, по-прежнему сохраняя его высоту в плоскости картины, то мы получим обратную перспективу всего параллелепипеда. Еще раз обратим внимание на "странность" обратной перспективы: видимые размеры фигуры в обратной перспективе по мере удаления от глаза наблюдателя не сокращаются (как в прямой перспективе), а увеличиваются. До тех пор пока ваши построения обратной перспективы носили чисто геометрический характер, в них, может быть, и не было бы ничего странного, кроме замеченного расхождения обратной перспективы с нашим зрительным опытом. Но уж совсем удивительным оказывается то, что именно обратная перспектива является геометрической основой древнерусской живописи. Такая странная геометрия живописи Древней Руси до сих пор не дает покоя ее исследователям. Некоторые называют ее просто "ошибочным приемом". Другие связывают "потустороннее" геометрическое происхождение обратной перспективы (вспомните наш взгляд из-за картины) с тем "потусторонним" неземным ирреальным миром, который призвана была изображать древнерусская икона. Наконец, есть и третий, как нам кажется, наиболее реалистичный и научный взгляд на обратную перспективу.

Итак, перспектива - это очень просто. Это чистая геометрия. Так что же, овладев геометрией перспективы, каждый может стать художником? К сожалению, нет. Математически точная перспектива - это еще не живопись, а только чертеж, хотя бы и такой прекрасный, как воспроизведенный здесь нами. Перспектива - это только геометрическая основа живописи. Но эта основа мертва, до тех пор пока художник не вложит в нее частичку своей души, не сделает ее живописью.

4.3 Геометрия и живопись: страницы истории

И, поистине, живопись - это наука и законная дочь природы, ибо она порождена природой...

Леонардо да Винчи

Геометрия и живопись... Пути науки и искусства переплетались в них на протяжении столетий. Геометрия дарила живописи новые изобразительные возможности, обогащала язык живописи, а живопись эпохи Возрождения стимулировала исследования по геометрии, дала начало проективной геометрии. Сейчас нам предстоит взглянуть на геометрию с неожиданной, быть может, стороны. Мы увидим, что геометрия, будучи могучей ветвью древа математики, является в то же время и тем связующим стержнем, который проходит через всю историю живописи.

В самом деле, существуют три принципиальных геометрических метода отображения трехмерного пространства на двумерную плоскость картины: метод ортогональных проекций, аксонометрия и перспектива (см. рис. на с. 277). Перспектива, как явствует из рисунка, может быть прямой или обратной. Все эти принципиальные возможности изображения пространства на плоскости были реализованы в искусстве живописи, причем в разных пластах художественной культуры каждый из этих методов находил свое наиболее полное и чистое выражение. Так, система ортогональных проекций составила геометрическую основу живописи

Древнего Египта; аксонометрия (параллельная перспектива) характерна для живописи средневекового Китая и Японии; обратная перспектива - для фресок и икон Византии и Древней Руси; прямая перспектива - это геометрический язык ренессансной живописи, а также станковой и монументальной живописи европейского искусства XVII века и русского искусства XVIII- XIX веков.

Итак, ортогональные проекции - аксонометрия - перспектива. Именно по такой схеме шло развитие геометрии живописи. Видимо, простота метода прежде всего определяла его положение в этой схеме. Метод ортогональных проекций как наиболее простой занял в ней первое место. Ортогональные проекции передавали без искажений контуры реальных предметов, а идея метода, как справедливо заметил Леонардо да Винчи (см. с. 274), была подсказана человеку самой природой: тень, отброшенная вечерним солнцем на стену, и была первой картиной, нарисованной этим методом. Однако ортогональные проекции никак не передавали глубину реального пространства, поэтому уже в искусстве Древнего Египта появились робкие ростки аксонометрии.

Аксонометрия при надлежащем выборе точки зрения передавала без искажений фронтальную плоскость изображаемого предмета; она давала представление о глубине пространства, хотя и трудно было понять, сколь протяженна эта глубина. Строгий математический взгляд на аксонометрию как центральную проекцию с бесконечно удаленным центром сложился сравнительно недавно, в XVIII веке, в трудах немецкого математика и философа Иоганна Генриха Ламберта (1728- 1777). Однако как нестрогий метод изображения пространства на плоскости аксонометрия, именуемая тогда вольной перспективой, известна давно. Начиная с Птолемея (II в.) и вплоть до XVIII века (до появления начертательной геометрии) планы городов изображались в вольной перспективе, как бы с высоты птичьего полета. (Этот принцип и сегодня широко используется на туристских схемах.)

Недостатки аксонометрии в передаче глубины пространства вместе с "вольностями" вольной перспективы были исправлены в ренессансной системе перспективы. Эта система имела единые правила, основанные на математических доказательствах, отчего за ней закрепилось название научной системы перспективы. Ренессансная перспектива - наиболее сложный геометрический метод в живописи. Построенный с учетом геометрических закономерностей зрения (геометрической оптики), он наиболее точно воспроизводил видимый человеком мир. Ренессансная перспектива, как и вся философия эпохи Возрождения, распахнула перед человеком "окно в Природу", беспредельно расширила горизонты человеческого мироощущения.

Таким образом, каждый из трех геометрических методов был очередным этапом в развитии искусства живописи, новой ступенью в поисках более точной и совершенной системы передачи зрительных ощущений. Любопытно, что по такой же схеме идет развитие и детского рисунка, хотя многие так и не поднимаются выше ее первой ступени. Психологи много спорят, почему дети начинают рисовать именно с "ортогональных проекций", хотя, как нам кажется, главной причиной тому является простота и естественность метода, который с рождения демонстрирует ребенку само Солнце.

"Ортогональная" живопись Древнего Египта. Идея незыблемости, вечности абсолютной власти фараона, почитавшегося сыном бога, пронизывала всю философию и весь жизненный уклад древнеегипетского общества. Эта идея не только откристаллизовалась в острых гранях пирамид - апофеозе вечности, но и нашла воплощение в древнеегипетской живописи. Согласно "философии вечности" образы древнеегипетской живописи также должны были вбирать в себя все непреходящее и наиболее устойчивое. Каждый предмет как бы вычленялся художником из окружающего мира, осмыслялась "идея" этого предмета, отбрасывалось все сиюминутное, нехарактерное, и в результате возникал живописный образ, который не зависел ни от места, ни от времени его создания и который сегодня удачно называют "образом-существительным".

"Параллельная" живопись средневекового Китая и Японии. Попытки передать глубину пространства на плоскости картины, согласовать умозрение со зрением, которые мы обнаружили еще в живописи Древнего Египта, привели к образованию новой геометрической системы в живописи - аксонометрии, или параллельной перспективы. Явные признаки параллельной перспективы, точнее, суммы двух идущих навстречу друг другу параллельных перспектив, легко увидеть в живописи Древней Греции. Такая геометрическая система в живописи, именуемая искусствоведами "рыбья кость", имела ось схода и, безусловно, тяготела к линейной перспективе, хотя так и не переросла в нее. Та же "рыбья кость" имела место и в знаменитых помпейских росписях Древнего Рима, именуемых, впрочем, "запоздалым эхом древнегреческой живописи". Рим пал, не успев, а может, и не сумев развить живописную систему греков, и свое законченное развитие аксонометрия нашла много веков спустя на другом конце земли в живописи средневекового Китая и Японии.

Линейная перспектива Возрождения. Ветер Возрождения распахнул пыльные окна мастерских средневековых художников и впервые заставил их посмотреть на изумительный вид, открывающийся из окна.

Из дряхлой Византии в жизнь - весна

Вошла, напомнив о любви, о теле;

В своих созданьях Винчи, Рафаэли

Блеск бытия исчерпали до дна.

(В. Брюсов)

Вера в идеалы гуманизма, в могущество человеческого разума, основанного не на проповедях теологов, а на непосредственном опыте, будоражила воображение и придавала силы разбуженным умам Возрождения. Новое мышление пришло и в живопись. В условиях ломки старых канонов, в условиях торжества эмпирического знания язык живописи также должен был опираться на непосредственный зрительный опыт человека. Таким геометрическим языком живописи стала перспектива.

Обратная перспектива живописи Древней Руси. У древнерусской живописи трагическая судьба. Дело в том, что олифа, которой для лучшей сохранности покрывали живопись, со временем темнела и по прошествии ста лет превращалась в черную непроницаемую пелену. Такие "черные доски" ждало два исхода: либо от них избавлялись - пускали плыть по реке, сжигали, выносили на чердаки и колокольни, либо их "подновляли" - звали новых иконописцев, и они по едва просвечивающим контурам, а более по собственному наитию и разумению заново писали. В любом случае старая живопись безвозвратно уходила.

Так было до конца прошлого века, когда кто-то как-то случайно под одним черным слоем обнаружил другой, потом третий и даже четвертый и пятый, пока вдруг из глубины веков не вспыхнули на иконе пронзительно-звонкие древние краски. Это было потрясающее открытие, вызволившее из небытия целую эпоху в культуре русского народа. Появились первые крупные коллекционеры: И. С. Остроухов, Н. П. Лихачев, А. В. Морозов, С. П. Рябушинский, В. М. Васнецов...

Об этом счастливом для древнерусской живописи времени вспоминает советский живописец и искусствовед, действительный член Академии наук и Академии художеств И. Э. Грабарь (1871 - 1960): "По северу разъезжали офени (бродячие торговцы.- А. В.), выменивая у попов и церковных старост старые иконы на новые "благолепные". Древние иконы обыкновенно валялись на колокольнях и в рухлядных, выброшенные туда за ветхостью... Офени привозили иконы возами во Мстеру, где их поджидали перекупщики-иконники, а иногда и прямо в Москву, также к перекупщикам..." Но чудом открытая древнерусская живопись чуть было вновь не погибла в руках воинствующих иконоборцев. К счастью, этого не случилось. Собранная в лучших музеях древнерусская живопись радует сегодня чистотою своих красок и нравственных идеалов. Но вместе с радостью древнерусская живопись преподнесла и немало загадок, в том числе и загадок чисто геометрических. Воспитанные на ренессансной перспективе искусствоведы поспешили назвать ее "неправильной", "наивной", "примитивной". Это было продолжение трагедии живописи Древней Руси.

Вот, к примеру, прославленная "Троица" Андрея Рублева - шедевр древнерусской живописи. Сотни статей написаны об этом совершенном творении великого мастера, о его величавом и мудром спокойствии, о его нежных красках, созвучных краскам русской природы: цвету поспевающей ржи и цветущего льна. Однако вопрос о геометрии пространства иконы либо обходят молчанием, либо глубокомысленно называют его "абстрактным пространством" или "пространством сердца" (о том, что прячется за этими фразами не говорится ни слова). А вопрос этот и в самом деле не простой! Приглядимся внимательнее. Подножие правого ангела показано в аксонометрии, в то время как подножие левого - в слабой обратной перспективе. Но даже если бы и левое подножие было дано в аксонометрии, то легко видеть, что показаны они с разных точек зрения: на правого ангела мы смотрим слева, а на левого - справа. Далее нетрудно обнаружить, что край правого табурета, не параллелен соответствующему краю правого подножия, а край левого табурета и края левого подножия не имеют общей точки схода. Следовательно, ни аксонометрия правой части иконы, ни обратная перспектива левой части строго не выдержаны. Наконец, легко представить, как ведут себя края стола, закрытые коленями ангелов. Следуя логике построения левой и правой частей иконы, им ничего не остается, как расходиться.

Но как объяснить появление в Византии столь странной системы? Ведь обратная перспектива явно выпадает из общего направления развития геометрии живописи (ортогональные проекции - параллельная перспектива - прямая перспектива), идущего от изображения реального пространства к изображению пространства видимого. Вопрос этот во многом остается открытым. И все-таки, как объяснить обратную перспективу? Чем вызвано расхождение параллельных линий в обратной перспективе? Есть два подхода к этому вопросу. В первом корни обратной перспективы ищутся в идейных задачах, которые она решала. Икона призвана была убедить верующего в реальности ирреального, она должна была "отстранить" молящегося от грешной земли. Поэтому, как считают сторонники философско-богословских взглядов на истоки обратной перспективы, изображение на иконе не должно было в точности походить на видимый человеком мир. Икона должна была походить и не походить на видимый мир. Именно так она и могла заставить верующего поверить в чудо, которое также есть одновременно реальное и сверхъестественное. Мир иконы не мог быть отображением мира реального; поэтому и появляются расходящиеся параллели обратной перспективы, которые дают некую "потустороннюю", "сверхъестественную" точку зрения на мир, некий отстраненный "взгляд изнутри". Другая точка зрения на истоки oбратной перспективы основана на чистом естествознании и прежде всего на закономерностях зрительного восприятия. Когда в 1966 г. Б. В. Раушенбах случайно попал в Музей древнерусского искусства имени Андрея Рублева, его порази необычный мир иконы. Но в то же время и покоробили слова экскурсовода, щедро раздававшей древнерусским живописцам ярлыки: "не умели", "не знали", "не смогли". И это мудрые, образованнейшие мастера, чьи произведения имена пережили столетия?! Раушенбах спешил назвать их "простодушными и наивными". Он задумался... 20 лет спустя появилась на свет oбщая теория перспективы, в которой древнерусская обратная перспектива заняла свое достойное место.

http://www.smekalka.pp.ru/picture

задачи по картинкам

5 Математическое изобразительное искусство 6 часов.

Исторически, математика играла важную роль в изобразительном искусстве, в частности при изображении перспективы, подразумевающем реалистичное изображение трехмерной сцены на плоском холсте или листе бумаги. Согласно современным взглядам, математика и изобразительное искусство очень удаленные друг от друга дисциплины, первая - аналитическая, вторая - эмоциональная. Математика не играет очевидной роли в большинстве работ современного искусства, и, фактически, многие художники редко или вообще никогда не используют даже использование перспективы. Однако, есть много художников, у которых математика находится в центре внимания. Несколько значительных фигур в изобразительном искусстве проложили дорогу этим индивидуумам.

Вообще-то не существует каких-либо правил или ограничений на использование различных тем в математическом в математическом искусстве. Однако, есть несколько тем, которые достаточно часто различным художниками. Среди них есть использование многогранников, тесселяций, невозможных фигур, лент Мебиуса, искаженных или необычных систем перспективы, а также фракталов.

Тесселляции, известные также как покрытие плоскости плитками (tiling), являются коллекциями фигур, которые покрывают всю математическую плоскость, совмещаясь друг с другом без наложений и пробелов. Правильные тесселляции состоят из фигур в виде правильных многоугольников, при совмещении которых все углы имеют одинаковую форму. Существует всего три многоугольника, пригодные для использования в правильных тесселляциях. Это - правильный треугольник, квадрат и правильный шестиугольник. Полуправильными тесселляциями называют такие тесселляции, в которых использованы правильные многоугольники двух или трех типов и все вершины одинаковы. Существует всего 8 полуправильных тесселляций. Вместе три правильных тесселляции и восемь полуправильных носят название Архимедовых. Тесселляции, в которых отдельные плитки являются узнаваемыми фигурами, являются одной из основных тем творчества Эшера. В его записных книгах содержатся более 130 вариантов тесселляций.[3] Он использовал их в огромном количестве своих картин, среди которых "День и ночь" (1938), серия картин "Предел круга" I-IV, и знаменитые "Метаморфозы" I-III (1937-1968). Примеры ниже - картины современных авторов Холлистера Девида (Hollister David) и Роберта Фатауэра (Robert Fathauer). Hollister David "Семь птиц". На этой картине изображены семь птиц, две из которых изображены в негативе на фоне ландшафта города Ахо в Аризоне. Последовательно уменьшающиеся фигуры птиц совмещаются друг с другом в виде фрактальной тесселляции. Хвостовые перья каждой птицы являются разделяют конструкцию напополам, отсекая примерно треть расстояния между кончиками крыльев. Каждая меньшая птица в свою очередь делит свою область аналогичным образом. Если этот процесс продолжать до бесконечности, получится набор точек, известный как множество Кантора или Канторова пыль. Robert Fathauer "Фрактальные рыбы - сгруппированные группы". Это компьютерная работа, распечатанная на фотобумаге. Сквозь иллюминатор видны волны, но при ближайшем рассмотрении видно, что волны являются на самом деле фрактальной тесселляцией, состоящей из рыб.

5.1 Выдающиеся люди в истории математического изобразительного искусства 2

Голландский художник М.К. Эшер (1898-1972) в некотором роде является отцом математического искусства. Математические идеи играют центральную роль в большинстве его картин за исключением лишь ранних работ. Большинство идей, часто используемых современными математическими художниками, были использованы Эшером, и его работы часто являются источником вдожновения для современных авторов. Надеемся, что читатель знаком с работами Эшера, которые детально рассмотрены в литературе [1]-[3]. В данном разделе перечислены другие выдающиеся личности, которые не так часто ассоциируются с математическим искусством.

Одной из частых тем математического искусства является использование многогранников, которые были изучены достаточно давно. Платон (427-348 до н.е.) описал пять правильных многогранников, которые также иногда называются телами Платона. Однако открыты они были раньше Платона, и детали открытия правильных многогранников остаются загадкой. Платон соотносил эти тела с четырьмя элементами: огонь - тетраэдр, воздух - октаэдр, вода - икосаэдр, земля - куб. Далее, он писал, что существует пятая комбинация, которой Бог ограничил Мир, это додекаэдр. Архимед (290/280-212/211 до н.э) описал 13 полуправильных многогранников. Так же как правильные многогранники называют Платоновыми, полуправильные многогранники называют архимедовыми. Записи Архимеда об этих многогранниках были утеряны вместе с фигурами многогранников. Они были открыты вновь лишь в эпоху Ренессанса, и описание всех 13 многогранников было впервые опубликовано в книге Иоганна Кеплера "Harmonices Mundi" в 1619 году, почти через две тысячи лет после смерти Архимеда.

Леонардо да Винчи (Leonardo da Vinci ) (1452-1519) известен своими достижениями в качестве изобретателя и художника. В его записных книгах содержатся первые из известных примеров анаморфного искусства, использующего искаженные сетки перспективы. Его наклонные анаморфные изображения представляют объекты, которые должны рассматриваться по углом, чтобы они выглядели неискаженными.

Иоганн Кеплер (Johannes Kepler) (1580-1630) более известен своими работами в астрономии, но также имел большой интерес к геометрическим тесселяциям и многогранникам. В своей книге "Harmonices Mundi" (1619) он опубликовал примеры заполнения плоскости плитками в виде правильных и звездчатых многоугольников в дополнение к многогранникам, о которых было сказано выше.

Коломан Мозер (Koloman Moser) (1868-1918) - художник-график, преподававший в Вене и работавший в стиле модернизма. Он исполнил пару тесселляций в виде рыб в период 1899-1900 гг., выглядящие вполне в стиле Эшера. Однако, несомненно, Эшер не мог знать о работах Мозера вплоть до 1964 года.

Некоторые известнейшие художники XX века активно использовали математику в искусстве. Пит Мондриан (Piet Mondriaan) (1872-1944) - голландский художник, известный своими геометрическими абстракциями; несколько его работ изображают цветные блоки, разделенные черными линиями.

Сальвадо Дали (Salvador Dali) (1904-1989) - яркий и парадоксальный испанский художник использовал математические идеи в некоторых своих картинах. На картине "Распятие" ("Crucifixion") (1954) изображен гиперкуб, а на картине "La Visage de la Guerre" (1940) изображена фрактальная последовательность уменьшающихся гротескных лиц. Он также создал несколько эротических анаморфиных изображений.

Макс Биль (Max Bill) (1908-1994) - художник-график и скульптор, обучавшийся в Баухаузе (Bauhaus), создавал скульптуры, основанные на ленте Мебиуса, многие из которых высталены в общественных местах.

Виктор Васарели (1908-1997) - художник, родившийся в Венгрии, известен как пионер и практик направления оптического искусства Оп-арт (Op Art). Он использовал окрашенные простые геометрические формы, часто объединенные в массивы, для создания эффекта движения, выпуклости или вогнутости на плоском рисунке.

Бенуа Мандельброт (Benoit Mandelbrot) (1924-...) - математик, в значительной степени ответственный за формализацию и популяризация концепции фракталов. Он открыл множество Мандельброта, наиболее известный фрактальный объект. Он также изобрел термин "фрактал" ("fractal"), полученный из латинского слова "fractus", означающий "разбитый на куски", "сломанный". О его понимании эстетического содержания фракталов говорит следующая цитата: "Может ли чистая геометрия 'человеку с улицы' показаться прекрасной? Точнее, может ли фигура, описываемая простым уравнением или правилом построения, быть воспринята человеком, не связанным с геометрией, как фигура имеющая эстетическое значение, а именно, быть декоративной, а возможно и видом искусства? Если эта геометрическая фигура - фрактал, то ответ - да."

5.2 Общие темы в математическом искусстве 4

5.2.1 Многогранники 1

Правильные геометрические тела - многогранники - имели особое очарование для Эшера. Во его многих работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов. Существует лишь пять правильных многогранников, то есть таких тел, все грани которых состоят из однаковых правильных многоугольников. Они еще называются телами Платона. Это - тетраэдр, гранями которого являются четыре правильных треугольника, куб с шестью квадратными гранями, октаэдр, имеющий восемь треугольных граней, додекаэдр, гранями которого являются двенадцать правильных пятиугольников, и икосаэдр с двадцатью треугольными гранями. На гравюре "Четыре тела" Эшер изобразил пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники выглядят полупрозрачными, и сквозь любой из них можно увидеть остальные.

Многогранник называется правильным, если он лежит по одну сторону от плоскости любой его грани, т. е. является выпуклым, и все его грани есть равные правильные многоугольники. Простой подсчет суммы углов при вершине правильного многогранника показывает, что существует только пять правильных многогранников^*. Доказательство этого факта имеется в XIII книге "Начал" Евклида, но сам факт был, безусловно, известен Платону, а правильные многогранники знали пифагорейцы задолго до Платона. Форму правильных тел, по-видимому, подсказала древним грекам сама природа: кристаллы поваренной соли имеют форму куба, кристаллы квасцов - октаэдра, а кристаллы пирита - додекаэдра. Последний, как показали раскопки в итальянских Альпах, был любимой игрушкой этрусских детей задолго до нашей эры.

^* ( В самом деле, сумма плоских углов s при вершине выпуклого многогранника должна быть строго меньше 360°, а число граней при вершине m≥3. Тогда гранями правильного многогранника могут быть только три плоские фигуры: правильные треугольник, четырехугольник (квадрат) и пятиугольник, ибо уже для шестиугольников s = 120°*3 = 360°. Название правильному многограннику дается по общему числу граней М. Таким образом, из равносторонних треугольников можно составить три правильных многогранника при m = 3, 4, 5 (при m = 6 s = 60°*6 = 360°):

1. Тетраэдр (четырехгранник): m = 3, М = 4.

2. Октаэдр (восьмигранник): m = 4, М = 8.

3. Икосаэдр (двадцатигранник): m = 5, М = 20, а из квадратов и правильных пятиугольников - только по одному при m = 3 (при m = 4 s = 90°*4 = 360° - для квадратов и s = 108°*4 = 432° - для пятиугольников).

4. Гексаэдр (шестигранник), или куб: m = 3, М = 6.

5. Додекаэдр (двенадцатигранник): m = 3, М = 12.

В любом выпуклом многограннике числа вершин L, граней М и ребер N связаны формулой Эйлера L + M - N = 2.)

Правильные многогранники всегда восхищали пытливые умы симметрией, простотой и мудростью своих форм. Леонардо да Винчи любил изготовлять из дерева каркасы правильных тел и преподносить их в виде подарка различным знаменитостям.

Рисунки тел Платона, выполненные Леонардо да Винчи к книге Луки Пачоли 'О божественной пропорции'. Венеция. 1509

Ко времени Платона в античной философии уже созрела концепция четырех элементов (стихий) - первооснов материального мира: огня, воздуха, воды ц земли. Огонь и землю Платон считает основными компонентами для образования космоса: "...всему, что имело произойти, надлежало, конечно, быть телесным, видимым и осязаемым. Но быть видимым ничто не может без посредства огня, точно так же и осязаемым ничто не может быть без чего-нибудь твердого, твердым же ничто не может быть без земли (Тимей)". Между основными стихиями помещаются две средние - вода и воздух, и все они связываются музыкальными отношениями. Атомам земли Платон придает форму куба, так как и земля, и куб отличаются неподвижностью и устойчивостью. Атомам воды - форму икосаэдра, так как вода отличается текучестью, а из всех правильных тел икосаэдр - наиболее "катящийся". Атомам воздуха - форму октаэдра, ибо воздух движется взад и вперед и октаэдр как бы направлен одновременно в разные стороны. Атомам огня - форму тетраэдра как наиболее острого, мечущегося в разные стороны. Не у дел остался пятый правильный многогранник - додекаэдр. Для него Платон вводит пятый элемент - "пятую сущность"^* - мировой эфир, атомам которого придается форма додекаэдра как наиболее близкого к шару - самому совершенному по форме телу. С тех пор правильные многогранники называются также платоновыми телами.

^* (Пятая сущность - по-латыни квинтэсенция - у средневековых алхимиков ста означать тончайший элемент, составляющий якобы сущность вещей. В настоящее время квинтэссенция - синоним самого главного, иболее существенного.)

Практическая работа: Модели правильных многогранников

5.2.3 Искажённые и необычные перспективы 1

Среди наиболее важных работ Эшера с математической точки зрения являются картины, оперирующие с природой самого пространства. Литография "Три пересекающиеся плоскости" - хороший пример для начала обзора таких картин. Этот пример демонстрирует интерес художника к размерности пространства и способность мозга распознавать трехмерные изображения на двухмерных рисунках. Как будет ниже, Эшер позже использовал данный принцип для создания изумительных визуальных эффектов.

Невозможные фигуры - эти фигура, изображенная в перспективе таким способом, чтобы выглядеть на первый взгляд обычной фигурой. Однако при более внимательном рассмотрении зритель понимает, что такая фигура не может существовать в трехмерном пространстве. Эшер изобразил невозможные фигуры на своих известных картинах "Бельведер" (1958), "Восхождение и спуск" (1960) и "Водопад" (1961). Одним из примеров невозможной фигуры служит картина современного венгерского художника Иштвана Ороса (Istvan Orosz). Istvan Orosz "Перекрестки" (1999). Репродукция гравюры по металлу. На картине изображены мосты, которые не могут существовать в трехмерном пространстве. Например, есть отражения в воде, которые не могут быть исходными мостами.

Необычные системы перспективы, содержащие две или три исчезающие точки, также являются излюбленной темой многих художников. К ним также относится родственная область - анаморфное искусство. Эшер использовал искаженную перспективу в нескольких своих работах "Наверху и внизу" (1947), "Дом лестниц" (1951) и "Картинная галерея" (1956). Дик Термес (Dick Termes) использует шеститочечную перспективу для рисования сцен на сферах и многогранниках, как показано на примере ниже. Dick Termes "Клетка для человека" (1978). Это разукрашенная сфера, в процессе создания которой использовалась шеститочечная перспектива. На ней изображения геометрическая структура в виде сетки, сквозь которую виден ландшафт. Три ветки проникают внутрь клетки, а также по ней ползают рептилии. В то время как одни изучают мир, другие обнаруживают себя, находящимися в клетке. Слово анаморфный (anamorthic) сформировано из двух греческих слов "ana" (снова) и morthe (форма). К анаморфным относятся изображения настолько сильно искаженные, что разобрать их без специального зеркала бывает невозможно. Такое зеркало иногда называют анаморфоскопом. Если смотреть в анаморфоскоп, то изображение "формируется снова" в узнаваемую картину. Европейские художники раннего Ренессанса были очарованы линейными анаморфными картинами, когда вытянутая картина становилась снова нормальном при обзоре под углом. Известный премер - картина Ханса Хольбейна (Hans Holbein) "Послы" ("The Ambassadors") (1533), в которой изображен вытянутый череп. Картина может быть наклонена в верхней части лестницы так, что люди, поднимающиеся по лестнице будут напуганы изображением черепа. Анаморфные картины, для просмотра которых необходимы цилиндрические зеркала, были популярны в Европе и на Востоке в XVII-XVIII веках. Часто такие изображения несли сообщения политического протеста или были эротического содержания. Эшер не использовал в своей работе классические анаморфные зеркала, однако, в некоторых своих картинах он использовал сферические зеркала. Самая известная его работа в этом стиле "Рука с отражающей сферой" (1935). Пример ниже показывает классическое анаморфное изображение работы Иштвана Ороса (Isvan Orosz). Istvan Orosz "Колодец" (1998). Картина "Колодец" полученая печаться с гравюры по металлу. Работа была создана к столетию со дня рождения М.К. Эшера. Эшер писал об экскурсиях в математическое искусство, как о прогулся по прекрасному саду, где ничто не повторяется. Ворота в левой части картины отделяют эшеровский математический сад, находящийся в мозге, от физического мира. В разбитом зеркале в правой части картины присутствует вид маленького городка Атрани (Atrani) на побережье Амалфи (Amalfi) в Италии. Эшер любил это место и прожил там некоторое время. Он изобразил этот город на второй и третьей картинах из серии "Метаморфозы". Если поместить цилиндрическое зеркало на место колодца, как это показано справа, то в нем, как по волшебству, появится лицо Эшера.

Оптические иллюзии (http://www.smekalka.pp.ru/optic.html)

5.2.4 Лента Мёбиуса 1

Лента Мебиуса - это трехмерный объект, имеющий только одну сторону. Такая лента может быть легко получена из полоски бумаги, перекрутив один концов полоски, а затем склеив оба конца друг с другом. Эшер изобразил ленту Мебиуса на работах "Всадники" (1946), "Лента Мебиуса II (Красные мурвьи)" (1963) и "Узлы" (1965). Позднее, поверхности минимальной энергии стали вдохновением для многих математических художников. Брент Коллинз (Brent Collins), использует ленты Мебиуса и поверхности минимальной энергии, а также другие виды абстракций в скульптуре.

Проект «В нём бесконечность свёрнута кольцом…»

5.2.5 Фракталы 1

Фрактал - это объект, повторяющий сам себя в различных масштабах, которые связаны математическим способом. Фракталы формируются итерационно, многократно повторяя вычисления так, что получается объект высокой сложности с множеством мелких деталей. К сожалению, фракталы как таковые были недоступны Эшеру, потому что были формализованы и выделены в отдельную область математики лишь после его смерти. Эшер очень интересовался изображением бесконечного в пределах конечной области, в частности бесконечными тесселляциями. Он использовал сжимающиеся координатные сетки и гиперболическую геометрию для достижения этого эффекта, как показано в картинах "Предел круга" I-IV (1958-1960) и "Предел квадрата" (1964). Ниже приведены примеры современных художников Кэри Митчелл (Kerry Mitchell) и Роберта Фатауэра (Robert Fathauer). Kerry Mitchell "Будда" - компьютерная картина основанная на множестве Мандельброта, исследованного Бенуа Мандельбротом (Benoit Mandelbrot) Robert Fathauer "Композиция кругов" (2001) - не является вычисляемым фракталом, однако может быть получен графически, упаковывая меньшие круги в больших.

Проект «Печенье-фракталы» (http://www.evilmadscientist.com/2009/fractal-snowflake-cupcakes/)

Математические изобразительное искусство процветает сегодня, и многие художники создают картины в стиле Эшера и в своем собственном стиле. Эти художники работают в различных направлениях, включая скульптуру, рисование на плоских и трехмерных поверхностях, литографию и компьютерную графику. А наиболее популярными темами математического искусства остаются многогранники, тесселляции, невозможные фигуры, ленты Мебиуса, искаженные системы перспективы и фракталы.

6 Математика и литература 3 часа

6.1 Математики-поэты (Ломоносов М.В., Ковалевская С.В., Лобачевский Н.И., Омар Хайам,..) 1

Математика и поэзия. Что роднит их, казалось, на первой взгляд они такие разные… Ученым не чужда поэзия. Как показывает история науки, еще со времен пифагорейцев выдающиеся математики увлекались поэзией и даже сами пробовали писать.

Ж. Дьедонне говорил: “Стимулы математиков всех времен: любознательность и стремление к красоте”. Большое математическое дарование нередко сочетается с проявлением творческого интереса к поэзии.

Ученые и поэзия.

Женщина-математик Софья Васильевна Ковалевская говорит о математике так: “Это наука, требующая наиболее фантазии, нельзя быть математиком, не будучи в то же время поэтом в душе”.

Она – великий математик, она – признанный писатель и поэт. Вот одно из ее стихотворений.

“ЕСЛИ ТЫ В ЖИЗНИ…”

Если ты в жизни, хотя на мгновенье

Истину в сердце своем ощутил,

Если луч правды сквозь мрак и сомненье

Ярким сияньем твой путь озарил:

Чтобы в решеньи своем неизменном

Рок ни назначил тебе впереди –

Память об этом мгновеньи священном

Вечно храни, как святыню, в груди.

Тучи сберутся громадой нестройной,

Небо покроется черною мглой,

С ясной решимостью, с верой спокойной

Бурю ты встреть и померься с грозой.

Великий русский ученый М. В. Ломоносов говорил о математике так: “Математику уже затем учить надо, что она ум в порядок приводит”. И вот отрывок из его стихотворения:

О вы, которых ожидает

Отечество от недр своих

И видеть таковых желает,

Каких зовет от стран чужих,

О, ваши дни благословенны!

Дерзайте ныне ободрены

Раченьем вашим показать,

Что может собственных Платонов

И быстрых разумом Невтонов

Российская земля рожать.

Писал стихи и великий русский геометр Лобачевский. Ректор Казанского университета и известный математик вдруг в 1834 году “рискнул” опубликовать свое стихотворение “Разлив Волги при Казани”. Вот отрывок его:

“Ты поражаешь ли поля опустошеньем?

Ты похищаешь ли надежды поселян?

Нет! На водах твоих всегда благословенье

Почиет благодарных стран,

Тобой, питаемых, тобой обогащенных!

Ты и земли безвредная краса,

И светлые в струях твоих невозмущенных,

Как в чистой совести, сияют небеса.

Вот образ мирного могущества России!

Ее разлив не страшен никому.

Великодушие обуздывает силы,

Всегда, везде покорные ему.

Эта публикация, по-видимому, связана с приездом Пушкина в Казань в сентябре 1833 года, где он собирал материалы о восстании Пугачева. Жена Лобачевского – сестра Великопольского, давнишнего приятеля Пушкина, на вечерах которого бывали Пушкин и Лобачевский. Встретились два гения. Может быть, после встречи с Лобачевским Пушкин сказал: “Вдохновение нужно в поэзии, как в геометрии”.

3. Пушкин и математика.

Широко распространено мнение, что А.С. Пушкин был не совсем в ладах с математикой. На самом деле, из воспоминаний старшей сестры Ольги, мы узнаем, что в детстве бывало он плакал над задачами по математике. На страницах гениальных творений Пушкина нашли отражение математические понятия, термины и идеи. Связи поэта с современной ему математикой весьма многообразны. По результатам вступительных экзаменов в лицей об Александре Пушкине записано: что «в познании языков: российского – очень хорошо, французского – хорошо, немецкого – не учился, в арифметике – знает до тройного правила, в познании общих свойств тел – хорошо. В воспоминаниях об учебе в лицее «первый друг» и «друг бесценный» Иван Пущин рассказывал: «Учитель физики и математики Яков Иванович Карцев вызвал Пушкина к доске решать алгебраическую задачу. Переминаясь с ноги на ногу, Пушкин молча делал на доске какие-то записи чисел. На вопрос учителя: «Ну, что же у Вас получилось? Чему равняется икс?» - ученик улыбнулся и ответил: «Нулю!». «Хорошо, - подытожил Карцев. – У вас, Пушкин, все в моем классе кончается нулем. Садитесь на место и пишите лучше стихи».

Как видно в лицейские годы математика не всегда принималась юным А. Пушкиным как «милые сердцу предметы». Зато в последствии, когда он писал о своем стремлении «в просвещении стать с веком на равнее», поэт несомненно проявлял большой интерес к математике, что нашло отражение в его гениальных творениях. В материалах записных книжек Пушкина за 1835 год содержится гипотеза о происхождении формы цифр: «Форма цифр арабских составлена из следующей фигуры: AD (1), ABDC (2), ABECD (3), ABD+AE (4). Русские цифры составлены по тому же образцу». Хотя, существует мнение об индийском происхождении «арабских» цифр.

Индийские цифры попади в Европу от арабов в 12 в. через Мавриатнию. Пушкин, сравнивая татарское иго с игом мавританским в Испании, отметил: «Татары не походили на мавров. Они, завоевав Россию, не подарили ей ни алгебры, ни Аристотеля».

Поистине крылатыми стали слова из трагедии «Моцарт и Сальери» «проверил я алгеброй гармонию». Считается, что эта фраза проводит разделение между искусством Моцарта и ремесленничеством Сальери и сводится к противопоставлению искусства и науки.

В творчестве Пушкина в различных вариациях встречаются слова, загадочным образом связанные с наукой о случайном.

Дар напрасный, дар случайный,

Жизнь, зачем ты мне дана?

Иль зачем судьбою тайной

Ты на казнь осуждена?

В незаконченном стихотворении о научном творчестве Пушкин дает глубокие определения случаю, опыту и гению:

О, сколько нам открытий чудных

Готовят просвещенья дух

И опыт, сын ошибок трудных,

И гений, парадоксов друг,

И случай, бог изобретатель

Глубину этих определений специально отмечал еще академик С.И. Вавилов

В настоящее время на основе произведений Пушкина авторы современных задачников по теории вероятностей с удовольствием включают задачи на классическое определение вероятности. Например: Из колоды карт (52 карты) Герман наугад извлекает три карты. Найдите вероятность того, что это будут 3, 7 и туз.

Друг поэта П.А. Вяземский писал о Пушкине, что от был «страстен и к наукам естественным и особенно математическим, которые составляли значительный каптал его познаний и были до конца любимым предметом его ученых занятий и глубоких исследований».

6.2 Математика в литературных произведениях 1 http://www.smekalka.pp.ru/old.html

старинные сказочные литературные

6.3 Вечер поэзии:

- стихи, посвящённые великим математикам;

- стихи, в которых встречаются математические понятия;

- стихи – задачи; 1

Задачи со словами (http://www.smekalka.pp.ru/word_other.html)

7 Математика и театр 3 часа

Подготовка и выступление "Математического театра": странички из жизни древних ученых-математиков; значение и роль некоторых математических кривых

Примеры миниатюр, пьес, сказок.

1. История возникновения дробных чисел

2. «Колесо истории»

3. Сказка о геометрических фигурах.

4. Дед равняло (о решении уравнения)

5. Сказка о хитром и жадном короле (о процентах)

6. Случай в вагоне

7. Делители и кратные

8. Точка. Прямая. Отрезок. Луч.

9. Сказка о четырехугольнике и сварливой жене его трапеции

10. Среднее арифметическое

11. Задача – сказка о Балде

12. Бесплатный обед

13. Рене Декарт

14. Карл Гаусс на уроке

15. Царский путь в геометрию

16. Уроки Евклида

17. Притча о трех учениках

18. Посвящается Архимеду

ДРАМА + ДРАМА = ТЕАТР

Ответ: 18969 + 18969 = 37938

Резерв 4 часа

То, что я понял - превосходно.

Думаю, таково же и то, чего я не понял.

Сократ

Только кончая задуманное сочинение, мы уясняем себе, с чего нам следовало его начать.

Б. Паскаль

Как сказал один мудрец задолго до Паскаля, "идет ветер к югу и переходит к северу, кружится, кружится на ходу своем, и возвращается ветер на круги свои". Поэтому, подойдя к заключению, хочется вернуться к началу книги, к мудрому древнему знаку Ин-Ян. Невозможно навести "математический" порядок в искусстве, а то и вовсе "математизировать" искусство, как это происходит сегодня со многими науками.

Гармонии стиха божественные тайны

Не думай разгадать по книгам мудрецов:

У брега сонных вод, один бродя, случайно,

Прислушайся душой к шептанью тростников... (Аполлон Майков)

Искусство - самостоятельная форма познания реальной действительности, оно живет своей жизнью, оно соткано из хитросплетения диалектически противоположных начал - материального и духовного, рационального и иррационального, объективного и субъективного, логичного и алогичного, сконструированного и сотворенного, рассчитанного и угаданного... Ни в науке, ни в технике нет подобного переплетения противоположностей. Поэтому в той своей части, которая описывается первыми прилагательными, искусство доступно точному и прежде всего математическому анализу. А в части, описываемой вторыми прилагательными, искусство неподвластно математике, да и не нужно разрушать эту волшебную часть искусства логикой. К этой части искусства необходимо "прислушаться душой". Вот почему словосочетание "Математика и искусство" на протяжении столетий вызывает диаметрально противоположные суждения. Приведем только два и только служителей муз. Английский художник У. Хогарт писал о сущности художественного метода: "Все математические представления следует совершенно устранить из нашего метода, потому что они для него не имеют никакого смысла". А вот французский скульптор Антуан Бурдель (1861-1929) считал: "Искусство - это завуалированная алгебра, отнимающая жизнь у тех, кто стремится приподнять ее покрывало".

Однако есть третье мнение, отражающее глубокое понимание диалектики искусства, мнение, которое высказал в дискуссии ученых и художников профессор М. Каган: "... невозможно проверить алгеброй гармонию и невозможно проверить - т. е. познать - гармонию без алгебры". Именно такой взгляд на математику и искусство символизирует древнекитайский знак гармонии Ин-Ян.

Искусство - это не только "содержание", но и "форма". Последняя, по всей видимости, имеет сходные законы построения (формообразования) как в природе, так и в искусстве. И, как все закономерное форма, должна подчиняться прежде всего математическим законам. Но не убьет ли знание законов формообразования искусство, не превратит ли искусство в технологический процесс изготовления штампов? Истинному искусству это не грозит. Имхотеп и Хесира, Поликлет и Пракситель, Дюрер и Леонардо да Винчи, Моцарт и Бах, Палладио и Ле Корбюзье - все они на каких-то этапах отдавали поискам законов формообразования (в том числе и математических) больше усилий, чем "беспорядочному" и "безрассудному" искусству. Однако эти поиски, эта "математика искусства" не убили в них художников, а, скорее, наоборот, помогли стать великими. Более того, знание законов формообразования часто было для художника тем "магическим кристаллом", который помогал найти живое русло истины в мучительно тревожных сумерках, сопровождающих начало любого пути.

И даль свободного романа

Я сквозь магический кристалл

Еще не ясно различал. (Пушкина А.С.)

Симметрия форм живой природы обязана своим существованием прежде всего закону тяготения. Но тяготение - вечный закон природы; значит, вечна и симметрия, и, значит, вечно симметрия будет ассоциироваться с красотой. С доисторических времен симметрия играла огромную роль в искусстве. Та же заглавная роль симметрии в природе в полной мере осознана наукой нашего времени. Таким образом, математические законы симметрии становятся крепким связующим звеном между наукой и искусством. Но не только законы симметрии являются "математикой искусства". Гамма в музыке и шкала пропорциональности в архитектуре (в частности, знаменитые ряд золотого сечения и модулор Ле Корбюзье) имеют одинаковое математическое строение. Таким образом, в основе основ музыки и архитектуры - гамме и пропорции - лежит математика.

Красота не является избранницей только искусства. Красота есть всюду. Есть она и в науке, и в особенности в ее жемчужине - математике. К сожалению, эстетика науки до сих пор живет на положении Золушки и о красоте науки сказано мало. Но те, кто собирается посвятить свою жизнь науке, должны ясно представлять, что наука во главе с "царицей всех наук" - математикой - откроет перед ними сказочные сокровища красоты.

Информационно-методическое обеспечение для учителя;

http://www.smekalka.pp.ru/old.html

http://www.smekalka.pp.ru/word_bred.html?page=1

http://livescience.ru/Статьи:Музыка-математика-в-цифрах

http://www.stonot.ru/

http://www.krugosvet.ru/

http://www.wikipedia.org/

http://ru.wikibooks.org/wiki

http://www.piano-notes.net/

http://festival.1september.ru/articles/508853/

http://im-possible.info/russian/articles/vis_math_art/

http://Letopisi.ru Проект «Музыкальная математика»

http://physmatica.ru/zhivaya-matematika-matematicheskie-rasskazy-i-golovolomki/zadachka-65-besplatnyj-obed.html

Алтынов М. В. и др. Искусство: Живопись: Скульптура: Архитектура: Графика: Книга для учителя в 3-х ч. М.: Просвещение,1987.

Волошинов А. В. Математика и искусство. М.: Просвещение,1992.

Жмудь Л. Я. Пифагор и его школа М.: Наука, 1990, 192с.

Кордемский Б.А. Увлечь школьников математикой. М.: Просвещение, 1986.

К. Левитил "Геометрическая рапсодия". М.: Просвещение,1995.

Матвиевская Г.П. Альбрехт Дюрер – учёный. М.:Наука,1987.

Перли С.С. Перли Б.С. Страницы русской истории на уроках математики. М.: Педагогика, 1994.

Тэн И. Философия искусства. М.: Просвещение,1996.

Журнал «Квант»

№ 2-79. Михайлов О. Одиннадцать правильных паркетов. Невозможные Объекты (обложка и статья к ней).

№ 4-79. Гиндикин С. Арифметика на клетчатой бумаге.

№ 2-84. Фукс Д. В. Перспектива.

№ 9-84. Прохоров Золотая спираль.

№ 8-80 Тарзиманова Г. Стихотворение Лобачевского.

№ 4-82 Фабрикант В. Можно ли услышать рёв мамонта?

№ Казанджан Э. Поэзия? Математика?

Журнал «Знание – сила» № 12-94 Пельцер А. Кто вы, Пифагор?

Журнал «Наука и религия» № 3-98 Величко. Как Софья Ковалевская изменила свою судьбу и чем за это заплатила; № 4-90 Зримая математика (обложка).

Математика Приложение к газете «Первое сентября»

№ 1-99 Мурадова Р. Золотое сечение.

№ 1-99 Магический квадрат

№ 34-94.Поздняков Э. Г. Симметрия.

№7-96. Рисунки Морица Эшера.

№ 32-97 Стихотворение «Зодчие».

№ 9-98 Григорьева С. Вечер, посвящённый Софье Ковалевской.

Информационно-методическое обеспечение для обучающихся;

http://www.smekalka.pp.ru/old.html

http://livescience.ru/Статьи:Музыка-математика-в-цифрах

http://www.krugosvet.ru/

http://www.wikipedia.org/

http://www.piano-notes.net/

http://Letopisi.ru Проект «Музыкальная математика»

Деплан И. Я. Мир чисел. М.: «Просвещение», 2005

Детская энциклопедия – 2. Числа и фигуры (стр. 266-299).

Журнал «Квант»

Журнал «Знание – сила»

Журнал «Наука и религия»

Энциклопедия для детей. Т. 7. Искусство. Ч. 1. – Э68-е изд., испр./Глав. Ред. М.Д. Аксенова. – М..6 Аванта +, 2006 – 688 с.: ил.

К. Левитил "Геометрическая рапсодия".

Леман И. Увлекательная математика.М.: Знание,1985.

Энциклопедический словарь юного математика. М.; «Педагогика» 1985г

Энциклопедический словарь юного музыканта Э68/сост. В.В. Медушевский, О.О. Очаковская. – М.: Педагогика, 2007. – 352с., ил.

Энциклопедический словарь юного художника. М.: Педагогика,1983.

Я познаю мир: Детская энциклопедия: Музыка /авт. А.С. Кленов. Под общей ред. О.Г. Хинн. – М.: ООО Фирма «Издательство АСТ», 2010. – 46