Прогрессии в реальной жизни

Арифмети́ческая прогре́ссия —

числовая последовательность, в которой каждое последующее число, начиная со второго, получается из предыдущего увеличением его на определённое число .

Имеет вид: a 1 , a 1 +d, a 1 +2d, a 1 +3d, …, a 1 +(n-1)d,…

Геометри́ческая прогре́ссия — последовательность чисел, в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число .

Имеет вид: b 1 , b 1 q, b 1 q 2 , b 1 q 3 ,… ,b 1 q n-1 ,…

Арифметическая прогрессия:

Геометрическая прогрессия:

Определения

арифметической

и геометрической

прогрессий

очень похожи.

Заменяется лишь

сложение

умножением.

А из формулы n-го члена

арифметической

прогрессии,

можно получить

формулу

для геометрической

прогрессии,

если заменить сложение

умножением и умножение –

возведением в степень

a n+1 =a n +d

b n+1 =b n · q

q = b n+1 :b n

d = a n - а 1

a n =а 1 +d (n-1)

b n = b 1 q n-1

Числовая последовательность, каждый

член которой, начиная со второго,

равен предшествующему члену,

сложенному с одним и тем же числом,

Называется арифметической прогрессией.

Числовая последовательность, каждый

член которой, начиная со второго,

равен предшествующему члену,

умноженному на одно и то же число,

называется геометрической прогрессией

В соревновании по стрельбе за каждый промах в серии из 25 выстрелов стрелок получал штрафные очки: за первый промах — одно штрафное очко, за каждый последующий — на 0,5 очка больше, чем за предыдущий. Сколько раз попал в цель стрелок, получивший 7 штрафных очков?

Решение. Составим математическую модель задачи. Система штрафных очков составляет арифметическую прогрессию, первый член которой равен 1, а разность – 0,5. Сумма первых n членов ( количество промахов) равно 7. Найдем число промахов - n .

0. S n = (2 a 1 + d ( n -1)) n /2; 525= (2 · 30+ 5( n -1)) n /2; 1050= (60+ 5( n -1)) n ; 1050= 55 n + 5 n 2 ; n 2 +11 n -210=0, n 1 =-21, n 2 =10 ( n 0). Улитка достигнет вершины за 10 минут. " width="640"

Улитка ползет по дереву. За первую минуту она проползла 30 см, а за каждую следующую минуту — на 5 см больше, чем за предыдущую. За какое время достигнет улитка вершины дерева длиной 5,25 м, если считать, что движение начато от его основания?

Решение. a 1 =30, d =5, S n = 525, n 0.

S n = (2 a 1 + d ( n -1)) n /2;

525= (2 · 30+ 5( n -1)) n /2;

1050= (60+ 5( n -1)) n ;

1050= 55 n + 5 n 2 ;

n 2 +11 n -210=0, n 1 =-21, n 2 =10 ( n 0).

Улитка достигнет вершины за 10 минут.

При свободном падении тело прошло в первую секунду 5м, а в каждую следующую на 10м больше. Найдите глубину шахты, если свободно падающее тело достигло его дна через 5 с. после начала падения.

Решение.(1 способ)

в первую секунду: 5м,

во вторую секунду: 15м,

в третью секунду: 25м,

в четвертую секунду: 35м,

в пятую секунду: 45м.

Всего за пять секунд: 5+15+25+35+45=125(м).

Ответ: глубина шахты 125м.

Решение.(2 способ)

а1=5, d=10.

а5=а1+4d; а5=45.

S5=(a1+a5)·n/2; S5=(5+45)·5/2=125;

глубина шахты 125м.

Ответ: 125м.

Первые теоретические сведения, связанные с прогрессиями, дошли до нас в документах Древней Греции.

В Древнем Египте в V в. до н.э. греки знали прогрессии и их суммы:

1+2+3+…+n = =2+4+6+…+2n = n · (n+1).

Некоторые формулы, относящиеся к прогрессиям, были известны китайским и индийским ученым ( V в.)

В клинописных табличках вавилонян, как и в египетских папирусах, относящихся ко второму тысячелетию до нашей эры, встречаются примеры арифметических и геометрических прогрессий.

Пример:

«Пусть тебе сказано: раздели 10 мер ячменя между 10 человеками и, разность же между каждым человеком и его соседом равна меры».

Задачи на прогрессии, дошедшие до нас из древности, были связаны с запросами хозяйственной жизни: распределение продуктов, деление наследства и другие.

В трудах АРХИМЕДА (ок. 287-212 гг. до н.э.) излагаются первые сведения о прогрессиях.

В ходе своих исследований Архимед нашел сумму бесконечной геометрической прогрессии со знаменателем 1/4, что явилось первым примером появления в математике бесконечного ряда…

В “Исчислении песчинок” Архимед впервые сопоставляет арифметическую и геометрическую прогрессии:

1, 2, 3, 4, 5, …

10, 10 2 , 10 3 , 10 4 , 10 5 , …

и указывает на связь между ними, например:

10 3 · 10 5 =10 3+5 =10 8 ,

т.е. для умножения двух членов геометрической

прогрессии достаточно сложить соответствующие

члены арифметической прогрессии и взять

полученную сумму в качестве показателя 10.

Одно из доказательств Архимеда, изложенное в его произведении “Квадратура параболы”, сводится к суммированию бесконечно убывающей геометрической прогрессии:

Для решения некоторых задач из геометрии и механики Архимед вывел формулу суммы квадратов натуральных чисел, хотя ею пользовались и до него:

• Пифагор (IV в. до н. э.) и его ученики рассматривали последовательности, связанные с геометрическими фигурами. Подсчитывая число кружков в треугольниках, квадратах, пятиугольниках, они получали:

- последовательность (а п ) треугольных чисел 1, 3, 6, 10, 15, ... ;

- последовательность ( b п ) квадратных чисел 1, 4, 9, 16, 25, ... ;

- последовательность (с п ) пятиугольных чисел 1, 5, 12, 22, 35, ...

• Зададим эту последовательностей формулой п- ого члена.
• Последовательность (а п ) треугольных чисел получается из последовательности натуральных чисел 1, 2, 3, ... , т. е. из арифметической прогрессии, в которой первый член и разность равны 1, следующим образом:

а 1 = 1, а 2 = 1 + 2, а 3 = 1 + 2 + 3, а п = 1 + 2 + 3 + ... + п.

• Значит, а п = ( 1 + п ): 2 · п.

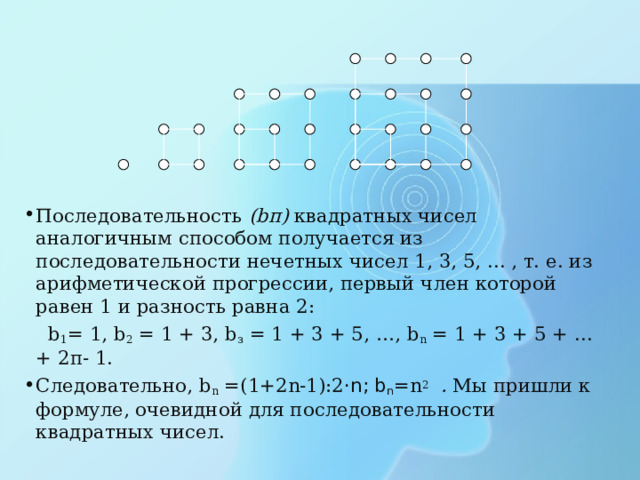
• Последовательность ( b п) квадратных чисел аналогичным способом получается из последовательности нечетных чисел 1, 3, 5, ... , т. е. из арифметической прогрессии, первый член которой равен 1 и разность равна 2:

b 1 = 1, b 2 = 1 + 3, b з = 1 + 3 + 5, …, b n = 1 + 3 + 5 + ... + 2п- 1.

• Следовательно, b n = (1+2n-1):2 ·n; b n =n 2 . Мы пришли к формуле, очевидной для последовательности квадратных чисел.

• Последовательность ( c п ) пятиугольных чисел аналогичным способом получается из последовательности нечетных чисел 1, 4, 7, ... , т. е. из арифметической прогрессии, первый член которой равен 1 и разность равна 3: с 1 = 1, с 2 = 1 + 4,

b з = 1 + 4 + 7, …, с n = 1 + 4 + 7 + ... +(1+3( п- 1)).

• Следовательно, с n = ( 1+1+3( п- 1)) :2 ·n; с n = (3 n -1) · n / 2

Леонардо Пизанский

(Фибоначчи)

• Числа Фибоначчи — элементы числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … в которой каждое последующее число равно сумме двух предыдущих чисел.

• 1.Сумма первых n -чисел Фибоначчи: u 1 + u 2 +…+ u n = u n +2 -1.
• 2.Сумма чисел Фибоначчи с нечетными номерами:

u 1 + u 3 + u 5 +…+ u 2 n -1 = u 2 n .

• 3.Сумма чисел Фибоначчи с четными номерами:

u 2 + u 4 +…+ u 2 n = u 2 n +1 -1.

• 4.Сумма квадратов первых n -чисел Фибоначчи:

Летом инфузории размножаются бесполым способом делением пополам.

Вопрос: сколько будет инфузорий после 15-го размножения?

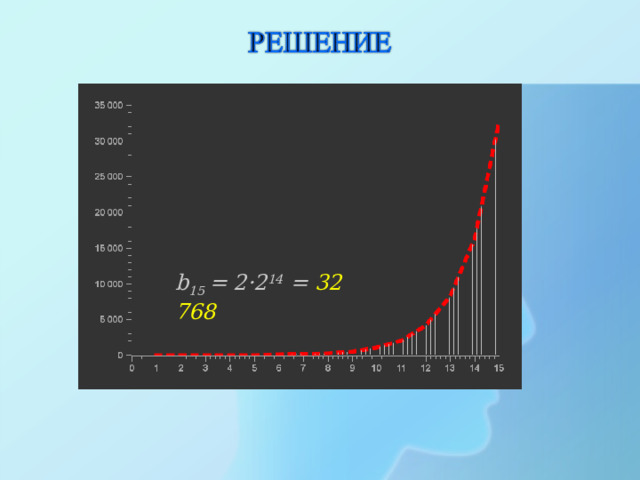
• Численность любого вида при отсутствии ограничений растёт в соответствии с геометрической прогрессией;
• Кривая роста численности любого вида при отсутствии ограничений называется экспонентой .

b 15 = 2·2 14 = 32 768

Бактерии

Известно, что бактерии размножаются делением: одна бактерия делится на две; каждая из этих двух в свою очередь тоже делится на две, и получаются четыре бактерии; из этих четырех в результате деления получаются восемь бактерий и т. д. Результат каждого удвоения будем называть поколением.

Способность к размножению у бактерий настолько велика, что если бы они не гибли от разных причин, а беспрерывно размножались, то за трое суток общая масса потомства одной только бактерии могла бы составить 7500 тонн. Таким громадным количеством бактерий можно было бы заполнить около 375 железнодорожных вагонов.

• Бактерия, попав в живой организм, к концу 20-й минуты делится на две бактерии, каждая из них к концу следующих 20 минут делится опять на две и т.д. Найдите число бактерий, образующихся из одной бактерии к концу суток.
• Решение. В сутках 1440 минут, каждые двадцать минут появляется новое поколение - за сутки 72 поколения. По формуле суммы n первых членов геометрической прогрессии, у которой b 1 =1, q=2, n=72, находим, что S 72 =2 72 -1= 4 722 366 482 869 645 213 696 - 1=

= 4 722 366 482 869 645 213 695.

Одуванчик

“ Потомство одного одуванчика за 10 лет может покрыть пространство в 15 раз больше суши земного шара”.

К. А. Тимирязев

• Одно растение одуванчика занимает на земле площадь 1 кв. метр и даёт в год около 100 летучих семян.

• а) Сколько кв. км площади покроет всё потомство одной особи одуванчика через 10 лет при условии, если он размножается беспрепятственно по геометрической прогрессии?
• б) Хватит ли этим растениям на 11-й год места на поверхности суши земного шара?

• Одно растение одуванчика занимает на земле площадь 1 кв. метр и даёт в год около 100 летучих семян.

• а) Сколько кв. км площади покроет всё потомство одной особи одуванчика через 10 лет при условии, если он размножается беспрепятственно по геометрической прогрессии?

[ 1012 км 2 ]

• б) Хватит ли этим растениям на 11-й год места на поверхности суши земного шара?

[ нет, Sсуши = 148 млн км 2 ]

Царь древней Индии Шерам пригласил к себе изобретателя шахмат Сета и спросил, какую бы

награду хотел бы он получить за изобретение столь

мудрой игры.

Тогда Сета попросил царя на первую клетку

шахматной доски положить 1 зерно, на вторую – 2 зерна,

на третью – 4, на четвертую – 8 и т.д., т.е. на каждую

клетку вдвое больше зерна, чем на предыдущую клетку.

Поначалу царь удивился столь “скромному” запросу

изобретателя и поспешно повелел выполнить ту просьбу.

Однако, как выяснилось, казна царя оказалось слишком

“ ничтожной” для выполнения этой просьбы.

Действительно, чтобы выполнить эту просьбу, потребовалось бы количество зерен, равное сумме 1 + 2 + 2 2 +.. + 2 63 , а эта сумма равна 18446744073709551615.

Если считать, что 1 пуд зерна содержит 40000 зерен, то для выполнения просьбы потребовалось бы 230 584 300 921 369 пудов зерна. Если полагать, что в среднем ежегодно собирается 1 000 000 000 пудов зерна, то для выполнения указанной просьбы нужно работать (не расходуя ни одного зерна) на протяжении 230584 лет.

S 64 =2 64 -1=

=18446744073704551615

Это задача из «Сборника старинных занимательных задач по математике» Игнатьева Е.И.

Однажды богач заключил выгодную, как ему казалось, сделку с человеком, который целый месяц ежедневно должен был приносить по 100 тыс. руб., а взамен в первый день месяца богач должен был отдать 1 коп., во второй-2 коп., в третий-4 коп., в четвертый-8 коп. и т. д. в течении 30 дней. Сколько денег получил богач и сколько отдал? Кто выиграл от этой сделки?

Считают “мужик” и “купец”

“ Мужик” заплатил: S 30 = 100 000• 30 = 3 000 000 (рублей).

“ Купец” заплатил: 1; 2; 4;… q=2/1=2.

S 30 =1• (2 30 – 1):(2-1)= 2 30 -1= =1 073 741 824 -1 =1 073 741 823 (коп.) т.е. 10 738 418 руб.23коп

Удивительно, как быстро разбегаются по посёлку слухи! Иной раз не пройдет и двух часов со времени какого– нибудь происшествия, которое видели всего несколько человек, а новость уже облетела весь посёлок: все о ней знают, все слышали.

Пример:

В поселке 16 000 жителей. Приезжий в 8.00 рассказывает новость трем соседям; каждый из них рассказывает новость уже трем своим соседям и т. д. Во сколько эта новость станет известна половине посёлка?

Решение. Итак, в 8. 15 утра новость была известна только четверым: приезжему и трём местным жителям. Узнав эту новость, каждый из трёх граждан поспешил рассказать её трём другим. Это потребовало также четверти часа. Значит, спустя полчаса после прибытия новости в город о ней узнали уже 4+3 · 3=13 человек. Каждый из девяти вновь узнавших поделился в ближайшие четверть часа с тремя другими гражданами, так что к 8.45 утра новость стала известна 13+9 · 3= 40 гражданам. Если слух распространяется по посёлку и далее таким способом, то есть каждый узнавший эту новость успевает в ближайшие четверть часа передать её трём согражданам, то осведомление посёлка будет происходить по следующему расписанию:

в 9.00 новость узнают 40+27 · 3=121 (человек);

9.15 121+81 · 3 =364 (человек);

9.30 364+243 · 3=1093 (человек);

9.45 1093+729 · 3=3280 (человек);

10.00 3280 + 2187 · 3 =9841(человек).

Прогрессии в литературе:

строки из “Евгения Онегина”.

«…Не мог он ямба от хорея Как мы не бились отличить…». Отличие ямба от хорея состоит в различных расположениях ударных слогов стиха.

Ямб – это стихотворный размер с ударением на четных слогах 2; 4; 6; 8;…Номера ударных слогов образуют арифметическую прогрессию с первым членом 2 и разностью прогрессии 2.

Хорей – это стихотворный размер с ударением на нечетные слогах стиха. Номера ударных слогов образуют арифметическую прогрессию 1; 3; 5; 7;..

Примеры.

• Ямб . «Мой д Я дя с А мых ч Е стных пр А вил…», прогрессия 2; 4; 6; 8;…
• Хорей. « Я проп А л, как зв Е рь в заг О не»Б.Л.Пастернак, « Б У ря  мгл О ю  н Е бо  кр О ет» А.С. Пушкин, прогрессия 1; 3; 5;7.

• Разберёмся в механизмах этих организаций. Организатор начинает вовлекать в свою организацию и говорит, что, если внести указанную плату по указанным адресам по 1 рублю, а затем заплатить ещё по 5 таким же адресам, вычеркнув первый адрес и дописав свой последним, то через некоторое время вы получите уйму денег. Хотя желающих разбогатеть по щучьему веленью немало, но в выигрыше оказываются только учредители такой игры.
• Решение. Дело в том, что число участников увеличивается в 5 раз с каждым кругом. Если пятёрка устроителей подпишет, допустим, 120 человек со своими адресами, то в первом круге участвуют 120 человек, во втором – 600, в третьем – 3 000, …, в десятом – 234  375  000 человек; это намного больше населения страны. Так что участник, включившийся в восьмом или девятом круге, уже ничего не получит.