Проект "Математика на шахматной доске"

Муниципальное автономное общеобразовательное учреждение "Лицей №14 имени Заслуженного учителя Российской Федерации А.М. Кузьмина"

ИНДИВИДУАЛЬНЫЙ ПРОЕКТ

по теме:

«Математика на шахматной доске»

Выполнил:

Учащийся 11 класса «Б»

Пыкин Даниил Иванович

Подпись

Научный руководитель:

Ондрикова Елена Вячеславовна,

учитель математики

Тамбов, 2017

Оглавление
Ведение……………………………………………………………………………3

История…………………………………………………………………………...4

Геометрия шахматной доски…………………………………………………..5

Задачи о шахматной доске……………………………………………………..7

Задачи, связанные с шахматными фигурами……………………………...11

Перестановочные задачи……………………………………………………..18

Математические игры на шахматной доске……………………………….20

Заключение …………………………………………………………………….21

ВВЕДЕНИЕ

Ша́хматы — настольная логическая игра со специальными фигурами на 64-клеточной доске для двух соперников, сочетающая в себе элементы искусства (в части шахматной композиции), науки и спорта. Название берёт начало из персидского языка: шах мат, что значит буквально: «шах умер».

Игра подчиняется определённым правилам; в официальных турнирах применяются правила ФИДЕ, которые регламентируют не только передвижение фигур, но и права судьи, правила поведения игроков и т.п.

Существует множество вариантов шахмат с нестандартными правилами, фигурами, размерами доски. Соответствующий раздел шахматной композиции — сказочные шахматы. В математике изучаются различные аспекты шахматной игры (например, классические «Задача о ходе коня» и «Задача о восьми ферзях»), в том числе с помощью компьютерного моделирования.

Объект изучения

Объектом изучения являются математические задачи на шахматную тему.

Предмет исследования

Телом исследования являются различные свойства шахматной доски, фигур, а также задачи, связанные с математикой.

Актуальность

Шахматы не перестают быть актуальными с древних времён. Даже сейчас шахматы пользуются популярностью у многих детей и взрослых, потому что это игра имеет такие свойства, как увлекательность и спортивный азарт, развивают логическое мышление, память, внимание. В математике существуют множество задач, связанных с шахматным столом и свойствами фигур.

Цель

Целью проекта является рассмотрение различных свойств, связанных с геометрией шахматной доски и фигурами, а также решение сопутствующих задач.

ИСТОРИЯ

Считается, что история шахмат насчитывает не менее полутора тысяч лет. Известно множество версий, объясняющих развитие шахмат и их распространение во всём мире — «индийская», «византийская» и др. Согласно наиболее распространённой из них, первая известная игра-прародитель, чатуранга, появилась в Индии не позже VI века нашей эры. Попав в соседние с Индией страны, чатуранга претерпела ряд изменений. Потомком её на Арабском Востоке стал шатрандж, а в Юго-Восточной Азии — сянци (Китай), макрук (Таиланд) и сёги (Япония). Шатрандж в IX—X веках от арабов попал в Европу и Африку. Европейские игроки продолжили модификацию игры, в результате к XV веку были те правила, которые сегодня известны как «классические». Окончательно правила были стандартизованы в XIX веке, когда стали систематически проводиться международные турниры. С 1886 года разыгрывается звание чемпиона мира по шахматам. С1924 года существует Международная шахматная федерация — ФИДЕ, под эгидой которой, начиная с середины XX века, проводится большинство международных соревнований.

ГЕОМЕТРИЯ ШАХМАТНОЙ ДОСКИ

Наиболее интересное свойство шахматной доски заключается в весьма необычном измерении расстояний на ней. Например, в обычной, евклидовой геометрии расстояние от поля a1 до h8 больше, чем до a8 (имеются в виду центры полей), однако король оба пути может преодолеть ровно за семь ходов! Расстояние между полями шахматной доски можно определять как число ходов, за которое данная фигура попадает с одного из этих полей в другое. Расстояние, введенное таким образом, зависит от конкретной фигуры. При этом для всех фигур, кроме пешки и рокирующего короля, расстояние от поля а до поля b равно расстоянию от b до а, а расстояние от а до с не больше, чем сумма расстояний от а до b и от b до с (так называемое неравенство треугольника).

Свойства наших «расстояний» не во всем похожи на обычные. На плоскости две точки соединяет лишь один кратчайший путь, а на шахматной доске король, например, может перейти с f7 на a7 за пять ходов 46 различными способами - и, значит, здесь у нас 46 «отрезков», соединяющих эти поля.

♔               ♚   ♙                       ♟

Рис. 1. Р. Рети.

Белые начинают и делают ничью 

Эффектную иллюстрацию указанного свойства представляет собой известный этюд Р. Рети (рис. 11). Кажется невозможным, что в этом положении белый король в состоянии справиться с черной пешкой. Это можно сделать, если он отправится за ней не по обычной прямой, а по «королевской». 
1.Крh8-g7 h5-h4 

2. Крg7-f6! 

Теперь грозит 3. Крe6, после чего белая пешка при поддержке короля проходит в ферзи одновременно с неприятельской. Такая угроза не могла бы возникнуть, если бы белый король двигался за пешкой h прямолинейно. 

2 Крa6-b6 

3. Крf6-e5!

 Снова король хочет помочь своей пешке, и хотя он довольно далеко удалился от вертикали h, после вынужденного 

3. Крb6:c6 

он догоняет неприятельскую пешку как раз на пороге ее превращения: 
4.Крe5-f4 h4-h3 

5.Крf4-g3 h3-h2 6.

Крg3:h2.

Ничья!

Рис. 2. И. Майзелис. Белые начинают и выигрывают 

Движение короля по прямой в случае необходимости можно заменить движением по ломаной линии. В этюде И. Майзелиса (рис. 12) пешка на a7 беззащитна, единственный шанс черных заключается в том, чтобы на неизбежное взятие Кр:a7 ответить Крc7, не выпуская короля противника из заточения. Путь белого короля до пешки a7 занимает пять ходов, причем существует 30 способов съесть эту пешку за столько ходов (на 16 меньше, чем число путей с f7 на a7, так как движение через b6 запрещено). Но лишь один из 30 путей приводит к цели (рис. 12):

1.Крf7-e6! Крb2-c3

2.Крe6-d5!!

Белый король, как говорят шахматисты, «отталкивает плечом» своего черного оппонента. Теперь тот не может пойти на d4, и это оказывается для него губительпым. Не проходит, например, 1. Крe6 Крc3 2. Крd6 Крd4 3. Крc6 Крe5! 4. Крb7 Крd6 5. Кр:a7 Крc7 с ничьей.

ЗАДАЧИ О ШАХМАТНОЙ ДОСКЕ

Задача 1

Рассмотрим задачу о покрытии доски костями домино размером 2×1. Всюду предполагается, что каждое домино покрывает два поля доски, а каждое поле покрыто одной половиной домино. Начнем со следующей задачи.

Условие.

Можно ли покрыть домино квадрат размером 8×8, из которого вырезаны противоположные угловые клетки (рис. 2,а)?

Рис. 3, 4. Задача о домино: а - квадрат с вырезанными углами; б - шахматная доска с вырезанными полями 

Можно воспользоваться алгебраическими рассуждениями, однако «шахматное» решение проще. Окрасим урезанный квадрат в черно-белый цвет, превратив его в шахматную доску без двух угловых полей a8 и h1 (рис. 2,б). При любом покрытии доски каждое домино покрывает одно белое и одно черное поле. У нас белых полей на два меньше, чем черных (вырезанные поля - белые), и поэтому необходимого покрытия не существует! Раскраска доски не только позволяет шахматисту легче ориентироваться во время игры, но и служит средством решения математических задач.

В рассмотренной задаче существенным было не то, что из доски вырезаны угловые поля, а то, что они одного цвета.

Задача 2

 Условие.
Сколькими способами можно расставить 8 ладей на чёрных полях шахматной доски так, чтобы они не били друг друга?
Решение.
Если не выдвигать ограничений на цвет полей, то для доски nn число способов расстановки n ладей так, чтобы они не били друг друга, равно n!. Раскрасим чёрные поля доски в два цвета: красный и синий (см. рис.). 4 ладьи окажутся на красных полях, 4 – на синих. Красные и синие поля образуют как бы отдельные доски 44, поэтому число способов расстановки 4 ладей, как на красных, так и на синих полях равно 4!. Отсюда число способов расстановки 8 ладей на чёрных полях шахматной доски равно 4!2.
Ответ: 4!2.

Рис. 5. Задача 2

Задача 3

Условие.
Расставить на доске 88 наименьшее возможное число коней так, чтобы каждое поле доски было бито (поле, на котором конь стоит, является битым).
Решение.
12 коней (пример на рисунке). Меньше 12 не хватит, т. к. каждое из 12 красных полей (см. рис.) бьют разные кони.
Ответ: 12 коней.

Рис. 6. Задача 3

Задача 4

Условие.
Можно ли доску 4n обойти конём, побывав на каждом поле ровно 1 раз, и последним ходом вернуться на исходное поле?
Решение.
Раскрасим доску в 4 цвета (см. рис). С синих полей можно попасть только на красные, с зелёных – только на жёлтые. Синих клеток столько же, сколько красных. Попав на красное поле, конь должен пойти на синее, иначе, если он пойдёт на жёлтое, в обходе коня красные поля встретятся чаще, чем синие. Аналогично, попав на синее поле, конь должен пойти на красное. Но тогда конь будет ходить только по синим и красным полям, что невозможно.
Ответ: Нет.

Рис. 7. Задача 4

Задача 5

 Условие.
Можно ли из шахматной доски 88 выкинуть а) 32, б) 48 клеток так, чтобы на оставшихся клетках нельзя было разместить доминошку 12, но при добавлении любой из выкинутых клеток доминошку расположить было бы можно?
Решение.
а) Можно, например, выкинуть все чёрные клетки.
б) Можно (см. рис., серым обозначены оставшиеся клетки, белым – выкинутые).
На самом деле 48 – наибольшее число клеток, которые можно выкинуть подобным образом, но доказательство этого факта слишком скучное (надо заметить, что если мы разобьём доску на 16 квадратов 22, то при выбрасывании 49 или более клеток в одном из таких квадратов не останется клеток (назовём такой квадрат “пустым”); далее надо рассматривать три случая расположения пустого квадрата…).
Ответ: можно.

Рис. 8. Задача 5

Задача 6

 Условие.
На всех клетках шахматной доски расставлены натуральные числа. Разрешается выделить любой квадрат размером 33 или 44 и увеличить все числа в нём на 1. Мы хотим в результате нескольких таких операций добиться, чтобы числа во всех клетках делились на 10. Всегда ли удастся это сделать?
Решение.
Будем рассматривать числа по модулю 10. Возьмём набор, состоящий только из нулей, и подсчитаем, сколько наборов мы сможем получить, исходя из него с помощью указанных в условии операций. На доске 88 можно выделить 62=36 квадратов 33 и 52=25 квадратов 44. Поэтому искомых наборов не больше 1025+36=1061. Но всего наборов 1064. Значит, существует набор, который с помощью указанных операций из набора, состоящего из нулей, получить не удастся. Если мы примем такой набор за исходный, то набор из нулей из такого набора получить не удастся.
Ответ: нет, не всегда.

Задача 7

Условие.
Какое наибольшее число ладей можно расставить на доске mn так, чтобы каждая била не более двух других?
Решение.
Посчитаем общее число ладей, которых бьёт ладья, обходящая доску по периметру (см. левый рисунок). Их не более чем 2(m+n). При этом каждую из стоящих на доске ладей мы посчитали по крайней мере дважды. Поэтому число ладей на доске не более m+n. Пример расстановки m+n ладей показан на правом рисунке.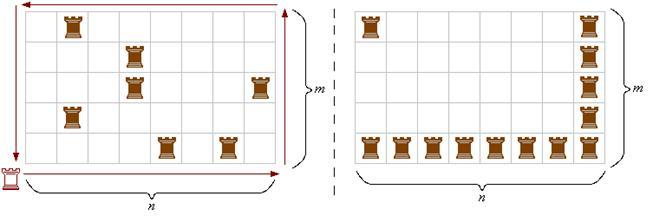

Рис. 9. Задача 7

Ответ: m+n.

ЗАДАЧИ, СВЯЗАННЫЕ С ШАХМАТНЫМИ ФИГУРАМИ КОНЬ

Основное отличительное свойство коня состоит в том, что он на каждом ходу меняет цвет своего поля. Многие задачи о коне удается эффектно решить, если воспользоваться этим важным свойством коня.

Рассмотрим два примера на эту тему.

На всех полях доски с нечетным числом полей стоят кони. Могут ли все они за один ход переместиться так, чтобы на каждом поле по-прежнему стоял один конь?

Доказательство того, что это невозможно, опирается на «нечетность» доски и свойство копя-хамелеона: оно аналогично данному для задачи о сдвиге фигур на доске.

Может ли конь с a1 добраться до h8, ступив на каждое поле доски ровно один раз?

И это невозможно. Исходное поле a1 - черное, и, значит, на каждом нечетном ходу конь попадает на белое поле. Однако число 63 (именно на этом ходу конь прибывает на b8) нечетно, а поле b8 - черное.

Перейдем к задачам о маршрутах коня. Под маршрутом коня понимаем такое последовательное перемещение, при котором каждое поле доски он посещает один и только один раз. Маршрут замкнут, если последним ходом конь возвращается на исходное поле. Если не требуется, чтобы конь посетил все поля доски, то мы говорим о пути коня по доске. Те же термины - «маршрут» и «путь» - используются и для других фигур. Каждому маршруту или пути коня или другой фигуры соответствует некоторый график, получающийся в результате последовательного соединения отрезками центров полей, посещаемых данной фигурой.

Доказать, что на доске m×n замкнутый маршрут коня может существовать только в том случае, если доска содержит четное число полей.

Окунев приводит чисто алгебраическое доказательство, однако «четность» доски сразу вытекает из следующего простого соображения. В любом замкнутом маршруте конь-хамелеон посещает одинаковое число белых и черных полей, т. е. тех и других на доске поровну, а значит - общее число полей четно.

Но для существования замкнутого маршрута коня важна не столько «четность» доски, сколько наличие на ней одинакового числа белых и черных полей. Таким образом, если некоторая доска произвольной формы содержит различное число белых и черных полей, то можно сразу сказать, что замкнутого маршрута коня на ней не существует. Ясно также, что произвольный маршрут коня (не обязательно замкнутый) можно искать лишь на таких досках, у которых число полей разного цвета, либо одинаковое, либо отличается на единицу.

Следующая задача показывает, что даже «четность» и прямоугольность доски еще не гарантируют существования замкнутого маршрута.

Доказать, что ни при каком n на доске n×4 не существует замкнутого маршрута коня.

Докажем это от противного. Пусть при некотором n на доске n×4 замкнутый маршрут коня существует. Поля, которые расположены на верхней в нижней горизонталях, назовем крайними, а остальные - средними. Так как с крайних полей конь может попасть только на средние, которых имеется 2n, то из 4n ходов, образующих маршрут, 2n сделаны с крайних на средние. Тогда оставшиеся 2n ходов конь совершил со средних на крайние. Поскольку каждым ходом конь-хамелеон меняет цвет поля, то все поля крайних горизонталей должны быть окрашены в один цвет, а средних - в другой. Противоречие.

Задача о «коне Аттилы». На шахматной доске стоят белый конь и черный король. Некоторые поля доски считаются «горящими», недоступными для коня. Конь должен дойти до неприятельского короля, повергнуть его и вернуться на исходное место. При этом ему запрещено становиться на «горящие» поля и на поля, которые уже пройдены. «Трава не растет там, где ступил мой конь!» - похвалялся вождь гуннов Аттила, намекая, что предводительствуемые им полчища уничтожают все живое на своем пути.

На рис. 20,а конь Аттилы стоит на поле g4, неприятельский король - на b3, а «горящие» поля заштрихованы. Задачи такого типа решаются в теории графов, неоднократно упоминаемой в нашей книге. Геометрически граф проще всего определить как множество точек (вершин графа), некоторые пары которых (возможно, все) соединены прямолинейными отрезками или дугами (ребрами графа). Путем в графе называется такая последовательность ребер, в которой каждые два соседних ребра имеют общую вершину.

На рис. 20,б изображен «граф коня» для рассматриваемой задачи. Его вершины расположены в центрах полей, доступных коню, и пары вершин соединены ребрами, если между соответствующими полями возможен ход коня.

Рис. 10. Задача о коне Аттилы: а - конь Аттилы; б - граф коня Атолы
 

В результате задача свелась к нахождению такого пути в полученном графе, который не содержит ни одной вершины более одного раза и, кроме того, проходит через обе заданные (на рис. 20, 6 они обведены кружками).. Для коня Аттилы на нашей доске искомый путь нетрудно найти и непосредственно, он состоит из следующих восемнадцати ходов: Кg4-f6-e8-g7-e6-f8-g6-e7-c6-a5:b3-d2-b1-a3-b5-d6-f7-h6-g4. Для своей «победы» коню Аттилы пришлось побывать на всех полях, не «сожженных» в начале сражения.

Аналогия между графиком движения фигуры и ее графом очевидна. Отличие состоит в том, что граф отражает все возможные ходы фигуры (в данной задаче), а график - лишь ее определенный путь по доске.

Введем на бесконечной шахматной доске прямоугольную систему координат. В этой системе шахматные вертикали и горизонтали обозначаются целыми числами (положительными и отрицательными), а всякое поле задается парой таких чисел - абсциссой и ординатой. При этом вертикали обычной доски можно обозначить не буквами, а числами 1, 2, ..., 8. С поля (s, t) копь в один ход может попасть на восемь полей (х, у), координаты которых отвечают целочисленным решениям следующего неопределенного уравнения:

(х - s)² + (у - t)² = 5.

Это уравнение (оно легко получается из теоремы Пифагора) лежит в основе многих чисто математических исследований свойств коня.

ЛАДЬЯ

Ладья является самой распространенной фигурой в комбинаторных задачах на шахматной доске и часто упоминается даже в серьезной математической литературе. Американский математик Дж. Риордан связывает понятия “Ладья” и “многочлен”. Это вызвано тем, что большой класс важных комбинаторных задач сводится к подсчету числа тех или иных расстановок ладей на шахматной доске. При рассмотрении ряда сложных задач существенную роль играет многочлен

r₀ +r₁x+r₂x²+...+r_kx^k +...+r_nxⁿ, 
где r_k - число размещений k ладей на доске n×n, не угрожающих друг другу (к = 1, ..., n). Этот многочлен Риордан и называет ладейным.

Многие задачи из комбинаторики, теории групп и теории чисел удобно интерпретируются в «ладейных» терминах. Приведем один комбинаторный пример. Пусть n рабочих назначаются на n различных работ, причем каждая из них должна выполняться только одним рабочим.

Спрашивается, сколькими способами можно осуществить такое назначение?

Поставим в соответствие рабочим горизонтали шахматной доски n×n, а работам - ее вертикали. Если i-й рабочий назначается на j-ю работу, то на поле, соответствующее пересечению i-й горизонтали и j-й вертикали, поставим ладью. Так как каждая работа выполняется одним рабочим и каждый рабочий назначаете! на одну работу, то в результате на любой вертикали и горизонтали будет стоять по одной ладье. Другими словами, никакая пара из этих n ладей не будет угрожать друг другу. Таким образом, нашей задаче о назначении можно придать вполне шахматный характер.

Сколькими различными способами на доске n×n можно расставить n не угрожающих друг другу ладей?

Заметим, что при расстановке более n ладей хотя бы на одной вертикали или горизонтали их окажется не менее двух. Таким образом, n есть наибольшее число ладей на доске n×n, не угрожающих друг другу. Одна из простейших расстановок заключается в расположении ладей вдоль главной диагонали доски (на полях a1, b2, c3, d4, e5, f6, g7, h8 для обычной доски).

Выясним теперь, сколько существует указанных расположений n ладей. Назовем ладью, стоящую на первой вертикали, - первой, стоящую на второй вертикали - второй, и т. д., вплоть до n-й ладьи, стоящей на n-й вертикали. Первую ладью можно поместить на любую из n горизонталей, затем вторую - на любую из (n - 1) оставшихся горизонталей (занятая первой ладьей исключается, так как никакие две ладьи не должны угрожать друг другу), третью ладью - на любую из (n - 2) оставшихся горизонталей и т. д., вплоть до (n - 1)-й ладьи, для которой остается выбор из двух горизонталей, и последней, n-й ладьи, которая ставится на единственную оставшуюся горизонталь. Комбинируя n различных расположений первой ладьи с (n - 1) расположениями второй, (n - 2) - третьей и т. д., получаем n (n - 1) ... 2 · 1 = n! различных расположений всех n ладей. Это число и является искомым. В частности, на обыкновенной шахматной доске восемь ладей, не угрожающих друг другу, можно расположить 8! = 40320 различными способами.

Если ладьи занумерованы, то существует уже (n!)² различных расположений n ладей, не угрожающих друг другу. Это следует из того, что n подходящих полей можно выбрать n! способами и столько же способов имеется для расположения на этих полях n занумерованных ладей.

Сколькими различными способами на доске n×n можно расставить n ладей, не угрожающих друг другу и не стоящих на главной диагонали (для обычной доски - на диагонали a1 - h8)?

Дополнительное условие значительно затрудняет решение задачи. Даже Эйлеру не удалось найти общую формулу для числа А_n указанных расстановок. Правда, он вывел рекуррентное соотношение А_n = (n - 1) (A_n-1 + А_n-2), с помощью которого можно последовательно определить значения А_n для любого n ≥ 3 (А₁ = 0, А₂ = 1). Окунев приводит элементарный вывод формулы для A_n, она имеет следующий вид:

An = n!

(

1 2!

-

1 3!

+

1 4!

- ... +

(-1)n    n!

).

Для n = 8 получаем

A8 = 8!

(

1 2!

-

1 3!

+

1 4!

- ... +

1 8!

) = 14833,

т. е. при дополнительном условии число расстановок восьми ладей, не угрожающих друг другу, уменьшается почти втрое.

На полях a1 и h1 стоят белые ладьи, а на полях a8 и h8 - черные. Сколькими способами могут кратчайшим путем поменяться местами белые и черные ладьи?

Кратчайшая перестановка осуществляется за четыре хода белых и черных, например: 
1. Лa1-d1 Лa8-a1 

2. Лd1-d8 Лh8-g8 

3. Лd8-a8 Лg8-g1 

4. Лh1-h8 Лg1-h1.

Подсчет показывает, что всего существует 330 необходимых перестановок.

ФЕРЗЬ

Если конь - самая «хитрая» шахматная фигура, а ладья - самая «неповоротливая», то ферзь является самой сильной шахматной фигурой. Возможности ферзя чрезвычайно богаты, и ему принадлежат многие рекорды на шахматной доске. Большинство нерешенных шахматно-математических проблем связано именно с ферзями.

Задача о часовых. Около каждой тюремной камеры можно поставить часового. Находясь у одной из камер, часовой видит также, что происходит в некоторых других камерах, из которых к данной ведут коридоры. Каково наименьшее число часовых, необходимое для наблюдения за всеми камерами?

Если шахматную доску рассматривать как тюрьму, причем ее поля считать камерами, а вертикали, горизонтали и диагонали - коридорами, то «часовыми» назначить ферзей, которые могут вести наблюдение в произвольном направлении. При этом задаче о часовых можно придать следующую шахматную интерпретацию.

Какое наименьшее число ферзей можно расставить на шахматной доске при условии, что они держат под обстрелом все свободные поля доски?

Пять ферзей вполне способны справиться со всей шахматной «тюрьмой». Доказано, что существует ровно 4860 способов, которыми можно расставить на доске пять ферзей-часовых. В расстановке на рис. 35,а ферзи держат под обстрелом все свободные поля доски, но сами не угрожают друг другу. На рис. 35,б все ферзи стоят на одной диагонали и, значит, защищают друг друга. Таким образом, во второй расстановке ферзи обстреливают не только свободные поля доски, но и занятые.

♕         ♕                   ♕                   ♕         ♕

♕                           ♕             ♕             ♕                           ♕

Рис. 11. Пять ферзей, доминирующих на шахматной доске: 
а - ферзи не угрожают друг другу; б - под боем все 64 поля доски
 

Как бы мы ни расставляли на доске четырех ферзей, по меньшей мере два ее поля уже останутся «без присмотра. Пусть четыре ферзя стоят на полях a1, b1, g1, h1.

Пусть теперь на доске стоит всего один ферзь - на поле d1. Какой геометрически самый длинный несамопересекающийся путь он может сделать за пять ходов?

Искомый путь состоит из таких пяти ходов: Фd1-h1-a8-h8-h2-c7. Любопытно, что большинство решающих эту задачу предлагают другой путь: Фd1-h1-h8-a1-a8-g8. По числу посещаемых полей он действительно длиннее (32 30), однако в геометрическом смысле (см. гл. 3) - короче. Если ширину одного поля Доски считать равной 1, то первый путь длиннее второго всего на 0,05, но все-таки длиннее! В самом деле, получаем:

d₁ = (4 + 7√2 + 7 + 6 + 5√2) = (17 + 12√2);

d₂ = (4 + 7 + 7√2 + 7 + 6) = (24 + 7√2);

d₁ - d₂ = (5√2 - 7) ≈ 0,05

 

ПЕРЕСТАНОВОЧНЫЕ ЗАДАЧИ

Любая шахматная задача связана с какими-нибудь перестановками фигур на доске. Однако к перестановочным относят обычно такие задачи па перестановку фигур, задания в которых далеки от обычных. Вот типичный пример задачи с «нешахматным» заданием.

Задача Доусона. У белых лишь король на e1 и пешка на d2; у черных же на доске полный комплект фигур, все они находятся на своих первоначальных местах. Черным разрешается ходить только в том случае, если они дают своим ходом шах. Учитывая это, белые должны заставить черных дать мат их королю.

Конечно, эту задачу. Доусона на обратный мат нельзя считать настоящей шахматной задачей, так как правила игры здесь сильно нарушены. Для того чтобы добиться своей цели, белый король должен весьма умело перемещаться по доске, вызывая огонь на себя. Он получает мат лишь на 33-м (!) ходу после следующих перемещений: 
1-4.Крe1-d1-c2-b3-a4

4....b7-b5+ 
5-6.Крa4-b3-c3 b5-b4+ 

7.Крc3-d3 Сc8-a6+ 

8.Крd3-e3 
9. d2-d3 (единственный раз в «партии» ход делает белая пешка) 
10-13.Крe3-d2-c1-b2-b3 Сa6-c4+ 

14-20.Крb3-b2-c1-d2-e3-f2-g3-h3 Сc4-e6+ 

21.Крh3-h4 g7-g5+ 

22-24.Крh4-g3-h2-h1 Сe6-d5+ 

25-26.Крh1-g1-f1 Сd5-g2+ 

27-29.Крf1-e1-d2-c2 b4-b3+ 

30.Крc2-b2 Сf8-g7+ 

31.Крb2-a3 Сg7-b2+ 

32.Крa3-a4 Сg2-c6+ 

33. Крa4-a5 Сb2-c3 мат!

На доске 4×4 расставлены 15 ладей, занумерованных числами от 1 до 15. Переставить ладьи так, чтобы их номера расположились в возрастающем порядке, а пустым было поле в правом нижнем углу доски.

Так как ход ладьи на нашей доске совпадает с перестановкой квадрата в игре «Пятнадцать», то данная задача фактически сводится к ней. Другими словами, существование решения зависит от числа транспозиций ладей в исходной расстановке.

Задача с ладьями легко обобщается и для доски 8×8. Можно показать, что все позиции с 63 ладьями, занумерованными числами от 1 до 63, распадаются на два класса: в половине из 64! позиций ладьи удается расположить в возрастающем порядке (с пустым полем h1), а в половине - нет. Любопытно, что для коней имеет место та же самая ситуация, что и для ладей. Все позиции с 03 занумерованными конями также распадаются на два равных по численности класса.

Для ферзей и королей задача имеет решение уже при любой начальной позиции, так как эти фигуры ходят ле только по прямой (как ладья), но и по диагонали. А для слонов задача вообще не интересна, поскольку они не могут менять своего цвета.

Рис. 12. «Пистолет» Т. Доусона. Белые начинают и дают мат в 21 ход
 

В противоположных углах шахматной доски 3×3 стоят два белых и два черных коня (рис. 61,а). За минимальное число ходов поменять местами белых коней с черными.

Эта задача, придуманная итальянцем Гуарини еще в XVI в. Наиболее изящно она решается при помощи так называемого метода пуговиц и нитей, придуманного известным изобретателем головоломок Г. Дьюдени.

Занумеруем поля нашей маленькой доски, как показано на рис. 61,б (центральное поле осталось без номера, но оно нас сейчас не интересует, так как кони все равно не могут на него попасть). После этого поместим на каждое из занумерованных полей по пуговице и если между двумя полями возможен ход коня, то расположенные на них пуговицы свяжем нитью. Полученный клубок пуговиц и нитей распутаем так, чтобы все пуговицы расположились по кругу (рис. 61,в).

Теперь решение находится почти автоматически. Выбрав одно из направлений по кругу, достаточно переставлять коней до тех пор, пока они не поменяются местами. Необходимое перемещение на доске получается заменой занумерованных пуговиц соответствующими полями. Нетрудно убедиться, что решение состоит из 16 перестановок коней (8 ходов белых и 8 ходов черных), причем белые и черные кони могут ходить по очереди. Если дополнительно потребовать, чтобы кони. разного цвета при своем движении не угрожали друг другу (очередность ходов в этом случае произвольна), то решение также непосредственно следует из рис. 61,в. Нужно следить лишь за тем, чтобы белые и черные кони не оказались на нашем круге рядом. Будем считать, что круговое движение (против часовой стрелки) начинает белый конь a1 (на нем помещена пуговица с номером 1). Тогда в шахматной нотации решение можно записать так: Кa1-b3, Кa3-c2, Кc3-b1-a3, Кc1-a2-c3, Кb3-c1-a2, Кc2-a1-b3, Кa3-c2-a1, Кc3-b1-a3, Кa2-c3, Кb3-c1.

Математические игры на шахматной доске.

Шахматная игра создавалась на протяжении многих веков и ее правила неоднократно менялись. С точки зрения математики, движение шахматных фигур и форма доски имеют весьма условный характер. Существует множество самых разнообразных игр на прямоугольных досках, теория которых занимает значительное место в математической литературе. Одних только шашечных игр. известно больше десятка: русские, стоклеточные, шашка Ласкера, поддавки, уголки и др. Даже современные шахматы имеют ряд разновидностей, в основном - в неевропейских странах. Например, Гарднер рассказывает о японских шахматах (соги), китайских (цюнь ки), корейских (тьян-кеуи). Сейчас мы остановимся на некоторых шахматных играх и задачах (содержащих математические элементы), в которых доска или правила игры отличаются от обычных.

До первого шаха. В этой игре все, как в настоящих шахматах, только выигрывает не тот, кто «первым» дает мат, а тот, кто первым объявляет шах. При нормальной начальной позиции белые форсированно побеждают, причем не позднее пятого хода. 
1. Кb1-c3. Грозит выпад коня на e4, d5 или b5 с неизбежным шахом, у черных единственный ответ: 

1. ... e7-e6 (1. ... e5 не спасает из-за 2. Кd5 и 3. Кf6 с шахом). Теперь после 

2. Кc3-e4 Крe8-e7 

3. Кg1-f3 второй конь с решающим эффектом вступает в игру. 

3. ... Фd8-e8 (3. ... d6 4. Кd4) 

4. Кf3-e5 и шах следующим ходом.

Чтобы «оживить» игру, следует каким-либо образом изменить начальную позицию, например передвинув белую пешку с c2 на c3, а черную - с c7 на c6. Теперь невозможен первый ход 1. Кc3, и форсированного выигрыша уже не видно, например после 1. Фb3 d5 2. Фb4 Фd6! 3. Фa4 Сd7 4. Фh4 Кf6 черный король надежно защищен.

Двухходовые шахматы. В этой игре каждый ход белых и черных состоит из двух обычных. Такое изменение правил позволяет доказать следующий неочевидный и неожиданный факт.

При правильной игре в двухходовые шахматы белым, по меньшей мере, гарантирована ничья.

Попробуем доказать это от противного. Пусть прн наилучшей игре обеих сторон белые проигрывают. После 1. Кb1-c3-b1 сохраняется начальная позиция, а первый ход уже принадлежит черным. Фактически теперь черные играют белыми и, по предположению, проигрывают. Противоречие.

Кажется, все правильно Однако это доказательство не совсем точно. После первого хода белых позиция действительно повторяется, но ситуация иная! Так, после 1. ... Кg8-f6-g8 2. Кb1-c3-b1 белые еще не могут требовать ничью, а черные могут, поскольку 2. ... Кg8-f6-g8 приводит к троекратному повторению исходной позиции при ходе белых. Таким образом, нельзя считать, что после 1. Кb1-c3-b1 «черные играют белыми» - возможности сторон разные. Кстати, аналогичный пример можно привести и на «правило 50 ходов».

Примечательно, что эту весьма тонкую ошибку в доказательстве обнаружил академик А. Н. Колмогоров.

Приведем теперь строгое доказательство. По-прежнему считаем, что черные при безукоризненной игре обеих сторон выигрывают. Будем играть одновременно на двух досках. На первой пойдем 1. Кb1-c3-b1, а ответный ход черных воспроизведем на второй доске со стороны белых. Затем ответ черных на второй доске повторим ва первой за белых, ход черных на первой - за белых на второй и т. д. По нашему.предположению, черные выигрывают и, значит, наступит момент, когда на первой доске своим очередным ходом они объявят мат белому королю. Но тогда на второй доске при повторении этого хода 8а белых возникнет позиция, в которой мат пол у чарт черный король! Но ведь черные и на второй доске играли безошибочно. Противоречие.

Заметим, что в отличие от ловкого обманщика, игралшего с Ласкером и Капабланкой одну партию белыми, а другую черными (см. главу 12), мы действовали абсолютно честно - обе партии играли одним цветом!

Наше доказательство, как говорят математики, неконструктивно. Мы доказали, что белые могут не проиграть в двухходовые шахматы, но не выяснили, как им нужно играть. Более того, если будет показано, что белые выигрывают (как, например, в игре «до первого шаха»), то тогда, очевидно, первый ход 1.Кb1-c3-b1 проигрывает! Таким образом, не исключено, что наше доказательство беспроигрышности белых проведено с помощью проигрывающего хода!

Вот одна из распространенных модификаций двухходовых шахмат. У одного игрока полный комплект фигур, которые ходят, как обычно, а у другого лишь король и несколько пешек, но делают они по два хода. Цель слабейшей стороны - взять неприятельского короля. Тот, кто впервые знакомится с этой игрой, всегда выбирает обычные фигуры и... быстро проигрывает, даже если у противника всего лишь король и пара пешек. По-видимому, примерное равенство «сил» в этой игре сохраняется в том случае, если этого короля сопровождают 5-6 пешек.

Шахматы без цугцванга. Если в некоторой позиции любой ход белых проигрывает, то мы говорим, что они в цугцванге (если проигрывает и любой ход черных, то цугцванг взаимный). Шахматы без цугцванга отличаются от обычных добавлением одного хода - хода на месте. В них цугцванга не бывает, так как всегда можно передать очередь хода партнеру.

Приведенное выше доказательство того, что при правильной игре в двухходовые шахматы белым гарантирована ничья, полностью проходит и для шахмат без цугцванга. Однако, в отличие от двухходовых шахмат, иоиск непосредственного мата здесь безнадежен! Напомним, что в настоящих шахматах, где шансы белых, судя по статистике, заметно выше, вовсе не доказано, что даже при наилучшей игре им обеспечена хотя бы ничья.

Среди студентов мехмата большой популярностью пользуется следующая игра в крестики и нолики. На клетчатой бумаге произвольной формы (хоть «бесконечной») двое по очереди ставят крестики и нолики. Побеждает тот, кто первым ставит пять своих значков подряд (по вертикали, горизонтали или диагонали). Подобно двухходовым шахматам и шахматам без цугцванга, можно доказать, что и здесь начинающий при безупречной игре не проигрывает. Правда, доказательство в данном случав сложнее, чем в шахматных играх.

Поддавки. Эта игра более популярна в шашках, однако и ее шахматный вариант весьма интересен. Победителем в ней становится тот, кто первый отдает все свои фигуры. Взятие в этой игре обязательно (в том числе и короля, которого можно ставить под бой), а если возможно несколько взятий, то выбор произволен.

Идеи и комбинации, возникающие в поддавках, довольно оригинальны и совершенно не похожи на те, которые встречаются в обычных шахматах. Рассмотрим один несложный эндшпиль: белая пешка на a2, а черная на b6 (больше ничего на доске нет), белые начинают и проигрывают (а значит - выигрывают в поддавки).

На доске всего две пешки, но посмотрите, сколько тонкостей содержит позиция. 
1. a2-a3! Но не a2-a4, так как белая пешка должна превратиться только после черной. 

1. ... h6-h5 

2. a3-a4 h5-h4 

3. a4-a5 h4-h3 

4. a5-a6 h3-h2 

5. a6-a7 h2-h1Л!

 Именно ладья, при других превращениях черной пешки (в ферзя, слона и коня) белые ставят ферзя и либо сразу, либо на следующем ходу отдают его. 
6. a7-a8С!! Белая пешка превращается в еще более слабую фигуру, иначе черная ладья моментально встает под удар. Теперь на любой ее ход следует 
7. Сa8-h1!, и белые избавляются от слона.

Рассмотрим еще одну позицию: у белых пешка на d7, а у черных конь на f5 (других фигур нет). Чем закончится игра в поддавки при ходе белых и при ходе черных?

Белые выигрывают в поддавки, независимо от очереди хода. Если ход их, то после превращения 1. d7-d8K!конь быстро приносит себя в жертву. Если первый ход делают черные, то на любой скачок их коня следует d7-d8C!, и слон без труда встает под удар коня.

Задача X. Клювера и К. Фабеля. Белый король на f3, а у черных две фигуры - король на d7 и ферзь на c8. Белые начинают и проигрывают (выигрывают в поддавки).

1. Крe4! Фd8! (иначе белый король уже на втором ходу встанет под бой) 2. Крd4!, и следующим ходом король кончает «самоубийством». Не проходит 1. Крg4? Фa6! Теперь нельзя идти королем на f4, f5 и g5 (например, 2. Крg5 Фf6! 3. Кр:f6 Крe6, и черные сами отдают обе фигуры), а другие ходы короля приводят к ничьей - черные «жертвуют» ферзя, после чего короли не могут приблизиться друг к другу.

Многочисленные математические игры и задачи возникают при переходе к другим шахматным доскам. Мы уже встречались с прямоугольными досками m×n (в частности, квадратной n×n) при тех или иных значениях m и n, а также бесконечной шахматной доской. При желании большинство задач, упомянутых в книге, можно сформулировать и для этих досок. Сейчас мы рассмотрим шахматные игры на досках, получающихся из обычной при помощи более сложных математических преобразований.

Проективные шахматы. Правила игры в зти шахматы основываются на свойствах прямых, которые изучаются в проективной геометрии. В этой геометрии любое семейство параллельных прямых пересекается в некоторой бесконечно удаленной точке. Соответственно этому, введем бесконечно удаленные поля бесконечной доски: поле Р_х есть пересечение ее горизонталей, Р_у - вертикалей, Р₁ - диагоналей, параллельных a1 - h8, Р₂ - диагоналей, параллельных a8 - h1. Проективная доска получается из бесконечной добавлением этих четырех полей Р_х, Р_у, P₁, Р₂.

На проективной доске сохраняются многие правила обычных шахмат, а основное дополнение состоит в том, что дальнобойная фигура может переместиться на бесконечно удаленное поле (с учетом ее способа передвижения) и оттуда вернуться на конечное поле доски. Проективные шахматы особенно популярны среди югославских шахматных композиторов, много проективных задач составлено Петровичем. Рассмотрим одну из них (рис. 13).

♞           ♙ ♞   ♙   ♙         ♕     ♙   ♙     ♙     ♚           ♟         ♙             ♔

Рис. 13. Н. Петрович. Проективная шахматная доска. Белые начинают и дают мат в два хода 

Первый ход решения: 1. Крh2-g1! Теперь у черного короля несколько ответов. Если он идет на e4, то мат дает белый ферзь, удаляясь в бесконечность через a5: 2. Фc5-Р_х мат. Действительно, с поля Р_х ферзь нападает на черного короля и держит все поля вокруг него: e3, f3 - через b3; d4, e4, f4 - через b4; d5, e5, f5 - через a5. Ход 2. Фc5-Р_хматует и при 1. ... Крf4-f3. Поля e4, f4, g4 в этом случае ферзь держит через h4, e3, f3, g3 - через h3, а e2, f2, g2 - через h2 (белый король предусмотрительно ушел с h2).

При отступлениях черного короля на линию g, а также при 1. ... d3-d2 матует 2. Фc5-Р₁ (ферзь уходит в бесконечность по диагонали c5 - a3). Например, после 1. ... Крf4-g5 2. Фc5-P₁ поля f4, g5, h6 ферзь держит через c1, поле f6 - через a1, f5 - через h7, g4, h5 - через d1 и поле h4 - через e1.

Осталось рассмотреть ходы черных коней. На любой ход коня d6 следует 2. Фc5-Р₂ мат, а на любой ход коня c7 - 2. Фc5-Р_у мат (в первом случае ферзь уходит в бесконечность через a7, а во втором через c8).

При решении разобранной задачи использовались все четыре бесконечно удаленных поля. Кстати, в начальном положении после 1. Фc5-Р_х черный король скрывается на g5, а после 1. Фc5-Р₁ - на e4, с поля Р₂ ферзь даже не дает шаха, а хода Фc5-Р_у и вовсе нет.

Все до сих пор рассмотренные нами доски, как и привычная шахматная доска, плоские. Остановимся теперь на некоторых пространственных досках.

Объемные шахматы. В них играют на трехмерной доске m×n×k. В гл. 5 были приведены маршруты коня по всем полям доски 4×4×4 и по поверхности доски 8×8×8. Следующая, довольно сложная задача касается расстановки ладей на объемной доске n×n×n.

Какое минимальное число ладей следует расставить на доске n×n×n так, чтобы они держали под угрозой все остальные поля доски?

Фактически здесь требуется найти число «ладей-часовых», доминирующих на объемной доске n×n×n.

Оказывается, что оно равно n²/2 при четных n и (n² + 1)/2 при нечетных. В частности, для «охраны» доски 8×8×8 достаточно иметь 32 ладьи. Число независимых ладей на доске n×n×n равно n² (но n ладей в каждом слое доски). На доске 8×8×8 удается расставить 64 ладьи так, чтобы они не угрожали друг другу и в то же время держали под обстрелом все свободные поля доски. Наши задачи о доминировании и независимости ладей на доске n×n×n можно сформулировать следующим образом в терминах линейной алгебры.

Рассмотрим множество всех трехмерных векторов (t₁, t₂, t₃), компоненты которых принимают одно из значений 1, 2, ..., n (всего таких векторов n³). Какое минимальное число векторов следует выбрать из этого множества так, чтобы каждый из оставшихся векторов имел хотя бы с одним из выбранных не менее одной общей компоненты? Какое максимальное-число векторов можно выбрать так, чтобы никакие два из них не имели ни одной общей компоненты?

Первый вопрос эквивалентен определению числа доминирования ладей на доске n×n×n, а второй - определению числа независимости. Таким образом, ответ такой: в первом случае n²/2 или (n² + 1)/2 векторов, во втором случае - n² векторов. Рассмотрение последней задачи наводит на мысль о следующем обобщении.

Многомерные шахматы. Полями доски для игры в такие шахматы являются многомерные кубики 1×1×...×1. В указанной терминологии наши задачи о ладьях можно обобщить для k-мерной шахматной доски.

Рассмотрим множество всех k-мерных векторов (t₁, t₂, ..., t_k), компоненты которых принимают одно из значений 1, 2, ..., n (всего таких векторов n^k). Какое минимальное число k-мерных векторов следует выбрать из этого множества так, чтобы каждый из оставшихся векторов имел хотя бы с одним из выбранных не менео одной общей компоненты? Какое максимальное число k-мерных векторов можно выбрать так, чтобы никакие два из них не имели ни одной общей компоненты?

Решение этой задачи неизвестно. Аналогичные задачи о доминировании и независимости на многомерных досках можно поставить и для других шахматных фигур. В упомянутой статье Васильева показана связь между задачами такого типа и некоторыми вопросами, возникающими в теории информации (в ее разделе, называемом кодированием).

 

Магараджа. У одного игрока - полный комплект фигур, стоящих на первоначальных местах, а у другого - лишь один магараджа, которого он ставит на произвольное поле. Магараджа проигрывает, если его удастся взять, и выигрывает, если ставит мат неприятельскому королю.

В этой игре пешкам запрещено превращаться, так как в противном случае выигрыш слишком прост - достаточно провести обе крайние пешки в ферзей, после чего три ферзя и две ладьи без труда окружают магараджу. При сделанной оговорке магараджа оказывает упорное сопротивление, а у неопытного игрока быстро выигрывает (здесь имеет место та же ситуация, что и в борьбе полного комплекта фигур против короля и пешек, делающих по два хода). И все же у того, кто играет полным комплектом фигур, имеется форсированный выигрыш. Гарднер предлагает план окружения магараджи, состоящий из 25 ходов. Однако цель достигается, по крайней мере, десятью ходами раньше!

Не обращая внимания на перемещения магараджи, белые делают следующие 14 ходов подряд: 1-14. a4, h4, Лa3, Лh3, Кc3, Кf3, Лb3, Лg3, d4, Фd3, Фe4, Лb7, Фd5, Лg8. Легко проверить, что при этих ходах магараджа не мог дать мат или взять белую фигуру. Теперь у него имеются лишь два свободных поля - a6 и f6: на a6 он гибнет после 15. Сg5, а на f6 - после 15. e4.

Различные сказочные фигуры получаются из «обобщенного коня» (а, b) при выборе тех или иных значений а, b (см. гл. 4). Конь (1, 3) называется верблюдом, (1, 4) - жирафом, (2, 3) - зеброй. Если одно из чисел а, b равно нулю, то мы получаем ладью, перемещающуюся на фиксированное число полей. Если же а = b, то имеем слона, обладающего тем же свойством. Конго, который за один ход делает несколько скачков подряд, присваивается «звание» всадника. Интересной игре, в которой одной и той же фигурой ходят и как конем, и как верблюдом, посвящена следующая задача.

В углу доски n×n (n ≥ 4) стоит фигура. Двое ходят по очереди. Один играет этой фигурой, как обычным конем, но с двойным ходом, а второй - как верблюдом. Первый стремится к тому, чтобы поставить фигуру в противоположный угол доски, а второй - ему помешать. Чем закончится игра?

В этом, несколько странном соперничестве коня и верблюда (а точнее было бы сказать: хамелеона, превращающегося то в одну фигуру, то в другую) победителем выходит конь! Это вытекает из следующего соображения. Бели наша фигура стоит на диагонали, проходящей через исходное угловое поле доски, то на любое отступление верблюда с диагонали конь возвращается на нее, причем продвигается, по крайней мере, на одно поле ближе к цели, а то и сразу попадает в нужный угол.

Следующая игра и задачи к ней были предложены на Всесоюзной олимпиаде школьников (Ереван, 1974 г.)

 

Шашматы. В этой игре, представляющей собой смесь шахмат и шашек (по-английски: chess + checkers = cheskers), шахматные фигуры ходят по черным полям доски (как в шашках). Обычный конь (1, 2) не в состоянии здесь сделать ни одного хода (он сразу же попадает на запрещенное белое поле), и его следует заменить верблюдом (1, 3), который перемещается по полям одного цвета.

На рис. 72 последовательно занумерованы поля маршрута, который верблюд проходит по всем полям «шашматной» доски, причем этот маршрут замкнутый.

Как мы знаем, на шахматной доске можно расставить максимум 32 коня, не угрожающих друг другу. Максимальное число «мирных» верблюдов равно 16, т. е. они также могут занять половину всей доски (шашматной).

На рис. 72 их можно поставить на поля со всеми четными или со всеми нечетными числами. Таким образом, этот рисунок дает решение сразу двух задач на шашматной доске. Более подробный рассказ о шашматах (в частности, расстановку фигур перед пачалом игры) можно найти у Гарднера.

В заключение главы - еще о нескольких сказочных фигурах, которые вообще уже ни на что не похожи!

Сверчок ходит, как ферзь, и перепрыгивает через свои и чужие фигуры, останавливаясь сразу вслед за ними. Лев, в отличие от сверчка, приземляется на любом поле за перепрыгнутой фигурой.

Существуют нейтральные фигуры, которыми могут играть и белые, и черные. Фигура, которая делает ход только со взятием; называется бьющей. Бьющий конь называется гиппопотамом, а бьющий ферзь - динозавром. Фигура дипломат - не ходит, но и ее нельзя брать. Мало того, около дипломата фигуры того же цвета неприкосновенны! А фигура камикадзе (самоубийца) убирается с доски вместе со взятой фигурой!

До сих пор речь шла исключительно о сказочных фигурах. Однако и для пешек существует много разновидностей. Пешка-хамелеон при взятии неприятельской фигуры превращается в такую же фигуру, но своего цвета. Сверхпешка ходит на любое число полей по прямой и бьет на любое число полей по диагонали. Пешка-такси ходит и вперед, и назад. Наконец, один раз в партии пешке можно разрешить превращение в «атомную бомбу»! Эта фигура сразу же после появления ставится на любое поле доски и в заданном радиусе уничтожает все вокруг себя.

ЗАКЛЮЧЕНИЕ

В ходе проделанной работы были рассмотрены некоторые свойства шахматной доски, примеры задач, связанных с шахматной доской, свойства некоторых фигур, а также задачи на перестановку. Эта тема может быть интересна начинающим игрокам в шахматы или людям, ищущим нестандартные задачи по математике.