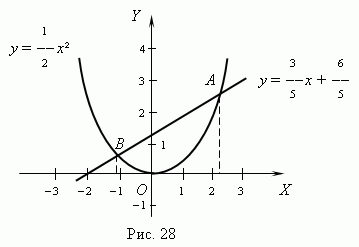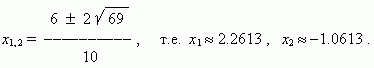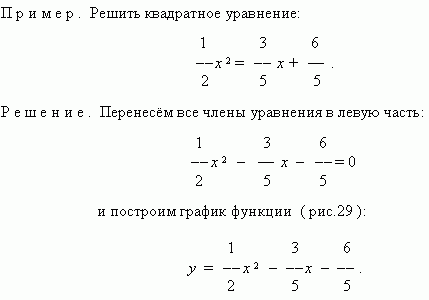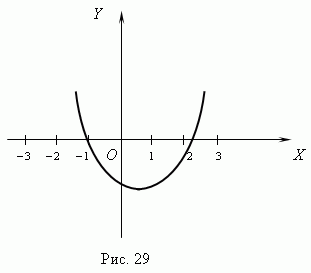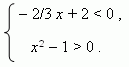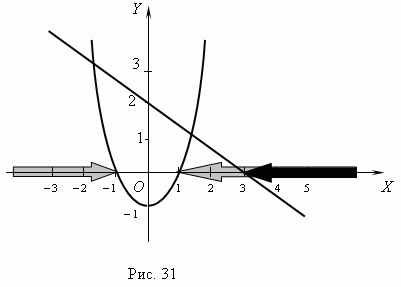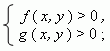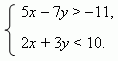Государственное бюджетное образовательное
учреждение среднего профессионального образования
«Санкт – Петербургский политехнический колледж»
ПРОЕКТНАЯ РАБОТА
по дисциплине МАТЕМАТИКА

Выполнили студенты группы 171
Корецкая Екатерина
Корчигина Валерия
Гармаш Эдуард
Преподаватель:
Рахаева Елена Анатольевна
Санкт-Петербург
2014 год
Содержание
Введение
Из истории возникновения функций
Определение и виды функций
Свойства функций в пословицах и поговорках
Решение задач
Заключение
Литература
1. Введение.
Функция – это одно из основных математических и общенаучных понятий, выражающее зависимость между переменными величинами.
Каждая область знаний: физика, химия, биология, социология, лингвистика и т. д. имеет свои объекты изучения, устанавливает свойства и, что особенно важно, взаимосвязи этих объектов.
В различных науках и областях человеческой деятельности возникают количественные соотношения, и математика изучает их в виде свойств чисел. Математика рассматривает абстрактные переменные величины и в отвлеченном виде, изучает различные законы их взаимосвязи, которые на математическом языке называются функциональными зависимостями, или функциями.
Например, в соотношении y = х2 геометр или геодезист увидит зависимость площади у квадрата от величины x его стороны, а физик, авиаконструктор или кораблестроитель может усмотреть в нем зависимость силы y сопротивления воздуха или воды от скорости x движения. Математика же изучает зависимость y = x2и ее свойства в отвлеченном виде. Она устанавливает, например, что при зависимости y = x2 увеличение x в 2 раза приводит к четырехкратному увеличению y. И где бы конкретно ни появилась эта зависимость, сделанное абстрактное математическое заключение можно применять в конкретной ситуации к любым конкретным объектам.
2. Из истории возникновения функций.
Понятие функции уходит своими корнями в ту далёкую эпоху, когда люди впервые поняли, что окружающие их явления взаимосвязаны. Они ещё не умели считать, но уже знали, что, чем больше оленей удастся убить на охоте, тем дольше племя будет избавлено от голода, чем сильнее натянута тетива лука, тем дальше полетит стрела, чем дольше горит костёр, тем теплее будет в пещере.
С развитием скотоводства и земледелия, ремесла и обмена увеличилось количество известных людям зависимостей между величинами.
Начиная с XVII в. одним из важнейших понятий является понятие функции. Оно сыграло и поныне большую роль в познании реального мира.
Идея функциональной зависимости восходит к древности, она содержится уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами, в первых формулах для нахождения площади и объема тех или иных фигур.
Однако явное и вполне сознательное применение понятия функции и систематическое изучение функциональной зависимости берут своё начало в XVII в. в связи с проникновением в математику идеи переменных.

Чёткого представления понятия функции в XVII в. ещё не было, однако путь к первому такому определению проложил Декарт, который систематически рассматривал в своей «Геометрии» лишь те кривые, которые можно точно представить с помощью уравнений, притом преимущественно алгебраических. Постепенно понятие функции стало отождествляться таким образом с понятием аналитического выражения – формулы.


Слово «функция» (от латинского functio – совершение, выполнение) Лейбниц употреблял с 1673 г. в смысле роли (величина, выполняющая ту или иную функцию).
Явное определение функции было впервые дано в 1718 г. одним из учеников и сотрудников Лейбница, выдающимся швейцарским математиком Бернулли: «Функцией переменной величины называют количество, образованное каким угодно способом из этой переменной величины и постоянных»..
Явное определение функции было впервые дано в 1718 г. одним из учеников и сотрудников Лейбница, выдающимся швейцарским математиком Бернулли: «Функцией переменной величины называют количество, образованное каким угодно способом из этой переменной величины и постоянных». Оно привело в восхищение престарелого Лейбница, увидевшего, что отход от геометрических образов знаменует новую эпоху в изучении функций. Многие из этих функций нельзя было явно выразить с помощью ранее известных операций. Поэтому один из самых замечательных математиков XVII в. Леонард Эйлер (1707 – 1783), вводя в своём учебнике понятие функции, говорит лишь, что «когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называются функциями вторых». Леонард Эйлер во «Введении в анализ бесконечных» (1748) примыкает к определению своего учителя И. Бернулли несколько уточняя его. Определение Л. Эйлера гласит: « Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого количества и чисел или постоянных количеств». Так понимали функцию на протяжении почти всего XVII в. Даламбер, Лагранж и другие видные математики. В формировании современного понимания функциональной зависимости приняли участие многие крупные математики. Описание функции, почти совпадающее с современным, встречается уже в учебниках математики начала XIX в. Активным сторонником такого понимания функции был Н.И. Лобачевский.
3. Определение и виды функций
Функция – это одно из основных математических и общенаучных понятий, выражающее зависимость между переменными величинами. Каждая область знаний: физика, химия, биология, социология, лингвистика и т. д. имеет свои объекты изучения, устанавливает свойства и, что особенно важно, взаимосвязи этих объектов. В различных науках и областях человеческой деятельности возникают количественные соотношения, и математика изучает их в виде свойств чисел. Математика рассматривает абстрактные переменные величины и в отвлеченном виде, изучает различные законы их взаимосвязи, которые на математическом языке называются функциональными зависимостями, или функциями. Например, в соотношении 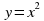 геометр или геодезист увидит зависимость площади у квадрата от величины x его стороны, а физик, авиаконструктор или кораблестроитель может усмотреть в нем зависимость силы y сопротивления воздуха или воды от скорости x движения. Математика же изучает зависимость
геометр или геодезист увидит зависимость площади у квадрата от величины x его стороны, а физик, авиаконструктор или кораблестроитель может усмотреть в нем зависимость силы y сопротивления воздуха или воды от скорости x движения. Математика же изучает зависимость 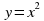 и ее свойства в отвлеченном виде. Она устанавливает, например, что при зависимости
и ее свойства в отвлеченном виде. Она устанавливает, например, что при зависимости 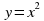 увеличение x в 2 раза приводит к четырехкратному увеличению y. И где бы конкретно ни появилась эта зависимость, сделанное абстрактное математическое заключение можно применять в конкретной ситуации к любым конкретным объектам.
увеличение x в 2 раза приводит к четырехкратному увеличению y. И где бы конкретно ни появилась эта зависимость, сделанное абстрактное математическое заключение можно применять в конкретной ситуации к любым конкретным объектам.
В школьном учебнике математики дается следующее определение функции: Зависимость переменной y от переменной x называется функцией, если каждому значению x соответствует единственное значение у.
Переменную x называют независимой переменной или аргументом, а переменную у – зависимой переменной. Значение у, соответствующее заданному значению x, называют значением функции. Записывают: y =f(x) (читается: «Эф от икс»). Буквой f обозначается данная функция, т. е. функциональная зависимость между переменными x и y; f(x) есть значение функции, соответствующее значению аргумента х. Говорят также, что f(x) есть значение функции в точке х. Все значения, которые принимает независимая переменная, образуют область определения функции. Все значения, которые принимает функция f(x) (при x, принадлежащих области ее определения), образуют область значений функции.
Может возникнуть вопрос: почему мы обозначаем функцию символом f, и когда он появился. Этот символ изобрел в 1733 г. французский математик Клеро. А появился этот символ, когда формировался общий подход к понятию функции, когда потребовалось обозначение «функции вообще».
4. Свойства функций в пословицах и поговорках
Функции – это математические портреты устойчивых закономерностей, познаваемых человеком. Чтобы проиллюстрировать характерные свойства функций обратимся к пословицам и поговоркам. Ведь пословицы – это тоже отражение устойчивых закономерностей, выверенное многовековым опытом народа.
1. Возрастание функции.
Определение: Функция y= f(x) называется возрастающей на промежутке Х, если для любых х1 и х2 из Х, таких, что х1 2, выполняется неравенство f(x1)2). Иными словами, функция возрастает на промежутке Х, если, какие бы два значения аргумента, принадлежащие этому промежутку, ни взять, окажется, что большему значению аргумента соответствует большее значение функции.
«Чем дальше в лес, тем больше дров», - гласит пословица.
Такое свойство функции называется монотонным возрастанием.
2. Неубывающая функция.
Определение: Если для любых х1 и х2 из множества Х таких, что х1 2, выполняется неравенство f(x1) f(x2). Иными словами, функция убывает на промежутке Х, если, какие бы два значения аргумента, принадлежащие этому промежутку, ни взять, окажется, что большему значению аргумента соответствует меньшее значение функции.
«Дальше кумы – меньше греха». Функция, которая показывает, как изменяется мера греха по мере удаления от кумы, монотонно убывающая. м е р а г р е х а Расстояние до кумы
3.Ограниченные функции.
Определение: Функция f, определённая на множестве Х, называется ограниченной на множестве Х1, если f (x1), т.е. множество её значений на множестве Х1, ограничено, т.е. если существуют постоянные m и M такие, что для всех значений x из Х1 выполняется неравенство m ≤f(x)≤M. В противном случае функция называется неограниченной.
Функция y=f(x) называется ограниченной сверху (снизу) на промежутке Х, если существует такое число k, что для всех выполняется неравенство f(x)≤k (f(x)≥k).
Функция ограничена снизу, если весь ее график расположен выше некоторой горизонтальной прямой y=m;
Функция ограничена сверху, если весь ее график расположен ниже некоторой горизонтальной прямой y=M. «Выше меры конь не скачет». Если изобразить траекторию скачущего коня, то высота скачков в полном соответствии с пословицей будет ограничена сверху некоторой «мерой». «Мера» Расстояние
4. Максимум функции.
Определение: Пусть функция у =f(x) определена в некоторой окрестности точки x0. Функция у =f (x) имеет максимум в точке x0, если существует такая  – окрестность точки x0, что при x0 –
– окрестность точки x0, что при x0 –  0 +
0 +  выполняется неравенство f (x) 0),т.е. значение функции в этой точке больше, чем её значение во всех других точках, достаточно близких к x0.
выполняется неравенство f (x) 0),т.е. значение функции в этой точке больше, чем её значение во всех других точках, достаточно близких к x0.
«Пересев хуже недосева», - издавна говорили земледельцы. Вековой опыт свидетельствовал: урожай лишь до некоторой поры растет вместе с плотностью посева, дальше он снижается, потому что при чрезмерной густоте ростки начинают глушить друг друга. Эта закономерность станет особенно наглядной, если изобразить её графиком, где урожай представлен как функция плотности посева. Урожай максимален, когда поле засеяно в меру. Максимум – это наибольшее значение функции по сравнению с её значениями во всех соседних точках. Это как бы вершина горы, с которой все дороги ведут только вниз, куда ни шагни. «Недосол на столе – пересол на спине». Качество пищи зависит, является функцией от количества соли в ней. Мало соли – невкусно, много – тоже в рот не возьмёшь. А где-то в промежутке, в золотой середине, когда соли в самый раз, кушанье становится особенно лакомым. В этой точке кулинарная функция достигает максимума. Малейший щепотью соли больше или меньше – и дегустатор с утончённым вкусом скажет, что качество пищи снизилось.
5. Вогнутость и выпуклость функции.
«Не круто начинай, круто кончай». Эта пословица заслуживает того, чтобы быть включённой в правила научной организации труда. Тем более что за ней так и видится графическое выражение. Повелительное звучание пословицы явно рассчитано на борьбу с противоположной, весьма распространенной манерой работы. На нее тоже есть своя пословица: «Горяч на почине, да скоро остыл». Парабола вершиной вниз представляет собой вогнутую функцию: сначала она спадает всё замедляющимися темпами, потом нарастает всё ускоряющимися. Вогнутой функцией является и гипербола, построенная для положительных значений аргумента. Наклон другой кривой неизменно уменьшается. Рост функции слабеет с ростом аргумента. Такое свойство функции называется выпуклостью. Выпуклую параболу выписывает и снаряд, выпущенный из пушки под углом к горизонту. Но присмотритесь подольше к его полёту: достигнув максимальной высоты, он начинает падать; однако искривление его траектории сохраняет прежний характер. Всё усиливающийся спад – это выпуклость. Выпуклой функцией является и гипербола, построенная для отрицательных значений аргумента.
6. Периодичность функции.
Определение: Функция y = f(x) называется периодической, если существует такое отличное от нуля число Т, что для любого x из области определения функции справедливо равенство f (x + T) = f(x) = f(x – T). Число Т называется периодом функции y = f(x).
«Это сказка про белого бычка». Так говорят, когда какое-то дело безнадёжно затягивается, когда раз за разом попытки уладить его приводят к пустому или бессмысленному результату. Поговорку знают все, но не каждый знает, как рассказывается сказка. Важная деталь рассказа – реакция слушателя.
Сказка представляет собой диалог:
- Рассказать тебе сказку про белого бычка?
- Расскажи.
- Ты расскажи, я расскажи. Рассказать тебе сказку про белого бычка?
- Так давай же!
- Ты так давай же, я так давай же. Рассказать тебе сказку про белого бычка?
- Ну хватит!
- Ты ну хватит… и так далее.
Ссылку на сказку про белого бычка часто заменяют цитированием первых слов песни «У попа была собака». Ради полноты приведём и её. «У попа была собака. Он её любил. Она съела кусок мяса. Он её убил. И в землю закопал. И надпись написал: «У попа была собака. Он её любил…» и так далее. Белый бычок и поповская собака нужны нам для разговора о периодических функциях, для уяснения математического понятия периода и тех искажений, которые привносятся в него обыденной речью. Периодичностью в обыденной речи называют чуть ли не всякую повторяемость. Но повторяемость может быть более или менее строгой. Достаточно сравнить между собой приведенные тексты: во втором, какую букву ни возьми, она обязательно повториться через 89 букв. Про первый текст такого не скажешь.
В обыденной речи утвердилось выражение «период солнечной активности». Если бы все явления на Солнце подчинялись строгой периодичности, их можно было бы предсказывать на сколь угодный долгий срок. Стала бы не нужна всемирная служба Солнца с её круглосуточными наблюдениями за дневным светилом, потеряли бы свой хлеб астрономы, пытающиеся определить, как в ближайшее время изменится количество солнечных пятен, интенсивность солнечных вспышек и т.п. Прекрасные примеры периодических функций даёт тригонометрия: синус, косинус, тангенс… Для синуса и косинуса период составляет 3600, для тангенса – 1800.
Современная математика знает множество функций, и у каждой свой неповторимый облик, как неповторим облик каждого из миллиардов людей, живущих на Земле. Однако при всей непохожести одного человека на другого у каждого есть руки и голова, уши и рот. Точно также облик каждой функции можно представить сложенным из набора характерных деталей. В них проявляются основные свойства функций. Наблюдая различные процессы и явления, мы стараемся разглядеть самые существенные их черты, самые глубокие закономерности. Часто они оказываются общими для широчайшего круга наблюдаемых событий. Общей оказывается и математическая модель, построенная на основе этих закономерностей.
5. Решение задач
Графическое решение уравнений
Приближённое решение уравнений.
Графическое решение уравнений с одним неизвестным.
Графическое решение систем уравнений с двумя неизвестными.
Графическое представление функций позволяет приближённо решить любое уравнение с одним неизвестным и систему двух уравнений с двумя неизвестными. Чтобы решить систему двух уравнений с двумя неизвестными x и y, мы рассматриваем каждое из уравнений как функциональную зависимость между переменными x и y и строим графики этих двух функций. Координаты точек пересечения этих графиков дают нам искомые значения неизвестных x и y ( т.e. решение этой системы уравнений ).
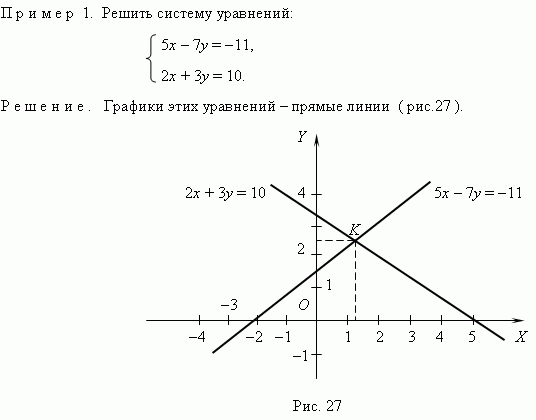
В соответствии с графиками координаты точки пересечения
K приближённо равны: x = 1.25, y = 2.5. Точное решение
этой системы уравнений:
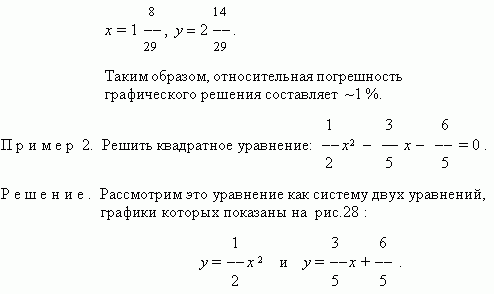
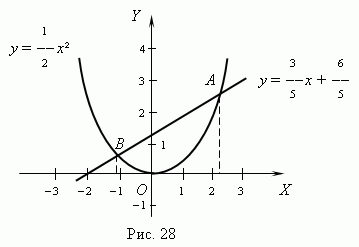
После построения графиков находим абсциссы точек
пересечения A и B: x1 » 2.25, x2 » -1.1. Точные значения
корней этого уравнения:
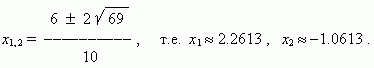
Относительная погрешность графического решения в этом
примере ~3.5 %.
Чтобы решить графически уравнение с одним неизвестным, необходимо перенести все его члены в одну часть, т.e. привести к виду:
f ( x ) = 0 ,
и построить график функции y = f ( x ). Абсциссы точек пересечения графика с осью Х будут корнями этого уравнения ( нулями этой функции ).
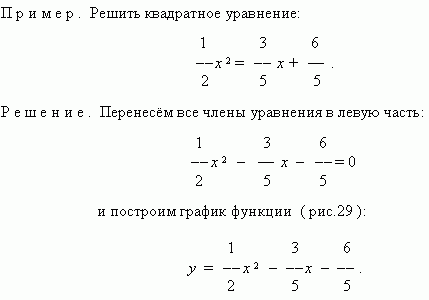
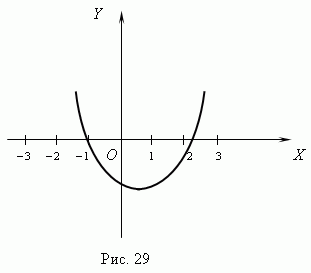
По этому графику находим нули функции: x1 » 2.25, x2 » -1.1.
Графическое решение неравенств
Приближённое решение неравенств.
Графическое решение неравенств с одним неизвестным.
Графическое решение систем неравенств с двумя неизвестными.
Пересечение решений.
Графическое представление функций позволяет приближённо решать неравенства с одним неизвестным и системы неравенств с одним и двумя неизвестными.
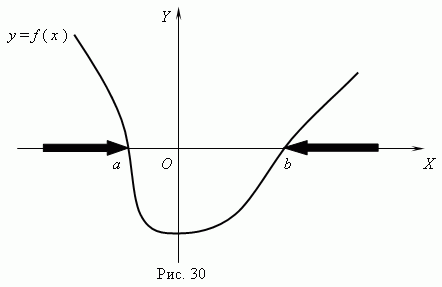
Чтобы решить графически неравенство с одним неизвестным, необходимо перенести все его члены в одну часть, т.e. привести к виду: f ( x ) 0 , и построить график функции y = f ( x ). После этого, используя построенный график, можно найти нули функции, которые разделят ось Х на несколько интервалов.
Теперь на основе этого определим интервалы x, внутри которых знак функции соответствует знаку неравенства. Например, нули нашей функции: a и b ( рис.30 ). Тогда из графика очевидно, что интервалы, внутри которых f ( x ) 0: x a и x b ( они выделеныжирными стрелками ). Ясно, что знак здесь условный; вместо него может быть любой другой: 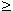 ,
, 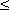 .
.
Чтобы решить графически систему неравенств с одним неизвестным, нужно перенести в каждом из них все члены в одну часть, т.e. привести неравенства к виду:

и построить графики функций y = f ( x ), y = g ( x ) , ... , y = h ( x ). Каждое из этих неравенств решается графическим методом, описанным выше. После этого нужно найти пересечение решений всех неравенств, т.e. их общую часть.
П р и м е р . Решить графически систему неравенств:
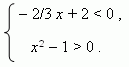
Р е ш е н и е . Сначала построим графики функций y = - 2 / 3 x + 2 и
y = x2 -1 ( рис.31 ):
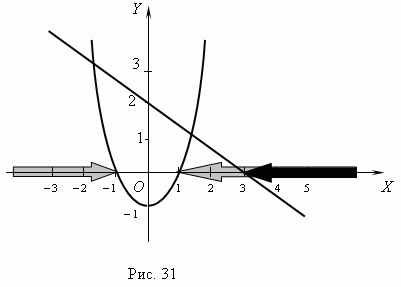
Решением первого неравенства является интервал x 3, обозначенный на рис.31 чёрной стрелкой; решение второго неравенства состоит из двух интервалов: x -1 и x 1, обозначенных на рис.31 серыми стрелками.
Из графика видно, что пересечением этих двух решений является интервал x 3. Это и есть решение заданной системы неравенств.
Чтобы решить графически систему двух неравенств сдвумя неизвестными, надо:
1) в каждом из них перенести все члены в одну часть, т.e. привести
неравенства к виду:
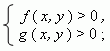
2) построить графики функций, заданных неявно: f ( x, y ) = 0 и g ( x, y ) = 0;
3) каждый их этих графиков делит координатную плоскость на две части:
в одной из них неравенство справедливо, в другой – нет; чтобы решить
графически каждое из этих неравенств, достаточно проверить
справедливость неравенства в одной произвольной точке внутри любой
части плоскости; если неравенство имеет место в этой точке, значит
эта часть координатной плоскости является его решением, если нет – то
решением является противоположная часть плоскости;
4) решением заданной системы неравенств является пересечение
(общая область) частей координатной плоскости.
П р и м е р . Решить систему неравенств:
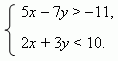
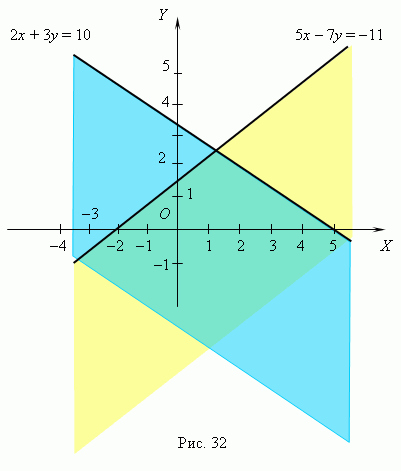
Р е ш е н и е . Сначала строим графики линейных функций: 5x – 7y = -11 и
2x + 3y = 10 ( рис.32 ). Для каждой из них находим полуплоскость,
внутри которой соответствующее заданное неравенство
справедливо. Мы знаем, что достаточно проверить справедливость
неравенства в одной произвольной точке области; в данном
случае легче всего использовать для этого начало координат O ( 0, 0 ).
Подставляя его координаты в наши неравенства вместо x и y,
получим: 5 · 0 – 7 · 0 = 0 -11, следовательно, нижняя
полуплоскость ( жёлтого цвета ) является решением первого
неравенства; 2 · 0 + 3 · 0 = 0 неравенство
имеет своим решением также нижнюю полуплоскость ( голубого
цвета ). Пересечение этих полуплоскостей ( область цвета бирюзы )
является решением нашей системы неравенств.
6. Заключение.
"Функция есть произвольный способ отображения множества А = {а} во множество В = {в}, по которому каждому элементу аА поставлен в соответствие определенный элемент вВ". Уже в этом определении не накладывается никаких ограничений на закон соответствия (этот закон может быть задан формулой, таблицей, графиком, словесным описанием). Под элементами множеств А и В
понимаются при этом элементы произвольной природы.
Это определение вполне устраивало всех математиков: под него попадали все функциональные зависимости в то время известные в математике. Оно столь широко, что им действительно охватывается все содержание и современной математики. Более того, с точки зрения общего учения о функциях та или иная отдельная математическая дисциплина характеризуется типом рассматриваемых в ней функций.
Всякая функция, которая получается из основных элементарных функций путем конечного числа суперпозиций и четырех арифметических действий (сложение, вычитание, умножение и деление), называется элементарной функцией.
Функции, тригонометрические, логарифмическая, показательная, степенная, постоянная называются основными элементарными функциями.
7. Литература:
1.Дорофеев Г. В. и др. Математика. Алгебра. Анализ данных. 9 кл.: Учебник для общеобразовательных учреждений. – М.: Дрофа, 2004.
2.Гусев В. А., Мордкович А.Г. Математика: Справочные материалы: кн. для учащихся. – М.: Просвещение, 1998.
3. Глейзер Г. И. История математики в школе. – М.: Просвещение, 1982.
4. Виленкин Н. Я. Функции в природе и технике. –М. 5. Пухначев Ю., Попов Ю. Математика без формул. – М.: АО «Столетие», 1995.











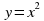 геометр или геодезист увидит зависимость площади у квадрата от величины x его стороны, а физик, авиаконструктор или кораблестроитель может усмотреть в нем зависимость силы y сопротивления воздуха или воды от скорости x движения. Математика же изучает зависимость
геометр или геодезист увидит зависимость площади у квадрата от величины x его стороны, а физик, авиаконструктор или кораблестроитель может усмотреть в нем зависимость силы y сопротивления воздуха или воды от скорости x движения. Математика же изучает зависимость  – окрестность точки x0, что при x0 –
– окрестность точки x0, что при x0 –