Проектно-исследовательская работа по геометрии "Применение подобия треугольников и фигур в жизни "

Применение подобия треугольников и фигур в жизни

Работу выполнила: Олейникова Дарья

ученица 8 класса

Руководитель: учитель математики

Матюшина Е.Г.

Цель :

• Закрепить понятие подобия треугольников
• Узнать где применяется подобие в жизни
• Рассмотреть решение задач на местности по иллюстрациям из книг.

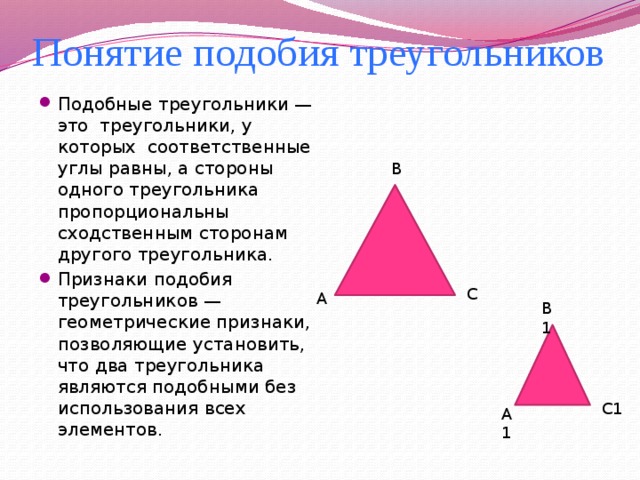
Понятие подобия треугольников

• Подобные треугольники —это треугольники, у которых соответственные углы равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
• Признаки подобия треугольников — геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов.

В

С

А

В1

С1

А1

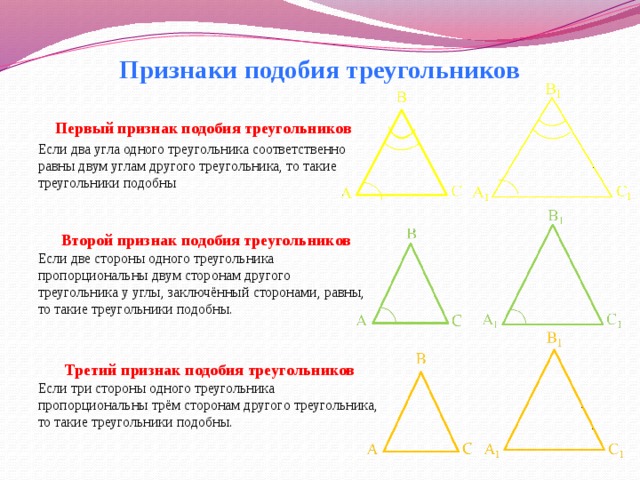
Признаки подобия треугольников

Первый признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны

Второй признак подобия треугольников

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника у углы, заключённый сторонами, равны, то такие треугольники подобны.

Третий признак подобия треугольников

Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.

Фалес Милетский

За шесть веков до нашей эры греческий мудрец Фалес Милетский

вычислил высоту египетской пирамиды, измерив длину её тени.

Как это было, рассказывается в книге Я.И.Перельмана

«Занимательная геометрия».

Фалес, говорит предание, избрал день и час,

когда длина собственной его тени

равнялась его росту. В этот момент высота пирамиды

должна также равняться

длине отбрасываемой

его тени.

Вот, пожалуй, единственный

случай, когда человек

извлёк пользу из своей тени.

ПРИТЧА:

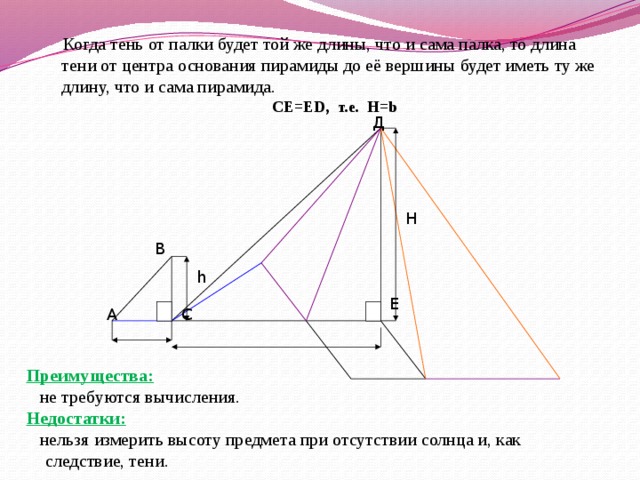
Когда тень от палки будет той же длины, что и сама палка, то длина тени от центра основания пирамиды до её вершины будет иметь ту же длину, что и сама пирамида.

СЕ=ED, т.е. H=b

Д

Н

В

h

Е

С

А

Преимущества:

не требуются вычисления.

Недостатки:

нельзя измерить высоту предмета при отсутствии солнца и, как следствие, тени .

Жюль Верн

Жюль Верн Это писатель, предвосхитивший возможности современного технического прогресса. Из 108 гипотез писателя 64 были реализованы. Увлекавшийся идеями технического прогресса, Ж.Верн был поэтом природы.

В романе Жюля Верна «Таинственный остров» описан один из способов измерения высоких предметов.

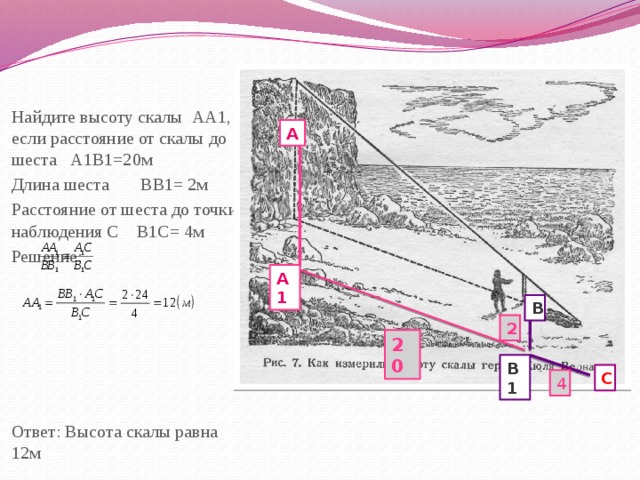
Найдите высоту скалы АА1, если расстояние от скалы до шеста А1В1=20м

Длина шеста ВВ1= 2м

Расстояние от шеста до точки наблюдения С В1С= 4м

Решение:

Ответ: Высота скалы равна 12м

А

А1

В

2

20

В1

С

4

Нахождения четвертого неизвестного члена

пропорции.

Преимущества:

• можно производить измерения в любую
• погоду;

простота формулы.

Недостатки:

нельзя

измерить высоту

предмета

не испачкавшись,

так как приходится

ложиться на землю.

Определение высоты предмета

по зеркалу

 АВD подобен  EFD (по двум углам):

 ВАD=  FED=90°;

• АDВ =  EDF, т.к. угол падения равен углу отражения.

В подобных треугольниках сходственные стороны пропорциональны:

;

;

;

.

.

.

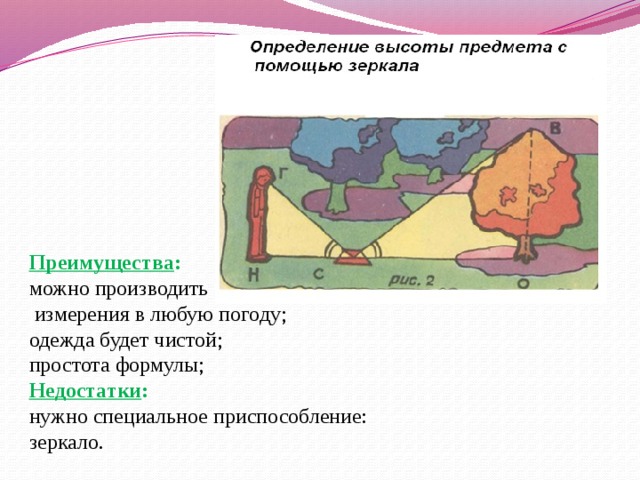
Преимущества :

можно производить

измерения в любую погоду;

одежда будет чистой;

простота формулы;

Недостатки :

нужно специальное приспособление: зеркало.

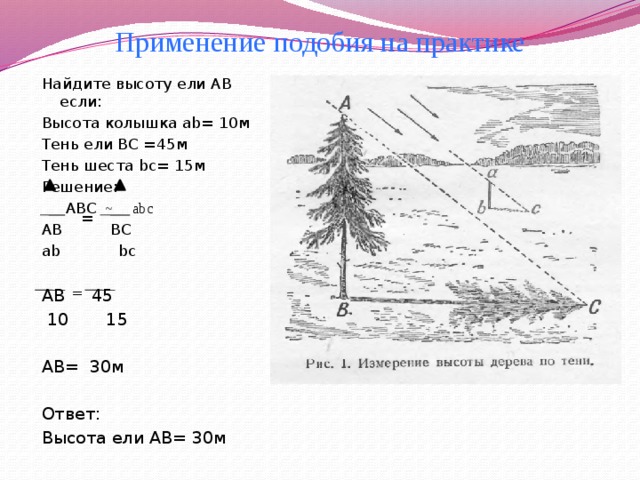
Применение подобия на практике

Найдите высоту ели АВ если:

Высота колышка ab= 10м

Тень ели ВС =45м

Тень шеста bc= 15м

Решение:

АВС ~ abc

АВ ВС

ab bc

AB 45

10 15

AB= 30м

Ответ:

Высота ели AB= 30м

=

=

Задача – измерение расстояния до недоступной точки.

Чтобы найти ширину реки АВ необходимо поставить колышек С на продолжение АВ, вдоль берега отмерить на прямой  CF перпендикулярной АС, расстояние одно в несколько раз меньше другого. Например : отмеряют  FE  в четыре раза меньше  ЕС. По направлению FG,  перпендикулярному к  FD  отыскивают точку  Н   из которой точка Е перекрывает точку А . Треугольники  АСЕ  и  EFH подобны (объясните почему). Из подобия треугольников следует пропорция AC:FH=CE:EF=4:1.

Значит, измерив  FH, можно   узнать искомую ширину реки.

Дано:

CE:EF=4:1 FH=6 м, BC=4 м

Найти: АВ.

Ответ: 20 м .

Решение задачи на конкретном примере

• Измерим высоту ели с помощью полученных знаний о подобных треугольниках. Для этого сделаем следующее: выйдем на местность, выберем объект измерения, в нашем случае ель, на некотором расстоянии от неё установим шест, в нашем случае я = D. Затем измерим расстояние от объекта до шеста. Но для измерения нам необходимо знать не только эту величину. Нам так же потребуется знать расстояние от меня до пересечения гипотенузы с землёй.

• Дано:
• Дано:

СС1- 8м, расстояние от ели до

меня (шеста)

АС-1,5м, мой рост

ВС- 1 м, расстояние от меня до

точки пересечения гипотенузы с

землёй.

• Найти:
• Найти:

А1С1- высота ели.

• Решение:
• Решение:

А1С1 =

А1

?

А

С

С1

В

АС*ВС₁ 1,5*9

13,5

=

=

ВС 1

Ответ: высота ели = 13,5м

Подобие в жизни и архитектуре

Всемирный торговый центр в Нью-Йорке

комплекс из семи зданий, спроектированный Минору Ямасаки и официально открытый 4 апреля 1973 года в Нью-Йорке (США). Архитектурной доминантой комплекса были две башни, каждая по 110 этажей — Северная (высотой 526,3 м) и Южная (высотой 415 м). 11 сентября 2001 года комплекс ВТЦ был разрушен в результате террористической атаки.

Всемирный торговый центр в Коломбо

самое высокое законченное здание в Шри-Ланке. Высота — 152 метра, таким образом башни занимают третье место по высоте среди башен-близнецов в Южной Азии. Он один из 320 Всемирных торговых центров в 90 странах мира.

Башни Петронас в Куала-Лумпуре

88-этажный небоскрёб. Высота — 451,9 метров. Находится в столице Малайзии Куала-Лумпуре. В проектировании небоскрёба участвовал премьер-министр Малайзии Махатхир Мохамад, который предложил построить здания в «исламском» стиле. Поэтому в плане комплекс представляет собой две восьмиконечные звезды.

Торрес-де-Санта-Крус в Испании

пара небоскрёбов, представляющих собой жилые башни-близнецы. Небоскрёбы расположены в городе Санта-Крус-де-Тенерифе (Канарские острова, Испания). Первое здание было построено в 2004 году, а второе — в 2006 году.

Башни-близнецы Банка Германии

два небоскрёба, высотой по 155 м.,являющиеся штаб-квартирой Банка Германии, находящиеся во Франкфурте-на-Майне, Германия. Занимают 80 место по высоте в Европе, 53 место в Евросоюзе, 11 место в Германии и 10 место во Франкфурте-на-Майне.

«Ворота Европы» в Мадриде

башни-близнецы, находящиеся в Мадриде, Испания. Башни «Ворота Европы» были завершены в 1994 году, имея в высоту по 114 метров, стали вторыми по высоте башнями-близнецами в Испании (после Торрес-де-Санта-Крус на Канарских островах) и первыми по высоте башнями-близнецами в континентальной Испании. Построенные в стиле постмодернизма, башни наклонены друг к другу под углом в 15°, они стали первыми в мире наклонными небоскрёбами. На крышах обустроены посадочные площадки для вертолётов: окрашенные в синий цвет - на западной башне, в красный — на восточной.

Самый большой макет центральной части Москвы

Это та же Москва только уменьшенная в 400 раз

Готовая часть нового архитектурного макета Москвы выставлена в павильоне №75 на Выставке достижений народного хозяйства.

Завершить работу над макетом планируется к 2017 году, он сможет войти в Книгу рекордов Гиннеса как самый большой макет города.

Площадь этого макета — 70 квадратных метров, 6500 зданий.

Общая площадь макета после окончания всех работ составит 950 квадратных метров, на нем будет представлена часть города, охватывающая Третье транспортное кольцо, все железнодорожные вокзалы, а также территорию Воробьевых гор и активно развивающиеся территории промышленной зоны ЗИЛ(Завод Имени Лихачева).

Русские матрешки

Вывод:

• В результате проведенной работы я повторила признаки подобия треугольников и разобрала решения задач различного уровня сложности, решаемые методом подобия. Я думаю, что это поможет мне при подготовке к экзаменам по математике.
• Я научилась видеть подобные треугольники в различных ситуациях, умею правильно записывать отношения сходственных сторон, по известным элементам, вычислять неизвестные, используя свойства пропорции.
• Подобие треугольников применяется в повседневной жизни довольно часто. Для себя я выяснила на конкретных примерах, что с помощью подобия можно найти высоту или расстояние до недоступной точки. Я смогу применять метод подобия для решения практических задач.
• Интересен материал из истории подобия, с которым я ознакомилась. Думаю, что те, кто изучит данный материал, тоже углубят свои знания в одной из областей геометрии.