Промежуточная аттестация по геометрии

Итоговый тест по геометрии 7 класс

Вариант 1

Часть 1

А1. Найдите длину отрезка FE, если FD = 7 см, ED = 5 см.

А) 2 см Б) 12 см В) 11 мм Г) 14 см

А2. Луч MP проходит внутри ∠AMC = 121°. Найдите градусную меру ∠CMP, если ∠AMP = 39°.

А) 180° Б) 82° В) 160° Г) 82 см

А3. Если ∠AOD = 55°, ∠BOC = 55°, то эти углы:

А) невозможно определить Б) тупые

В) вертикальные Г) смежные

H

1) АМ A) медиана АBC

2) ВК Б) высота АBC

3) CH В) секущая АBC

Г) биссектриса АBC

А5. Определите по какому признаку равенства треугольников ABC и CDA равны, если AD = BC, AB = DC.

А) по двум катетам Б) по двум сторонам и углу между ними

В) по трем сторонам Г) по стороне и двум прилежащим углам

А 6. Определите вид ∠3 и ∠5, изображенных на рисунке

А) вертикальные

Б) соответсвенные

В) односторонние

Г) накрест лежащие

A7. Сумма двух односторонних углов, образованных при пересечении двух прямых m и n секущей k, равна 148°. Определите взаимное расположение прямых m и n.

А) такая ситуация невозможна Б) прямые m и n перпендикулярны

В) прямые m и n параллельны Г) прямые m и n пересекаются

А8. Укажите, треугольника с какими сторонами НЕ существует.

А) 2 см, 2 см, 3 см Б) 1 см, 2 см, 3 см

В) 4 см, 5 см, 8 см Г) 3 см, 3 см, 3 см

А9. В прямоугольном треугольнике ABC из вершины прямого угла проведена высота CD. Найдите катет AC, если угол CBA равен 30°, а гипотенуза АВ равна 8 см.

А) 2 см Б) 6 см В) 4 см Г) 10 см

А10. Определите по данным рисунка по какому признаку равны прямоугольные треугольники.

А) по двум катетам Б) по гипотенузе и острому углу

В) по катету и острому углу Г) по катету и гипотенузе

Часть 2

В1. Известно, что углы MNK и KNP смежные. Если ∠KNP = 35°, то градусная мера ∠MNK равна ______

В2. Треугольник ABC – равнобедренный с основанием AC, ∠С = 50°. Градусная мера ∠А равна _____

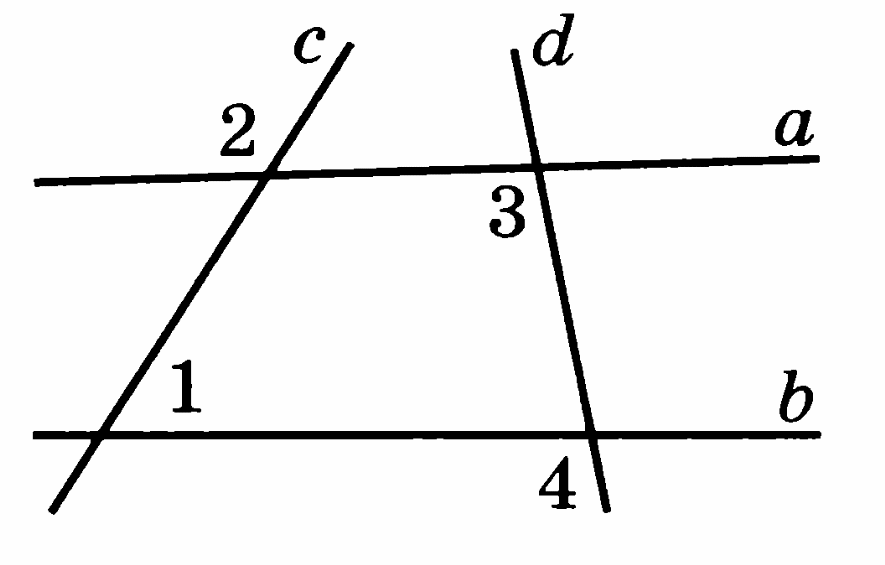В3. Известно, что a∥b, ∠1 = 55°, ∠2 = 125°, ∠3=123°. Найдите угол 4.

В4. В треугольнике ABC ∠С=90°, ∠А = 58°. Найдите угол В.

В5. В равностороннем треугольнике сторона равна 7 см. Найдите периметр треугольника.

Часть 3

С1. Два угла треугольника равны 15° и 65°. Найдите угол между высотой и биссектрисой, проведенными из третьей вершины треугольника.

С2. Отрезки AB и CD пересекаются в точке О, которая является серединой каждого из них. Докажите равенство треугольников ACD и BDC.

Итоговый тест по геометрии 7 класс

Вариант 2

Часть 1

А1. Найдите длину отрезка FD, если FE = 3 см, ED = 5 см.

А) 8 см Б) 2 см В) 10 мм Г) 35 см

А2. Луч MP проходит внутри ∠AMP = 61°. Найдите градусную меру ∠CMP, если ∠AMC = 109°.

А) 180° Б) 48° В) 170° Г) 61 см

А3. Если ∠AOD = 60°, ∠BOC = 60°, то эти углы:

А) невозможно определить Б) тупые

В) вертикальные Г) смежные

H

1) АМ A) медиана АBC

2) ВК Б) высота АBC

3) CH В) секущая АBC

Г) биссектриса АBC

А5. Определите по какому признаку равенства треугольников ABC и CDA равны, если ∠СBD = ∠ADB, ∠ABD = ∠CDB.

А) по двум сторонам и углу между ними Б) по двум катетам

В) по стороне и двум прилежащим углам Г) по трем сторонам

А 6. Определите вид ∠4 и ∠5, изображенных на рисунке

А) вертикальные

Б) соответсвенные

В) накрест лежащие

Г) односторонние

A7. Сумма двух односторонних углов, образованных при пересечении двух прямых m и n секущей k, равна 180°. Определите взаимное расположение прямых m и n.

А) прямые m и n пересекаются Б) прямые m и n перпендикулярны

В) такая ситуация невозможна Г) прямые m и n параллельны

А8. Укажите, треугольника с какими сторонами НЕ существует.

А) 4 см, 4 см, 3 см Б) 3 см, 6 см, 9 см

В) 4 см, 5 см, 8 см Г) 3 см, 3 см, 3 см

А9. В прямоугольном треугольнике ABC из вершины прямого угла проведена высота CD. Найдите катет AC, если угол CBA равен 30°, а гипотенуза АВ равна 10 см.

А) 2 см Б) 6 см В) 5 см Г) 10 см

А10. Определите по данным рисунка по какому признаку равны прямоугольные треугольники.

А) по двум катетам Б) по гипотенузе и острому углу

В) по катету и острому углу Г) по катету и гипотенузе

Часть 2

В1. Известно, что углы MNK и KNP смежные. Если ∠KNP = 45°, то градусная мера ∠MNK равна ______

В2. Треугольник ABC – равнобедренный с основанием AC, ∠С = 65°. Градусная мера ∠А равна _____

В3. Известно, что a∥b, ∠1 = 50°, ∠2 = 110°, ∠3=124°. Найдите угол 4.

В4. В треугольнике ABC ∠С=90°, ∠А = 28°. Найдите угол В.

В5. В равностороннем треугольнике сторона равна 5 см. Найдите периметр треугольника.

Часть 3

С1. Два угла треугольника равны 15° и 65°. Найдите угол между высотой и биссектрисой, проведенными из третьей вершины треугольника.

С2. Отрезки AB и CD пересекаются в точке О, которая является серединой каждого из них. Докажите равенство треугольников ACD и BDC.