КОМПЛЕКТ ЗАДАНИЙ ДЛЯ ВЫПОЛНЕНИЯ ПРОВЕРОЧНЫХ РАБОТ
ПО ДИСЦИПЛИНЕ ЕН.01 МАТЕМАТИКА
Контрольная работа №1
Тема: «Действия над комплексными числами»
1. Записать тригонометрическую форму записи комплексного числа.
2. Перевести число из алгебраической формы записи в показательную форму:

3.Дано комплексное число

Записать число противоположное и сопряженное исходному.
4. Выполнить действие

5.Выполнить умножение

6.Выполнить деление

7.Выполнить действия

8. Найти:  если: a)
если: a) 
b) 
9. Выполнить в тригонометрической форме записи следующие операции:
 , если: a)
, если: a)  b)
b) 
Самостоятельная работа №1
Тема: Вычисление определителей
Даны матрицы:




Вычислить определитель матрицы Н.
| Вариант | Матрица Н | Вариант | Матрица Н |
| 1 | 
| 2 | 
|
| 3 | 
| 4 | 
|
| 5 | 
| 6 | 
|
| 7 | 
| 8 | 
|
Самостоятельная работа №2
Тема: Методы решения системы 3 уравнений
с 3 переменными
Решить систему линейных алгебраических уравнений: 1) методом Крамера, 2) методом Гаусса.
Вариант № 1

Вариант № 2.

Самостоятельная работа №3
Тема: Правила вычисления производных
А1. Найдите производную функции:
a)  b)
b)  c)
c)  d)
d)  .
.
А2. Найдите производную функции: a)  b)
b)
А3. Найдите значение производной функции  в точке
в точке  .
.
В1. Найдите значения х, при которых значения производной функции:  положительны.
положительны.
В2. Найдите производную функции:  .
.
Самостоятельная работа №4
Тема: Применение производной к исследованию функции
1. Найдите угловой коэффициент касательной, проведённой к графику функции y = f(x) в точке с абсциссой x0, если:
 , если x0 = 1
, если x0 = 1
2. Составьте уравнение касательной к графику функции  в точке x0 = 2.
в точке x0 = 2.
3. Определите промежутки монотонности функции:
а) y = 3x2 – 6x + 1
б) y = x9 — 9x
4. Определите критические точки функции:
а) f(x) = x3 – 9x
б) 
5. Найдите точки экстремума функции:

6. Найдите наименьшее и наибольшее значение функции на заданном отрезке:
f(x) =  , [0,5 ; 3]
, [0,5 ; 3]
Контрольный тест №1
по теме «Применение производной к исследованию функции
Определить угловой коэффициент касательной, проведённой к графику функции  в точке А(16; 96).
в точке А(16; 96).
О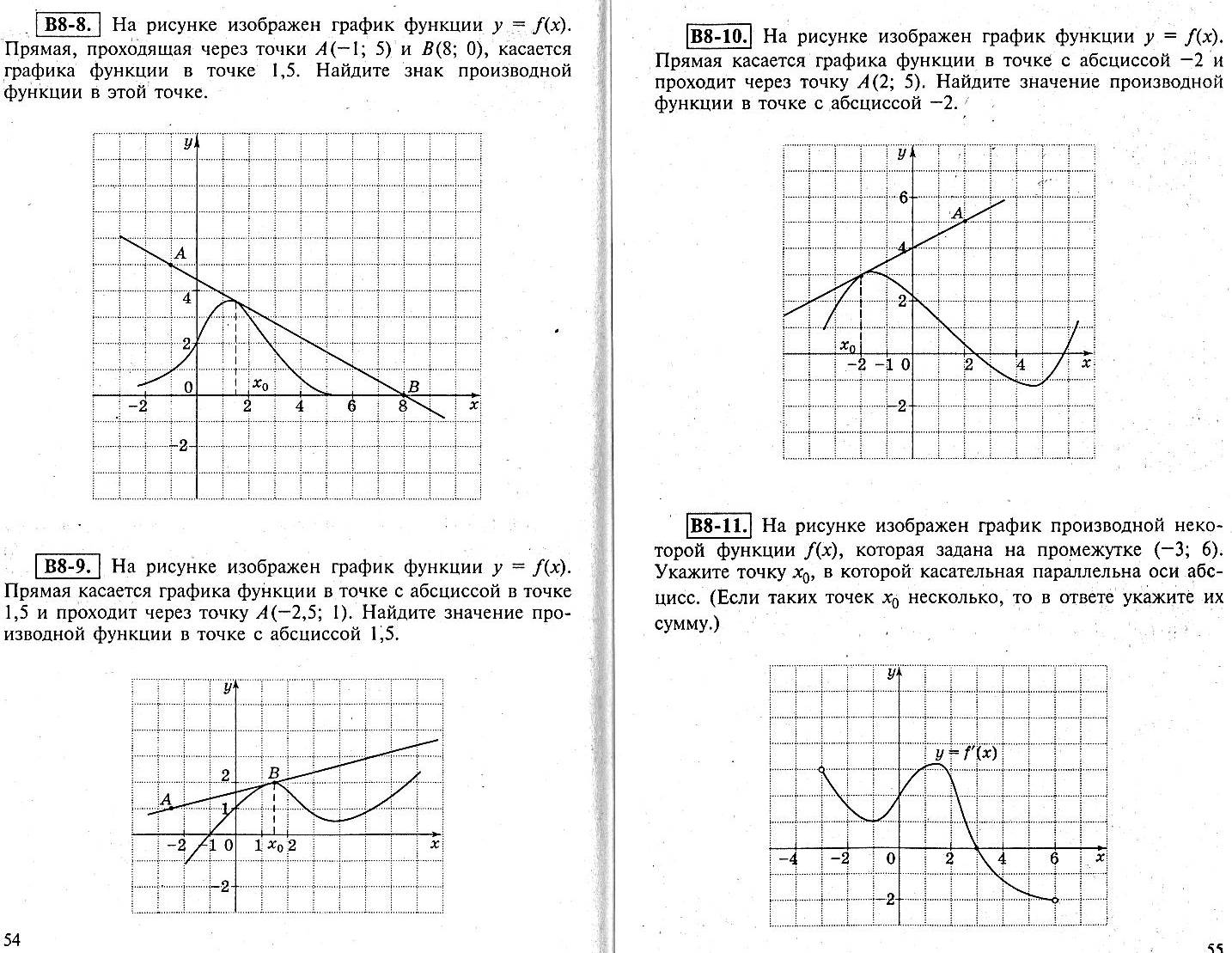 пределить наибольшее значение функции
пределить наибольшее значение функции  на промежутке
на промежутке  .
.
На рисунке изображён график функции  . Прямая касается графика функции в точке с абсциссой –2 и проходит через точку А(2; 5). Найдите
. Прямая касается графика функции в точке с абсциссой –2 и проходит через точку А(2; 5). Найдите  .
.
Н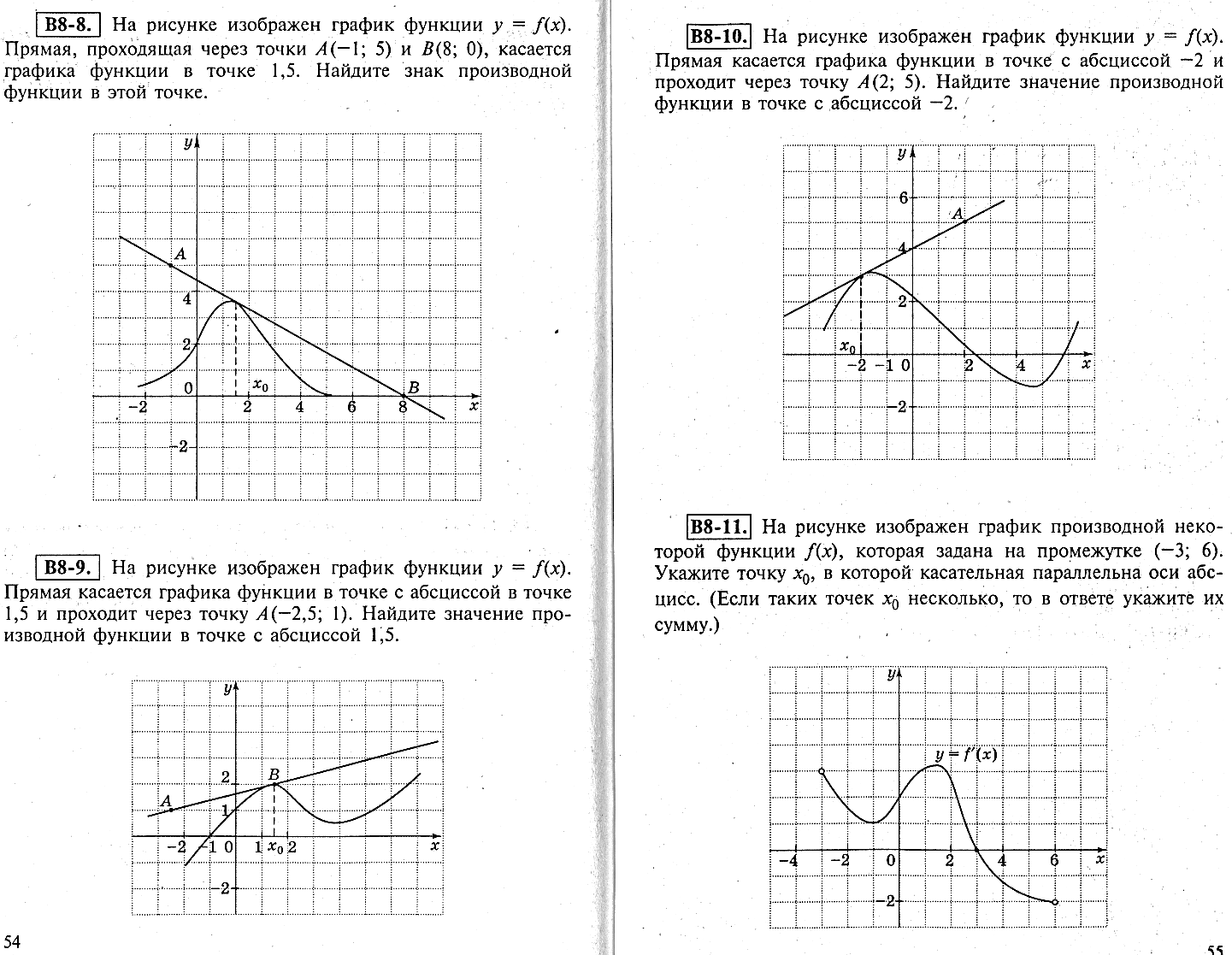 а рисунке изображён график производной некоторой функции
а рисунке изображён график производной некоторой функции  , которая задана на промежутке (-3; 6). Укажите абсциссу точки, в которой касательная к графику функции параллельна оси абсцисс (если таких точек несколько, то в ответе укажите их сумму).
, которая задана на промежутке (-3; 6). Укажите абсциссу точки, в которой касательная к графику функции параллельна оси абсцисс (если таких точек несколько, то в ответе укажите их сумму).
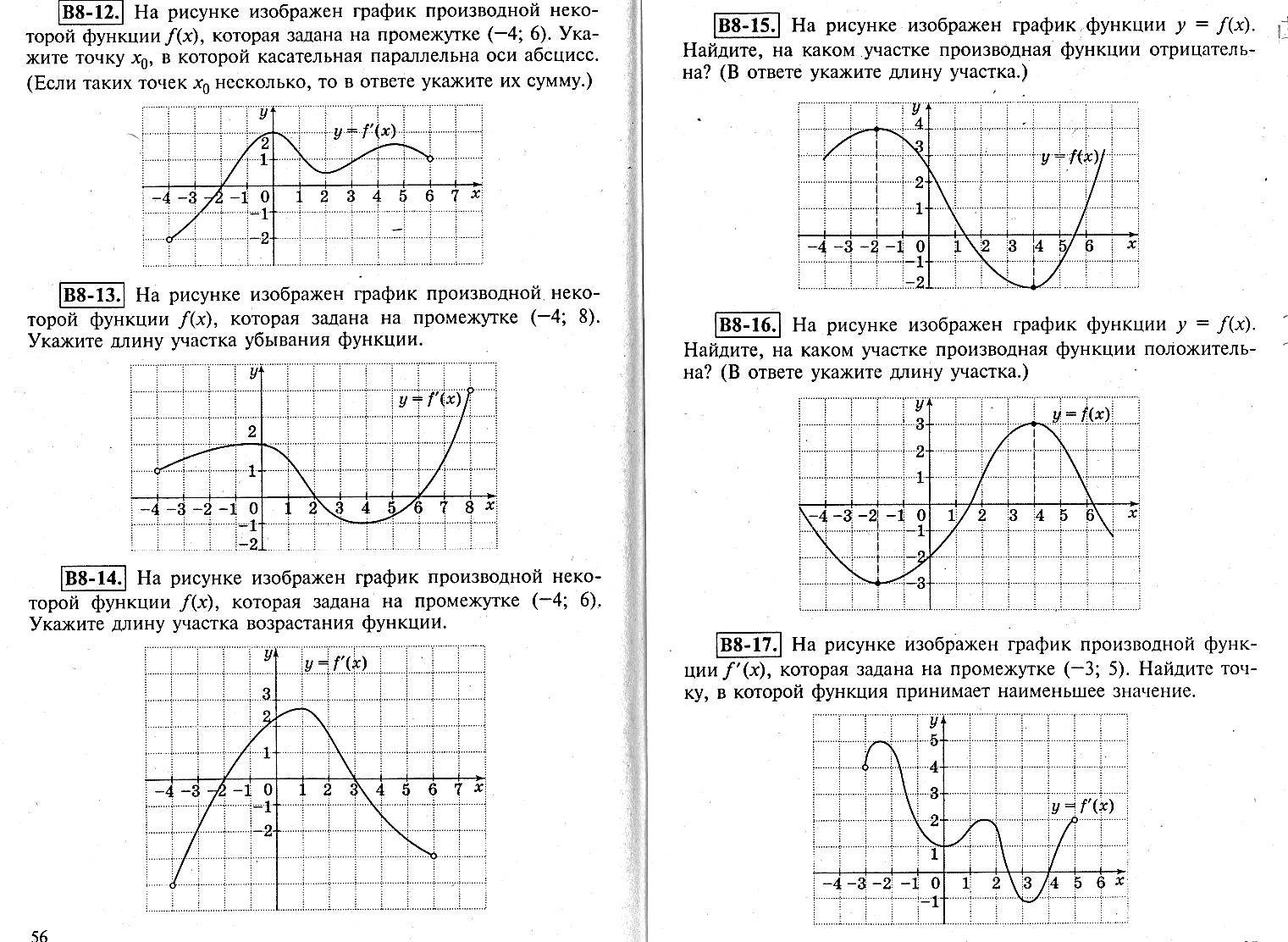
На рисунке изображён график производной некоторой функции  , которая задана на промежутке (–4; 8). Укажите длину промежутка убывания функции.
, которая задана на промежутке (–4; 8). Укажите длину промежутка убывания функции.
Н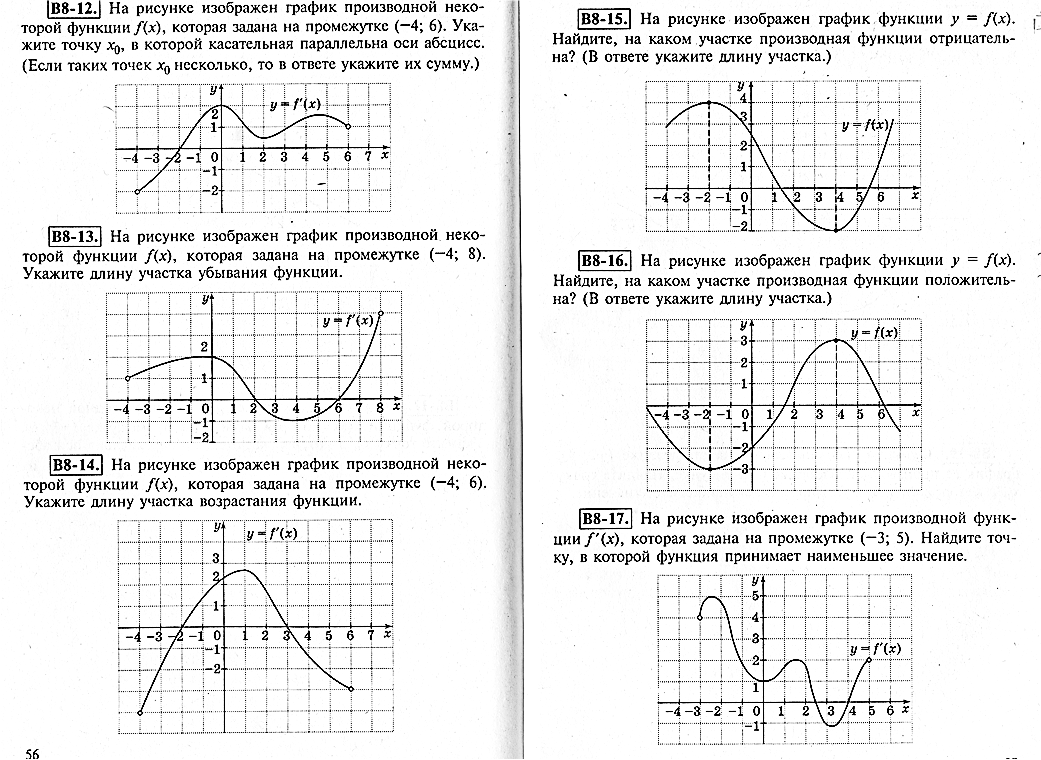 а рисунке изображён график функции
а рисунке изображён график функции  . Найдите на каком промежутке производная функции положительна? (в ответе укажите длину промежутка)
. Найдите на каком промежутке производная функции положительна? (в ответе укажите длину промежутка)
Ответы
| № вопроса | 1 | 2 | 3 | 4 | 5 | 6 |
| Ответ | 5,5 | 17 | 0,5 | 0,5 | 3 | 4 |
Самостоятельная работа №5
Тема: «Приложение определенного интеграла»
Вычислить площадь фигуры, ограниченной линиями
 ,
,
 ,
, 
Самостоятельная работа №6
Тема: «Решение задач с применением вероятностных методов»
Вариант 1
1. Из 10 билетов выигрышными являются два. Чему равна вероятность того, что среди взятых наудачу пяти билетов один выигрышный?
2. Из партии, содержащей 10 изделий, среди которых 3 бракованных, наудачу извлекают 3 изделия. Найдите вероятность того, что в полученной выборке одно изделие бракованное.
3. В ящике 10 шаров, из которых 2 белых, 3 красных и 5 голубых. Наудачу извлечено 3 шара. Найдите вероятность того, что все 3 шара разного цвета.
4. В бригаде 4 женщины и 3 мужчины. Среди членов бригады разыгрываются 4 билета в театр. Какова вероятность, того, что среди обладателей билетов окажется 2 женщины и 2 мужчины?
5. В ящике 4 голубых и 5 красных шаров. Из ящика наугад вынимают 2 шара. Найдите вероятность того, что эти шары разного цвета.
Вариант 2
1. Эксперт оценивает качественный уровень трех видов изделий по потребительским признакам. Вероятность того, что изделию первого вида будет присвоен знак качества, равна 0,9; для изделия второго вида эта вероятность равна 0,8; для изделия третьего вида 0,7. Найти вероятность того, что знак качества будет присвоен: а) всем изделиям; б) только одному изделию; в) хотя бы одному изделию.
2. В партии из 10 радиоприемников имеется 2 неисправных. Наудачу отобраны 2 радиоприемника. Найти вероятность того, что: а) оба радиоприемника несправны; б) оба радиоприемника исправны; в) один исправный, другой неисправный.
3. Для трех различных торговых предприятий определен плановый уровень прибыли. Вероятность того, что первое предприятие выполнит план прибыли, равна 90%, для второго она составляет 95%, для третьего 100%. Какова вероятность того, что плановый уровень прибыли будет достигнут: а) всеми предприятиями; б) только двумя предприятия; в) хотя бы одним предприятием?
4. Для магазина куплены два холодильника. Вероятность того, что каждый из них выдержит гарантийный срок службы составляет 90%. Найти вероятность того, что в течение гарантийного срока: а) оба холодильника не потребуют ремонта; б) оба холодильника потребуют ремонта; в) хотя бы один не потребует ремонта.
5. В партии из 80 одинаковых по внешнему виду изделий смешаны 30 изделий 1 сорта и 50 изделий 2 сорта. Найти вероятность того, что наудачу взятые два изделия окажутся: а) одного сорта; б) разных сортов.












 если: a)
если: a) 

 , если: a)
, если: a)  b)
b) 






 b)
b)  c)
c)  d)
d)  .
. b)
b)
 в точке
в точке  .
. положительны.
положительны. .
.  , если x0 = 1
, если x0 = 1 в точке x0 = 2.
в точке x0 = 2.

 , [0,5 ; 3]
, [0,5 ; 3] в точке А(16; 96).
в точке А(16; 96).  пределить наибольшее значение функции
пределить наибольшее значение функции  на промежутке
на промежутке  .
. . Прямая касается графика функции в точке с абсциссой –2 и проходит через точку А(2; 5). Найдите
. Прямая касается графика функции в точке с абсциссой –2 и проходит через точку А(2; 5). Найдите  .
. а рисунке изображён график производной некоторой функции
а рисунке изображён график производной некоторой функции 
 , которая задана на промежутке (–4; 8). Укажите длину промежутка убывания функции.
, которая задана на промежутке (–4; 8). Укажите длину промежутка убывания функции.  а рисунке изображён график функции
а рисунке изображён график функции  ,
,
 ,
, 










