Муниципальное бюджетное образовательное учреждение
«Новокулундинская средняя общеобразовательная школа»
Благовещенского района Алтайского края
| «Рассмотрено»
на заседании МО учителей естественно-математического цикла
Протокол №__от _________
______________/Федорова Л.Н. | «Согласовано»
заместитель директора по УВР
Мосина Л.В./_________
«__»____________20__г. | «Утверждено» директор МБОУ НСОШ Сушков А.И./_____________ Приказ №____ от «__»____20__ г. |
РАБОЧАЯ ПРОГРАММА
АЛГЕБРА 7 КЛАСС
предмет, класс
Карачаровой Оксаны Александровны
Ф.И.О. учителя
на 2015 - 2016 учебный год
| Составлено на основе программы общеобразовательных учреждений. Алгебра 7 – 9 классы / Т.А.Бурмистрова. – М.: Просвещение, 2011.
|
п. Новокулундинка
2015 год
Содержание
Пояснительная записка.
Содержание программы.
Требования к математической подготовке учащихся.
Планирование учебного материала
Требование к оценке знаний и умений учащихся
Календарно – тематическое планирование
Лист дополнений и изменений.
Список учебников и учебных пособий.
-
Пояснительная записка
Рабочая программа разработана на основе Федерального компонента образовательного стандарта образовательной области «Математика». Рабочая программа составлена на основании следующих нормативно-правовых документов:
Закона Российской Федерации «Об образовании» (статья 7, 9, 32).
Федерального компонента государственного образовательного стандарта основного общего образования (МО РФ 05.03.2004 г. № 1089).
Федеральный базисный учебный план для среднего общего образования (МО №322 от 09.02.1998 г. и №1312 от 09.03.2004 г.)
Федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в образовательных учреждениях.
«Программа планирование учебного материала» алгебра 7 класс автора-составителя Бурмистровой Т.А. - М., «Просвещение», 2009-2011.
Программа авторского коллектива Ю.Н. Макарычева, Н.Г.Миндюк, К.И.Нешкова, С.Б.Суворовой, которая ориентирована на учащихся 7 классов.
Базисного учебного плана для среднего общего образования Положение о рабочей программе МБОУ «НовокулундинскаяСОШ» на 2015-2016 учебный год
Программа соответствует учебникам Макарычев Ю.Н., Миндюк Н.Г. Нешков К.И.,Суворова С.Б. Алгебра. 7 класс. М. Просвещение. 2012г.
Согласно Федеральному учебному плану для образовательных учреждений Российской Федерации, учебному плану МБОУ «Новокулундинская СОШ» для обязательного изучения алгебре в 7 классе отводится 5 часов в неделю I четверть, 3 часа в неделю II, III, IV четверть Преподавание ведется по первому варианту «Программы общеобразовательных учреждений». Алгеба 7 класс. Автора-составителя Бурмистровой Т.А. (120 ч). В связи с наличием 35 учебных недель, программа включает резервные уроки (3 ч.), которые отводятся на повторение изученного материала за курс 7 класса.(всего 123ч.)
Цели обучения математике.
Изучение алгебры в 7 классе направлено на достижение следующих целей:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Основные развивающие и воспитательные цели
Развитие:
Ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
Математической речи;
Сенсорной сферы; двигательной моторики;
Внимания; памяти;
Навыков само и взаимопроверки.
Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов.
Воспитание:
Культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;
Волевых качеств;
Коммуникабельности;
Ответственности.
Содержание программы
1. Выражения и их преобразования. Уравнения.
Числовые выражения и выражения с переменными. Простейшие преобразования выражений. Уравнение с одним неизвестным и его корень, линейное уравнение. Решение задач методом уравнений.
2. Функции.
Функция, область определения функции, Способы задания функции. График функции. Функция y=kx+b и её график. Функция y=kx и её график.
3. Степень с натуральным показателем.
Степень с натуральным показателем и её свойства. Одночлен. Функции y=x2, y=x3, и их графики.
4. Многочлены.
Многочлен. Сложение, вычитание и умножение многочленов. Разложение многочлена на множители.
5. Формулы сокращённого умножения.
Формулы. Применение формул сокращённого умножения к разложению на множители.
6. Системы линейных уравнений.
Система уравнений с двумя переменными. Решение систем двух линейных уравнений с двумя переменными. Решение задач методом составления систем уравнений.
7. Повторение.
Закрепление знаний, умений и навыков, полученных на уроках по данным темам (курс алгебры 7 класса).
Требования к математической подготовке учащихся.
1. Выражения и их преобразования. Уравнения - 24 ч
Числовые выражения и выражения с переменными. Простейшие преобразования выражений. Уравнение с одним неизвестным и его корень, линейное уравнение. Решение задач методом уравнений.
Цель – систематизировать и обобщить сведения о преобразовании выражений и решении уравнений с одним неизвестным, полученные учащимися в курсе математики 5,6 классов.
Знать: какие числа являются целыми, дробными, рациональными, положительными, отрицательными и др.; свойства действий над числами; знать и понимать термины «числовое выражение», «выражение с переменными», «значение выражения», тождество, «тождественные преобразования».
Уметь: осуществлять в буквенных выражениях числовые подстановки и выполнять соответствующие вычисления; сравнивать значения буквенных выражений при заданных значениях входящих в них переменных; применять свойства действий над числами при нахождении значений числовых выражений.
2. Функции - 14 ч
Функция, область определения функции, Способы задания функции. График функции. Функция y=kx+b и её график. Функция y=kx и её график.
Цель – познакомить учащихся с основными функциональными понятиями и с графиками функций y=kx+b, y=kx.
Знать: определения функции, области определения функции, области значений, что такое аргумент, какая переменная называется зависимой, какая независимой; понимать, что функция – это математическая модель, позволяющая описывать и изучать разнообразные зависимости между реальными величинами, что конкретные типы функций (прямая и обратная пропорциональности, линейная) описывают большое разнообразие реальных зависимостей.
Уметь: правильно употреблять функциональную терминологию (значение функции, аргумент, график функции, область определение, область значений), понимать ее в тексте, в речи учителя, в формулировке задач; находить значения функций, заданных формулой, таблицей, графиком; решать обратную задачу; строить графики линейной функции, прямой и обратной пропорциональности; интерпретировать в несложных случаях графики реальных зависимостей между величинами, отвечая на поставленные вопросы
3. Степень с натуральным показателем - 15ч
Степень с натуральным показателем и её свойства. Одночлен. Функции y=x2, y=x3, и их графики.
Цель – выработать умение выполнять действия над степенями с натуральными показателями.
Знать: определение степени, одночлена, многочлена; свойства степени с натуральным показателем, свойства функций у=х2, у=х3.
Уметь: находить значения функций, заданных формулой, таблицей, графиком; решать обратную задачу; строить графики функций у=х2, у=х3; выполнять действия со степенями с натуральным показателем; преобразовывать выражения, содержащие степени с натуральным показателем; приводить одночлен к стандартному виду.
4. Многочлены – 20ч
Многочлен. Сложение, вычитание и умножение многочленов. Разложение многочлена на множители.
Цель – выработать умение выполнять сложение, вычитание, умножение многочленов и разложение многочленов на множители.
Знать: определение многочлена, понимать формулировку заданий: «упростить выражение», «разложить на множители».
Уметь: приводить многочлен к стандартному виду, выполнять действия с одночленом и многочленом; выполнять разложение многочлена вынесением общего множителя за скобки; умножать многочлен на многочлен, раскладывать многочлен на множители способом группировки, доказывать тождества.
5. Формулы сокращённого умножения – 20ч
Формулы. Применение формул сокращённого умножения к разложению на множители.
Цель – выработать умение применять в несложных случаях формулы сокращённого умножения для преобразования целых выражений в многочлены и для разложения многочленов на множители.
Знать: формулы сокращенного умножения: квадратов суммы и разности двух выражений; различные способы разложения многочленов на множители.
Уметь: читать формулы сокращенного умножения, выполнять преобразование выражений применением формул сокращенного умножения: квадрата суммы и разности двух выражение, умножения разности двух выражений на их сумму; выполнять разложение разности квадратов двух выражений на множители; применять различные способы разложения многочленов на множители; преобразовывать целые выражения; применять преобразование целых выражений при решении задач.
6. Системы линейных уравнений – 17ч
Система уравнений с двумя переменными. Решение систем двух линейных уравнений с двумя переменными. Решение задач методом составления систем уравнений.
Цель – познакомить учащихся со способами решения систем линейных уравнений с двумя переменными, выработать умение решать системы уравнений и прменять их при решении текстовых задач.
Знать: что такое линейное уравнение с двумя переменными, система уравнений, знать различные способы решения систем уравнений с двумя переменными: способ подстановки, способ сложения; понимать, что уравнение – это математический аппарат решения разнообразных задач из математики, смежных областей знаний, практики.
Уметь: правильно употреблять термины: «уравнение с двумя переменными», «система»; понимать их в тексте, в речи учителя, понимать формулировку задачи «решить систему уравнений с двумя переменными»; строить некоторые графики уравнения с двумя переменными; решать системы уравнений с двумя переменными различными способами.
7. Повторение – 10ч
Закрепление знаний, умений и навыков, полученных на уроках по данным темам (курс алгебры 7 класса).
Планирование учебного плана
| № п/п | Модуль (глава) | Примерное количество часов | Контрольные работы в течение года
|
| 1. | Выражения, тождества, уравнения. | 24ч | 2 |
| 2. | Функции. | 14ч | 1 |
| 3. | Степень с натуральным показателем. | 15ч | 1 |
| 4. | Многочлены. | 20ч | 2 |
| 5. | Формулы сокращённого умножения. | 20ч | 2 |
| 6. | Системы линейных уравнений. | 17ч | 1 |
| 7. | Повторение. | 10ч | 1 |
| 8. | Резервные уроки | 3ч |
|
| - | Итого: | 123ч | 10 |
Требование к оценке знаний и умений учащихся
1.Оценка письменных контрольных работ обучающихся по математике.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится, если:
работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2.Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя
Отметка «1» ставится, если:
ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.
Общая классификация ошибок.
При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
3.1. Грубыми считаются ошибки:
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
неумение пользоваться первоисточниками, учебником и справочниками;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.
3.2. К негрубым ошибкам следует отнести:
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.
3.3. Недочетами являются:
нерациональные приемы вычислений и преобразований;
небрежное выполнение записей, чертежей, схем, графиков.
Список учебников и учебных пособий.
1. Учебник Алгебра 7. / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Пешков, С.В. Суворова. Под редакцией С.А. Теляковского. / М.: Просвещение, 2010.
2. Рабочая тетрадь по алгебре./ Н.Г. Миндюк, И.С. Шыков /- М.: Просвещение ,2014.
Литература для учителя
Федеральный базисный учебный план для образовательных учреждений Российской Федерации, реализующих программы общего образования.
Примерная программа общеобразовательных учреждений. Алгебра 7-9 кл./ Составитель: Т.А.Бурмистрова .- М.: Просвещение, 2011г.
Б.Г.Зив, В.М. Мейлер. Дидактические материалы.- М.: Просвещение ,2014.
Жохов В.И. Уроки алгебры в 7 классе.- М.: Просвещение. 2009г.
Миндюк Н.Г Методические рекомендации. – М.: Просвещение. 2014г.
Дудницын Ю.П., Кронгаус В.Л. Тематические тесты.- М.: Просвещение.2014г.
М.А. Иченская. Самостоятельные и контрольные работы.- М.: Просвещение ,2014
Изучение алгебры в 7-9классах./ Ю.Н. Макарычев, Н.Г. Миндюк, , С.В. Суворова. И.С. Шлыкова/Просвещение, 2011







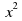 ,
,










