

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Рабочая программа 8 класс (алгебра, геометрия).
Просмотр содержимого документа
«ктп 8класс алгебра»
6. Календарно – тематическое планирование.
| № п/п | Тема урока | Кол-во часов
| Формы и методы обучения | Основное содержание | Требование к уровню подготовки (знать/уметь) Критерии оценивания (см. поясн. записка | Оборудование, оснащение | Календарно - учебный график | |||||||
|
| Глава 1. Рациональные дроби (23 ч) | |||||||||||||
| 1-5 | Рациональные дроби и их свойства | 5ч | Словесные, наглядные, практические | Дробные выражения, рациональные выражения, рациональные выражения, рациональная дробь. Основное свойство дроби, тождество, сокращение дробей. | Знать рациональные, целые, дробные выражения; рациональная дробь. основное свойство дроби, термины «выражение», «тождественное преобразование», правило сокращение дробей. Уметь осуществлять в рациональных выражениях числовые подстановки и выполнять соответствующие вычисления , сокращать дробь. | Карточки: устный счет | 1,2 неделя сентября | |||||||
| 6-11 | Сумма и разность дробей. | 6ч | Словесные, наглядные, практические | Правила сложения и вычитания дробей с одинаковым знаменателем и с разными знаменателями | Знать правила сложения и вычитания дробей с одинаковым знаменателем и с разными знаменателями. Уметь выполнять сложение и вычитание дробей с одинаковыми знаменателями и с разными знаменателями. | Интерактивная доска, проектор Печатные пособия | 2,3,4 неделя сентября
| |||||||
| 12 | Контрольная работа № 1 по теме: «Рациональные выражения. Сложение и вычитание дробей». | 1ч | Самостоятельная работа |
| Уметь: применять изученный теоретический материал при выполнении письменной работы | Карточки с заданиями | 4 неделя сентября
| |||||||
| 13-22 | Произведение и частное дробей. | 10ч | Словесные, наглядные, практические
| Правило умножения рациональных дробей, правило возведения в степень рациональных дробей, правило деления рациональных дробей . | Знать правило умножения рациональных дробей, правило возведения в степень рациональных дробей, правило деления рациональных дробей Уметь применять правило умножения рациональных дробей, применять правило возведения в степень рациональных дробей правило деления рациональных дробей. | Интерактивная доска, проектор Печатные пособия | 5 неделя сентября 1-4 неделя октября
| |||||||
| 23 | Контрольная работа № 2 по теме: «Произведение и частное дробей». | 1ч | Самостоятельная работа |
| Уметь: применять изученный теоретический материал при выполнении письменной работы | Карточки с заданиями | 4 неделя октября | |||||||
| Глава 2. Квадратные корни (19 ч) | ||||||||||||||
| 24-25 | Действительные числа | 2ч | Словесные, наглядные, практические
| Рациональные числа, несократимая дробь Иррациональные числа. Действительные числа. | Знать какие числа называются рациональными, действительными их обозначение Уметь представлять рациональное число в виде десятичной дроби и наоборот, сравнивать действительные числа
| Интерактивная доска, проектор Печатные пособия | 4,5 неделя октября
| |||||||
| 26-30 | Арифметический квадратный корень. | 5ч | Словесные, наглядные, практические
| Квадратные корни. Арифметический квадратный корень Приближенные значения квадратного корня. Функция y= | Знать определения квадратного корня, арифметического квадратного корня , график функции y= Уметь выполнять преобразование числовых выражений, содержащих квадратные корни, находить приближенные значения квадратного корня. Строить график функции | Интерактивная доска, проектор Печатные пособия
| 5 неделя октября 2 неделя ноября | |||||||
| 31-33 | Свойства арифметического квадратного корня | 3ч | Словесные, наглядные, практические | Теоремы о квадратном корне из произведения и дроби. Теорема о квадратном корне из степени | Знать теоремы о квадратном корне из произведения и дроби Теорему о квадратном корне из степени Уметь находить квадратный корень из произведения и дроби Находить квадратный корень из степени. |
| 3 неделя ноября | |||||||
| 34 | Контрольная работа № 3 по теме: «Квадратные корни». | 1ч | Самостоятельная работа |
| Уметь: применять изученный теоретический материал при выполнении письменной работы | Карточки с заданиями | 4 неделя ноября | |||||||
| 35-41 | Применение свойств арифметического квадратного корня | 7ч | Словесные, наглядные, практические | Вынесение множителя из-под знака корня. Внесение множителя под знак корня. Преобразование выражений, содержащих квадратные корни
| Знать: свойства арифметического квадратного корня Уметь выносить множитель из-под знака корня; вносить множитель под знак корня выполнять преобразование выражений, содержащих квадратные корни , | Интерактивная доска, проектор | 4 неделя ноября 1,2 неделя декабря | |||||||
| 42 | Контрольная работа № 4 по теме: «Применение свойств арифметического квадратного корня» | 1ч | Самостоятельная работа |
| Уметь: применять изученный теоретический материал при выполнении письменной работы | Карточки с заданиями | 2 неделя декабря | |||||||
| Глава 3. Квадратные уравнения. (21 ч) | ||||||||||||||
| 43-52 | Квадратное уравнение и его корни | 10ч | Словесные, наглядные, практические | Неполные квадратные уравнения. Приведенное квадратное уравнение; формулы дискриминанта и корней квадратного уравнения. Решение задач с помощью квадратных уравнений
| Знать что такое квадратное уравнение; неполное квадратное уравнение определение приведённого квадратного уравнения; формулы дискриминанта и корней квадратного уравнения. Уметь решать неполные квадратные уравнения, решать квадратные уравнения выделением квадрата двучлена; решать квадратные уравнения по формуле; решать текстовые задачи с помощью квадратных уравнений
| Интерактивная доска, проектор Печатные пособия | 3,4 неделя декабря 3,4 неделя января | |||||||
| 53 | Контрольная работа № 5 по теме: «Квадратные уравнения». | 1ч | Самостоятельная работа |
| Уметь: применять изученный теоретический материал при выполнении письменной работы | Карточки с заданиями | 4 неделя января | |||||||
| 54-62 | Дробные рациональные уравнения | 9ч | Словесные, наглядные, практические | Определение дробных рациональных уравнений и способы их решения. Решение дробных рациональных уравнений и задач с помощью рациональных уравнений
| Знать определение дробных рациональных уравнений и способы их решения. Уметь решать дробно-рациональные уравнения; решать уравнения графическим способом; решать текстовые задачи с помощью рациональных уравнений | Интерактивная доска, проектор Печатные пособия | 4,5 неделя января 1,2 неделя февраля | |||||||
| 63 | Контрольная работа № 6 по теме: «Дробные рациональные уравнения» | 1ч | Самостоятельная работа |
| Уметь: применять изученный теоретический материал при выполнении письменной работы | Карточки с заданиями | 2 неделя февраля | |||||||
| Глава 4. Неравенства (20 ч) |
| |||||||||||||
| 64-71 | Числовые неравенства и их свойства | 8ч | Словесные, наглядные, практические | Числовые неравенства Свойства числовых неравенств. Теоремы о сложении и умножении неравенств. Абсолютная и относительная погрешности
| Знать определение числового неравенства с одной переменной; свойства числовых неравенств; теоремы о сложении и умножении неравенств; определения абсолютной и относительной погрешностей. Уметь доказывать неравенства; применять свойства числовых неравенствпри решении и оценивании неравенств; применять эти теоремы при оценке неравенств; применять погрешности при оценке качества измерений | Интерактивная доска, проектор Печатные пособия | 3,4 неделя февраля 1неделя марта | |||||||
| 72 | Контрольная работа № 7 по теме: «Числовые неравенства и их свойства». | 1ч | Самостоятельная работа |
| Уметь: применять изученный теоретический материал при выполнении письменной работы | Карточки с заданиями | 1 неделя марта | |||||||
| 73-82 | Неравенства с одной переменной и их системы. | 10ч | Словесные, наглядные, практические | Пересечение и объединение множеств. Числовые промежутки и их виды. Числовое неравенство с одной переменной, решение неравенств с одной переменной. Система неравенств с одной переменной, решение систем неравенств с одной переменной | Знать определения пересечение и объединение множеств; определение системы неравенств с одной переменной; что значит решить систему неравенств Уметь находить пересечение и объединение множеств записывать и читать числовые промежутки; изображать их на числовой прямой; решать линейные неравенства с одной переменной; решать системы неравенств с одной переменной | Интерактивная доска, проектор Печатные пособия | 2-4 неделя марта 2 неделя апреля | |||||||
| 83 | Контрольная работа № 8 по теме: «Неравенства с одной переменной и их системы». | 1ч | Самостоятельная работа
|
| Уметь: применять изученный теоретический материал при выполнении письменной работы | Карточки с заданиями | 2 неделя апреля | |||||||
| Глава 5. Степень с целым показателем. Элементы статистики. (11 ч) | ||||||||||||||
| 84-89 | Степень с целым показателем и её свойства | 6ч | Словесные, наглядные, практические. | Определение степени с целым отрицательным показателем; выражение вида 0n .Стандартный вид числа. | Знать определение степени с целым и целым отрицательным показателем. Уметь выполнять действия со степенями с натуральным и целым показателями используя свойства степеней; записывать числа в стандартном виде. | Интерактивная доска, проектор Печатные пособия | 3,4 неделя апреля | |||||||
| 90 | Контрольная работа №9 по теме «Степень с целым показателем». | 1ч | Самостоятельная работа |
| Уметь: применять изученный теоретический материал при выполнении письменной работы | Карточки с заданиями | 5 неделя апреля | |||||||
| 91-94 | Элементы статистики | 4 | Словесные, наглядные, практические | Частота, таблица частот, относительная частота, таблица относительных частот, интервальный ряд, выборочное исследование, генеральная совокупность, выборочная совокупность.
| Знать что такое: частота, таблица частот, относительная частота, таблица относительных частот, интервальный ряд; выборочное исследование, генеральная совокупность, выборочная совокупность. Уметь собирать и группировать статистические данные. Наглядно представлять статистические данные в виде столбчатых, круговых диаграмм, полигона, гистограмма |
| 5 неделя апреля
| |||||||
|
| Повторение. (8ч) | |||||||||||||
| 95-96 | Повторение. Рациональные дроби. | 2ч | Словесные, наглядные, практические | Преобразования рациональных выражений, используя все действия с алгебраическими дробями. | Уметь выполнять преобразования рациональных выражений, используя все действия с алгебраическими дробями. | Интерактивная доска, проектор | 1неделя мая | |||||||
| 97 | Повторение. Квадратные корни. | 1ч | Словесные, наглядные, практические | Преобразование выражений, содержащих операцию извлечения квадратного корня | Уметь упрощать выражения, с помощью извлечения квадратного корня и освобождение от иррациональности в знаменателе | Интерактивная доска, проектор | 1 неделя мая | |||||||
| 98-99 | Повторение. Квадратные уравнения | 2ч | Словесные, наглядные, практические. | Решение квадратных уравнений | Уметь решать неполное квадратное уравнение; используя дискриминант, решать квадратные уравнения по алгоритму; решать задачи на составление квадратных уравнений; решать рациональные уравнения, используя метод введения новой переменной; биквадратные уравнения; уравнения с применением нескольких способов упрощения выражений входящих в уравнение; | Интерактивная доска, проектор | 2 неделя мая | |||||||
| 100-101 | Повторение. Неравенства | 2ч | Словесные, наглядные, практические | Решение неравенств и систем неравенств с одной переменной | Уметь решать неравенства и системы неравенств с одной переменной | Интерактивная доска, проектор | 3 неделя мая | |||||||
| 102 | Итоговая контрольная работа. | 1ч | Самостоятельная работа |
| Уметь: применять изученный теоретический материал при выполнении письменной работы | Карточки с заданиями | 3 неделя мая | |||||||
| 103-105 | Резервный урок | 3ч |
|
|
|
| 4 неделя мая | |||||||
|
| Итого: | 105ч |
|
|
|
|
| |||||||
Просмотр содержимого документа
«ктп 8класс геометрия»
6. Календарно – тематическое планирование.
| № п/п | Тема урока | Кол-во часов
| Формы и методы обучения | Основное содержание | Требование к уровню подготовки (знать/уметь) Критерии оценивания (см. поясн. записка | Оборудование, оснащение | Календарно - учебный график | ||||||||||||||
|
| Глава 5. Четырехугольники (14 ч) | ||||||||||||||||||||
| 1,2 | Многоугольники | 2ч | Словесные, наглядные, практические | Многоугольники. Выпуклые многоугольники. Сумма углов выпуклого многоугольника | Знать: определение многоугольника; Формулу суммы углов выпуклого многоугольника. Уметь: распознавать на чертежах многоугольники, используя определение; Применять формулу суммы углов выпуклого многоугольника при нахождении элементов многоугольника | Карточки: устный счет | 1 неделя сентября | ||||||||||||||
| 3-8 | Параллелограмм и трапеция | 6ч | Словесные, наглядные, практические | Параллелограмм, его свойства и признаки. Трапеция, её свойства | Знать: определение параллелограмма и его свойства, формулировки признаков; определение трапеции, свойства равнобедренной трапеции Уметь: распознавать на чертежах среди четырёх- угольников параллелограммы; доказывать, что данный четырёхугольник- параллелограмм; выполнять чертежи по условию задачи, находить углы и стороны параллелограмма, используя свойство углов и сторон; распознавать трапецию, её элементы, виды на чертежах, находить углы и стороны равнобедренной трапеции, используя её свойства | Интерактивная доска, проектор Печатные пособия | 2-4 неделя сентября
| ||||||||||||||
| 9-12 | Прямоугольник, ромб, квадрат. | 4ч | Словесные, наглядные, практические | Прямоугольник, его элементы, свойства и признаки. Понятие ромба, квадрата, их свойства и признаки. | Знать: определение прямоугольника, его элементы, свойства и признаки; определения квадрата, ромба, их элементы, свойства и признаки Уметь: распознавать на чертежах прямоугольники, находить их стороны и углы, выполнять чертёж по условию задачи ; применять признаки при решении задач. распознавать на чертежах рассматриваемые 4-хугольники, находить их стороны и углы, используя свойства; выполнять чертёж по условию задачи ; применять признаки при решении задач; находить стороны квадрата, если известны части сторон, используя свойства прямоугольного треугольника. | Интерактивная доска, проектор Печатные пособия | 5 неделя сентября 1,2 неделя октября | ||||||||||||||
| 13. | Решение задач по теме «Четырёхугольники» | 1ч | Словесные, наглядные, практические
| Определения, свойства и признаки прямоугольника, трапеции, ромба, параллелограмма | Уметь находить: в прямоугольнике угол между диагоналями. Используя свойство диагоналей, углы в прямоугольной и равнобедренной трапециях, используя свойства трапеции и сторон параллелограмма | Интерактивная доска, проектор Печатные пособия | 3 неделя октября | ||||||||||||||
| 14 | Контрольная работа № 1по теме: «Четырёхугольники» | 1ч | Самостоятельная работа |
| Уметь: применять изученный теоретический материал при выполнении письменной работы | Карточки с заданиями | 3 неделя октября
| ||||||||||||||
| Глава 6. Площадь (14 ч) | |||||||||||||||||||||
| 15, 16 | Площадь многоугольника | 2ч | Словесные, наглядные, практические
| Единицы измерения площадей, площадь прямоугольника, основные свойства площадей | Знать: представление о способе измерения площадей многоугольников, свойства площадей. Формулу площади прямоугольника. Уметь: вычислять площади квадрата, прямоугольника, используя формулы | Интерактивная доска, проектор Печатные пособия | 4,5 неделя октября
| ||||||||||||||
| 17-22 | Площадь параллелограмма, треугольника и трапеции | 6ч | Словесные, наглядные, практические
| Параллелограмм, основание и высота параллелограмма, площадь параллелограмма Треугольник, основание и высота, площадь треугольника, соотношение площадей. Трапеция, высота трапеции, площадь трапеции. | Знать: формулу площади параллелограмма, треугольника,трапеции. Уметь: вычислять площадь параллелограмма, треугольника, трапеции используя формулу. Выводить формулу площади параллелограмма. Решать задачи на вычисление площадей. | Интерактивная доска, проектор Печатные пособия
| 5 неделя октября 2,3 неделя ноября | ||||||||||||||
| 23-25 | Теорема Пифагора | 3ч | Словесные, наглядные, практические | Теорема Пифагора и теорема ей обратная | Знать формулировку теоремы Пифагора и теорема ей обратная Уметь доказывать теорему Пифагора; решать задачи на нахождение гипотенузы или катета в прямоугольном треугольнике. Доказывать обратную теорему и применять её при решении задач.
| Интерактивная доска, проектор Печатные пособия
| 4 неделя ноября 1 неделя декабря | ||||||||||||||
| 26, 27 | Решение задач по теме «Площадь | 2ч | Словесные, наглядные, практические | Площадь параллелограмма, треугольника, трапеции, теорема Пифагора | Уметь находить площадь параллелограмма, треугольника, трапеции по формулам; Уметь применять теорему Пифагора при решении задач. | Интерактивная доска, Печатные пособия проектор.
| 1,2 неделя декабря | ||||||||||||||
| 28 | Контрольная работа № 2 по теме: «Площадь». | 1ч | Самостоятельная работа |
| Уметь: применять изученный теоретический материал при выполнении письменной работы | Карточки с заданиями | 2 неделя декабря | ||||||||||||||
| Глава 7. Подобные треугольники (19 ч) | |||||||||||||||||||||
| 29, 30 | Определение подобных треугольников | 2ч | Словесные, наглядные, практические | Подобие треугольников, коэффициент подобия Связь между площадями подобных фигур. | Знать: определение пропорциональных отрезков подобных треугольников, свойство биссектрисы треугольника; формулировку теоремы об отношении площадей подобных треугольников Уметь: находить элементы треугольника. Используя свойство биссектрисы; находить отношение площадей, составлять уравнения по условию задачи. | Интерактивная доска, проектор Печатные пособия | 3 неделя декабря
| ||||||||||||||
| 31-35 | Признаки подобия треугольников | 5ч | Словесные, наглядные, практические | Первый признак подобия треугольников. Второй и третий признаки подобия треугольников. Применение признаков подобия при решении задач | Знать: формулировк признаков подобия треугольников и его доказательство. Уметь: доказывать признаки, применять их при решении задач, выполнять чертёж по условию задачи. | Интерактивная доска, проектор Печатные пособия | 4 неделя декабря 3,4 неделя января | ||||||||||||||
| 36 | Контрольная работа № 3 по теме: «Подобные треугольники» | 1ч | Самостоятельная работа |
| Уметь: применять изученный теоретический материал при выполнении письменной работы | Карточки с заданиями | 4 неделя января | ||||||||||||||
| 37-43 | Применение подобия к доказательству теорем и решению задач | 7ч | Словесные, наглядные, практические | Средняя линия треугольника Свойство медианы треугольника. Среднее пропорциональное Пропорциональные отрезки в прямоугольном треугольнике. | Знать: формулировку о средней линии треугольника.; формулировку свойства медианы треугольника; понятие среднего пропорционального, Свойство высоты, проведённой из вершины прямого угла треугольника. Теоремы о пропорциональности отрезков в прямоугольном треугольнике. Уметь проводить доказательство теоремы о средней линии треугольника и находить её; находить элементы треугольника, используя свойство медианы; находить элементы прямоугольного треугольника, используя свойство высоты; использовать теоремы при решении задач | Интерактивная доска, проектор Печатные пособия | 5 неделя января 1,2,3 неделя февраля | ||||||||||||||
| 44-46 | Соотношение между сторонами и углами прямоугольного треугольника | 3ч | Словесные, наглядные, практические | Понятия синуса, косинуса, тангенса острого угла прямоугольного треугольника; основное тригонометрическое тождество. Значения синуса, косинуса, тангенса для углов 30ْ, 45ْ, 60ْ, 90.ْ Решение прямоугольных треугольников | Знать: понятия синуса, косинуса, тангенса острого угла прямоугольного треугольника; основное тригонометрическое тождество; значения синуса, косинуса, тангенса для углов 30ْ, 45ْ, 60ْ, 90.ْ ; соотношения между сторонами и углами прямоугольного треугольника; Уметь: находить значение одной из тригонометрических функций по значению другой; определять значения синуса, косинуса, тангенса по заданному значению углов решать прямоугольные треугольники, используя понятия синуса, косинуса, тангенса острого угла прямоугольного треугольника; | Интерактивная доска, проектор Печатные пособия | 3,4 неделя февраля | ||||||||||||||
| 47 | Контрольная работа № 4 по теме: «Подобные треугольники». | 1ч | Самостоятельная работа |
| Уметь: применять изученный теоретический материал при выполнении письменной работы | Карточки с заданиями | 1 неделя марта | ||||||||||||||
| Глава 8. Окружность (17 ч) |
| ||||||||||||||||||||
| 48-50 | Касательная к окружности | 3ч | Словесные, наглядные, практические | Взаимное расположение прямой и окружности. Касательная и секущая к окружности, точка касания. | Знать: случаи взаимного расположение прямой и окружности. Понятия касательной, секущей, точек касания, свойство касательной и её признак. | Интерактивная доска, проектор Печатные пособия | 1,2неделя марта | ||||||||||||||
| 51-54 | Центральные и вписанные углы | 4ч | Словесные, наглядные, практические | Центральные и вписанные углы. Градусная мера длины дуги окружности. Теорема о вписанном угле и следствие из неё. Теорема об отрезках пересекающихся хорд | Знать: понятие градусной меры дуги, центрального угла. Определение вписанного угла, теорему о вписанном угле и следствие из неё. Уметь: решать простейшие задачи на вычисление градусной меры дуги; распознавать на чертежах вписанные углы, находить величину вписанного угла. Доказывать и применять теорему при решении задач, выполнять чертёж по условию задачи. | Интерактивная доска, проектор Печатные пособия | 3,4 неделя марта
| ||||||||||||||
| 55-57 | Четыре замечательные точки треугольника | 3ч | Словесные, наглядные, практические | Понятие серединного перпендикуляра. Теорема о серединном перпендикуляре. Теорема о точке пересечения высот треугольника. Четыре замечательные точки треугольника.
| Знать: понятие серединного перпендикуляра, формулировку теоремы о нём. Четыре замечательные точки треугольника. Формулировку теоремы о пересечении высот треугольника Уметь: доказывать и применять теорему для решения задач на нахождение элементов треугольника; находить элементы треугольника | Интерактивная доска, проектор Печатные пособия | 2,3 неделя апреля | ||||||||||||||
| 58-61 | Вписанная и описанная окружности | 4ч | Словесные, наглядные, практические | Понятие вписанной окружности. Теорема об окружности, вписанной в треугольник. Теорема о свойстве описанного четырёхугольника, треугольника. | Знать: понятие вписанной окружности, теорему об окружности, вписанной в треугольник. Теорему о свойстве описанного четырёхугольника, треугольника и этапы её доказательства.
Уметь: распознавать на чертежах вписанные окружности, находить элементы треугольника, используя свойства вписанной окружности. Применять свойство описанного 4-хугольника при решении задач, выполнять чертёж по условию задачи. Доказывать теорему и применять её при решении задач, различать на чертежах описанные окружности. | Интерактивная доска, проектор Печатные пособия | 3-5 неделя апреля | ||||||||||||||
| 62, 63 | Решение задач по теме «Окружность» | 2ч | Словесные, наглядные, практические | Вписанная и описанная окружности, вписанные и описанные четырёхугольники | Знать: формулировки определений и свойств; Уметь: находить один из отрезков касательных, проведённых из одной точки по заданному радиусу окружности; центральные и вписанные углы по отношению дуг окружностей; отрезки, пересекающихся хорд окружности. Используя теорему о произведении отрезков пересекающихся хорд.
| Интерактивная доска, проектор Печатные пособия | 5 неделя апреля 1 неделя мая | ||||||||||||||
| 64 | Контрольная работа № 5 по теме: «Окружность». | 1ч | Самостоятельная работа
|
| Уметь: применять изученный теоретический материал при выполнении письменной работы | Карточки с заданиями | 1 неделя мая | ||||||||||||||
| Повторение. Решение задач. (4 ч) | |||||||||||||||||||||
| 65 | Повторение по теме «Четырехугольники» | 1ч | Словесные, наглядные, практические. | Задачи на построение. | Уметь: выполнять основные типы задач на построения. | Интерактивная доска, проектор Печатные пособия | 2 неделя мая | ||||||||||||||
| 66 | Повторение по теме «Площадь» | 1ч | Словесные, наглядные, практические | Формулы площадей прямоугольника, квадрата, параллелограмма, треугольника, трапеции | Уметь решать задачи на вычисление площадей. | Интерактивная доска, проектор Печатные пособия | 2 неделя мая | ||||||||||||||
| 67 | Повторение по теме «Подобные треугольники» | 1ч | Словесные, наглядные, практические | Применение признаков подобия при решении задач | Уметь: доказывать подобия треугольников и находить элементы треугольника, используя признаки подобия. | Интерактивная доска, проектор Печатные пособия | 3 неделя мая | ||||||||||||||
| 68 | Повторение по теме «Окружность»
| 1ч | Словесные, наглядные, практические | Преобразование выражений, содержащих операцию извлечения квадратного корня | Уметь упрощать выражения, с помощью извлечения квадратного корня и освобождение от иррациональности в знаменателе. | Интерактивная доска, проектор Печатные пособия | 3 неделя мая | ||||||||||||||
| 69, 70 | Резервный урок | 2ч |
|
|
|
| 4 неделя мая | ||||||||||||||
|
| Итого: | 70ч |
|
|
|
|
| ||||||||||||||
Просмотр содержимого документа
«ктп 8класс»
6. Календарно – тематическое планирование.
| № п/п | Тема урока | Кол-во часов
| Формы и методы обучения | Основное содержание | Требование к уровню подготовки (знать/уметь) Критерии оценивания (см. поясн. записка | Оборудование, оснащение | Календарно - учебный график | |||||||
|
| Глава 1. Рациональные дроби (23 ч) | |||||||||||||
| 1-5 | Рациональные дроби и их свойства | 5ч | Словесные, наглядные, практические | Дробные выражения, рациональные выражения, рациональные выражения, рациональная дробь. Основное свойство дроби, тождество, сокращение дробей. | Знать рациональные, целые, дробные выражения; рациональная дробь. основное свойство дроби, термины «выражение», «тождественное преобразование», правило сокращение дробей. Уметь осуществлять в рациональных выражениях числовые подстановки и выполнять соответствующие вычисления , сокращать дробь. | Карточки: устный счет | 1,2 неделя сентября | |||||||
| 6-11 | Сумма и разность дробей. | 6ч | Словесные, наглядные, практические | Правила сложения и вычитания дробей с одинаковым знаменателем и с разными знаменателями | Знать правила сложения и вычитания дробей с одинаковым знаменателем и с разными знаменателями. Уметь выполнять сложение и вычитание дробей с одинаковыми знаменателями и с разными знаменателями. | Интерактивная доска, проектор Печатные пособия | 2,3,4 неделя сентября
| |||||||
| 12 | Контрольная работа № 1 по теме: «Рациональные выражения. Сложение и вычитание дробей». | 1ч | Самостоятельная работа |
| Уметь: применять изученный теоретический материал при выполнении письменной работы | Карточки с заданиями | 4 неделя сентября
| |||||||
| 13-22 | Произведение и частное дробей. | 10ч | Словесные, наглядные, практические
| Правило умножения рациональных дробей, правило возведения в степень рациональных дробей, правило деления рациональных дробей . | Знать правило умножения рациональных дробей, правило возведения в степень рациональных дробей, правило деления рациональных дробей Уметь применять правило умножения рациональных дробей, применять правило возведения в степень рациональных дробей правило деления рациональных дробей. | Интерактивная доска, проектор Печатные пособия | 5 неделя сентября 1-4 неделя октября
| |||||||
| 23 | Контрольная работа № 2 по теме: «Произведение и частное дробей». | 1ч | Самостоятельная работа |
| Уметь: применять изученный теоретический материал при выполнении письменной работы | Карточки с заданиями | 4 неделя октября | |||||||
| Глава 2. Квадратные корни (19 ч) | ||||||||||||||
| 24-25 | Действительные числа | 2ч | Словесные, наглядные, практические
| Рациональные числа, несократимая дробь Иррациональные числа. Действительные числа. | Знать какие числа называются рациональными, действительными их обозначение Уметь представлять рациональное число в виде десятичной дроби и наоборот, сравнивать действительные числа
| Интерактивная доска, проектор Печатные пособия | 4,5 неделя октября
| |||||||
| 26-30 | Арифметический квадратный корень. | 5ч | Словесные, наглядные, практические
| Квадратные корни. Арифметический квадратный корень Приближенные значения квадратного корня. Функция y= | Знать определения квадратного корня, арифметического квадратного корня , график функции y= Уметь выполнять преобразование числовых выражений, содержащих квадратные корни, находить приближенные значения квадратного корня. Строить график функции | Интерактивная доска, проектор Печатные пособия
| 5 неделя октября 2 неделя ноября | |||||||
| 31-33 | Свойства арифметического квадратного корня | 3ч | Словесные, наглядные, практические | Теоремы о квадратном корне из произведения и дроби. Теорема о квадратном корне из степени | Знать теоремы о квадратном корне из произведения и дроби Теорему о квадратном корне из степени Уметь находить квадратный корень из произведения и дроби Находить квадратный корень из степени. |
| 3 неделя ноября | |||||||
| 34 | Контрольная работа № 3 по теме: «Квадратные корни». | 1ч | Самостоятельная работа |
| Уметь: применять изученный теоретический материал при выполнении письменной работы | Карточки с заданиями | 4 неделя ноября | |||||||
| 35-41 | Применение свойств арифметического квадратного корня | 7ч | Словесные, наглядные, практические | Вынесение множителя из-под знака корня. Внесение множителя под знак корня. Преобразование выражений, содержащих квадратные корни
| Знать: свойства арифметического квадратного корня Уметь выносить множитель из-под знака корня; вносить множитель под знак корня выполнять преобразование выражений, содержащих квадратные корни , | Интерактивная доска, проектор | 4 неделя ноября 1,2 неделя декабря | |||||||
| 42 | Контрольная работа № 4 по теме: «Применение свойств арифметического квадратного корня» | 1ч | Самостоятельная работа |
| Уметь: применять изученный теоретический материал при выполнении письменной работы | Карточки с заданиями | 2 неделя декабря | |||||||
| Глава 3. Квадратные уравнения. (21 ч) | ||||||||||||||
| 43-52 | Квадратное уравнение и его корни | 10ч | Словесные, наглядные, практические | Неполные квадратные уравнения. Приведенное квадратное уравнение; формулы дискриминанта и корней квадратного уравнения. Решение задач с помощью квадратных уравнений
| Знать что такое квадратное уравнение; неполное квадратное уравнение определение приведённого квадратного уравнения; формулы дискриминанта и корней квадратного уравнения. Уметь решать неполные квадратные уравнения, решать квадратные уравнения выделением квадрата двучлена; решать квадратные уравнения по формуле; решать текстовые задачи с помощью квадратных уравнений
| Интерактивная доска, проектор Печатные пособия | 3,4 неделя декабря 3,4 неделя января | |||||||
| 53 | Контрольная работа № 5 по теме: «Квадратные уравнения». | 1ч | Самостоятельная работа |
| Уметь: применять изученный теоретический материал при выполнении письменной работы | Карточки с заданиями | 4 неделя января | |||||||
| 54-62 | Дробные рациональные уравнения | 9ч | Словесные, наглядные, практические | Определение дробных рациональных уравнений и способы их решения. Решение дробных рациональных уравнений и задач с помощью рациональных уравнений
| Знать определение дробных рациональных уравнений и способы их решения. Уметь решать дробно-рациональные уравнения; решать уравнения графическим способом; решать текстовые задачи с помощью рациональных уравнений | Интерактивная доска, проектор Печатные пособия | 4,5 неделя января 1,2 неделя февраля | |||||||
| 63 | Контрольная работа № 6 по теме: «Дробные рациональные уравнения» | 1ч | Самостоятельная работа |
| Уметь: применять изученный теоретический материал при выполнении письменной работы | Карточки с заданиями | 2 неделя февраля | |||||||
| Глава 4. Неравенства (20 ч) |
| |||||||||||||
| 64-71 | Числовые неравенства и их свойства | 8ч | Словесные, наглядные, практические | Числовые неравенства Свойства числовых неравенств. Теоремы о сложении и умножении неравенств. Абсолютная и относительная погрешности
| Знать определение числового неравенства с одной переменной; свойства числовых неравенств; теоремы о сложении и умножении неравенств; определения абсолютной и относительной погрешностей. Уметь доказывать неравенства; применять свойства числовых неравенствпри решении и оценивании неравенств; применять эти теоремы при оценке неравенств; применять погрешности при оценке качества измерений | Интерактивная доска, проектор Печатные пособия | 3,4 неделя февраля 1неделя марта | |||||||
| 72 | Контрольная работа № 7 по теме: «Числовые неравенства и их свойства». | 1ч | Самостоятельная работа |
| Уметь: применять изученный теоретический материал при выполнении письменной работы | Карточки с заданиями | 1 неделя марта | |||||||
| 73-82 | Неравенства с одной переменной и их системы. | 10ч | Словесные, наглядные, практические | Пересечение и объединение множеств. Числовые промежутки и их виды. Числовое неравенство с одной переменной, решение неравенств с одной переменной. Система неравенств с одной переменной, решение систем неравенств с одной переменной | Знать определения пересечение и объединение множеств; определение системы неравенств с одной переменной; что значит решить систему неравенств Уметь находить пересечение и объединение множеств записывать и читать числовые промежутки; изображать их на числовой прямой; решать линейные неравенства с одной переменной; решать системы неравенств с одной переменной | Интерактивная доска, проектор Печатные пособия | 2-4 неделя марта 2 неделя апреля | |||||||
| 83 | Контрольная работа № 8 по теме: «Неравенства с одной переменной и их системы». | 1ч | Самостоятельная работа
|
| Уметь: применять изученный теоретический материал при выполнении письменной работы | Карточки с заданиями | 2 неделя апреля | |||||||
| Глава 5. Степень с целым показателем. Элементы статистики. (11 ч) | ||||||||||||||
| 84-89 | Степень с целым показателем и её свойства | 6ч | Словесные, наглядные, практические. | Определение степени с целым отрицательным показателем; выражение вида 0n .Стандартный вид числа. | Знать определение степени с целым и целым отрицательным показателем. Уметь выполнять действия со степенями с натуральным и целым показателями используя свойства степеней; записывать числа в стандартном виде. | Интерактивная доска, проектор Печатные пособия | 3,4 неделя апреля | |||||||
| 90 | Контрольная работа №9 по теме «Степень с целым показателем». | 1ч | Самостоятельная работа |
| Уметь: применять изученный теоретический материал при выполнении письменной работы | Карточки с заданиями | 5 неделя апреля | |||||||
| 91-94 | Элементы статистики | 4 | Словесные, наглядные, практические | Частота, таблица частот, относительная частота, таблица относительных частот, интервальный ряд, выборочное исследование, генеральная совокупность, выборочная совокупность.
| Знать что такое: частота, таблица частот, относительная частота, таблица относительных частот, интервальный ряд; выборочное исследование, генеральная совокупность, выборочная совокупность. Уметь собирать и группировать статистические данные. Наглядно представлять статистические данные в виде столбчатых, круговых диаграмм, полигона, гистограмма |
| 5 неделя апреля
| |||||||
|
| Повторение. (8ч) | |||||||||||||
| 95-96 | Повторение. Рациональные дроби. | 2ч | Словесные, наглядные, практические | Преобразования рациональных выражений, используя все действия с алгебраическими дробями. | Уметь выполнять преобразования рациональных выражений, используя все действия с алгебраическими дробями. | Интерактивная доска, проектор | 1неделя мая | |||||||
| 97 | Повторение. Квадратные корни. | 1ч | Словесные, наглядные, практические | Преобразование выражений, содержащих операцию извлечения квадратного корня | Уметь упрощать выражения, с помощью извлечения квадратного корня и освобождение от иррациональности в знаменателе | Интерактивная доска, проектор | 1 неделя мая | |||||||
| 98-99 | Повторение. Квадратные уравнения | 2ч | Словесные, наглядные, практические. | Решение квадратных уравнений | Уметь решать неполное квадратное уравнение; используя дискриминант, решать квадратные уравнения по алгоритму; решать задачи на составление квадратных уравнений; решать рациональные уравнения, используя метод введения новой переменной; биквадратные уравнения; уравнения с применением нескольких способов упрощения выражений входящих в уравнение; | Интерактивная доска, проектор | 2 неделя мая | |||||||
| 100-101 | Повторение. Неравенства | 2ч | Словесные, наглядные, практические | Решение неравенств и систем неравенств с одной переменной | Уметь решать неравенства и системы неравенств с одной переменной | Интерактивная доска, проектор | 3 неделя мая | |||||||
| 102 | Итоговая контрольная работа. | 1ч | Самостоятельная работа |
| Уметь: применять изученный теоретический материал при выполнении письменной работы | Карточки с заданиями | 3 неделя мая | |||||||
| 103-105 | Резервный урок | 3ч |
|
|
|
| 4 неделя мая | |||||||
|
| Итого: | 105ч |
|
|
|
|
| |||||||
Просмотр содержимого документа
«пояснительная записка 8 класс алгебра»
Муниципальное бюджетное образовательное учреждение
«Новокулундинская средняя общеобразовательная школа»
Благовещенского района Алтайского края
| «Рассмотрено» естественно-математического цикла | «Согласовано» | «Утверждено» директор МБОУ НСОШ Сушков А.И./_____________ Приказ №____ от «__»____20__ г. |
РАБОЧАЯ ПРОГРАММА
АЛГЕБРА 8 КЛАСС
предмет, класс
Карачаровой Оксаны Александровны
Ф.И.О. учителя
на 2015 - 2016 учебный год
| Составлено на основе программы общеобразовательных учреждений. Алгебра 7 – 9 классы / Т.А.Бурмистрова. – М.: Просвещение, 2011.
|
п. Новокулундинка
2015 год
Содержание
Пояснительная записка.
Содержание программы.
Требования к математической подготовке учащихся.
Планирование учебного материала
Требование к оценке знаний и умений учащихся
Календарно – тематическое планирование
Лист дополнений и изменений.
Список учебников и учебных пособий.
Пояснительная записка
Рабочая программа разработана на основе Федерального компонента образовательного стандарта образовательной области «Математика». Рабочая программа составлена на основании следующих нормативно-правовых документов:
Закона Российской Федерации «Об образовании» (статья 7, 9, 32).
Федерального компонента государственного образовательного стандарта основного общего образования (МО РФ 05.03.2004 г. № 1089).
Федеральный базисный учебный план для среднего общего образования (МО №322 от 09.02.1998 г. и №1312 от 09.03.2004 г.)
Федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в образовательных учреждениях.
«Программа планирование учебного материала» алгебра 8 класс автора-составителя Бурмистровой Т.А. - М., «Просвещение», 2009-2011.
Программа авторского коллектива Ю.Н. Макарычева, Н.Г.Миндюк, К.И.Нешкова, С.Б.Суворовой, которая ориентирована на учащихся 8 классов.
Базисного учебного плана для среднего общего образования Положение о рабочей программе МБОУ «Новокулундинская СОШ» на 2015-2016 учебный год
Программа соответствует учебникам Макарычев Ю.Н., Миндюк Н.Г. Нешков К.И., Суворова С.Б. Алгебра. 8 класс. М. Просвещение. 2012г.
Согласно Федеральному учебному плану для образовательных учреждений Российской Федерации, учебному плану МБОУ «Новокулундинская СОШ» для обязательного изучения алгебре в 8 классе отводится 3 часа в неделю. Преподавание ведется по первому варианту «Программы общеобразовательных учреждений». Алгебра 8 класс. Автора-составителя Бурмистровой Т.А. (102 ч). В связи с наличием 35 учебных недель, программа включает резервные уроки (3 ч.), которые отводятся на повторение изученного материала за курс 8 класса (всего 105ч.)
Цели обучения математике.
Изучение алгебры в 8 классе направлено на достижение следующих целей:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Основные развивающие и воспитательные цели
Развитие:
Ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
Математической речи;
Сенсорной сферы; двигательной моторики;
Внимания; памяти;
Навыков само и взаимопроверки.
Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов.
Воспитание:
Культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;
Волевых качеств;
Коммуникабельности;
Ответственности.
Содержание программы
1. Рациональные дроби.
Рациональная дробь. Основное свойство дроби, сокращение дробей.
Тождественные преобразования рациональных выражений. Функция 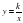 и ее график.
и ее график.
2. Квадратные корни.
Понятие об иррациональных числах. Общие сведения о действительных числах. Квадратный корень. Понятие о нахождении приближенного значения квадратного корня. Свойства квадратных корней. Преобразования выражений, содержащих квадратные корни. Функция 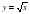 ее свойства и график.
ее свойства и график.
3. Квадратные уравнения.
Квадратное уравнение. Формула корней квадратного уравнения. Решение рациональных уравнений. Решение задач, приводящих к квадратным уравнениям и простейшим рациональным уравнениям.
4. Неравенства.
Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Погрешность и точность приближения. Линейные неравенства с одной переменной и их системы.
5. Степень с целым показателем. Элементы статистики.
Степень с целым показателем и ее свойства. Стандартный вид числа. Приближенный вычисления. Начальные представления об организации статистических исследований. Статистические характеристики: среднее арифметическое, мода, размах.
6. Повторение.
Требования к математической подготовке учащихся.
1. Рациональные дроби (23ч)
Рациональная дробь. Основное свойство дроби, сокращение дробей.
Тождественные преобразования рациональных выражений. Функция 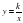 и ее график.
и ее график.
Основная цель – выработать умение выполнять тождественные преобразования рациональных выражений.
В результате изучения данной главы учащиеся должны:
Знать: понятия области определения и области допустимых значений; основное свойство дроби; алгоритм сложения и вычитания дробей с разными знаменателями; свойство (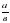 )n =
)n =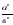 ; определение функции у=k/x.
; определение функции у=k/x.
Уметь: выделять целые и дробные выражения, определять область допустимых значений переменой; находить значения переменных, при которых значение рационального выражения равно 0; применять основное свойство дроби при сокращении рациональных дробей, при приведении рациональных дробей к новому знаменателю; выполнять преобразование суммы и разности дробей с одинаковыми знаменателями и противоположными знаменателями в дробь; находить алгебраическую сумму дробей с разными знаменателями; преобразовывать произведение рациональных дробей в дробь; выполнять возведение дроби в степень; строить график функции y= 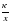 , «читать график»; выполнять тождественные преобразования рациональных выражений.
, «читать график»; выполнять тождественные преобразования рациональных выражений.
2. Квадратные корни (19ч)
Понятие об иррациональных числах. Общие сведения о действительных числах. Квадратный корень. Понятие о нахождении приближенного значения квадратного корня. Свойства квадратных корней. Преобразования выражений, содержащих квадратные корни. Функция 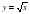 ее свойства и график.
ее свойства и график.
Основная цель – систематизировать сведения о рациональных числах и дать представление об иррациональных числах, расширив тем самым понятие о числе; выработать умение выполнять преобразования выражений, содержащих квадратные корни.
В результате изучения данной главы учащиеся должны:
Знать: понятие квадратного корня и арифметического квадратного корня; алгоритм решения уравнения х2=а; свойства функции у=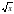 ; свойства квадратных корней из произведения и дроби; формулу
; свойства квадратных корней из произведения и дроби; формулу 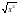 =│х│; понятия: вынесение множителя из-под знака корня и внесение множителя под знак корня.
=│х│; понятия: вынесение множителя из-под знака корня и внесение множителя под знак корня.
Уметь: представлять рациональные числа в виде десятичных дробей; пользоваться таблицей квадратов натуральных чисел для квадрата числа и вычисления арифметического квадратного корня из числа; микрокалькулятором , решать уравнения вида 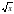 =а; решать уравнения вида х2=а; иметь навыки применения тождества (
=а; решать уравнения вида х2=а; иметь навыки применения тождества (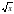 )2=х; строить график функции у=
)2=х; строить график функции у=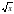 и применять свойства функции при решении задач; применять теоремы о квадратных корнях из произведения и дроби для вычисления значений квадратных корней; применять формулу
и применять свойства функции при решении задач; применять теоремы о квадратных корнях из произведения и дроби для вычисления значений квадратных корней; применять формулу 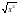 =│х│ для преобразования выражений, содержащих квадратные корни; выносить множитель из-под знака корня; вносить множитель под знак корня; освобождаться от иррациональности в знаменателе в выражениях вида
=│х│ для преобразования выражений, содержащих квадратные корни; выносить множитель из-под знака корня; вносить множитель под знак корня; освобождаться от иррациональности в знаменателе в выражениях вида 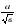 и
и 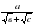 .
.
3. Квадратные уравнения (21ч)
Квадратное уравнение. Формула корней квадратного уравнения. Решение рациональных уравнений. Решение задач, приводящих к квадратным уравнениям и простейшим рациональным уравнениям.
Основная цель – выработать умения решать квадратные уравнения и простейшие рациональные уравнения и применять их к решению задач.
В результате изучения данной главы учащиеся должны:
Знать: понятие: неполное квадратное уравнение; приемы решения неполных квадратных уравнений; формулу корней квадратного уравнения; теорему Виета и формулу, обратную ей; алгоритм решения дробно-рациональных уравнений; графический способ решения уравнений.
Уметь: решать неполные квадратные уравнения; решать квадратные уравнения по формуле и по формуле с четным вторым коэффициентом; применять теорему Виета и обратную ей, находить p и q по х1 и х2; применять алгоритм при решении дробно-рациональных уравнений; применять дробные рациональные уравнения при решении задач; строить графики функций у=кх; у=кх+в; у=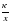 ; у=х2; у=х3; у=
; у=х2; у=х3; у= 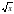 ; у=│х│ и с помощью этих граф решать уравнения.
; у=│х│ и с помощью этих граф решать уравнения.
4. Неравенства (20ч)
Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Погрешность и точность приближения. Линейные неравенства с одной переменной и их системы.
Основная цель – ознакомить учащихся с применением неравенств для оценки значений выражений, выработать умение решать линейные неравенства с одной переменной и их системы.
В результате изучения данной главы учащиеся должны:
Знать: определение понятий «больше» и «меньше»; свойства числовых неравенств; теоремы о почленном сложении и умножении числовых неравенств.
Уметь: применять «меньше» и «больше» к доказательству неравенств; применять свойства неравенств для оценки значений выражений; применять теоремы о почленном умножении и сложении к решению простейших задач на оценку по методу границ; решать простейшие неравенства вида ахв, ах
5. Степень с целым показателем. Элементы статистики (11ч)
Степень с целым показателем и ее свойства. Стандартный вид числа. Приближенный вычисления. Начальные представления об организации статистических исследований. Статистические характеристики: среднее арифметическое, мода, размах.
Основная цель – выработать умение применять свойства степени с целым показателем в вычислениях и преобразованиях.
В результате изучения данной главы учащиеся должны:
Знать: алгоритм вычисления степени с целым отрицательным показателем; свойства степени с целым показателем.
Уметь: вычислять степень с целым отрицательным показателем а-n=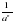 ; применять свойства степени с целым показателем в вычислениях и преобразованиях; представлять числа в стандартном виде и выполнять действия над числами, записанными в стандартном виде; интерпретировать результаты статистических исследований, широко представленных в средствах массовой информации.
; применять свойства степени с целым показателем в вычислениях и преобразованиях; представлять числа в стандартном виде и выполнять действия над числами, записанными в стандартном виде; интерпретировать результаты статистических исследований, широко представленных в средствах массовой информации.
6. Повторение (8ч)
Планирование учебного плана
| № п/п | Модуль (глава) | Примерное количество часов | Контрольные работы в течение года
|
| 1. | Рациональные дроби | 23ч | 2 |
| 2. | Квадратные корни | 19ч | 2 |
| 3. | Квадратные уравнения | 21ч | 2 |
| 4. | Неравенства | 20ч | 2 |
| 5. | Степень с целым показателем. Элементы статистики. | 11ч | 1 |
| 7. | Повторение. | 8ч | 1 |
| 8. | Резервные уроки | 3ч |
|
| - | Итого: | 105ч | 10 |
Требование к оценке знаний и умений учащихся
1.Оценка письменных контрольных работ обучающихся по математике.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится, если:
работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2.Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя
Отметка «1» ставится, если:
ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.
Общая классификация ошибок.
При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
3.1. Грубыми считаются ошибки:
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
неумение пользоваться первоисточниками, учебником и справочниками;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.
3.2. К негрубым ошибкам следует отнести:
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.
3.3. Недочетами являются:
нерациональные приемы вычислений и преобразований;
небрежное выполнение записей, чертежей, схем, графиков.
Список учебников и учебных пособий.
1. Учебник Алгебра 8. / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Пешков, С.В. Суворова. Под редакцией С.А. Теляковского. / М.: Просвещение, 2010.
2. Рабочая тетрадь по алгебре./ Н.Г. Миндюк, И.С. Шыков /- М.: Просвещение ,2014.
Литература для учителя
Федеральный базисный учебный план для образовательных учреждений Российской Федерации, реализующих программы общего образования.
Примерная программа общеобразовательных учреждений. Алгебра 7-9 кл./ Составитель: Т.А.Бурмистрова .- М.: Просвещение, 2011г.
Б.Г.Зив, В.М. Мейлер. Дидактические материалы.- М.: Просвещение ,2014.
Жохов В.И. Уроки алгебры в 8 классе.- М.: Просвещение. 2009г.
Миндюк Н.Г Методические рекомендации. – М.: Просвещение. 2014г.
Дудницын Ю.П., Кронгаус В.Л. Тематические тесты.- М.: Просвещение.2014г.
М.А. Иченская. Самостоятельные и контрольные работы.- М.: Просвещение ,2014
Изучение алгебры в 7-9классах./ Ю.Н. Макарычев, Н.Г. Миндюк, , С.В. Суворова. И.С. Шлыкова/Просвещение, 2011
Просмотр содержимого документа
«пояснительная записка 8 класс геометрия»
Муниципальное бюджетное образовательное учреждение
«Новокулундинская средняя общеобразовательная школа»
Благовещенского района Алтайского края
| «Рассмотрено» естественно-математического цикла | «Согласовано» | «Утверждено» директор МБОУ НСОШ Сушков А.И./_____________ Приказ №____ от «__»____20__ г. |
РАБОЧАЯ ПРОГРАММА
ГЕОМЕТРИЯ 8 КЛАСС
предмет, класс
Карачаровой Оксаны Александровны
Ф.И.О. учителя
на 2015 - 2016 учебный год
| Составлено на основе программы общеобразовательных учреждений. Геометрия 7 – 9 классы / Т.А.Бурмистрова. – М.: Просвещение, 2011.
|
п. Новокулундинка
2015 год
Содержание
Пояснительная записка.
Содержание программы.
Требования к математической подготовке учащихся.
Планирование учебного материала
Требование к оценке знаний и умений учащихся
Календарно – тематическое планирование
Лист дополнений и изменений.
Список учебников и учебных пособий.
Пояснительная записка
Рабочая программа разработана на основе Федерального компонента образовательного стандарта образовательной области «Математика». Рабочая программа составлена на основании следующих нормативно-правовых документов:
Закона Российской Федерации «Об образовании» (статья 7, 9, 32).
Федерального компонента государственного образовательного стандарта основного общего образования (МО РФ 05.03.2004 г. № 1089).
Федеральный базисный учебный план для среднего общего образования (МО №322 от 09.02.1998 г. и №1312 от 09.03.2004 г.)
Федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в образовательных учреждениях.
«Программа планирование учебного материала» геометрия 8 класс автора-составителя Бурмистровой Т.А. - М., «Просвещение», 2009-2011.
Программа авторского коллектива Ю.Н. Макарычева, Н.Г.Миндюк, К.И.Нешкова, С.Б.Суворовой, которая ориентирована на учащихся 8 классов.
Базисного учебного плана для среднего общего образования Положение о рабочей программе МБОУ «НовокулундинскаяСОШ» на 2015-2016 учебный год
Программа соответствует учебникам «Геометрия» для 7-9 классов образовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.– М., «Просвещение», 2007 -2011 гг.
Согласно Федеральному учебному плану для образовательных учреждений Российской Федерации, учебному плану МБОУ «Новокулундинская СОШ» для обязательного изучения геометрии в 8 классе отводится 2 часа в неделю Преподавание ведется по первому варианту «Программы общеобразовательных учреждений». Геометрия 7-9 классы. Автора-составителя Бурмистровой Т.А. (68 ч)В связи с наличием 35 учебных недель, программа включает резервные уроки (2 ч.), которые отводятся на повторение изученного материала за курс 8 класса.(всего 70 ч.)
Цели обучения математике.
Изучение геометрии в 8 классе направлено на достижение следующих целей:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Основные развивающие и воспитательные цели
Развитие:
Ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
Математической речи;
Сенсорной сферы; двигательной моторики;
Внимания; памяти;
Навыков само и взаимопроверки.
Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов.
Воспитание:
Культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;
Волевых качеств;
Коммуникабельности;
Ответственности.
Содержание программы
.
1. Четырёхугольники.
Многоугольники. Выпуклые многоугольники. Сумма углов выпуклого многоугольника. Параллелограмм, его свойства и признаки. Прямоугольник, квадрат, ромб, их свойства и признаки. Трапеция, средняя линия трапеции; равнобедренная трапеция. Осевая и центральная симметрии.
2. Площади фигур.
Понятие о площади плоских фигур. Равносоставленные и равновеликие фигуры.
Площадь прямоугольника. Площадь параллелограмма, треугольника и трапеции (основные формулы). Формулы, выражающие площадь треугольника: через две стороны и угол между ними, через периметр и радиус вписанной окружности, формула Герона. Площадь четырехугольника. Теорема Пифагора
3. Подобные треугольники.
Теорема Фалеса. Подобие треугольников; коэффициент подобия. Признаки подобия треугольников.
4. Окружность.
Центр, радиус, диаметр. Дуга, хорда.. Центральный, вписанный угол; величина вписанного угла. Взаимное расположение прямой и окружности, двух окружностей. Касательная и секущая к окружности; равенство касательных, проведенных из одной точки. Метрические соотношения в окружности: свойства секущих, касательных, хорд.
Замечательные точки треугольника: точки пересечения серединных перпендикуляров, биссектрис, медиан. Окружность Эйлера.
Окружность, вписанная в треугольник, и окружность, описанная около треугольника.
5 .Итоговое повторение курса 8 класса
Требования к математической подготовке учащихся.
1. Четырёхугольники (14ч)
Многоугольники. Выпуклые многоугольники. Сумма углов выпуклого многоугольника. Параллелограмм, его свойства и признаки. Прямоугольник, квадрат, ромб, их свойства и признаки. Трапеция, средняя линия трапеции; равнобедренная трапеция. Осевая и центральная симметрии.
В результате изучения данной главы учащиеся должны:
Знать: определения рассматриваемых четырехугольников; формулировки и доказательства теорем, выражающих признаки и свойства этих четырехугольников; определения симметричных точек и фигур относительно прямой и точки.
Уметь: распознавать на рисунке и по определению четырехугольники; применять признаки в решении задач; строить симметричные точки и распознавать фигуры, обладающие осевой и центральной симметрией
2. Площади фигур (14ч)
Понятие о площади плоских фигур. Равносоставленные и равновеликие фигуры.
Площадь прямоугольника. Площадь параллелограмма, треугольника и трапеции (основные формулы). Формулы, выражающие площадь треугольника: через две стороны и угол между ними, через периметр и радиус вписанной окружности, формула Герона. Площадь четырехугольника. Теорема Пифагора
В результате изучения данной главы учащиеся должны:
Знать: основные свойства площади, формулы площади прямоугольника, параллелограмма, треугольника, трапеции; формулировки теоремы Пифагора и обратной к ней теоремы;
Уметь: применять их в решении задач.
3. Подобные треугольники (19ч)
Теорема Фалеса. Подобие треугольников; коэффициент подобия. Признаки подобия треугольников.
В результате изучения данной главы учащиеся должны:
Знать: определения пропорциональных отрезков, подобных треугольников, формулировки и доказательства теорем, выражающих признаки и свойства подобных треугольников; определения синуса, косинуса, тангенса острого угла прямоугольного треугольника;
Уметь: воспроизводить доказательства признаков подобия треугольников, доказывать основное тригонометрическое тождество, применять их в решении задач.
4. Окружность (17ч)
Центр, радиус, диаметр. Дуга, хорда. Центральный, вписанный угол; величина вписанного угла. Взаимное расположение прямой и окружности, двух окружностей. Касательная и секущая к окружности; равенство касательных, проведенных из одной точки. Метрические соотношения в окружности: свойства секущих, касательных, хорд.
Замечательные точки треугольника: точки пересечения серединных перпендикуляров, биссектрис, медиан. Окружность Эйлера.
Окружность, вписанная в треугольник, и окружность, описанная около треугольника.
В результате изучения данной главы учащиеся должны:
Знать: случаи расположения прямой и окружности; определение, свойство и признак касательной; определения центрального, вписанного углов, теорему о вписанном угле и следствия из нее; какая окружность называется вписанной, описанной, теоремы о свойствах окружностей.
Уметь: доказывать и применять их в решении задач.
5. Повторение. Решение задач (4ч).
Планирование учебного плана
| № п/п | Модуль (глава) | Примерное количество часов | Контрольные работы в течение года
|
| 1. | Четырехугольники | 14ч | 1 |
| 2. | Площадь | 14ч | 1 |
| 3. | Подобные треугольники | 19ч | 2 |
| 4. | Окружность | 17ч | 1 |
| 5. | Повторение. | 4ч | 1 |
| 6. | Резервные уроки | 2ч |
|
|
| Итого: | 70ч | 5 |
Требование к оценке знаний и умений учащихся
1.Оценка письменных контрольных работ обучающихся по математике.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится, если:
работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2.Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя
Отметка «1» ставится, если:
ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.
Общая классификация ошибок.
При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
3.1. Грубыми считаются ошибки:
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
неумение пользоваться первоисточниками, учебником и справочниками;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.
3.2. К негрубым ошибкам следует отнести:
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.
3.3. Недочетами являются:
нерациональные приемы вычислений и преобразований;
небрежное выполнение записей, чертежей, схем, графиков.
Список учебников и учебных пособий.
Геометрия 7 – 9. Учебник для общеобразовательных учреждений. / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г.Позняк, И.И. Юдина. / М.: Просвещение, 2007 (и последующие издания) – 384 с.:ил.
Рабочая тетрадь по геометрии./С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г.Позняк, И.И. Юдина. / М.: Просвещение,
.
Литература для учителя
Федеральный базисный учебный план для образовательных учреждений Российской Федерации, реализующих программы общего образования.
Примерная программа общеобразовательных учреждений. Геометрия 7-9 кл./ Составитель: Т.А.Бурмистрова .- М.: Просвещение, 2011г.
Б.Г. Зив, В.М. Мейлер, А.П. Баханский. Задачи по геометрии для 7 – 11 классов. – М.: Просвещение, 2003.
С.М. Саакян, В.Ф. Бутузов. Изучение геометрии в 7-9 классах: Методические рекомендации к учебнику. Книга для учителя. – М.: Просвещение, 2001.
Б.Г.Зив, В.М. Мейлер. Дидактические материалы.- М.: Просвещение ,2014.
Миндюк Н.Г Методические рекомендации. – М.: Просвещение. 2014г.
М.А. Иченская. Самостоятельные и контрольные работы.- М.: Просвещение ,2014.




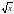 и её график
и её график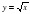 и находить значения этой функции по графику или по формуле
и находить значения этой функции по графику или по формуле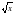 и её график
и её график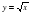 и находить значения этой функции по графику или по формуле
и находить значения этой функции по графику или по формуле









