СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Обо мне Блог Файлы Тесты Галерея Активность Награды

Рабочая программа по геометрии 7-9 класс к УМК Смирнова И.М., Смирнов В.А

Категория: Математика

Нажмите, чтобы узнать подробности

рабочая программа по геометрии 7-9 классов составлена с учетом требований ФГОС к УМК Смирнова И.М., Смирнов В.А не содержит календарно-тематическое планирование .     Рабочая программа основного общего образования по геометрии составлена на основе Фундаментального ядра содержания образования и Требований к результатам освоения основной образовательной программы основного общего образования, представленных в Федеральном государственном образовательном стандарте общего образования. В ней также учитываются основные идеи и положения программы развития и формирования универсальных учебных действий для основного общего образования, программа по геометрии для 7-9 классов  Смирнова И.М., Смирнов В.А.Смирнова И.М., Смирнов В.А. Геометрия. 7-9 кл.: учебн. для общеобразовательных учреждений. – М.: Мнемозина

Просмотр содержимого документа
«геометрия 7-9 Смрнов»



И.М. СМИРНОВА, В.А. СМИРНОВ















Г Е О М Е Т Р И Я


7-9 КЛАССЫ


ПРОГРАММА И ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ










Москва

2012

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Данная программа и тематическое планирование составлены на основе Федерального государственного образовательного стандарта второго поколения, Примерной программы основного общего образования, Примерной программы среднего (полного) общего образования и предназначены для работы по учебнику, рекомендованному к использованию Министерством образования и науки РФ и входящему в Федеральный перечень учебной литературы:

Смирнова И.М., Смирнов В.А. Геометрия. 7-9 кл.: учебн. для общеобразовательных учреждений. – М.: Мнемозина.

Известно, какую большую роль играет геометрия в науке и образовании. На протяжении всей истории человечества она служила источником развития не только математики, но и многих других наук. Именно в ней появились первые теоремы и доказательства. Сами законы математического мышления формировались с помощью геометрии.

Многие геометрические задачи способствовали появлению новых научных направлений. Наоборот, решение многих научных проблем получено с использованием геометрических методов.

Вообще современная наука и её приложения немыслимы без геометрии и её разделов, таких как топология, теория графов, дифференциальная геометрия, алгебраическая геометрия, компьютерная геометрия и др.

Появление компьютеров не только не снижает, но и увеличивает роль и значение геометрического образования школьников, поскольку при этом существенно расширяются возможности графического представления материала и компьютерного моделирования.

Мы исходим из того, что геометрия это элемент общей культуры человека, который вносит неоценимый вклад в развитие мышления, воображения, исследовательских способностей.

Об этом говорили и говорят многие видные учёные-математики. Например, Н.Ф. Четверухин подчеркивал важность развития пространственных представлений для всех учащихся вне зависимости от направления их дальнейшего образования и выбора будущей профессии. «Хорошее пространственное воображение нужно конструктору, создающему новые машины, геологу, разведывающему недра земли, архитектору, сооружающему здания современных городов, хирургу, производящему тончайшие операции среди кровеносных сосудов и нервных волокон, скульптору, художнику и т. д.».

А.Д. Александров, говоря о целях преподавания геометрии, указывал, что «особенность геометрии, выделяющая её среди других наук вообще, состоит в том, что в ней самая строгая логика соединена с наглядным представлением. Геометрия в своей сущности и есть такое соединение живого воображения и строгой логики, в котором они взаимодействуют и дополняют друг друга». В соответствии с этим он делал вывод о том, что преподавание геометрии в школе должно включать в себя три тесно связанные, но вместе с тем и противоположныё элементы: логику, наглядное представление и применение к реальным вещам. Задача геометрии заключается в развитии у учащихся трёх соответствующих качеств: логического мышления, пространственного воображения и практического понимания.

В.Г. Болтянский в статье «Математическая культура и эстетика» говорил о том, что природа геометрии предоставляет богатые возможности для воспитания у школьников эстетического чувства красоты в самом широком значении этого слова. Красота геометрии заключается в её проявлениях в живой природе, архитектуре, живописи, декоративно-прикладном искусстве, строительстве и т. д., а также в смелых, оригинальных, нестандартных доказательствах, выводах и решениях.

Обучение геометрии по предлагаемой программе направлено на достижение следующих целей:

1) в направлении личностного развития:

– формирование представлений о геометрии как части общечеловеческой культуры, о значимости геометрии в развитии цивилизации и современного общества;

– развитие геометрических представлений, логического мышления, культуры речи, способности к умственному эксперименту;

– формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;

– воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;

– формирование качеств мышления, необходимых для адаптации в современном информационном обществе;

  • развитие интереса к математике;

  • развитие математических способностей;

2) в метапредметном направлении:

– развитие представлений о геометрии как форме описания и методе познания действительности, создание условий для приобретения опыта математического моделирования;

– формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;

3) в предметном направлении:

– овладение геометрическими знаниями и умениями, необходимыми для продолжения образования, изучения смежных дисциплин, применения в повседневной жизни;

– создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.

Задача, которую ставили перед собой авторы предлагаемой программы по геометрии для 7-9 классов, состояла в том, чтобы, опираясь на достигнутый отечественной школой уровень геометрического образования, сделать геометрию современным и интересным предметом, учитывающим склонности и способности учеников, направленным на формирование математической культуры, интеллектуальное развитие личности каждого ученика, его творческих способностей, формирование представлений учащихся о математике, её месте и роли в современном мире.

В седьмом классе изучаются основные геометрические фигуры и их свойства; рассматривается взаимное расположение точек и прямых на плоскости; вводятся понятия равенства отрезков и углов; доказываются признаки равенства треугольников; свойства равнобедренного треугольника; выясняются соотношения между сторонами и углами треугольника, между перпендикуляром и наклонной; исследуются случаи взаимного расположения двух окружностей, прямой и окружности; рассматриваются основные геометрические места точек и решаются задачи на построение.

Восьмой класс начинается с изучения понятия параллельности. Доказываются: теоремы о сумме углов треугольника и выпуклого многоугольника; признаки параллелограмма; теоремы о средних линиях треугольника и трапеции; теорема Фалеса; вводится понятие движения и рассматриваются различные виды движений (центральная симметрия, поворот, осевая симметрия, параллельный перенос); определяется понятие равенства фигур и устанавливаются его свойства; вводится понятие подобия и доказываются признаки подобия треугольников; доказывается теорема Пифагора; изучаются тригонометрические функции угла; доказываются теоремы синусов и косинусов.

В девятом классе изучается вопрос об измерении площадей. В частности, выводятся формулы площади прямоугольника, параллелограмма, треугольника, трапеции, правильного многоугольника, круга. Рассматривается прямоугольная система координат, векторы и их свойства, аналитическое задание фигур на плоскости.

В конце 9-го класса изучаются начала стереометрии. Здесь не ста­вится цель доказывать теоремы стереометрии и дублировать тем самым соответствующий курс для старших классов. Целью изучения этого раздела является, с одной стороны, повторение, систематизация и обобщение зна­ний по планиметрии, распространение изученных понятий и свойств на случай пространства, а с другой стороны, пропедевтика стереометрии, развитие пространственных представлений учащихся. В частности, здесь рассматриваются: понятие параллельности в пространстве; основные пространственные фигуры; многогранники, в том числе правильные, полуправильные и звёздчатые; кристаллы – природные многогранники. Вводится понятие ориентируемой и неориентируемой поверхностей. В качестве примера неориентируемой поверхности приводится лист Мёбиуса.

Опыт работы школы показывает, что учащиеся живо интересуются современными и прикладными аспектами математики. Этому, в частности, во многом способствует развитие средств массовой информации, появление большого количества научно-популярной литературы, электронных ресурсов и т. п. Желание узнать о новых иде­ях, направлениях развития математики вполне естественное желание для молодого человека, и это необходимо выпускнику школы для ори­ентации в современном мире, правильному представлению о про­цессах, происходящих в природе и обществе, осознания собственной роли в движении общества вперёд.

В учебниках соответствующий материал относится к необязательному и помечен звёздочкой.

Для того чтобы познакомить учащихся с современным состоянием развития геометрии, вовсе необязательно вводить элементы высшей геометрии в курс основной школы. Для этого мы включаем в содержание курса геометрии следующие элементы:

а) знакомство с жизнью и творчеством известных современных ученых-геометров;

б) работа с научно-популярной литературой;

в) решение современных прикладных задач;

г) использование современных компьютерных технологий.

Так, в конце седьмого класса после изучения темы «Геометрические места точек» в качестве дополнительного материала предлагается рассмотреть кривые как геометрические места точек. Среди таких кривых: парабола, эллипс, гипербола.

Например, парабола является геометрическим местом точек, равноудалённых от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Вопрос о нахождении такого геометрического места точек возникает естественным образом после нахождения геометрического места точек, равноудалённых от двух заданных точек (серединный перпендикуляр) и геометрического места внутренних точек угла, равноудалённых от его сторон (биссектриса угла).

Эллипс является геометрическим местом точек, сумма расстояний от которых до двух заданных точек, называемых фокусами, есть величина постоянная. Если фокусы приближаются друг к другу, сливаясь в одну точку, то эллипс превращается в окружность.

Кроме кривых, в конце седьмого класса в качестве дополнительного материала в учебник включены графы и их применение, в том числе: уникурсальные графы, задача Эйлера о кёнигсбергских мостах, задача о трёх домиках и трёх колодцах, теорема Эйлера о числе вершин, рёбер и граней сетки из многоугольников, проблема четырёх красок и др.

Изучение данного материала значительно повышает интерес учащихся к геометрии, способствует формированию комбинаторных геометрических представлений и развитию их мышления.

В качестве дополнительного материала в восьмом классе рассматривается золотое сечение и его использование в живописи, скульптуре, архитектуре; паркеты; кривые как траектории движения точек, среди которых: циклоида – траектория движения точки, закреплённой на окружности, катящейся по прямой; кардиоида – траектория движения точки, закреплённой на окружности, катящейся по другой окружности того же радиуса; астроида – траектория движения точки, закреплённой на окружности, катящейся с внутренней стороны другой окружности в четыре раза большего радиуса.

В качестве дополнительного материала в девятом классе, после изучения понятия площади, рассматривается изопериметрическая задача (задача Дидоны) о нахождении замкнутой кривой заданной длины, охватывающей наибольшую площадь, изучается понятие равносоставленности и предлагаются задачи на разрезание. Кроме того, в теме «Координаты и векторы» рассматриваются полярные координаты, кривые, заданные уравнениями в декартовых и полярных координатах, в том числе: спираль Архимеда, золотая спираль, n-лепестковые розы и др., предлагаются задачи оптимального управления.

Включение в учебники разнообразного материала, учитывающего интересы каждого ученика, повышает желание учащихся заниматься геометрией. Опираясь на этот интерес и желание, можно преодолеть и известные трудности обучения.


ПРОГРАММА ПО ГЕОМЕТРИИ ДЛЯ 7-9 КЛАССОВ

Смирнова И.М., Смирнов В.А. Геометрия. 7-9 кл.: учебн. для общеобразовательных учреждений. – М.: Мнемозина.

Вариант I программы – 2 часа в неделю, всего 68 часов за год.

Вариант II программы составлен с учётом дополнительного материала, 2 часа в неделю, всего 68 часов за год.

Вариант III программы составлен для классов с углублённым изучением математики, 3 часа в неделю, всего 102 часа за год.

7 КЛАСС


Параграф учебника

Содержание

Количество часов

I

II

III


1

2

3

4

5

6


7

8

9

10

11


12


13


14

15


16

17


18


19

20


21*

22*

23*

24*

25*

26*

Вводная беседа

Основные геометрические фигуры

Отрезок и луч

Измерение длин отрезков

Полуплоскость и угол

Измерение величин углов

Ломаные и многоугольники

Контрольная работа № 1

Треугольники

Первый признак равенства треугольников

Второй признак равенства треугольников

Равнобедренные треугольники

Третий признак равенства треугольников

Контрольная работа № 2

Соотношения между сторонами и углами треугольника

Соотношения между сторонами треугольника

Прямоугольные треугольники

Перпендикуляр и наклонная

Контрольная работа № 3

Окружность и круг

Взаимное расположение прямой и окружности

Взаимное расположение двух окружностей

Контрольная работа № 4

Геометрические места точек

Задачи на построение

Контрольная работа № 5

Парабола

Эллипс

Гипербола

Графы

Теорема Эйлера

Проблема четырёх красок

Контрольная работа № 6

Итоговое повторение

1

2

3

2

4

4

3

1

2

3

3

3

3

1


3

3


2

2

1

2

3


3

1

3

3

1

-

-

-

-

-

-

-

6

1

2

2

2

2

3

3

1

2

2

2

2

2

1


2

2


2

2

1

2

3


3

1

3

3

1

2

2

2

2

2

2

1

3

2

3

3

3

4

4

3

2

3

3

3

3

3

2


3

3


3

3

2

3

3


3

2

4

4

2

3

3

3

3

3

3

2

6


8 КЛАСС


Параграф учебника

Содержание

Количество часов

I

II

III

27

28


29

30

31

32

33

34


35

36

37


38


39

40

41

42

43

44*


45


46


47

48*

49


50

51

52

53

54

55

56*

Параллельные прямые

Сумма углов многоугольника

Контрольная работа № 1

Параллелограмм

Признаки параллелограмма

Прямоугольник, ромб, квадрат

Средняя линия треугольника

Трапеция

Теорема Фалеса

Контрольная работа № 2

Углы, связанные с окружностью

Многоугольники, вписанные в окружность

Многоугольники, описанные около окружности

Замечательные точки в треугольнике

Контрольная работа № 3

Центральная симметрия

Поворот. Симметрия n-го порядка

Осевая симметрия

Параллельный перенос

Движение. Равенство фигур

Паркеты

Контрольная работа № 4

Подобие треугольников. Первый признак подобия треугольников

Второй и третий признаки подобия треугольников

Подобие фигур. Гомотетия

Золотое сечение

Теорема Пифагора

Контрольная работа № 5

Тригонометрические функции острого угла

Тригонометрические тождества

Тригонометричские функции тупого угла

Теорема косинусов

Теорема синусов

Длина окружности

Циклоидальные кривые

Контрольная работа № 6

Итоговое повторение

3

2

1

2

2

3

2

3

2

1

2

2

2


2

1

2

2

2

2

2

-

1

2


3


2

-

2

1

2

2

2

2

2

2

-

1

4

2

2

1

2

2

2

2

2

2

1

2

2

2


2

1

2

2

2

2

2

2

1

2


2


2

2

2

1

2

2

2

2

2

2

2

1

2

3

3

2

3

3

3

3

3

3

2

3

3

3


3

2

3

3

3

3

3

3

2

3


3


2

3

3

2

2

2

2

3

3

2

3

2

5



9 КЛАСС


Параграф учебника

Содержание

Количество часов

I

II

III

57


58

59

60


61

62

63

64*

65*


66

67



68

69

70

71


72

73*

74*

75


76*


77-90

Измерение площадей. Площадь прямоугольника

Площадь параллелограмма

Площадь треугольника

Площадь трапеции

Контрольная работа № 1

Площадь многоугольника

Площадь круга и его частей

Площади подобных фигур

Изопериметрическая задача

Равносоставленность и задачи на разрезание

Контрольная работа № 2

Прямоугольная система координат

Расстояние между точками. Уравнение окружности

Контрольная работа № 3

Векторы. Сложение векторов

Умножение вектора на число

Координаты вектора

Скалярное произведение векторов

Контрольная работа № 4

Уравнение прямой

Аналитическое задание фигур на плоскости

Задачи оптимизации

Тригонометрические функции произвольного угла

Полярные координаты

Контрольная работа № 5

Начала стереометрии

Контрольная работа № 6

Итоговое повторение

3


3

3

3

1

3

3

2

-

-

1

2

2


1

2

2

2

2

1

2

-

-

2


-

1

16

1

10

2


2

2

2

1

2

2

2

2

2

1

2

2


1

2

2

2

2

1

2

2

2

2


2

1

15

1

7

3


3

3

3

2

3

3

3

3

3

2

3

3


2

3

3

3

3

2

3

3

3

3


3

2

18

2

12



СОДЕРЖАНИЕ КУРСА ГЕОМЕТРИИ ДЛЯ 7-9 КЛАССОВ


1. Начала геометрии

История возникновения и развития геометрии. Основные геометрические фигуры и их свойства. Взаимное расположение точек на прямой.

Отрезок и луч. Равенство отрезков. Операции сложения и вычитания отрезков, умножения и деления отрезка на натуральное число. Измерение длины отрезка. Исторические сведения об измерении длин.

Полуплоскость и угол. Виды углов: прямой угол, острые и тупые углы, развёрнутый угол, смежные и вертикальные углы. Равенство углов. Биссектриса угла. Операции сложения и вычитания углов, умножения и деления угла на натуральное число. Теорема о равенстве вертикальных углов. Перпендикулярные прямые. Измерение величин углов. Исторические сведения об измерении углов.

Ломаные. Виды ломаных. Длина ломаной. Многоугольники. Элементы многоугольника. Периметр многоугольника. Выпуклые и невыпуклые многоугольники. Правильные многоугольники.

2. Треугольники

Треугольники. Виды треугольников: остроугольные, прямоугольные, тупоугольные, равнобедренные, равносторонние. Медиана, биссектриса и высота треугольника.

Равенство треугольников. Первый и второй признаки равенства треугольников. Равнобедренные треугольники и их свойства. Признак равнобедренного треугольника. Третий признак равенства треугольников.

Соотношения между сторонами и углами треугольника. Соотношения между сторонами треугольника.

Прямоугольные треугольники. Признаки равенства прямоугольных треугольников. Перпендикуляр и наклонная и их свойства.

3. Окружность и геометрические места точек

Понятия окружности и круга. Элементы окружности и круга: центр, радиус, диаметр, хорда. Взаимное расположение прямой и окружности. Касательная и секущая к окружности. Взаимное расположение двух окружностей.

Понятие о геометрическом месте точек. Примеры геометрических мест точек на плоскости. Построения с помощью циркуля и линейки. Примеры задач на построение.

4*. Кривые и графы

Парабола и её свойства. Касательная к параболе. Построение параболы и касательных к ней.

Эллипс и его свойства. Касательная к эллипсу. Построение эллипса и касательных к нему.

Гипербола и её свойства. Касательная к гиперболе. Построение гиперболы и касательных к ней.

Графы и их элементы: вершины, рёбра.

Задачи, приводящие к понятию графа. Задача Эйлера о кёнигсбергских мостах.

Уникурсальные графы и их свойства. Теорема Эйлера о числе вершин, рёбер и граней плоского графа.

Задача о трех домиках и трех колодцах. Проблема четырёх красок.

5. Параллельность

Параллельные прямые. Признаки параллельных прямых. Аксиома параллельных прямых. Свойства параллельных прямых. Исторические сведения.

Сумма углов треугольника. Сумма углов выпуклого n-угольника.

Параллелограмм. Прямоугольник. Ромб. Квадрат. Их свойства. Признаки параллелограмма.

Средняя линия треугольника. Трапеция. Равнобедренная и прямоугольная трапеции. Средняя линия трапеции. Теорема Фалеса.

6. Многоугольники и окружность

Углы, связанные с окружностью. Многоугольники, вписанные в окружность. Многоугольники, описанные около окружности. Вписанные и описанные окружности правильного многоугольника. Замечательные точки треугольника.

7. Движение

Понятие движения и его свойства. Центральная симметрия. Центрально-симметричные фигуры. Поворот. Симметрия n-го порядка. Осевая симметрия. Фигуры, симметричные относительно некоторой оси. Параллельный перенос. Равенство фигур.

8. Подобие

Подобие треугольников. Признаки подобия треугольников. Подобие фигур. Гомотетия. *Золотое сечение. Теорема Пифагора.

9. Элементы тригонометрии

Тригонометрические функции острого угла прямоугольного треугольника: синус, косинус, тангенс, котангенс.

Тригонометрические тождества. Тригонометрические функции тупого угла. Теорема косинусов. Теорема синусов. Длина окружности. Число . Длина дуги окружности. *Циклоидальные кривые.

10. Площадь

Понятие площади плоской фигуры. Измерение площадей. Равновеликие и равносоставленные фигуры.

Площадь прямоугольника. Площади параллелограмма, треугольника, трапеции. Формула Герона.

Площадь многоугольника. Площадь правильного многоугольника. Площади круга, сектора и сегмента.

Соотношение между площадями подобных фигур. *Изопериметрическая задача. *Задачи на разрезание.

11. Координаты и векторы

Прямоугольная система координат. Исторические сведения. Кординаты середины отрезка. Расстояние между точками. Уравнение окружности.

Векторы. Сложение векторов. Умножение вектора на число. Координаты вектора. Скалярное произведение векторов.

Уравнение прямой. *Аналитическое задание фигур на плоскости. *Задачи оптимизации.

Тригонометрические функции произвольного угла. *Полярные координаты.

12. Начала стереометрии

Основные понятия стереометрии. Фигуры в пространстве. Многогранники, их элементы. Примеры многогранников.

Угол в пространстве. Взаимное расположение прямых и плоскостей в пространстве. Параллельность в пространстве.

Сфера и шар. Их основные элементы.

Выпуклые многогранники. Теорема Эйлера для выпуклых многогранников.

Правильные, полуправильные, звёздчатые многогранники. Моделирование многогранников. Кристаллы – природные многогранники. Исторические сведения.

Ориентация плоскости. Лист Мёбиуса.

Площадь поверхности и объём.

ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ

7 КЛАСС

Вариант I (2 ч в неделю, всего 68 ч)


Основное содержание по темам

Характеристика основных видов деятельности ученика

(на уровне учебных действий)

1. Начала геометрии (20 ч)

История возникновения и развития геометрии. Основные геометрические фигуры и их свойства. Взаимное расположение точек на прямой.

Отрезок и луч. Равенство отрезков. Операции сложения и вычитания отрезков, умножения и деления отрезка на натуральное число. Измерение длины отрезка. Исторические сведения об измерении длин.

Полуплоскость и угол. Виды углов: прямой угол, острые и тупые углы, развёрнутый угол, смежные и вертикальные углы. Равенство углов. Биссектриса угла. Операции сложения и вычитания углов, умножения и деления угла на натуральное число. Теорема о равенстве вертикальных углов. Перпендикулярные прямые. Измерение величин углов. Исторические сведения об измерении углов.

Ломаные. Виды ломаных. Длина ломаной. Многоугольники. Элементы многоугольника. Периметр многоугольника. Выпуклые и невыпуклые многоугольники. Правильные многоугольники.

Приводить исторические сведения о возникновении и развитии геометрии.

Изображать точки и прямые на плоскости.

Формулировать определения и иллюстрировать понятия: отрезка, равенства отрезков, длины отрезка. Производить операции сложения и вычитания отрезков, умножения и деления отрезка на натуральное число.

Изверять длину отрезка с помощью линейки.

Решать задачи на нахождение длины отрезка.

Формулировать определения и иллюстрировать понятия: луча, угла, равенства углов. Различать виды углов. Производить операции сложения и вычитания углов, умножения и деления угла на натуральное число.

Измерять величину угла с помощью транспортира. Решать задачи на нахождение величины угла.

Формулировать определения и иллюстрировать понятия ломаной и многоугольника. Распознавать и приводить примеры ломаных и многоугольников. Решать задачи на нахождение длины ломаной и периметра многоугольника.

2. Треугольники (26 ч)

Треугольники. Виды треугольников: остроугольные, прямоугольные, тупоугольные, равнобедренные, равносторонние. Медиана, биссектриса и высота треугольника.

Равенство треугольников. Первый и второй признаки равенства треугольников. Равнобедренные треугольники и их свойства. Признак равнобедренного треугольника. Третий признак равенства треугольников.

Соотношения между сторонами и углами треугольника. Соотношения между сторонами треугольника.

Прямоугольные треугольники. Признаки равенства прямоугольных треугольников. Перпендикуляр и наклонная и их свойства.

Формулировать определения: треугольника, равенства треугольников, медианы, биссектрисы и высоты треугольника. Различать виды треугольников.

Формулировать признаки равенства треугольников, применять их при решении задач.

Устанавливать соотношения между сторонами и углами треугольника, применять их при решении задач.

Формулировать определения перпендикуляра и наклонной. Использовать соотношение между ними при решении задач.

3. Окружность и геометрические места точек (16 ч)

Понятия окружности и круга. Элементы окружности и круга: центр, радиус, диаметр, хорда. Взаимное расположение прямой и окружности. Касательная и секущая к окружности. Взаимное расположение двух окружностей.

Понятие о геометрическом месте точек. Примеры геометрических мест точек на плоскости. Построения с помощью циркуля и линейки. Примеры задач на построение.

Формулировать определения и иллюстрировать понятия окружности, круга и их элементов.

Изображать, распознавать и описывать взаимное расположение прямой и окружности, двух окружностей.

Приводить примеры геометрических мест точек.

Решать задачи на нахождение геометрических мест точек.

Решать задачи на построение с с помощью циркуля и линейки.

Итоговое повторение (6 ч)


Вариант II (2 ч в неделю, всего 68 ч)


Основное содержание по темам

Характеристика основных видов деятельности ученика

(на уровне учебных действий)

1. Начала геометрии (16 ч)

История возникновения и развития геометрии. Основные геометрические фигуры и их свойства. Взаимное расположение точек на прямой.

Отрезок и луч. Равенство отрезков. Операции сложения и вычитания отрезков, умножения и деления отрезка на натуральное число. Измерение длины отрезка. Исторические сведения об измерении длин.

Полуплоскость и угол. Виды углов: прямой угол, острые и тупые углы, развернутый угол, смежные и вертикальные углы. Равенство углов. Биссектриса угла. Операции сложения и вычитания углов, умножения и деления угла на натуральное число. Теорема о равенстве вертикальных углов. Перпендикулярные прямые. Измерение величин углов. Исторические сведения об измерении углов.

Ломаные. Виды ломаных. Длина ломаной. Многоугольники. Элементы многоугольника. Периметр многоугольника. Выпуклые и невыпуклые многоугольники. Правильные многоугольники.

Приводить исторические сведения о возникновении и развитии геометрии.

Изображать точки и прямые на плоскости.

Формулировать определения и иллюстрировать понятия: отрезка, равенства отрезков, длины отрезка. Производить операции сложения и вычитания отрезков, умножения и деления отрезка на натуральное число.

Изверять длину отрезка с помощью линейки.

Решать задачи на нахождение длины отрезка.

Формулировать определения и иллюстрировать понятия: луча, угла, равенства углов. Различать виды углов. Производить операции сложения и вычитания углов, умножения и деления угла на натуральное число.

Измерять величину угла с помощью транспортира.

Решать задачи на нахождение величины угла.

Формулировать определения и иллюстрировать понятия ломаной и многоугольника. Распознавать и приводить примеры ломаных и многоугольников. Решать задачи на нахождение длины ломаной и периметра многоугольника.

2. Треугольники (20 ч)

Треугольники. Виды треугольников: остроугольные, прямоугольные, тупоугольные, равнобедренные, равносторонние. Медиана, биссектриса и высота треугольника.

Равенство треугольников. Первый и второй признаки равенства треугольников. Равнобедренные треугольники и их свойства. Признак равнобедренного треугольника. Третий признак равенства треугольников.

Соотношения между сторонами и углами треугольника. Соотношения между сторонами треугольника.

Прямоугольные треугольники. Признаки равенства прямоугольных треугольников. Перпендикуляр и наклонная и их свойства.

Формулировать определения: треугольника, равенства треугольников, медианы, биссектрисы и высоты треугольника. Различать виды треугольников.

Формулировать признаки равенства треугольников, применять их при решении задач.

Устанавливать соотношения между сторонами и углами треугольника, применять их при решении задач.

Формулировать определения перпендикуляра и наклонной. Использовать соотношение между ними при решении задач.

3. Окружность и геометрические места точек (16 ч)

Понятия окружности и круга. Элементы окружности и круга: центр, радиус, диаметр, хорда. Взаимное расположение прямой и окружности. Касательная и секущая к окружности. Взаимное расположение двух окружностей.

Понятие о геометрическом месте точек. Примеры геометрических мест точек на плоскости. Построения с помощью циркуля и линейки. Примеры задач на построение.

Формулировать определения и иллюстрировать понятия окружности, круга и их элементов.

Изображать, распознавать и описывать взаимное расположение прямой и окружности, двух окружностей.

Приводить примеры геометрических мест точек.

Решать задачи на нахождение геометрических мест точек.

Решать задачи на построение с помощью циркуля и линейки.

4*. Кривые и графы (13 ч)

Парабола и её свойства. Касательная к параболе. Построение параболы и касательных к ней.

Эллипс и его свойства. Касательная к эллипсу. Построение эллипса и касательных к нему.

Гипербола и её свойства. Касательная к гиперболе. Построение гиперболы и касательных к ней.

Графы и их элементы: вершины, рёбра.

Задачи, приводящие к понятию графа. Задача Эйлера о кёнигсбергских мостах.

Уникурсальные графы и их свойства. Теорема Эйлера о числе вершин, рёбер и граней плоского графа.

Задача о трёх домиках и трёх колодцах. Проблема четырёх красок.

Формулировать определения параболы, эллипса и гиперболы.

Решать задачи на построение касательных и нахождение элементов параболы, эллипса и гиперболы.

Выполнять проекты на построение кривых, как геометрических мест точек.

Формулировать определение и иллюстрировать понятие графа и его элементов.

Решать задачи на установление уникурсальности графов.

Формулировать теорему Эйлера о числе вершин, рёбер и граней плоского графа и применять её при решении задач.

Решать задачи на раскрашивание карт.

Приводить исторические сведения о Л. Эйлере.

Выполнять проекты по темам, связанным с графами и их применением.

Итоговое повторение (3 ч)



Вариант III (3 ч в неделю, всего 102 ч)


Основное содержание по темам

Характеристика основных видов деятельности ученика

(на уровне учебных действий)

1. Начала геометрии (24 ч)

История возникновения и развития геометрии. Основные геометрические фигуры и их свойства. Взаимное расположение точек на прямой.

Отрезок и луч. Равенство отрезков. Операции сложения и вычитания отрезков, умножения и деления отрезка на натуральное число. Измерение длины отрезка. Исторические сведения об измерении длин.

Полуплоскость и угол. Виды углов: прямой угол, острые и тупые углы, развернутый угол, смежные и вертикальные углы. Равенство углов. Биссектриса угла. Операции сложения и вычитания углов, умножения и деления угла на натуральное число. Теорема о равенстве вертикальных углов. Перпендикулярные прямые. Измерение величин углов. Исторические сведения об измерении углов.

Ломаные. Виды ломаных. Длина ломаной. Многоугольники. Элементы многоугольника. Периметр многоугольника. Выпуклые и невыпуклые многоугольники. Правильные многоугольники.

Приводить исторические сведения о возникновении и развитии геометрии.

Формулировать аксиомы о взаимном расположении точек и прямых на плоскости.

Формулировать определения и иллюстрировать понятия: отрезка, равенства отрезков, длины отрезка. Производить операции сложения и вычитания отрезков, умножения и деления отрезка на натуральное число.

Изверять длину отрезка с помощью линейки.

Решать задачи на нахождение длины отрезка.

Формулировать определения и иллюстрировать понятия: луча, угла, равенства углов. Различать виды углов. Производить операции сложения и вычитания углов, умножения и деления угла на натуральное число.

Измерять величину угла с помощью транспортира.

Решать задачи на нахождение величин углов.

Формулировать определения и иллюстрировать понятия ломаной и многоугольника. Распознавать и приводить примеры ломаных и многоугольников. Решать задачи на нахождение длины ломаной и периметра многоугольника.

Решать задачи комбинаторного характера на взаимное расположение точек и прямых на плоскости.

Решать задачи с практическим содержанием.

2. Треугольники (31 ч)

Треугольники. Виды треугольников: остроугольные, прямоугольные, тупоугольные, равнобедренные, равносторонние. Медиана, биссектриса и высота треугольника.

Равенство треугольников. Первый и второй признаки равенства треугольников. Равнобедренные треугольники и их свойства. Признак равнобедренного треугольника. Третий признак равенства треугольников.

Соотношения между сторонами и углами треугольника. Соотношения между сторонами треугольника.

Прямоугольные треугольники. Признаки равенства прямоугольных треугольников. Перпендикуляр и наклонная и их свойства.

Формулировать определения: треугольника, равенства треугольников, медианы, биссектрисы и высоты треугольника. Различать виды треугольников.

Формулировать признаки равенства треугольников, применять их при решении задач.

Доказывать соотношения между сторонами и углами треугольника, применять их при решении задач.

Формулировать определения перпендикуляра и наклонной. Использовать соотношение между ними при решении задач.

Решать задачи на нахождение наибольших и наименьших значений.

Решать задачи с практическим содержанием.

3. Окружность и геометрические места точек (21 ч)

Понятия окружности и круга. Элементы окружности и круга: центр, радиус, диаметр, хорда. Взаимное расположение прямой и окружности. Касательная и секущая к окружности. Взаимное расположение двух окружностей.

Понятие о геометрическом месте точек. Примеры геометрических мест точек на плоскости. Построения с помощью циркуля и линейки. Примеры задач на построение.

Формулировать определения и иллюстрировать понятия окружности, круга и их элементов.

Изображать, распознавать и описывать взаимное расположение прямой и окружности, двух окружностей.

Приводить примеры геометрических мест точек.

Решать задачи на нахождение геометрических мест точек.

Решать задачи на построение с с помощью циркуля и линейки.

4*. Кривые и графы (20 ч)

Парабола и её свойства. Касательная к параболе. Построение параболы и касательных к ней.

Эллипс и его свойства. Касательная к эллипсу. Построение эллипса и касательных к нему.

Гипербола и её свойства. Касательная к гиперболе. Построение гиперболы и касательных к ней.

Графы и их элементы: вершины, рёбра.

Задачи, приводящие к понятию графа. Задача Эйлера о кёнигсбергских мостах.

Уникурсальные графы и их свойства. Теорема Эйлера о числе вершин, рёбер и граней плоского графа.

Задача о трёх домиках и трёх колодцах. Проблема четырёх красок.

Формулировать определения параболы, эллипса и гиперболы.

Решать задачи на построение касательных и нахождение элементов параболы, эллипса и гиперболы.

Выполнять проекты на построение кривых, как геометрических мест точек.

Формулировать определение и иллюстрировать понятие графа и его элементов.

Решать задачи на установление уникурсальности графов.

Формулировать теорему Эйлера о числе вершин, рёбер и граней плоского графа и применять её при решении задач.

Решать задачи на раскрашивание карт.

Приводить исторические сведения о Л. Эйлере.

Выполнять проекты по темам, связанным с графами и их применением.

Итоговое повторение (6 ч)


8 КЛАСС

Вариант I (2 ч в неделю, всего 68 ч)


Основное содержание по темам

Характеристика основных видов деятельности ученика

(на уровне учебных действий)

5. Параллельность (21 ч)

Параллельные прямые. Признаки параллельных прямых. Аксиома параллельных прямых. Свойства параллельных прямых. Исторические сведения.

Сумма углов треугольника. Сумма углов выпуклого n-угольника.

Параллелограмм. Прямоугольник. Ромб. Квадрат. Их свойства. Признаки параллелограмма.

Средняя линия треугольника. Трапеция. Равнобедренная и прямоугольная трапеции. Средняя линия трапеции. Теорема Фалеса.

Формулировать определение параллельных прямых и аксиому параллельных.

Распознавать на рисунках и изображать параллельные прямые.

Называть углы, образованные при пересечении двух параллельных прямых секущей.

Приводить исторические сведения об аксиоме параллельных и Н.И. Лобачевском.

Формулировать и доказывать теоремы о сумме углов треугольника и выпуклого n-угольника.

Распознавать, формулировать определение и изображать: параллелограмм, прямоугольник, ромб, квадрат, трапецию, равнобедренную и прямоугольную трапеции.

Формулировать и доказывать свойства и признаки параллелограмма, прямоугольника, ромба, квадрата.

Формулировать определение и изображать среднюю линию: треугольника, трапеции.

Формулировать и доказывать теоремы о срединих линиях треугольника и трапеции, теорему Фалеса.

Решать задачи на построение, доказательство и вычисление.

6. Многоугольники и окружность (9 ч)

Углы, связанные с окружностью. Многоугольники, вписанные в окружность. Многоугольники, описанные около окружности. Вписанная и описанная окружности правильного многоугольника. Замечательные точки треугольника.

Формулировать определения и изображать углы, связанные с окружностью.

Формулировать и доказывать теоремы об углах, связанных с окружностью.

Решать задачи на нахождение углов, связанных с окружностью.

Формулировать определения и изображать многоугольники, вписанные в окружность и описанные около окружности.

Формулировать и доказывать теоремы о вписанной и описанной окружностях треугольника и правильного многоугольника.

Изображать замечательные точки треугольника.

Формулировать и доказывать теоремы о замечательных точках треугольника.

7. Движение (11 ч)

Понятие движения и его свойства. Центральная симметрия. Центрально-симметричные фигуры. Поворот. Симметрия n-го порядка. Осевая симметрия. Фигуры, симметричные относительно некоторой оси. Параллельный перенос. Равенство фигур.

Формулировать определение и иллюстрировать понятие: движения, центральной симметрии, поворота, симметрии n-го порядка, осевой симметрии, параллельного переноса.

Приводить примеры симметричных фигур.

Изображать фигуры, симметричные данным.

Формулировать определение равенства фигур.

Решать задачи на нахождение элементов симметрии и установление равенства фигур.

8. Подобие (10 ч)

Подобие треугольников. Признаки подобия треугольников. Подобие фигур. Гомотетия. Теорема Пифагора.

Формулировать определение и иллюстрировать понятие подобия треугольников.

Распознавать подобные треугольники на рисунках.

Формулировать и доказывать признаки подобия треугольников.

Решать задачи на нахождение элементов подобных треугольников.

Формулировать определения подобия и гомотетии.

Изображать фигуры, подобные и гомотетичные данным.

Формулировать и доказывать теорему Пифагора. Применять её при решении задач.

Приводить исторические сведения о Пифагоре.

Решать задачи с практическим содержанием с использованием подобия и теоремы Пифагора.

9. Элементы тригонометрии (13 ч)

Тригонометрические функции острого угла прямоугольного треугольника: синус, косинус, тангенс, котангенс.

Тригонометрические тождества. Тригонометрические функции тупого угла. Теорема косинусов. Теорема синусов. Длина окружности. Число . Длина дуги окружности.


Формулировать определения и иллюстрировать понятия синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника.

Выражать тригонометрические функции острого угла прямоугольного треугольника через его стороны.

Формулировать и доказывать тригонометрические тождества.

Формулировать определения и выражать тригонометрические функции тупого угла через тригонометрические функции острых углов.

Формулировать и доказывать теоремы косинусов и синусов.

Решать задачи на нахождение тригонометрических функций и сторон треугольника.

Формулировать определения длины окружности.

Указывать приближённые значения числа .

Устанавливать соответствие между величиной центрального угла и длиной дуги окружности.

Решать задачи на нахождение длины дуги окружности.

Итоговое повторение (4 ч)


Вариант II (2 ч в неделю, всего 68 ч)


Основное содержание по темам

Характеристика основных видов деятельности ученика

(на уровне учебных действий)

5. Параллельность (18 ч)

Параллельные прямые. Признаки параллельных прямых. Аксиома параллельных прямых. Свойства параллельных прямых. Исторические сведения.

Сумма углов треугольника. Сумма углов выпуклого n-угольника.

Параллелограмм. Прямоугольник. Ромб. Квадрат. Их свойства. Признаки параллелограмма.

Средняя линия треугольника. Трапеция. Равнобедренная и прямоугольная трапеции. Средняя линия трапеции. Теорема Фалеса.

Формулировать определение параллельных прямых и аксиому параллельных.

Распознавать на рисунках и изображать параллельные прямые.

Называть углы, образованные при пересечении двух параллельных прямых секущей.

Приводить исторические сведения об аксиоме параллельных и Н.И. Лобачевском.

Формулировать и доказывать теоремы о сумме углов треугольника и выпуклого n-угольника.

Распознавать, формулировать определение и изображать: параллелограмм, прямоугольник, ромб, квадрат, трапецию, равнобедренную и прямоугольную трапеции.

Формулировать и доказывать свойства и признаки параллелограмма, прямоугольника, ромба, квадрата.

Формулировать определение и изображать среднюю линию: треугольника, трапеции.

Формулировать и доказывать теоремы о срединих линиях треугольника и трапеции, теорему Фалеса.

Решать задачи на построение, доказательство и вычисление.

6. Многоугольники и окружность (9 ч)

Углы, связанные с окружностью. Многоугольники, вписанные в окружность. Многоугольники, описанные около окружности. Вписанная и описанная окружности правильного многоугольника. Замечательные точки треугольника.

Формулировать определения и изображать углы, связанные с окружностью.

Формулировать и доказывать теоремы об углах, связанных с окружностью.

Решать задачи на нахождение углов, связанных с окружностью.

Формулировать определения и изображать многоугольники, вписанные в окружность и описанные около окружности.

Формулировать и доказывать теоремы о вписанной и описанной окружностях треугольника и правильного многоугольника.

Изображать замечательные точки треугольника.

Формулировать и доказывать теоремы о замечательных точках треугольника.

7. Движение (13 ч)

Понятие движения и его свойства. Центральная симметрия. Центрально-симметричные фигуры. Поворот. Симметрия n-го порядка. Осевая симметрия. Фигуры, симметричные относительно некоторой оси. Параллельный перенос. Равенство фигур.

Формулировать определение и иллюстрировать понятие: движения, центральной симметрии, поворота, симметрии n-го порядка, осевой симметрии, параллельного переноса.

Приводить примеры симметричных фигур.

Изображать фигуры, симметричные данным.

Формулировать определение равенства фигур.

Решать задачи на нахождение элементов симметрии и установление равенства фигур.

*Формулировать определение и изображать паркеты на плоскости.

*Выполнять проекты на составление паркетов.

8. Подобие (11 ч)

Подобие треугольников. Признаки подобия треугольников. Подобие фигур. Гомотетия. *Золотое сечение. Теорема Пифагора.

Формулировать определение и иллюстрировать понятие подобия треугольников.

Распознавать подобные треугольники на рисунках.

Формулировать и доказывать признаки подобия треугольников.

Решать задачи на нахождение элементов подобных треугольников.

Формулировать определения подобия и гомотетии.

Изображать фигуры, подобные и гомотетичные данным.

*Формулировать определения и изображать золотое сечение, золотые прямоугольники и золотые треугольники.

Формулировать и доказывать теорему Пифагора. Применять её при решении задач.

Приводить исторические сведения о золотом сечении и Пифагоре.

Решать задачи с практическим содержанием с использованием подобия и теоремы Пифагора.

Выполнять проекты на тему *золотого сечения и теоремы Пифагора.

9. Элементы тригонометрии (15 ч)

Тригонометрические функции острого угла прямоугольного треугольника: синус, косинус, тангенс, котангенс.

Тригонометрические тождества. Тригонометрические функции тупого угла. Теорема косинусов. Теорема синусов. Длина окружности. Число . Длина дуги окружности. *Циклоидальные кривые.

Формулировать определения и иллюстрировать понятия синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника.

Выражать тригонометрические функции острого угла прямоугольного треугольника через его стороны.

Формулировать и доказывать тригонометрические тождества.

Формулировать определения и выражать тригонометрические функции тупого угла через тригонометрические функции острых углов.

Формулировать и доказывать теоремы косинусов и синусов.

Решать задачи на нахождение тригонометрических функций и сторон треугольника.

Формулировать определение длины окружности.

Указывать приближённые значения числа .

Устанавливать соответствие между величиной центрального угла и длиной дуги окружности.

Решать задачи на нахождение длины дуги окружности.

*Формулировать определения и изображать циклоидальные кривые.

Итоговое повторение (2 ч)



Вариант III (3 ч в неделю, всего 102 ч)


Основное содержание по темам

Характеристика основных видов деятельности ученика

(на уровне учебных действий)

5. Параллельность (28 ч)

Параллельные прямые. Признаки параллельных прямых. Аксиома параллельных прямых. Свойства параллельных прямых. Исторические сведения.

Сумма углов треугольника. Сумма углов выпуклого n-угольника.

Параллелограмм. Прямоугольник. Ромб. Квадрат. Их свойства. Признаки параллелограмма.

Средняя линия треугольника. Трапеция. Равнобедренная и прямоугольная трапеции. Средняя линия трапеции. Теорема Фалеса.

Формулировать определение параллельных прямых и аксиому параллельных.

Распознавать на рисунках и изображать параллельные прямые.

Называть углы, образованные при пересечении двух параллельных прямых секущей.

Приводить исторические сведения об аксиоме параллельных и Н.И. Лобачевском.

Формулировать и доказывать теоремы о сумме углов треугольника и выпуклого n-угольника.

Распознавать, формулировать определение и изображать: параллелограмм, прямоугольник, ромб, квадрат, трапецию, равнобедренную и прямоугольную трапеции.

Формулировать и доказывать свойства и признаки параллелограмма, прямоугольника, ромба, квадрата.

Формулировать определение и изображать среднюю линию: треугольника, трапеции.

Формулировать и доказывать теоремы о срединих линиях треугольника и трапеции, теорему Фалеса.

Решать задачи на построение, доказательство и вычисление.

6. Многоугольники и окружность (14 ч)

Углы, связанные с окружностью. Многоугольники, вписанные в окружность. Многоугольники, описанные около окружности. Вписанная и описанная окружности правильного многоугольника. Замечательные точки треугольника.

Формулировать определения и изображать углы, связанные с окружностью.

Формулировать и доказывать теоремы об углах, связанных с окружностью.

Решать задачи на нахождение углов, связанных с окружностью.

Формулировать определения и изображать многоугольники, вписанные в окружность и описанные около окружности.

Формулировать и доказывать теоремы о вписанной и описанной окружностях треугольника и правильного многоугольника.

Изображать замечательные точки треугольника.

Формулировать и доказывать теоремы о замечательных точках треугольника.

7. Движение (20 ч)

Понятие движения и его свойства. Центральная симметрия. Центрально-симметричные фигуры. Поворот. Симметрия n-го порядка. Осевая симметрия. Фигуры, симметричные относительно некоторой оси. Параллельный перенос. Равенство фигур.

Формулировать определение и иллюстрировать понятие: движения, центральной симметрии, поворота, симметрии n-го порядка, осевой симметрии, параллельного переноса.

Приводить примеры симметричных фигур.

Изображать фигуры, симметричные данным.

Формулировать определение равенства фигур.

Решать задачи на нахождение элементов симметрии и установление равенства фигур.

*Формулировать определение и изображать паркеты на плоскости.

*Выполнять проекты на составление паркетов.

8. Подобие (16 ч)

Подобие треугольников. Признаки подобия треугольников. Подобие фигур. Гомотетия. *Золотое сечение. Теорема Пифагора.

Формулировать определение и иллюстрировать понятие подобия треугольников.

Распознавать подобные треугольники на рисунках.

Формулировать и доказывать признаки подобия треугольников.

Решать задачи на нахождение элементов подобных треугольников.

Формулировать определения подобия и гомотетии.

Изображать фигуры, подобные и гомотетичные данным.

*Формулировать определения и изображать золотое сечение, золотые прямоугольники и золотые треугольники.

Формулировать и доказывать теорему Пифагора. Применять её при решении задач.

Приводить исторические сведения о золотом сечении и Пифагоре.

Решать задачи с практическим содержанием с использованием подобия и теоремы Пифагора.

Выполнять проекты на тему *золотого сечения и теоремы Пифагора.

9. Элементы тригонометрии (19 ч)

Тригонометрические функции острого угла прямоугольного треугольника: синус, косинус, тангенс, котангенс.

Тригонометрические тождества. Тригонометрические функции тупого угла. Теорема косинусов. Теорема синусов. Длина окружности. Число . Длина дуги окружности. *Циклоидальные кривые.

Формулировать определения и иллюстрировать понятия синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника.

Выражать тригонометрические функции острого угла прямоугольного треугольника через его стороны.

Формулировать и доказывать тригонометрические тождества.

Формулировать определения и выражать тригонометрические функции тупого угла через тригонометрические функции острых углов.

Формулировать и доказывать теоремы косинусов и синусов.

Решать задачи на нахождение тригонометрических функций и сторон треугольника.

Формулировать определение длины окружности.

Указывать приближенные значения числа .

Устанавливать соответствие между величиной центрального угла и длиной дуги окружности.

Решать задачи на нахождение длины дуги окружности.

*Формулировать определения и изображать циклоидальные кривые.

*Выполнять проекты на построение кривых как траекторий движения точек.

Итоговое повторение (5 ч)


9 КЛАСС

Вариант I (2 ч в неделю, всего 68 ч)


Основное содержание по темам

Характеристика основных видов деятельности ученика

(на уровне учебных действий)

10. Площадь (22 ч)

Понятие площади плоской фигуры. Измерение площадей. Равновеликие и равносоставленные фигуры.

Площадь прямоугольника. Площади параллелограмма, треугольника, трапеции. Формула Герона.

Площадь многоугольника. Площадь правильного многоугольника. Площади круга, сектора и сегмента.

Соотношение между площадями подобных фигур.

Формулировать определение и иллюстрировать понятие площади плоской фигуры.

Выводить формулы площадей прямоугольника, параллелограмма, треугольника и трапеции, правильного многоугольника, круга, сектора и сегмента.

Решать задачи на нахождение площадей плоских фигур.

11. Координаты и векторы (19 ч)

Прямоугольная система координат. Исторические сведения. Кординаты середины отрезка. Расстояние между точками. Уравнение окружности.

Векторы. Сложение векторов. Умножение вектора на число. Координаты вектора. Скалярное произведение векторов.

Уравнение прямой. Тригонометрические функции произвольного угла.


Формулировать определение и иллюстрировать понятие прямоугольной системы координат.

Приводить исторические сведения о Р. Декарте.

Выводить и использовать формулы координат середины отрезка, расстояния между точками, уравнения прямой и окружности.

Формулировать определение и иллюстрировать понятие: вектора, длины (модуля) вектора, коллинеарных и равных векторов, угла между векторами, суммы и разности векторов, умножения вектора на число, скалярного произведения векторов.

Выполнять операции над векторами.

Находить длину вектора, координаты вектора, угол между векторами и скалярное произведение векторов.

Формулировать определение и находить тригонометрические функции прозвольного угла.

Выполнять проекты, связанные с использованием координатного и векторного методов при решении задач на вычисление и доказательство.

12. Начала стереометрии (17 ч)

Основные понятия стереометрии. Фигуры в пространстве. Многогранники, их элементы. Примеры многогранников.

Угол в пространстве. Взаимное расположение прямых и плоскостей в пространстве. Параллельность в пространстве.

Сфера и шар. Их основные элементы.

Выпуклые многогранники. Теорема Эйлера для выпуклых многогранников.

Правильные, полуправильные и звёздчатые многогранники. Моделирование многогранников. Кристаллы – природные многогранники.

Исторические сведения.

Площадь поверхности и объём.


Изображать точки, прямые и плоскости в пространстве.

Формулировать определение и изображать: куб, параллелепипед, призму, пирамиду, правильные многогранники, цилиндр, конус, сферу и шар.

Устанавливать взаимное расположение прямых и плоскостей в пространстве.

Формулировать определения и приводить примеры выпуклых и невыпуклых многогранников.

Формулировать теорему Эйлера о выпуклых многогранниках и использовать её при решении задач.

Формулировать определения и приводить примеры полуправильных и звёздчатых многогранников.

Моделировать многогранники, используя развёртки и геометрический конструктор.

Приводить примеры кристаллов и устанавливать их форму.

Находить площади поверхностей и объёмы некоторых многогранников и круглых тел.

Итоговое повторение (10 ч)


Вариант II (2 ч в неделю, всего 68 ч)


Основное содержание по темам

Характеристика основных видов деятельности ученика

(на уровне учебных действий)

10. Площадь (20 ч)

Понятие площади плоской фигуры. Измерение площадей. Равновеликие и равносоставленные фигуры.

Площадь прямоугольника. Площади параллелограмма, треугольника, трапеции. Формула Герона.

Площадь многоугольника. Площадь правильного многоугольника. Площади круга, сектора и сегмента.

Соотношение между площадями подобных фигур. *Изопериметрическая задача. *Задачи на разрезание.

Формулировать определение и иллюстрировать понятие площади плоской фигуры.

Выводить формулы площадей прямоугольника, параллелограмма, треугольника и трапеции, правильного многоугольника, круга, сектора и сегмента.

Решать задачи на нахождение площадей плоских фигур.

*Формулировать и решать изопериметрические задачи и задачи на разрезание.

11. Координаты и векторы (25 ч)

Прямоугольная система координат. Исторические сведения. Кординаты середины отрезка. Расстояние между точками. Уравнение окружности.

Векторы. Сложение векторов. Умножение вектора на число. Координаты вектора. Скалярное произведение векторов.

Уравнение прямой. *Аналитическое задание фигур на плоскости. *Задачи оптимизации.

Тригонометрические функции произвольного угла. *Полярные координаты.

Формулировать определение и иллюстрировать понятие прямоугольной системы координат.

Приводить исторические сведения о Р. Декарте.

Выводить и использовать формулы координат середины отрезка, расстояния между точками, уравнения прямой и окружности.

Формулировать определение и иллюстрировать понятие: вектора, длины (модуля) вектора, коллинеарных и равных векторов, угла между векторами, суммы и разности векторов, умножения вектора на число, скалярного произведения векторов.

Выполнять операции над векторами.

Находить длину вектора, координаты вектора, угол между векторами и скалярное произведение векторов.

*Приводить примеры аналитического задания фигур на плоскости.

*Приводить примеры и решать задачи оптимизации.

Формулировать определение и находить тригонометрические функции прозвольного угла.

*Формулировать определение и иллюстрировать понятие полярных координат на плоскости.

*Устанавливать связь между полярными и декартовыми координатами.

*Решать задачи с использованием полярных координат.

12. Начала стереометрии (16 ч)

Основные понятия стереометрии. Фигуры в пространстве. Многогранники, их элементы. Примеры многогранников.

Угол в пространстве. Взаимное расположение прямых и плоскостей в пространстве. Параллельность в пространстве.

Сфера и шар. Их основные элементы.

Выпуклые многогранники. Теорема Эйлера для выпуклых многогранников.

Правильные, полуправильные, звёздчатые многогранники. Моделирование многогранников. Кристаллы – природные многогранники. Исторические сведения.

Ориентация плоскости. Лист Мёбиуса.

Площадь поверхности и объём.


Изображать точки, прямые и плоскости.

Формулировать определение и изображать: куб, параллелепипед, призму, пирамиду, правильные многогранники, цилиндр, конус, сферу и шар.

Устанавливать взаимное расположение прямых и плоскостей в пространстве.

Формулировать определения и приводить примеры выпуклых и невыпуклых многогранников.

Формулировать теорему Эйлера о выпуклых многогранниках и использовать её при решении задач.

Формулировать определения и приводить примеры полуправильных и звёздчатых многогранников.

Моделировать многогранники, используя развёртки и геометрический конструктор.

Приводить примеры кристаллов и устанавливать их форму.

Находить площади поверхностей и объёмы некоторых многогранников и круглых тел.

Итоговое повторение (7 ч)


Вариант III (3 ч в неделю, всего 102 ч)


Основное содержание по темам

Характеристика основных видов деятельности ученика

(на уровне учебных действий)

10. Площадь (31 ч)

Понятие площади плоской фигуры. Измерение площадей. Равновеликие и равносоставленные фигуры.

Площадь прямоугольника. Площади параллелограмма, треугольника, трапеции. Формула Герона.

Площадь многоугольника. Площадь правильного многоугольника. Площади круга, сектора и сегмента.

Соотношение между площадями подобных фигур. *Изопериметрическая задача. *Задачи на разрезание.

Формулировать определение и иллюстрировать понятие площади плоской фигуры.

Выводить формулы площадей прямоугольника, параллелограмма, треугольника и трапеции, правильного многоугольника, круга, сектора и сегмента.

Решать задачи на нахождение площадей плоских фигур.

*Формулировать и решать изопериметрическую задачу.

*Выполнять проекты, связанные с изопериметрической задачей и решением задач на разрезание.

11. Координаты и векторы (39 ч)

Прямоугольная система координат. Исторические сведения. Кординаты середины отрезка. Расстояние между точками. Уравнение окружности.

Векторы. Сложение векторов. Умножение вектора на число. Координаты вектора. Скалярное произведение векторов.

Уравнение прямой. *Аналитическое задание фигур на плоскости. *Задачи оптимизации.

Тригонометрические функции произвольного угла. *Полярные координаты.

Формулировать определение и иллюстрировать понятие прямоугольной системы координат.

Приводить исторические сведения о Р. Декарте.

Выводить и использовать формулы координат середины отрезка, расстояния между точками, уравнения прямой и окружности.

Формулировать определение и иллюстрировать понятие: вектора, длины (модуля) вектора, коллинеарных и равных векторов, угла между векторами, суммы и разности векторов, умножения вектора на число, скалярного произведения векторов.

Выполнять операции над векторами.

Находить длину вектора, координаты вектора, угол между векторами и скалярное произведение векторов.

*Приводить примеры аналитического задания фигур на плоскости.

*Приводить примеры и решать задачи оптимизации.

Формулировать определение и находить тригонометрические функции прозвольного угла.

*Формулировать определение и иллюстрировать понятие полярных координат на плоскости.

*Устанавливать связь между полярными и декартовыми координатами.

*Решать задачи с использованием полярных координат.

Выполнять проекты, связанные с использованием координатного и векторного методов при решении задач на вычисление и доказательство.

12. Начала стереометрии (20 ч)

Основные понятия стереометрии. Фигуры в пространстве. Многогранники, их элементы. Примеры многогранников.

Угол в пространстве. Взаимное расположение прямых и плоскостей в пространстве. Параллельность в пространстве.

Сфера и шар. Их основные элементы.

Выпуклые многогранники. Теорема Эйлера для выпуклых многогранников.

Правильные, полуправильные, звёздчатые многогранники. Моделирование многогранников. Кристаллы – природные многогранники. Исторические сведения.

Ориентация плоскости. Лист Мёбиуса.

Площадь поверхности и объём.


Изображать точки, прямые и плоскости.

Формулировать определение и изображать: куб, параллелепипед, призму, пирамиду, правильные многогранники, цилиндр, конус, сферу и шар.

Устанавливать взаимное расположение прямых и плоскостей в пространстве.

Формулировать определения и приводить примеры выпуклых и невыпуклых многогранников.

Формулировать теорему Эйлера о выпуклых многогранниках и использовать её при решении задач.

Формулировать определения и приводить примеры полуправильных и звёздчатых многогранников.

Моделировать многогранники, используя развёртки и геометрический конструктор.

Приводить примеры кристаллов и устанавливать их форму.

Находить площади поверхностей и объёмы некоторых многогранников и круглых тел.

Выполнять проекты на темы, связанные с ориентацией поверхности и листом Мёбиуса.

Итоговое повторение (12 ч)



ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ ОБУЧЕНИЯ

ГЕОМЕТРИИ в 7-9 КЛАССАХ


Предполагается, что в результате обучения выпускники 9-го класса будут обладать необходимыми знаниями, умениями и навыками:


Иметь сформированные представления

  • об истории возникновения и развития геометрии, учёных, внёсших существенный вклад в геометрическую науку;

  • о сущности аксиоматического метода построения геометрии и роли математического доказательства;

  • о значении геометрии в системе других наук и в познании окружающего нас мира;

  • о некоторых современных направлениях развития геометрии и её приложениях.


Знать

  • основные геометрические понятия и отношения между ними;

  • определения и примеры геометрических фигур на плоскости и в пространстве;

  • формулировки основных свойств и теорем.


Уметь

  • пользоваться геометрическими инструментами для изображения, построения и изготовления моделей геометрических фигур;

  • проводить доказательства основных свойств и теорем;

  • решать задачи на доказательство, вычисление и построение;

  • применять геометрию для решения практических задач.


Готовы

  • к сдаче Государственной итоговой аттестации (ГИА) по математике (часть «Геометрия») за курс основной школы;

  • к самостоятельному изучению литературы по геометрии, статей в научно-популярных журналах, материалов в электронных ресурсах;

  • к участию в турнирах, конкурсах и олипиадах по математике.





48



Просмотр содержимого документа
«рабочая программа по геометрии 7-9 кл»









Рабочая программа по геометрии 7-9 классы

Составлена к УМК Смирнова И.М., Смирнов В.А.





























Учитель: Рыбникова Л.В.

2015г.

Пояснительная записка.

Рабочая программа основного общего образования по геометрии составлена на основе Фундаментального ядра содержания образования и Требований к результатам освоения основной образовательной программы основного общего образования, представленных в Федеральном государственном образовательном стандарте общего образования. В ней также учитываются основные идеи и положения программы развития и формирования универсальных учебных действий для основного общего образования, программа по геометрии для 7-9 классов Смирнова И.М., Смирнов В.А.Смирнова И.М., Смирнов В.А. Геометрия. 7-9 кл.: учебн. для общеобразовательных учреждений. – М.: Мнемозина

Овладение учащимися системой геометрических знаний и умений необходимо в повседневной жизни, для изучения смежных дисциплин и продолжения образования.

Практическая значимость школьного курса геометрии обусловлена тем, что его объектом являются пространственные формы и количественные отношения действительного мира. Геометрическая подготовка необходима для понимания принципов устройства и использования современной техники, восприятия научных и технических понятий и идей. Математика является языком науки и техники. С её помощью моделируются и изучаются явления и процессы, происходящие в природе.

Геометрия является одним из опорных предметов основной школы: она обеспечивает изучение других дисциплин. В первую очередь это относится к предметам естественно - научного цикла, в частности к физике. Развитие логического мышления при обучении геометрии способствует усвоению предметов гуманитарного цикла. Практические умения и навыки геометрического характера необходимы для трудовой деятельности и профессиональной подготовки школьников.

Развитие у учащихся правильных представлений о сущности и происхождении геометрических абстракций, соотношении реального и идеального, характере отражения математической наукой явлений и процессов реального мира ,месте геометрии в системе наук и роли математического моделирования в научном познании и в практике способствует формированию научного мировоззрения учащихся, а также формированию качеств мышления, необходимых для адаптации в современном информационном обществе.

Требуя от учащихся умственных и волевых усилий, концентрации внимания, активности развитого воображения, геометрия развивает нравственные черты личности ( настойчивость, целеустремлённость, творческую активность самостоятельность, ответственность, трудолюбие, дисциплину и критичность мышления ) и умение аргументировано отстаивать свои взгляды и убеждения, а также способность принимать самостоятельные решения.

Геометрия существенно расширяет кругозор учащихся, знакомя их с индукцией и дедукцией, обобщением и конкретизацией, анализом и синтезом, классификацией и систематизацией, абстрагированием, аналогией. Активное использование задач на всех этапах учебного процесса развивает творческие способности школьников.

При обучении геометрии формируются умения и навыки умственного труда- планирование своей работы, поиск рациональных путей её выполнения, критическая оценка результатов. В процессе обучения геометрии школьники должны научиться излагать свои мысли ясно и исчерпывающе, лаконично и ёмко, приобрести навыки чёткого, аккуратного и грамотного выполнения математических записей.

Важнейшей задачей школьного курса геометрии является развитие логического мышления учащихся. Сами объекты геометрических умозаключений и принятые в геометрии правила их конструирования способствуют формированию умений обосновывать и доказывать суждения, приводить чёткие определения, развивают логическую интуицию, кратко и наглядно вскрывают механизм логических построений и учат их применению. Тем самым геометрия занимает ведущее место в формировании научно – теоретического мышления школьников. Раскрывая внутреннюю гармонию математики , формируя понимание красоты и изящества математических рассуждений, способствуя восприятию геометрических форм усвоению понятия симметрии, геометрия вносит значительный вклад в эстетическое воспитание учащихся. Её изучение развивает воображение школьников, существенно обогащает и развивает их пространственные представления.

Общая характеристика курса.

Линия «Геометрия в историческом развитии» предназначена для формирования представлений о геометрии как части человеческой культуры, для общего развития школьников, для создания культурно- исторической среды обучения.

Для того чтобы познакомить учащихся с современным состоянием развития геометрии, включаем в содержание курса геометрии следующие элементы:

а) знакомство с жизнью и творчеством известных современных ученых-геометров;

б) работа с научно-популярной литературой;

в) решение современных прикладных задач;

г) использование современных компьютерных технологий.

Так, в конце седьмого класса после изучения темы «Геометрические места точек» в качестве дополнительного материала предлагается рассмотреть кривые как геометрические места точек. Среди таких кривых: парабола, эллипс, гипербола.

Например, парабола является геометрическим местом точек, равноудалённых от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Вопрос о нахождении такого геометрического места точек возникает естественным образом после нахождения геометрического места точек, равноудалённых от двух заданных точек (серединный перпендикуляр) и геометрического места внутренних точек угла, равноудалённых от его сторон (биссектриса угла).

Эллипс является геометрическим местом точек, сумма расстояний от которых до двух заданных точек, называемых фокусами, есть величина постоянная. Если фокусы приближаются друг к другу, сливаясь в одну точку, то эллипс превращается в окружность.

Кроме кривых, в конце седьмого класса в качестве дополнительного материала в учебник включены графы и их применение, в том числе: уникурсальные графы, задача Эйлера о кёнигсбергских мостах, задача о трёх домиках и трёх колодцах, теорема Эйлера о числе вершин, рёбер и граней сетки из многоугольников, проблема четырёх красок и др.

Изучение данного материала значительно повышает интерес учащихся к геометрии, способствует формированию комбинаторных геометрических представлений и развитию их мышления.

В качестве дополнительного материала в восьмом классе рассматривается золотое сечение и его использование в живописи, скульптуре, архитектуре; паркеты; кривые как траектории движения точек, среди которых: циклоида – траектория движения точки, закреплённой на окружности, катящейся по прямой; кардиоида – траектория движения точки, закреплённой на окружности, катящейся по другой окружности того же радиуса; астроида – траектория движения точки, закреплённой на окружности, катящейся с внутренней стороны другой окружности в четыре раза большего радиуса.

В качестве дополнительного материала в девятом классе, после изучения понятия площади, рассматривается изопериметрическая задача (задача Дидоны) о нахождении замкнутой кривой заданной длины, охватывающей наибольшую площадь, изучается понятие равносоставленности и предлагаются задачи на разрезание. Кроме того, в теме «Координаты и векторы» рассматриваются полярные координаты, кривые, заданные уравнениями в декартовых и полярных координатах, в том числе: спираль Архимеда, золотая спираль, n-лепестковые розы и др., предлагаются задачи оптимального управления.

Включение в учебники разнообразного материала, учитывающего интересы каждого ученика, повышает желание учащихся заниматься геометрией. Опираясь на этот интерес и желание, можно преодолеть и известные трудности обучения.

Место предмета в учебном плане.

Базисный учебный ( образовательный ) план на изучение геометрии в основной школе отводит два часа в неделю (всего 210 часов).


Требования к результатам освоения содержания курса.

Программа обеспечивает достижение следующих результатов освоения образовательной программы основного общего образования:

Личностные:

  1. Формирование ответственного отношения к учению, готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования на базе ориентировки в мире профессий и профессиональных предпочтений, осознанному построению индивидуальной образовательной траектории с учётом устойчивых познавательных интересов.

  2. формирование целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики;

  3. формирование коммуникативной компетенции в общении и сотрудничестве со сверстниками, старшими и младшими в образовательной ,общественно полезной, учебно- исследовательской, творческой и других видах деятельности;

  4. умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры

  5. критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;

  6. креативность , инициативу, находчивость, активность при решении геометрических задач;

  7. умение контролировать процесс и результат учебной математической деятельности;

  8. способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;

метапредметные:

  1. умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач:.

  2. умение осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы:

  3. умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения:

  4. осознанное владение логическими действиями определения понятий, обобщения, установления аналогий, классификаций на основе самостоятельного выбора оснований и критериев, установления родовидовых связей:

  5. умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение 9 индуктивное, дедуктивное и по аналогии) и выводы;

  6. умение создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач:

  7. умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников, общие способы работы; умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение;

  8. формирование и развитие учебной и общепользовательской компетентности в области использования ИКТ;

  9. первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;

  10. умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни:

  11. умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной , точной и вероятностной информации;

  12. умение понимать и использовать математические средства наглядности ( рисунки, чертежи, схемы и др) для иллюстрации, интерпретации, аргументации;

  13. умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки:

  14. умение применять индуктивные и дедуктивные способы рассуждений. видеть различные стратегии решения задач;

  15. понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;

  16. умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;

  17. умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;

предметные:

  1. овладение базовым понятийным аппаратом по основным разделам содержания; представление об основных изучаемых понятиях (число, геометрическая фигура, вектор, координаты) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;

  2. умение работать с геометрическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений;

  3. овладение навыками устных, письменных, инструментальных вычислений;

  4. овладение геометрическим языком, умение использовать его для описания предметов окружающего мира, развитие пространственных представлений и изобразительных умений, приобретение навыков геометрических построений;

  5. усвоение систематических знаний о плоских фигурах и их свойствах, а также на наглядном уровне- о простейших пространственных телах, умение применять систематические знания о них для решения геометрических и практических задач;

  6. умение измерять длины отрезков, величины углов, использовать формулы для нахождения периметров, площадей объёмов геометрических фигур;

  7. умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, калькулятора, компьютора.



СОДЕРЖАНИЕ КУРСА ГЕОМЕТРИИ ДЛЯ 7-9 КЛАССОВ



1. Начала геометрии

История возникновения и развития геометрии. Основные геометрические фигуры и их свойства. Взаимное расположение точек на прямой.

Отрезок и луч. Равенство отрезков. Операции сложения и вычитания отрезков, умножения и деления отрезка на натуральное число. Измерение длины отрезка. Исторические сведения об измерении длин.

Полуплоскость и угол. Виды углов: прямой угол, острые и тупые углы, развёрнутый угол, смежные и вертикальные углы. Равенство углов. Биссектриса угла. Операции сложения и вычитания углов, умножения и деления угла на натуральное число. Теорема о равенстве вертикальных углов. Перпендикулярные прямые. Измерение величин углов. Исторические сведения об измерении углов.

Ломаные. Виды ломаных. Длина ломаной. Многоугольники. Элементы многоугольника. Периметр многоугольника. Выпуклые и невыпуклые многоугольники. Правильные многоугольники.

2. Треугольники

Треугольники. Виды треугольников: остроугольные, прямоугольные, тупоугольные, равнобедренные, равносторонние. Медиана, биссектриса и высота треугольника.

Равенство треугольников. Первый и второй признаки равенства треугольников. Равнобедренные треугольники и их свойства. Признак равнобедренного треугольника. Третий признак равенства треугольников.

Соотношения между сторонами и углами треугольника. Соотношения между сторонами треугольника.

Прямоугольные треугольники. Признаки равенства прямоугольных треугольников. Перпендикуляр и наклонная и их свойства.

3. Окружность и геометрические места точек

Понятия окружности и круга. Элементы окружности и круга: центр, радиус, диаметр, хорда. Взаимное расположение прямой и окружности. Касательная и секущая к окружности. Взаимное расположение двух окружностей.

Понятие о геометрическом месте точек. Примеры геометрических мест точек на плоскости. Построения с помощью циркуля и линейки. Примеры задач на построение.

4*. Кривые и графы

Парабола и её свойства. Касательная к параболе. Построение параболы и касательных к ней.

Эллипс и его свойства. Касательная к эллипсу. Построение эллипса и касательных к нему.

Гипербола и её свойства. Касательная к гиперболе. Построение гиперболы и касательных к ней.

Графы и их элементы: вершины, рёбра.

Задачи, приводящие к понятию графа. Задача Эйлера о кёнигсбергских мостах.

Уникурсальные графы и их свойства. Теорема Эйлера о числе вершин, рёбер и граней плоского графа.

Задача о трех домиках и трех колодцах. Проблема четырёх красок.

5. Параллельность

Параллельные прямые. Признаки параллельных прямых. Аксиома параллельных прямых. Свойства параллельных прямых. Исторические сведения.

Сумма углов треугольника. Сумма углов выпуклого n-угольника.

Параллелограмм. Прямоугольник. Ромб. Квадрат. Их свойства. Признаки параллелограмма.

Средняя линия треугольника. Трапеция. Равнобедренная и прямоугольная трапеции. Средняя линия трапеции. Теорема Фалеса.

6. Многоугольники и окружность

Углы, связанные с окружностью. Многоугольники, вписанные в окружность. Многоугольники, описанные около окружности. Вписанные и описанные окружности правильного многоугольника. Замечательные точки треугольника.

7. Движение

Понятие движения и его свойства. Центральная симметрия. Центрально-симметричные фигуры. Поворот. Симметрия n-го порядка. Осевая симметрия. Фигуры, симметричные относительно некоторой оси. Параллельный перенос. Равенство фигур.

8. Подобие

Подобие треугольников. Признаки подобия треугольников. Подобие фигур. Гомотетия. *Золотое сечение. Теорема Пифагора.

9. Элементы тригонометрии

Тригонометрические функции острого угла прямоугольного треугольника: синус, косинус, тангенс, котангенс.

Тригонометрические тождества. Тригонометрические функции тупого угла. Теорема косинусов. Теорема синусов. Длина окружности. Число 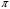. Длина дуги окружности. *Циклоидальные кривые.

10. Площадь

Понятие площади плоской фигуры. Измерение площадей. Равновеликие и равносоставленные фигуры.

Площадь прямоугольника. Площади параллелограмма, треугольника, трапеции. Формула Герона.

Площадь многоугольника. Площадь правильного многоугольника. Площади круга, сектора и сегмента.

Соотношение между площадями подобных фигур. *Изопериметрическая задача. *Задачи на разрезание.

11. Координаты и векторы

Прямоугольная система координат. Исторические сведения. Кординаты середины отрезка. Расстояние между точками. Уравнение окружности.

Векторы. Сложение векторов. Умножение вектора на число. Координаты вектора. Скалярное произведение векторов.

Уравнение прямой. *Аналитическое задание фигур на плоскости. *Задачи оптимизации.

Тригонометрические функции произвольного угла. *Полярные координаты.

12. Начала стереометрии

Основные понятия стереометрии. Фигуры в пространстве. Многогранники, их элементы. Примеры многогранников.

Угол в пространстве. Взаимное расположение прямых и плоскостей в пространстве. Параллельность в пространстве.

Сфера и шар. Их основные элементы.

Выпуклые многогранники. Теорема Эйлера для выпуклых многогранников.

Правильные, полуправильные, звёздчатые многогранники. Моделирование многогранников. Кристаллы – природные многогранники. Исторические сведения.

Ориентация плоскости. Лист Мёбиуса.

Площадь поверхности и объём.

Планируемые результаты изучения курса геометрии.

Начала стереометрии : • распознавать на чертежах, рисунках, моделях и в окружающем мире плоские и пространственные геометрические фигуры;

• распознавать развёртки куба, прямоугольного параллелепипеда, правильной пирамиды, цилиндра и конуса;

• строить развёртки куба и прямоугольного параллелепипеда;

• определять по линейным размерам развёртки фигуры линейные размеры самой фигуры, и наоборот;

• вычислять объём прямоугольного параллелепипеда.

Выпускник получит возможность:

• научиться вычислять объёмы пространственных геометрических фигур, составленных из прямоугольных параллелепипедов;

• углубить и развить представления о пространственных геометри-ческих фигурах;

• научиться применять понятие развёртки для выполнения практических расчётов.


Геометрические фигуры (треугольники, окружность и геометрические места точек, многоугольники и окружность элементы тригонометрии, подобие)

Выпускник научится:

• пользоваться языком геометрии для описания предметов окружающего мира и их взаимного расположения;

• распознавать и изображать на чертежах и рисунках геометрические фигуры и их конфигурации;

• находить значения длин линейных элементов фигур и их отношения, градусную меру углов от 0 до 180°, применяя определения, свойства и признаки фигур и их элементов, отношения фигур (равенство, подобие, симметрии, поворот, параллельный перенос);

• оперировать с начальными понятиями тригонометрии и выполнять элементарные операции над функциями углов;

• решать задачи на доказательство, опираясь на изученные свойства фигур и отношений между ними и применяя изученные методы доказательств;

• решать несложные задачи на построение, применяя основные алгоритмы построения с помощью циркуля и линейки;

• решать простейшие планиметрические задачи в пространстве.

Выпускник получит возможность:

• овладеть методами решения задач на вычисления и доказательства: методом от противного, методом подобия, методом перебора вариантов и методом геометрических мест точек;

• приобрести опыт применения алгебраического и тригонометрического аппарата и идей движения при решении геометрических задач;

• овладеть традиционной схемой решения задач на построение с помощью циркуля и линейки: анализ, построение, доказательство и исследование;

• научиться решать задачи на построение методом геометрического места точек и методом подобия;

• приобрести опыт исследования свойств планиметрических фигур с помощью компьютерных программ;

• приобрести опыт выполнения проектов по темам: «Геометрические преобразования на плоскости», «Построение отрезков по формуле».

Измерение геометрических величин ( площади, треугольники, окружность и геометрические места точек, многоугольники и окружность)

Выпускник научится:

• использовать свойства измерения длин, площадей и углов при решении задач на нахождение длины отрезка, длины окружности, длины дуги окружности, градусной меры угла;

• вычислять площади треугольников, прямоугольников, параллелограм-мов, трапеций, кругов и секторов;

• вычислять длину окружности, длину дуги окружности;

• вычислять длины линейных элементов фигур и их углы, используя формулы длины окружности и длины дуги окружности, формулы площадей фигур;

• решать задачи на доказательство с использованием формул длины окружности и длины дуги окружности, формул площадей фигур;

• решать практические задачи, связанные с нахождением геометрических величин (используя при необходимости справочники и технические средства).

Выпускник получит возможность научиться:

• вычислять площади фигур, составленных из двух или более прямоу-гольников, параллелограммов, треугольников, круга и сектора;

• вычислять площади многоугольников, используя отношения равновели-кости и равносоставленности;

• применять алгебраический и тригонометрический аппарат и идеи движения при решении задач на вычисление площадей многоугольников.

Координаты и векторы

Выпускник научится:

• вычислять длину отрезка по координатам его концов; вычислять координаты середины отрезка;

• использовать координатный метод для изучения свойств прямых и окружностей.

Выпускник получит возможность:

• овладеть координатным методом решения задач на вычисления и доказательства;

• приобрести опыт использования компьютерных программ для анализа частных случаев взаимного расположения окружностей и прямых;

• приобрести опыт выполнения проектов на тему «Применение координатного метода при решении задач на вычисления и доказательства».

Векторы

Выпускник научится:

• оперировать с векторами: находить сумму и разность двух векторов, заданных геометрически, находить вектор, равный произведению заданного вектора на число;

• находить для векторов, заданных координатами: длину вектора, координаты суммы и разности двух и более векторов, координаты произведения вектора на число, применяя при необходимости сочетательный, переместительный и распределительный законы;

• вычислять скалярное произведение векторов, находить угол между векторами, устанавливать перпендикулярность прямых.

Выпускник получит возможность:

• овладеть векторным методом для решения задач на вычисления и доказательства;

• приобрести опыт выполнения проектов на тему «применение векторного метода при решении задач на вычисления и доказательства».

ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ

Содержание

Количество часов

Количество контрольных работ


7 КЛАСС.

Начала геометрии

20

1


Равенство треугольников

26

2


Окружность и геометрические места точек.

16

2


Повторение

6

1


ИТОГО

68

6


8 КЛАСС.

Параллельность

21

1


Многоугольники и окружность

9

1


Движение

14

1


Подобие.

20

1


Итоговое повторение

4

1


Итого.

68

5


9 класс

Площадь.

22

1


Координаты и векторы

20

3


Начала стереометрии

16

1


Итоговое повторение

10

1


Итого

68

6



7 КЛАСС

Вариант I (2 ч в неделю, всего 68 ч)



Основное содержание по темам

Характеристика основных видов деятельности ученика

(на уровне учебных действий)

1. Начала геометрии (20 ч)

История возникновения и развития геометрии. Основные геометрические фигуры и их свойства. Взаимное расположение точек на прямой.

Отрезок и луч. Равенство отрезков. Операции сложения и вычитания отрезков, умножения и деления отрезка на натуральное число. Измерение длины отрезка. Исторические сведения об измерении длин.

Полуплоскость и угол. Виды углов: прямой угол, острые и тупые углы, развёрнутый угол, смежные и вертикальные углы. Равенство углов. Биссектриса угла. Операции сложения и вычитания углов, умножения и деления угла на натуральное число. Теорема о равенстве вертикальных углов. Перпендикулярные прямые. Измерение величин углов. Исторические сведения об измерении углов.

Ломаные. Виды ломаных. Длина ломаной. Многоугольники. Элементы многоугольника. Периметр многоугольника. Выпуклые и невыпуклые многоугольники. Правильные многоугольники.

Приводить исторические сведения о возникновении и развитии геометрии.

Изображать точки и прямые на плоскости.

Формулировать определения и иллюстрировать понятия: отрезка, равенства отрезков, длины отрезка. Производить операции сложения и вычитания отрезков, умножения и деления отрезка на натуральное число.

Измерять длину отрезка с помощью линейки.

Решать задачи на нахождение длины отрезка.

Формулировать определения и иллюстрировать понятия: луча, угла, равенства углов. Различать виды углов. Производить операции сложения и вычитания углов, умножения и деления угла на натуральное число.

Измерять величину угла с помощью транспортира. Решать задачи на нахождение величины угла.

Формулировать определения и иллюстрировать понятия ломаной и многоугольника. Распознавать и приводить примеры ломаных и многоугольников. Решать задачи на нахождение длины ломаной и периметра многоугольника.

2. Треугольники (26 ч)

Треугольники. Виды треугольников: остроугольные, прямоугольные, тупоугольные, равнобедренные, равносторонние. Медиана, биссектриса и высота треугольника.

Равенство треугольников. Первый и второй признаки равенства треугольников. Равнобедренные треугольники и их свойства. Признак равнобедренного треугольника. Третий признак равенства треугольников.

Соотношения между сторонами и углами треугольника. Соотношения между сторонами треугольника.

Прямоугольные треугольники. Признаки равенства прямоугольных треугольников. Перпендикуляр и наклонная и их свойства.

Формулировать определения: треугольника, равенства треугольников, медианы, биссектрисы и высоты треугольника. Различать виды треугольников.

Формулировать признаки равенства треугольников, применять их при решении задач.

Устанавливать соотношения между сторонами и углами треугольника, применять их при решении задач.

Формулировать определения перпендикуляра и наклонной. Использовать соотношение между ними при решении задач.

3. Окружность и геометрические места точек (16 ч)

Понятия окружности и круга. Элементы окружности и круга: центр, радиус, диаметр, хорда. Взаимное расположение прямой и окружности. Касательная и секущая к окружности. Взаимное расположение двух окружностей.

Понятие о геометрическом месте точек. Примеры геометрических мест точек на плоскости. Построения с помощью циркуля и линейки. Примеры задач на построение.

Формулировать определения и иллюстрировать понятия окружности, круга и их элементов.

Изображать, распознавать и описывать взаимное расположение прямой и окружности, двух окружностей.

Приводить примеры геометрических мест точек.

Решать задачи на нахождение геометрических мест точек.

Решать задачи на построение с с помощью циркуля и линейки.

Итоговое повторение (6 ч)



8 КЛАСС

Вариант I (2 ч в неделю, всего 68 ч)



Основное содержание по темам

Характеристика основных видов деятельности ученика

(на уровне учебных действий)

5. Параллельность (21 ч)

Параллельные прямые. Признаки параллельных прямых. Аксиома параллельных прямых. Свойства параллельных прямых. Исторические сведения.

Сумма углов треугольника. Сумма углов выпуклого n-угольника.

Параллелограмм. Прямоугольник. Ромб. Квадрат. Их свойства. Признаки параллелограмма.

Средняя линия треугольника. Трапеция. Равнобедренная и прямоугольная трапеции. Средняя линия трапеции. Теорема Фалеса.

Формулировать определение параллельных прямых и аксиому параллельных.

Распознавать на рисунках и изображать параллельные прямые.

Называть углы, образованные при пересечении двух параллельных прямых секущей.

Приводить исторические сведения об аксиоме параллельных и Н.И. Лобачевском.

Формулировать и доказывать теоремы о сумме углов треугольника и выпуклого n-угольника.

Распознавать, формулировать определение и изображать: параллелограмм, прямоугольник, ромб, квадрат, трапецию, равнобедренную и прямоугольную трапеции.

Формулировать и доказывать свойства и признаки параллелограмма, прямоугольника, ромба, квадрата.

Формулировать определение и изображать среднюю линию: треугольника, трапеции.

Формулировать и доказывать теоремы о срединих линиях треугольника и трапеции, теорему Фалеса.

Решать задачи на построение, доказательство и вычисление.

6. Многоугольники и окружность (9 ч)

Углы, связанные с окружностью. Многоугольники, вписанные в окружность. Многоугольники, описанные около окружности. Вписанная и описанная окружности правильного многоугольника. Замечательные точки треугольника.

Формулировать определения и изображать углы, связанные с окружностью.

Формулировать и доказывать теоремы об углах, связанных с окружностью.

Решать задачи на нахождение углов, связанных с окружностью.

Формулировать определения и изображать многоугольники, вписанные в окружность и описанные около окружности.

Формулировать и доказывать теоремы о вписанной и описанной окружностях треугольника и правильного многоугольника.

Изображать замечательные точки треугольника.

Формулировать и доказывать теоремы о замечательных точках треугольника.

7. Движение (11 ч)

Понятие движения и его свойства. Центральная симметрия. Центрально-симметричные фигуры. Поворот. Симметрия n-го порядка. Осевая симметрия. Фигуры, симметричные относительно некоторой оси. Параллельный перенос. Равенство фигур.

Формулировать определение и иллюстрировать понятие: движения, центральной симметрии, поворота, симметрии n-го порядка, осевой симметрии, параллельного переноса.

Приводить примеры симметричных фигур.

Изображать фигуры, симметричные данным.

Формулировать определение равенства фигур.

Решать задачи на нахождение элементов симметрии и установление равенства фигур.

8. Подобие (10 ч)

Подобие треугольников. Признаки подобия треугольников. Подобие фигур. Гомотетия. Теорема Пифагора.

Формулировать определение и иллюстрировать понятие подобия треугольников.

Распознавать подобные треугольники на рисунках.

Формулировать и доказывать признаки подобия треугольников.

Решать задачи на нахождение элементов подобных треугольников.

Формулировать определения подобия и гомотетии.

Изображать фигуры, подобные и гомотетичные данным.

Формулировать и доказывать теорему Пифагора. Применять её при решении задач.

Приводить исторические сведения о Пифагоре.

Решать задачи с практическим содержанием с использованием подобия и теоремы Пифагора.

9. Элементы тригонометрии (13 ч)

Тригонометрические функции острого угла прямоугольного треугольника: синус, косинус, тангенс, котангенс.

Тригонометрические тождества. Тригонометрические функции тупого угла. Теорема косинусов. Теорема синусов. Длина окружности. Число . Длина дуги окружности.


Формулировать определения и иллюстрировать понятия синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника.

Выражать тригонометрические функции острого угла прямоугольного треугольника через его стороны.

Формулировать и доказывать тригонометрические тождества.

Формулировать определения и выражать тригонометрические функции тупого угла через тригонометрические функции острых углов.

Формулировать и доказывать теоремы косинусов и синусов.

Решать задачи на нахождение тригонометрических функций и сторон треугольника.

Формулировать определения длины окружности.

Указывать приближённые значения числа .

Устанавливать соответствие между величиной центрального угла и длиной дуги окружности.

Решать задачи на нахождение длины дуги окружности.

Итоговое повторение (4 ч)

9 КЛАСС

Вариант I (2 ч в неделю, всего 68 ч)



Основное содержание по темам

Характеристика основных видов деятельности ученика

(на уровне учебных действий)

10. Площадь (22 ч)

Понятие площади плоской фигуры. Измерение площадей. Равновеликие и равносоставленные фигуры.

Площадь прямоугольника. Площади параллелограмма, треугольника, трапеции. Формула Герона.

Площадь многоугольника. Площадь правильного многоугольника. Площади круга, сектора и сегмента.

Соотношение между площадями подобных фигур.

Формулировать определение и иллюстрировать понятие площади плоской фигуры.

Выводить формулы площадей прямоугольника, параллелограмма, треугольника и трапеции, правильного многоугольника, круга, сектора и сегмента.

Решать задачи на нахождение площадей плоских фигур.

11. Координаты и векторы (19 ч)

Прямоугольная система координат. Исторические сведения. Кординаты середины отрезка. Расстояние между точками. Уравнение окружности.

Векторы. Сложение векторов. Умножение вектора на число. Координаты вектора. Скалярное произведение векторов.

Уравнение прямой. Тригонометрические функции произвольного угла.


Формулировать определение и иллюстрировать понятие прямоугольной системы координат.

Приводить исторические сведения о Р. Декарте.

Выводить и использовать формулы координат середины отрезка, расстояния между точками, уравнения прямой и окружности.

Формулировать определение и иллюстрировать понятие: вектора, длины (модуля) вектора, коллинеарных и равных векторов, угла между векторами, суммы и разности векторов, умножения вектора на число, скалярного произведения векторов.

Выполнять операции над векторами.

Находить длину вектора, координаты вектора, угол между векторами и скалярное произведение векторов.

Формулировать определение и находить тригонометрические функции прозвольного угла.

Выполнять проекты, связанные с использованием координатного и векторного методов при решении задач на вычисление и доказательство.

12. Начала стереометрии (17 ч)

Основные понятия стереометрии. Фигуры в пространстве. Многогранники, их элементы. Примеры многогранников.

Угол в пространстве. Взаимное расположение прямых и плоскостей в пространстве. Параллельность в пространстве.

Сфера и шар. Их основные элементы.

Выпуклые многогранники. Теорема Эйлера для выпуклых многогранников.

Правильные, полуправильные и звёздчатые многогранники. Моделирование многогранников. Кристаллы – природные многогранники.

Исторические сведения.

Площадь поверхности и объём.


Изображать точки, прямые и плоскости в пространстве.

Формулировать определение и изображать: куб, параллелепипед, призму, пирамиду, правильные многогранники, цилиндр, конус, сферу и шар.

Устанавливать взаимное расположение прямых и плоскостей в пространстве.

Формулировать определения и приводить примеры выпуклых и невыпуклых многогранников.

Формулировать теорему Эйлера о выпуклых многогранниках и использовать её при решении задач.

Формулировать определения и приводить примеры полуправильных и звёздчатых многогранников.

Моделировать многогранники, используя развёртки и геометрический конструктор.

Приводить примеры кристаллов и устанавливать их форму.

Находить площади поверхностей и объёмы некоторых многогранников и круглых тел.

Итоговое повторение (10 ч)


Литература:

Составляющие УМК:

  • Программно-методические материалы "Геометрия" 7-11 кл.

  • Учебник "Геометрия" 7-9 кл. Авт.: И.М. Смирнова, В.А. Смирнов

  • Рабочие тетради "Геометрия" 7, 8, 9 классы.

  • Дидактические материалы "Геометрия" 7, 8, 9 классы. Авт.: И.М. Смирнова, В.А. Смирнов

  • Методические рекомендации для учителя "Геометрия" 7, 8, 9 классы. Авт.: И.М. Смирнова, В.А. Смирнов

  • Учебное пособие "Нестандартные и исследовательские задачи" 7-11 кл. Авт.: И.М. Смирнова, В.А. Смирнов

Литература для учителя

  1. Геометрия 7-9 класс / Авт.: И.М. Смирнова, В.А. Смирнов

  2. А. П. Ершова, В. В. Голобородько, А. С. Ершова «Самостоятельные и контрольные работы по алгебре и геометрии для 8 класса». Разноуровневые дидактические материалы. М: Илекса, 2002 год.

  3. Б. Г. Зив, В. М. Мейлер «Дидактические материалы по геометрии», Москва, «Просвещение», 1998 год

Литература для учащихся

  1. Геометрия 7-9 класс / Авт.: И.М. Смирнова, В.А. Смирнов

  2. А. П. Ершова, В. В. Голобородько, А. С. Ершова «Самостоятельные и контрольные работы по алгебре и геометрии для 8 класса». Разноуровневые ; дидактические материалы. М.: Илекса, 2002 год.

Для информационно-компьютерной поддержки учебного процесса предполагается использование следующих программно-педагогических средств, реализуемых с помощью компьютера:

1. CD «1С: Репетитор. Математика» (К и М)

2. «Математика, 5-11»

Для обеспечения плодотворного учебного процесса предполагается использование информации и материалов следующих Интернет - ресурсов:

  1. Министерство образования РФ: http://www.innformika.ru /; http://www.ed.gov.ru/; http://www.edu/ru/

  2. Тестирование^ - 11 классы: http://www.kokch.ru/cdo/

  3. Педагогическая мастерская, уроки в Интернет и многое другое: http://teacher.fio.ru

  4. Новые технологии в образовании: http://edu.secna.ru/main/

  5. Путеводитель «В мире науки» для школьников: http://www.uic.ssu.samara.ru/nauka/

  6. Мегаэнциклопедия Кирилла и Мефодия: http://mega.km.ru

  7. Сайты «Энциклопедий», например: http://www.rubicon.ru/; http://www.encyclopedia.ru

Интернет-сайты для математиков:

www.ege.moipkro.ru

www.fipi.ru
www/ruedu.ru

www.mioo.ru

www.1september.ru

www.math.ru

www.allmath.ru

www.uztest.ru

http://www.catalog.alledu.ru/predmet/math/more2.html

http://shade.lcm.msu.ru:8080/index.jsp

http://wwwexponenta.ru/

http://comp-science.narod.ru/

http://methmath.chat.ru/index.html

http://www.mathnet.spb.ru/

http://vip.km.ru/vschool/demo/education.asp?subj=292

http://www.uchportal.ru/load/25-2-2/

http://www. mirurokov.ru/gdz-po-algebre-7-klass-mordkovich.html

http://www.zavuch.info/component/mtree/tochnie/algebra/algurok/

http://www.unimath.ru/?mode=1&idstructure=40000

Геометрия 10 класс ФГОС

Геометрия 11 класс ФГОС

Математика 5 класс ФГОС

Алгебра 10 класс ФГОС

Электронная тетрадь по математике 5...

Геометрия 8 класс ФГОС

Наглядная геометрия 5-6 классы ФГОС

Электронная тетрадь по алгебре 8 класс...
Скачать

© 2015, 4092 263

Похожие файлы

0 Нет комментариев

Вебинар для учителей

Свидетельство об участии БЕСПЛАТНО!

Полезное для учителя

Новости проекта
03.06.24

Лайфхак учителя №1! Что делать с плохой накопляемостью отметок

12.05.24

Лайфхак учителя №2! Как перестать бегать от ученика к ученику во время практической работы

04.05.24

Лайфхак учителя №3! Что делать, если вы устали из урока в урок повторять одно и то же