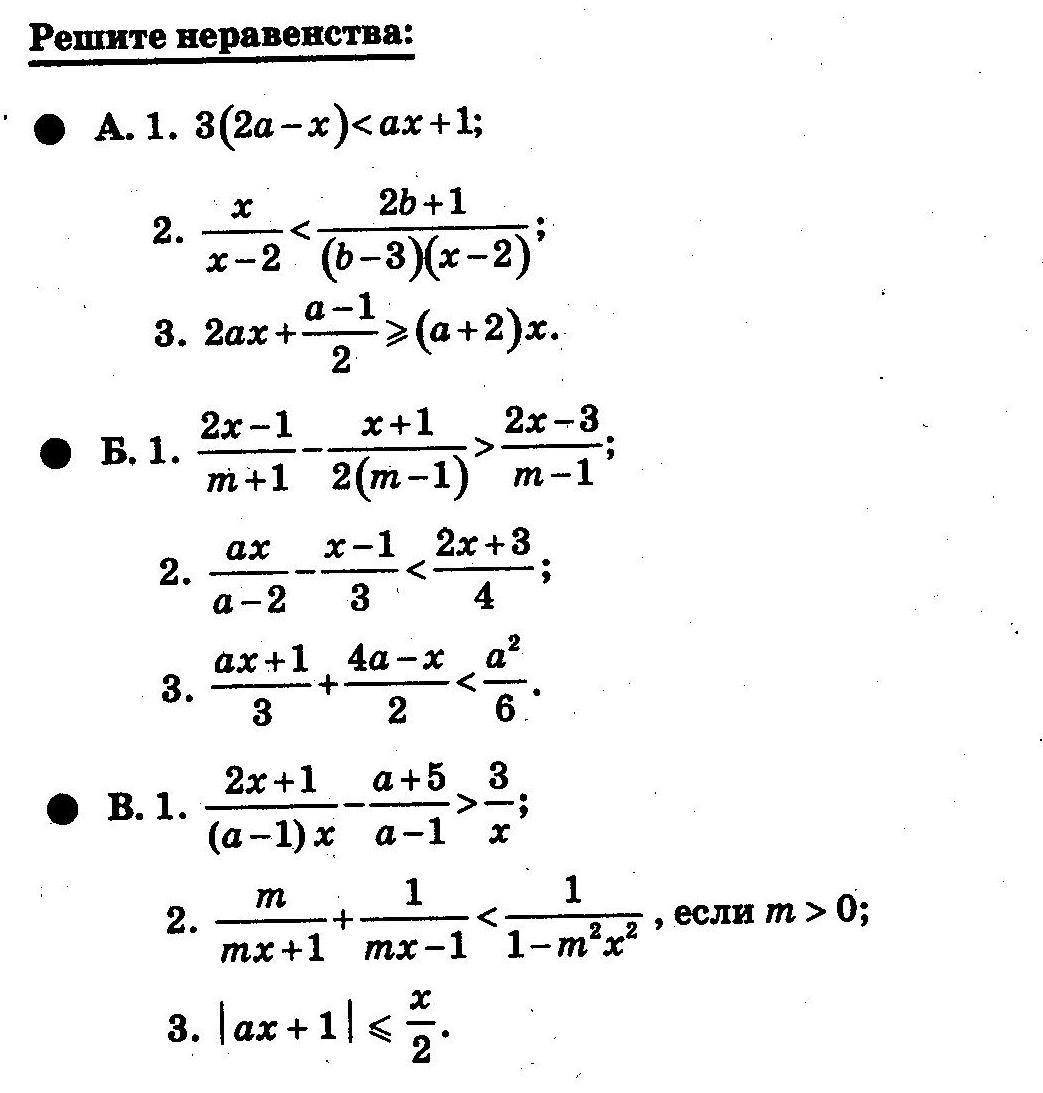Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа им. В.В.Николаева с.Чуваш-Карамалы
муниципального района Аургазинский район Республики Башкортостан
Рассмотрена Согласована Утверждена
на заседании ШМО зам.директора по УВР приказом № _112_
протокол № _1_ ________ /Леонтьева Л.Ф./ от «_18_» _августа_ 2017 г.
от «_17_» _августа_ 2017 г. от «_18_» _августа_ 2017 г. Директор ________ /Пашкин В.Х./ ________ /Леонтьев Ю.Х./
Рабочая программа
элективного курса «Решение примеров на параметры»
(указать предмет, курс, модуль)
По математике_______________________________________________________________
указать предмет, курс, модуль
Класс 10
Количество часов 34 Уровень базовый
(базовый, профильный)
Учитель Умова Надежда Леонидовна
2017 г.
Пояснительная записка
Рабочая программа элективного курса составлена на основе федерального компонента государственного стандарта среднего (полного) общего образования и на основе книги П.И.Горштейна, В.Б.Полонского, М.С.Якира «Решение примеров на параметры» и рассчитана на 34 часа (1 час в неделю).
Рабочая программа элективного курса по математике «Задачи с параметрами» рассчитана на учащихся 10-х классов, проявляющих интерес к предмету математика.
Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и дает примерное распределение учебных часов по разделам курса.
Примерная программа выполняет две основные функции.
Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета.
Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.
Изучение математики в основной школе направлено на достижение следующих целей:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
развитие вычислительных и формально-оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов (физика, химия, основы информатики и вычислительной техники), усвоение аппарата уравнений и неравенств как основного средства математического моделирования прикладных задач, осуществление функциональной подготовки школьников. В ходе изучения курса обучающиеся овладевают приёмами вычислений на калькуляторе.
Основным направлением модернизации математического школьного образования является отработка механизмов итоговой аттестации через введение единого государственного экзамена. В заданиях ЕГЭ по математике с развернутым ответом (часть С), а также с кратким ответом (часть В), встречаются задачи с параметрами. Появление таких заданий на экзаменах далеко не случайно, т.к. с их помощью проверяется техника владения формулами элементарной математики, методами решения уравнений и неравенств, умение выстраивать логическую цепочку рассуждений, уровень логического мышления учащегося и их математической культуры.
Решению примеров и задач с параметрами в школьной программе уделяется мало внимания. Большинство учащихся либо вовсе не справляются с такими задачами, либо приводят громоздкие выкладки. Причиной этого является отсутствие системы заданий по данной теме в школьных учебниках.
В связи с этим возникла необходимость в разработке и проведении элективного курса для старшеклассников по теме: «Решение примеров на параметры».
Решение примеров, задач, уравнений с параметрами, открывает перед учащимися значительное число эвристических приемов общего характера, ценных для математического развития личности, применяемых в исследованиях и на любом другом математическом материале. Именно такие задачи играют большую роль в формировании логического мышления и математической культуры у школьников, Поэтому учащиеся, владеющие методами решения задач с параметрами, успешно справляются с другими задачами.
Цели и задачи курса:
Формировать у учащихся умения и навыки по решению примеров, уравнений и задач с параметрами, сводящихся к исследованию линейных и квадратных уравнений, неравенств для подготовки к ЕГЭ и к обучению в вузе.
Изучение курса предполагает формирование у учащегося интереса к предмету, развитие их математических способностей, подготовку к ЕГЭ
Развивать исследовательскую и познавательную деятельность учащегося.
Обеспечить условия для самостоятельной творческой работы.
повышение математической культуры учащихся в рамках школьной программы по математике;
систематизация знаний и умений по стержневым темам курса математики старшей школы;
формирование и развитие у учащихся логического мышления, интеллектуальных и практических умений в области решения уравнений, неравенств, содержащих параметр;
умения самостоятельно приобретать и применять знания в различных ситуациях;
развитие творческих способностей; коммуникативных навыков, которые способствуют развитию умений работать в группе;
формирование навыков исследовательской деятельности учащихся; умение оценивать свои способности к математике и умению делать осознанный выбор профиля дальнейшего обучения;
подготовка к итоговой аттестации обучающихся.
Для реализации целей и задач данного курса предполагается использовать следующие формы занятий: лекции, практикумы по решению задач, семинары. Доминантной же формой учения должна стать исследовательская деятельность ученика, которая может быть реализована как на занятиях в классе, так и в ходе самостоятельной работы учащихся. Все занятия должны носить проблемный характер и включать в себя самостоятельную работу. Успешность усвоения курса определяется преобладанием самостоятельной творческой работы ученика. Такая организация занятий способствует реализации развивающих целей курса. Решение примеров на параметры дают прекрасный материал для настоящей учебно-исследовательской работы.
Образовательная программа «Решение примеров на параметры» направлена на реализацию концепции стандарта образования, на расширение школьного курса математики, подготовку к итоговой аттестации.
Отличительной особенностью курса является систематизация и классификация заданий с параметром и методов их решения по основным разделам курса математики 10 класса. Разделы программы свободно могут перемещаться в рамках курса, без ущерба для общей цели и результата, в зависимости от основной программы.
Прогнозируемый результат: овладение учащимися навыками решения уравнений и неравенств, содержащих параметры, интерпретации результатов своей деятельности; умением делать выводы и обсуждать результаты; успешная сдача ЕГЭ.
При составлении программы элективного курса использовались следующие принципы.
1. Принцип регулярности. Основная работа происходит в классе на совместных занятиях и дома, индивидуально. Полноценная подготовка невозможна без достаточно большого количества часов, посвященных работе над задачей. При этом лучше заниматься понемногу, но часто, скажем, по часу ежедневно, чем раз в неделю, но по многу часов. Хорошо бы еженедельно набирать по 10 часов, включая классные занятия. Заниматься математикой, думать можно, даже гуляя на улице (но не переходя при этом проезжую часть).
2. Принцип параллельности. Несмотря на то что учебное пособие разбито на отдельные главы по темам, было бы совершенно неправильно изучать эти темы последовательно, одну за другой. Следует постоянно держать в поле зрения несколько (две-три) тем, постепенно продвигаясь по ним вперед и вглубь.
3. Принцип опережающей сложности. Не следует загружать ученика большой по объему, но несложной работой, так же как и ставить его в положение лисицы перед виноградом, задавая непосильные для него задачи. Слишком легко и слишком трудно — равно плохо. Напомним, что оптимальными для развития цивилизации оказались широты, климатические условия которых, не позволяя человеку расслабиться, в то же время не превращали его жизнь в сплошную борьбу за существование. На практике реализовать этот принцип можно, например, следующим образом. Задавая на дом очередную недельную порцию задач (от 10 до 15), желательно подобрать их так, чтобы 7-8 из них были доступны практически всем слушателям элективного курса, 3-4 были бы по силам лишь некоторым, а 1-2, пусть не намного, но превышают возможности даже самых сильных учеников. Ученик имеет право отложить трудную задачу, если он потрудился над ее решением определенное время, скажем, один час, и она у него не получилась. В этом случае процесс усвоения новых идей будет более эффективным. Действие этого принципа будет тем лучше, чем ближе друг к другу по уровню математического развития члены факультатива. Кроме того, он развивает такие полезные качества, как сознательность, внутренняя честность, научное честолюбие.
4. Принцип смены приоритетов. Приоритет идеи. В период накопления идей, а также при решении достаточно трудных задач ученику прощаются небольшие и даже средние огрехи в решении задачи; главное — правильная идея решения, которая может быть доведена до числа за разумное время. Именно так действуют иногда и экзаменационные комиссии вузов при оценке решений наиболее сложных конкурсных задач. Приоритет ответа. При отработке уже известных идей, а также при решении наиболее простых, стандартных задач главное — правильный ответ.
5. Принцип вариативности. Очень полезно на примере одной задачи рассмотреть различные приемы и методы решения, а затем сравнить получившиеся решения с различных точек зрения: стандартность и оригинальность, объем вычислительной и объяснительной работы, эстетическая и практическая ценность.
6. Принцип самоконтроля. Большинство людей склонны прощать себе небольшие (да и крупные) ошибки. Школьники не исключение. Проявлением этого недостатка, имеющего большие последствия на экзамене, является привычка подстраиваться под ответ. Решив задачу, получив ответ и заглянув в конец учебника, обнаружив некоторые, иногда серьезные, расхождения, ученик делает кое-какие исправления, в результате которых его ответ соответствует ответу, данному в учебнике, и считает, что все в порядке, хотя задача не решена. Регулярный и систематический анализ своих ошибок и неудач должен быть непременным элементом самостоятельной работы.
7. Принцип быстрого повторения. По мере накопления числа решенных задач следует просматривать и некоторым образом раскладывать по полочкам образовавшийся задачный архив примерно по следующей схеме: эта задача простая — я ее без труда решил в свое время и сейчас вижу весь путь решения от начала до конца. Эта задача потруднее — я ее в свое время не решил (решил с трудом, нашел правильную идею, но запутался в вычислениях), но хорошо помню ее решение, данное учителем (товарищем). И наконец, эту задачу я не решил, объяснение вроде бы понял, но сейчас не могу восстановить в своей памяти. Надо разобраться в своих записях или же спросить об этой задаче учителя.
8. Принцип работы с текстом. Школьные учебники приучили учеников иметь дело с текстами разжеванными; более или менее сложные места, как правило, предваряются объяснениями учителя. Учебник читают, а не изучают с карандашом, бумагой и напряжением мысли. А ведь работа со сложными научными текстами, понять которые иногда не проще, чем решить небольшую проблему,— будни научного работника. В предлагаемом пособии немало трудных задач, снабженных лишь краткими указаниями. Понять эти указания, заполнить логические пробелы, выполнить промежуточные вычисления, рассмотреть самостоятельно варианты, сопровождающиеся оборотом «аналогично»,— главное назначение этих задач.
9. Принцип моделирования ситуаций. Полезно моделировать критические ситуации, которые могут возникнуть на экзамене, и отрабатывать стереотипы поведения.
Основные формы организации учебных занятий: беседа, практическая работа, семинар. Разнообразный дидактический материал дает возможность отбирать дополнительные задания для обучающихся разной степени подготовки: уровень сложности задач варьируется от простых до конкурсных и олимпиадных. Все занятия направлены на развитие интереса школьников к предмету, на расширение представлений об изучаемом материале, на решение новых и интересных задач. Одним из образовательных результатов является разработка и защита проектов обучающимися.
Требования к уровню подготовки учащихся
В результате изучения курса учащийся должен:
усвоить основные приемы и методы решения примеров, уравнений, неравенств систем уравнений с параметрами;
применять алгоритм решения уравнений, неравенств, содержащих параметр,
проводить полное обоснование при решении задач с параметрами;
овладеть исследовательской деятельностью.
Содержание тем учебного курса
Тема 1. Параметр: понятие, общие методы решения, поиск решений уравнений, неравенств, их систем (2 ч.)
Основная цель - определение уравнения и неравенства с параметром, области определения уравнения с параметром; общие приемы решения заданий с параметром. Учащимся раскрывается содержание понятия параметр, его интерпретация, основные теоремы.
Тема 2. Методы решения задач с параметром (2 ч.)
Основная цель - введение различных методов решения задач с параметром. Учащимся дается характеристика каждого метода решения задач с параметром; обоснование выбора метода решения в зависимости от условия, вопроса задачи.
Тема 3. Линейные уравнения и неравенства, уравнения и неравенства приводимые к линейным (2 ч.)
Основная цель - формирование навыка решения линейных уравнений и неравенств с параметром, а также уравнений и неравенств, приводимых к ним.
Тема 4. Квадратные уравнения и неравенства (4 ч.)
Основная цель - формирование навыка решения квадратных уравнений и неравенств с параметром, исследовать квадратный трехчлен, знаки корней в зависимости от параметра. определение квадратного трехчлена и квадратного уравнения, решения уравнений выделением полного квадрата, уравнений по формуле, методы решения неполных квадратных уравнений. Методы решения квадратных неравенств. В ходе практических занятий рассматриваются задания различной степени сложности,
Тема 5. Дробно-рациональные уравнения и неравенства (6 ч.)
Основная цель - формирование навыка решения дробных уравнений, содержащих параметр, различных типов и различными методами.
Тема 6. Графические интерпретации. Свойства функций в задачах с параметрами (3 ч.)
Основная цель - познакомить учащихся с графическим приемом решения заданий с параметрами, формировать умение использовать свойства функций при решении задач с параметрами. На практических занятиях рассмотреть свойства монотонности функций, ограниченности области значений, экстремальные свойства.
Тема 7. Тригонометрия (8 ч.)
Основная цель - введение методов решения тригонометрических задач с параметром: преобразование выражений, решение уравнений и неравенств. В ходе практических занятий рассматриваются задания различной степени сложности,
Тема 8. Показательные уравнения и неравенства (6 ч.)
Основная цель - формирование навыка оценки основания степени, решения показательных уравнений и неравенств различного вида.
Тема 9. Зачет (1 ч.)
Основная цель - подведение итогов изучения курса «Решение примеров на параметры» в 10 классе.
Календарно-тематический план
| № п/п | Раздел программы | Количество часов |
| 1 | Параметр: понятие, общие методы решения, поиск решений уравнений, неравенств, их систем | 2 |
| 2 | Методы решения задач с параметром | 2 |
| 3 | Линейные уравнения и неравенства, уравнения и неравенства приводимые к линейным | 2 |
| 4 | Квадратные уравнения и неравенства | 4 |
| 5 | Дробно-рациональные уравнения и неравенства | 6 |
| 6 | Графические интерпретации. Свойства функций в задачах с параметрами | 3 |
| 7 | Тригонометрия | 8 |
| 8 | Показательные уравнения и неравенства | 6 |
| 9 | Зачет | 1 |
Программа предусматривает: лекций - 9, практикумов - 18, практических работ – 1, проверочных работ - 1, самостоятельных работ - 3, тестов - 1, зачетов - 1.
| Тематическое планирование |
| № урока | № урока в теме | Содержание учебного материала (раздела, темы) | Кол-во часов | Форма проведения/ контроля | Дата проведения | Примечание |
| по плану | по факту |
| I ПОЛУГОДИЕ
1 урок неделю, 16 уроков за полугодие |
| Тема 1. Параметр: понятие, общие методы решения (2 ч.) |
| 1 | 1 | Параметр: понятие, общие методы решения, поиск решений уравнений, неравенств, их систем | 1 | Лекция | 08.09. |
|
|
| 2 | 2 | Параметр: понятие, общие методы решения, поиск решений уравнений, неравенств, их систем | 1 | Практикум | 15.09. |
|
|
| Тема 2. Методы решения задач с параметром (2 ч.) |
| 3 | 1 | Методы решения задач с параметром | 1 | Лекция | 23.09. |
|
|
| 4 | 2 | Методы решения задач с параметром | 1 | Практикум | 30.09. |
|
|
| Тема 3. Линейные уравнения и неравенства, уравнения и неравенства приводимые к линейным (2 ч.) |
| 5 | 1 | Линейные уравнения и неравенства, уравнения и неравенства приводимые к линейным | 1 | Лекция | 07.10. |
|
|
| 6 | 2 | Линейные уравнения и неравенства, уравнения и неравенства приводимые к линейным | 1 | Практическая работа | 14.10. |
|
|
| Тема 4. Квадратные уравнения и неравенства (4 ч.) |
| 7 | 1 | Квадратные уравнения | 1 | Лекция | 21.10. |
|
|
| 8 | 2 | Квадратные уравнения | 1 | Практикум | 28.10. |
|
|
| 9 | 3 | Квадратные неравенства | 1 | Практикум | 11.11. |
|
|
| 10 | 4 | Квадратные неравенства | 1 | С/р № 1 | 18.11. |
|
|
| Тема 5. Дробно-рациональные уравнения и неравенства (6 ч.) |
| 11 | 1 | Дробно-рациональные уравнения | 1 | Лекция | 25.11. |
|
|
| 12 | 2 | Дробно-рациональные уравнения | 1 | Практикум | 02.12. |
|
|
| 13 | 3 | Дробно-рациональные неравенства | 1 | Тест | 09.12. |
|
|
| 14 | 4 | Дробно-рациональные неравенства | 1 | Практикум | 16.12. |
|
|
| 15 | 5 | Решение дробно-рациональных уравнений и неравенств | 1 | Практикум | 23.12. |
|
|
| 16 | 6 | Решение дробно-рациональных уравнений и неравенств | 1 | С/р № 2 | 30.12. |
|
|
| II ПОЛУГОДИЕ
1 урок неделю, 18 уроков за полугодие |
| Тема 6. Графические интерпретации. Свойства функций в задачах с параметрами (3 ч.) |
| 17 | 1 | Графические интерпретации | 1 | Лекция | 20.01. |
|
|
| 18 | 2 | Свойства функций в задачах с параметрами | 1 | Практикум | 27.01. |
|
|
| 19 | 3 | Свойства функций в задачах с параметрами | 1 | Практикум | 03.02. |
|
|
| Тема 7. Тригонометрия (8 ч.) |
| 20 | 1 | Тригонометрические уравнения | 1 | Лекция | 10.02. |
|
|
| 21 | 2 | Тригонометрические уравнения | 1 | Лекция | 17.02. |
|
|
| 22 | 3 | Тригонометрические неравенства | 1 | Практикум | 24.02. |
|
|
| 23 | 4 | Тригонометрические неравенства | 1 | Практикум | 03.03. |
|
|
| 24 | 5 | Тригонометрические уравнения и системы уравнений | 1 | Практикум | 10.03. |
|
|
| 25 | 6 | Тригонометрические уравнения и системы уравнений | 1 | Практикум | 17.03. |
|
|
| 26 | 7 | Аналитические и графические приемы решения задач | 1 | Практикум | 24.03. |
|
|
| 27 | 8 | Аналитические и графические приемы решения задач | 1 | С/р № 3 | 07.04. |
|
|
| Тема 8. Показательные уравнения и неравенства (6 ч.) |
| 28 | 1 | Показательные уравнения | 1 | Лекция | 14.04. |
|
|
| 29 | 2 | Показательные уравнения | 1 | Практикум | 21.04. |
|
|
| 30 | 3 | Показательные неравенства | 1 | Практикум | 28.04. |
|
|
| 31 | 4 | Показательные неравенства | 1 | Практикум | 05.05. |
|
|
| 32 | 5 | Решение показательных уравнений и неравенств | 1 | Практикум | 12.05. |
|
|
| 33 | 6 | Решение показательных уравнений и неравенств | 1 | Проверочная работа | 19.05. |
|
|
| Тема 9. Зачет (1 ч.) |
| 34 | 1 | Зачет | 1 | Зачет | 26.05. |
|
|
Перечень учебно-методической литературы
1. Литература для учителя:
1. М.Я.Выгодский Справочник по элементарной математике. М. «Астель Аст», 2003
2. С.А. Субханкулова. Элективный курс «Задачи с параметрами», издательство «Илекса», 2010.
3. Горнштейн П.И., В.Б. Полонский, М.С.Якир «Задачи с параметрами». - М.: Гимназия, 2008.
4. И.С. Петряков Математические кружки. М. « Просвещение», 1997
5. Л.Я.Фальке Изучение сложных тем курса алгебры в средней школе. М. «Илекса», 2006
6. А.П.Карп Сборник задач по алгебре и началам анализа 10-11 кл. М., «Просвещение», 1999
7. В.В.Амелькин, В.Рабцевич. Задачи с параметром. Минск. 1996.
8. П.И.Горнштейн, В.Б.Полонский, М.С.Якир Задачи с параметрами. М. «Илекса».2005.
9. Г.А.Ястребинецкий. Уравнения и неравенства, содержащие параметры. М.1989.
10. А.Х.Шахмейстер. Задачи с параметрами в ЕГЭ.С.-Петербург.М. 2004.
11. http://www.internet-scool.ru - сайт Интернет – школы издательства Просвещение.
12. http://www.legion.ru – сайт издательства «Легион»
13. http://www.intellectcentre.ru – сайт издательства «Интеллект-Центр», где можно найти учебно-тренировочные материалы, демонстрационные версии, банк тренировочных заданий с ответами, методические рекомендации и образцы решений
14. http://www.fipi.ru - портал информационной поддержки
2. Литература для учителя:
1. С.А. Субханкулова. Элективный курс «Задачи с параметрами», издательство «Илекса», 2010.
Горнштейн П.И., В.Б. Полонский, М.С.Якир «Задачи с параметрами». - М.: Гимназия, 2008.
Крамор В.С. Математика. Типовые примеры на вступительных экзаменах. - М.: Аркти, 2009.
Математика для поступающих в вузы // сост. А.А.Тырымов. – Волгоград: Учитель, 2010.
Математика. Задачи М.И.Сканави. - Минск; В.М.Скакун, г. 2011.
Математика. «Первое сентября», № 4, 22, 23-2010 г; №12, 38-2010.
Нырко В.А.,Табуева В.А. Задачи с параметрами. - Екатеринбург; УГТУ, 2009.
Ястребинецкий Г.А. Задачи с параметрами. – М. Просвещение, 2009.
Потапов М.К., Олехник С.Н., Нестеренко Ю.В. Уравнения и реравенства с параметрами. Издат МГУ, 2011.
К.П.Сикорский Дополнительные главы по курсу математики. М., «Просвещение», 1996.
М.Л.Галицкий Сборник задач по алгебре 8-9 кл. М. «Просвещение», 2000.
Горбачев В.И. Методы решения уравнений и неравенств с параметрами, Брянск, 2010.
В.В.Локоть. Задачи с параметрами и их решения.Тригонометрия.М.Аркти.2002.
И.Ф.Шарыгин. Факультативный курс по математике. Решение задач. Учебное пособие для 10, 11 класса средней школы.М.1989.
Материалы по подготовке к ЕГЭ, 2013-2015.
Электронный учебник «Алгебра, 7 – 11».
Интерактивный курс подготовки к ЕГЭ «Математика», cd-диск, 2013.
http://www.intellectcentre.ru – сайт издательства «Интеллект-Центр», где можно найти учебно-тренировочные материалы, демонстрационные версии, банк тренировочных заданий с ответами, методические рекомендации и образцы решений.
http://www.fipi.ru - портал информационной поддержки ЕГЭ.
3. Интернет-ресурсы
http://www.ege.edu.ru/
http://site-infocenter.ru/
http://www.fipi.ru
http://4ege.ru/
http://www.ctege.org/razdel.php?s=&razdelid=239 – книги для подготовки к ЕГЭ
http://uztest.ru/exam
http://alexlarin.narod.ru/ege.html
http://zadachi.mccme.ru/work/JavaScript/treenow.htm
http://www.allmath.ru/
Методические рекомендации:
Тема 1. Лекция носит установочный характер и готовит учащихся к практической деятельности, а именно к решению упражнений, связанных с решением заданий с параметром. Во время практических занятий учащиеся коллективно, а затем по группам работают над примерами различной степени сложности, содержащими параметр.
Тема 2. Из содержания лекции учащиеся знакомятся с методами решения задач с параметрами: графический, аналитический, координатно-параметрический. Практические занятия рекомендуется проводить в форме фронтальной работы, отрабатывая применение различных методов решения задач с параметром. Завершающим этапом проводится практическая работа.
Тема 3. Краткая лекция на основе базовых знаний о линейных уравнениях и неравенствах, способах их решения. На практических занятиях отрабатываются навыки решения линейных уравнений и уравнений и неравенств и систем линейных уравнений и неравенств с параметром, графическим и аналитическим способом. Итогом служит проверочная работа.
Тема 4. Краткая лекция на основе базовых знаний о квадратных уравнениях и неравенствах, способах их решения. На практических занятиях отрабатываются навыки решения различных типов квадратных уравнений и неравенств с параметром, графическим и аналитическим способом, решения уравнений выделением полного квадрата, решения уравнений по формуле, методы решения неполных квадратных уравнений. Рассмотреть примеры применения теоремы Виета, обратной теореме Виета, определение знаков корней квадратного уравнения в зависимости от значений параметра, теоремы о расположении корней относительно заданной точки или заданного промежутка, алгоритм нахождения наибольшего и наименьшего значений квадратичной функции. Итоговое занятие по теме - проверочная работа.
Тема 5. Практические занятия проводить, используя как коллективную форму обучения, так и индивидуальную. На практических занятиях рассматривать решения уравнений, неравенств начиная с простых и заканчивая содержащими несколько параметров, используя метод интервалов.
Тема 6. На первом занятии целесообразно повторить свойства и графики основных функций. Определить, на каких свойствах основано решение задач с параметрами. На практических занятиях следует обратить внимание на аналитические и графические приемы решения задач. Провести самостоятельную работу с целью выявления уровня умения находить способы решения задач такого типа. В завершении – практикум по решению уравнений неравенств.
Тема 7. На первых занятиях целесообразно повторить теоретический материал по решению тригонометрических уравнений и неравенств, формул преобразования тригонометрических выражений. На практических занятиях следует обратить внимание на аналитические и графические приемы решения задач. При решении простейших неравенств необходимо опираться на геометрическую интерпретацию. Самостоятельная работа – итог работы по теме. В завершении – практикум по решению неравенств.
Тема 8. Из содержания лекции учащиеся на базовом уровне повторяют основные свойства показательной функции, методы оценки основания степени. Практические занятия рекомендуется проводить в группах, по карточкам-заданиям, с последующим обсуждением решения, его рациональности. Завершающим этапом проводится проверочная работа.
Тема 9. Завершающим этапом изучения элективного курса в 10 классе является зачет, который проводится в виде проверочной работы.
Приложения
Тема 3. Линейные уравнения и неравенства, уравнения и неравенства приводимые к линейным.

Тема 4. Квадратные уравнения и неравенства.

Тема 5. Дробно-рациональные уравнения и неравенства.
Дидактические материалы
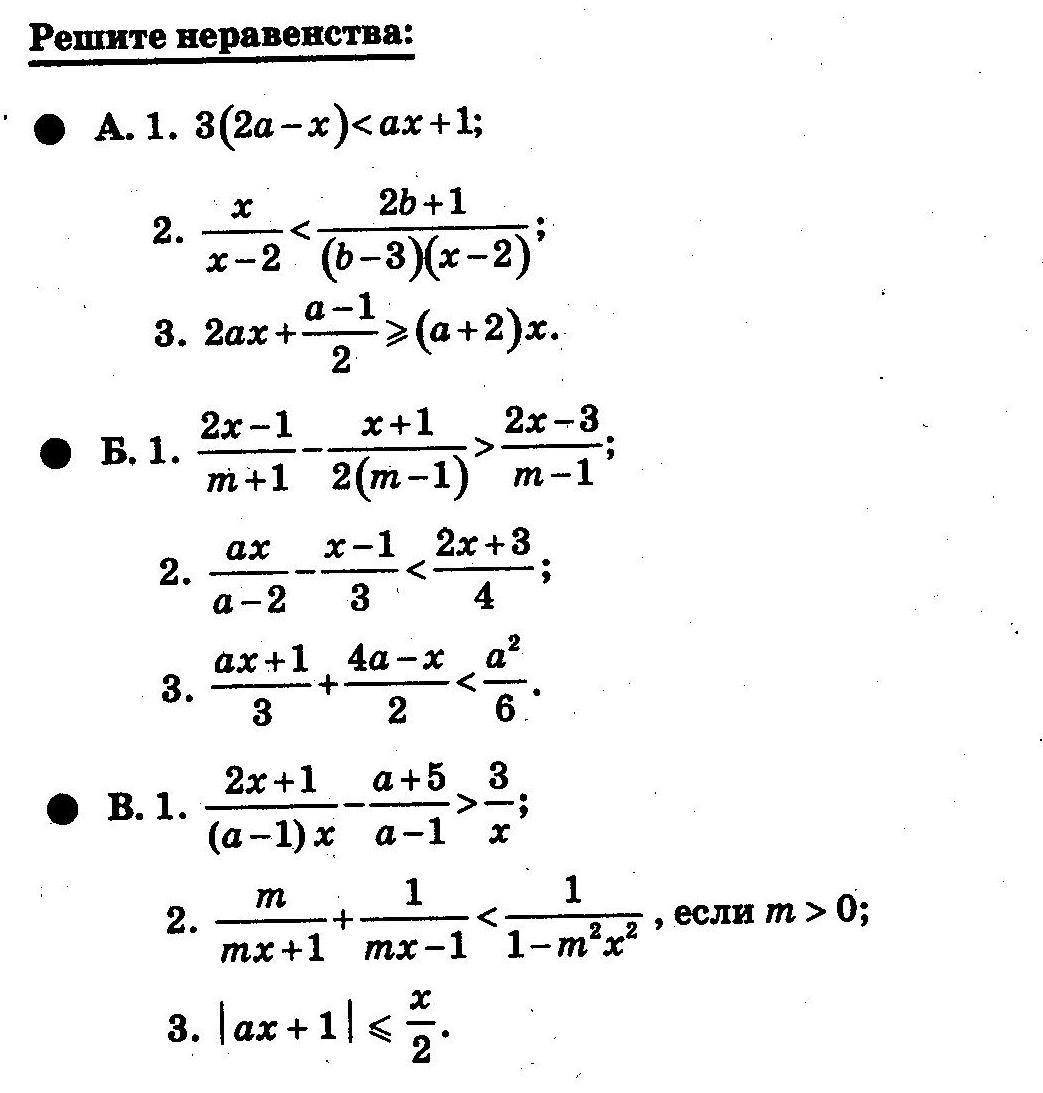



Тема 6. Графические интерпретации. Свойства функций в задачах с параметрами.
Дидактические материалы

Тема 7. Трансцендентные уравнения и неравенств.
Дидактические материалы


Тема 8. Иррациональные уравнения и неравенства.
Дидактические материалы
Самостоятельная работа № 1
Вариант 1
1. Решите уравнение a� �+3ax- (a+2) =0
�+3ax- (a+2) =0
2. Найдите все значения параметра а, при которых сумма корней и сумма квадратов корней уравнения равны� �2ах +2а - 1=0.
�2ах +2а - 1=0.
Вариант 2
1. Решите уравнение � �
�
2. Найдите все значения параметра а, при которых оба корня уравнения больше -1.
Самостоятельная работа № 2
Вариант 1
1. При каких значениях параметра а неравенство (а-1)� �-4х�
�-4х� �а+4 справедливо при всех х�
�а+4 справедливо при всех х� �0 ?
�0 ?
2. Решить неравенство при всех значениях параметра а� �.
�.
Вариант 2
1. При каких значениях параметра а неравенство (а+4)� �- 3ах +2�
�- 3ах +2� � -5а�
� -5а� �0 справедливо при всех х�
�0 справедливо при всех х� �0 ?
�0 ?
2. Решить неравенство при всех значениях параметра а� � �
� � �6.
�6.
Самостоятельная работа № 3
Вариант 1
1. При каких значениях параметра а уравнение � �-(а+0,5)�
�-(а+0,5)� �+0,5а=0 имеет ровно три корня на отрезке �
�+0,5а=0 имеет ровно три корня на отрезке � �?
�?
2. При каких значениях параметра а число π является периодом функции f(х)=� � ?
� ?
3. При каких значениях параметра а уравнения являются равносильными � �, 4�
�, 4� � а�
� а� �.
�.
Вариант 2
1. При каких значениях параметра а уравнение 2(� �+1) �
�+1) � �+1=0 не имеет решений?
�+1=0 не имеет решений?
2. Найдите наименьшее положительное значение параметра а, при котором функция f(х)=3а� �- 2�
�- 2� � ) является нечетной?
� ) является нечетной?
3. Сколько решений имеет уравнение � � на интервале � �?
�?
Самостоятельная работа № 4
Вариант 1
1. Найти все значения параметра а, при которых функция F(х) = 2� �+48ах +6х-5 возрастает на всей числовой прямой.
�+48ах +6х-5 возрастает на всей числовой прямой.
2. При каких значениях параметра а наибольшее значение функции f(х)=� �+5а�
�+5а� �+2а на отрезке �
�+2а на отрезке � � достигается в двух различных точках?
� достигается в двух различных точках?
3. В пирамиде АВСД проводятся сечения параллельные ребрам АД и ВС. В каком отношении сечение наибольшей площади делит ребро АС?
Вариант 2
1. При каких значениях параметра а из точки М(а,-1) можно провести три различные касательные к графику функции f(х)=� �?
�?
2. При каких значениях параметра а наименьшее значение функции f(х)=� � на промежутке �
� на промежутке � � достигается на правом конце?
� достигается на правом конце?
3. В правильную четырехугольную пирамиду вписан шар. Второй шар, имеющий радиус 1, касается первого шара и всех боковых граней пирамиды. При каком значении радиуса первого шара пирамида имеет наименьший объем?
Самостоятельная работа № 4
Вариант 1
1. Найдите все значения параметра а при которых множество решений � �неравенства содержит точку х = 1 .
�неравенства содержит точку х = 1 .
2. Для каждого значения с решите неравенство � �
�
Вариант 2
1. Найдите все значения параметра а, при котором уравнение � �= � � имеет два различных решения.
�= � � имеет два различных решения.
2. Для каждого значения с решите неравенство с -2� �(с-1)�
�(с-1)� �.
�.