РАБОЧАЯ ПРОГРАММА ПО АЛГЕБРЕ
8 КЛАСС
(профильный уровень)
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая программа по алгебре для 8 класса (профильный уровень) составлена в соответствии с Федеральным государственным образовательным стандартом основного общего образованиям на основе Фундаментального ядра содержания общего образования, Требований к результатам освоения основной образовательной программы основного общего образования. За основу взята Примерная программа основного общего образования по математике, а также программа для классов с углубленным изучением математики / А.Г.Мерзляк, В.Б.Полонский, М.С.Якир, Е.В.Буцко. – М.: Вентана-Граф, 2014
В рабочей программе учтены идеи и положения Концепции развития математического образования в Российской Федерации (утв. распоряжением Правительства РФ от 24.12.2013), Программы развития и формирования универсальных учебных действий, которые обеспечивают овладение ключевыми компетенциями, составляющими основу для саморазвития и непрерывного образования, целостность общекультурного, личностного и познавательного развития учащихся, в том числе коммуникативных качеств личности.
Данная программа ориентирована на реализацию системно-деятельностного подхода к процессу обучения, который обеспечивает соответствие учебной деятельности учащихся их возрасту и индивидуальному развитию, а так же построение разнообразных образовательных индивидуальных траекторий для каждого учащегося, в том числе для одарённых детей.
Рабочая программа составлена в соответствии с Основной образовательной программой основного общего образования МАОУ «Центр образования № 13 имени Героя Советского Союза Н.А.Кузнецова».
Рабочая программа по алгебре для 8 класса представляет собой целостный документ, включающий пояснительную записку, планируемые результаты изучения предмета, содержание учебного предмета, тематическое планирование, учебно-методическое и материально-техническое обеспечение.
Программа соответствует учебнику «Алгебра 8 класс» / А.Г.Мерзляк, В.М.Поляков. – М., Вентана-Граф, 2018.
Данная программа конкретизирует содержание предметных тем, дает примерное распределение учебных часов по разделам курса, рекомендуемую последовательность изучения тем и разделов с учетом межпредметных и внутрипредметных связей, логики учебного процесса, возрастных особенностей учащихся.
Предлагаемая программа выполняет две основные функции:
информационно-методическая - позволяет получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами математики;
организационно-планирующая – предусматривает выделение этапов обучения, определения качественных и количественных характеристик учебного материала на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.
Сознательное овладение учащимися системой алгебраических знаний и умений необходимо в повседневной жизни, для изучения смежных дисциплин и продолжения образования. Математическая подготовка необходима для понимания принципов устройства и использования современной техники, восприятия научных и технических понятий и идей. Математика является языком науки и техники. С ее помощью моделируются и изучаются явления и процессы, происходящие в природе. Практическая значимость школьного курса алгебры обусловлена тем, что его объектом являются количественные отношения действительного мира. Практические умения и навыки алгебраического характера необходимы для трудовой деятельности и профессиональной подготовки школьников.
Важнейшей задачей школьного курса алгебры является развитие логического мышления учащихся. Сами объекты математических умозаключений и принятые в алгебре правила их конструирования способствуют формированию умений обосновывать и доказывать суждения, приводить четкие определения, развивают логическую интуицию, кратко и наглядно вскрывают механизм логических построений и учат их применению. Раскрывая внутреннюю гармонию математики, формируя понимание красоты и изящества математических рассуждений, алгебра вносит значительный вклад в эстетическое воспитание учащихся.
Развитие у учащихся правильных представлений о сущности и происхождении алгебраических абстракций, соотношении реального и идеального, характере отражения математической наукой явлений и процессов реального мира, месте алгебры в системе наук и роли математического моделирования в научном познании и в практике способствует формированию научного мировоззрения учащихся, формированию качеств мышления, необходимых для адаптации в современном информационном обществе.
Язык алгебры подчеркивает значение математики как языка построения математических моделей, процессов и явлений реального мира. Одной из основных задач алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Изучение алгебры, в частности, функций, вероятности и статистики способствует расширению кругозора учащихся, знакомству их с индукцией и дедукцией, обобщением и конкретизацией, анализом и синтезом, классификацией и систематизацией, абстрагированием, аналогией. Активное использование задач на всех этапах учебного процесса развивает творческие способности школьников.
Алгебра, требуя от учащихся умственных и волевых усилий, концентрации внимания, активности развитого воображения, развивает нравственные черты личности (настойчивость, целеустремленность, самостоятельность, ответственность, трудолюбие, дисциплину, творческую активность и критичность мышления) и умение аргументировано отстаивать свои взгляды и убеждения, а также способность принимать самостоятельные решения.
Изучение алгебры позволяет формировать умения и навыки умственного труда – планирование работы, поиск рациональных путей ее выполнения, критическая оценка результатов. Использование в алгебре наряду с естественным языком нескольких математических дает возможность развивать у учащихся точную, экономную и информативную речь, умение отбирать наиболее подходящие языковые (в частности, символические, графические) средства. В процессе обучения алгебры школьники должны научиться излагать свои мысли ясно и исчерпывающе, лаконично и емко, приобрести навыки четкого, аккуратного и грамотного выполнения математических записей.
Изучение алгебры в 8 классе направлено на достижение следующих целей:
формирование целостного представления о современном мире;
развитие интеллектуальных и творческих способностей учащихся, а так же индивидуальности личности;
формирование осознанного выбора индивидуальной образовательной траектории.
В построении программы обучения алгебре ведущими методологическими ориентирами выступают интегративный подход к построению обучения с ориентацией на метапредметные святи, современные концепции математического образования в общеобразовательной школе, принцип личностно ориентированного развивающего обучения.
Задачи изучения курса алгебры 8 класса сформулированы в соответствии с ФГОС и с учетом особенностей общеобразовательного учреждения:
овладеть символьным языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений;
формировать специфические для математики качества мышления, необходимые человеку для полноценного функционирования в современном обществе, и в частности логического, алгоритмического и эвристического мышления;
продолжить формирование у учащихся способностей к организации своей учебной деятельности посредством освоения личностных, познавательных, регулятивных и коммуникативных универсальных учебных действий;
продолжить приобретение опыта самостоятельной математической деятельности по получению нового знания, его преобразованию и применению;
продолжить всестороннее развитие обучаемых, формирование у них способностей к самоизменению и саморазвитию;
способствовать развитию нравственных качеств, создающих условия для успешного вхождения в культуру и созидательную жизнь общества;
способствовать созданию здоровьесберегающей информационно-образовательной среды.
ОБЩАЯ ХАРАКТЕРИСТИКА УЧЕБНОГО ПРЕДМЕТА
Содержание курса алгебры 8 класса с углублённым изучением математики представлено в виде следующих содержательных разделов «Алгебра», «Множества», «Основы теории делимости», «Функции», «Элементы прикладной математики», «Алгебра в историческом развитии».
Содержание раздела «Алгебра» формирует знания о математическом языке, необходимые для решения математических задач, задач из смежных дисциплин, а так же практических задач. В данном разделе формируется целостная система преобразований алгебраических выражений, которая служит фундаментом аппарата, используемого в решении различных математических задач в курсе алгебры и математического анализа. Изучение материала способствует формированию у учащихся математического аппарата и задач с помощью уравнений и систем уравнений, а так же решения уравнений, систем уравнений с модулями и параметрами. Материал данного раздела представлен в аспекте, способствующем формированию у учащихся умения пользоваться алгоритмами. Существенная роль при этом отводится развитию алгоритмического мышления — важной составляющей интеллектуального развития человека.
Содержание раздела «Множества» нацелено на математическое развитие учащихся, формирование у них умения точно, сжато и ясно излагать мысли в устной и письменной речи. Материал раздела развивает понятие о числе, расширяет круг задач, при решении которых используются операции над множествами.
Изучение раздела «Основы теории делимости» раскрывает прикладное и теоретическое значение математики в окружающем мире, формирует представления об объектах исследования современной математики.
Цель содержания раздела «Функции» — получение школьниками конкретных знаний о функции как важнейшей математической модели для описания и исследования процессов и явлений окружающего мира. Материал способствует развитию воображения и творческих способностей учащихся, формирует умение использовать различные языки математики (словесный, символический, графический), расширяет круг методов математических доказательств, включая в него, в частности, метод математической индукции, позволяет раскрыть общенаучную роль современной математики.
Содержание раздела «Элементы прикладной математики» раскрывает прикладное и практическое значение математики в современном мире.
Раздел «Алгебра в историческом развитии» направлен на формирование ценностного отношения к алгебре как науке, воспитание уважения к учёным, которые внесли вклад в развитие науки, понимание основополагающих достижений классической и современной алгебры.
ОСОБЕННОСТИ ОРГАНИЗАЦИИ ОБРАЗОВАТЕЛЬНОГО ПРОЦЕССА
Согласно действующему в ОУ учебному плану программа ориентирована на детей 13 – 15 лет и составлена с учетом их возрастных особенностей. При организации учебного процесса надо обращать внимание на такую психологическую особенность данного возраста как избирательность внимания: дети легко откликаются на необычные, захватывающие формы работы, но быстрая переключаемость внимания не дает им возможности сосредоточиться долго на одном деле. дети в этом возрасте склонны к спорам и возражениям, особенностью их мышления является критичность. У ребят появляется свое мнение, которое они стараются демонстрировать. Этот возраст благоприятен для творческого развития. Учащимся нравиться решать проблемные ситуации, находить сходства и различия, различать причину и следствие, участвовать в дискуссиях, отстаивать и доказывать свою правоту.
Поэтому система уроков сориентирована не на передачу готовых знаний, а на формирование активной личности, мотивированной к самообразованию, обладающей достаточными навыками и психологически готовой к самообразованию.
Законом «Об образовании в РФ» учителю предоставляется право самостоятельного выбора методических путей и приемов решения образовательных и воспитательных задач. Рациональная система методов и приемов обучения, ее оптимизация с учетом возрастных особенностей учащихся, уровня их математической подготовки является важным условием правильной организации учебно-воспитательного процесса. В зависимости от указанных факторов необходимо сбалансировать сочетание традиционных и инновационных методов обучения, оптимизировать применение объяснительно-иллюстративных и эвристических методов, рационально использовать современные технические средства. Учебный процесс должен быть сориентирован на оптимальное сочетание устных и письменных видов работы как при изучении теории, так и при решении задач. Внимание направлено на развитие у учащихся навыков умственного труда (планирование своей работы, поиск рациональных путей ее выполнения, критическую оценку результатов), культуры устной и письменной математической речи.
В ходе изучения курса алгебры 8 класса обучающиеся должны развить умения по формированию собственного алгоритма решения познавательных задач: формулировать проблему и цели своей работы, определять адекватные способы и методы решения задачи, прогнозировать ожидаемый результат и сопоставлять его с собственными математическими знаниями. Обучающиеся должны научиться представлять результаты индивидуальной и групповой познавательной деятельности в формах конспекта, реферата, презентации.
Одной из главных особенностей курса алгебры является то, что в нем реализуется взаимосвязь принципов научности и доступности и уделяется особое внимание обеспечению прочного усвоения основ математических знаний всеми учащимися. Преподавание ведется с учетом принципов проблемного, развивающего, опережающего обучения. Такая особенность курса как практическая направленность служит стимулом для развития у учащихся интереса к алгебре, а также основой для формирования осознанных математических навыков и умений.
Принципиальным положением организации математического образования является дифференциация и индивидуализация обучения. Это означает, что осваивая курс математики, одни школьники в своих результатах ограничиваются уровнем базовой обязательной подготовки, зафиксированным в образовательном стандарте, другие, в соответствии со своими склонностями и способностями достигают более высоких результатов. При этом каждый имеет право самостоятельно решить ограничиться базовым уровнем или двигаться дальше. Развитие интереса к математике является важнейшей задачей учителя.
Особое место в овладении курсом отводится работе по формированию навыков саморегуляции: самоконтроля и самопроверки.
Для обеспечения достижения обязательных результатов обучения важное значение имеет организация контроля знаний и умений учащихся. Виды контроля: стартовый, текущий, тематический, промежуточный, итоговый. Формы контроля: фронтальный опрос, индивидуальная работа у доски, индивидуальная работа по карточкам, дифференцированная самостоятельная работа, дифференцированная проверочная работа, математический диктант, практическая работа, тесты, теоретические зачеты, контрольная работа. Текущий контроль осуществляется после изучения каждого основного раздела, форма проведения – контрольная работа. В конце года оценка результатов обучения проводится в виде переводного экзамена, который включает задания по основным вопросам курса алгебры 8 класса.
Формы работы – фронтальная, индивидуальная, групповая, парная.
Педагогическим инструментом реализации поставленных целей в курсе алгебры 8 класса являются следующие технологии - технология деятельностного метода, технология проблемного диалога, технология продуктивного чтения, технология развития критического мышления, технологии оценивания.
МЕСТО УЧЕБНОГО ПРЕДМЕТА В УЧЕБНОМ ПЛАНЕ
Учебный (образовательный) план на изучение алгебры в 8 классе в основной школе отводит 3 учебных часа в неделю в течение учебного года. Таким образом, рабочая программа рассчитана на 102 часа.
Методической особенностью курса «Алгебра» для классов физико-математического профиля является расширение традиционных учебных тем за счёт теоретико-множественной, вероятностно-статистической и историко-культурной линий. Содержание дополнительного материала не дублирует, а дополняет материал основного курса. Углубляется практическая направленность изучения тем «Вопросы теории делимости», «Уравнения и системы уравнений с модулями и параметрами» и некоторые другие. В течение учебного года предполагается включить обучающихся в проектную и научно-исследовательскую деятельность. Профильная дифференциация осуществляется за счет интенсификации обучения.
В программе предусмотрена возможность для реализации авторских подходов, использования разнообразных форм организации учебного процесса, внедрения современных методов обучения и педагогических технологий. В течение года возможны коррективы рабочей программы, связанные с объективными причинами.
ЛИЧНОСТНЫЕ, МЕТАПРЕДМЕТНЫЕ И ПРЕДМЕТНЫЕ
РЕЗУЛЬТАТЫ ОСВОЕНИЯ КУРСА
Программа выдвигает на первый план достижение учащимися следующих результатов освоения курса алгебры 8 класса:
в направлении личностного развития
воспитание российской гражданской идентичности: патриотизма, уважения к Отечеству, осознания вклада отечественных учёных в развитие мировой науки;
ответственное отношение к учению, готовность и способность обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию;
осознанный выбор и построение дальнейшей индивидуальной траектории образования с учётом устойчивых познавательных ин тересов, а также на основе формирования уважительного отношения к труду, развитие опыта участия в социально значимом труде;
умение контролировать, оценивать и анализировать процесс и результат учебной математической деятельности;
умение самостоятельно работать с различными источниками информации (учебные пособия, справочники, ресурсы Интернета и т.д.)
умение взаимодействовать со сверстниками, взрослыми в процессе образовательной, общественно полезной, учебно-исследовательской, творческой и других видов деятельности;
креативность, критичность мышления, инициатива, находчивость, активность при решении математических задач;
способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
освоение социальных норм, правил поведения, ролей и форм социальной жизни в группах и сообществах в пределах возрастных компетенций.
в метапредметном направлении
регулятивные универсальные учебные действия
умение самостоятельно определять цели своего обучения и приобретать новые знания, ставить и формулировать для себя новые задачи в учёбе, развивать мотивы и интересы своей познавательной деятельности;
умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией;
умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
умение оценивать правильность выполнения учебной задачи, ее объективную трудность и собственные возможности её решения;
понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
владение основами самоконтроля, самооценки, принятия решений и осуществления осознанного выбора в учебной и познавательной деятельности;
умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач.
познавательные универсальные учебные действия:
формирование первоначальных представлений об идеях и методах математики как универсальном языке науки и техники, средстве моделирования явлений и процессов;
умение определять понятия, выявлять их свойства и признаки, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации;
умения устанавливать причинно-следственные связи, строить логические рассуждения, умозаключения (индуктивные, дедуктивные, по аналогии), делать выводы;
развитие компетентности в области использования информационно-коммуникационных технологий;
умение видеть математическую задачу в контексте проблемной ситуации, в других дисциплинах, в окружающей жизни;
умение правильно и доступно излагать свои мысли в устной и письменной форме;
умение находить необходимую информацию в различных источниках (в справочниках, литературе, Интернете), представлять информацию в понятной форме, принимать решение в условиях неполной или избыточной, точной или вероятностной информации;
умение обрабатывать и анализировать полученную информацию;
умение понимать и использовать математические средства наглядности (диаграммы, таблицы, схемы и т.п.) для иллюстрации, интерпретации, аргументации;
умение выдвигать и реализовывать гипотезы для решения учебных задач, понимать необходимость их проверки;
умение находить различные способы решения математической задачи, решать познавательные и практические задачи;
приобретение опыта выполнения проектной деятельности
умения создавать, применять и преобразовывать знакосимволические средства, модели и схемы для решения учебных и познавательных задач;
умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач.
коммуникативные универсальные учебные действия:
умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников, общие способы работы;
работать индивидуально и в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов;
формулировать, аргументировать и отстаивать своё мнение.
в предметном направлении
осознание значения математики для повседневной жизни человека;
представление о математической науке как сфере математической деятельности, об этапах ее развития, о ее значимости для развития цивилизации;
развитие умений работать с учебным математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли с применением математической терминологии и символики, проводить классификации, логические обоснования;
умение оперировать понятиями по основным разделам содержания; проводить доказательства математических утверждений;
умение анализировать, структурировать и оценивать изученный предметный материал;
овладение системой функциональных понятий, развитие умения использовать функционально-графические представления для решения различных математических задач, для описания и анализа реальных зависимостей;
овладение символьным языком алгебры, практически значимыми математическими умениями и навыками, в том числе приемами выполнения тождественных преобразований рациональных выражений, решения уравнений, систем уравнений; умения моделировать реальные ситуации на языке алгебры, исследовать построенные модели с использованием аппарата алгебры, интерпретировать полученный результат;
развитие умений применять изученные понятия, результаты, методы для решения задач, в том числе практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, компьютера;
формирование информационной и алгоритмической культуры;
создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.
УЧЕБНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ КУРСА АЛГЕБРЫ 8 КЛАССА
| № п/п | Название темы, раздела | Кол-во часов на тему | Кол-во контр. работ |
| 1 | Множества и операции над ними | 6 | 1 |
| 2 | Рациональные выражения | 26 | 2 |
| 3 | Основы теории делимости | 8 | 1 |
| 4 | Неравенства | 14 | 1 |
| 5 | Квадратные корни. Действительные числа | 16 | 1 |
| 6 | Квадратные уравнения | 26 | 2 |
|
| Обобщающее повторение за курс алгебры 8 класса | 6 | 1 |
|
| Всего | 102 | 9 |
СОДЕРЖАНИЕ УЧЕБНОГО ПРЕДМЕТА
Множества и операции над ними ( 6 ч )
Множество. Подмножества данного множества. Операции над множествами. Формула включения-исключения. Взаимно-однозначное соответствие. Равномощные множества. Счетные множества.
Контрольная работа № 1 «Множества и операции над ними»
Рациональные выражения ( 26 ч )
Рациональные дроби. Допустимые значения переменных. Основное свойство рациональной дроби. Сложение и вычитание рациональных дробей с одинаковыми знаменателями. Сложение и вычитание рацональных дробей с разными знаменателями. Умножение и деление рациональных дробей. Возведение рациональной дроби в степень. Тождественные преобразования рациональных выражений.
Равносильные уравнения. Уравнение-следствие. Рациональные уравнения. Область определения уравнения. Рациональные уравнения с параметрами.
Степень с целым отрицательным показателем. Свойства степени с целым показателем. Функция у = 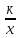 и ее график.
и ее график.
Контрольная работа № 2 «Рациональные выражения»
Контрольная работа № 3 «Рациональные уравнения. Степень с целым показателем»
Основы теории делимости ( 8 ч )
Делимость нацело и ее свойства. Деление с остатком. Сравнения по модулю и их свойства. Наибольший общий делитель и наименьшее общее кратное двух натуральных чисел. Взаимно простые числа. Алгоритм Евклида. Признаки делимости. Простые и составные числа. Основная теорема арифметики. Малая теорема Ферма.
Контрольная работа № 4 «Основы теории делимости»
Неравенства ( 14 ч )
Числовые неравенства и их свойства. Сложение и умножение числовых неравенств. Оценивание значения выражения. Основные методы доказательства неравенств.
Неравенства с одной переменной. Равносильные неравенства. Неравенства-следствия. Числовые промежутки. Линейные неравенства. Системы и совокупности линейных неравенств с одной переменной. Уравнения и неравенства, содержащие знак модуля.
Контрольная работа № 5 «Неравенства»
Квадратные корни. Действительные числа ( 16 ч )
Функция у = 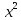 и ее график. Квадратные корни. Арифметический квадратный корень. Множество действительных чисел. Свойства арифметического квадратного корня. Тождественные преобразования выражений, содержащих арифметические квадратные корни. Функция у =
и ее график. Квадратные корни. Арифметический квадратный корень. Множество действительных чисел. Свойства арифметического квадратного корня. Тождественные преобразования выражений, содержащих арифметические квадратные корни. Функция у = 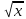 и ее график.
и ее график.
Контрольная работа № 6 «Квадратные корни. Действительные числа»
Квадратные уравнения ( 26 ч )
Квадратные уравнения. Решение неполных квадратных уравнений. Формула корней квадратного уравнения. Теорема Виета.
Квадратный трехчлен. Корни квадратного трехчлена. Свойства квадратного трехчлена. Разложение квадратного трехчлена на линейные множители.
Решение уравнений, сводящихся к квадратным уравнениям. Решение уравнений методом замены переменной. Уравнения, содержащие знак модуля.
Рациональные уравнения как математические модели реальных ситуаций.
Деление многочленов. Корни многочленов. Теорема Безу. Целое рациональное уравнение.
Контрольная работа № 7 «Квадратные уравнения»
Контрольная работа № 8 «Рациональные уравнения»
Обобщающее повторение за курс алгебры 8 класса ( 6 ч )
Итоговая контрольная работа № 9 (переводной экзамен)
ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ ИЗУЧЕНИЯ АЛГЕБРЫ В 8 КЛАССЕ
В результате изучения курса алгебры 8 класса
ученик научится:
оперировать понятием квадратного корня, применять понятие квадратного корня и его свойства в вычислениях;
выполнять преобразования выражений, содержащих степени с целыми показателями и квадратные корни;
выполнять тождественные преобразования рациональных выражений на основе правил действий над алгебраическими дробями;
выполять деление многочленов;
находить корни многочленов;
решать основные виды рациональных уравнений с одной переменной;
решать уравнения, содержащие знак модуля, уравнения с параметрами;
понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом;
применять графические представления для исследования уравнений с одной переменной;
понимать терминологию и символику, связанные с отношением неравенства, свойства числовых неравенств;
решать неравенства, системы и совокупности неравенств с одной переменной;
решать простейшие неравенства, содержащие знак модуля;
исследовать и решать простейшие неравенства с параметрами;
доказывать неравенства;
применять аппарат неравенств для решения задач из различных разделов курса и смежных дисциплин;
понимать терминологию и символику, связанные с понятием множества;
выполнять операции над множествами, устанавливать взаимно однозначное соответствие между множествами;
использовать начальные представления о множестве действительных чисел;
понимать терминологию и символику, связанные с понятием делимости;
применять основные свойства делимости нацело для решения простейших уравнений с двумя переменными в целых числах;
доказывать свойства и признаки делимости нацело;
использовать прием нахождения наибольшего общего делителя и наименьшего общего кратного двух натуральных чисел для решения задач;
использовать каноническое разложение составного числа на простые множители при решении задач;
понимать и использовать функциональные понятия и язык (термины, символические обозначения);
понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследования зависимостей между физическими, экономическими и тому подобными величинами;
строить графики элементарных функций, исследовать свойства числовых функций на основе изучения свойств их графиков;
работать с математическим текстом (анализировать, извлекать необходимую информацию), грамотно применять математическую терминологию и символику, использовать различные языки математики (словесный, символьный, графический, табличный), дополнительными источниками информации; точно и грамотно выражать свои мысли в устной и письменной речи;
составлять план решения задачи, выделять этапы ее решения, интерпретировать вычислительные результаты в задаче, исследовать полученное решение задачи.
ученик получит возможность научиться:
выполнять многошаговые преобразования рациональных выражений, применяя широкий набор способов и приемов;
применять тождественные преобразования рациональных выражений для решения задач из различных разделов курса;
овладеть специальными приемами решения уравнений с одной переменной; уверенно применять аппарат уравнений для решения разнообразных математических и практических задач, а также задач из смежных дисциплин;
применять графические представления для исследования уравнений с параметрами;
освоить разнообразные приемы доказательства неравенств; уверенно применять аппарат неравенств для решения разнообразных математических и практических задач, а также задач из смежных дисциплин;
применять графические представления для исследования неравенств с параметрами;
развивать представление о множествах;
применять операции над множествами для решения задач;
развивать представление о числе и числовых системах от натуральных до действительных чисел; о роли вычислений в практике;
развить и углубить знания о десятичной записи действительных чисел (периодические и непериодические дроби);
развивать представление о теории делимости;
использовать свойства делимости для решения математических задач из различных разделов курса;
проводить исследования, связанные с изучением свойств функций, в том числе с использованием компьютера; на основе графиков изученных функций строить более сложные графики (кусочно заданные, с «выколотыми» точками и т.п.);
использовать функциональные представления и свойства функций для решения математических задач из различных разделов курса;
использовать приемы, рационализирующие вычисления, приобрести привычку контролировать вычисления, выбирая подходящий для ситуации способ;
приобрести опыт построения и изучения математических моделей.
УЧЕБНО-МЕТОДИЧЕСКОЕ И МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ОБРАЗОВАТЕЛЬНОГО ПРОЦЕССА
Для учителя
Фундаментальное ядро содержания общего образования / под ред. В.В. Козлова, А.М. Кондакова. — М. : Просвещение, 2009.
Федеральный государственный образовательный стандарт основного общего образования.
Примерные программы основного общего образования.Математика. (Стандарты второго поколения.) — М. : Просвещение, 2010.
Программа по математике для классов с углубленным изучением математики / А.Г.Мерзляк, В.Б.Полонский, М.С.Якир, Е.В.Буцко. – М.: Вентана-Граф, 2014
Мерзляк А.Г. Алгебра : 8 класс : учебник для учащихся общеобразовательных учреждений / А.Г. Мерзляк, В.М. Поляков. — М. : Вентана-Граф, 2018.
Мерзляк А.Г. Алгебра : 8 класс : самостоятельные и контрольные работы : пособие для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, Е.М. Рабинович, М.С. Якир. — М. : Вентана-Граф, 2013.
Для учащихся
Мерзляк А.Г. Алгебра : 8 класс : учебник для учащихся общеобразовательных учреждений / А.Г. Мерзляк, В.М. Поляков. — М. : Вентана-Граф, 2018.
Мерзляк А.Г. Алгебра : 8 класс : самостоятельные и контрольные работы : пособие для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, Е.М. Рабинович, М.С. Якир. — М. : Вентана-Граф, 2013.
Агаханов Н.Х., Подли ский О.К. Математика : районные олимпиады : 6–11 классы. — М. : Просвещение, 1990.
Гаврилова Т.Д. Занимательная математика : 5–11 классы. — Волгоград : Учитель, 2008.
Левитас Г.Г. Нестандартные задачи по математике. —М. : ИЛЕК СА, 2007.
Пичугин Л.Ф. За страницами учебника алгебры. — М. :Просвещение, 2010.
Пойа Дж. Как решать задачу? — М. : Просвещение, 1975.
Фарков А.В. Математические олимпиады в школе : 5–11 классы. — М. : Айрис-Пресс, 2005.
Энциклопедия для детей. Т. 11 : Математика. — М. : Аванта+, 2003.
Научно-популярный физико-математический журнал для школьников и студентов «Квант».
Интернет-ресурсы
Министерство образования и науки РФ. http://www.mon.gov.ru
Федеральное государственное учреждение «Государственный научно-исследовательский институт информационных технологий и телекоммуникаций». http://www.informika.ru
Тестирование on-line: 5–11 классы. http://www.kokch.kts.ru/cdo
Путеводитель «В мире науки» для школьников. http://www.uic.ssu.samara.ru/~nauka
Мегаэнциклопедия Кирилла и Мефодия. http://mega.km.ru
Сайт энциклопедий. http://www.encyclopedia.ru
Технические средства обучения:
ПК учителя
Интерактивная доска
Мультимедийный проектор, колонки акустические, экран
Интерактивный диск «Алгебра 8 класс»
Учебно-практическое оборудование:
Таблицы по алгебре для 8 класса
Дидактический раздаточный материал
Портреты выдающихся деятелей в области математики
Шаблоны графиков элементарных функций
12







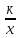 и ее график.
и ее график. 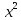 и ее график. Квадратные корни. Арифметический квадратный корень. Множество действительных чисел. Свойства арифметического квадратного корня. Тождественные преобразования выражений, содержащих арифметические квадратные корни. Функция у =
и ее график. Квадратные корни. Арифметический квадратный корень. Множество действительных чисел. Свойства арифметического квадратного корня. Тождественные преобразования выражений, содержащих арифметические квадратные корни. Функция у = 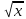 и ее график.
и ее график.









