© 2022, Евстифеева Ирина Викторовна 387 13


СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока


Рабочая программа курса по выбору (факультатива) «Повторим математику» 11 класс
Просмотр содержимого документа
«Рабочая программа курса по выбору (факультатива) «Повторим математику» 11 класс»
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«Школа № 116 города Донецка»
| РЕКОМЕНДОВАНО | СОГЛАСОВАНО
Заместитель директора
_____________А.Н. Потапенкова
« » августа 2022г. | УТВЕРЖДЕНО |
| решением педагогического совета | Директор | |
|
| ___________И.Е. Сташевская
| |
| Протокол от « » августа 2022 г. № |
Приказ от «31»августа 2022г. № |
Рабочая программа
курса по выбору (факультатива) «Повторим математику»
11 класс
Составитель программы:
Евстифеева Ирина Викторовна
Донецк 2022
Пояснительная записка.
Рабочая программа учителя курса по выбору (факультатива) «Повторим математику» составлена на основании примерной программа школьного курса по выбору (факультатива) «Повторим математику», Составители: Проскуренко Виталий Михайлович, учитель математики высшей категории Лисиченской ОШ I – III ступеней Амвросиевского района , учитель методист Беркес Инна Александровна, директор Лисиченской ОШ I – III_ступеней Амвросиевского района , учитель математики высшей категории,_старший учитель Бродяная Наталья Леонидовна, учитель математики высшей категории Благодатновской ОШ I – III ступеней Амвросиевского района , учитель-методист.
Программа курса по выбору (факультатива) «Повторим математику» предназначена для эффективной подготовки учащихся 10-11 классов общеобразовательных школ к Государственной Итоговой аттестации и вступительным испытаниям по математике в различном их виде и соответствует действующей школьной Программе по математике в условиях перехода на новые стандарты образования. Программа составлена на основании многолетнего опыта работы с учащимися старшей школы по подготовке их к ГИА и вступительным испытаниям по математике, в т.ч. и с использованием тестовых технологий в учебном процессе.
Основная идея Программы состоит в систематической дополнительной работе с учащимися по повторению, обобщению и систематизации их знаний по основным темам школьной математики.
Структура и содержание программы соответствует формату и программным требованиям вступительных испытаний и содержанию заданий Государственной Итоговой аттестации по математике. В Программе приведены основные опорные факты из разделов, входящих в программные требования школьной программы по математике и являющиеся их содержательными линиями: числа и выражения; уравнения и неравенства; функции; элементы комбинаторики, начала теории вероятностей и элементы статистики; геометрия (планиметрия и стереометрия).
Программа рассчитана на 1 учебный год в 11 классе по 1 часу в неделю (всего 35 часов). В связи с этим в содержательной части программы имеется раздел «Что надо знать и уметь применять», в котором подробно перечисляются опорные вопросы, определения, формулы из тем и по этому этот раздел имеет иллюстративно – справочный характер.
Задания для практической части занятий учитель может подобрать из школьных учебников, различных пособий для ГИА и для вступительных испытаний.
В порядке контроля учебных достижений учащихся к программе прилагаются комбинированные тематические тесты, разработанные составителями программы и ранее опубликованные в журнале «Математика в школе».
Тесты имеют традиционную структуру
- задания с выбором одного правильного ответа;
- задания открытой формы с кратким ответом;
-задания открытой формы с развернутым решением и ответом.
Методы проверки (самопроверки), систему оценивания устанавливает и объявляет учащимся учитель.
Занятия курса по выбору (факультатива) проводятся как правило, в виде спаренных уроков 1 раз в неделю. При недостаточном количестве или отсутствии часов школьного компонента возможна организация индивидуальной работы учащихся под руководством учителя в любом режиме. Повторение тем геометрии можно осуществлять параллельно с другими темами программы или в том порядке, какой имеется в программе. Возможна работа и по отдельным разделам программы.
Учебно – тематический план курса по выбору (факультатива)
«Повторим математику»
| Наименование разделов и тем | Количество часов | |
| Всего | ||
| Раздел 1. Числа и выражения Т-1. Делимость целых чисел и признаки делимости. Т-2. Проценты. Действительные числа. Т-3. Алгебраические выражения. Т-4. Корень n-й степени. Степени. Т-5. Логарифм числа. Свойства логарифмов. Т-6. Тригонометрические формулы. Т-7. Арксинус, арккосинус, арктангенс, арккотангенс. Т-8. Прогрессии. | 8 1 1 1 1 1
1 1 | |
| Раздел 2. Уравнения и неравенства Т-9. Рациональные уравнения. Т-10. Уравнения и неравенства с одной переменной. Системы уравнений. Т-11. Решение уравнений и неравенств с модулями. Т-12. Показательные уравнения. Показательные неравенства. Т-13. Логарифмические уравнения. Логарифмические неравенства. Т-14.Тригонометрические уравнения (примеры тригонометрических неравенств). Т-15. Решение более сложных уравнений и неравенств (общие методы). | 7 1 1 1 1 1
1 1 | |
| Раздел 3. Элементы комбинаторики, начала теории Т-16. Элементы комбинаторики, начала теории вероятностей и элементы статистики. Т-17.Элементы комбинаторики Т-18. Элементы статистики. Начала теории вероятностей. | 3 1
1 1 | |
| Раздел 4. Функции Т-19. Функция. Область определения и область значений. График функции. Т-20. Свойства функции. Обзор основных видов функции. Т-21. Производная. Геометрический и физический смысл производной. Применение производной к исследованию функций. Т-22. Интеграл и его применение. Т-23. Уравнения и неравенства с двумя переменными. | 5 1 1 1
1 1 |
|
| Раздел 5. Геометрия Т-24. Углы. Параллельные и перпендикулярные прямые Т-25. Треугольники, их виды и свойства. Подобие фигур. Т-26. Четырехугольники, их виды и свойства. Многоугольники. Т-27. Окружность и круг, хорды, дуги, касательные и секущие. Углы в окружности. Вписанные и описанные многоугольники. Правильные многоугольники Т-29. Площади треугольников и четырехугольников. Длина окружности и площадь круга. Т-30. Основные понятия стереометрии. Параллельность в пространстве. Перпендикулярность в пространстве. Углы и расстояния в пространстве. Т-31. Призмы, их виды и свойства. Т-32. Пирамида и ее свойства. Т-33. Цилиндр и его свойства. Конус и его свойства. Т-. Сфера и шар. Комбинация сферы (шара) с геометрическими телами. Т-47. Декартовы координаты. Векторы и операции над ними. Т-35. Обобщение и систематизация пройденного материал | 12 1 1 1 1
1
1
1 1 1 1 1 1 |
|
Содержание программы курса по выбору (факультатива)
«Повторим математику» в 11 классе (всего 35 ч.)
| Раздел программы | Кол-во часов | Основные темы и вопросы для повторения | Что знать и уметь применять (основное содержание тем) | |||||||||||||||||||||||||||||||||||||||
| 1. Числа и выражения | 8 | 1. Делимость целых чисел. 1) Определение делимости целого числа а на целое число в (в ≠0) |
а:в=с, тогда в*с=а
| |||||||||||||||||||||||||||||||||||||||
|
|
| 2) Свойства делимости чисел.
| если а:в и в:с, то а:с если а:в и в:с, mи n – любые целые числа, то (mа+nв):с. (при m=1и n=±1) если а:в и в:с, то (а±в):с если а:в и k≠0, то аk:вk если а:в и а:с, где в и с – взаимно простые числа, то а:вс | |||||||||||||||||||||||||||||||||||||||
|
|
| 3) Признаки делимости: на 2 на 5 на 10k на 4 на 8 на 3 и 9 | если последняя цифра числа делится на 2 (т.е четные) любое четное число n можно представить в виде:n=2k (kєZ), а нечетные числаn=2k + 1 (kєZ) Последняя цифра числа 0 или 5 Число оканчивается на k нулей Число, выраженное двумя последними цифрами данного числа, делится на 4 Число, выраженное тремя последними цифрами данного числа, делится на 8 сумма цифр числа делится на 3 или на 9 соответственно | |||||||||||||||||||||||||||||||||||||||
|
|
| 2. Проценты 1) Определение процента | Сотая часть целого (которое принимают за 1)
| |||||||||||||||||||||||||||||||||||||||
|
|
| 2) Основные задачи на проценты - Нахождение процентов от числа - Нахождение числа по данному значению его процентов
- Нахождение процентногоотношения двух чисел - увеличение на р% (уменьшение на р%)
- Формулы сложных процентов
| р%от числа а: Если р% некоторого числа равно в, то это число равнов: Число а составляет
Если число увеличить (уменьшить) на р%, то получим число Если А начальный вклад, р – годовые проценты, то на конец n-го года вклад составляет | |||||||||||||||||||||||||||||||||||||||
|
|
| 3. Действительные числа: 1) Числовые множества: - действительные числа R - рациональные числа Q - иррациональные числа - целые числа Z -дробные числа - натуральные числа N (целые положительные числа) - число 0 | Действительные числа, числа которые можно представить виде бесконечной десятичной дроби. Можно представить в виде несократимой дроби Нельзя представить в виде несократимой дроби Записываются в виде бесконечной непериодической десятичной дроби ( Включают натуральные числа, числа им противоположные и число 0. Числа, представляющие из себя целое число и части целой единицы ( Натуральное число – основное неопределяемое понятие математики Число, которое при сложении с любым числом не изменяет его (а+0=а; 0+а=а), а при умножении на любое число дает в произведении 0 (0*а=0; а*0=0) | |||||||||||||||||||||||||||||||||||||||
|
|
| 2) Пропорции, прямая и обратная пропорциональность. Пропорциональное деление числа. - определение пропорции | Пропорция – равенство двух отношений: а:в=с:dили | |||||||||||||||||||||||||||||||||||||||
|
|
| - свойства пропорции | Произведение крайних членов пропорции равно произведению средних ее членов Если Если Если | |||||||||||||||||||||||||||||||||||||||
|
|
| Масштаб | Масштаб – отношение расстояния на карте к соответствующему расстоянию на местности. Например, масштаб 1:100000 означает, что 1 см на карте соответствует 100000 см= 1000м=1км на местности. | |||||||||||||||||||||||||||||||||||||||
|
|
| - прямо пропорциональные величины | Две величины прямо пропорциональны, если с увеличением (уменьшением) значений одной из них в несколько раз значение второй увеличивается (уменьшается) во столько же раз | |||||||||||||||||||||||||||||||||||||||
|
|
| - обратно пропорциональные величины | Две величины обратно пропорциональны, если с увеличением (уменьшением) одной из них в несколько раз значение второй уменьшается (увеличивается) во столько же раз | |||||||||||||||||||||||||||||||||||||||
|
|
| - деление числа на части, пропорциональные данным числам | Числа у1, у2, у3 пропорциональны числам х1, х2, х3, если
Разделить число на части, пропорциональные данным числам. значит надо разделить его на сумму этих чисел и найденное частное умножить на каждое из них. | |||||||||||||||||||||||||||||||||||||||
|
|
| 3) Модуль числа: - определение | Модуль положительного числа – само это число. Модуль отрицательного числа –число, ему противоположное. Модуль 0 равно 0:
| |||||||||||||||||||||||||||||||||||||||
|
|
| - геометрический смысл модуля: |
| |||||||||||||||||||||||||||||||||||||||
|
|
| Свойства модуля:
а
| Модуль любого числа - число неотрицательное. Модули противоположных чисел равны. Любое число не превышает свой модуль. Модуль произведения равен произведению модулей
Модуль дроби равен модулю числителя, деленному на модуль знаменателя (если знаменатель не равен нулю) Модуль степени числа равен той же степени модуля этого числа | |||||||||||||||||||||||||||||||||||||||
|
|
| 4. Алгебраические выражения 1) Основные законы алгебры
| а+в=в+а; а*в=в*а а+(в+с)=(а+в)+с; а*(в*с)=(а*в)*с а+0=а; а*1=а а+(-а)=0 а* а(в±с)=ав±ас (а+в)(с+d)=ac+ad+bc+bd | |||||||||||||||||||||||||||||||||||||||
|
|
| 2) Правила раскрытия скобок | a+(b+c)=a+b+c; a-(b+c)=a-b-c; a+(b-c)=a+b-c; a-(b-c)=a-b+c; | |||||||||||||||||||||||||||||||||||||||
|
|
| 3) Умножение одночлена на многочлен | x(a+b)=xa+xb | |||||||||||||||||||||||||||||||||||||||
|
|
| 4) Умножение многочлена на многочлен | (а+в)(x+y)=ax+ay+bx+by | |||||||||||||||||||||||||||||||||||||||
|
|
| 5) формулы сокращенного умножения | (а+в)(а-в)=а2-в2; (а±в)2=а2±2ав+ в2; (а+в)(а2-ав +в2)= а3+в3; (а-в)(а2+ав +в2)= а3-в3; (а±в)3=а3±3а2в+3ав2±в3; (а+в+с)2= а2+в2+с2+2ав+2ас+2вс. | |||||||||||||||||||||||||||||||||||||||
|
|
| 6) разложение многочлена на множители: - вынесение общего множителя за скобки; -способ группировки:
- Применение формул сокращенного умножения
| ха+хв=х(а+в) ха+хв+уа+ув=(ха+хв)+ (уа+ув)=х(а+в)+у(а+в)= =(а+в)(х+у) а2-в2=(а+в)(а-в); а2±2ав+ в2= (а±в)2; а3±3а2в+3ав2±в3= (а±в)3 а2+в2+с2+2ав+2ас+2вс= (а+в+с)2. | |||||||||||||||||||||||||||||||||||||||
|
|
| Применение других формул | ах2+вх+с=а(х-х1) (х-х2), где х1и х2 корни уравнения ах2+вх+с=0 аn-1=(a-1)(an-1+ an-2+…+a+1) а2m+1=(a+1)(a2m- a2m-1- a2m-2-…-a-1) xn –an=(x-a)(xn-1+ axn-2+a2xn-3+…+an-2x+an-1) | |||||||||||||||||||||||||||||||||||||||
|
|
| 7) выделение квадрата двучлена | ах2+вх+с=а(х+ | |||||||||||||||||||||||||||||||||||||||
|
|
| 5. Корень n-й степени и его свойства 1) Квадратный корень
| Квадратным корнем из числа а называют такое число в, квадрат которого равен а.Если а=в2, то в= | |||||||||||||||||||||||||||||||||||||||
|
|
| 2) Корень n-й степени | Корнемn-й степени из числа а называют такое число в, n-я степень которого равна а Если а=вnn | |||||||||||||||||||||||||||||||||||||||
|
|
| 3) Арифметический корень | Арифметический корень – неотрицательное значение корня Тождества ( | |||||||||||||||||||||||||||||||||||||||
|
|
| 4) Область допустимых значений (ОДЗ) |
| |||||||||||||||||||||||||||||||||||||||
|
|
| 5) Свойства корняn-й степени |
| |||||||||||||||||||||||||||||||||||||||
|
|
| 6. Степени 1) Степень с натуральным и целым показателем
|
а nраз а0=1( | |||||||||||||||||||||||||||||||||||||||
|
|
| 2) Степень с дробным показателем |
| |||||||||||||||||||||||||||||||||||||||
|
|
| 3) Свойства степеней | aman=am+n; am:an=am-n; (am)n=amn; (ab)n= an bn
| - степень положительного числа – число положительное; - четная степень отрицательного числа – число положительное; - нечетная степень отрицательного числа – число отрицательное. | ||||||||||||||||||||||||||||||||||||||
|
|
| 7. Логарифм числа 1) Определение логарифма числа
| Логарифм положительного числа b по основанию а (а | |||||||||||||||||||||||||||||||||||||||
|
|
| 2) Основное логарифмическое тождество |
| |||||||||||||||||||||||||||||||||||||||
|
|
| 3) Свойства логарифмов и формулы логарифмирования (а | 1) 2)
3) 4) 5) 6) Формула перехода к логарифму с новым основаним
7) | |||||||||||||||||||||||||||||||||||||||
|
|
| 8. Основные тригонометрические формулы. 1) Соотношения между тригонометрическими функциями одного аргумента х | тождество
| |||||||||||||||||||||||||||||||||||||||
|
|
| 2) Тригонометрические функции двойного аргумента |
| |||||||||||||||||||||||||||||||||||||||
|
|
| 3) значения тригонометрических функций некоторых аргументов |
| |||||||||||||||||||||||||||||||||||||||
|
|
| 4) Формулы суммы (разности) аргументов |
| |||||||||||||||||||||||||||||||||||||||
|
|
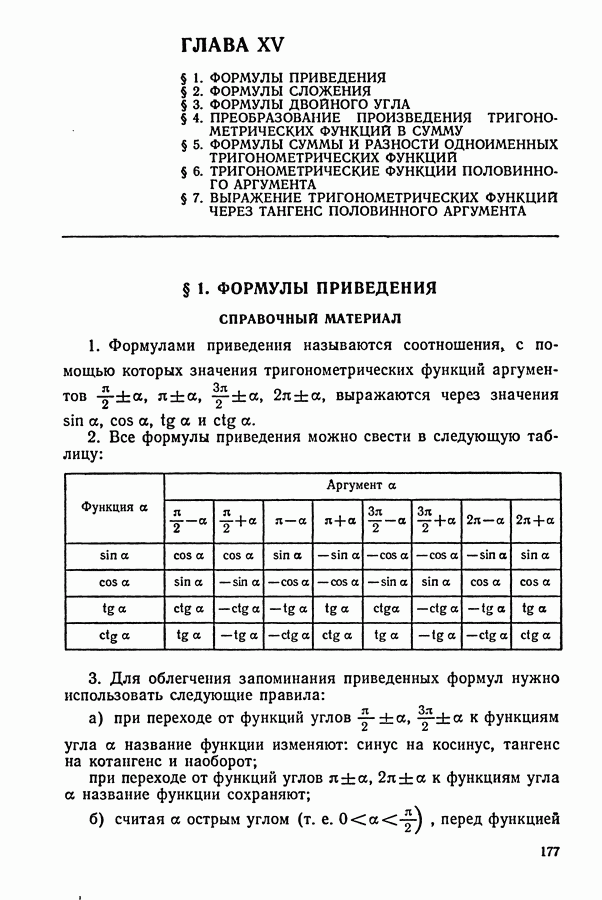
| 5) Формулы приведения |
| |||||||||||||||||||||||||||||||||||||||
|
|
| 6) Формулысуммы и разности тригонометрических функций |
| |||||||||||||||||||||||||||||||||||||||
|
|
| 7) Преобразование произведения тригонометрических функций в сумму |
| |||||||||||||||||||||||||||||||||||||||
|
|
| 8) Формулы преобразования выражения аsinα +всоsα | аsinα +всоsα = sin | |||||||||||||||||||||||||||||||||||||||
|
|
| 9.Арксинус,арккосинус, арктангенс, арккотангенс |
| |||||||||||||||||||||||||||||||||||||||
|
|
| определение | Арксинус числа а – это угол (число) t из промежутка т.е. arcsina=t означает, что Арккосинусчисла а – это угол (число) t из промежутка т.е. arccosa=t означает, что Арктангинс числа а – это угол (число) t из промежутка т.е. arctga=t означает, что Аркотангенс числа а – это угол (число) t из промежутка т.е. arcctga=t означает, что | |||||||||||||||||||||||||||||||||||||||
|
|
| основные соотношения для аркфункций | sin(arcsina)=а, cos(arccosa) =а, а tg(arctga) = а,сtg(arcсtga) = а, а arcsin(-a) = - arcsina; arccos(-a) = arctg(-a) = - arctga; arcсtg(-a) = arcsin (sin arccos (cos arctg (tg arcсtg (ctg arcsina+ arccosa= arctga + arcсtga= | |||||||||||||||||||||||||||||||||||||||
|
|
| некоторые соотношения для аркфункций | arcsin x = arccos arccos x = arcsin arctg x = arcctg arcctg x = arctg | |||||||||||||||||||||||||||||||||||||||
|
|
| 10. Прогрессии |
| |||||||||||||||||||||||||||||||||||||||
|
|
| 1) Определения |
| |||||||||||||||||||||||||||||||||||||||
|
|
| а) арифметической прогрессии | Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом (это число – разность d арифметической прогрессии) | |||||||||||||||||||||||||||||||||||||||
|
|
| б) геометрической прогрессии | Числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предшествующему, умноженному на одно и то же число, отличное от нуля (это число – знаменатель qгеометрической прогрессии). | |||||||||||||||||||||||||||||||||||||||
|
|
| 2) Обозначения |
| |||||||||||||||||||||||||||||||||||||||
| а) в арифметической прогрессии | a1, a2,a3, …, an-1, an, an+1- арифметическаяпрогрессия d= a2 - a1 = a3- a2 = an - an-1–разностьпрогрессии | |||||||||||||||||||||||||||||||||||||||||
|
|
| б) в геометрической прогрессии | b1, b2, b3, …, bn-1, bn, bn+1 –арифметическаяпрогрессия q= | |||||||||||||||||||||||||||||||||||||||
|
|
| 3) Характеристическое свойство |
| |||||||||||||||||||||||||||||||||||||||
|
|
| а) арифметической прогрессии | an= | |||||||||||||||||||||||||||||||||||||||
|
|
| б) геометрической прогрессии |
| |||||||||||||||||||||||||||||||||||||||
|
|
| 4) формулыn-го члена |
| |||||||||||||||||||||||||||||||||||||||
|
|
| а) арифметической прогрессии | an=an-1+d(по определению) an= a1+d(n-1). | |||||||||||||||||||||||||||||||||||||||
|
|
| б) геометрической прогрессии |
| |||||||||||||||||||||||||||||||||||||||
|
|
| 5) формулы суммы n первых членов |
| |||||||||||||||||||||||||||||||||||||||
|
|
| а) арифметической прогрессии |
| |||||||||||||||||||||||||||||||||||||||
|
|
| б) геометрической прогрессии |
| |||||||||||||||||||||||||||||||||||||||
|
|
| 6) бесконечно убывающая геометрическая прогрессия |
| |||||||||||||||||||||||||||||||||||||||
|
|
| а) определение | Бесконечная геометрическая прогрессия, у которой знаменатель | |||||||||||||||||||||||||||||||||||||||
|
|
| б) сумма членов | C S=lim Sn n формула для ее вычисления S = | |||||||||||||||||||||||||||||||||||||||
| Уравнения и неравенства | 7 | 11. Рациональные уравнения: |
| |||||||||||||||||||||||||||||||||||||||
| Определение уравнений | Уравнение –это равенство, содержащее неизвестное, обозначенное переменной. Корень уравнения (решение уравнения) – это значение переменной, при которой уравнение обращается в верное числовое равенство. Решить уравнение- значит найти все его корни или доказать, что их нет. | |||||||||||||||||||||||||||||||||||||||||
|
|
| Линейные уравнения: |
| |||||||||||||||||||||||||||||||||||||||
|
|
| а) определение | Общий вид: ах=b, где а и b- некоторые числа, х-неизвестное число. | |||||||||||||||||||||||||||||||||||||||
|
|
| б) решение | 1) а ≠0 – единственный корень х= 2 | |||||||||||||||||||||||||||||||||||||||
|
|
| Квадратные уравнения: |
| |||||||||||||||||||||||||||||||||||||||
|
|
| а) определение | Уравнение вида ах2+bx +c=0, где х - неизвестная переменная , а,b и с некоторые числа, причем а≠0 Если b=0 или с =0 – уравнение неполное: ах2=0, ах2+bx=0, ах2+c=0 | |||||||||||||||||||||||||||||||||||||||
|
|
| б) формулы корней полных квадратных уравнений | ах2+bx +c=0 (а ≠0)
(D – дискриминант) D D | |||||||||||||||||||||||||||||||||||||||
|
|
| в) приведенные квадратные уравнения | Если первыйкоэффициент равен 1: х2+px +q=0.
| |||||||||||||||||||||||||||||||||||||||
|
|
| г) теорема Виета для приведенных квадратных уравнений | х2+px +q=0, х1 и х2 – его корни, тогда х1 | |||||||||||||||||||||||||||||||||||||||
|
|
| д) уравнения, которые сводятся к квадратным | Если в уравнении переменная входит в одном и том же виде, то удобно соответствующее выражение с переменной обозначить новой переменной. Пример: биквадратное уравнение ах4+bx2 +c=0 (а ≠0) | |||||||||||||||||||||||||||||||||||||||
|
|
| 4)Дробно-рациональные уравнения | Схема решения: 1) Перенести все члены уравнения в левую часть; 2) выполнить все действия с алгебраическими дробями, т.е. получить уравнение, левая часть которой дробь, а правая – нуль; 3) использовать свойство равенства дроби нулю (дробь равна нулю, если ее числитель равен нулю, а знаменатель – не равен нулю) и приравнять числитель полученной дроби нулю; 4) решить получившееся уравнение; 5) проверить, все ли найденные решения удовлетворяют условие равенства дроби нулю (если получим в знаменателе нуль, то найденное число не является корнем данного уравнения). Или другая схема решения (с помощью ОДЗ). | |||||||||||||||||||||||||||||||||||||||
|
|
| 1)Определить ОДЗ данного уравнения; 2)Найти общий знаменатель всех дробей, которые входят в запись уравнения; 3)умножить обе части уравнения на общий знаменатель (полученное уравнение равносильно заданному на ОДЗ) 4)Решить получившееся целое уравнение; 5)Отобрать из всех найденных решений те, которые входят в ОДЗ. | ||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| Неравенства с одной переменной – это два выражения с переменной , соединённых знаком : Решением неравенства называют значения переменной, при которых неравенство превращается в верное числовое неравенство. Решить неравенство – значит найти все его решения или доказать , что их нет. | ||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| ОДЗ уравнения( или неравенства) – это общая область определения всех функций, которые имеются во всех частях уравнения ( неравенства) | ||||||||||||||||||||||||||||||||||||||||
|
|
| - Если каждый корень первого уравнения является корнем другого уравнения, то второе уравнение называется следствием первого. - Еслииз правильного первого равенства вытекает правильность каждого следующего, то получается уравнение- следствие. При этом возможно появление посторонних корней. Поэтому при использовании уравнений – следствий обязательна проверка полученных корней в начальном уравнении. | ||||||||||||||||||||||||||||||||||||||||
|
|
| Два уравнения ( два неравенства) равносильны на некотором множестве, если на этом множестве они имеют одни и те же решения. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1Если из одной части уравнения ( неравенства ) перенести в другую часть слагаемые с противоположным знаком, то получим уравнение ( неравенство) , равносильное данному на любом множестве . 2.Еслиобе части уравнения умножить или разделить на одно и то же число, не равное нулю( или на одну й ту же функцию, которая определена и не равна нулю на ОДЗ данного уравнения), то получим уравнение , равносильное данному на ОДЗ этого уравнения. 3. Если обе части неравенства умножить или разделить на одно и то же положительное число, ( или на одну й ту же функцию, которая определена и положительна на ОДЗ данного неравенства), не меняя знака неравенства, то получим неравенство, равносильное данному на ОДЗ этого неравенства. 4.Если обе части неравенства умножить или разделить на одно и то же отрицательное число, ( или на одну й ту же функцию, которая определена и отрицательна на ОДЗ данного неравенства) и при этомпоменять знак неравенства на противоположный, то получим неравенство, равносильное данному на ОДЗ данного неравенства. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1. с помощью уравнений- следствий: -преобразования, которые гарантируют сохранение правильности равенства; - проверка корней подстановкой в начальное уравнение. 2. с помощью равносильных преобразований : - учесть ОДЗ данного уравнения. - сохранять на ОДЗ правильное равенство при прямых и обратных преобразованиях. 3.применение свойств функций. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1. с помощью равносильных преобразований: - преобразования, которые гарантируютсохранение правильности неравенства. - проверка корней подстановкой в начальное неравенство. 2. с помощью метода интервалов ( f(x) - найти ОДЗ - найти нули функции: f(x) - обозначить нули на ОДЗ и найти знак функции f(x) на каждом промежутке, на которые разбивается ОДЗ. - записать ответ, учитывая знак данного неравенства.
| ||||||||||||||||||||||||||||||||||||||||
|
|
| -Если надо найти общие решения двух ( и более) уравнений с одной или несколькими переменными, то говорят , что надо решить систему уравнений ( запись этих уравнений объединяют фигурною скобкой). - Решением системы называют такое значение переменной или такой упорядоченный набор значений переменных( если их несколько), которые удовлетворяют все уравнения системы. - Решить систему уравнений – значит найти все её решения или доказать , что их нет, ( если система не имеет решений, то её называют несовместимой) | ||||||||||||||||||||||||||||||||||||||||
|
|
| - Две системы уравнений равносильны на некотором множестве, если на этом множестве они имеют одинаковые решения. (ОДЗ системы называют общую область определения всех выражений, входящих в её запись. Все равносильные преобразования систем выполняются на ОДЗ заданной системы). - Если изменить порядок записи уравнений заданной системы , то получим систему, равносильную заданной. - Если одно из уравнений системы заменить на равносильное емууравнение, то получим систему, равносильную данной. | ||||||||||||||||||||||||||||||||||||||||
|
|
| - способ подстановки - способ сложения - графический способ решения систем уравнений с двумя переменными | ||||||||||||||||||||||||||||||||||||||||
|
|
| - по определению модуля: - по геометрическому смыслу модуля: 1.f(x) = 2. 3. 4. - по общей схеме: 1.Найти ОДЗ 2.Найти нули всех подмодульных функций 3.Обозначить нули на ОДЗ и разбить ОДЗ на промежутки 4.Найти решение на каждом промежутке и проверить, входит ли это решение в данный промежуток. | ||||||||||||||||||||||||||||||||||||||||
|
|
|
2. 3. 4. | ||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Найти ОДЗ; 2. Найти нули всех подмодульных функций; 3.Разбить ОДЗ на промежутки нулями подмодульных функций; 4.Найти решения на каждом промежутке и объединить их. | ||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| - с помощью возведения обеих частей уравнения в одну и ту же степень ( при возведении обеих частей уравнения в чётную степень могут появиться посторонние корни, которые отбрасывают проверкой) -с помощью замены переменных ( введение вспомогательной переменной) | ||||||||||||||||||||||||||||||||||||||||
|
|
| - метод интервалов (для неравенств вида (f(x) 1.Найти ОДЗ неравенства. 2.Найти нули функцииf(x) : (f(x) = 3. Отметить нули функции на ОДЗ и найти знак функции f(x) на каждом промежутке, на которые разбивается ОДЗ. 4. Записать ответ, учитывая знак неравенства. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.При возведении обоих частей неравенства в нечётную степень (с сохранением знака неравенства) получаем неравенство, равносильное данному ( на ОДЗ данного неравенства). 2.Если обе части неравенства неотрицательны, то при возведении их в чётную степень (с сохранением знака неравенства) получаем неравенство, равносильное данному ( на ОДЗ данного неравенства). 3.Если на ОДЗ данного неравенства какая- либо его часть может принимать как положительные, так и отрицательные значения, то прежде чем возводить обе части неравенства в чётную степень, эти случаи надо рассмотреть отдельно.
| ||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Если в левой и правой части уравнения имеется только произведение, частное, корни или степени, то с помощью основных формул записываются обе части уравнения как степени с одинаковым основанием. 2.Если в одной части показательного уравнения все члены имеют выражение вида | ||||||||||||||||||||||||||||||||||||||||
|
|
| а)Замена переменной в показательном уравнении. 1.Избавляемся числовых слагаемых в показателях степеней( используя справа налево основные формулы действий со степенями) 2.Приводим все степени ( с переменной в показателе) к одному основанию и вводим новую переменную. 3.Если степени не приводятся к одному основанию, то приводятся все степени к двум основаниям так, чтобы получить однородное уравнение( которое можно решить делением обоих частей уравнения на наибольшую степень одного из видов переменных). б)Разложение левой части на множители( при этом правая часть должна быть равна нулю). | ||||||||||||||||||||||||||||||||||||||||
|
|
| Применение свойств возрастания ( убывания) показательной функции для сравнения выражений если 0 | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.При 2. При 0 | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.С помощью равносильных преобразований ( по схеме решения показательных уравнений) неравенство приводится к неравенству известного вида( квадратному, дробному). После решения полученного неравенства решается простейшее показательное неравенство. 2.Общий метод интервалов, приводя данное неравенство к виду f(x) 1.Найти ОДЗ. 2) Найти нули функцииf(x). 3)Отметить нули функции на ОДЗ и найти знак f(x) на каждом из промежутков, на которые разбита ОДЗ. 4)Записать ответ, учитывая знак неравенства | ||||||||||||||||||||||||||||||||||||||||
|
|
| Если | ||||||||||||||||||||||||||||||||||||||||
|
|
| Если из допуска того, что первое равенство заданного уравнения верное, следует верность каждого следующего равенства, что гарантированно получается уравнение- следствие. При этом корни начального уравнения не теряются, но возможно появление посторонних корней. Поэтому проверка корней подстановкой в начальное уравнение обязательна. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1)Замена переменных ( пример 2)Уравнение вида 3)Потенцирование в логарифмических уравнениях. а) Учитывается ОДЗ заданного уравнения ( избегаем преобразований, которые сужают ОДЗ) б) На ОДЗ каждое преобразование выполняется в прямом и обратном направлениях с сохранением верного равенства Пример: | ||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| 1) (знак неравенства не меняется , учитывая ОДЗ) 2. 0 ( знак неравенства меняется, учитывая ОДЗ)
| ||||||||||||||||||||||||||||||||||||||||
|
|
| 1)С помощью равносильных преобразований данное неравенство приводится к неравенству известного вида. Пример: 2)Применение общего метода интервалов (заданное неравенство приводится к видуf(x) | ||||||||||||||||||||||||||||||||||||||||
|
|
|
При Частные случаи:
2. При Частные случаи:
| ||||||||||||||||||||||||||||||||||||||||
|
|
|
2. Особый случай: | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1)Все тригонометрические функции с помощью формул тригонометрии сводятся к одной функции с одним аргументом ( если это возможно). 2)Если привести к одной функции не удалось, пробуем уравнение привести к однородному. 3) В других случаях переносим все члены уравнения в одну часть и пробуем разложить на множители или применяем специальные приёмы решения. | ||||||||||||||||||||||||||||||||||||||||
|
|
| Используем графики тригонометрических функций или единичную окружность. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1)Уравнение с конечной ОДЗ: Если ОДЗ уравнения ( неравенства ) состоит из конечного числа значений, то для решения достаточно проверить все эти значения. Пример: Ответ: x=1 – корень ( проверяется подстановкой). 2)Оценка левой и правой части уравнения:
Если в уравнении Пример : 1 - 3)Применение возрастания и убывания функций. Теоремы о корнях уравнения: Т-1. Если в уравнении Т-2.Если в уравнении Схема решений: 1.Подбираем один или несколько корней уравнения. 2.Доказываем , что других корней это уравнение не имеет( используя Т-1, Т-2 ( см. выше) или оценку левой и правой частей уравнения) | ||||||||||||||||||||||||||||||||||||||||
| Раздел 3 Функции | 5 |
| ||||||||||||||||||||||||||||||||||||||||
|
|
| Функция – зависимость, при которой каждому значению переменной х ( х – аргумент, независимая переменная) из некоторого множества D соответствует единственное значение переменной у ( у – функция от х). Множество D – область определения функции( для функций , заданных формулой, где ничего не сказано об области её определения, D – множество всех значений переменной , при которых заданная формула имеет смысл). Область значений функции( множество Е) – это множество тех значений , которые может принимать сама функция при всех значениях аргумента из области определения. | ||||||||||||||||||||||||||||||||||||||||
|
|
| График функции – множество всех точек координатной плоскости, абсциссы которых равны значению аргумента, а ординаты - соответствующим значениям функции. | ||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| Функцияf(x) возрастающая, если для Функцияf(x) убывающая,если для | ||||||||||||||||||||||||||||||||||||||||
|
|
| Функцияf(x)- чётная, если График чётной функции симметричен относительно оси Oy. Функцияf(x) – нечетная, еслиf(-x) = -f(x)для всех График нечётной функции симметричен относительно начала координат/ | ||||||||||||||||||||||||||||||||||||||||
|
|
| Функция f(x) периодическая с периодом ЕслиT – период функции, Функции Функции Если функцияy = f(x) периодическая с периодомT, то функцияy = Af(kx + b) также периодическая с периодом
| ||||||||||||||||||||||||||||||||||||||||
|
|
| Построение графиков функций и их свойства | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1) y = -f(x) - симметрия графика относительно оси Ох 2) y = f(-x) - симметрия графика относительно оси Оу 3) y = f(x-a) – параллельный перенос графика вдоль оси Ох 4) y =f(x) + c –параллельный перенос графика вдоль оси Оуна с единиц 5) y =kf(x) ( k 6) y = f( 7) y = 8) y = f | ||||||||||||||||||||||||||||||||||||||||
|
|
| y = f(x); Дифференцирование – операция нахождения производной | ||||||||||||||||||||||||||||||||||||||||
|
|
| S = S(t) – зависимость пути от времени V = S′(t) – скорость прямолинейного движения
Вообще, производная любой функции – это скорость изменения функции. | ||||||||||||||||||||||||||||||||||||||||
|
|
|
Тогдаf y= | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1)(C)′ = 0 C 2) (Cu)′ =C u′ 3)(u 4)(u 5)( 6)Сложнаяфункция :если y = f (u) иu (x), т. е. y = f (u(x)), тоf (u(x))′ = | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Достаточное условие возрастания функции (Если в каждой точке интервала (а,в)f′(x) 2.Достаточное условие убывания функции ( Если в каждой точке интервала (а,в)f′(x) 3.Необходимое и достаточное условие постоянства функции ( Функция f(x) является постоянной на интервале (а,в) тогда и только тогда, когда f′(x) | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Точки максимума функции. Точка
2.Точки минимума функции. Точка
3.Критические точки функции. Критические точки функции - это внутренние точки её области определения , в которых + производная функции равна нулю или не существует. 4. Необходимые и достаточные условия экстремума. - в точках экстремума производная функции f(x) равна нулю или не существует ( однако не в каждой точке - если функция f(x) непрерывна в точке а) в точке б) в точке 4. Точки экстремума – точки максимума и минимума функции. 5. Экстремумы (максимум и минимум функции) – значения функции в точках максимума и минимума:
| ||||||||||||||||||||||||||||||||||||||||
|
|
| Если функция f(x) непрерывна на отрезке и имеет на нём конечное число критических точек, то она принимает наибольшее и наименьшее значения на этом промежутке или в критических точках , которые принадлежат этому отрезку, или на концах отрезка. | ||||||||||||||||||||||||||||||||||||||||
|
|
| Функция F(x) - первообразная для функции f(x) на заданном промежутке, если для всех х из этого промежуткаF′(x) = f(x) ( Пример:F(x) = | ||||||||||||||||||||||||||||||||||||||||
|
|
| Если F(x) – первообразная для функции f(x) на заданном промежутке, то функция f(x) имеет бесконечное число первообразных и все эти первообразные можно записать в виде F(x) + С , где С – произвольное число. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Первообразная суммы функций равна сумме первообразных, т.е. если F(x) – первообразная для f(x), а G(x) – первообразная для g(x), то F(x) + G(x) = f(x) +g(x). 2.Постоянный множитель можно выносить за знак первообразной , т.е. еслиF(x) – первообразная для функцииf(x) и С – постоянное число , то СF(x) – первообразная для функции Сf(x). 3.Если F(x) – первообразная для f(x) и k | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.СовокупностьF(x) + С всех первообразных для данной функцииf(x) – неопределённый интеграл от функцииf(x) : 2.Основные правила интегрирования 1) 2) 3) Если k | ||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| 1. Определение: Пусть у =f(x) – непрерывная функция, определенная на промежутке[a;b]. Тогда определённый интеграл от а до b функцииf(x) – это приращение первообразной F(x) для этой функции, т.е. 2.Основные правила вычисления определённого интеграла: 1) 2) 3) 4) 5) 6) | ||||||||||||||||||||||||||||||||||||||||
|
|
| S = | ||||||||||||||||||||||||||||||||||||||||
|
|
| S = | ||||||||||||||||||||||||||||||||||||||||
|
|
| S = | ||||||||||||||||||||||||||||||||||||||||
|
|
| V= | ||||||||||||||||||||||||||||||||||||||||
|
|
| Уравнение( неравенство), которое имеет две переменные: f(x;y) = 0 ( f(x;y) Решение уравнения f(x;y) = 0 ( неравенстваf(x;y) | ||||||||||||||||||||||||||||||||||||||||
|
|
|
2. 3. 4. 5. 6. | ||||||||||||||||||||||||||||||||||||||||
|
|
|
2. 3. 4. | ||||||||||||||||||||||||||||||||||||||||
| Раздел 4 Элементы комбинаторики, начала теории вероятностей и элементы статистики | 3 |
| ||||||||||||||||||||||||||||||||||||||||
|
|
| Перестановка изn элементов – любое упорядоченное множество из nэлементов, т.е. такое множество, в котором указано, какой элемент на первом месте , какой – на втором…, какой на n -м. Формула числа перестановок
| ||||||||||||||||||||||||||||||||||||||||
|
|
| Размещение из nэлементов поk - это любое упорядоченное множество из kэлементов, составленное из элементов n– элементного множества Формула числа размещений | ||||||||||||||||||||||||||||||||||||||||
|
|
| Комбинация без повторений из n элементов по k- это любое k-элементное подмножество n- элементного множества Формула числа комбинаций Причём: 1) по определению 2) 3) | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1) Правило суммы:если элемент А можно выбрать m способами, а элемент В- n способами, то А или В можно выбрать(m+n) способами. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 2)Правило произведения: если элемент А можно выбрать m способами, а после этого элемент В- n способами, то А и В можно выбрать(m | ||||||||||||||||||||||||||||||||||||||||
|
|
| Событие, которое может произойти, а может и не произойти в процессе наблюдений или эксперимента в одних и тех же условиях, называется случайным событием( а сам эксперимент – случайным экспериментом) | ||||||||||||||||||||||||||||||||||||||||
|
|
| Если при неизменных условиях проведено n случайных экспериментов и в n(А)случаев осуществилось событие А , то числоn (А)- частота события А. Отношение | ||||||||||||||||||||||||||||||||||||||||
|
|
| Если при проведении большого количества случайных экспериментов, в каждом из которых событие А может произойти, а может и не произойти, значение относительной частоты близки к некоторому числу, то это число – вероятность случайного события А : Невозможное событие ( Событие U, которое обязательно произойдёт в каждом повторении эксперимента Р(U) = 1 | ||||||||||||||||||||||||||||||||||||||||
|
|
| Для равновозможных элементарных событий вероятность события А – это отношение количества благоприятных для неё событий ( m) к количеству всех равновозможных событий (n) в данном эксперименте: | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Ранжирование ряда данных –расположение элементов этого ряда в порядке возрастания, т.е. каждое следующее число или больше, или не меньше предыдущего. 2.Размах выборки (R) – это разность между наибольшим и наименьшим значениями случайной величины выборки. 3.Мода ( МО) – значения случайной величины, которые встречаются чаще всего. 4.Медиана ( МЕ) – т.н. серединное значение упорядоченного ряда значений случайной величины. 5.Среднее значение( а) ( б) m1,m2…mnсоответственно.
| ||||||||||||||||||||||||||||||||||||||||
|
|
| Полигон частот - ломаная, отрезки которой последовательно соединяют точки(х1;m1), (x2; m2) …(xn;mn), где х1,х2…хn.- значения случайных величин, m1,m2…mn– соответствующие им частоты | ||||||||||||||||||||||||||||||||||||||||
| Раздел 5 Геометрия | 12
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| Угол как фигура ,образованная двумя лучами с общим началом( вершиной угла) Плоский угол – часть плоскости, ограниченной двумя лучами с общим началом. | ||||||||||||||||||||||||||||||||||||||||
|
|
| Прямой угол, острый угол, тупой угол, развернутый угол, больший развернутого угла. | ||||||||||||||||||||||||||||||||||||||||
|
|
| Биссектриса угла – это луч , имеющий начало в вершине угла, лежащей в его внутренней области и делящий угол на два равных угла | ||||||||||||||||||||||||||||||||||||||||
|
|
|
∠1 + ∠2 = 180 ∠1 и ∠3, ∠2 и ∠4 - вертикальные углы . ∠1 = ∠3 , ∠2 =∠4 (рис. 2) | ||||||||||||||||||||||||||||||||||||||||
|
|
| ∠1 и ∠5, ∠2 и ∠8 – внутренние односторонние углы , ∠1 и ∠8 , ∠2 и ∠5 – внутренние накрест лежащие углы , ∠4 и∠5; ∠3 и ∠8 ;∠1 и ∠6 ; ∠2 и ∠7 – соответственные углы. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1. Две прямые параллельны, если они лежат в одной плоскости и не пересекаются: a 2. Через точку вне данной прямой можно провести одну прямую , параллельную данной. 3. Признаки параллельности прямых: 1) Если внутренние накрест лежащие или соответственные углы равны, то a 2) Если сумма внутренних односторонних углов равна 180 3) Если a ⊥ с и b ⊥ c, то a ‖ b 4) Если a ‖ b, b ‖ c, то a ‖ c. 4.Свойства параллельных прямых и секущей Если a ‖ b, а с- секущая , то 1) внутренние накрест лежащие углы равны; 2) соответственные углы равны; 3) сумма внутренних односторонних углов равна 180 4) если a ‖ b и c ⊥ a, то c ⊥ b | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1. Две прямые перпендикулярные, если они пересекаются под прямым углом: a ⊥ b, ∠AOB= 90 (рис. 1). 2. Через данную точку можно провести единственную прямую, перпендикулярную данной прямой. 3. Перпендикуляр к прямой – отрезок ОА , проведенный из точки О к прямой а под прямым углом (А – основание перпендикуляра, ОА – кратчайшее расстояние от точки О до прямой а) (рис. 2). | ||||||||||||||||||||||||||||||||||||||||
|
|
| Две фигуры равны, если они движением переходят одна в другую. ∆ ABC =∆ A1B1C1 , тогдаAB =A1B1BC=B1C1AC=A1C1, ∠A =∠A1 , ∠B =∠B1, ∠C=∠C1 | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.По двум сторонам и углу между ними 2.По стороне и двум прилежащим углам 3.По трём сторонам | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.По двум катетам 2.По катету и острому углу 3.По гипотенузе и острому углу 4.По гипотенузе и катету | ||||||||||||||||||||||||||||||||||||||||
|
|
| В ∆ ABC (AB = с, BC= a , AC = b , ∠A =∠1 , ∠B =∠2, ∠C=∠3, ∠4 - внешний при вершине C) 1.∠A +∠B +∠C = 180 2. 3.∠4 = ∠1+ ∠2 – свойство внешнего угла | ||||||||||||||||||||||||||||||||||||||||
|
|
| В равнобедренном треугольнике ∆ABC (AB=BC, AC- основание, BD- медиана к основанию AC) Свойства: 1.∠A = ∠C ( углы при основании равны) 2.Медиана BD является также высотой и биссектрисой. Признаки: 1.Если∠A = ∠C , то AB= BC 2.Треугольник ABC равнобедренный с основанием AC, если BD - медиана и высота или - высота и биссектриса или - медиана и биссектриса | ||||||||||||||||||||||||||||||||||||||||
|
|
| ∠C = 90 | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1. Медиана треугольника(рис. 1): 1) 2)В прямоугольном треугольнике с гипотенузой с и медианой 2.Биссектриса BD треугольника ABC(рис. 2): 1)∠ABD=∠CBD= 2) 3) О – точка пересечения биссектрис – центрвписанной окружности. | ||||||||||||||||||||||||||||||||||||||||
|
|
|
3. Высота треугольника: 1) BD – высота , BD⊥AC. 2) 4.Средняя линия треугольника M - середина AB, N- середина BC; MN - средняя линия. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1. Прямоугольный треугольник(рис. 1)
2) b = c 3)∆ACD ∆CBD ∆ACD 2.Произвольный треугольник (a,b ,c - стороны , R- радиус описанной окружности)(рис. 2) 1) 2) 3) Следствия: - если - если - если | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Подобие треугольников | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1) ∆ ABC | ||||||||||||||||||||||||||||||||||||||||
|
|
| 2) | ||||||||||||||||||||||||||||||||||||||||
|
|
| 2.Признаки подобия треугольников 1) По двум равным углам: ∆ ABC 2)По двум пропорциональным сторонам и углу между ними: ∆ ABC | ||||||||||||||||||||||||||||||||||||||||
|
|
| 3)По трём пропорциональным сторонам ∆ ABC | ||||||||||||||||||||||||||||||||||||||||
|
|
| 4)Прямая пересекающая две стороны треугольника и параллельная третьей его стороне , отсекает треугольник, подобный данному. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Параллелограммом называется четырёхугольник , у которого противоположные стороны попарно параллельны | ||||||||||||||||||||||||||||||||||||||||
|
|
| 2. Свойства параллелограмма: 1) равенство противоположных сторон и углов; 2)диагональ делит параллелограмм на два равных треугольника; 3)диагонали точкой пересечения делятся пополам; 4)ABCD– параллелограмма , ACи BD- его диагонали | ||||||||||||||||||||||||||||||||||||||||
|
|
| Четырёхугольник ABCD – параллелограмм, если : | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1)две стороны попарно равны и параллельны; | ||||||||||||||||||||||||||||||||||||||||
|
|
| 2) противоположные стороны попарно равны; 3)диагонали пересекаются и точкой пересечения делятся пополам. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Прямоугольник: - диагонали прямоугольника равны. 2. Ромб: -диагонали ромба перпендикулярны и являются биссектрисами его углов. 3. Квадрат: - имеет свойства любого из параллелограммов. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение трапеции, её элементы. Виды трапеции. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 2. Равнобокая трапеция и её свойства | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1)∠A =∠D;∠B =∠C. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 2)AC=BD. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 3)A | ||||||||||||||||||||||||||||||||||||||||
|
|
| 3.В прямоугольной трапеции высота равна боковой стороне, которая перпендикулярна основаниям. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 4. Средняя линия трапеции MN - MN ‖ AD; MN‖ BC. - MN = | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение выпуклого многоугольника, его диагонали. 2.Углы многоугольника. Внешний угол при данной вершине. 3.Свойства: - сумма всех внутренних углов вычисляется по формуле 180 - сумма всех внешних углов, взятых по одному при вершине, равна 360 | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Равные дуги стягивают равные хорды и наоборот. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 2.Параллеьные хорды отсекают на окружности равные дуги. 3.Диаметр, перпендикулярный к хорде, делит её и стягиваемую дугу пополам и наоборот. 4.S – точка пересечения хорд AB и CD ,тогда AS AB – хорда , AC – диаметр и BD⊥AC. Тогда - - B | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение секущей и касательной | ||||||||||||||||||||||||||||||||||||||||
|
|
| 2.Равенство двух касательных, проведенных из одной точки. 3. SM - касательная ,SA- секущая:S 4. SAи SC – секущие:SA | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение центральных и вписанных углов, их измерение | ||||||||||||||||||||||||||||||||||||||||
|
|
| 2.Свойства вписанных углов - опирающихся на одну и ту же дугу (эти углы равны) - опирающихся на диаметр ( эти углы – прямые) | ||||||||||||||||||||||||||||||||||||||||
|
|
| 3. Угол между касательной и секущей MA- касательная , MB - секущая:∠AMB= | ||||||||||||||||||||||||||||||||||||||||
|
|
| 4. Угол между двумя хордами ∠M = | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Вписанные многоугольники 2. Описанные многоугольники | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Центр окружности О – точка пересечения серединных перпендикуляров к сторонам треугольника. 2.OA = OB = OC = R – радиус окружности, описанной около ∆ ABC( О – центр этой окружности). 3. R = | ||||||||||||||||||||||||||||||||||||||||
|
|
| 4.Положение центра окружности, описанной около - остроугольного и тупоугольного треугольников; - прямоугольного треугольника ( центр - середина гипотенузы c и R = | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Центр О окружности, вписанной в∆ ABC - точка пересечения биссектрис внутренних углов этого треугольника. 2.OD⊥AB;OD = r – радиус вписанной окружности. 3.r = 4.В прямоугольном треугольнике с катетамиa и b и гипотенузой c: r = 5.Радиус окружности , вписанной в равнобедренный треугольник. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение правильного многоугольника. Его центр. 2. Формулы стороны 3.Формулы вычисления 4.Формулы площадей некоторых правильных многоугольников. 1)Правильный треугольник :S = S = 2) Квадрат: S = 3)Правильный 6 – угольникS =
| ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Площадь произвольного треугольника S = S = | ||||||||||||||||||||||||||||||||||||||||
|
|
| 2.Площадь прямоугольного треугольника S= | ||||||||||||||||||||||||||||||||||||||||
|
|
| 3.Площадь равностороннего треугольника S = | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Произвольный выпуклый: S = его диагонали , 2.Прямоугольник:S = a 3.Квадрат: S= 4.Параллелограмм :S = 5. Ромб: S = a 6.Трапеция: S = S = =
| ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Длина окружности C = 2 и длина дуги в | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Площадь круга радиуса R: S = 2.Площадь кругового сектора - в - в 3.Площадь кругового сегмента: Sсегм=Sсект | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Аксиомы: принадлежности точек плоскости; пересечения двух плоскостей, существования плоскости. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение прямой, параллельной плоскости 2.Признак параллельности прямой и плоскости 3. Свойство прямой, параллельной плоскости - если | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение параллельных плоскостей. 2.Признак параллельности плоскостей: - если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то плоскости параллельны. 3.Свойства параллельных плоскостей: - параллельность двух плоскостей третьей плоскости - параллельность прямых пересечения двух параллельных плоскостей третьей плоскостью - равенство отрезков параллельных прямых,пересекающих параллельные плоскости. 4.Правила параллельного проектирования при изображении пространственных фигур на плоскости: - отрезок проектируется в отрезок; - проекция параллельных прямых ( отрезков) – параллельные прямые ( отрезки); - если M - точка отрезка AB , аM1 - точкаA1B1 проекцииAB, то | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение. 2.Признак перпендикулярности прямой и плоскости:
3.Свойства: - если одна из двух параллельных прямых перпендикулярна плоскости, то и вторая прямая перпендикулярна этой плоскости; - две прямые, перпендикулярные к плоскости, параллельны; - прямая, перпендикулярная к одной из параллельных плоскостей, перпендикулярна другой плоскости; - если каждая из двух плоскостей перпендикулярна прямой, то плоскости параллельны. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение: 1)AO⊥α; O 2)Отрезок AO - перпендикуляр; AO – расстояние от точки A до плоскости α; до прямой 2.Свойства: - перпендикуляр из точки А к плоскости α короче любой наклонной, проведённой из той же точки А к плоскости α. - две наклонные, проведённые из точки А к плоскости α а) равны, если равны их проекции и наоборот; б) большая наклонная имеет большую проекцию и наоборот. | ||||||||||||||||||||||||||||||||||||||||
|
|
| OB- проекция наклонной AB на плоскость α, c – прямая на плоскости α, проходящая через основание В наклонной ABи OB⊥c, тогда и AB⊥c ( и наоборот) | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.определение перпендикулярных плоскостей. 2.Признак перпендикулярности двух плоскостей: - если прямаяb⊥α и β проходит через прямую b, то β ⊥α. 3. Свойство перпендикулярных плоскостей: -если β⊥α и β пересекает α по прямой | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Угол между прямой и плоскостью – угол между прямой и её проекцией на эту плоскость. 2.Угол между скрещивающимися (рис. 1) прямыми:
∠( 3.Угол между плоскостями: α Тогда угол между плоскостями – это угол между прямыми, по которой плоскость γпересекает плоскости α и β.
4.Двугранный угол (угол между полуплоскостями) (рис. 2): 1)определение двугранного угла: α 2.Линейный угол двугранного угла(рис. 3): γ ⊥ c, (γ ∩ α =MA, γ ∩ β =MB) ∠ AMB– линейный угол двугранного угла αcβ- свойство : плоскость γ⊥α и γ⊥β. 3. Практические способы построения линейного угла | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Расстояние от точки до плоскости. 2.Расстояние между прямой и параллельной ей плоскостью ( расстояние от любой точки этой прямой до плоскости, - т.е. длина перпендикуляра , опущенного из любой точки прямой на плоскость). 3.Расстояние между параллельными плоскостями – расстояние от любой точки одной плоскости до другой плоскости, т.е. длина перпендикуляра , опущенного из любой точки одной плоскости , на другую плоскость. 4.Расстояние между скрещивающимися прямыми – длина общего перпендикуляра к этим прямым. | ||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определениепроизвольной призмы,( наклонной призмы), её оснований, боковых рёбер, боковых граней, диагоналей и высоты | ||||||||||||||||||||||||||||||||||||||||
|
|
| 2.Сойства: 1)Основания призмы – равные многоугольники, лежащие в параллельных плоскостях. 2)Боковые рёбра призмы параллельны и равны. 3)Боковые грани призмы – параллелограммы. 4) V = Sосн. H 5) S бок. = Pперпен.сеч.· AA1 (AA1–бок.ребро) или S бок. – сумма площадей всех боковых граней. 6)Sпол. = Sбок. +2Sосн. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение прямой призмы ( все бок.рёбра перпендикулярны основаниям). 2.Свойства прямой призмы: 1)Высота призмы – любое боковое ребро, 2)Боковые грани – прямоугольники, 3) V = Sосн. H = Sосн. AA1(AA1 –бок. ребро), 4) ) S бок. = Pосн.· AA1 (AA1 –бок.ребро), 5)Sпол. = Sбок. +2Sосн. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение ( прямая призма, основание которой правильный многоугольник) | ||||||||||||||||||||||||||||||||||||||||
|
|
| 2.Свойства правильной призмы: 1)Высота призмы – любое боковое ребро, 2)Боковые грани – прямоугольники, 3) V = Sосн. H = Sосн. AA1(AA1 –бок. ребро), 4) ) S бок. = Pосн.· AA1 (AA1 –бок.ребро), 5)Sпол. = Sбок. +2Sосн. | ||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение – призма, основания которой параллелограммы. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 2. Свойства: 1)Все грани - параллелограммы. 2)Противолежащие грани параллельны и равны. 3)Диагонали параллелепипеда пересекаются в одной точке О и делятся ею пополам( О – центр симметрии параллелепипеда) | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение – параллелепипед, у которого боковые ребра перпендикулярны плоскостям оснований, т.е. боковые грани – прямоугольники. 2.Свойства: 1)Все боковые грани - прямоугольники. 2)Противолежащие грани параллельны и равны. 3)Диагонали параллелепипеда пересекаются в одной точке О и делятся ею пополам( О – центр симметрии параллелепипеда) | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1. Определение – параллелепипед, у которого все грани- прямоугольники ( a,b,c – измерения, три ребра , имеющие общую вершину. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 2. Свойства прямоугольного параллелепипеда: 1) 2) V= 3) S бок. = Pосн.· AA1 =2( 4) ) Sпол. = Sбок.+2Sосн. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение ( куб – прямоугольный параллелепипед, все измерения которого равны 2.Свойства куба: 1)Все грани – равные квадраты со стороной 2)Диагональ куба 3) V = 4)Sбок = 4 | ||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение, элементы пирамиды ( основание, вершина, боковые ребра и боковые грани, высота пирамиды, углы (плоские при вершине, между боковым ребром и плоскостью основания, двугранные при ребрах основания) 2. Свойства: 1)Vпир = 2)Sбок - сумма площадей боковых граней, Sпол. = Sбок. +Sосн. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение правильной пирамиды ( основание - | ||||||||||||||||||||||||||||||||||||||||
|
|
| правильный многоугольник,основание высоты пирамиды – центр этого многоугольника). 2.Свойства правильной пирамиды: 1)Все боковые рёбра равны и наклонены к плоскости основания под одним углом, 2)Все боковые грани – равные равнобедренные треугольники, плоскости которых наклонены к плоскости основания под одним углом. Апофема пирамиды – высота её боковой грани. 5)Vпир = Sбок = Sбок= Sбок грани 4)Sпол. = Sбок. +Sосн. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Если все боковые рёбра равны, или наклонены к плоскости основания под одним и темже углом , или образуют с высотой пирамиды равные углы - то основание пирамиды является центром окружности, описанной около основания пирамиды ( и наоборот). 2.Если все боковые грани пирамиды одинаково наклонены к основанию – то основание высоты пирамиды является центром окружности, вписанной в основание ( и наоборот). Для таких пирамид :Sбок = 3)Если лишь одна боковая грань пирамиды перпендикулярна к плоскости основания - товысотой пирамиды является высота этой грани. 4)Если две смежные боковые грани пирамиды перпендикулярны к плоскости основания - то высотой пирамиды является их общее боковое ребро. | ||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение прямого кругового цилиндра. Элементы цилиндра: основания, образующие, высота. 2.Свойства цилиндра: 1)Основание цилиндра - круги одинакового радиуса, лежащие в параллельных плоскостях. 2)Образующие цилиндра параллельны и равны. 3)Высота цилиндра равна образующей. 4)Цилиндр как тело вращения, полученное вращением прямоугольника ОАА1О1 вокруг стороны ОО1 (ОО1 –ось вращения, ОА =ОА1 = R- радиус цилиндра, ОО1 = АА1=H- его высота). 5)Sосн = 6) Vцил. = Sосн | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1. Осевое сечение. 2. Сечение плоскостью, параллельной его оси. 3. Сечение плоскостью, параллельной основанию. 4. Плоскость, касательная к цилиндру, если она проходит через образующую и перпендикулярна к плоскости осевого сечения, которая содержит эту образующую. | ||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение конус. Элементы – вершина , основание, образующие, высота. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1) Все образующие равны между собой. 2) Высота конуса H = SO (S– вершина, O –центр основания) 3) Конус как тело вращения прямоугольного треугольника вокруг одного из его катетов 4) Sосн = 5) Vкон = | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1. Осевое сечение. 2. Сечение конуса плоскостью, проходящей через его вершину. 3. Сечение конуса плоскостью, параллельной его основанию. Усечённый конус. 4. Плоскость, касательная к конусу | ||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение сферы ( О – центр сферы, А – точка сферы, ОА =R –радиус)Sсф. =4 2.Определение шара. Vш. = | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Любое сечение шара плоскостью – круг 2.Центр сечения – основание перпендикуляра из центра шара на плоскость сечения: О –центр шара, О1 – центр круга сечения, А – точка окружности сечения: ОО1⊥α ( α – плоскость сечения); ∆ ОО1А – прямоугольный и АО1 =Rсеч. = 3.Сечение, которое проходит через центр шара – большой круг: R, бол. круга = Rшара. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение: шар, описан около прямой призмы, если все вершины призмы лежат на поверхности шара. - шар можно описать только около прямой призмы, около основания которой можно описать окружность. О –центр шара, точка, равноудалённая от плоскостей оснований и от вершин призмы. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение шара , вписанного в прямую призму ( все грани призмы касаются этого шара). 2. Центр шара , вписанного в прямую призму - это середина отрезка, соединяющего центры окружностей, вписанных в основания призмы (радиус шара равен радиусу этой окружности, а диаметр шара равен высоте призмы). | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение шара, описанного около пирамиды( если все вершины пирамиды лежат на поверхности шара) Пирамида, вписанная в шар, у которой основание высоты –центр окружности, описанной около её основания. | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение шара, вписанного в пирамиду. 2.Пирамида, описанная около шара, у которой основание высоты – центр окружности, вписанной в основание пирамиды | ||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| На плоскости:
В пространстве:
| ||||||||||||||||||||||||||||||||||||||||
|
|
| На плоскости: A (
В пространстве: A (
| ||||||||||||||||||||||||||||||||||||||||
|
|
| На плоскости: AB = В пространстве:AB = | ||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| Определение вектора, как направленного отрезка, модуль ( длина, абсолютная величина) вектора | ||||||||||||||||||||||||||||||||||||||||
|
|
| На плоскости:
В пространстве:
| ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение
2.В координатах: на плоскости
В пространстве:
| ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Определение коллинеарных векторов. 2.Условие коллинеарности векторов ( в координатах)
| ||||||||||||||||||||||||||||||||||||||||
|
|
| 1.Сумма векторов на плоскости: 1) Правило треугольника: 2)Правило параллелограмма
В координатах:
3) Сумма векторов в пространстве – правило параллелепипеда
В координатах: | ||||||||||||||||||||||||||||||||||||||||
|
|
| 2. Разность векторов 1)
2)В координатах на плоскости:
3)В координатах в пространстве:
| ||||||||||||||||||||||||||||||||||||||||
|
|
| 3.Умножение вектора | ||||||||||||||||||||||||||||||||||||||||
|
|
| 1)
2)В координатах на плоскости: 3) В координатах в пространстве:
| ||||||||||||||||||||||||||||||||||||||||
|
|
| 4. .Скалярное произведение векторов 1). 2) В координатах на плоскости:
В координатах в пространстве:
3)Некоторые свойства скалярного произведения: -
- если - если - если
| ||||||||||||||||||||||||||||||||||||||||
Информационное обеспечение программы курса по выбору (факультатива)
«Повторим математику»
Литература:
1.Закон ДНР «Об образовании»
2.Программа по математике для общеобразовательных организаций 5-6 классы, 7-9 классы, 10-11 классы .
3.Учебники «Математика» 5 класс и 6 класс /С.И. Никольский, М.К. , Н.Н. Решетников, А.В. Шевкин / М.Просвещение,2016
4. Учебники «Алгебра» 7 класс, 8 класс, 9 класс / Ю.М. Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б. Суворова, под редакцией С.А. Теляковского/ М.Просвещение,2016
5. Учебник «Алгебра и начала математического анализа», 10-11 классы / Ш.А. Алимов, Ю.М.Колягин, М.В. Ткачева, Н.Е. Федорова, М.И. Шабунин/ М.Просвещение,2016
6.Учебник «Геометрия» 7-9 классы /Л.С.Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, , Э.Г. Позняк, И.И. Юдина/ М.Просвещение,2016
7. Учебник «Геометрия»10-11 классы /Л.С. Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Л.С.Киселева / М.Просвещение,2016.
8. Тематические и итоговые контрольные работы по математике 5 класс, 6 класс, /Л.Я.Федченко, Д.Каштан, 2009.
9. Сборник заданий для тематических и итоговых аттестаций, алгебра 7-9 классы, /Л.Я.Федченко ,Д.Каштан, 2009.
10. Сборник заданий для тематических и итоговых аттестаций, геометрия 7-9 классы. /Л.Я.Федченко , Д.Каштан, 2009.
11. Разноуровневые задания для тематических и итоговых контрольных работ по геометрии в 10-11 классах / Л.Я.Федченко , Д.Каштан, 2009.
12. Разноуровневые задания для тематических и итоговых контрольных работ по алгебре и началам анализа в 10-11 классах / Л.Я.Федченко , Д.Каштан, 2009.
13. Алгебраический тренажер, пособие для школьников и абитуриентов /А.Г.Мерзляк, Д.А.Немировский, В.Б.Полонский, М.С.Якир/ Х.Гимназия, 2009.
14. Полный курс математики в тестах. Энциклопедия тестовых заданий /Ю.А.Захарийченко, А.В.Школьный, Л.И.Захарийченко, Е.В.Школьная/ Х.Ранок, 2012.
15.Сборник заданий для государственной итоговой аттестации по математике, 11 класс в 2-х книгах; книга 1 и книга 2 / М.И.Бурда, О.Я. Билянина, О.П. Вашуленко, Н.С.Прокопенко / Х.Гимназия, 2009.
16. Математика ( профильный уровень). Экзаменационные тесты. Практикум по выполнению типовых тестовых заданий ЕГЭ. /Л.Д.Лаппо, М.А.Попов. М. «Экзамен», 2016
17. Математика ( базовый уровень). Экзаменационные тесты. Практикум по выполнению типовых тестовых заданий ЕГЭ. /Л.Д.Лаппо, М.А.Попов. М. «Экзамен», 2016
18. Математика. Подготовка к ЕГЭ в 2016 году. Диагностические работы. Профильный уровень. М. МЦНМО, 2016
19. Математика. Подготовка к ЕГЭ в 2016 году. Диагностические работы. Базовый уровень. М. МЦНМО, 2016
20. Электронный ресурс. Тематические комбинированные тесты для систематизации , обобщения учебного материала и контроля (самоконтроля) знаний учащихся 10 -11 классов по математике.


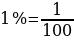

 .
.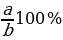 от числа в.
от числа в.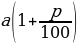 ,
, 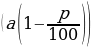
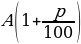 n
n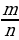 , где m– целое, n – натуральное число.Записываются в виде бесконечной периодической десятичной дроби.
, где m– целое, n – натуральное число.Записываются в виде бесконечной периодической десятичной дроби.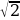 =1,4142135…
=1,4142135…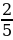 - обыкновенная дробь; 1,37 – десятичная дробь: 1,37=
- обыкновенная дробь; 1,37 – десятичная дробь: 1,37=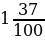 =
=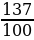 )
) 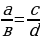 (а и d – крайние члены, в и с – средние члены)
(а и d – крайние члены, в и с – средние члены)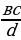 , с=
, с= 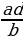 ,b=
,b= 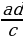 , d=
, d= 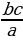
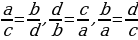
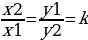 (k - коэффициент пропорциональности)
(k - коэффициент пропорциональности)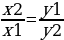
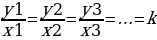


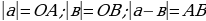
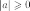
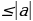
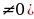
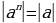 n, в частности
n, в частности 2,
2,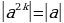 2k
2k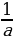 =1 (а
=1 (а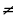 0)
0)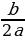 )2+
)2+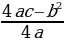
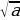
 , то в=
, то в= 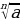
 )n=a.
)n=a. (k
(k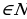 )
)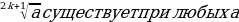
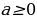 и
и 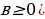
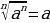
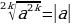
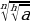 =
=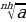
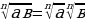
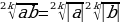
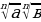 =
=
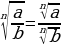
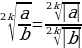
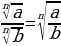
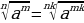 и наоборот
и наоборот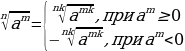
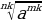 =
= 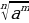
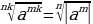
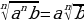
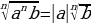
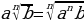
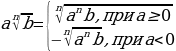 , где b≥0
, где b≥0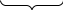 1=а; аn=а
1=а; аn=а a
a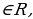 n
n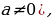 a-n=
a-n=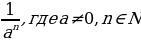
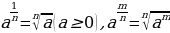
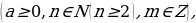
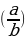 n=
n=
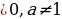 ) – показатель степени, в которую нужно возвести а, чтобы получить b.
) – показатель степени, в которую нужно возвести а, чтобы получить b.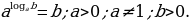
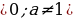
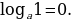


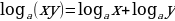
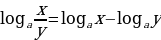
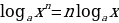
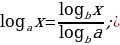
 b
b
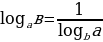
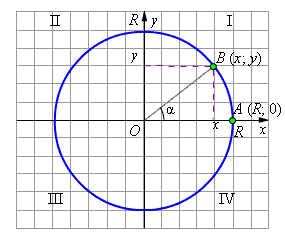 2+у2=1; соsα=x; sinα=y
2+у2=1; соsα=x; sinα=y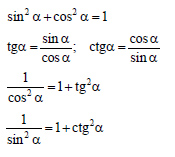 - основное тригонометрическое
- основное тригонометрическое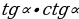 =1
=1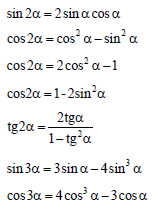
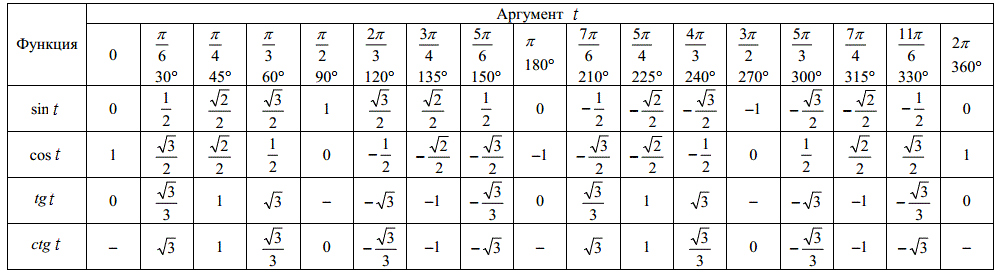
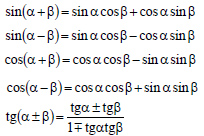
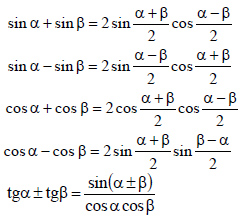
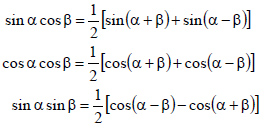
 sin(α+
sin(α+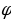 ), где аргумент
), где аргумент 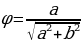 ,
, 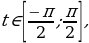 синус которого равен а:
синус которого равен а: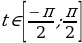 и sint=a
и sint=a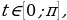 косинус которого равен а:
косинус которого равен а: и cost=a
и cost=a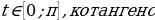 которого равен а:
которого равен а: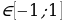 ;
;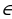 R;
R;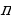 - arccosa;
- arccosa;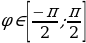 ;
; ;
;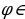 (
(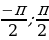 );
);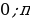 ).
).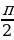 ,а
,а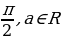 .
.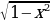 = arctg
= arctg 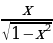 , 0
, 0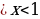 ;
;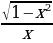 = arcctg
= arcctg 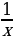 = arcsin
= arcsin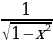 , x
, x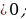
 =
= 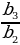 = … =
= … = 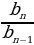 –знаменательпрогрессии
–знаменательпрогрессии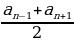 – любой член арифметической прогрессии – равен среднему арифметическому предыдущего и последующего членов.
– любой член арифметической прогрессии – равен среднему арифметическому предыдущего и последующего членов. – квадрат любого члена геометрической прогрессии равен произведению предыдущего и последующего членов.
– квадрат любого члена геометрической прогрессии равен произведению предыдущего и последующего членов.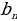 =
=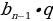 (по определению)
(по определению)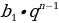
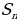 =
= 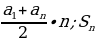 =
= 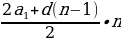 .
. =
=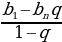 ;
; 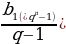 =
=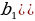 .
.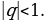

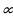 :
: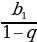
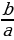
 ) a=0 0x=b
) a=0 0x=b 
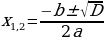 , где D =
, где D = 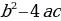 . При D
. При D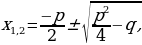 где D1=
где D1=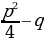 - дискриминант
- дискриминант 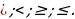
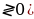 :
: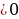 .
.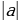 =
=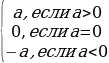
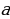

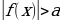
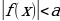
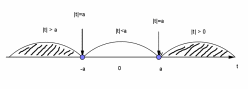 1.
1.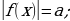 f(x) =
f(x) = 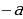 .
.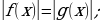 f(x)
f(x)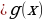 или f(x)
или f(x)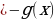 .
.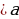 или f(x)
или f(x) 
 f(x)
f(x)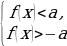
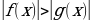 равносильно
равносильно  или (f(x) -
или (f(x) - 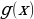 ) (f(x) +
) (f(x) +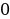 ).
).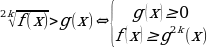 или
или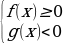
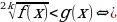
 =
=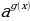 (
( равносильно f (x)
равносильно f (x)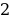 .
.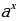 = b (
= b (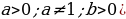 ; x =
; x =  .
.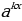 ( показатели степеней отличаются только свободными членами), а в другой части стоит число, то в этом случае выносится за скобку наименьшая степень
( показатели степеней отличаются только свободными членами), а в другой части стоит число, то в этом случае выносится за скобку наименьшая степень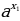 ≷
≷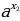 ; если
; если 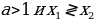 ,
, 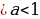 и
и 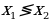 .
.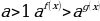 равносильно f(x)
равносильно f(x)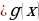 –знак неравенства сохраняется
–знак неравенства сохраняется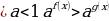 равносильно f(x)
равносильно f(x)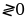 :
: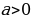 и
и 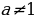 ), то
), то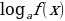 =c равносильно f(x) =
=c равносильно f(x) =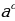
 )
)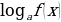 =
= );
);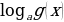 равносильно
равносильно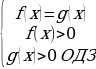
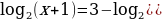
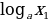 ≷
≷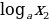 . если
. если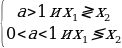
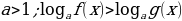 равносильно
равносильно 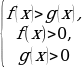 или
или 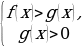
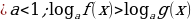 равносильно
равносильно 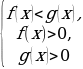 или
или 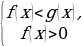
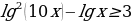
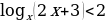
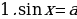 . При
. При или а
или а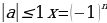 arc
arc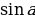 +
+
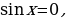 x =
x =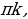 k
k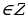 ,
,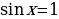 , x =
, x =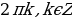 ,
,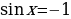 , x =
, x =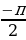 +
+ 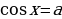 , При
, При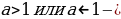 корней нет.
корней нет.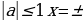 arc
arc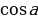 +
+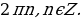
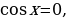 x =
x =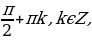
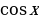 = 1, x = 2
= 1, x = 2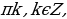
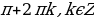
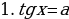 , x = arctg
, x = arctg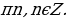
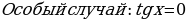 , х =
, х =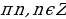
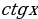 =
=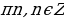
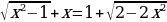 ( ОДЗ:x =
( ОДЗ:x = 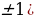
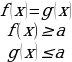 равносильно
равносильно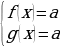
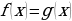 оказалось , что
оказалось , что 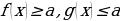 , то равенство в уравнении возможно только тогда, когда
, то равенство в уравнении возможно только тогда, когда 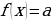 и
и 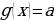 одновременно.
одновременно.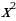 =
= 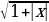 . Ответ : 0
. Ответ : 0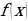 возрастает на некотором промежутке, а функция
возрастает на некотором промежутке, а функция 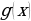 убывает на этом же промежутке( или наоборот), то это уравнение может иметь не более одного корня на этом промежутке.
убывает на этом же промежутке( или наоборот), то это уравнение может иметь не более одного корня на этом промежутке.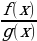
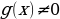
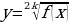 ;
;
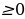
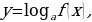
 ,
,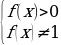
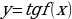
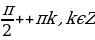
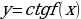
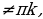


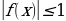 , -1
, -1
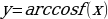
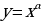
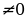
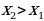 и
и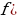 )
)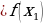 для всех
для всех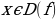 .
.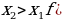 )
)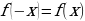 для всех
для всех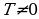 если для любогоx (
если для любогоx (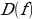 и выполняется равенство:
и выполняется равенство: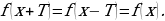
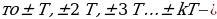 также периоды этой функции(k
также периоды этой функции(k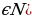 и T- наименьший её положительный период.
и T- наименьший её положительный период.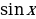 иcosx имеют период T = 2
иcosx имеют период T = 2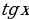 и
и 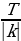 , где A, k, и b некоторые числа иk
, где A, k, и b некоторые числа иk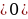 –растяжение или сжатие графика вдоль оси Оу (при k
–растяжение или сжатие графика вдоль оси Оу (при k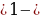 растяжение, при 0
растяжение, при 0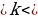 1 -сжатие)
1 -сжатие)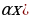 (
( 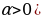 –растяжение или сжатие графика вдоль оси Ох ( при
–растяжение или сжатие графика вдоль оси Ох ( при 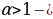 сжатие ,при
сжатие ,при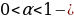 растяжение)
растяжение)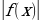 –выше оси Ох ( и на самой оси) график остается без изменений; ниже оси Ох- симметрично отображается относительно оси Ох.
–выше оси Ох ( и на самой оси) график остается без изменений; ниже оси Ох- симметрично отображается относительно оси Ох.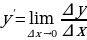 =
=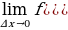 т.е. Производная – предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
т.е. Производная – предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.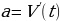 - ускорение прямолинейного движения
- ускорение прямолинейного движения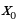 - абсцисса точки касания прямой с графиком
- абсцисса точки касания прямой с графиком  ) =
) =  = k ( k– угловой коэффициент касательной)
= k ( k– угловой коэффициент касательной)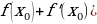 ) уравнение касательной к графику функцииy = f(x) в точке с абсциссой
) уравнение касательной к графику функцииy = f(x) в точке с абсциссой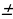 v )′ = u′
v )′ = u′ 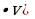 = u
= u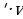 +u·v′
+u·v′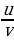 )′ =
)′ =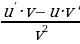
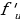 (u)·
(u)· 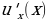
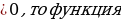 f(x) возрастает на этом интервале).
f(x) возрастает на этом интервале).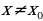 из окрестностей
из окрестностей 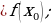
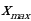 =
=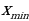 =
= то
то 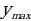 = f(
= f(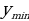 = f(
= f(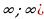 ).
).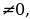 b - число, то
b - число, то 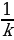 F( kx + b) - первообразная для функцииf ( kx + b).
F( kx + b) - первообразная для функцииf ( kx + b).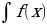 dx =F(x) + С.
dx =F(x) + С.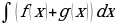 =
= 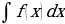 +
+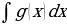 .
.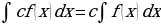 .
.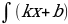 =
= 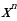 (n
(n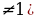
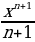 + C
+ C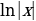 + C
+ C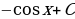
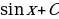
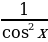
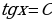
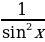
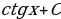
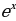
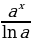 + C
+ C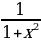
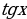 + Cили
+ Cили + C
+ C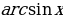 +C или
+C или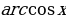 + C
+ C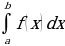 = F(b) – F (a) – формула Ньютона – Лейбница.
= F(b) – F (a) – формула Ньютона – Лейбница.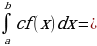 c
c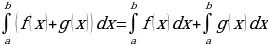
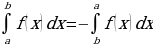
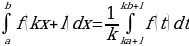
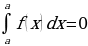
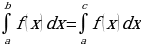 +
+ 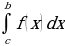
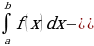 площадь S криволинейной трапеции (фигура , ограниченная графиком непрерывной положительной на промежутке [a;b] функцииf(x), осью Ох и прямыми
площадь S криволинейной трапеции (фигура , ограниченная графиком непрерывной положительной на промежутке [a;b] функцииf(x), осью Ох и прямыми )
) путь при прямолинейном движении за время от
путь при прямолинейном движении за время от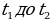 со скоростью
со скоростью 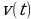
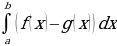
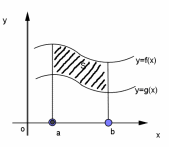
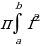 (x)dx
(x)dx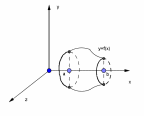
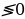 ) – упорядоченная пара чисел(
) – упорядоченная пара чисел(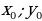 ,) которая обращает его в верное равенство( числовое неравенство).
,) которая обращает его в верное равенство( числовое неравенство).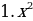 +
+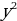 =
= 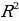 окружность с центром в точке (0;0) и радиусом R.
окружность с центром в точке (0;0) и радиусом R.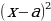 +
+ 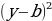 =
= 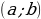 и радиусом R
и радиусом R + by + c = 0 - прямая, с координатами точек пересечения осей
+ by + c = 0 - прямая, с координатами точек пересечения осей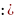 ;0) и ( 0;
;0) и ( 0;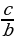 )
) 
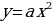 + bx + c (
+ bx + c (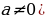 парабола с вершиной в точке с координатами
парабола с вершиной в точке с координатами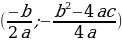 ( при
( при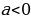 - ветви вниз).
- ветви вниз).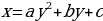 - парабола с вершиной (
- парабола с вершиной (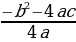 ;
;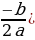 ( при
( при 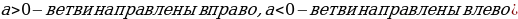
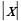 +
+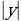 =1 квадрат с центром в точке ( 0;0); диагонали квадрата лежат на осях Ох и Оу ( т.е. вершины квадратов в точках (1;0) ;(0;1; ( -1 ;0); (0 ;-1).
=1 квадрат с центром в точке ( 0;0); диагонали квадрата лежат на осях Ох и Оу ( т.е. вершины квадратов в точках (1;0) ;(0;1; ( -1 ;0); (0 ;-1).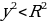 круг с центром в точке (0;0) и радиусом R.
круг с центром в точке (0;0) и радиусом R.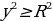 плоскость вне круга с центром в точке (0;0) и радиусом R.
плоскость вне круга с центром в точке (0;0) и радиусом R.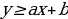 - полуплоскость над прямой
- полуплоскость над прямой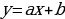
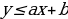 - полуплоскость под прямой
- полуплоскость под прямой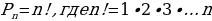
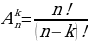
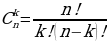
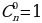
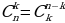
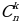 +
+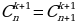
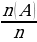 – относительная частота случайного события
– относительная частота случайного события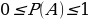 .
.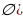 не происходит ни при каком повторении эксперимента Р
не происходит ни при каком повторении эксперимента Р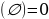 .
.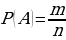 .
.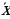 )случайной величины x – среднее арифметическое всех её значений.
)случайной величины x – среднее арифметическое всех её значений.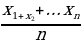 ,если случайная величина х имеетn значенийх1,х2…хn.
,если случайная величина х имеетn значенийх1,х2…хn.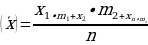 , если случайная величина Х имеет значения х1,х2…хn., а их частоты
, если случайная величина Х имеет значения х1,х2…хn., а их частоты
 (рис. 1)
(рис. 1)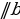
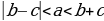 - неравенство треугольника
- неравенство треугольника =
=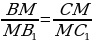 =
= ;
;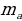 =
=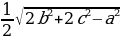
 к ней
к ней 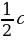
 ∠B;
∠B;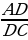 =
= - пропорциональное свойство биссектрисы;
- пропорциональное свойство биссектрисы;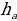 :
: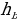 :
: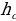 =
=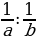 :
: – высоты обратно пропорциональны сторонам.
– высоты обратно пропорциональны сторонам.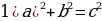 –Теорема Пифагора
–Теорема Пифагора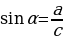 ; a= c
; a= c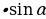 ;
; 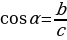 ;
;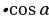 ;
;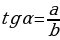 ; a= b
; a= b 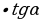 .
. ∆ABC ,
∆ABC , 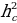 =
=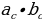
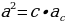
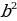 = c
= c .
.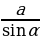 =
= 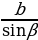 =
= 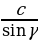 =
= 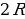 –теорема синусов
–теорема синусов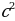 =
= 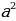 +
+ 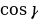 - теорема косинусов
- теорема косинусов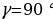
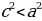 +
+ 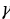 – острый угол
– острый угол +
+ 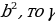 – тупой угол
– тупой угол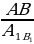 =
=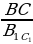 =
=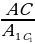 =
= =
=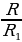 =k (k-коэффициент подобия)
=k (k-коэффициент подобия)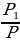 =
= 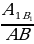 = k;
= k;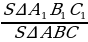 =
=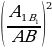 =
=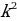
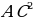 + B
+ B = 2
= 2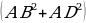
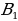 =
= D =
D =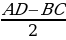 .
.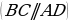 :
: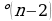 ( n- число углов многоугольника);
( n- число углов многоугольника);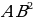 = AC
= AC 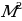 =SA
=SA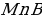
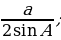 R =
R = 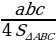 (a,b,c– стороны ∆ ABC, S – его площадь , R – радиус описанной окружности)
(a,b,c– стороны ∆ ABC, S – его площадь , R – радиус описанной окружности)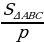 ; где p =
; где p =  (a,b,c– стороны ∆ ABC, S – его площадь, r– радиус вписанной окружности)
(a,b,c– стороны ∆ ABC, S – его площадь, r– радиус вписанной окружности)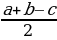 .
.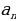 правильного n- угольника через R и r(радиусы описанной и вписанной окружностей)
правильного n- угольника через R и r(радиусы описанной и вписанной окружностей) 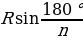 ;
;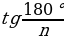 .
.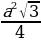 S = 3
S = 3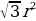
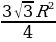 .
.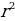 ; S = 2
; S = 2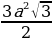 ;S = 2
;S = 2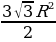 .
.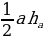 ; S =
; S = 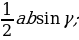 S =
S =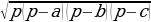 гдеp =
гдеp =  )
)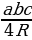 , где R–радиус описанной окружности S =rp , где r – радиус вписанной окружности
, где R–радиус описанной окружности S =rp , где r – радиус вписанной окружности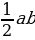 ; S =
; S =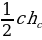 ;S =
;S = 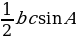 .
.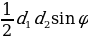 ,
, 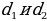 -
-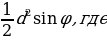 aи b -
aи b - 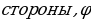 - угол между диагоналями, d - диагональ
- угол между диагоналями, d - диагональ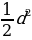 .
.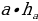 ; S =
; S = 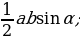 S =
S = 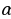 – угол между сторонами., ,
– угол между сторонами., ,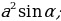 S =
S = 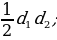 ( a – сторона ,
( a – сторона , 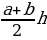 или S = m
или S = m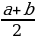 , h- высота)
, h- высота)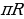 ( R- радиус),
( R- радиус),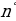 ℓ
ℓ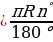 или 𝓵 =
или 𝓵 =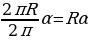 (
(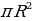 .
.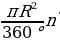
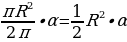
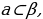 причём
причём то
то 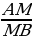 =
= 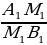
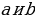 –скрещивающееся прямые
–скрещивающееся прямые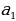 ‖
‖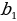 ‖b; O=
‖b; O=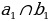
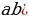 =∠(
=∠(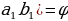 ( 0
( 0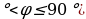 .
.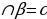 ; γ ⊥с .
; γ ⊥с . =
=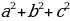 (
(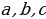 -измерения, d –диагональ)
-измерения, d –диагональ)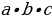
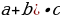
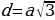 ,
,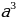 ,
,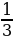 Sосн. H.
Sосн. H.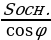 (
( 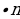 (n- количество боковых граней),
(n- количество боковых граней), H.
H.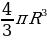
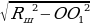 .
.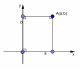
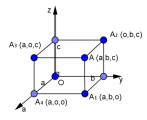
 ;
;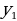 ),B(
),B(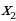 ;
;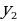 ),C- середина AB:
),C- середина AB: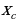 =
=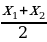 ;
;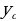 =
=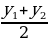 .
.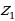 ),B(
),B(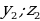 ) С- середина AB:
) С- середина AB: =
= 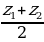 .
.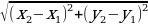
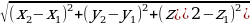
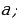 b) – координаты её центра
b) – координаты её центра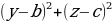 =
= 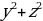 =
= 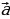 =
= 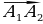 , где A1 (
, где A1 (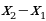 ,
,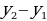 и
и 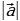 =
=
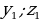 ) – начало, А2(
) – начало, А2(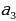 ) , где
) , где 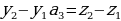 и
и 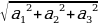 .
. , если
, если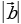 и
и  и
и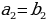 .
.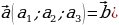 ;
; 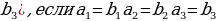
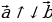 , если
, если 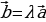 , т.е.
, т.е.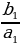 =
=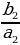 =
= 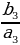 (т.е.соответствующие координаты пропорциональны)
(т.е.соответствующие координаты пропорциональны)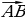 +
+ =
=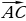

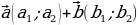 =
= 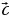 (
(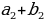 )
)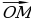 =
= 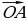 +
+ 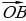 +
+ =
=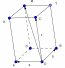
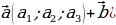 ;
;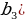 =
= 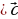 (
(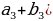
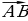 =
=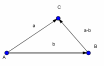
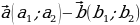 =
= 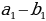 ;
; 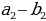 )
)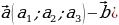 ;
; 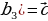 (
(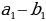 ;
; 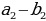 ;
; 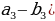
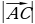 =
=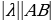 и при
и при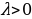 вектор λ
вектор λ 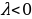 вектор λ
вектор λ 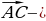 противоположно направлены.
противоположно направлены.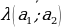 =
=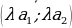 .
.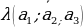 =
=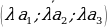
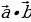 =
= 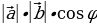 (
( 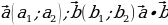 =
= 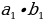 +
+ 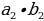 .
.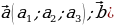 ;
; 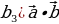 =
= 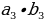 .
.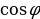 =
=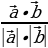 (
( 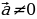 и
и 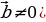 , то
, то 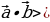 0 (
0 (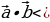 0 (
0 (









