

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока


Рабочая программа по алгебре 7-9 класс. ФГОС
Рабочая программа по алгебре 7-9 класс. ФГОС
Просмотр содержимого документа
«Рабочая программа по алгебре 7-9 класс. ФГОС»
Муниципальное бюджетное общеобразовательное учреждение
«средняя школа № 43» города Иванова
Предметная область: «Математика и информатика»
Предмет: Алгебра
Название программы: Рабочая программа основного общего образования по алгебре.
| «Рассмотрено» Руководитель МО учителей естественно-научного цикла_______Морева Е.Н. Протокол № ____ от «____» ________20___ г.
| «Согласовано» Заместитель директора по УВР __________Емельянова Н.С.
«____» __________ 20 ____г. | «Утверждаю» Директор МБОУ СОШ № 43 _____________Виткина Н.В. Приказ № _______ от «____»___________20___г.
|
Составители:
учитель математики Шляпцева Н.Н.
Год составления программы: 2015.
Пояснительная записка
Настоящая программа курса алгебры для 7–9 классов продолжает соответствующую программу курса математики 5–6 классы и ставит перед собой главной целью формирование у школьников основ научного (математического) мышления, позволяющих продолжать обучение в старшей школе или путем самообразования, и применять их в своей практической деятельности.
Данная рабочая программа разработана на основе Федерального государственного образовательного стандарта основного общего образования, Фундаментального ядра содержания общего образования, Образовательной программы основного общего образования школы, авторской программы «Алгебра 7-9 классы», авторы: И.И.Зубарева, А.Г.Мордкович.
Нормативно правовым основанием разработки программы также является:
Закон «Об образовании в Российской Федерации» – ФЗ №273 от 29.12.12.
Постановление Главного государственного санитарного врача РФ от 29.12.2010 №189 «Об утверждении СанПин 2.4.2.2821-10. Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях» - зарегистрирован в Минюсте России 03.03.2011.
О введении федеральных государственных образовательных стандартов общего образования - Инструктивно-методическое письмо Департамента общего образования Минобрнауки России от 19.04.2011 № 03255.
Об организации внеурочной деятельности при введении Федерального государственного образовательного стандарта общего образования - Инструктивно-методическое письмо Департамента общего образования Минобрнауки России от 12.05.2011 № 03296.
Рекомендации по оснащению общеобразовательных учреждений учебным и учебно-лабораторным оборудованием, необходимым для реализации Федерального государственного образовательного стандарта основного общего образования, организации проектной деятельности, моделирования и технического творчества обучающихся - приложение к письму Минобрнауки России от 24.11.2011 № МД1552/03.
Приказ Министерства образования и науки Российской Федерации (Минобрнауки России) от 19 декабря 2012 г. N 1067 г. Москва "Об утверждении федеральных перечней учебников, рекомендованных (допущенных) к использованию в образовательном процессе в образовательных учреждениях, реализующих образовательные программы общего образования и имеющих государственную аккредитацию, на 2013/14 учебный год".
Приказ Департамента образования Ивановской области №594 от 8 июля 2011.
Устав МБОУ «СШ № 43".
Положения о порядке разработки, утверждения, реализации и корректировки рабочих программ учебных курсов, предметов, дисциплин (модулей).
Курс «Алгебра» является продолжением курса «Математики», начатого в 5-6 классах. Однако он нацелен на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Данная программа ориентирована, главным образом, на формирование научных (математических) понятий, а не только лишь на выработку практических навыков и умений. Это предполагает особую организацию учебного процесса в форме учебной деятельности школьников. Содержание учебной деятельности развертывается в теоретической форме – от общего к частному, от абстрактного к конкретному. Освоение понятий происходит не в форме отработки словесных формулировок, а путем вхождения учащихся в новый круг задач и в деятельность по поиску общего способа их решения. Поиск способа решения новой задачи является мотивационным ядром учебной деятельности, той ценностной установкой учеников, которая складывается в виде формального эффекта обучения как личностно-смысловое образование, основа желания и умения учиться. Необходимость поиска способа решения новой задачи не диктуется требованиями учителя, учебника или программы, она должна быть обусловлена для детей внутренней логикой содержания обучения. Когда ученики обнаруживают, что задача не может быть решена теми способами, которыми они уже владеют, они сами заявляют о необходимости поиска новых способов действия. Иными словами, уже начав действовать, уже стремясь получить результат, дети фиксируют невозможность его немедленного достижения и необходимость открытия «чего-то нового». Т.о. новое понятие или способ действия не возникает для детей случайно; каждое следующее понятие с необходимостью вытекает из предыдущего. При этом принципиально, что поисковые действия детей (их пробы, мнения, предложения, вопросы) должны быть направлены не на внешние чувственно-представленные, непосредственно наблюдаемые свойства вещей, а на общий принцип их строения. Вскрывая этот общий принцип посредством собственных действий, осуществляемых не в словесной, а предметно-чувственной форме, ребенок тем самым обнаруживает существенное отношение, лежащее в основании нового понятия.
Отношение, которое дети обнаруживают, преобразуя объект изучения, не обладает чувственной наглядностью, оно нуждается в особом – модельном способе презентации. При этом не всякое изображение можно назвать учебной моделью, а лишь такое, которое отображает внутренние особенности объекта, не наблюдаемые непосредственно, и обеспечивает их дальнейший анализ. Учебная модель, выступая как продукт мыслительного анализа, затем сама может стать особым средством мыслительной деятельности. С одной стороны, в процессе построения модели происходит абстракция отношения от его предметных носителей. С другой стороны, уже построенная модель, в которой отношение представлено материально, позволяет преобразовывать ее, открывая новые свойства этого отношения. Преобразовывая и переконструируя учебную модель, школьники получают возможность изучать свойства отношения как такового, без «затемнения» привходящими обстоятельствами. Представленная моделью абстракция затем конкретизируется в различных частных условиях, что позволяет применять найденный общий способ к целому классу частных задач. Для того чтобы дети смогли через собственные поисковые действия открыть новый способ действия, необходимы особые формы организации совместной учебной деятельности класса и учителя. Основой этой организации является общеклассная дискуссия, в которой каждое высказанное предложение оценивается остальными участниками обсуждения с точки зрения соответствия способа действия и достигнутого результата. Предложения учителя подлежат такому же контролю и оценке, что и предложения учеников. При этом достоинства и недостатки предлагаемых способов действия оцениваются содержательно и ученики участвуют в выработке критериев контроля и оценки наряду с учителем. Благодаря этому у школьников складывается способность к самоконтролю и самооценке как базисным компонентам умения учиться. Осуществление школьниками учебной деятельности способствует формированию у них таких мыслительных действий, как рефлексия, анализ и планирование, являющихся основой теоретического мышления и, одновременно развитию других познавательных процессов – восприятия, воображения, памяти. Это дает основание говорить о развивающем значении специальной организации учебной деятельности школьников.
Традиционно курсы алгебры включают две содержательные области. Одна из них, касается собственно алгебраической тематики (преобразование выражений, решение уравнений и неравенств и т.п.). Вторая относится к изучению элементарных функций (исследование функций, построение графиков и т.п.). Обычно в школьных курсах алгебры эти области рассматриваются изолированно друг от друга, более того, даже темы, относящиеся к одной области, идейно не всегда связаны друг с другом: например, понятие равносильности рассматривается отдельно для уравнений, отдельно для неравенств, отдельно для систем, как будто это совершенно разные понятия; общее понятие функции вводится только после рассмотрения отдельных частных видов функциональных зависимостей и т.п. Как следствие, эти и другие общие понятия у детей остаются не сформированными, а по-прежнему сводятся к их частным проявлениям. Исходные «узкие» определения не позволяют формировать у детей позиционный (в зависимости от рассматриваемой ситуации) взгляд на математические объекты. Так, например, в математике многочлен может рассматриваться и как выражение определенного вида, и как функция, что не одно и то же: с первой точки зрения выражение (х – 3)(х + 1) не является многочленом, а со второй – является.
Понимание переменной только как буквы, а не места в выражении, препятствует видению общей структуры выражения, что затрудняет сведение сложных выражений к простым «базовым» (например, дети могут не увидеть возможности применить способ решения квадратных уравнений к тригонометрическим или логарифмическим). В результате освоенные способы решения определенных классов задач не переносятся на задачи, требующие комплексных методов решения.
В основе предлагаемой программы лежит идея математического моделирования и использования для этого специальных языков описания объектов. С различными описаниями (моделями) учащиеся знакомились и ранее. Теперь главной задачей становится соотнесение разных языков описания. Главным образом, речь идет о двух языках: геометрическом и алгебраическом (языке знаковых моделей). Геометрический язык более наглядный и позволяет непосредственно представлять отношения между числами и величинами; алгебраический (знаковый) – более абстрактный, он является языком действий.
Связующим звеном между этими языками является координатный метод, который становится основным средством исследований на протяжении всего курса, выступая в двух взаимосвязанных и взаимодополняющих ролях: как средство описания геометрических объектов – точечных множеств на прямой и на плоскости и как средство графической интерпретации алгебраических объектов – уравнений, неравенств и их систем. Центральным понятием, в котором происходит синтез двух языков, является понятие функции. Причем сначала понятие функции вводится в общем контексте описания зависимостей между переменными величинами, формулируются в общем виде основные задачи исследования этих зависимостей (здесь основными средствами являются графическое представление и общефункциональная символика) и лишь затем происходит конкретизация – рассмотрение частных видов функций, описываемых определенными алгебраическими выражениями – линейной, включая прямую пропорциональность (7 класс), квадратичной (8 класс), степенной функций, арифметической и геометрической прогрессий (9 классы). Такой подход делает открытой для учащихся перспективу их продвижения в предметном содержании, поскольку позволяет им самостоятельно выделять конкретные виды функций, исследуя и классифицируя алгебраические выражения, либо, открывая новые зависимости как модели «реальных» ситуаций.
Исследования, связанные с собственно алгебраическим языком, составляют линию алгебраических преобразований, которая выстраивается по тому же принципу – от общих понятий о выражениях и их преобразовании к конкретным их видам – целым рациональным выражениям (7, 8 классы), дробным рациональным выражениям, иррациональным выражениям (8, 9 классы). При этом линия алгебраических преобразований разворачивается во времени таким образом, чтобы обеспечивать необходимым инструментарием ведущую линию – линию математических моделей.
Такой подход позволяет рассматривать основные виды математических моделей не изолированно друг от друга, а в тесной взаимосвязи, когда, например, уравнения и неравенства (а также их системы) выступают как средство решения задач, связанных с исследованием функций, а функциональные представления, наоборот, положены в основу способов решения уравнений и неравенств. Тем самым возникает возможность рассмотрения различных понятий, традиционно составляющих содержание курса алгебры, с единых позиций.
В курсе также продолжается начатая в 6 классе содержательная линия, посвященная элементам теории вероятностей и статистики.
Изучение алгебры в основной школе направлено на достижение следующих целей:
1) в направлении личностного развития
развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
развитие интереса к математическому творчеству и математических способностей;
2) в метапредметном направлении
формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сферчеловеческой деятельности;
3) в предметном направлении
овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни;
создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.
Для реализации поставленных целей выбран учебно-методический комплект, который обеспечивает преемственность курсов математики в начальной школе и математики в 5-6 классах. УМК позволяет проводить разноуровневое обучение и качественную подготовку школьников к изучению курса алгебры в 7-9 классах, а также смежных дисциплин — геометрии, информатики, физики, химии, географии и др. Математическое содержание учебников «Алгебра 7-9» позволяет достичь планируемых результатов обучения, предусмотренных ФГОС. Кроме того, данная линия учебников обусловлена логикой внутрипредметных связей, возрастными особенностями развития учащихся и имеет следующие особенности:
последовательное изложение теории с привлечением большого числа примеров, способствующее эффективной организации учебного процесса;
создание математическим взаимопроникновению содержательно-методических линий курса условий для глубокого аппаратом усвоения благодаря теории взаимосвязи и овладения;
обеспечение усвоения основных теоретических знаний и формирования необходимых умений и навыков с помощью системы упражнений;
выделение заданий обязательного уровня в каждом пособии, входящем в УМК.
Учебно-методический комплект:
1. А.Г.Мордкович. Алгебра-7. Часть 1. Учебник. М: Мнемозина, 2014 г.
2. А.Г.Мордкович и др. Алгебра-7. Часть 2. Задачник. М: Мнемозина, 2014 г.
3. А.Г.Мордкович. Алгебра-8. Часть 1. Учебник. М: Мнемозина, 2014 г.
4. А.Г.Мордкович и др. Алгебра-8. Часть 2. Задачник. М: Мнемозина, 2014 г.
5. А.Г.Мордкович. Алгебра-8. Часть 1. Учебник. М: Мнемозина, 2014 г.
6. А.Г.Мордкович и др. Алгебра-8. Часть 2. Задачник. М: Мнемозина, 2014 г.
В МБОУ «СШ № 43» для обязательного изучения учебного предмета «Алгебра» на этапе основного общего образования отводится 306 учебных часов, в том числе: в VII, VIII и IX классах по 102 часа, из расчета 3 учебных часа в неделю.
Содержание математического образования в основной школе представлено в виде следующих содержательных разделов. Это арифметика; алгебра; функции; вероятность и статистика. Наряду с этим в содержание основного общего образования включены два дополнительных методологических раздела: логика и множества; математика в историческом развитии, что связано с реализацией целей обще интеллектуального и общекультурного развития учащихся. Содержание каждого из этих разделов разворачивается в содержательно-методическую линию, пронизывающую все основные разделы содержания математического образования на данной ступени обучения. При этом первая линия - «Логика и множества» - служит цели овладения учащимися некоторыми элементами универсального математического языка, вторая - «Математика в историческом развитии» - способствует созданию общекультурного, гуманитарного фона изучения курса.
Содержание раздела «Арифметика» служит базой для дальнейшего изучения учащимися алгебры, способствует развитию их логического мышления, формированию умения пользоваться алгоритмами, а также приобретению практических навыков, необходимых в повседневной жизни. Развитие понятия о числе в основной школе связано с рациональными и иррациональными числами, формированием первичных представлений о действительном числе. Завершение числовой линии (систематизация сведений о действительных числах, о комплексных числах), так же как и более сложные вопросы арифметики (алгоритм Евклида, основная теорема арифметики), отнесено к ступени общего среднего (полного) образования.
Содержание раздела «Алгебра» способствует формированию у учащихся математического аппарата для решения задач из разных разделов математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей процессов и явлений реального мира. В задачи изучения алгебры входят также развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики, овладение навыками дедуктивных рассуждений. Преобразование символьных форм вносит специфический вклад в развитие воображения учащихся, их способностей к математическому творчеству. В основной школе материал группируется вокруг рациональных выражений, а вопросы, связанные с иррациональными выражениями, с тригонометрическими функциями и преобразованиями, входят в содержание курса математики на старшей ступени обучения в школе.
Содержание раздела «Функции» нацелено на получение школьниками конкретных знаний о функции как важнейшей математической модели для описания и исследования разнообразных процессов. Изучение этого материала способствует развитию у учащихся умения использовать различные языки математики (словесный, символический, графический), вносит вклад в формирование представлений о роли математики в развитии цивилизации и культуры.
Раздел «Вероятность и статистика» - обязательный компонент школьного образования, усиливающий его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования у учащихся функциональной грамотности - умения воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и вероятности обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.
Особенностью раздела «Логика и множества» является то, что представленный в нем материал преимущественно изучается при рассмотрении различных вопросов курса. Соответствующий материал нацелен на математическое развитие учащихся, формирование у них умения точно, сжато и ясно излагать мысли в устной и письменной речи.
Раздел «Математика в историческом развитии» предназначен для формирования представлений о математике как части человеческой культуры, для общего развития школьников, для создания культурно-исторической среды обучения. На него не выделяется специальных уроков, усвоение его не контролируется, но содержание этого раздела органично присутствует в учебном процессе как своего рода гуманитарный фон при рассмотрении проблематики основного содержания математического образования.
В учебно-тематическом планировании отведены первые уроки на повторение материала за предшествующий год.
При организации процесса обучения в рамках данной программы предполагается применением следующих педагогических технологий обучения: личностно-ориентированная (педагогика сотрудничества), позволяющую увидеть уровень обученности каждого ученика и своевременно подкорректировать её; технология уровневой дифференциации, позволяющая ребенку выбирать уровень сложности, информационно-коммуникационная технология, обеспечивающая формирование учебно-познавательной и информационной деятельности учащихся. Основные виды учебной деятельности:
- Чтение формул, правил, теорем, записанных на математическом языке в знаково-символьном виде. Перевод словесных формулировок математических утверждений на математический язык.
- Описание реальных ситуаций с помощью математических моделей: функций, уравнений, неравенств, систем уравнений и неравенств.
- Планирование хода решения задач с использованием трех этапов математического моделирования. Прогнозирование результата решения, оценка реальности полученного ответа.
- Узнавание, построение и описание графических моделей элементарных функций, изучаемых в 7 – 9 классах. Применение графического метода решения уравнений, неравенств, систем уравнений.
- Составление алгоритма построения графика, решения уравнения, неравенства, систем уравнений или неравенств, выполнения алгебраических преобразований.
- Выполнение алгебраических преобразований, пошаговый контроль правильности и полноты выполнения алгоритма преобразования.
- Поиск, обнаружение и устранение ошибок арифметического, алгебраического и логического характера.
- Сравнение разных способов вычислений, преобразований, решений задач, выбор оптимального способа.
- Осуществление исследовательской деятельности: наблюдение, анализ, выявление закономерности, выдвижение гипотезы, доказательство, обобщение результата.
- Вывод формул, доказательство свойств, формулирование утверждений.
- Сбор, анализ, обобщение и представление статистических данных.
- Поиск информации в учебной и справочной литературе и в Интернете.
Внеурочная деятельность по предмету предусматривается в формах: факультативов, элективного курса по предмету, участие в конкурсах, творческие проекты.
В практике используются формы организации работы на уроке:
индивидуальные;
групповые;
индивидуально-групповые;
фронтальные;
практикумы.
В качестве методов обучения применяются:
словесные методы (рассказ, объяснение, беседа, дискуссия, лекция, работа с книгой),
наглядные методы (метод иллюстраций, метод демонстраций),
практические методы (упражнения, практические работы).
Промежуточная аттестация и текущий контроль проводится в соответствии с локальным актом школы.
Тематическое планирование
Алгебра 7 класс
| № | Содержание учебного материала | Количество часов (102) | Количество контрольных работ (7) |
|
| Глава 1. МАТЕМАТИЧЕСКИЙ ЯЗЫК. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ | 13 |
|
| | Числовые и алгебраические выражения | 3 |
|
| | Что такое математический язык | 1 |
|
| | Что такое математическая модель | 3 |
|
| | Линейное уравнение с одной переменной | 3 |
|
| | Координатная прямая | 2 |
|
|
| Контрольная работа № 1 | 1 | 1 |
|
| Глава 2. ЛИНЕЙНАЯ ФУНКЦИЯ | 12 |
|
| | Координатная плоскость | 2 |
|
| | Линейное уравнение с двумя переменными | 3 |
|
| | Линейная функция | 3 |
|
| | Линейная функция | 2 |
|
| | Взаимное расположение графиков линейных функций | 1 |
|
|
| Контрольная работа № 2 | 1 | 1 |
|
| Глава 3. СИСТЕМЫ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ | 11 |
|
| | Основные понятия | 2 |
|
| | Метод подстановки | 3 |
|
| | Метод алгебраического сложения | 2 |
|
| | Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций | 3 |
|
|
| Контрольная работа № 3 | 1 | 1 |
|
| Глава 4. СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ И ЕЕ СВОЙСТВА | 9 |
|
| | Что такое степень с натуральным показателем | 2 |
|
| | Таблица основных степеней | 1 |
|
| | Свойства степени с натуральным показателем | 3 |
|
| | Умножение и деление степеней с одинаковым показателем | 2 |
|
| | Степень с нулевым показателем | 1 |
|
|
| Глава 5. ОДНОЧЛЕНЫ. ОПЕРАЦИИ НАД ОДНОЧЛЕНАМИ | 7 |
|
| | Понятие одночлена. Стандартный вид одночлена | 1 |
|
| | Сложение и вычитание одночленов | 2 |
|
| | Умножение одночленов. Возведение одночлена в степень | 2 |
|
| | Деление одночлена на одночлен | 1 |
|
|
| Контрольная работа № 4 | 1 | 1 |
|
| Глава 6. МНОГОЧЛЕНЫ. ОПЕРАЦИИ НАД МНОГОЧЛЕНАМИ | 14 |
|
| | Основные понятия | 1 |
|
| | Сложение и вычитание многочленов | 2 |
|
| | Умножение многочлена на одночлен | 2 |
|
| | Умножение многочлена на многочлен | 3 |
|
| | Формулы сокращенного умножения | 4 |
|
| | Деление многочлена на одночлен | 1 |
|
|
| Контрольная работа № 5 | 1 | 1 |
|
| Глава 7. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ | 17 |
|
| | Что такое разложение многочлена на множители и зачем оно нужно | 1 |
|
| | Вынесение общего множителя за скобки | 2 |
|
| | Способ группировки | 2 |
|
| | Разложение многочлена на множители с помощью формул сокращенного умножения | 4 |
|
| | Разложение многочлена на множители с помощью комбинации различных приемов | 3 |
|
|
| Контрольная работа № 6 | 1 | 1 |
| | Сокращение алгебраических дробей | 3 |
|
| | Тождества | 1 |
|
|
| Глава 8. ФУНКЦИЯ | 9 |
|
| | Функция | 3 |
|
| | Графическое решение уравнений | 2 |
|
| | Что означает в математике запись | 3 |
|
|
| Контрольная работа № 7 | 1 | 1 |
|
| ЭЛЕМЕНТЫ ОПИСАТЕЛЬНОЙ СТАТИСТИКИ (Приложение к задачнику) | 9 |
|
| | Данные и ряды данных. Упорядоченные ряды данных, таблицы распределения | 2 |
|
| | Частота результата, таблица распределения частот. Процентные частоты | 2 |
|
| | Группировка данных | 2 |
|
|
| ИТОГОВОЕ ПОВТОРЕНИЕ | 1 |
|
Алгебра 8 класс
| № | Содержание учебного материала | Количество часов (102) | Количество контрольных работ (10) |
|
| ПОВТОРЕНИЕ КУРСА АЛГЕБРЫ 7 класса | 3 | 1 |
|
| Глава 1. АЛГЕБРАИЧЕСКИЕ ДРОБИ | 20 |
|
| | Основные понятия | 1 |
|
| | Основное свойство алгебраической дроби | 2 |
|
| | Сложение и вычитание алгебраических дробей с одинаковыми знаменателями | 2 |
|
| | Сложение и вычитание алгебраических дробей с разными знаменателями | 3 |
|
|
| Контрольная работа № 1 | 1 | 1 |
| | Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень | 2 |
|
| | Преобразование рациональных выражений | 3 |
|
| | Первые представления о решении рациональных уравнений | 2 |
|
| | Степень с отрицательным целым показателем | 3 |
|
|
| Контрольная работа № 2 | 1 | 1 |
|
| Глава 2. ФУНКЦИЯ | 18 |
|
| | Рациональные числа | 2 |
|
| | Понятие квадратного корня из неотрицательного числа | 2 |
|
| | Иррациональные числа | 1 |
|
| | Множество действительных чисел | 1 |
|
| | Функция | 2 |
|
| | Свойства квадратных корней | 2 |
|
| | Преобразование выражений, содержащих операцию извлечения квадратного корня | 4 |
|
|
| Контрольная работа № 3 | 1 | 1 |
| | Модуль действительного числа | 3 |
|
|
| Глава 3. КВАДРАТИЧНАЯ ФУНКЦИЯ. ФУНКЦИЯ | 18 |
|
| | Функция | 3 |
|
| | Функция | 3 |
|
|
| Контрольная работа № 4 | 1 | 1 |
| | Как построить график функции | 2 |
|
| | Как построить график функции | 2 |
|
| | Как построить график функции | 2 |
|
| | Функция | 3 |
|
| | Графическое решение квадратных уравнений | 2 |
|
|
| Контрольная работа № 5 | 1 | 1 |
|
| Глава 4. КВАДРАТНЫЕ УРАВНЕНИЯ | 19 |
|
| | Основные понятия | 2 |
|
| | Формула корней квадратных уравнений | 3 |
|
| | Рациональные уравнения | 3 |
|
|
| Контрольная работа № 6 | 1 | 1 |
| | Рациональные уравнения как математические модели реальных ситуаций | 4 |
|
| | Еще одна формула корней квадратного уравнения | 2 |
|
| | Теорема Виета. Разложение квадратного трехчлена на множители | 3 |
|
|
| Контрольная работа № 7 | 1 | 1 |
|
| Глава 5. НЕРАВЕНСТВА | 15 |
|
| | Свойства числовых неравенств | 3 |
|
| | Исследование функций на монотонность | 2 |
|
| | Решение линейных неравенств | 3 |
|
| | Решение квадратных неравенств | 3 |
|
|
| Контрольная работа № 8 | 1 | 1 |
| | Приближенные значения действительных чисел | 2 |
|
| | Стандартный вид числа | 1 |
|
|
| ЭЛЕМЕНТЫ КОМБИНАТОРИКИ | 6 |
|
|
| (Приложение к задачнику) Простейшие комбинаторные задачи. Организованный перебор вариантов. Дерево вариантов. Комбинаторное правило умножения
| 6 |
|
|
| ИТОГОВОЕ ПОВТОРЕНИЕ | 3 | 1 |
Алгебра 9 класс
| № | Содержание учебного материала | Количество часов (102) | Количество контрольных работ (8) |
|
| ПОВТОРЕНИЕ КУРСА АЛГЕБРЫ 8 класса | 3 | 1 |
|
| Глава 1. НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ | 16 |
|
| | Линейные и квадратные неравенства | 3 |
|
| | Рациональные неравенства | 5 |
|
| | Множества и операции над ними | 3 |
|
| | Системы рациональных неравенств | 4 |
|
|
| Контрольная работа № 1 | 1 | 1 |
|
| Глава 2. СИСТЕМЫ УРАВНЕНИЙ | 15 |
|
| | Основные понятия, связанные с системами уравнений и неравенств с двумя переменными | 4 |
|
| | Методы решения систем уравнений | 5 |
|
| | Системы уравнений как математические модели реальных ситуаций | 5 |
|
|
| Контрольная работа № 2 | 1 | 1 |
|
| Глава 3. ЧИСЛОВЫЕ ФУНКЦИИ | 25 |
|
| | Определение числовой функции. Область определения, область значений функции | 4 |
|
| | Способы задания функции | 2 |
|
| | Свойства функций | 4 |
|
| | Четные и нечетные функции | 3 |
|
|
| Контрольная работа № 3 | 1 | 1 |
| | Функции | 4 |
|
| | Функции | 3 |
|
| | Функция | 3 |
|
|
| Контрольная работа № 4 | 1 | 1 |
|
| Глава 4. ПРОГРЕССИИ | 16 |
|
| | Числовые последовательности | 4 |
|
| | Арифметическая прогрессия | 5 |
|
| | Геометрическая прогрессия | 6 |
|
|
| Контрольная работа № 5 | 1 | 1 |
|
| Глава 5. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ | 12 |
|
| | Комбинаторные задачи | 3 |
|
| | Статистика – дизайн информации | 3 |
|
| | Простейшие вероятностные задачи | 3 |
|
| | Экспериментальные данные и вероятности событий | 2 |
|
|
| Контрольная работа № 8 | 1 | 1 |
|
| ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА АЛГЕБРЫ 9 класса | 15 | 1 |
Содержание учебного предмета. Алгебра.
Натуральные числа. Натуральные числа. Натуральный ряд. Десятичная система счисления. Арифметические действия с натуральными числами. Свойства арифметических действий. Степень с натуральным показателем. Числовые выражения, значение числового выражения. Порядок действий в числовых выражениях, использование скобок. Решение текстовых задач арифметическими способами. Делители и кратные. Свойства и признаки делимости. Простые и составные числа. Разложение натурального числа на простые множители. Деление с остатком.
Дроби. Обыкновенные дроби. Основное свойство дроби. Сравнение обыкновенных дробей. Арифметические действия с обыкновенными дробями. Нахождение части от целого и целого по его части. Десятичные дроби. Сравнение десятичных дробей. Арифметические действия с десятичными дробями. Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде десятичной. Проценты; нахождение процентов от величины и величины по её процентам. Отношение; выражение отношения в процентах. Пропорция; основное свойство пропорции. 275 Решение текстовых задач арифметическими способами.
Рациональные числа. Положительные и отрицательные числа, модуль числа. Множество целых чисел. Множество рациональных чисел; рациональное число как отношение m/n, где т — целое число, а n — натуральное. Сравнение рациональных чисел. Арифметические действия с рациональными числами. Свойства арифметических действий. Степень с целым показателем.
Действительные числа. Квадратный корень из числа. Корень третьей степени. Понятие об иррациональном числе. Иррациональность числа 2 и несоизмеримость стороны и диагонали квадрата. Десятичные приближения иррациональных чисел. Множество действительных чисел; представление действительных чисел бесконечными десятичными дробями. Сравнение действительных чисел. Координатная прямая. Изображение чисел точками координатной прямой. Числовые промежутки.
Измерения, приближения, оценки. Размеры объектов окружающего мира (от элементарных частиц до Вселенной), длительность процессов в окружающем мире. Выделение множителя — степени десяти в записи числа. Приближённое значение величины, точность приближения. Округление натуральных чисел и десятичных дробей. Прикидка и оценка результатов вычислений.
Алгебраические выражения. Буквенные выражения (выражения с переменными). Числовое значение буквенного выражения. Допустимые значения переменных. Подстановка выражений вместо переменных. Преобразование буквенных выражений на основе свойств арифметических действий. Равенство буквенных выражений. Тождество. Степень с натуральным показателем и её свойства. Одночлены и многочлены. Степень многочлена. Сложение, вычитание, умножение многочленов. Формулы сокращённого умножения: квадрат суммы и квадрат 276 разности. Формула разности квадратов. Преобразование целого выражения в многочлен. Разложение многочленов на множители. Многочлены с одной переменной. Корень многочлена. Квадратный трёхчлен; разложение квадратного трёхчлена на множители. Алгебраическая дробь. Основное свойство алгебраической дроби. Сложение, вычитание, умножение, деление алгебраических дробей. Степень с целым показателем и её свойства. Рациональные выражения и их преобразования. Доказательство тождеств. Квадратные корни. Свойства арифметических квадратных корней и их применение к преобразованию числовых выражений и вычислениям.
Уравнения. Уравнение с одной переменной. Корень уравнения. Свойства числовых равенств. Равносильность уравнений. Линейное уравнение. Квадратное уравнение: формула корней квадратного уравнения. Теорема Виета. Решение уравнений, сводящихся к линейным и квадратным. Примеры решения уравнений третьей и четвёртой степеней. Решение дробно-рациональных уравнений. Уравнение с двумя переменными. Линейное уравнение с двумя переменными, примеры решения уравнений в целых числах. Система уравнений с двумя переменными. Равносильность систем. Системы двух линейных уравнений с двумя переменными; решение подстановкой и сложением. Примеры решения систем нелинейных уравнений с двумя переменными. Решение текстовых задач алгебраическим способом. Декартовы координаты на плоскости. Графическая интерпретация уравнения с двумя переменными. График линейного уравнения с двумя переменными; угловой коэффициент прямой; условие параллельности прямых. Графики простейших нелинейных уравнений: парабола, гипербола, окружность. Графическая интерпретация систем уравнений с двумя переменными.
Неравенства. Числовые неравенства и их свойства. Неравенство с одной переменной. Равносильность неравенств. Линейные неравенства с одной переменной. Квадратные неравенства. Системы неравенств с одной переменной.
Функции. Примеры зависимостей; прямая пропорциональность; обратная пропорциональность. Задание зависимостей формулами; вычисления по формулам. Зависимости между величинами. Примеры графиков зависимостей, отражающих реальные процессы.
Числовые функции. Понятие функции, область определения и область значения функции. Способы задания функции. График функции. Свойства функции, их отображение на графике. Функции, описывающие прямую и обратную пропорциональные зависимости, их графики и свойства. Линейная функция, её график и свойства. Квадратичная функция, её график и свойства. Степенные функции с натуральными показателями 2 и 3, их графики и свойства. Графики функций 
Числовые последовательности. Понятие числовой последовательности. Задание последовательности рекуррентной формулой и формулой n-го члена. Арифметическая и геометрическая прогрессии. Формулы n-го члена арифметической и геометрической прогрессий, суммы первых п-х членов. Изображение членов арифметической и геометрической прогрессий точками координатной плоскости. Линейный и экспоненциальный рост. Сложные проценты.
Описательная статистика. Представление данных в виде таблиц, диаграмм, графиков. Случайная изменчивость. Статистические характеристики набора данных: среднее арифметическое, медиана, наибольшее и наименьшее значения, размах. Представление о выборочном исследовании.
Случайные события и вероятность. Понятие о случайном опыте и случайном событии. Частота случайного события. Статистический подход к понятию вероятности. Вероятности противоположных событий. Достоверные и невозможные события. Равновозможность событий. Классическое определение вероятности.
Комбинаторика. Решение комбинаторных задач перебором вариантов. Комбинаторное правило умножения. Перестановки и факториал.
Математика в историческом развитии. История формирования понятия числа: натуральные числа, дроби, недостаточность рациональных чисел для геометрических измерений, иррациональные числа. Старинные системы записи чисел. Дроби в Вавилоне, Египте, Риме. Открытие десятичных дробей. Старинные системы мер. Десятичные дроби и метрическая система мер. Появление отрицательных чисел и нуля. Л. Магницкий. Л. Эйлер. Зарождение алгебры в недрах арифметики. Ал-Хорезми. Рождение буквенной символики. П. Ферма. Ф. Виет. Р. Декарт. История вопроса о нахождении формул корней алгебраических уравнений, неразрешимость в радикалах уравнений степени, большей четырёх. Н. Тарталья, Дж. Кардано, Н. X. Абель. Э. Галуа. Изобретение метода координат, позволяющего переводить геометрические объекты на язык алгебры. Р. Декарт и П. Ферма. Примеры различных систем координат на плоскости. Задача Леонардо Пизанского (Фибоначчи) о кроликах, числа Фибоначчи. Задача о шахматной доске. Истоки теории вероятностей: страховое дело, азартные игры. П. Ферма и Б. Паскаль. Я. Бернулли. А. Н. Колмогоров. От землемерия к геометрии. Пифагор и его школа. Фалес. Архимед. Построения с помощью циркуля и линейки. Построение правильных многоугольников. Трисекция угла. Квадратура круга. Удвоение куба. История числа π. Золотое сечение. «Начала» Евклида. Л. Эйлер. Н. И. Лобачевский. История пятого постулата. Софизм, парадоксы.
Содержание курса «Алгебра-7»
| Содержание курса | Характеристика видов деятельности | Планируемые результаты обучения |
| Математический язык. Математическая модель Числовые и алгебраические выражения. Что такое математический язык и математическая модель. Линейное уравнение с одной переменной. Линейное уравнение с одной переменной как математическая модель реальной ситуации. Координатная прямая. | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Вычисление значений числовых выражений, применение свойств и правил арифметических действий, выбор рациональных способов вычислений. Чтение выражений, формул, правил, записанных на математическом языке, перевод словесных формулировок на математический язык. Использование символики для записи математических утверждений. Работа в паре и группе. Участие в деловой игре. Описание реальных ситуаций с помощью математических моделей. Планирование хода решения задач с использованием трех этапов математического моделирования. Прогнозирование результата решения, оценка реальности полученного ответа. Применение алгоритма при решении линейного уравнения. Изображение чисел и числовых промежутков на числовой прямой. Чтение учебника, извлечение информации в соответствии с темой урока и заданием учителя. Выполнение упражнений по правилу, образцу и алгоритму. Подведение итогов. Самооценка знаний. | Умение составлять числовые и буквенные выражения, записывать математические свойства, правила, формулы на математическом языке; осуществлять числовые подстановки в алгебраические выражения и формулы и выполнять соответствующие вычисления; выражать из формулы одну переменную через другие; находить область допустимых значений переменных в выражении. Умение распознавать и решать линейные уравнения и уравнения, сводящиеся к ним; решать текстовые задачи алгебраическим методом: описывать реальную ситуацию в виде математической модели – линейного уравнения, решать полученное уравнение и интерпретировать результат. Умение изображать числа и числовые промежутки на координатной прямой, определять принадлежность точки данному числовому промежутку. УУД Умение ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку. Умение находить информацию в учебнике по заданной теме. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу, работать в паре и группе. |
| Линейная функция Координатная плоскость. Линейное уравнение с двумя переменными. Линейная функция. Взаимное расположение графиков линейных функций. | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Построение точек и геометрических фигур в координатной плоскости. Построение прямой, заданной линейным уравнением с двумя переменными. Моделирование реальной ситуации с помощью линейного уравнения с двумя переменными. Исследование графической модели с точки зрения реальности результата. Проведение аналогии между линейным уравнением с двумя переменными и линейной функцией. Работа в паре и в группе. Построение графика линейной функции, в том числе на заданном промежутке. Чтение графика, нахождение наибольшего и наименьшего значений функции. Анализ поведения графика линейной функции в зависимости от значений коэффициентов k и m на основе наблюдения и сравнения. Работа в группе. Исследование взаимного расположения графиков линейных функций. Работа в группе. Самостоятельное изучение материала учебника, извлечение учебной информации, осмысление ее и применение в учебной деятельности. Выполнение упражнений по аналогии, алгоритму, образцу. Самоконтроль решения. Участие в мини проектной деятельности «Линейная функция как модель описания реальных ситуаций». Поиск, обнаружение и устранение ошибок при построении графиков линейного уравнения с двумя переменными и линейной функции. Подведение итогов: что нового узнали, чему научились. Самооценка знаний. | Умение строить на координатной плоскости точки и фигуры по заданным координатам, фигуры, симметричные данным относительно координатных осей и начала координат, а также определять координаты точек, данных на координатной плоскости. Первоначальные умения записывать уравнения прямых, параллельных координатным осям. Понимание, что такое линейное уравнение с двумя переменными. Умение узнавать указанные уравнения, выражать в них одну переменную через другую, определять, является ли пара чисел решением уравнения с двумя переменными. Умение строить прямую, которая является графиком данного линейного уравнения с двумя переменными. Понимание, что такое линейная функция, что такое независимая переменная – аргумент, зависимая переменная – функция. Знание способов задания функции формулой и графически, умение составлять таблицы значений функции. Умение строить и читать графики линейной функции, находить по графику значение одной переменной по значению другой, определять наименьшее и наибольшее значения функции, решать графически линейные уравнения и неравенства. Умение показывать схематически положение на координатной плоскости графиков функций УУД Умение ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку. Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение на наглядно-интуитивном уровне проводить наблюдение, исследование, анализ, делать выводы. Умение осуществлять проектную деятельность: ставить цель, собирать и представлять информацию. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации. |
| Системы двух линейных уравнений с двумя переменными Основные понятия о системах двух линейных уравнений с двумя переменными. Методы решения систем двух линейных уравнений с двумя переменными: графический, подстановки и алгебраического сложения. Системы двух линейных уравнений как математические модели реальных ситуаций. | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Изучение новой математической модели – системы двух линейных уравнений с двумя переменными. Проведение аналогии между взаимным расположением двух прямых на координатной плоскости и графическим методом решения систем двух линейных уравнений с двумя переменными. Составление алгоритма решения систем графическим методом. Исследование систем уравнений на предмет числа решений с помощью функционально-графических представлений. Поиск решения в проблемной ситуации в случаях неточности и недостаточности применения графического метода решения систем (точка пересечения неточна или слишком удалена). Работа в группе. Составление алгоритма решения систем методом постановки и алгебраического сложения. Работа в паре. Выполнение самоконтроля при решении систем. Поиск, обнаружение и устранение ошибок при решении систем. Описание реальных ситуаций с помощью систем двух линейных уравнений с двумя переменными. Решение задач в три этапа математического моделирования. Участие в мини проектной деятельности «Моделирование реальных ситуаций с помощью систем линейных уравнений». Отыскание информации на заданную тему в учебнике. Подведение итогов: что нового узнали, чему научились. Самооценка знаний. | Понимание того, что такое система двух линейных уравнений с двумя переменными. Умение узнавать указанные системы, определять, является ли пара чисел решением системы двух линейных уравнений с двумя переменными. Умение решать системы двух линейных уравнений с двумя переменными графическим методом, использовать функционально-графические представления для исследования систем уравнений на предмет числа решений. Умение решать системы двух линейных уравнений с двумя переменными методом подстановки и алгебраического сложения. Умение решать текстовые задачи алгебраическим методом, составляя математическую модель задачи в виде системы двух линейных уравнений с двумя переменными, решать полученную систему и интерпретировать результат. УУД Умение ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку. Умение осознанно читать математический текст, находить информацию в учебнике по заданной теме. Умение на наглядно-интуитивном уровне проводить наблюдение, исследование, анализ, делать выводы. Умение решать по образцу и алгоритму, проводить аналогии. Умение осуществлять проектную деятельность. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение быстро включаться в деятельность взаимодействовать с товарищами по классу в деловой ситуации. |
| Степень с натуральным показателем и ее свойства Понятие степени с натуральным показателем и ее свойства. Умножение и деление степеней с одинаковым показателем. Степень с нулевым показателем.
| Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Чтение и запись степени выражения, свойств степени на математическом языке. Составление таблицы степеней. Изучение по учебнику этапов теоретического исследования. Самостоятельное проведение исследования. Доказательство свойств степени. Конструирование предложений с помощью связок «если…, то…». Работа в паре. Применение определения и свойств степени при решении простейших уравнений, моделирование реальных ситуаций, приводящих к простейшему степенному уравнению. Мини проект. Осуществление самоконтроля решения, поиск и устранение ошибок. Подведение итогов: что нового узнали, чему научились. Самооценка знаний. | Знание определения степени с натуральным показателем и ее свойств, умение вычислять степень числа. Знание табличных значений степеней 2, 3, 5, 10. Понятие степени с нулевым показателем. Умение применять свойства степени для преобразования выражений и вычислений. Умение конструировать математические предложения с помощью связок «если…, то…», воспроизводить несложные доказательства изученных теорем о свойствах степени с натуральным показателем. Умение решать простейшие уравнения, используя определение степени с неотрицательным целым показателем. УУД Умение ставить цели, планировать свою деятельность, прогнозировать результат, осуществлять самоконтроль и самооценку. Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение на наглядно-интуитивном уровне проводить наблюдение, исследование, анализ, делать выводы. Первичное умение проводить доказательство утверждения. Умение выполнять действия по правилу и образцу. Умение осуществлять мини проектную деятельность. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации, работать в паре и группе. |
| Одночлены. Арифметические операции над одночленами Понятие одночлена. Стандартный вид одночлена. Сложение и вычитание одночленов. Умножение одночленов. Возведение одночленов в натуральную степень. Деление одночлена на одночлен. | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Самостоятельное чтение учебника с целью поиска информации на заданную тему. Выполнение алгебраических преобразований с одночленами, пошаговый контроль правильности выполнения алгоритма преобразования. Работа в паре. Сравнение двух дробей по виду и выявление, которая из них является одночленом, а которая нет, обоснование вывода. Составление алгоритма приведения одночлена к стандартному виду, сложения одночленов. Работа в паре. Выполнение действий с одночленами. Описание реальных ситуаций с помощью модели (уравнения) с подобными одночленами. Решение задач в три этапа математического моделирования. Мини проект. Наблюдение и вывод, в каком случае один одночлен можно разделить на другой одночлен и как это сделать. Выполнение заданий, связанных с выявлением некорректных высказываний. Самоконтроль выполнения действий и преобразований с одночленами, поиск и устранение ошибок. Подведение итогов: что нового узнали, чему научились. Самооценка знаний. | Понимание, что такое одночлен. Умение записывать одночлены в стандартном виде, умение приводить одночлены к стандартному виду. Умение выполнять сложение и вычитание подобных одночленов, умножение одночленов, возведение одночлена в степень, деление одночлена на одночлен в корректных случаях. УУД Умение ставить цели, планировать свою деятельность, прогнозировать результат, осуществлять самоконтроль и самооценку. Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение проводить наблюдение, сравнивать, анализировать ситуацию, делать выводы. Умение работать по правилу и образцу. Умение осуществлять мини проектную деятельность. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации, работать в паре и группе. |
| Многочлены. Арифметические операции над многочленами Понятие многочлена. Сложение и вычитание многочленов. Умножение многочлена на одночлен. Умножение многочлена на многочлен. Формулы сокращенного умножения. Деление многочлена на одночлен. | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Извлечение информации из учебника, связанной с изучением нового материала. Выполнение действий с многочленами по правилам. Работа в паре. Описание реальных ситуаций с помощью математической модели, представляющей собой многочлены. Решение задач в три этапа математического моделирования. Мини проект. Вывод формул сокращенного умножения. Чтение их и запись на математическом языке. Применение геометрической модели, иллюстрирующей вывод формул разности квадратов и квадрата суммы и разности. Выполнение преобразований многочленов, пошаговый контроль правильности и полноты выполнения алгоритма. Поиск, обнаружение и устранение арифметических и алгебраических ошибок. Подведение итогов: что нового узнали, чему научились. Самооценка знаний. | Понимание, что такое многочлен. Умение записывать многочлены в стандартном виде, умение выполнять сложение и вычитание многочленов, умножение многочлена на одночлен, умножение многочлена на многочлен. Умение применять правило умножения многочленов для выведения формул разности квадратов, квадрата двучлена и суммы (разности) кубов. Умение применять формулы сокращенного умножения для преобразования алгебраических выражений. Умение выполнять деление многочлена на одночлен, если такое деление корректно. УУД Умение ставить учебные цели и задачи, планировать свою деятельность, прогнозировать результат, осуществлять самоконтроль и самооценку, преодолевать трудности, корректировать свои знания. Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение работать по аналогии, образцу, алгоритму, формуле. Умение сравнивать, обобщать, делать выводы, проводить обоснованный вывод формул. Умение осуществлять мини проектную деятельность. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации, работать в паре и группе. |
| Разложение многочленов на множители Понятие о разложении многочлена на множители и его необходимости. Вынесение общего множителя за скобки. Способ группировки. Разложение многочлена на множители с помощью формул сокращенного умножения и комбинации различных приемов. Сокращение алгебраических дробей. Тождества. | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Извлечение информации из учебника по заданной теме. Выделение существенного, главного. Чтение и запись на математическом языке при выполнении разложения на множители. Комментирование решений, разобранных в учебнике. Работа в паре. Выполнение преобразования в виде разложения многочлена на множители по алгоритму и образцу. Решение уравнений, построение графиков уравнений, выполнение арифметических действий, связанных с разложением на множители, сокращение дробей. Пошаговый самоконтроль за выполнением указанных действий. Поиск и устранение ошибок. Подведение итогов. Самооценка знаний. | Умение видеть способ, которым данный многочлен можно разложить на множители и выполнять это разложение. Умение применять формулы сокращенного умножения для разложения многочлена на множители. Умение применять разложение многочлена на множители для решения уравнений, сокращения алгебраических дробей, доказательства делимости значения числового выражения на число, а также как способ рациональных вычислений. Понимание, что такое тождество и тождественное преобразование выражений. УУД Умение ставить учебные цели и задачи, планировать свою деятельность, прогнозировать результат, осуществлять самоконтроль и самооценку, преодолевать трудности, корректировать свои знания. Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение работать по аналогии, образцу, алгоритму, формуле. Умение сравнивать, обобщать, делать выводы, проводить обоснованный вывод формул. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации, работать в паре. |
| Функция Функция | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Чтение учебника и извлечение информации по заданной теме. Изучение новых функций Построение и чтение графиков, в том числе кусочных функций. Проведение простейших исследований. Участие в проектной деятельности «Описание реальных ситуаций с помощью кусочных функций». Применение графических моделей для решения уравнений, неравенств, систем неравенств. Проверка найденных корней. Исследование взаимного расположения графика кусочной функции и прямой y = a на предмет числа общих точек при различных значениях а. Подведение итогов. Самооценка знаний. | Понятие о функциях УУД Умение ставить учебные цели и задачи, планировать свою деятельность, прогнозировать результат, осуществлять самоконтроль и самооценку, преодолевать трудности, корректировать свои знания. Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение работать по аналогии, образцу, алгоритму, формуле. Умение сравнивать, обобщать, делать выводы. Умение проводить графическое исследование, читать графики. Умение осуществлять мини проектную деятельность. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации, работать в паре и группе. |
| Элементы описательной статистики Данные и ряды данных. Упорядоченные ряды данных, таблицы распределения. Частота результата, таблица распределения частот, процентные частоты. Группировка данных. | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Сбор, анализ, обобщение и представление статистической информации в виде таблиц и диаграмм. Мини проект. | Умение извлекать информацию из таблиц и диаграмм, выполнять вычисления по табличным данным, организовывать информацию в виде таблиц и диаграмм, приводить примеры числовых данных, находить среднее значение, объем, моду, размах. УУД Умение ставить цель и задачи, планировать деятельность, проводить самоанализ и самоконтроль деятельности. Умение собирать, анализировать, обобщать и представлять информацию в виде таблиц и диаграмм. Умение контактировать со всеми участниками учебного процесса. |
| Итоговое повторение | Постановка цели и задач на при повторении материала. Планирование учебной деятельности на уроке и дома. Подведение итога, коррекция знаний. Самоконтроль. |
|
Содержание курса «Алгебра-8»
| Содержание курса | Характеристика видов деятельности | Планируемые результаты обучения |
| Повторение курса алгебры 7 класса |
| Актуализация знаний за курс алгебры 7 класса |
| Алгебраические дроби Основные понятия об алгебраических дробях. Основное свойство алгебраической дроби. Сложение и вычитание, умножение и деление алгебраических дробей, возведение алгебраической дроби в степень. Преобразование рациональных выражений. Первые представления о простейших рациональных уравнениях. Степень с отрицательным целым показателем. | Постановка цели и задач. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль и коррекция знаний. Чтение учебника с целью освоения новых знаний, извлечение информации в соответствии с темой урока и заданием учителя. Выполнение упражнений по правилу, образцу и алгоритму при нахождении допустимых значений алгебраической дроби, сокращении алгебраических дробей, приведении к наименьшему общему знаменателю, сложении, вычитании, умножении и делении дробей, возведении дроби в степен, преобразовании выражений, содержащих степень с отрицательным показателем, решении рациональных уравнений. Поиск и отбор корней рационального уравнения. Моделирование реальных ситуаций с помощью рациональных уравнений. Работа в паре и группе. Подведение итогов. Самооценка знаний. | Представление о допустимых значениях алгебраической дроби и умение их находить. Знание основного свойства алгебраической дроби и умение применять его для преобразования дробей; умение выполнять действия с алгебраическими дробями, доказывать тождества. Понятие степени с целым показателем, умение вычислять значения степеней с отрицательным показателем, иллюстрировать примерами свойства степени с целым показателем. Первичные представления о рациональных уравнениях, методах их решения, отборе корней. УУД Умение ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку. Умение находить информацию в учебнике по заданной теме. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение работать по правилу, алгоритму, по аналогии. Умение анализировать свои действия, прогнозировать и оценивать результат. Умение взаимодействовать с товарищами по классу, работать в паре и группе. |
| Функция Рациональные, иррациональные числа, множество действительных чисел, стандартный вид числа. Квадратный корень из неотрицательного числа. Функция | Постановка цели и задач. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Самостоятельное изучение материала учебника, извлечение учебной информации о множестве рациональных и иррациональных чисел как части множества действительных чисел, осмысление ее и применение в учебной деятельности. Изображение чисел на числовой прямой, сравнение, выполнение арифметических и алгебраических действий на множестве действительных чисел. Запись рациональных чисел в виде обыкновенной и десятичной периодической дроби. Прикидка возможности представления обыкновенной дроби в виде конечной десятичной дроби. Работа по правилу и по образцу. Составление алгоритма. Знакомство с методом доказательства от противного. Изучение свойств функций Проведение преобразований выражений, содержащих квадратный корень. Работа в паре. Поиск, обнаружение и устранение ошибок при выполнении вычислений, построении графиков и преобразовании выражений. Подведение итогов: что нового узнали, чему научились. Самооценка знаний. | Систематизация знания о рациональных числах, понятия иррационального числа, множества действительных чисел. Умение находить приближения рациональных и иррациональных чисел, сравнивать и упорядочивать действительные числа. Освоение понятие квадратного корня из неотрицательного числа, умение строить график функции УУД Умение ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку. Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение на наглядно-интуитивном уровне проводить наблюдение, исследование, анализ, делать выводы.Умение переводить информацию с наглядно-интуитивного уровня на рабочий уровень восприятия. Умение работать по правилу, алгоритму, образцу. Умение осуществлять прикидку и оценку результата действий, примерно определять положение точки на числовой прямой. Умение логически мыслить, рассуждать, доказывать утверждения. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации. |
| Квадратичная функция. Функция Функции
| Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль и самооценка знаний. Изучение графических моделей и свойств функций . Исследование зависимости графиков функций от значений коэффициентов. Проведение аналогии между аналитическим заданием квадратичной функции в виде Наблюдение и исследование взаимного расположения графика функции Составление алгоритмов построение параболы, гиперболы, построения графика функции с учетом параллельного переноса, решения квадратного уравнения графическим методом. Участие в мини проектной деятельности «Гипербола и парабола как математические модели реальных ситуаций». Поиск решения в проблемной ситуации в случаях неточности и недостаточности применения графического метода решения квадратного уравнения (точки пересечения неточны или слишком удалены). Работа в паре и группе. Подведение итогов: что нового узнали, чему научились. Самооценка знаний. | Умение вычислять значения функций, заданных формулами, составлять таблицы значений функции, распознавать виды изучаемых функций, строить графики, описывать свойства функций, осуществлять параллельный перенос графика функции УУД Умение ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку. Умение осознанно читать математический текст, находить информацию в учебнике по заданной теме. Умение на наглядно-интуитивном уровне проводить наблюдение, исследование, анализ, делать выводы. Умение переводить информацию с наглядно-интуитивного уровня на рабочий уровень восприятия. Умение решать по образцу и алгоритму, проводить аналогии. Умение осуществлять проектную деятельность. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение быстро включаться в деятельность, взаимодействовать с товарищами по классу в деловой ситуации. |
| Квадратные уравнения Квадратные уравнения. Формулы корней квадратных уравнений. Рациональные уравнения. Рациональные уравнения как математические модели реальных ситуаций. Теорема Виета. Разложение квадратного трехчлена на линейные множители. | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль и самооценка достижений. Изучение материала учебника с целью освоения понятия квадратного уравнения, его коэффициентов, понятия дискриминанта. Исследование квадратных уравнений на предмет числа корней. Вывод формулы для вычисления корней квадратного уравнения. Применение формул для решения квадратных уравнений. Составление алгоритма решения квадратного уравнения. Исследование соотношения между корнями квадратного уравнения и его коэффициентами, изучение теоремы Виета (прямой и обратной). Применение теоремы Виета для составления квадратных уравнений, подбора корней приведенного квадратного уравнения, разложения квадратного трехчлена на множители. Освоение методов решения алгебраических уравнений, сводящихся к квадратным. Моделирование реальных ситуаций с помощью квадратных и рациональных уравнений. Участие в мини проектной деятельности «Квадратные уравнения как математические модели реальных ситуаций». Осуществление самоконтроля решения, поиск и устранение ошибок. | Освоение понятия квадратного уравнения, умение распознавать квадратные уравнения, проводить исследование на предмет количества корней квадратного уравнения по дискриминанту и коэффициентам, умение применять формулы корней для решения квадратных уравнений. Умение решать рациональные уравнения и уравнения, сводящиеся к квадратным, умение решать текстовые задачи алгебраическим методом: составлять математическую модель – квадратное либо рациональное уравнение, решать его и интерпретировать результат. УУД Умение ставить цели, планировать свою деятельность, прогнозировать результат, осуществлять самоконтроль и самооценку. Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение проводить анализ, исследование, делать выводы. Умение проводить доказательство утверждений. Умение выполнять действия по формуле, правилу, образцу. Умение моделировать с помощью уравнений реальные ситуации. Умение осуществлять мини проектную деятельность. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации, работать в паре и группе. |
| Неравенства Свойства числовых неравенств. Исследование функций на монотонность. Линейные и квадратные неравенства. Приближенные значения действительных чисел. Стандартный вид числа. | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль и самооценка достижений. Самостоятельное чтение учебника с целью поиска информации и изучения материала на заданную тему. Иллюстрация свойств числовых неравенств на координатной прямой. Исследование функций на монотонность с помощью свойств числовых неравенств. Применение правил при решении неравенств. Исследование взаимосвязи решений квадратного неравенства и расположения параболы относительно прямой Ох. Установление взаимосвязи между коэффициентом а квадратного неравенства, знаком неравенства и наличием решений при отрицательном дискриминанте. Исследование квадратного уравнения с параметром на число корней. Поиск, обнаружение и устранение ошибок в решении линейных и квадратных неравенств. Участие в проектной деятельности «Моделирование реальных ситуаций с помощью квадратных неравенств» и «Где используются числа, записанные в стандартном виде?». Оценка и прикидка результата в приближенных вычислениях.
| Знание свойств числовых неравенств, умение иллюстрировать их на координатной прямой, применять при исследовании функции на монотонность, доказательстве и решении неравенств. Умение распознавать линейные и квадратные неравенства, решать их, показывать решение неравенства в виде числового промежутка на числовой прямой. Умение находить приближенные значение числа с недостатком и с избытком, умение прикидывать и примерно оценивать результат. Умение представлять числа в стандартном виде и выполнять арифметические действия с числами, записанными в стандартном виде, использовать запись числа в стандартном виде для выражения размеров объектов, длительности процессов в реальном мире, сравнивать числа, записанные в стандартном виде. УУД Умение ставить цели, планировать свою деятельность, прогнозировать результат, осуществлять самоконтроль и самооценку. Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение проводить наблюдение, сравнение, анализ, исследование, обобщение. Умение работать по правилу и образцу. Умение выполнять прикидку, оценку размера объектов, длительности реальных процессов. Умение осуществлять мини проектную деятельность. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации, работать в паре и группе. |
| Элементы комбинаторики, статистики и теории вероятностей Простейшие комбинаторные задачи. Организованный перебор вариантов, дерево вариантов. Комбинаторное правило умножения.
| Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль и самооценка достижений. Наблюдение, установление закономерности при переборе вариантов, построении дерева вариантов, вывод правила комбинаторного умножения. Мини проект «Комбинаторика вокруг нас». | Ознакомление с основными методами решения простейших комбинаторных задач: перебор вариантов, построение дерева вариантов, правило умножения. Умение применять правило комбинаторного умножения для решения задач на нахождение числа объектов или комбинаций. УУД Умение ставить цель и задачи, планировать деятельность, проводить самоанализ и самоконтроль деятельности. Умение проводить организованный перебор вариантов, работать по правилу и образцу. Умение контактировать со всеми участниками учебного процесса. |
| Итоговое повторение | Постановка цели и задач при повторении материала. Планирование учебной деятельности на уроке и дома. Подведение итога, коррекция знаний. Самоконтроль. |
|
Содержание курса «Алгебра-9»
| Содержание курса | Характеристика видов деятельности | Планируемые результаты обучения |
| Повторение курса алгебры 8 класса |
| Актуализация знаний за курс алгебры 8 класса |
| Неравенства и системы неравенств Линейные и квадратные неравенства. Рациональные неравенства. Метод интервалов. Множества и операции над ними. Системы неравенств. | Постановка цели и задач. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль и коррекция знаний. Чтение учебника с целью освоения новых знаний, извлечение информации в соответствии с темой урока и заданием учителя. Выполнение упражнений по правилу, образцу и алгоритму при решении неравенств и систем неравенств. Исследование знаков неравенства на числовых промежутках, отбор результатов решения. Поиск, обнаружение и исправление ошибок. Подведение итогов. Самооценка знаний. | Умение распознавать виды неравенств: линейное, квадратное, рациональное, и выбирать способ решения. Освоение различных методов решения неравенств и систем неравенств. Умение строить геометрическую модель решения неравенства и систем неравенств. Умение интерпретировать результат. Освоение понятий множество, элемент множества, пустое множество, подмножество, объединение и пересечение множеств. Умение показывать объединение и пересечение множеств с помощью кругов Эйлера, на числовой прямой и координатной плоскости. УУД Умение ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку. Умение находить информацию в учебнике по заданной теме. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение работать по правилу, алгоритму, по аналогии. Умение анализировать свои действия, прогнозировать и оценивать результат. Умение взаимодействовать с товарищами по классу, работать в паре и группе. |
| Системы уравнений Рациональное уравнение с двумя переменными. Решение уравнения | Постановка цели и задач. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Самостоятельное изучение материала учебника, извлечение учебной информации о методах решения систем уравнений. Интеграция знаний по алгебре и геометрии при изучении и применении в решении задач тем расстояние между двумя точками в координатной плоскости, уравнение окружности и уравнение прямой. Применение графических методов при решении уравнений, неравенств и систем уравнений. Исследование взаимного расположения графиков уравнений прямой, параболы, гиперболы и др. с окружностью. Моделирование реальных ситуаций в виде систем уравнений. Освоение нового вида задач на производительность. Участие в проектной деятельности «Системы уравнений как математические модели реальных ситуаций», «Жизнь вокруг нас: задачи на производительность». Работа в паре, группе. Поиск, обнаружение и устранение ошибок при выполнении вычислений, построении графиков и преобразовании выражений, решении уравнений, входящих в систему. Оценка достоверности и интерпретация результата решения. Подведение итогов: что нового узнали, чему научились. Самооценка знаний. | Знание уравнений окружности, прямой, параболы, гиперболы, уравнений с модулем. Умение применять в решении систем уравнений графические и аналитические методы. Умение выполнять преобразование уравнений, входящих в систему, вводить новую переменную, интерпретировать и оценивать результат. Умение применять системы уравнений в решении задач. Освоение приемов решения задач на производительность труда. Умение проводить анализ и графическое исследование решения систем уравнений, в том числе с уравнением окружности, делать выводы и интерпретировать результат исследования. УУД Умение ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку. Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение на наглядно-интуитивном уровне проводить наблюдение, исследование, анализ, делать выводы. Умение переводить информацию с наглядно-интуитивного уровня на рабочий уровень восприятия. Умение работать по правилу, алгоритму, образцу. Умение осуществлять прикидку и оценку результата с точки зрения его достоверности. Умение логически мыслить, рассуждать, доказывать утверждения. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации. |
| Числовые функции Функция. Независимая и зависимая переменные. Определение числовой функции. Область определения и область значений функции. Естественная область определения функции. Способы задания функции. Свойства функций. Четные и нечетные функции. Алгоритм исследования функции на четность. Графики четной и нечетной функций. Функции
| Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль и самооценка знаний. Описание свойств функций . Исследование функций. Задание функций разными способами и построение графиков. Изучение новых свойств функций: четность и нечетность. Исследование функций на четность и нечетность согласно алгоритму. Изучение свойств функций Участие в проектной деятельности «Описание реальных процессов с помощью графиков функций Поиск решения в проблемной ситуации: неточность и недостаточность применения графического метода решения уравнения Работа в паре и группе. Подведение итогов: что нового узнали, чему научились. Самооценка знаний. | Умение вычислять значения функций, заданных формулами, составлять таблицы значений функции, распознавать виды изучаемых функций, способы их задания, строить графики, описывать свойства функций, осуществлять параллельный перенос графика функции УУД Умение ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку. Умение осознанно читать математический текст, находить информацию в учебнике по заданной теме. Умение на наглядно-интуитивном уровне проводить наблюдение, исследование, анализ, делать выводы. Умение переводить информацию с наглядно-интуитивного уровня на рабочий и далее на формальный уровень восприятия. Умение решать по образцу и алгоритму, проводить аналогии. Умение осуществлять проектную деятельность. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение быстро включаться в деятельность, взаимодействовать с товарищами по классу в деловой ситуации. |
| Прогрессии Числовые последовательности. Способы задания числовых последовательностей (аналитический, словесный, рекуррентный). Свойства числовых последовательностей. Арифметическая прогрессия. Формула n-го члена. Формула суммы членов конечной арифметической прогрессии. Характеристическое свойство. Геометрическая прогрессия. Формула n-го члена. Формула суммы членов конечной геометрической прогрессии. Характеристическое свойство. Прогрессии и банковские расчеты. | Постановка цели и задач на уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль и самооценка достижений. Изучение материала учебника с целью освоения понятиями: последовательность, задание последовательности, график последовательности, формула n-го члена. Освоение понятий арифметическая и геометрическая прогрессии, вывод формул n-го члена, суммы членов конечной арифметической и геометрической прогрессии, характеристических свойств. Исследование последовательностей, в том числе арифметической и геометрической прогрессий. Выполнение упражнений на применение формул n-го члена, суммы членов конечной арифметической и геометрической прогрессии, характеристических свойств. Моделирование банковских расчетов с помощью прогрессий. Работа в группе. Участие в проекте «Прогрессии как математические модели реальных ситуаций». Осуществление самоконтроля решения, обнаружение, поиск и устранение ошибок. | Ознакомление с новой математической моделью – числовая последовательность, арифметическая и геометрическая прогрессии, способами задания последовательностей, формуламиn-го члена, графиками числовых последовательностей. Знание формул n-го члена, суммы членов конечной арифметической и геометрической прогрессии, характеристических свойств. Освоение новой терминологии, новых символов и обозначений. Умение распознавать арифметическую и геометрическую прогрессии, находить неизвестный компонент формулы n-го члена, формулы суммы конечной арифметической или геометрической прогрессии, применять характеристическое свойство прогрессии. Знание формулы сложных процентов. Умение производить несложные расчеты процентов банковских операций. Умение моделировать реальные ситуации с помощью последовательностей. УУД Умение ставить цели, планировать свою деятельность, прогнозировать результат, осуществлять самоконтроль и самооценку. Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение читать утверждения, записанные на математическом языке в знаково-символьной форме. Умение наблюдать, находить закономерности, выдвигать гипотезы, проводить обоснование. Умение переходить от наглядно-интуитивного уровня восприятия к рабочему и далее формальному уровню. Умение проводить анализ, исследование, делать обоснованные выводы. Умение выполнять действия по формуле, правилу, образцу. Умение моделировать реальные ситуации. Умение осуществлять мини проектную деятельность. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации, работать в паре и группе. |
| Элементы комбинаторики, статистики и теории вероятностей Комбинаторные задачи. Правило умножения. Факториал. Перестановки. Статистика – дизайн информации. Группировка информации. Общий ряд данных. Кратность варианты измерения. Табличное представление информации. Частота варианты. Графическое представление информации. Полигон распределения данных. Гистограмма. Числовые характеристики данных измерения. Вероятность. Событие. Классическая вероятностная схема. Противоположные события. Несовместные события. Вероятность суммы двух событий. Вероятность противоположного события. Экспериментальные данные и вероятности событий. Статистическая устойчивость и статистическая вероятность.
| Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль и самооценка достижений. Наблюдение, установление закономерности при переборе вариантов, построении дерева вариантов, вывод правила комбинаторного умножения. Участие в проведении эксперимента. Сбор, обработка и представление информации. Ознакомление с новой математической моделью – классической вероятностной схемой и применение формулы для подсчета вероятности. Математическое моделирование простейших вероятностных ситуаций.
Мини проект «Игры и вероятности событий». | Умение применять основные методы решения комбинаторных задач: перебор вариантов, построение дерева вариантов, правило умножения. Умение применять правило комбинаторного умножения для решения задач на нахождение числа объектов или комбинаций. Освоение понятия факториал, умение применять определение факториала в решении комбинаторных задач. Ознакомление с новой математической моделью – классической вероятностной схемой и формулой для подсчета вероятности. Знание основных видов случайных событий: достоверные, невозможные, несовместные события, события, противоположные данным; сумма двух случайных событий. Умение проводить доказательство формул и теорем. Знание числовых характеристик информации, полученной в результате эксперимента. Умение проводить эксперимент. Умение использовать методы статистической обработки результатов измерений, полученных при проведении эксперимента. Умение группировать данные, проводить обработку данных, представлять информацию в виде таблиц, диаграмм, гистограмм, графиков. УУД Умение ставить цель и задачи, планировать деятельность, проводить самоанализ и самоконтроль деятельности. Умение проводить эксперимент, добывать, обрабатывать и представлять информацию, работать по правилу и образцу. Умение контактировать со всеми участниками учебного процесса. |
| Итоговое повторение Числовые выражения. Алгебраические выражения. Функции и графики. Уравнения и системы уравнений. Неравенства и системы неравенств. Задачи на составление уравнений или систем уравнений. Арифметическая и геометрическая прогрессии. | Постановка цели и задач при повторении материала. Планирование учебной деятельности на уроке и дома. Подведение итога, коррекция знаний. Подготовка к итоговой аттестации по математике. Самоконтроль. |
|
Планируемые результаты обучения.
К концу изучения курса алгебры в основной школе будет обеспечена готовность учащихся к дальнейшему образованию, достигнут необходимый уровень их математического развития:
- осознание возможностей и роли математики в познании и описании реальных ситуаций окружающего мира, понимание математики как части общечеловеческой культуры;
- осознание того, как математически определенные функции описывают реальные процессы и зависимости, умение приводить примеры;
- умение моделировать реальные ситуации;
- понимание того, как потребности практической деятельности человека привели к расширению понятия числа;
- понимание того, как используются математические формулы, уравнения и неравенства; умение приводить примеры их применения для решения математических и практических задач;
- способность понимать существо понятия математического доказательства, алгоритма действия, приводить их примеры;
- способность проводить математическое исследование, анализировать, обобщать, делать выводы;
- применение универсальных учебных действий (анализ, сравнение, обобщение, классификация) для упорядочивания, установления закономерностей на основе математических фактов;
- осознание вероятностного характера многих закономерностей окружающего мира; понимание статистических закономерностей и выводов;
- осуществление поиска необходимой информации в учебной и справочной литературе и в Интернете;
- осуществление проверки хода решения и оценки результата выполнения математического задания, обнаружение и исправление ошибок.
В направлении личностного развития:
умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации;
креативность мышления, инициатива, находчивость, активность при решении математических задач;
умение контролировать процесс и результат учебной математической деятельности;
способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
В метапредметном направлении:
первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять ее в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении учебных задач и понимать необходимость проверки;
умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
В предметном направлении:
Натуральные числа. Дроби. Рациональные числа
Выпускник научится:
• понимать особенности десятичной системы счисления;
• оперировать понятиями, связанными с делимостью натуральных чисел;
• выражать числа в эквивалентных формах, выбирая наиболее подходящую в зависимости от конкретной ситуации;
• сравнивать и упорядочивать рациональные числа;
• выполнять вычисления с рациональными числами, сочетая устные и письменные приёмы вычислений, применение калькулятора;
• использовать понятия и умения, связанные с пропорциональностью величин, процентами, в ходе решения математических задач и задач из смежных предметов, выполнять несложные практические расчёты.
Выпускник получит возможность:
• познакомиться с позиционными системами счисления с основаниями, отличными от 10;
• углубить и развить представления о натуральных числах и свойствах делимости;
• научиться использовать приёмы, рационализирующие вычисления, приобрести привычку контролировать вычисления, выбирая подходящий для ситуации способ.
Действительные числа
Выпускник научится:
• использовать начальные представления о множестве действительных чисел;
• оперировать понятием квадратного корня, применять его в вычислениях.
Выпускник получит возможность:
• развить представление о числе и числовых системах от натуральных до действительных чисел; о роли вычислений в практике;
• развить и углубить знания о десятичной записи действительных чисел (периодические и непериодические дроби).
Измерения, приближения, оценки
Выпускник научится:
• использовать в ходе решения задач элементарные представления, связанные с приближёнными значениями величин.
Выпускник получит возможность:
• понять, что числовые данные, которые используются для характеристики объектов окружающего мира, являются преимущественно приближёнными, что по записи приближённых значений, содержащихся в информационных источниках, можно судить о погрешности приближения;
• понять, что погрешность результата вычислений должна быть соизмерима с погрешностью исходных данных.
Алгебраические выражения
Выпускник научится:
• оперировать понятиями «тождество», «тождественное преобразование», решать задачи, содержащие буквенные данные, работать с формулами;
• выполнять преобразования выражений, содержащих степени с целыми показателями и квадратные корни;
• выполнять тождественные преобразования рациональных выражений на основе правил действий над многочленами и алгебраическими дробями;
• выполнять разложение многочленов на множители.
Выпускник получит возможность научиться:
• выполнять многошаговые преобразования рациональных выражений, применяя широкий набор способов и приёмов; применять тождественные преобразования для решения задач из различных разделов курса (например, для нахождения наибольшего/наименьшего значения выражения).
Уравнения
Выпускник научится:
• решать основные виды рациональных уравнений с одной переменной, системы двух уравнений с двумя переменными;
• понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом;
• применять графические представления для исследования уравнений, исследования и решения систем уравнений с двумя переменными.
Выпускник получит возможность:
• овладеть специальными приёмами решения уравнений и систем уравнений; уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики;
• применять графические представления для исследования уравнений, систем уравнений, содержащих буквенные коэффициенты.
Неравенства
Выпускник научится:
• понимать и применять терминологию и символику, связанные с отношением неравенства, свойства числовых неравенств;
• решать линейные неравенства с одной переменной и их системы; решать квадратные неравенства с опорой на графические представления;
• применять аппарат неравенств для решения задач из различных разделов курса.
Выпускник получит возможность научиться:
• разнообразным приёмам доказательства неравенств; уверенно применять аппарат неравенств для решения разнообразных математических задач и задач из смежных предметов, практики;
• применять графические представления для исследования неравенств, систем неравенств, содержащих буквенные коэффициенты.
Основные понятия. Числовые функции
Выпускник научится:
• понимать и использовать функциональные понятия и язык (термины, символические обозначения);
• строить графики элементарных функций; исследовать свойства числовых функций на основе изучения поведения их графиков;
• понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследования зависимостей между физическими величинами.
Выпускник получит возможность научиться:
• проводить исследования, связанные с изучением свойств функций, в том числе с использованием компьютера; на основе графиков изученных функций строить болеесложные графики (кусочно-заданные, с «выколотыми» точками и т. п.);
• использовать функциональные представления и свойства функций для решения математических задач из различных разделов курса.
Числовые последовательности
Выпускник научится:
• понимать и использовать язык последовательностей (термины, символические обозначения);
• применять формулы, связанные с арифметической и геометрической прогрессией, и аппарат, сформированный при изучении других разделов курса, к решению задач, в том числе с контекстом из реальной жизни.
Выпускник получит возможность научиться:
• решать комбинированные задачи с применением формул n-го члена и суммы первых n членов арифметической и геометрической прогрессии, применяя при этом аппарат уравнений и неравенств;
• понимать арифметическую и геометрическую прогрессию как функции натурального аргумента; связывать арифметическую прогрессию с линейным ростом, геометрическую — с экспоненциальным ростом.
Описательная статистика
Выпускник научится использовать простейшие способы представления и анализа статистических данных.
Выпускник получит возможность приобрести первоначальный опыт организации сбора данных при проведении опроса общественного мнения, осуществлять их анализ, представлять результаты опроса в виде таблицы, диаграммы.
Случайные события и вероятность
Выпускник научится находить относительную частоту и вероятность случайного события.
Выпускник получит возможность приобрести опыт проведения случайных экспериментов, в том числе с помощью компьютерного моделирования, интерпретации их результатов.
Комбинаторика
Выпускник научится решать комбинаторные задачи на нахождение числа объектов или комбинаций.
Выпускник получит возможность научиться некоторым специальным приёмам решения комбинаторных задач.
Формирование ИКТ-компетентности обучающихся
Создание графических объектов.
Выпускник научится:
• создавать различные геометрические объекты с использованием возможностей специальных компьютерных инструментов;
• создавать диаграммы различных видов (алгоритмические, концептуальные, классификационные, организационные, родства и др.) в соответствии с решаемыми задачами;
• создавать специализированные карты и диаграммы: географические, хронологические;
• создавать графические объекты проведением рукой произвольных линий с использованием специализированных компьютерных инструментов и устройств.
Выпускник получит возможность научиться:
• создавать мультипликационные фильмы;
• создавать виртуальные модели трёхмерных объектов.
Создание, восприятие и использование гипермедиа сообщений.
Выпускник научится:
• организовывать сообщения в виде линейного или включающего ссылки представления для самостоятельного просмотра через браузер;
• работать с особыми видами сообщений: диаграммами (алгоритмическими, концептуальными, классификационными, организационными, родства и др.), спутниковыми фотографиями, в том числе в системах глобального позиционирования;
• проводить деконструкцию сообщений, выделение в них структуры, элементов и фрагментов;
• использовать при восприятии сообщений внутренние и внешние ссылки;
• формулировать вопросы к сообщению, создавать краткое описание сообщения; цитировать фрагменты сообщения;
• избирательно относиться к информации в окружающем информационном пространстве, отказываться от потребления ненужной информации.
Выпускник получит возможность научиться:
• проектировать дизайн сообщений в соответствии с задачами и средствами доставки;
• понимать сообщения, используя при их восприятии внутренние и внешние ссылки, различные инструменты поиска, справочные источники (включая двуязычные).
Коммуникация и социальное взаимодействие.
Выпускник научится:
• выступать с аудио- или видео- поддержкой, включая выступление перед дистанционной аудиторией;
• участвовать в обсуждении (аудио-видео-форум, текстовый форум) с использованием возможностей Интернета;
• использовать возможности электронной почты для информационного обмена;
• осуществлять образовательное взаимодействие в информационном пространстве образовательного учреждения (получение и выполнение заданий, получение комментариев, совершенствование своей работы, формирование портфолио);
• соблюдать нормы информационной культуры, этики и права; с уважением относиться к частной информации и информационным правам других людей.
Выпускник получит возможность научиться:
• взаимодействовать в социальных сетях, работать в группе над сообщением (вики);
• участвовать в форумах в социальных образовательных сетях;
• взаимодействовать с партнёрами с использованием возможностей Интернета (игровое и театральное взаимодействие).
Поиск и организация хранения информации
Выпускник научится:
• использовать различные приёмы поиска информации в Интернете, поисковые сервисы, строить запросы для поиска информации и анализировать результаты поиска;
• использовать приёмы поиска информации на персональном компьютере, в информационной среде учреждения и в образовательном пространстве;
• использовать различные библиотечные, в том числе электронные, каталоги для поиска необходимых книг;
• искать информацию в различных базах данных, создавать и заполнять базы данных, в частности использовать различные определители;
• формировать собственное информационное пространство: создавать системы папок и размещать в них нужные информационные источники, размещать информацию в Интернете.
Выпускник получит возможность научиться:
• создавать и заполнять различные определители;
• использовать различные приёмы поиска информации в Интернете в ходе учебной деятельности.
Анализ информации, математическая обработка данных в исследовании
Выпускник научится:
• вводить результаты измерений и другие цифровые данные для их обработки, в том числе статистической, и визуализации;
• строить математические модели;
• проводить эксперименты и исследования в виртуальных лабораториях по естественным наукам, математике и информатике.
Выпускник получит возможность научиться:
• проводить естественнонаучные и социальные измерения, вводить результаты измерений и других цифровых данных и обрабатывать их, в том числе статистически и с помощью визуализации;
• анализировать результаты своей деятельности и затрачиваемых ресурсов.
Моделирование и проектирование, управление
Выпускник научится:
• моделировать с использованием виртуальных конструкторов;
• конструировать и моделировать с использованием материальных конструкторов с компьютерным управлением и обратной связью;
• моделировать с использованием средств программирования;
• проектировать и организовывать свою индивидуальную и групповую деятельность, организовывать своё время с использованием ИКТ.
Выпускник получит возможность научиться:
• проектировать виртуальные и реальные объекты и процессы, использовать системы автоматизированного проектирования.
Условия реализации программы
| № п/п | Наименование модуля | Состав и предназначение оборудования, входящего в модуль | Количественный состав | |||
| педагога | обучающихся | |||||
| 1 | Модуль: технические средства обучения | |||||
| 1.1 | Специализированный программно-аппаратный комплекс педагога (СПАК) | СПАК является составной частью информационно - образовательной среды образовательного учреждения, обеспечивает решение профессиональных задач педагога с применением информационно-коммуникационных технологий (ИКТ). СПАК должен обеспечивать сетевое взаимодействие всех участников образовательного процесса. Все технические средств СПАК с коммутированы между собой. СПАК включает: | 4 | - | ||
| 1. Персональный или мобильный компьютер (ноутбук) с предустановленным программным обеспечением | 4 | - | ||||
| 2. Интерактивное оборудование 2.1. Интерактивная доска | 1 | - | ||||
| 2.2. Проектор мультимедийный | 4 | - | ||||
| 3. Копировально-множительная техника 4.1. Печатное, копировальное, сканирующие устройства (отдельные элементы или в виде многофункционального устройства, в соответствии с целями и задачами использования оборудования в образовательном процессе) | 4 | - | ||||
| 4. Прочее оборудование Аппаратное и программное обеспечение компьютера обеспечивает: управление учебным процессом; создание и редактирование электронных таблиц, текстов и презентаций; создание, обработку и редактирование звука; создание, обработку и редактирование растровых, векторных и видеоизображений; создание и редактирование интерактивных учебных материалов, образовательных ресурсов, творческих работ со статическими и динамическими графическими и текстовыми объектами; возможность размещения, систематизирования и хранения (накапливания) материалов образовательного процесса; проведение мониторинга и фиксацию хода учебного процесса и результатов освоения основной образовательной программы общего образования; проведение различных видов и форм контроля знаний, умений и навыков, осуществление адаптивной (дифференцированной) подготовки к государственной (итоговой) аттестации; осуществление взаимодействия между участниками учебного процесса, в том числе дистанционное (посредством локальных и глобальных сетей) использование данных, формируемых в ходе учебного процесса для решения задач управления образовательной деятельностью; возможность безопасного доступа к печатным и электронным образовательным ресурсам и пр. | 4 | - | ||||
|
|
| Интерактивное оборудование предназначено для визуализации учебного материала, полученного с цифровых и нецифровых носителей, на интерактивном экране, сохранения результатов образовательного процесса и образовательных достижений (в том числе формирование портфолио) обучающихся. Копировально-множительная техника предназначена для тиражирования учебного материала, сохранения в цифровом формате результатов образовательного процесса и образовательных достижений (формирование портфолио) обучающихся. Прочее оборудование включает фото и/или видео технику, гарнитуру, устройства для коммутации оборудования |
|
| ||
| 2 | Модуль: наглядные пособия по предметам | |||||
| 2.1 | Наглядные пособия по предметам | Представлены учебной техникой, обеспечивающей визуально-звуковое представление объекта изучения. Наглядные пособия по предметам включают: электронные образовательные ресурсы (ЭОР), а также традиционные: объёмные пособия - макеты, модели,; плоскостные пособия - таблицы, картины, фотографии, карты, схемы, чертежи и т.п. |
|
| ||
| 3 | Модуль: информационно-методической поддержки педагогического работника | |||||
| 3.1 | Методические материалы для педагогического работника по использованию комплекта или отдельных компонентов комплекта в образовательном процессе | Материалы содержат руководство пользователя по подключению, наладке комплекта или отдельных модулей комплекта, описание конструктивных особенностей и технологии работы с оборудованием, примеры практической работы с оборудованием, описание порядка постановки экспериментов с использованием оборудования и пр. | ||||
| 3.2 | Программы (модули, курсы) повышения квалификации педагогических работников по использованию комплекта или отдельных компонентов комплекта в образовательном процессе | Разработанные программы (модули, курсы) являются частью программ повышения квалификации, обеспечивающих в соответствии с требованиями ФГОС ООО непрерывность профессионального развития педагогических работников образовательного учреждения, в объеме не менее 108 часов и не реже одного раза в пять лет. | ||||
| 3.3. | Нормативно-методические материалы для учителя |
| 1 ед.
1 ед. 1 ед. |
| ||
| 3.4 | Учебные материалы |
| 1 эд. 1 эд. | Кол-во уч-ся | ||
| 3.5. | Методические материалы |
| необходимое кол-во |
| ||
Список литературы
Примерные программы по учебным предметам «Стандарты второго поколения. Математика 5 – 9 класс» – М.: Просвещение, 2011 г.
Сборник рабочих программ. Алгебра 7–9 классы, Т.А.Бурмистрова, М: Просвещение, 2011г.
А.Г.Мордкович. Алгебра-7. Часть 1. Учебник, М: Мнемозина, 2014 г.
А.Г.Мордкович и др. Алгебра-7. Часть 2. Задачник, М: Мнемозина, 2014 г.
А.Г.Мордкович. Алгебра-7. Методическое пособие для учителя, М: Мнемозина, 2014 г.
Л.А.Александрова. Алгебра-7. Контрольные работы, М: Мнемозина, 2014 г.
Л.А.Александрова. Алгебра-7. Самостоятельные работы, М: Мнемозина, 2014 г.
Л.А.Александрова. Алгебра-7. Тематические проверочные работы в новой форме, М: Мнемозина, 2014 г.
Е.Е.Тульчинская. Алгебра-7. Блицопрос, М: Мнемозина, 2014 г.
М.С.Мильштейн, И.И.Зубарева. Алгебра-7. Рабочая тетрадь, ч. 1, ч. 2, М: Мнемозина, 2014 г.
О.В.Кирюшкина. Алгебра-7. Живые иллюстрации. Учебное мультимедийное пособие, М: Мнемозина, 2014 г.
В.В.Шеломовский. Алгебра-7. Электронный помощник, М: Мнемозина, 2014 г.
А.Г.Мордкович. Алгебра-8. Часть 1. Учебник, М: Мнемозина, 2014 г.
А.Г.Мордкович и др. Алгебра-8. Часть 2. Задачник, М: Мнемозина, 2014 г.
А.Г.Мордкович. Алгебра-8. Методическое пособие для учителя, М: Мнемозина, 2014 г.
Л.А.Александрова. Алгебра-8. Контрольные работы, М: Мнемозина, 2014 г.
Л.А.Александрова. Алгебра-8. Самостоятельные работы, М: Мнемозина, 2014 г.
Л.А.Александрова. Алгебра-8. Тематические проверочные работы в новой форме. М: Мнемозина, 2014 г.
Е.Е.Тульчинская. Алгебра-8. Блицопрос. М: Мнемозина, 2014 г.
А.Г.Мордкович. Алгебра-9. Часть 1. Учебник, М: Мнемозина, 2014 г.
А.Г.Мордкович и др. Алгебра-9. Часть 2. Задачник, М: Мнемозина, 2014 г.
А.Г.Мордкович. Алгебра-9. Методическое пособие для учителя, М: Мнемозина, 2014 г.
Л.А.Александрова. Алгебра-9. Контрольные работы, М: Мнемозина, 2014 г.
Л.А.Александрова. Алгебра-9. Самостоятельные работы, М: Мнемозина, 2014 г.
Л.А.Александрова. Алгебра-9. Тематические проверочные работы в новой форме, М: Мнемозина, 2014 г.
Е.Е.Тульчинская. Алгебра-9. Блицопрос, М: Мнемозина, 2014 г.
Список интернет сайтов:
http://www.edu.ru
http://www.internet-scool.ru
http://www.intellectcentre.ru
http://www.fipi.ru
http://mathege.ru
http://www.egetrener.ru/
http://www.uchportal.ru/load/25
http://school-collection.edu.ru/
http://videouroki.net/
http://www.prosv.ru
40





 . СВОЙСТВА КВАДРАТНОГО КОРНЯ
. СВОЙСТВА КВАДРАТНОГО КОРНЯ
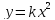 , ее свойства и график
, ее свойства и график , если известен график функции
, если известен график функции  , если известен график функции
, если известен график функции , если известен график функции
, если известен график функции , ее свойства и график
, ее свойства и график , их свойства и графики
, их свойства и графики , их свойства и графики
, их свойства и графики , ее свойства и график
, ее свойства и график в зависимости от значений коэффициентов k и b.
в зависимости от значений коэффициентов k и b. , графических моделей этих функций, свойств.
, графических моделей этих функций, свойств.









