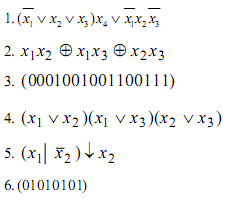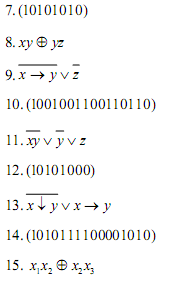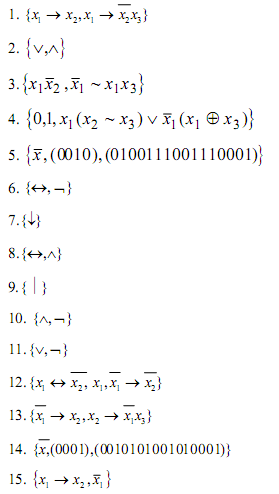Рабочая тетрадь по дисциплине ЕН.02. Элементы математической логики для студентов специальности 09.02.02. Компьютерные сети - 2 часть

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение высшего образования

«КРЫМСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ им. В.И. Вернадского»

ПРИБРЕЖНЕНСКИЙ АГРАРНЫЙ КОЛЛЕДЖ (ФИЛИАЛ)

«Методическая разработка:
«Рабочая тетрадь по дисциплине ЕН.02. Элементы математической логики
для обучающихся специальности 09.02.02 Компьютерные сети — 2 часть»

Автор: Тулова Ю.Ф., преподаватель специальных и общетехнических дисциплин

с.Прибрежное, 2019

АННОТАЦИЯ

Методическая разработка: «Рабочая тетрадь по дисциплине ЕН.02. Элементы математической логики для обучающихся специальности 09.02.02 Компьютерные сети» предназначена для оказания методической помощи обучающимся специальности 09.02.02 Компьютерные сети при выполнении практических занятий по разделам: 3. Булевы функции, 4. Логика предикатов и 5. Элементы теории алгоритмов.

Методическая разработка может быть рекомендована для использования в работе преподавателям, преподающим дисциплину ЕН.02. Элементы математической логики и обучающимся, выполняющим практические занятия по данной дисциплине.

Автор методической разработки: Тулова Юлия Фёдоровна, преподаватель общетехнических и специальных дисциплин Прибрежненского аграрного колледжа (филиал) ФГАОУ ВО «КФУ им. В.И. Вернадского», высшей квалификационной категории, контактный телефон +7(978)7147317.

Рецензент методической разработки: Вильчевский Александр Викторович, преподаватель общетехнических и специальных дисциплин Прибрежненского аграрного колледжа (филиал) ФГАОУ ВО «КФУ им. В.И. Вернадского», высшей квалификационной категории, контактный телефон +7(978)7985854.

Рассмотрено и одобрено на заседании цикловой методической

комиссии информационно-технических дисциплин

Протокол № 5 от « 10» января 2019 г.

Председатель комиссии __________ Тулова Ю.Ф.

Рассмотрено и одобрено на заседании Методического совета

Прибрежненского аграрного колледжа (филиал)

ФГАОУ ВО «КФУ им. В.И. Вернадского»

Протокол № ___ от «____» __________ 2019 г.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ 5

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА 6

ВЫВОДЫ 47

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 48

ВВЕДЕНИЕ.

Предлагаемая методическая разработка предназначена для обучающихся, изучающих дисциплину ЕН.02. Элементы математической логики.

Знания, полученные при изучении дисциплины ЕН.02 Элементы математической логики, являются необходимыми при работе с информацией, что в современном мире является неотъемлемой частью при получении среднего профессионального образования и дальнейшей работы выпускников колледжа.

Актуальность методической разработки заключается в том, что она позволяет за достаточно короткий промежуток времени разъяснить обучающимся требования к выполнению практической работы, с применением конкретных примеров.

Цель предлагаемой методической разработки – это оказание методической помощи обучающимся при написании практических работ, систематизация материалов по выполнению практических занятий обучающимися специальности 09.02.02 Компьютерные сети по дисциплине ЕН.02. Элементы математической логики.

Ожидаемым результатом методических рекомендаций является овладение обучающимися знаниями и умениями, предусмотренными ФГОС по специальности 09.02.02 Компьютерные сети при изучении дисциплины ЕН.02. Элементы математической логии:

В результате освоения дисциплины обучающийся должен уметь:

• формулировать задачи логического характера и применять средства математической логики для их решения;

В результате освоения дисциплины обучающийся должен знать:

• основные принципы математической логики, теории множеств и теории алгоритмов;

• формулы алгебры высказываний;

• методы минимизации алгебраических преобразований;

• основы языка и алгебры предикатов

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение высшего образования

«КРЫМСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ им. В.И. Вернадского»

ПРИБРЕЖНЕНСКИЙ АГРАРНЫЙ КОЛЛЕДЖ (ФИЛИАЛ)

Рабочая тетрадь по дисциплине
ЕН.02. Элементы математической логики
обучающегося группы ________
специальности 09.02.02 Компьютерные сети»

____________________________________________

____________________________________________

с.Прибрежное, 2019

Инструкционная карта 9.

на выполнение практического занятия по дисциплине
ЕН.02. Элементы математической логики
для обучающихся специальности 09.02.02 Компьютерные сети

Тема: Упрощение формул логики до минимальной ДНФ..

Цель: Научиться упрощать формулы логики используя основные законы и формулы булевой алгебры.

Норма времени: 2 часа.

Оснащение рабочего места: инструкционные карты, конспект.

Литература: Е.Л Рабкин, Ю.Б. Фарфоровская, «ДИСКРЕТНАЯ МАТЕМАТИКА. БУЛЕВЫ ФУНКЦИИ И ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ», МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ, http://dvo.sut.ru/libr/himath/w163rabk/index.htm

Основные умения и навыки, которыми должны овладеть обучающиеся в процессе изучения этой темы:

• применять формулы булевой алгебры,

• минимизировать формулы логики.

Вопросы для актуализации опорных знаний:

1. Что такое ДНФ, СДНФ?

2. Что такое КНФ, СКНФ

3. Формулы минимизации.

Задания для практического занятия и инструктаж по их выполнению

1. Записать теоретические сведения в тетрадь.

2. Выполнить письменно практические задания по данной теме.

Теоретические сведения

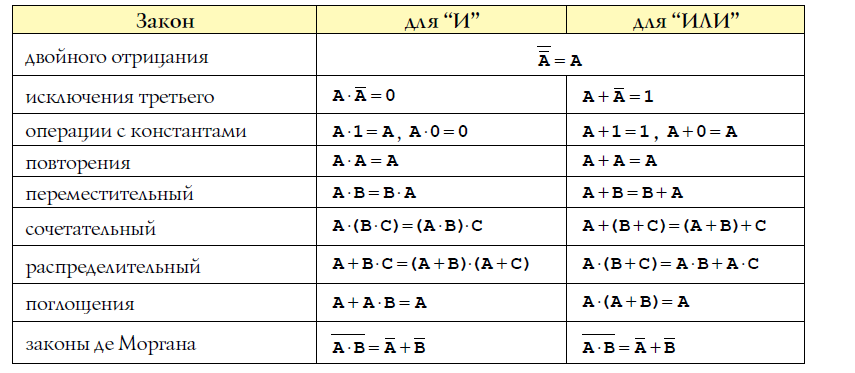
Для упрощения логических выражений используют законы алгебры логики. Они формулируются для базовых логических операций — "НЕ", "И" и "ИЛИ".

Используя законы логики, формулы склеивания и поглощения и свойства логических операций, можно сложную логическую функцию заменить более простой, но равносильной ей функцией. Этот процесс называется минимизацией функции.

Минимизация необходима для того, чтобы функциональные схемы не были слишком громоздкими и не использовали лишних элементов. Чем меньше в функции, получаемой при минимизации, входных переменных и используемых логических операций, тем проще логическая схема, меньше в ней логических элементов. Минимизация необходима и при составлении сложных логических выражений в программах.

Пример 1. Упростить формулу (А+В)·(А+С)

Решение.

а) Раскроем скобки (A+B)·(A+C)C+B·A+B·C

б) По закону идемпотентности A·A, следовательно, C+B·A+B·CC+B·A+B·C

в) В высказываниях А и А·C вынесем за скобки А и используя свойство А+11, получим А+АСCССС

гАналогично пункту в) вынесем за скобки высказывание А.

ССС

Таким образом, доказан закон дистрибутивности (распределительный).

Преобразования “поглощение” и “склеивание”

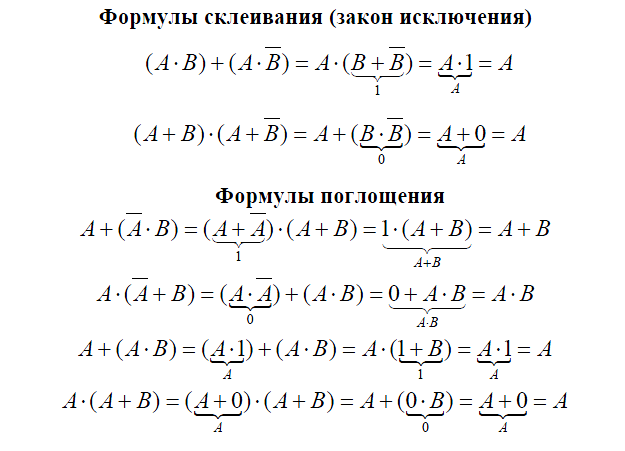
Пример 2. Упростить выражение А.Решение.  - поглощение

Пример 3. Упростить выражение   Решение.    - склеивание

Всякую формулу можно преобразовать так, что в ней не будет отрицаний сложных высказываний - все отрицания будут применяться только к простым высказываниям.

Пример 4. Преобразовать формулу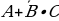 так, чтобы не было отрицаний сложных высказываний.

Решение. 1. Воспользуемся формулой де Моргана, получим: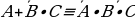

2. Для выражения 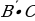применим еще раз формулу де Моргана, получим: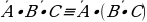

Любую формулу можно тождественно преобразовать так, что в ней

не будут использованы:

- знаки логического сложения;

- знаки логического умножения,

а будут использованы:

- знаки отрицания и логического умножения

- знаки отрицания и логического сложения.

Пример 5. Преобразовать формулу 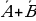так, чтобы в ней не использовались знаки логического сложения.

Решение. Воспользуемся законом двойного отрицания, а затем формулой де Моргана.

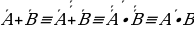
Пример 6. Преобразовать формулу 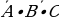так, чтобы в ней не использовались знаки логического умножения.

Решение. Используя формулы де Моргана и закон двойного отрицания получим:

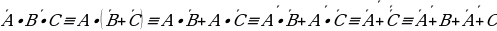
Замена эквиваленции и импликации на конъюнкцию, дизъюнкцию и отрицание.

До сих пор мы занимались равносильными преобразованиями формул, не содержащих знаков импликации и эквиваленции ““ и ““. Сейчас покажем, что всякую формулу, содержащую  или , можно заменить равносильной ей формулой, не содержащей этих знаков.

Имеют место следующие равносильности:

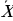  (1)

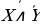 (2)

Докажем равносильность (1) с помощью таблицы истинности:

X	Y	X		
0	0	1	1	1
0	1	1	1	1
1	0	0	0	0
1	1	1	0	1

Эквиваленция выражается через конъюнкцию и импликацию

 

Из (3) и (1) получаем

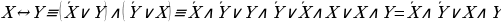(4)

Эта равносильность выражает эквиваленцию через конъюнкцию, дизъюнкцию и отрицание. Из равносильностей (3) и (2) получаем равносильность

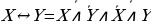, (5)

выражающая эквиваленцию через конъюнкцию и отрицание.

Вывод:

В алгебре логики всякую логическую функцию можно выразить через другие логические функции, но их должно быть, по меньшей мере, 2 операции, при этом одной из них обязательно должно быть отрицание.

Примеры выполнения заданий:

Задание №1. Формулы данных высказываний преобразовать в эквивалентные, исключив логическое сложение:

а) ;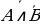

б) ;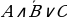

в) ) .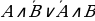

Задание №2. Формулы данных высказываний преобразовать в эквивалентные, исключить логическое умножение.

а) ;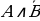

б) ;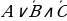

в) .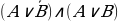

Задание №3. Упростить:

а)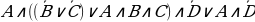

б) ;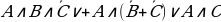

Ответы.

1. Формулы данных высказываний преобразовать в эквивалентные, исключив логическое сложение:

а) ;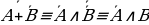

б) ;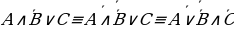

в) .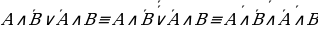

2. Формулы данных высказываний преобразовать в эквивалентные, исключить логическое умножение.

а) ;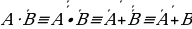

б) ;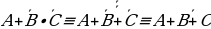

в) .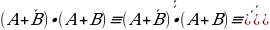

3. Упростить:

а)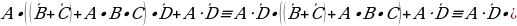

б)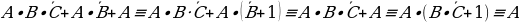

Ход работы.

1. Замените эквиваленции и импликации на конъюнкцию, дизъюнкцию и отрицание

1.1. (A→ B) →(B  A)

1.2. A ∧ (B ∨ C)→ В

1.3. (A→ A ∧ B) → C

1.4. (A→ B) ∧ (C→ D) ∧ B

2.1. (A→ B) ∧ (C→ D) ∧ D

2.2. (A ∧ B ∧ C)→(A ∨ B)→ B ∧ C

2.3. (A  B) →( C ∧ D

2.4. (A ∨ B) →( C ∨ D)

3.1. A∧B ∨ (A→ B) ∧ A

3.2. (A→ B) →(A B)

3.3. (A→ B) → A

3.4. (A→ B) ∧ (B →C)

4.1. (A ∧ B) ∨ (A→ B)

4.2. (A→ B) →(C ∨ A)

4.3. (A→ B)  C

4.4. . (A ∧ С) →(A→ B)

№ ________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

№ _________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

№ .________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

№ .________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

Вариант 1 Составить таблицы истинности: а) б) в) Упростить высказывания: а) б) в)	Вариант 2 Составить таблицы истинности: а) б) в) Упростить высказывания: а) б) в)
Вариант 3 Составить таблицы истинности: а) б) в) Упростить высказывания: а) б) в)	Вариант 4 Составить таблицы истинности: а) б) в) Упростить высказывания: а) б) в)
Вариант 5 Составить таблицы истинности: а) б) в) Упростить высказывания: а) б) в)	Вариант 6 Составить таблицы истинности: а) б) в) Упростить высказывания: а) б) в)
Вариант 7 Составить таблицы истинности: а) б) в) Упростить высказывания: а) б) в)	Вариант 8 Составить таблицы истинности: а) б) в) Упростить высказывания: а) б) в)

Контрольные вопросы:

1. Oтрицание. Свойства

2. Конъюнкция. Свойства

3. Правила поглощения, де Моргана и Блейка.

4. ДНФ, СДНФ.

5. Алгоритм представления булевой функции (по таблице истинности) в виде СДНФ.

6. КНФ, СКНФ.

7. Алгоритм представления булевой функции (по таблице истинности) в виде СКНФ.

1. _________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

2. _________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

3. _________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

4. _________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

Инструкционная карта 10.

на выполнение практического занятия по дисциплине
ЕН.02. Элементы математической логики
для обучающихся специальности 09.02.02 Компьютерные сети

Тема: Минимизация в классе дизъюнктивных нормальных форм.

Цель: Научиться минимизировать функции при помощи минимизирующих карт и карт Карно.

Норма времени: 2 часа.

Оснащение рабочего места: инструкционные карты, конспект.

Литература: Е.Л Рабкин, Ю.Б. Фарфоровская, «Дискретная математика. Булевы функции и элементы теории графов», методические указания и контрольные задания, http://dvo.sut.ru/libr/himath/w163rabk/index.htm

Основные умения и навыки, которыми должны овладеть обучающиеся в процессе изучения этой темы:

• уметь минимизировать функции при помощи минимизирующих карт;

• уметь минимизировать функции при помощи карт Карно.

Вопросы для актуализации опорных знаний:

1. Что такое минимизирующая карта?

2. Что такое карта Карно?

3. Правила склеивания карт Карно.

Задания для практического занятия и инструктаж по их выполнению

1. Записать теоретические сведения в тетрадь.

2. Разобрать и проанализировать примеры.

3. Выполнить письменно практические задания по данной теме.

Теоретические сведения.

Метод минимизирующих карт.

Построение минимальной ДНФ осуществляется следующим образом:

1. Отметим в таблице строки, в которых соответствующая конъюнкция не принадлежит СДНФ. Вычеркнем все конъюнкции в этих строках.

2. Все вычеркнутые конъюнкции вычеркнем также во всех остальных строках.

3. В каждой строке выберем из оставшихся конъюнкций только те, которые содержат наименьшее число “сомножителей”, а остальные вычеркнем.

4. В каждой строке выберем по одному оставшемуся элементу и составим из них ДНФ.

5. Из всех ДНФ, полученных в п.4, выберем минимальную.

Пример:

X1	X2	X3	X1X2	X1X3	X2X3	X1X2X3	0
X1	X2	¬Х3	Х1Х2	Х1¬Х3	X2¬X3	X1X2¬X3	1
X1	¬X2	X3	X1¬X2	X1X3	¬X2X3	X1¬X2X3	1
X1	¬X2	¬X3	X1¬X2	Х1¬Х3	¬X2¬X3	X1¬X2¬X3	1
¬X1	X2	X3	¬X1X2	¬X1X3	X2X3	¬X1X2X3	0
¬X1	X2	¬X3	¬X1X2	¬X1¬X3	X2¬X3	¬X1X2¬X3	0
¬X1	¬X2	X3	¬X1¬X2	¬X1X3	¬X2X3	¬X1¬X2X3	1
¬X1	¬X2	¬X3	¬X1¬X2	¬X1¬X3	¬X2¬X3	¬X1¬X2¬X3	0

X1	X2	X3	X1X2	X1X3	X2X3	X1X2X3	0
X1	X2	¬Х3	Х1Х2	Х1¬Х3	X2¬X3	X1X2¬X3	1
X1	¬X2	X3	X1¬X2	X1X3	¬X2X3	X1¬X2X3	1
X1	¬X2	¬X3	X1¬X2	Х1¬Х3	¬X2¬X3	X1¬X2¬X3	1
¬X1	X2	X3	¬X1X2	¬X1X3	X2X3	¬X1X2X3	0
¬X1	X2	¬X3	¬X1X2	¬X1¬X3	X2¬X3	¬X1X2¬X3	0
¬X1	¬X2	X3	¬X1¬X2	¬X1X3	¬X2X3	¬X1¬X2X3	1
¬X1	¬X2	¬X3	¬X1¬X2	¬X1¬X3	¬X2¬X3	¬X1¬X2¬X3	0

	X2	X3	X1X2	X1X3	X2X3	X1X2X3	0
X1	X2	¬Х3	Х1Х2	Х1¬Х3	X2¬X3	X1X2¬X3	1
X1	¬X2	X3	X1¬X2	X1X3	¬X2X3	X1¬X2X3	1
X1	¬X2	¬X3	X1¬X2	Х1¬Х3	¬X2¬X3	X1¬X2¬X3	1
¬X1	X2	X3	¬X1X2	¬X1X3	X2X3	¬X1X2X3	0
¬X1	X2	¬X3	¬X1X2	¬X1¬X3	X2¬X3	¬X1X2¬X3	0
¬X1	¬X2	X3	¬X1¬X2	¬X1X3	¬X2X3	¬X1¬X2X3	1
¬X1	¬X2	¬X3	¬X1¬X2	¬X1¬X3	¬X2¬X3	¬X1¬X2¬X3	X1

Метод карт Карно.

Карты Карно - это специально организованные таблицы соответствия, на которых удобно производить операции склеивания или упрощения функции на пути к минимальным формам.

Столбцы и строки этих таблиц соответствуют всем наборам значений переменных, причём эти наборы расположены в таком порядке, что каждый последующий (соседний) отличается от предыдущего значением только одной из переменных. Краевые ячейки таблиц тоже считаются “соседними”.  

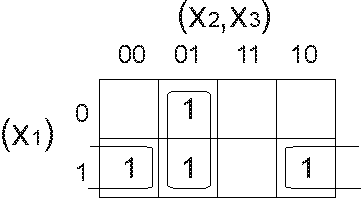
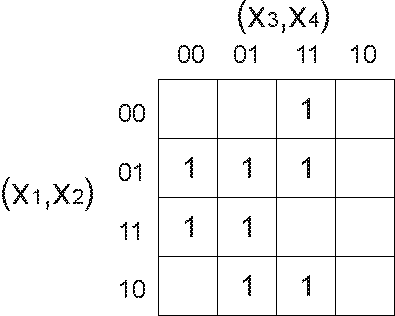
В ДНФ входят только те переменные, которые сохраняют свои значения в данной группе, причём значениям 1 соответствует сама переменная, 0 - её отрицание.

Ход работы_1 вариант.

1.Выполнить следующие действия:

1. Минимизируйте функции при помощи минимизирующих карт и при помощи карт Карно. Сравните полученный результат.

1. f(x₁,x₂,x₃)= ¬x₁¬x₂¬x₃ ∨ x₁x₂¬x₃∨ x₁¬x₂x₃∨¬x₁x₂x₃

2. f(x₁,x₂,x₃)=x₁x₂x₃ ∨¬x₁¬x₂¬x₃∨ x₁¬x₂x₃∨¬x₁¬x₂x₃

3. f(x₁,x₂,x₃)=x₁¬x₂¬x₃ ∨ x₁x₂¬x₃∨¬x₁¬x₂¬x₃∨¬x₁¬x₂x₃

4. f(x₁,x₂,x₃)=x₁¬x₂x₃ ∨ x₁x₂¬x₃∨¬x₁¬x₂x₃∨x₁¬x₂¬x₃

5. f(x₁,x₂,x₃)= ¬x₁¬x₂x₃ ∨ x₁x₂¬x₃∨ x₁¬x₂¬x₃∨¬x₁¬x₂¬x₃

6. f(x₁,x₂,x₃)= ¬x₁¬x₂¬x₃ ∨ x₁x₂x₃∨ x₁¬x₂x₃∨x₁¬x₂¬x₃

7. f(x₁,x₂,x₃)= ¬x₁¬x₂¬x₃ ∨ x₁x₂x₃∨ x₁¬x₂¬x₃∨¬x₁x₂¬x₃

8. f(x₁,x₂,x₃)= ¬x₁¬x₂x₃ ∨ x₁x₂¬x₃∨ x₁¬x₂¬x₃∨¬x₁x₂¬x₃

9. f(x₁,x₂,x₃)= ¬x₁x₂¬x₃ ∨ x₁¬x₂x₃∨ x₁¬x₂¬x₃∨¬x₁¬x₂¬x₃

10. f(x₁,x₂,x₃)= x₁¬x₂¬x₃ ∨ x₁x₂x₃∨ x₁¬x₂x₃∨¬x₁x₂¬x₃

Задача 2. 2. С помощью карт Карно по данной таблице истинности для функции 4-х переменных найти её сокращённую ДНФ.

2.1.						2.2.					2.3.
	x3 , x4					x3 , x4					x3 , x4
х1 ,х2	00	01	11	10	х1, х2	00	01	11	10	х1 ,х2	00	01	11	10
00	1	0	0	1	00	1	0	0	1	00	1	0	0	1
01	1	0	1	1	01	1	0	0	1	01	1	0	0	1
11	1	1	0	1	11	1	0	0	1	11	0	1	1	0
10	1	1	1	1	10	0	1	1	0	10	0	0	0	1
2.4						2.5					2.6
	x3 , x4					x3 , x4					x3 , x4
х1 ,х2	00	01	11	10	х1 ,х2	00	01	11	10	х1 ,х2	00	01	11	10
00	0	1	1	0	00	0	1	1	1	00	1	1	0	1
01	0	1	1	0	01	1	1	0	1	01	1	0	0	1
11	0	0	0	0	11	1	1	0	0	11	0	1	0	1
10	1	0	0	1	10	0	0	1	0	10	1	0	0	1
2.7						2.8					2.9
	x3 , x4					x3 , x4					x3 , x4
х1 ,х2	00	01	11	10	х1 ,х2	00	01	11	10	х1 ,х2	00	01	11	10
00	1	1	0	0	00	1	0	0	1	00	1	1	0	0
01	0	1	1	0	01	1	0	0	1	01	0	1	0	0
11	0	0	0	0	11	0	1	1	0	11	0	1	0	0
10	1	0	0	1	10	0	1	1	0	10	1	1	0	0

Контрольные вопросы:

1. Что такое минимизирующая карта ? Сформулируйте правило применения минимизирующих карт.

2. Что такое карта Карно? Сформулируйте правило применения карт Карно
   

1. _________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

2. _________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

Инструкционная карта 11.

на выполнение практического занятия по дисциплине
ЕН.02 Элементы математической логики
для обучающихся специальности 09.02.02 Компьютерные сети

Тема: Построение полинома Жегалкина для булевой функции.

Цель: Изучить булевые функции, приобрести навыки по определению полинома Жегалкина.

Норма времени: 2 часа.

Оснащение рабочего места: инструкционные карты, конспект.

Литература: Спирин М.С., Спирина П.А. Дискретная математика. – М.: Издательский центр «Академия», 2014.

Основные умения и навыки, которыми должны овладеть обучающиеся в процессе изучения этой темы:

• формулировать задачи логического характера и применять средства математической логики для их решения.

Вопросы для актуализации опорных знаний:

1. Основные формулы математической логики, теории множеств и теории алгоритмов;

2. Формулы алгебры высказываний.

Задания для практического занятия и инструктаж по их выполнению

1. Записать теоретические сведения в тетрадь.

2. Выполнить письменно практические задания по данной теме.

Теоретические сведения.

Методом неопределенных коэффициентов найдем многочлен Жегалкина для функции от двух переменных, которая задана вектором значений f( x,y ) = ( 0, 1, 1, 0 ).

Составим  таблицу истинности для данной функции:

Обозначение вектора	x	y	f
	0	0	0
	0	1	1
	1	0	1
	1	1	0

Канонический многочлен Жегалкина для функции от двух переменных ищем в следующем виде:

f( x, y ) = k₀  k₁·x  k₂·y  k₁₂·x∙y (1)

Для определения коэффициентов многочлена подставляем значения переменных и соответствующее значение функции в формулу (1) − в соответствии с таблицей истинности.

Подставляя набор переменных (0,0) в (1) получаем:

Р( )= k₀  k₁·0  k₂·0  k₁₂·0·0 = k₀ = 0 = f( )  k₀ = 0.

Аналогично для набора (0,1) получаем:

Р(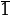 )= 0  k₁·0  k₂·1  k₁₂·0·1 = k₂ = 1 = f( 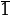)  k₂ = 1.

Для набора (1,0) получаем:

Р(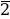 )= 0  k₁·1  k₂·0  k₁₂·1·0 = k₁ = 1 = f( 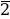)  k₁ = 1.

Для набора (1,1) получаем:

Р(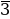 )= 0= 0 1·1  1·1  k₁₂·1·1 = 1  1  k₁₂ = 0  k₁₂ = k₁₂ = 0 = f( 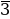)  k₁₂=0.

Подставляя в (1) найденные значения коэффициентов, получаем искомый многочлен для данной функции: f( x, y ) = x  y.

Ход работы

1. Для заданной функции постройте полином Жегалкина любым способом.

1. f= (00101101)

2. ( x₁↓ x₂ ) | x₃

3. (x₁ →x₂) ↔ (x₂ ↔x₃)

4. (x₁ →x₃)(x₂⊕x₃)

5.

6. (z₁ ↔z₂) → z₃

7. f = (10101100)

8. f = ( 11000100)

9.

10.

11.

12.

13.

14.

15.

Ответ: ________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

Задание 2.

Вариант 1

1. Для заданной функции выполнить следующее:

• постройте таблицу истинности;

• по таблице истинности запишите СДНФ или СКНФ;

• постройте многочлен Жегалкина двумя способами - с помощью эквивалентных преобразований над исходной формулой и методом неопределенных коэффициентов;

• сравнив оба результата, проверьте правильность построенного многочлена.

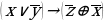
Вариант 2

1. Для заданной функции выполнить следующее:

• постройте таблицу истинности;

• по таблице истинности запишите СДНФ или СКНФ;

• постройте многочлен Жегалкина двумя способами - с помощью эквивалентных преобразований над исходной формулой и методом неопределенных коэффициентов;

• сравнив оба результата, проверьте правильность построенного многочлена.

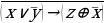
Вариант 3

1. Для заданной функции выполнить следующее:

• постройте таблицу истинности;

• по таблице истинности запишите СДНФ или СКНФ;

• постройте многочлен Жегалкина двумя способами - с помощью эквивалентных преобразований над исходной формулой и методом неопределенных коэффициентов;

• сравнив оба результата, проверьте правильность построенного многочлена.

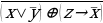
Вариант 4

1. Для заданной функции выполнить следующее:

• постройте таблицу истинности;

• по таблице истинности запишите СДНФ или СКНФ;

• постройте многочлен Жегалкина двумя способами - с помощью эквивалентных преобразований над исходной формулой и методом неопределенных коэффициентов;

• сравнив оба результата, проверьте правильность построенного многочлена.

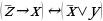
Вариант 5

1. Для заданной функции выполнить следующее:

• постройте таблицу истинности;

• по таблице истинности запишите СДНФ или СКНФ;

• постройте многочлен Жегалкина двумя способами - с помощью эквивалентных преобразований над исходной формулой и методом неопределенных коэффициентов;

• сравнив оба результата, проверьте правильность построенного многочлена.

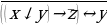
Ответ:

Контрольные вопросы:

1. Что такое полином Жегалкина?

2. Запишите в общем виде полином Жегалкина для функции 3-х переменных.

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________

Инструкционная карта 12.

на выполнение практического занятия по дисциплине
ЕН.02 Элементы математической логики
для обучающихся специальности 09.02.02 Компьютерные сети

Тема: Проверка булевой функции на принадлежность к классам ТО, Tl, S, L, М; проверка множества булевых функций на полноту

Цели занятия: изучить булевые функции, а также приобрести навыки по определению полноты множества будевых функций

Норма времени: 2 часа.

Оснащение рабочего места: инструкционные карты, конспект.

Литература: Спирин М.С., Спирина П.А. Дискретная математика. – М.: Издательский центр «Академия», 2014.

Основные умения и навыки, которыми должны овладеть обучающиеся в процессе изучения этой темы:

уметь: - формулировать задачи логического характера и применять средства математической логики для их решения.

знать: - основные принципы математической логики, теории множеств и теории алгоритмов;

- формулы алгебры высказываний.

Задания для практического занятия и инструктаж по их выполнению

1. Записать теоретические сведения в тетрадь.

2. Разобрать и проанализировать примеры.

3. Выполнить письменно практические задания по данной теме.

Теоретические сведения

Основные понятия полноты функции.

Пусть B — некоторое множество функций алгебры логики. Замыканием [B] множества B называется совокупность всех функций из Р₂, являющихся суперпозициями функций из множества B. Множество B называется замкнутым классом, если [B]=B. Пусть B – замкнутый класс в Р₂ . Множество B называется функционально полной системой в Р₂, если [B] = Р₂.

Замкнутые классы Поста

1. Говорят, что функция 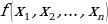сохраняет константу 0, если f(0,0,...,0)=0.

T₀ − класс функций, сохраняющих ноль: T₀ = {f  P₂  f (0,0,...,0) = 0}.

2. Говорят, что функция 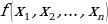сохраняет константу 1, если f (1,1,...,1)=1.

T₁ − класс функций, сохраняющих единицу: T₁ = {f  P₂  f (1,1,...,1) = 1}.

3. Функция 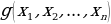называется двойственной к 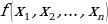, если на противоположных наборах она принимает противоположные значения, т.е. 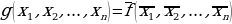. Двойственная функция обозначается .

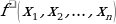Функция 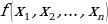называется самодвойственной, если она совпадает со своей двойственной функцией.

S -- класс самодвойственных функций: S = {f  P₂  f (a₁,a₂ ,...,a_n ) = ( , ,..., )}.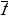

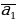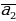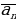4. Для двоичных векторов 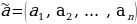и 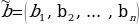, где i=1,2,…,n, введем следующее отношение частичного порядка, называемое отношением предшествования. Будем говорить, что набор 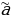предшествует набору 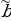и писать 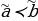, если a_i≤b_i для всех i=1,2,…,n. Функция f(x₁,x₂,…,x_n) называется монотонной, если для любых векторов 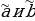, находящихся в отношении предшествования 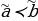, выполняется соотношение .

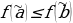М − класс монотонных функций: М ={ f  P₂ (n) f − монотонна}.

5. L − класс линейных функций составляют функции, которые представляются полиномом Жегалкина первой степени: L={ f  P₂ (n) f = k₀k₁x₁ k₂x₂  … k_nx_n }, где k_i{0,1}.

Проверка принадлежности булевой функции замкнутым классам 1-4 осуществляется по таблице истинности. Проверка принадлежности булевой функции классу L осуществляется путем построения многочлена Жегалкина.

Каждое из множеств T₀, T₁, S, L, M является замкнутым классом в P₂ .

Критерий полноты системы булевых функций

Теорема Поста. Система булевых функций В функционально полна в Р₂ тогда и только тогда, когда она содержит:

1.хотя бы одну функцию, не сохраняющую ноль;

2.хотя бы одну функцию, не сохраняющую единицу;

3.хотя бы одну немонотонную функцию;

4.хотя бы одну несамодвойственную функцию;

5.и хотя бы одну нелинейную функцию.

Для проверки функциональной полноты системы булевых функций строится так называемая таблица Поста, в которой отмечается принадлежность функций замкнутым классам. Если в каждом столбце таблицы Поста есть хотя бы один минус, система полна, в противном случае – нет.

Пример 1. Проверить систему булевых функций В = {x  y, x  y,1} на функциональную полноту.

Проверим принадлежность замкнутым классам функции f (x, y) = x  y. Построим таблицу истинности данной функции.

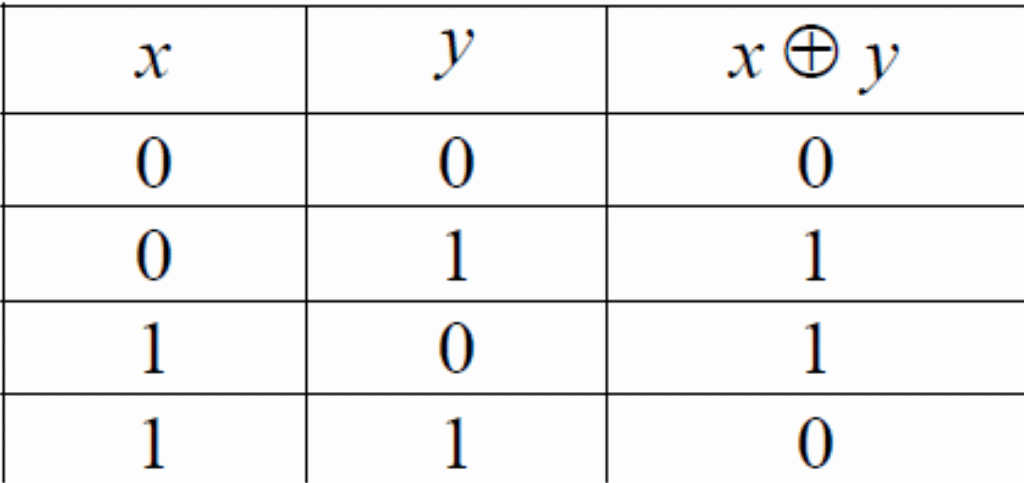
f (0,0) = 0 , следовательно f (x, y) T₀ .

f (1,1) = 0 , следовательно f (x, y) T₁ .

f (0,0) = f (1,1) , следовательно, f (x, y) S .

f (1,0) = 1 0 = f (1,1) , следовательно, f (x, y) M .

Функция представляет собой полином Жегалкина первой степени, следовательно, f (x, y)  L .

Результаты заносим в первую строку таблицы Поста. Остальные функции исследуются аналогично. Окончательно таблица Поста имеет вид:

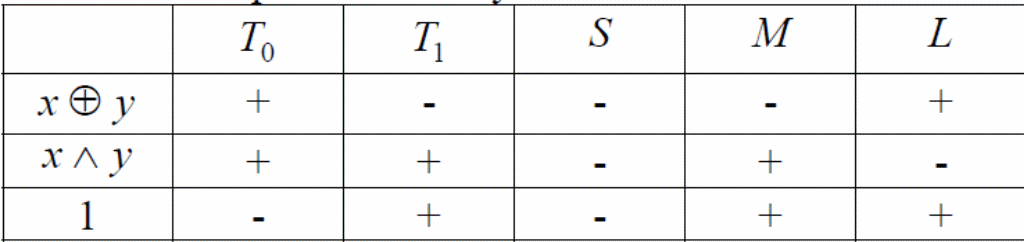
В каждом столбце таблицы имеется минус, следовательно, система В функционально полна.

Ход работы.

Вариант 1

1. Для заданной функции выполнить следующее:

• постройте СДНФ и СКНФ методом эквивалентных преобразований.;

• проверьте правильность по таблице истинности;

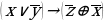
2. С помощью теоремы Поста выяснить, полна ли заданная система булевых функций.

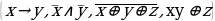
Вариант 2

1. Для заданной функции выполнить следующее:

• постройте СДНФ и СКНФ методом эквивалентных преобразований.;

• проверьте правильность по таблице истинности;

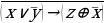
2. С помощью теоремы Поста выяснить, полна ли заданная система булевых функций.

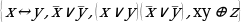
Вариант 3

1. Для заданной функции выполнить следующее:

• постройте СДНФ и СКНФ методом эквивалентных преобразований.;

• проверьте правильность по таблице истинности;

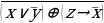
2. С помощью теоремы Поста выяснить, полна ли заданная система булевых функций.

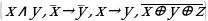
Вариант 4

1. Для заданной функции выполнить следующее:

• постройте СДНФ и СКНФ методом эквивалентных преобразований.;

• проверьте правильность по таблице истинности;

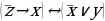
2. С помощью теоремы Поста выяснить, полна ли заданная система булевых функций.

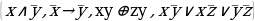
Вариант 5

1. Для заданной функции выполнить следующее:

• постройте СДНФ и СКНФ методом эквивалентных преобразований.;

• проверьте правильность по таблице истинности;

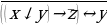
2. С помощью теоремы Поста выяснить, полна ли заданная система булевых функций.

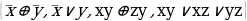
Задание 2, 3:

2. Проверить самодвойственность функций.

3. Проверить полноту следующих систем.

Контрольные вопросы:

1. При каком условии множество B называется замкнутым классом?

2. Когда функцию можно назвать самодвойственной? Приведите пример самодвойственной функции.

3. Что должна содержать система булевых функций В чтобы быть функционально полной в Р₂ ?

Ответ:

1. _________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

2. _________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

3. _________________________________________________________________________

___________________________________________________________________________

Инструкционная карта 13.

на выполнение практического занятия по дисциплине
ЕН.02. Элементы математической логики
для обучающихся специальности 09.02.02 Компьютерные сети

Тема: Предикат. Логические операции над предикатами

Цели занятия: Научиться находить истинность и ложность предикатов.

Норма времени: 2 часа.

Оснащение рабочего места: инструкционные карты, конспект.

Литература: Спирин М.С., Спирина П.А. Дискретная математика. – М.: Издательский центр «Академия», 2014.

Основные умения и навыки, которыми должны овладеть обучающиеся в процессе изучения этой темы:

• уметь выделять предикаты и определять для них область истинности;

• уметь изображать графически область истинности предикатов.

Задания для практического занятия и инструктаж по их выполнению

1. Записать теоретические сведения в тетрадь.

2. Разобрать примеры.

3. Выполнить письменно практические задания по данной теме.

Теоретические сведения

Одноместным предикатом Р(х) называется произвольная функция переменного х, опреде­ленная на множестве М и принимающая значения из множества {1,0}.

Множество М, на котором определен предикат P(х) , называется областью определения предиката.

Множество всех элементов х  М , при которых предикат принимает значение «истина», называется множеством истинности предиката Р(х), то есть множество истиннос­ти предиката Р(х) - это множество 1р = {х| х  М, Р(х) = 1}.

Так, предикат -Р(х) - «х - простое число» определен на множестве N, а множество Iр для него есть множество всех простых чисел.

Предикат Р(х), определенный на множестве М, называется тождественно истинным (тож­дественно ложным), если 1р = М (1р = )

Ход работы.

Задание № 1. Определите значения истинности следующих высказываний:

1. Для следующих предложений выделить предикаты и для каждого из них указать область истинности, если область определения для одноместного М=R, для двухместного M=R² :

1. х+5=1;

2. при х=2 выполняется равенство х² – 1 = 0;

3. существует такое число х, что х² – 2х + 1 =0;

4. х² – 2х + 1 =0;

5. х+2x – 4;

6. однозначное число х кратно 3;

7. (х+2)-(3х-4);

8. х² + у² 0.

Ответ: 1.________________________________________________________________________

2.________________________________________________________________________

3.________________________________________________________________________

4.________________________________________________________________________

5.________________________________________________________________________

6.________________________________________________________________________

7.________________________________________________________________________

8.________________________________________________________________________

2. Какие из предикатов тождественно истинны?

1. х² + у²  0;

2. sin²x + cos²x =1;

3. x² + 1(x+1)²;

4. х² + у² 0;

5. (x+1)²x-1.

Ответ:

.________________________________________________________________________

.________________________________________________________________________

3. Найти области истинности предикатов, если хR:

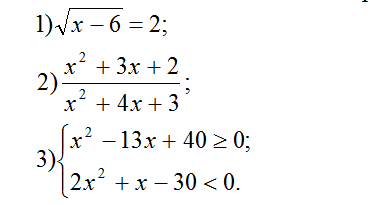
Ответ: 1.________________________________________________________________________

2.________________________________________________________________________

3.________________________________________________________________________

4. Изобразить на декартовой плоскости области истинности предикатов:

1. х+у=1;

2. х+3у=3;

3. sinx=siny;

4. (x-2)²+(y+3)²=0;

5. (x-2)²+(y+3)²4;

6. ((x2)v(y1))((x

Ответ:

5.На множестве М = {1,2,3,4,5,6,7,8,9,10} заданы предикаты А(х): «х не делится на 5», В(х): «х – четное число», С(х): «х кратно 3». Найти множество истинности предиката: А(х)VB(x)C(x).

6. Изобразить на диаграмме Эйлера -Венна область истинности предиката: (P(x)Q(x))VR(x)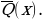

Ответ: .________________________________________________________________________

.________________________________________________________________________

.________________________________________________________________________

.________________________________________________________________________

.________________________________________________________________________

.________________________________________________________________________

Контрольные вопросы:

1. Структура простого высказывания.

2. Определение одноместного предиката.

3. Область истинности одноместного предиката.

4. Определение тождественно истинного (тождественно ложного) предиката.

5. Определение двухместного предиката.

6. Определение n – местного предиката.

7. Какие предикаты являются равносильными? В каком случае предикат Р(х) является следствием предиката Q(x)?

8. Перечислить логические операции над предикатами и показать области истинности на диаграммах Эйлера- Венна.

1. _________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

2. _________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

3. _________________________________________________________________________

___________________________________________________________________________

Инструкционная карта 14.

на выполнение практического занятия по дисциплине
ЕН.02 Элементы математической логики
для обучающихся специальности 09.02.02 Компьютерные сети

Тема: Логические операции над предикатами.

Цели занятия: обобщение, систематизация, углубление, закрепление полученных знаний по теме Логические операции над предикатами

Норма времени: 2 часа.

Оснащение рабочего места: инструкционные карты, конспект.

Литература: Спирин М.С., Спирина П.А. Дискретная математика. – М.: Издательский центр «Академия», 2014.

Основные умения и навыки, которыми должны овладеть обучающиеся в процессе изучения этой темы:

• уметь оперировать понятиями алгебры предикатов,

• формирование умений и навыков применения алгебры предикатов

Вопросы для актуализации опорных знаний:

Задания для практического занятия и инструктаж по их выполнению

1. Записать теоретические сведения в тетрадь.

2. Разобрать примеры.

3. Выполнить письменно практические задания по данной теме.

Теоретические сведения

Высказывания имеют определенную логическую форму. Понятие о предмете мысли называется субъектом и обозначается буквой S, а понятие о свойствах и отношениях предмета мысли называются предикатом и обозначается буквой P. Оба этих понятия - субъект и предикат называются терминами суждения. Отношения между субъектом и предикатом выражаются связкой «есть», «не есть», «является», «состоит» и т.д.

Т.о., каждое высказывание состоит из трех элементов - субъекта, предиката и связки. Состав суждения можно выразить общей формулой «S есть P» или «S не есть P».

Пример, P(N) = "В городе N живут более 2 миллионов человек".

Если мы задаем конкретные значения переменных, предикат превращается в логическое высказывание. Напри­мер, для предиката Р (N) полученное высказывание будет истинно для N = "Москва" и ложно для N = "Якутск".

Предикат, зависящий от одной переменной, — это свойство. Например, только что рассмотренный предикат Р (N) характеризует свойство города. Вот еще примеры предикатов-свойств:

Простое (х) = "х —простое число"

Студент (х) = "х-студент"

Спит(х) = "х всегда спит на уроке"

Пример 1.

Пусть предметное множество М есть класс млекопитающих. Рассмотрим одно­местный предикат Р(х): у х четыре ноги. Тогда Р(слон) = 1, Р(кошка) = 1, Р(человек) =0.

Пусть М - множество натуральных чисел. Рассмотрим двухместный предикат G(x,y): хТогда, например, G(l,3) = l, G(8,5) = 0.

Предикат называется

А) тождественно истинным, если значение его для любых аргументов есть «истина» (Предикат Р(х) называется тождественно истинным на множестве М, если )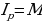

Б) тождественно ложным, если значение его для любых аргументов есть «ложь» (Предикат Р(х) называется тождественно истинным на множестве М, если );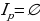

В) выполнимым, если существует, по крайней мере, одна n-система его аргументов, для которой значение предиката есть «истина».

Пример 2. Предикат “x+y=y+x” является тождественно истинным, предикат “x+1=x” – тождественно ложным, предикат “x+y=5” – выполнимым.

Ход работы.

Задание №1. Среди следующих предложений выделите предикаты:

1) Луна есть спутник Венеры

2) Планеты х и y принадлежат Солнечной системе

3)

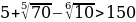
4)

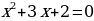
5)

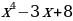
6) Любое простое число Р не имеет делителей, отличных от себя и 1

7) Натуральное число n не меньше 1

8) Треугольник АВС равен треугольнику А₁В₁С₁

9)

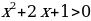
10)

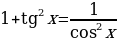
11)

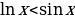
Ответ:

__________________________________________________________________________

__________________________________________________________________________

__________________________________________________________________________

__________________________________________________________________________

__________________________________________________________________________

__________________________________________________________________________

__________________________________________________________________________

Задание №2. Среди следующих предложений выделить предикаты и для каждого из них указать область истинности.

1) х+5=1

2) при х=2 выполняется равенство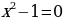

3)

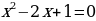
4) существует такое число х, что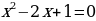

5) x+2x-4

6) однозначное число х кратно3;

7) (х+2)-(3х-4).

Ответ:

__________________________________________________________________________

__________________________________________________________________________

__________________________________________________________________________

__________________________________________________________________________

__________________________________________________________________________

__________________________________________________________________________

__________________________________________________________________________

Задание №3. Составив соответствующие таблицы истинности, докажите, что все следующие формулы являются тавтологиями:

Ответ:

Задание №4. Составьте таблицы истинности для следующих высказываний:

а)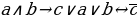

б)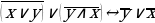

в)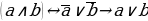

Ответ:

Контрольные вопросы:

1. Что такое таблица истинности формулы?

2. Какая функция называется тождественно ложной?

3. Какая функция называется тождественно истинной?

4. Какая функция называется тождественно истинной?

5. Какая функция называется вычислимой?

1. _________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

2. _________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

3. _________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

4. _________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

Инструкционная карта 15.

на выполнение практического занятия по дисциплине
ЕН.02. Элементы математической логики
для обучающихся специальности 09.02.02 Компьютерные сети

Тема: Машина Поста.

Цели занятия: Научиться решать задачи с использованием машины Поста.

Норма времени: 2 часа.

Оснащение рабочего места: инструкционные карты, конспект.

Литература:

Основные умения и навыки, которыми должны овладеть обучающиеся в процессе изучения этой темы:

• знать принцип работы машины Поста;

• уметь составлять алгоритмы для решения поставленной задачи;

• уметь применять команды машины Поста

Задания для практического занятия и инструктаж по их выполнению

1. Записать теоретические сведения в тетрадь.

2. Разобрать примеры.

3. Выполнить практические задания по данной теме.

Теоретические сведения

1. Устройство машины Поста. Машина Поста - абстрактная машина. Машина Поста состоит из ленты и каретки (считывающая и записывающая головка). Лента бесконечна и разделена на секции одинакового размера. В каждую секцию ленты заносится один символ двоичного информации, который подлежит обработке. Один из символов двоичного алфавита - метка "√", другой - пустота. Если в секцию занесена "√" - секция отмеченная, если в секции "√" нет - секция пустая или неотмеченная. Каретка может передвигаться вдоль ленты влево и вправо. Когда она неподвижна, она стоит против ровно одной секции ленты; говорят, что каретка обозревает эту секцию. А такая секция называется текущей или обозреваемой. За единицу времени, которая называется шагом, каретка может сдвинуться на одну секцию влево или вправо. Кроме того, каретка может также распознать стоит или нет метка в обозреваемой ею секции, может заносить метку в пустую секцию и может удалять метку из отмеченной ячейки. Команды, по которым каретка должна занести метку в отмеченную секцию или удалить метку из пустой секции являются недопустимыми.

2. Команды машины Поста. Формат команды: nKm, где: n - номер текущей команды, K - команда из системы команд машины Поста, m - отсылка - номер команды, которая будет выполняться следующей. Последовательность команд из системы команд - программа, если:

1) на n - ом месте этой программы будет стоять команда с номером n.

2) отсылке m соответствует реальная команда в программе.

Система команд машины Поста:

1). a→b

Сдвиг каретки вправо, содержимое ленты не меняется.

2). a←b

Сдвиг каретки влево, содержимое ленты не меняется.

3). a√b

В обозреваемую секцию ставится метка "√". Выполнение этой команды возможно только в том случае, если обозреваемая секция пустая, в противном случае команда считается невыполнимой.

4). a↨b

Каретка стирает метку в обозреваемой секции. Выполнение этой команды возможно только в том случае, если обозреваемая секция содержит метку, в противном случае команда считается невыполнимой.

5). a?b1, b2

Команда передачи. Проверяется содержимое текущей секции, если метки нет, то происходит передача управления команде с номером b1, иначе, если метка есть - команде с номером b2. Содержимое ленты не меняется.

6). a![b]

Команда останова машины. Содержимое ленты не меняется. У команды остановки отсылка не обязательна.

3. Порядок работы машины Поста. Работа машины Поста состоит в том, что каретка передвигается вдоль ленты и печатает или стирает метки. Чтобы машина Поста работала, надо задать некоторую программу и некоторое состояние машины (т.е. нужно как-то расставить метки по секциям ленты, в частности, можно все секции оставить пустыми, и поставить каретку против одной из секций). Работа машины на основании заданной программы происходит следующим образом. Машина приводится в начальное состояние и приступает к выполнению первой команды программы. Эта команда выполняется за один шаг, после чего машины приступает к выполнению той команды, номер которой равен отсылке первой команды. Эта команда также выполняется за один шаг, после чего начинается выполнение той команды, номер команды которой равен отсылке предыдущей команды. Вообще каждая команда выполняется за один шаг, а переход от выполнения одной команды к выполнению другой происходит по следующему правилу: пусть на k-ом шаге выполнялась команда с номером a, тогда:

1) если эта команда имеет единственную отсылку b, то на (k+1)-ом шаге выполняется команда с номером b;

2) если эта команда имеет две отсылки b1 и b2, то на (k + 1)-ом шаге выполняется одна из двух команд - с номером b1 или с номером b2;

3) если же выполняющаяся на k-ом шаге команда вовсе не имеет отсылки, то на (k+1) - ом шаге и на всех последующих шагах не выполняется никакая команда – машина останавливается.

Возможные случаи останова машины Поста:

1) в ходе выполнения программы машина дойдет до выполнения невыполнимой команды; выполнение программы прекращается, машина останавливается - происходит безрезультатная остановка.

2) в ходе выполнения программы машина дойдет до выполнения команды остановки; программа в этом случае считается выполненной, машина останавливается - происходит результативная остановка.

3) в ходе выполнения программы машина не дойдет до выполнения ни одной из команд, указанных в первых двух вариантах; выполнение программы при этом никогда не прекращается, машина никогда не останавливается - процесс работы машины происходит бесконечно.

Ход работы.

Задание 1. Исследуйте программу для машины Поста. В тетрадь запишите результаты работы программы.

Варианты заданий:

Задача №1

Даны два массива меток, которые находятся на некотором расстоянии друг от друга. Требуется соединить их в один массив. Каретка находится над крайней левой меткой первого массива.

Решение:
1 удалить 2
2 вправо 3
3 ? 4,2
4 метка 5
5 вправо 6
6 ? 8,7
7 стоп 7
8 влево 9
9 ? 10,8
10 вправо 1

Задача №2

Нахождение суммы любого количества массивов, которые отделены друг от друга одной ячейкой. Каретка находится над крайней левой меткой первого массива.

Решение:
1 удалить 2
2 вправо 3
3 ? 4,2
4 метка 5
5 вправо 6
6 ? 10,7
7 влево 8
8 ? 9,7
9 вправо 1
10 стоп 10

Задача №3

Дан массив меток. Проверить, делится ли он нацело на 3. Если да, то слева от него, через одну пустую ячейку поставить метку; если нет, то ничего не делать. Каретка располагается над первой пустой ячейкой, примыкающей к массиву слева.

Решение:
1 вправо 2
2 ? 3,4
3 стоп 3
4 вправо 5
5 ? 3,6
6 вправо 7
7 ? 8,1
8 вправо 9
9 метка 3

Задача №4

Дано несколько массивов меток. Удалить четные массивы. Каретка находится где-то над первым массивом.

Решение:
1 вправо 2
2 ? 3,1
3 вправо 4
4 вправо 5
5 вправо 6
6 ? 14,7
7 удалить 8
8 вправо 9
9 ? 10,7
10 вправо 11
11 вправо 12
12 вправо 13
13 ? 14,1
14 стоп 14

Задача №5

Дано некоторое число (в виде меток). Найти остаток от деления его на 3. Каретка располагается над первой пустой ячейкой, примыкающей к массиву меток справа.

Решение:
1 влево 2
2 ? 1,3
3 влево 4
4 ? 5,6
5 стоп 5
6 влево 7
7 ? 5,8
8 влево 9
9 ? 5,10
10 вправо 11
11 удалить 12
12 вправо 13
13 удалить 14
14 вправо 15
15 удалить 1

Задача №6

Удвоить данный массив справа от него, через ячейку, и затем стереть исходный. Каретка находится над крайней левой меткой.

Решение:
1 влево 2
2 ? 3,1
3 вправо 4
4 удалить 5
5 вправо 6
6 ? 7,5
7 вправо 8
8 ? 9,7
9 метка 10
10 вправо 11
11 метка 12
12 влево 13
13 ? 14,12
14 влево 15
15 ? 16,1
16 стоп 16

Задача №7

Даны два целых положительных числа. Найти их разность по модулю.

Решение:

1 вправо 2
2 ? 3,1
3 влево 4
4 удалить 5
5 влево 6
6 ? 14,7
7 вправо 8
8 ? 7,9
9 удалить 10
10 вправо 11
11 ? 17,12
12 влево 13
13 ? 12,4
14 вправо 15
15 ? 14,16
16 удалить 17
17 стоп 17

Задача №8

Дано несколько массивов. Определить их количество. Каретка находится над крайней левой меткой первого массива.

Решение:
1 влево 2
2 влево 3
3 метка 4
4 вправо 5
5 вправо 6
6 ? 7,5
7 метка 8
8 вправо 9
9 ? 18,10
10 влево 11
11 ? 12,10
12 влево 13
13 ? 14,12
14 метка 15
15 вправо16
16 ? 17,15
17 вправо 6
18 влево 15
19 удалить 20
20 влево 21
21 ? 22,19
22 стоп 22

Задача №9

Найти массив и встать на его начало. Каретка располагается в любом месте, но не над массивом.

Решение:

1 влево 2
2 ? 3,2
3 вправо 4
4 вправо 5
5 ? 6,23
6 влево 7
7 метка 8
8 влево 9
9 ? 10,8
10 влево 11
11 ? 12,20
12 вправо 13
13 метка 14
14 вправо 15
15 ? 16,14
16 вправо 17
17 ? 18,23
18 влево 19
19 метка 8
20 влево 21
21 ? 22,20
22 вправо 23
23 стоп 23

Задача №10

Дан массив из 2N-1 меток. Найти и удалить среднюю. Каретка над второй меткой, если считать справа.

Решение:
1 влево 2
2 ? 3,1
3 вправо 4
4 удалить 5
5 вправо 6
6 ? 7,5
7 влево 8
8 удалить 9
9 влево 10
10 ? 11,9
11 метка 12
12 вправо 13
13 удалить 14
14 вправо 15
15 ? 22,16
16 влево 17
17 вправо 18
18 ? 19,17
19 метка 20
20 влево 21
21 удалить 9
22 метка 23
23 стоп 23

Задача №11

Дано N массивов меток. После последнего массива на расстоянии более трёх пустых ячеек находится одна метка. Массивы разделены тремя пустыми ячейками. Количество меток в массиве =2. Если количество меток в массиве кратно трём, то стереть метки в этом массиве через одну, в противном случае стереть весь массив. Каретка находится над крайней левой меткой первого массива.

Решение:
1 вправо 2
2 ? 7,3
3 вправо 4
4 ? 7,5
5 вправо 6
6 ? 13,1
7 влево 8
8 ? 9,7
9 вправо 10
10 удалить 11
11 вправо 12
12 ? 19,10
13 влево 14
14 ? 15,13
15 вправо 28
16 удалить 17
17 вправо 18
18 вправо19
19 ? 20,16
20 вправо 21
21 ? 20,22
22 вправо 23
23 ? 25,24
24 влево 1
25 влево 26
26 удалить 27
27 стоп 27
28 вправо 16

Задача №12

Дан массив меток. Каретка располагается где-то над массивом, но не над крайними метками. Стереть все метки, кроме крайних, и поставить каретку в исходное положение.

Решение:
1 удалить 2
2 влево 3
3 ? 4,2
4 вправо 5
5 вправо 6
6 вправо 7
7 ? 13,8
8 влево 9
9 ? 31,10
10 удалить 11
11 вправо 12
12 вправо 13
13 ? 14,8
14 влево 15
15 удалить 16
16 вправо 17
17 метка 18
18 вправо19
19 вправо 20
20 ? 26,21
21 влево 22
22 удалить 23
23 вправо 24
24 вправо 25
25 ? 26,20
26 влево 27
27 влево 28
28 ? 27,30
29 удалить 30
30 удалить 31
31 стоп 31

Задача №13

Составить программу нахождения разности двух целых неотрицательных чисел a и b. Если a меньше b, то перед разностью через одну пустую ячейку поставить метку. Каретка находится над крайней левой меткой левого числа.

Решение:
1 вправо 2
2 ? 18,3
3 влево 4
4 удалить 5
5 вправо 6
6 ? 7,5
7 вправо 8
8 ? 7,9
9 вправо 10
10 ? 29,11
11 влево 12
12 удалить 13
13 влево 14
14 ? 13,15
15 влево 16
16 ? 17,15
17 вправо 1
18 влево19
19 удалить 20
20 вправо 21
21 ? 20,22
22 удалить 23
23 вправо 24
24 ? 28,25
25 влево 26
26 влево 27
27 метка 28
28 стоп 28
29 влево 30
30 удалить 31
31 стоп 31

Задача №14

Произвести умножение двух чисел. Каретка располагается над пустой ячейкой, которая разделяет данные массивы.

Решение:
1 вправо 2
2 ? 1,3
3 влево 4
4 ? 5,14
5 вправо 6
6 удалить 7
7 вправо 8
8 ? 7,9
9 удалить 10
10 вправо 11
11 ? 12,10
12 метка 13
13 стоп 13
14 вправо 15
15 удалить 16
16 вправо 17
17 ? 16,18
18 удалить 19
19 вправо 20
20 ? 21,19
21 вправо 22
22 ? 23,21
23 метка 24
24 влево 25
25 ? 26,24

26 влево 27
27 ? 28,26
28 метка 29
29 вправо 30
30 ? 31,18
31 влево 32
32 ? 1,31

Задача №15

Дан массив из N Меток. Сделать из него массив, в котором будет 2N+1 меток. Если полученный массив делится нацело на 3, то справа от него, через одну пустую ячейку, поставить две метки; если нет - то три метки. Каретка находится над крайней левой меткой.

Решение:
1 удалить 2
2 вправо 3
3 ? 4,2
4 вправо 5
5 ? 6,4
6 метка 7
7 вправо 8
8 метка 9
9 влево 10
10 ? 11,9
11 влево 12
12 ? 13,15
13 вправо 14
14 метка 18
15 влево 16
16 ? 17,15
17 вправо 1
18 вправо 19
19 вправо 20
20 вправо 21
21 ? 22,18
22 влево 23
23 ? 24,37
24 влево 25
25 ? 38,26
26 вправо 38
27 метка 28
28 вправо 29
29 метка 30
30 вправо 31
31 метка 36
32 вправо 33
33 метка 34
34 вправо 35
35 метка 36
36 стоп 36
37 вправо 32
38 вправо 27

Решение:

Контрольные вопросы:

1. Объясните устройство машины Поста.

2. Перечислите и объясните команды машины Поста.

3. Объясните порядок работы машины Поста.

4. Что представляет собой таблица машины Поста?

5. Какие возможны ошибки в работе машины Поста?

6. Что предусматривает анализ алгоритма?

7. Назовите способы анализа алгоритма. Какой способ предпочтительнее?

8. Приведите примеры и способы проверки правильности алгоритма.

9. Как классифицируют алгоритмы по временной сложности

10. Какие существуют формы представления алгоритма?

__________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

_______________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

Инструкционная карта 16.

на выполнение практического занятия по дисциплине
ЕН.02. Элементы математической логики
для обучающихся специальности 09.02.02 Компьютерные сети

Тема: Машина Тьюринга.

Цели занятия: Научиться решать задачи с использованием машины Тьюринга.

Норма времени: 2 часа.

Оснащение рабочего места: инструкционные карты, конспект.

Литература:

В.Н. Пильщиков, В.Г. Абрамов, А.А. Вылиток, И.В. Горячая. Машина Тьюринга и алгоритмы Маркова. Решение задач. М.: МГУ, 2006

Основные умения и навыки, которыми должны овладеть обучающиеся в процессе изучения этой темы:

• знать принцип работы машины Тьюринга;

• уметь составлять алгоритмы для решения поставленной задачи;

• уметь применять команды машины Тьюринга

Задания для практического занятия и инструктаж по их выполнению

1. Записать теоретические сведения в тетрадь.

2. Разобрать примеры.

3. Выполнить практические задания по данной теме.

Теоретические сведения

1. Устройство машины Тьюринга. Машина Тьюринга - абстрактная машина. Машина Тьюринга состоит из информационной ленты, каретки (считывающая и записывающая головка), лентопротяжного механизма и операционного исполнительного устройства. Лента ограничена (т.е. жестко закреплена) слева и бесконечна справа. Лента разделена на секции одинакового размера. В каждую секцию ленты заносятся символы внешнего алфавита машины Тьюринга A = {a0, a1,... aN}, где а0, как правило, пробел. Каретка может передвигаться вдоль ленты влево и вправо. Когда она неподвижна, она стоит против ровно одной секции ленты; говорят, что каретка обозревает эту секцию. А такая секция называется текущей или обозреваемой. За единицу времени, которая называется шагом, каретка может сдвинуться на одну секцию влево или вправо. Кроме того, каретка может также распознать содержимое обозреваемой секции, может заносить символ внешнего алфавита в текущую секцию и может стирать содержимое текущей ячейки. Операционное исполнительное устройство может находиться в одном из дискретных состояний: Q = {q0, q1,...qM} - внутренний алфавит машины Тьюринга или алфавит внутренних состояний.

2. Команды и порядок работы машины Тьюринга.

Порядок работы машины Тьюринга обычно задается в виде таблицы: в каждый столбец верхней строчки заносятся символы внутреннего алфавита, в каждую строчку первого столбца - символы внешнего алфавита. В ячейках на пересечении других столбцов и строчек помещаются команды. Если на пересечении какой-либо строки и какого-либо столбца мы получим пустую клетку, то это означает, что в данном внутреннем состоянии данный символ встретиться не может.

A/Q	q0	q1	…	qn
a0
a1
…
ai	aKq
…
am

Формат команды: aKq, где:

a - новое содержание текущей ячейки (новый символ внешнего алфавита, который заносится в текущую ячейку);

K - команда лентопротяжного механизма машины Тьюринга (влево, вправо, стоп);

q - новое внутренне состояние машины Тьюринга.

Работа машины Тьюринга состоит в том, что каретка передвигается вдоль ленты и печатает или стирает символы. Чтобы машина Тьюринга работала, первым делом надо задать внешний алфавит, т.е. указать какие символы в него входят. Затем надо задать некоторую программу и некоторое состояние машины (т.е. нужно как-то расставить символы внешнего алфавита по секциям ленты, в частности, можно все секции оставить пустыми, и поставить каретку против одной из секций). Работа машины на основании заданной программы происходит следующим образом. Предположим, что в данный момент времени машина Тьюринга находится во внутреннем состоянии q[i], а в обозреваемой кареткой ячейке ленты находится символ a[j]. Тогда машина переходит к выполнению команды aKq в ячейке, на пересечении столбца q[i] и строчки a[j]:

1) в текущую секцию ленты заносится новый символ a.

2) происходит сдвиг каретки влево (K = влево), или сдвиг каретки вправо (K = вправо), или происходит остановка машины (K = стоп).

3) машины переходит в новое внутреннее состояние q.

3. Возможные случаи останова машины Тьюринга:

1) в ходе выполнения программы машина дойдет до выполнения команды остановки; программа в этом случае считается выполненной, машина останавливается - происходит результативная остановка.

2) машина никогда не останавливается, происходит зацикливание.

Ход работы.

Задание 1. Выполнить команды для машины Тьюринга на предложенных исходных данных. Записать полученную последовательность символов. Определить алгоритм выполнения.

Задача №1

Заменить в двоичной записи числа все нули на единицы и все единицы на нули. Каретка стоит слева от числа.

Задача №2

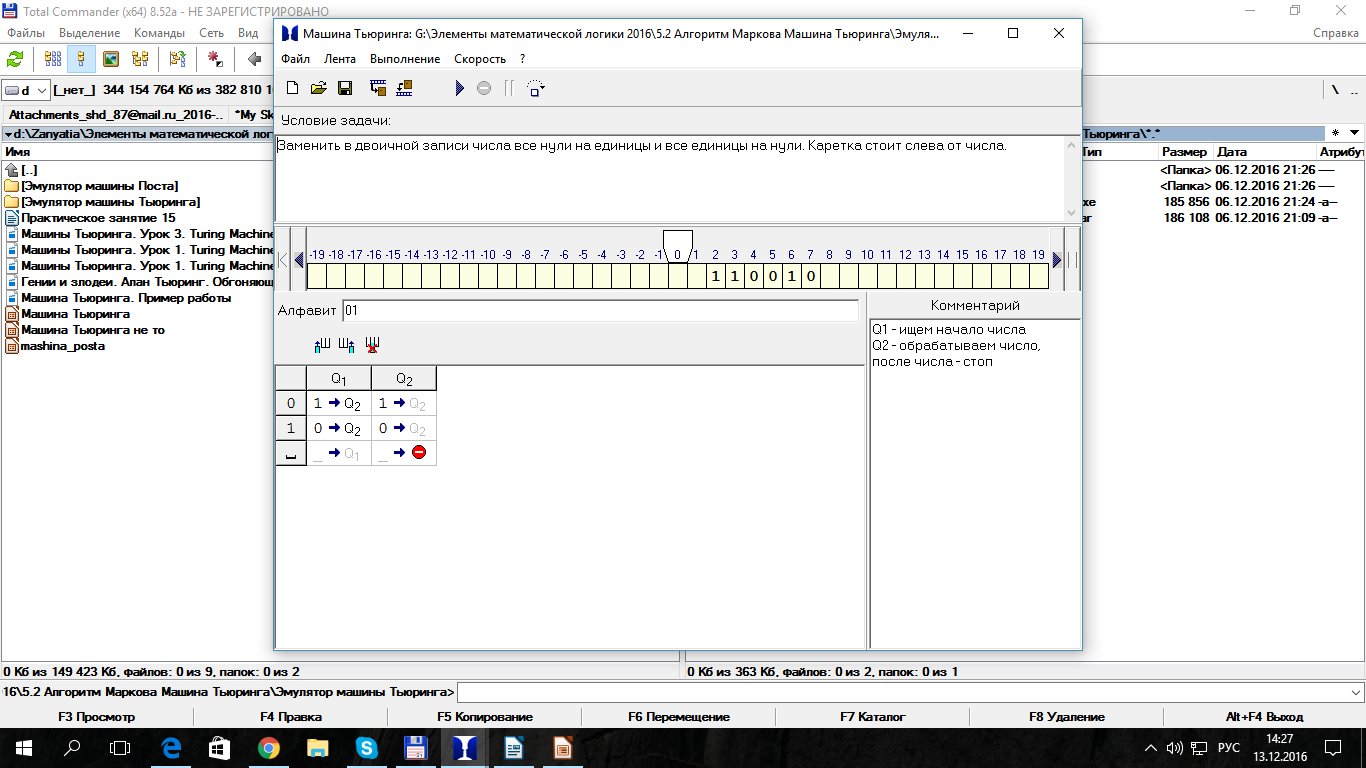
Сортировка цепочки из букв "а" и "б" так, чтобы сначала стоял все буквы "а", а потом - все буквы "б". Каретка стоит над строкой.

Задача №3

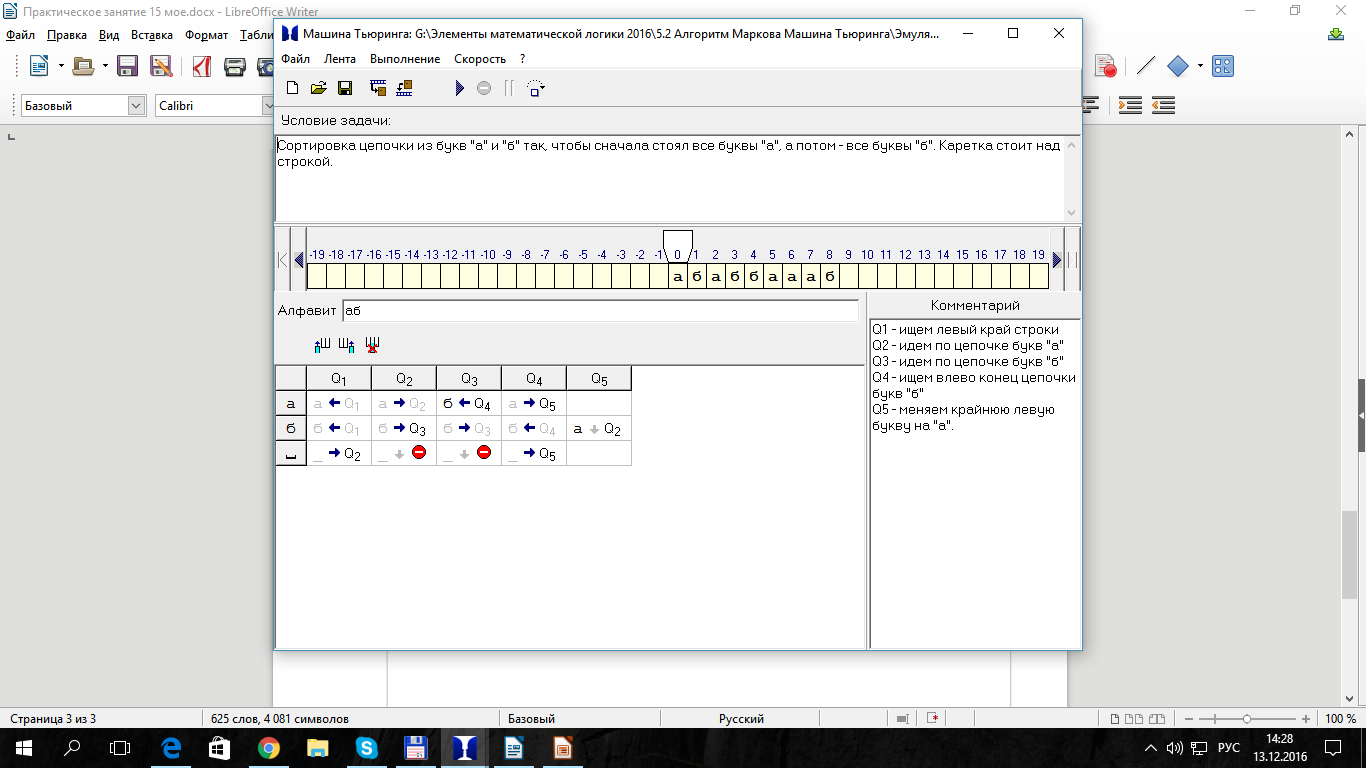
Сортировка цепочки из букв "а" и "б" так, чтобы сначала стоял все буквы "а", а потом - все буквы "б". Каретка стоит над первым символом строки.

Задача №4

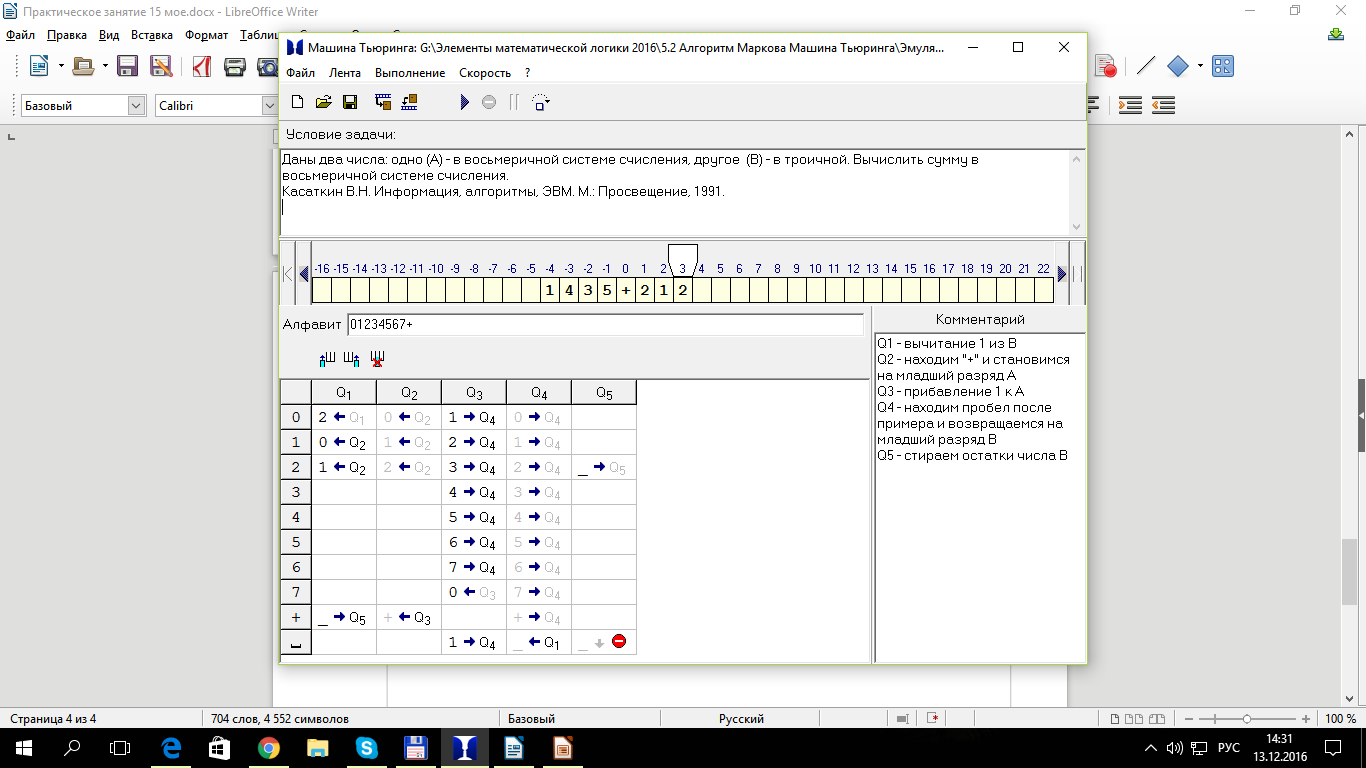
Даны два числа: одно (A) - в восьмеричной системе счисления, другое (B) - в троичной. Вычислить сумму в восьмеричной системе счисления.

Задача №5

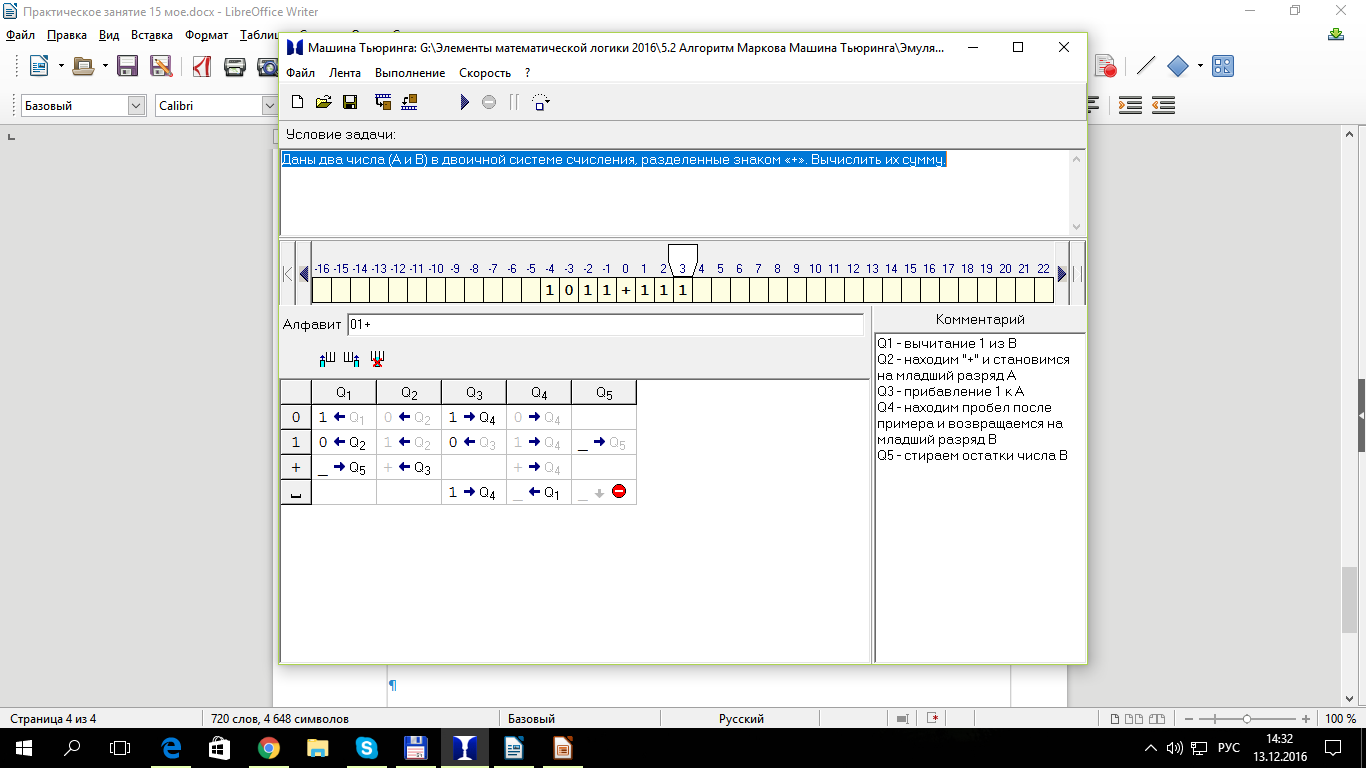
Даны два числа (A и B) в двоичной системе счисления, разделенные знаком «+». Вычислить их сумму.

Задача №6

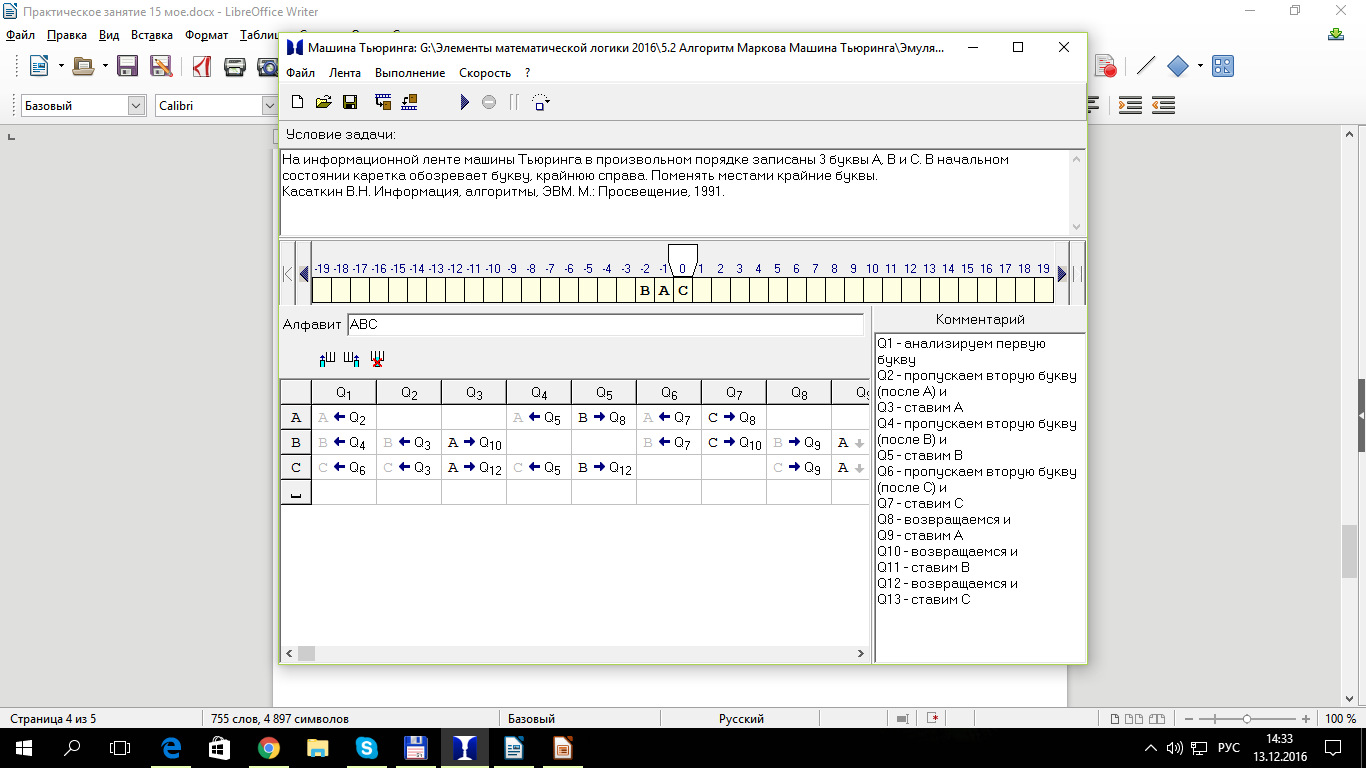
На информационной ленте машины Тьюринга в произвольном порядке записаны 3 буквы A, B и C. В начальном состоянии каретка обозревает букву, крайнюю справа. Поменять местами крайние буквы.

Задача №7

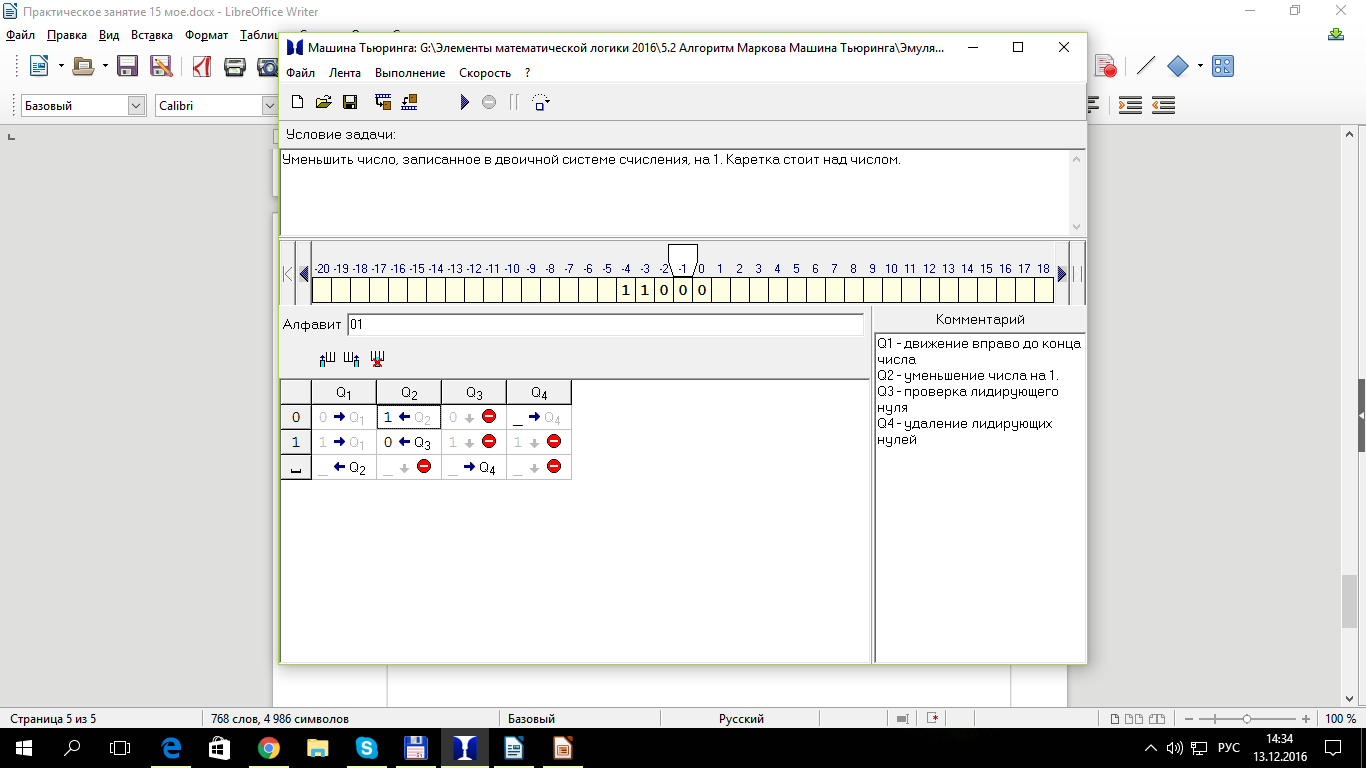
Уменьшить число, записанное в двоичной системе счисления, на 1. Каретка стоит над числом.

Задача №8

Удалить все вхождения символа 'a'. Каретка находится на первом символе слова.

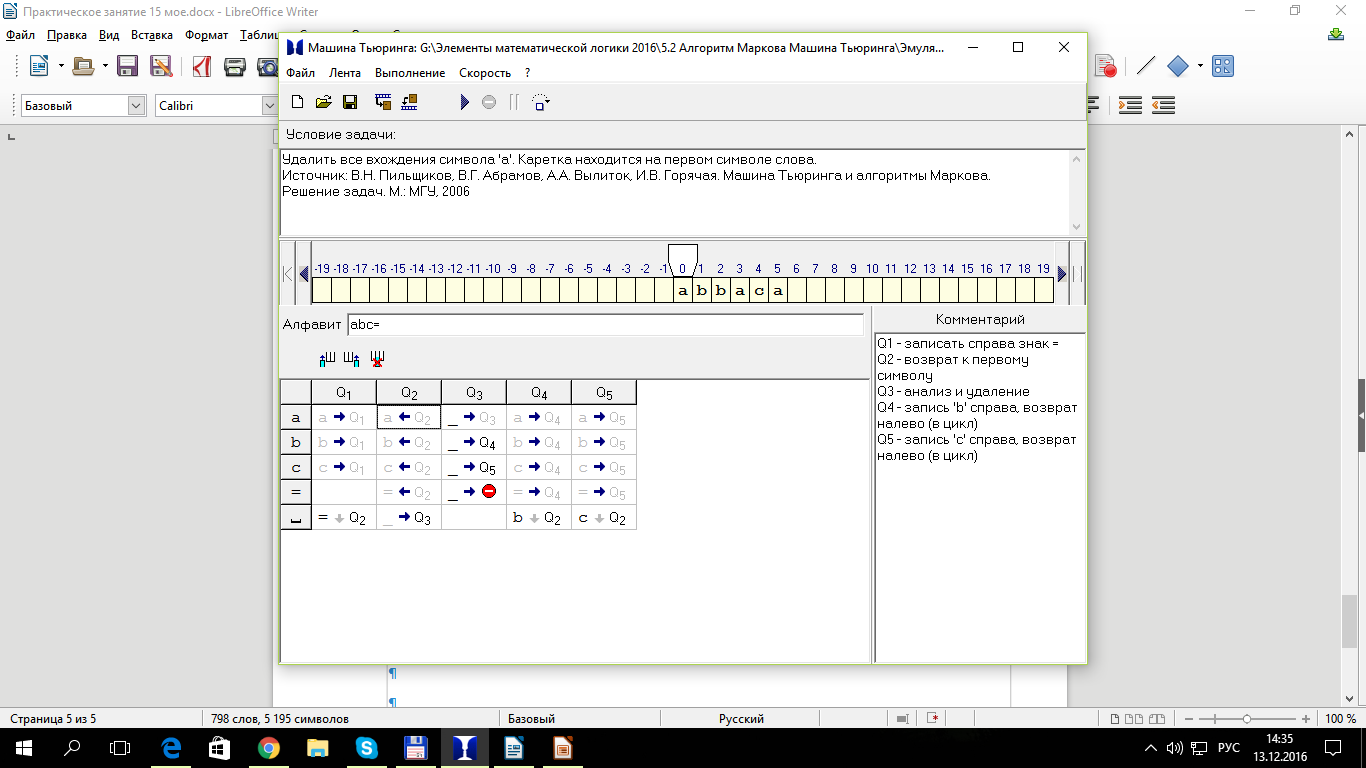
Задача №9

Удалить из слова второй символ, если он есть. Каретка находится в начале слова.

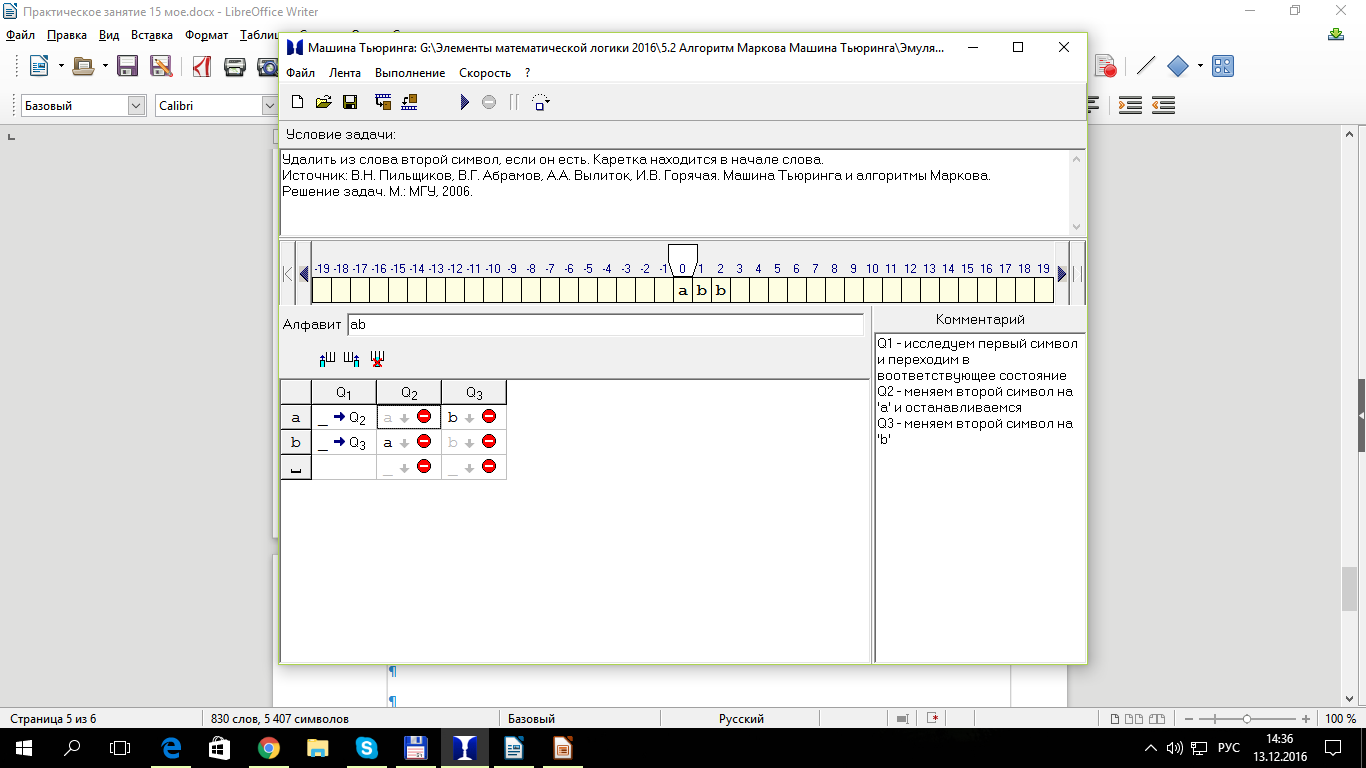
Задача №10

Машина выдает результат 1, если число, записанное в унарной системе четное, и стирает все метки, если число нечетное. Каретка расположена над самой левой отметкой.

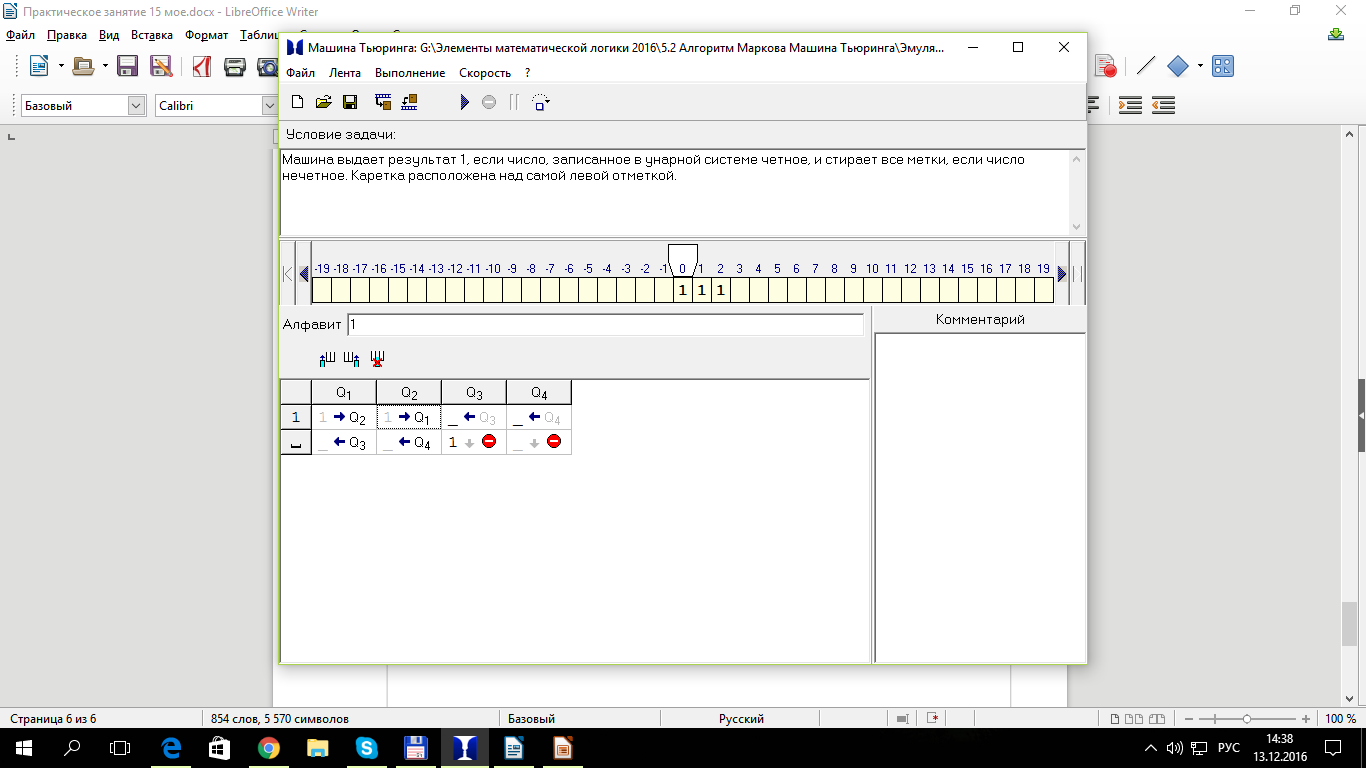
Задача №11

Удвоить слово, поставив между ним и его копией знак =. Каретка находится на первом символе слова.

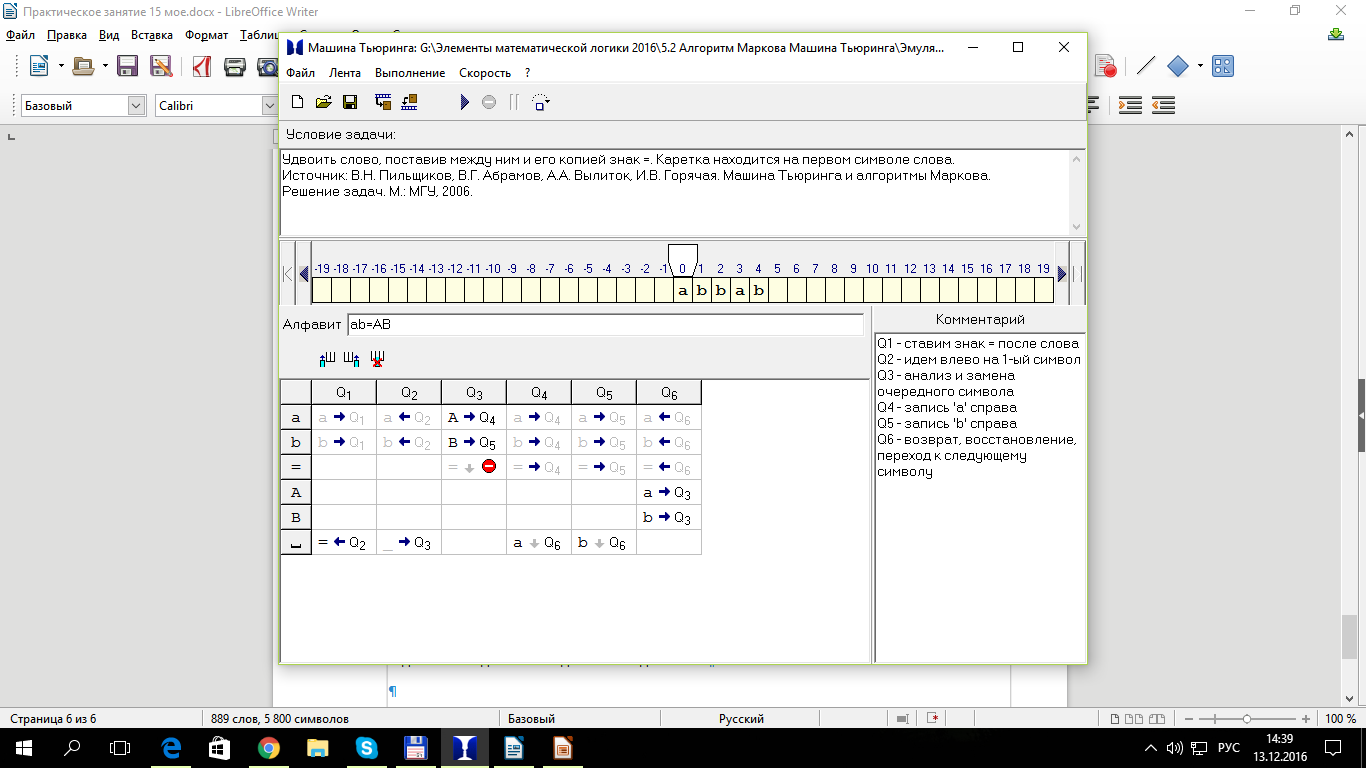
Задача №12

Если первый и последний символы (непустого) слова одинаковы, тогда это слово не менять, а иначе заменить его на пустое слово. Каретка стоит на первом символе слова.

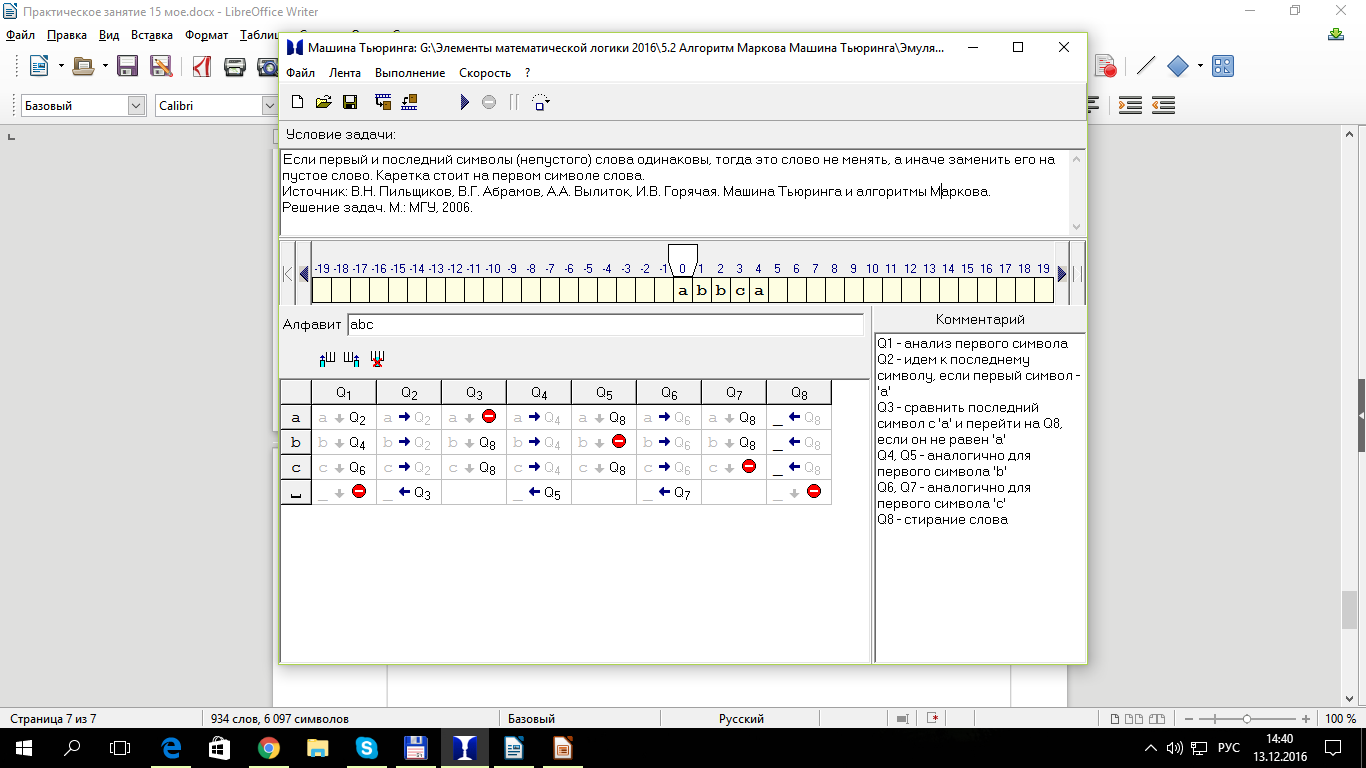
Задача №13

Увеличить число, записанное в двоичной системе счисления, на 1. Каретка стоит над числом.

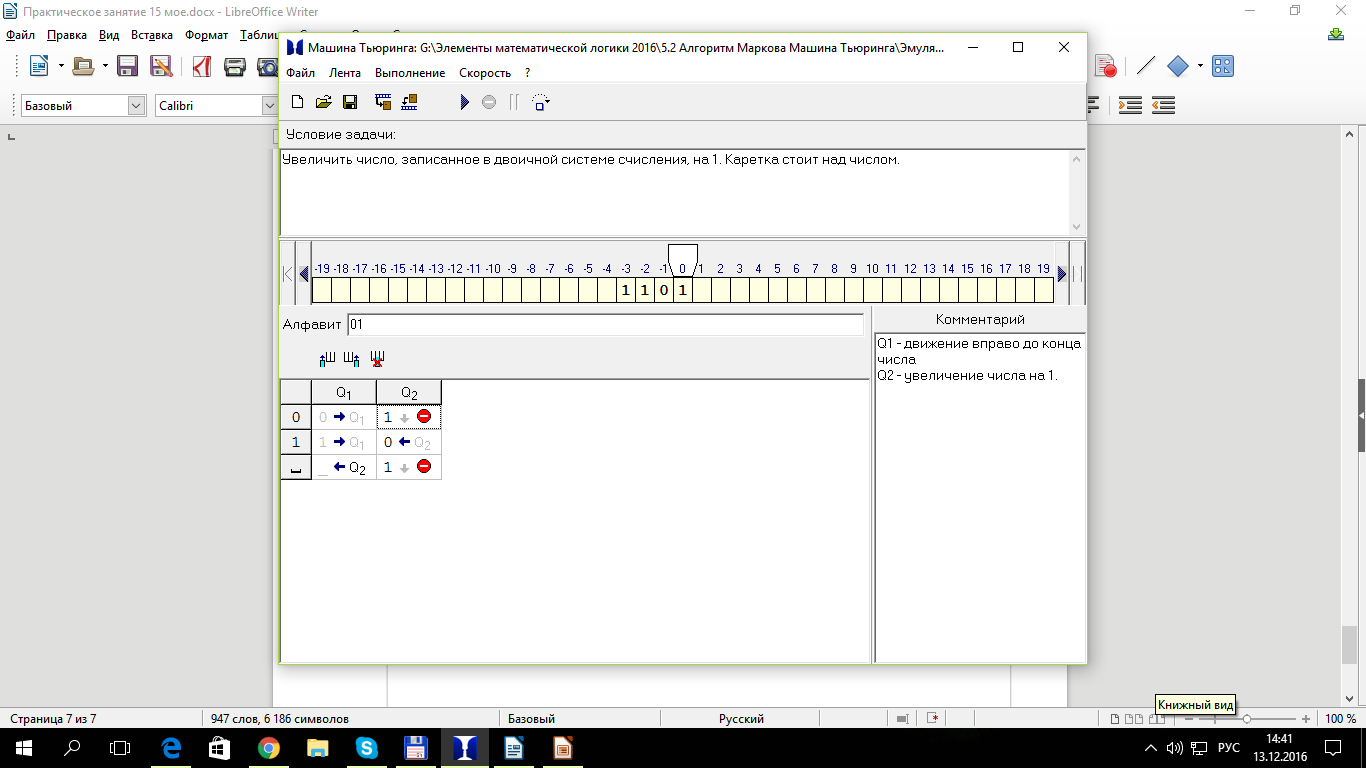
Задача №14

Увеличить число, записанное в троичной системе счисления, на 1. Каретка стоит справа от числа.

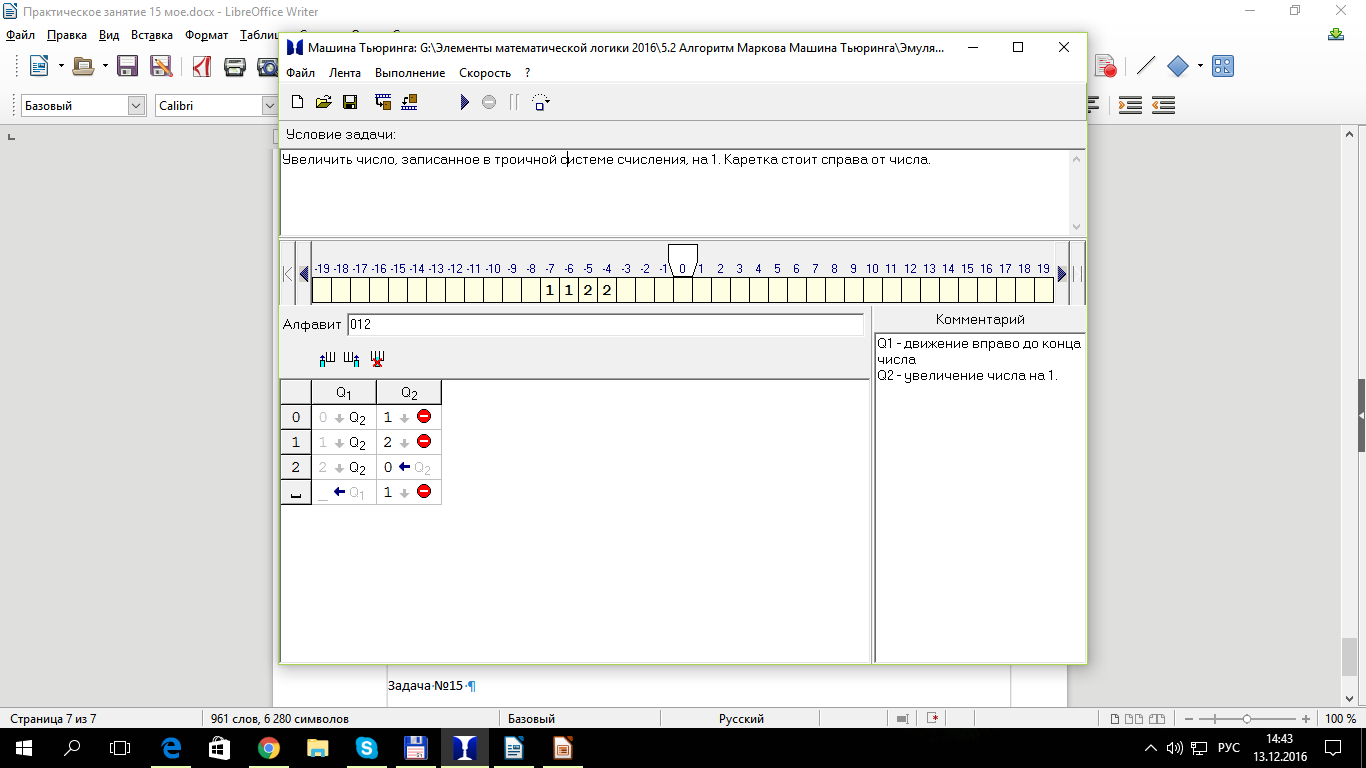
Задача №15

Вставить символ 'a' за первым вхождением символа 'c', если он есть. Каретка находится на первом символе слова.

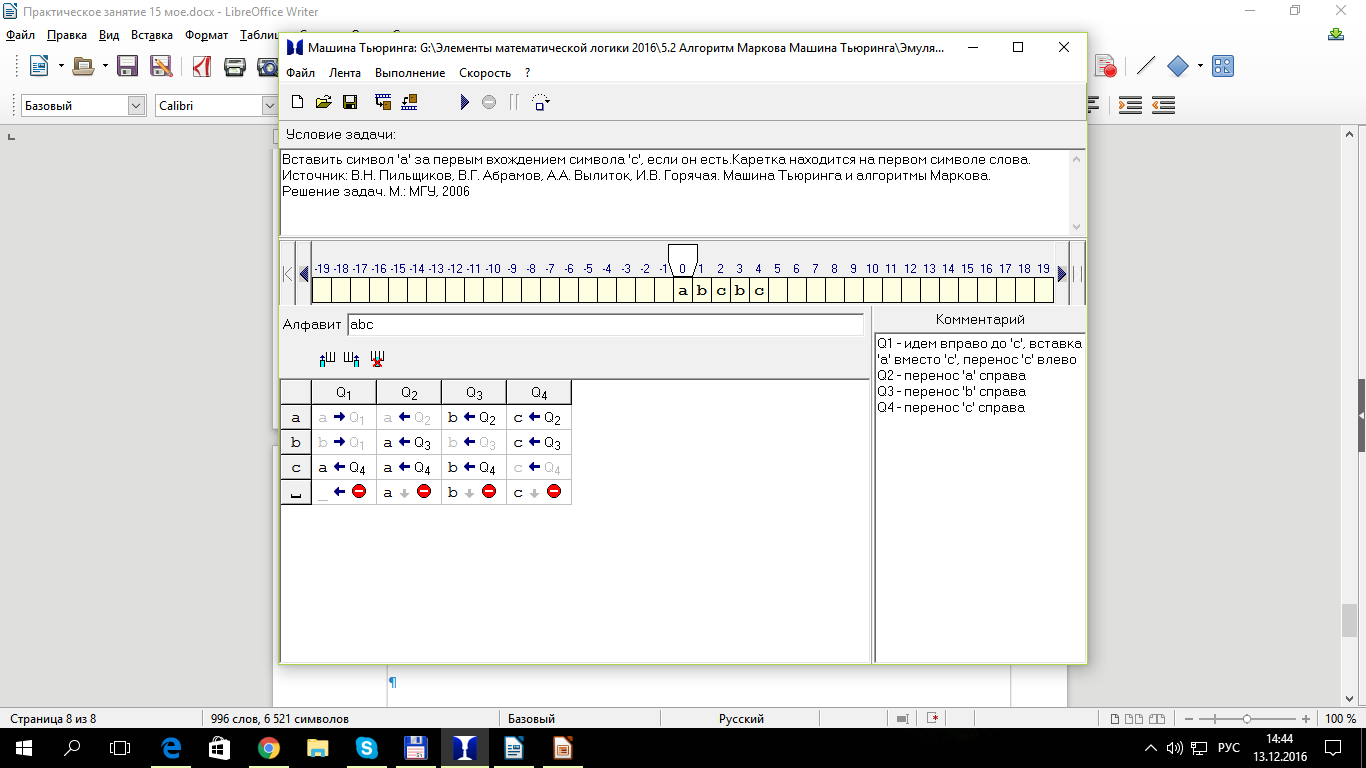
Контрольные вопросы:

1. Объясните устройство машины Тьюринга.

2. Перечислите и объясните команды машины Тьюринга.

3. Объясните порядок работы машины Тьюринга.

4. Что представляет собой таблица машины Тьюринга?

5. Какие возможны ошибки в работе машины Тьюринга?

6. Что предусматривает анализ алгоритма?

7. Назовите способы анализа алгоритма. Какой способ предпочтительнее?

8. Приведите примеры и способы проверки правильности алгоритма.

9. Как классифицируют алгоритмы по временной сложности

10. Какие существуют формы представления алгоритма?

_________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

ВЫВОДЫ

«Методическая разработка: «Рабочая тетрадь по дисциплине ЕН.02 Элементы математической логики для обучающихся специальности 09.02.02 Компьютерные сети», разработанная преподавателем общетехнических и специальных дисциплин Туловой Ю.Ф., предназначена для обучающихся, 2 курса, специальности 09.02.02 Компьютерные сети.

Цель методической разработки – систематизировать материалы для выполнения практических занятий обучающимися специальности 09.02.02 Компьютерные сети по дисциплине ЕН.02. Элементы математической логики.

В методической разработке освещаются вопросы, связанные с выполнением практических занятий обучающимися по программам среднего профессионального образования.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Канцедал С.А., Дискретная математика М.: Инфра-М, 2011

2. Спирин М.С., Спирина П.А. Дискретная математика. – М.: Издательский центр «Академия», 2014.

Интернет-ресурсы:

1. Дискретная математика: электронный учебник. Форма доступа: http://lvf2004.com/dop_t3.html

2. Бабичева, И.В. Дискретная математика. Контролирующие материалы к тестированию [Электронный ресурс] : учебное пособие / И.В. Бабичева. — Электрон. дан. — Санкт-Петербург : Лань, 2013. — 160 с. — Режим доступа: https://e.lanbook.com/book/30193. — Загл. с экрана.

3. Русская логика: электронные книги, статьи. Форма доступа: http://logicrus.ru

4. Российская государственная библиотека. Форма доступа: http://www.rsl.ru

5. Дискретная математика: каталог электронных книг. Форма доступа: http://www.ph4s.ru/book_pc_diskretka.html