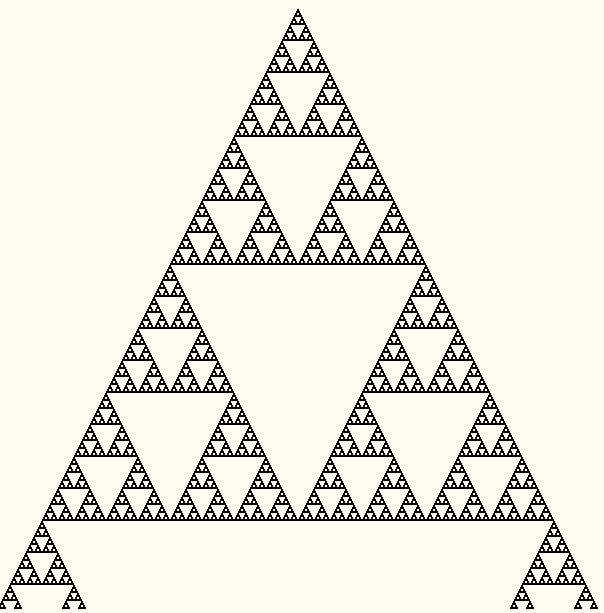Муниципальное Казённое Общеобразовательное Учреждение
Средняя Общеобразовательная Школа с. Лохово
Школьная НПК
Секция математика
«Треугольник Паскаля»
Выполнил: Абраменко Сергей
7 класс
Проверила: Шаянова С.Б.
Учитель математики
С. Лохово ул. Школьная -25
2015г.
Содержание:
Треугольник Паскаля. Определение - с.2
Задачи Исследования -с.2
Цель исследования -с.3
Гипотеза -с.3
Ход исследования -с.3
Свойства треугольника -с.5-6
Применение треугольника - с.7-8
Список литературы -с.9
ТРЕУГОЛЬНИК ПАСКАЛЯ
—это бесконечная числовая таблица
"треугольной формы", в которой по боковым
сторонам стоят единицы и всякое число,
кроме этих боковых единиц равно
сумме двух вышестоящих чисел.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
. . . . . . . . . . . . . . .
ЗАДАЧИ ИССЛЕДОВАНИЯ
1.Выявить свойства чисел, входящих в состав треугольника Паскаля
2. Определить применение свойств чисел треугольника Паскаля
3. Сформулировать вывод и итоги исследования
ЦЕЛЬ ИССЛЕДОВАНИЯ
Привести достаточное количество
примеров свойств чисел треугольника
Паскаля и примеров применения
треугольника для доказательства
гипотезы.
ГИПОТЕЗА
Если числа
треугольника Паскаля
обладают особыми
свойствами, то его
можно считать
удивительный.
ХОД ИССЛЕДОВАНИЯ
Выяснить, что высказывали о треугольнике Паскаля ученые или математики.
Собрать первоначальные сведения о треугольнике в энциклопедической и учебно-научной литературе.
"Треугольник Паскаля так прост,что выписать его сможет даже
десятилетний ребенок.В тоже время он таит в себенеисчерпаемые сокровища и связывает
воедино различные аспекты математики,не имеющие на первый взгляд между
собой ничего общего.Столь необычные свойства позволяют
считать треугольник Паскаля одной изнаиболее изящных схемво всей математике".
Мартин Гарднер
"Математические новеллы"
1974
ЭНЦИКЛОПЕДИЯ ЮНОГО МАТЕМАТИКА
ТРЕУГОЛЬНИК ПАСКАЛЯ
—это бесконечная числовая таблица
"треугольной формы", в которой по боковым
сторонам стоят единицы и всякое число,
кроме этих боковых единиц.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
. . . . . . . . . . . . . . .
ХОД ИССЛЕДОВАНИЯ
Выявить самые «Удивительные» свойства чисел треугольника
Выяснить, какими еще свойствами обладает треугольник Паскаля
САМЫЕ УДИВИТЕЛЬНЫЕ СВОЙСТВА
Каждое число равно сумме двух расположенных
над ним чисел.
Треугольник можно продолжать неограниченно.
ЭНЦИКЛОПЕДИЯ ЮНОГО МАТЕМАТИКА
Свойство 1: Каждое число А в таблице равно сумме чисел предшествующего вертикального ряда, начиная с самого верхнего вплоть до стоящего непосредственно левее числа А.
Свойство 2: Каждое число в таблице, будучи уменьшенным на единицу, равно сумме всех чисел, заполняющих прямоугольник, ограниченный теми вертикальными и горизонтальными рядами, на пересечении которых стоит число А (сами эти ряды в рассматриваемый прямоугольник не включаются).
СВОЙСТВА ТРЕУГОЛЬНИКА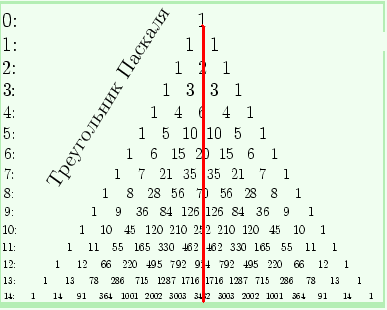
1.Он обладает симметрией
относительно вертикальной
оси, проходящей через его
вершину.
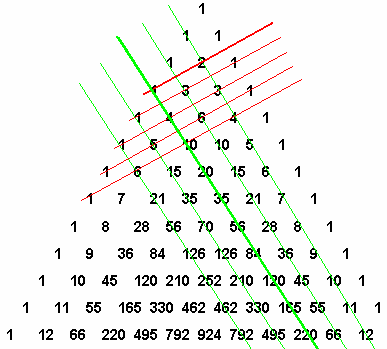
2. Вдоль прямых,
параллельных сторонам 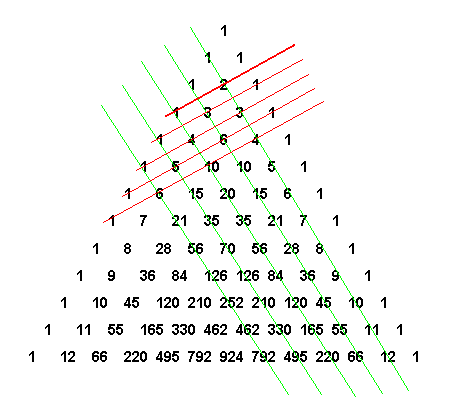
треугольника (на рисунке
отмечены зелеными линиями)
выстроены треугольные
числа и их обобщения на
случай пространств всех
размерностей.
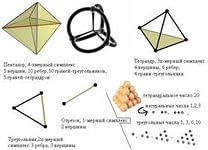
3.Треугольные числа показывают, сколько касающихся кружков можно расположить в виде треугольника
Классический пример начальная расстановка шаров в бильярде.

4.Следующая зеленая
линия покажет нам
тетраэдральные числа
- один шар мы можем
положить на три –
итого четыре, под три
подложим шесть
далее.
ЗАМЕЧАНИЕ
В нашем мире такое невозможно, только в
четырехмерном, виртуальном. И тем более
пятимерный тетраэдр, о котором
свидетельствует
следующая зеленая линия, он может существовать только в рассуждениях
топологов… или фантастов.
Хотя… Попробуйте с вишнями или яблоками одинакового размера, только не пытайтесь выйти с ними в четвертое измерение, они могут исчезнуть
НАВЕРНОЕ ВЫ ХОТИТЕ СПРОСИТЬ…
А о чем же говорит нам самая верхняя зеленая линия, на которой расположились числа натурального ряда?
Это тоже треугольные числа, но одномерные, показывающие, сколько шаров можно выложить вдоль линии - сколько есть, столько и выложите. Если уж идти до конца, то самый верхний ряд из единиц - это тоже треугольные числа в нульмерном пространстве - сколько бы шаров мы не взяли - больше одного расположить не сможем, ибо просто негде - нет ни длины, ни ширины, ни высоты.
4.Удивительное свойство треугольника Паскаля
Заменим каждое число в
треугольнике Паскаля точкой. 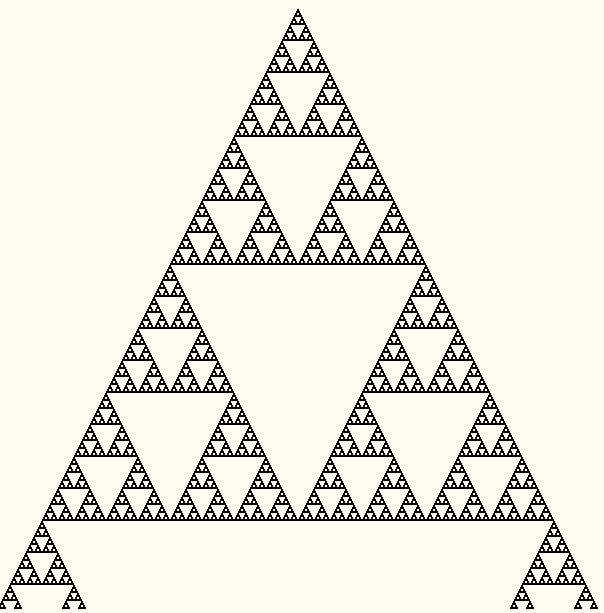
Причем, нечетные точки
выведем контрастным цветом,
а четные - прозрачным, или
цветом фона.
Результат
окажется непредсказуемо-
удивительным: треугольник
Паскаля разобьется на более
мелкие треугольники,
образующие изящный узор.
ХОД ИССЛЕДОВАНИЯ
Изучить возможности применения треугольника Паскаля
Продемонстрировать примеры
ПРИМЕНЕНИЕ
1.Пусть, например, мы хотим 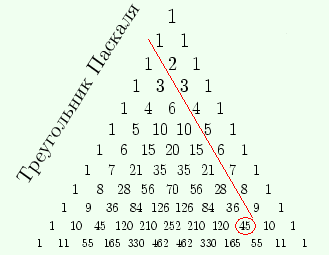
вычислить сумму чисел
натурального ряда от 1 до 9.
"Спустившись" по диагонали
До числа 9, мы увидим слева
снизу от него число 45.
Оно то и дает искомую сумму.
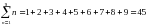
2..Биномиальные коэффициенты естькоэффициэнты разложения многочлена
по степеням x иy

3.Предположим , что некий шейх, следуя законам гостеприимства, решает отдать вам трех из семи своих жен. Сколько различных выборов вы можете сделать среди прекрасных обитательниц гарема? Для ответа на этот волнующий вопрос необходимо лишь найти число, стоящее на пересечении диагонали 3 и строки 7: оно оказывается равным 35.
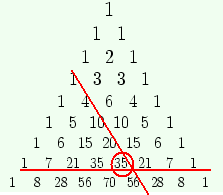
Если, охваченные радостным волнением, вы перепутаете номера диагонали и строки и будете искать число, стоящее на пересечении диагонали 7 со строкой 3, то обнаружите, что они не пересекаются. То есть сам метод не дает вам ошибиться
5.
6.
Формулируем итоги и выводы
ПОДТВЕРЖДЕНИЕ ГИПОТЕЗЫ
ОБЛАДАЯ ТАКИМИ СВОЙСТВАМИ, ТРЕУГОЛЬНИК МОЖЕТ НАЗЫВАТЬСЯ УДИВИТЕЛЬНЫМ.
Вывод:
Треугольник Паскаля используется во многих науках, помогает решать сложные задачи и расширяет кругозор
числа треугольника Паскаля Имеют особые свойства, значит его можно считать удивительным.
Список Литературы
Интернет ресурсы
Учебник Алгебры
Дополнительная Литература
Задачи по планиметрии. Прасолов В. В.
Планиметрия. Пособие для углублённого изучения математики - Бутузов, Кадомцев. 2005
Я познаю мир. Детская энциклопедия. Математика 2002 изд. «Просвещение»
12