Просмотр содержимого документа
«Расчет сложных электрических цепей постоянного тока методом преобразования схем.»
Расчет сложных электрических цепей постоянного тока методом преобразования схем.
Краткие теоретические сведения:
Метод преобразования электрических схем применяют для расчета сложных цепей путем преобразований треугольника сопротивлений в эквивалентную звезду или звезды сопротивлений в эквивалентный треугольник.

Рис. 1.
Контур, состоящий из трех сопротивлений RAB, RВСиRСА, имеющий три узловые точкиА, В и С, образует треугольник сопротивлений (рис. 1. а).
Электрическая цепь, состоящая из трех сопротивлений RA, RBи RС, соединенных в одной узловой точкеО, образует звезду сопротивлений (рис. 1. б).
Расчет некоторых сложных цепей значительно упрощается, если соединение звездой в них заменить соединением треугольником или наоборот.
Преобразование схемы должно производиться так, чтобы при неизменном напряжении между точкамиА, В и С токи IА, IВи IСзвезды и треугольника оставались без изменений.
Треугольник и звезда, удовлетворяющие этому условию, называются эквивалентными.
Для такого преобразования рекомендуется изображать схему цепи без заменяемого треугольника (или звезды), но с обозначенными вершинамиА, В и С и к этим обозначенным вершинам подсоединить эквивалентную звезду (или треугольник).
При замене треугольника эквивалентной звездой сопротивления звезды определяются следующими выражениями:

Таким образом, каждое сопротивление эквивалентной звезды равно отношению произведения двух примыкающих к соответствующей узловой точке сопротивлений треугольника к сумме трех его сопротивлений.
При замене звезды эквивалентным треугольником каждое сопротивление треугольника определяется следующими выражениями:

Каждое сопротивление эквивалентного треугольника равно сумме трех слагаемых: двух примыкающих к соответствующим точкам сопротивлений звезды и отношению произведения этих сопротивлений к третьему сопротивлению звезды.
Пример расчёта:
В исходной схеме (рис. 2. а) преобразовать треугольник сопротивлений R1=10 Ом, R2=30 Ом и R3= 60 Ом в эквивалентную звезду. Выполнить проверку.
Решение
На рис. 34 б представлена расчётная схема с учётом преобразования.
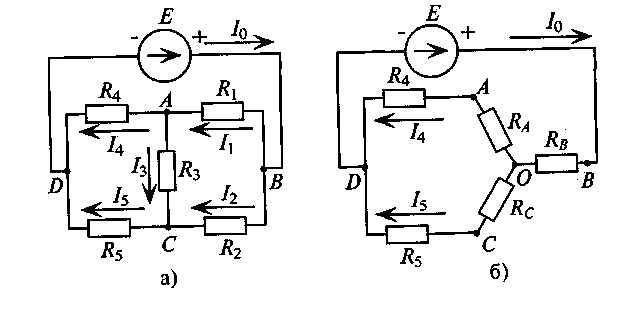
Рис. 34
Определим величины сопротивлений эквивалентной звезды:

Проверка

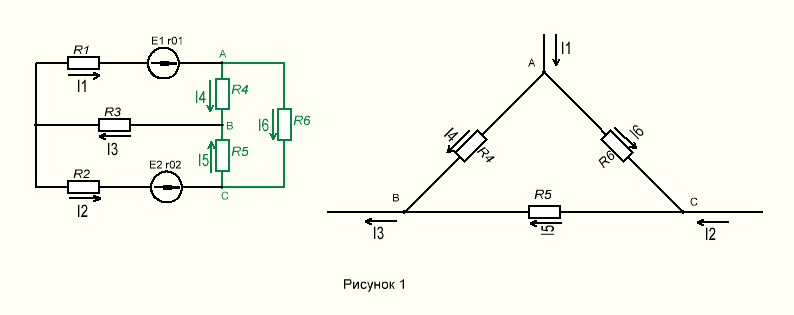
Выполнить задание:Определить токи во всех ветвях цепи при следующих исходных данных согласно варианта по таблице.
| №вар. | E1,В | R01,Ом | E2,В | R02,Ом | R1,Ом | R2,Ом | R3,Ом | R4,Ом | R5,Ом | R6,Ом |
| 1 | 6 | 0.1 | 20 | 0.5 | 1 | 7 | 7 | 9 | 7 | 6 |
| 2 | 8 | 0.2 | 18 | 0.4 | 2 | 1 | 10 | 10 | 8 | 7 |
| 3 | 10 | 0.3 | 16 | 0.3 | 3 | 2 | 1 | 7 | 9 | 8 |
| 4 | 12 | 0.4 | 14 | 0.2 | 4 | 3 | 2 | 1 | 10 | 9 |
| 5 | 14 | 0.5 | 12 | 0.1 | 5 | 4 | 3 | 2 | 1 | 10 |
| 6 | 16 | 0.1 | 10 | 0.5 | 6 | 5 | 4 | 3 | 2 | 1 |
| 7 | 18 | 0.2 | 8 | 0.4 | 7 | 6 | 5 | 4 | 3 | 2 |
| 8 | 20 | 0.3 | 6 | 0.3 | 8 | 8 | 6 | 5 | 4 | 3 |
| 9 | 22 | 0.4 | 4 | 0.2 | 9 | 10 | 8 | 6 | 5 | 4 |
| 10 | 24 | 0.5 | 2 | 0.1 | 10 | 9 | 9 | 8 | 6 | 5 |
Ответить на контрольные вопросы:
1. Чему равно каждое эквивалентное сопротивление треугольника?
2. Чему равно каждое эквивалентное сопротивление звезды?























