Лабораторная работа № 1.
Расчет погрешностей емкости с помощью коэффициента Стьюдента.
Расчет погрешности измерения мощности и сопротивления
Цели занятия:
Общеобразовательная – Умение решать задачи по теме погрешности.
Развивающая - Углубление знаний .
Воспитательная – Проверить сформированность качеств знаний.
Теоретическая часть
Отклонение результата измерения от истинного измеряемой величины называют погрешностью измерения.
Абсолютная погрешность измерения ΔА равна разности между результатом измерения Ах и истинным значением измеренной величины А:
ΔА = Ах – А (1)
Действительная относительная погрешность  представляет собой отношение абсолютной погрешности измерения к действительному значению измеряемой величины, выраженное в процентах:
представляет собой отношение абсолютной погрешности измерения к действительному значению измеряемой величины, выраженное в процентах:
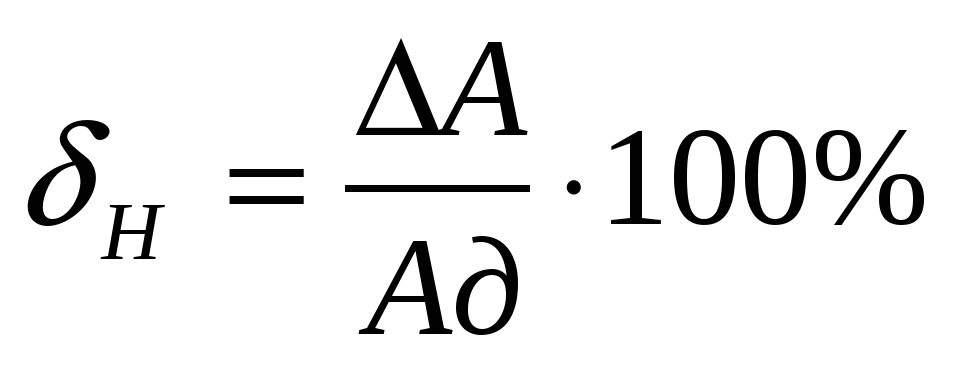 (2)
(2)
Номинальная относительная погрешность, равная отношению абсолютной погрешности к измеренному значению исследуемой величины,
т .е. к показанию прибора
 (3)
(3)
Приведенная относительная погрешность измерения представляет собой отношение абсолютной погрешности измерения к максимальному значению измерительного прибора
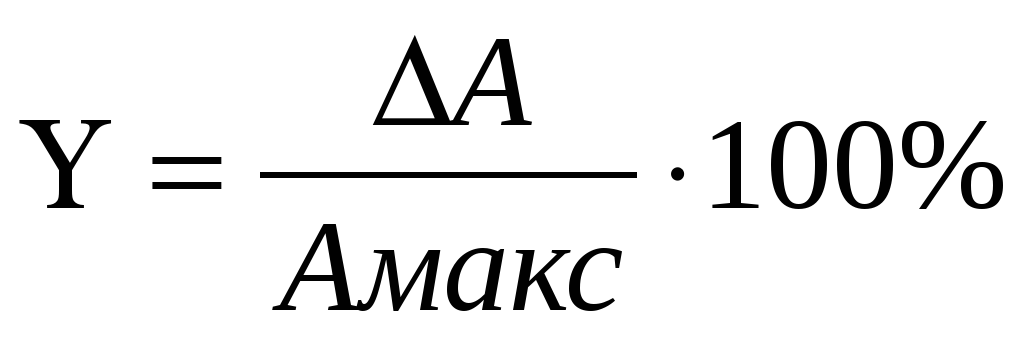 (4)
(4)
Для приборов с двухсторонней шкалой Амакс определяется как сумма абсолютных величин положительного и отрицательного пределов измерения.
Если шкала начинается не с нуля, а с какого-то минимального значения, то Амакс равно разности между конечным и начальным значениями шкалы.
Случайными называются погрешности, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Случайные погрешности нельзя исключить опытным путем, т. к. они возникают случайно. Для того, чтобы исключить случайные погрешности производят неоднократные измерения и определяют среднее арифметическое из полученных значений, определяемое как
 ,
,
где а1, а2, …, аn – результаты отдельных измерений;
n – число измерений.
Для оценки точности результата измерений необходимо знать закон распределения случайных погрешностей, таким законом является нормальный закон Гаусса. Среднее квадратическое отклонение может быть выражено через случайные отклонения результатов наблюдения Р:

где Р1 = а1 – Аср; Р2 = а2 – Аср; Рn = аn – Аср.
Этот способ определения доверительных интервалов справедлив толко для больших количеств измерений (20-30). Для небольшого количества измерений для определения доверительного интервала нужно пользоваться коэффициентами Стьюдента tn, которые зависят от задаваемой доверительной вероятности Р и количества измерений n.
Для определения доверительного интервала среднюю квадратическую погрешность  надо умножить на коэффициент Стьюдента. Окончательный результат измерения можно записать так:
надо умножить на коэффициент Стьюдента. Окончательный результат измерения можно записать так:
А = Аср  tn
tn
Контрольное задание
Задача 1. Для уменьшения влияния случайных погрешностей на результат измерения, емкость конденсатора С измерялась многократно в одинаковых условиях (таблица 1). Считая, что случайные погрешности имеют нормальный закон распределения, определить на основании заданного количества измерения (табл. 1, табл. 2):
Действительное значение измеряемой емкости;
Среднюю квадратическую и максимальную погрешности однократного измерения;
Доверительный интервал для результата измерения при доверительной вероятности Рд (табл.3).
Имеется ли систематическая составляющая в погрешности измерения емкости и с какой доверительной вероятностью ее можно оценить, если принять в качестве действительного значения емкости значения Сср (таб.1, таб.2).
Таблица 1
| №№из мере ния | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| С, пФ | 2430 | 2440 | 2435 | 2438 | 2439 | 2441 | 2438 | 2440 | 2441 | 2439 |
| №№из мере ния | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| С, пФ | 2500 | 2564 | 2550 | 2480 | 2450 | 2528 | 2440 | 2556 | 2562 | 2550 |
Таблица 2
| № вари анта | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| №№из мере ния | 1-3 | 6-10 | 2-6 | 1-4 | 2-8 | 2-4 | 7-9 | 4-7 | 3-5 | 5-7 |
| С0, пФ | 2428 | 2429 | 2430 | 2432 | 2436 | 2424 | 2440 | 2441 | 2440 | 2442 |
| Рд | 0,89 | 0,9 | 0,99 | 0,95 | 0,85 | 0,94 | 0,97 | 0,9 | 0,96 | 0,98 |
| № вари анта | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| №№из мере ния | 11-14 | 12-15 | 16-19 | 13-16 | 14-17 | 17-20 | 15-18 | 11-13 | 12-16 | 15-20 |
Примечание. Количество и номера наблюдений значений емкости для каждого варианта определяются данными таблицы 1 и 2, например для варианта 1 следует взять результаты измерений 1-3 табл.2.
Указания к решению
Для удобства выполнения и проверки расчетов по заданию целесообразно представить промежуточное вычисление в виде таблицы
Таблица 3
| №№ пп | №№ наблюдения | Сi, пФ | Сi – Cср, пФ | (Сi – Cср)2, пФ |
| 1 2 3 4 |
|
|
|
|
|
|
| Сумма Сi, пФ | Сумма Сi – Cср, пФ | Сумма (Сi – Cср)2, пФ |
Далее определить среднеквадратическую погрешность :

По таблице (4) определить коэффициент Стьюдента.
В конце решения следует записать окончательный (с учетом округления) результат измерения в требуемой форме, например: С = 1231 12 пФ, Р
12 пФ, Р
Задание 2.. Используя формулы (1-7 примера) произвести расчет абсолютной и относительной погрешностей измерения мощности и сопротивления. Расчет выполняется в соответствии с вариантами указанными в задании.
Задача 1. Для определения сопротивления резистора и мощности, выделяемой на этом сопротивлении, измерены напряжение и ток. Зная основные параметры измерительных приборов (амперметра и вольтметра), определить ошибку косвенных измерений мощности и сопротивления.
Пример. Определить абсолютную и относительную погрешности измерения мощности, выделяемой на резисторе, если известны показания вольтметра класс точности Кв = 2,5, номинальное значение Umax = 150 В, показание 120 В и амперметра – класс точности КА = 1,0, номинальное значение шкалы 10 МА, показания 6 МА.
Решение:
Определяем мощность Р = U * I ( Вт)
Абсолютная ошибка измерения напряжения, В

Абсолютная ошибка измерения тока, М А

В соответствии с таблицей абсолютная ошибка измерения мощности, Вт

Относительная ошибка 
Формула для сопротивления R = U / I

Относительная погрешность

Примечание:
Для вычисления погрешностей измерения мощности используются формулы 1,2,3,4,
Для вычисления погрешностей измерения сопротивления используются формулы 2,3,5,6,7.
Формулы для выполнения контрольной работы и письменного экзамена по предмету «Электрические измерения»
1.Абсолютная погрешность измерения
ΔА = Ах – А
2. Действительная относительная погрешность
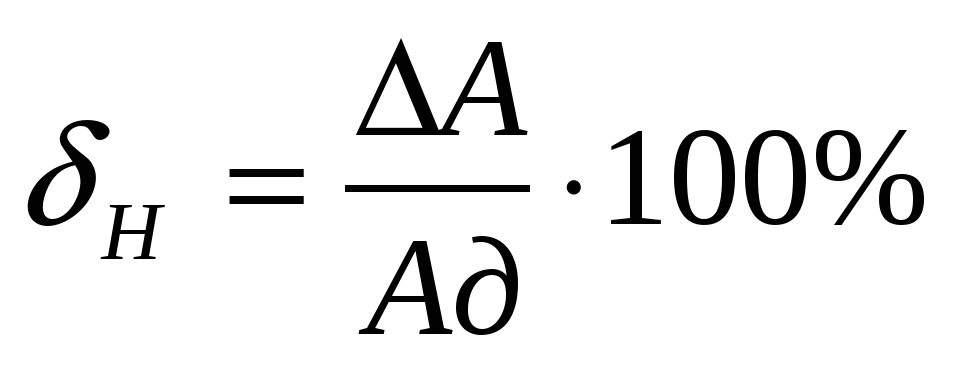
3 Номинальная относительная погрешность

4.Приведенная относительная погрешность
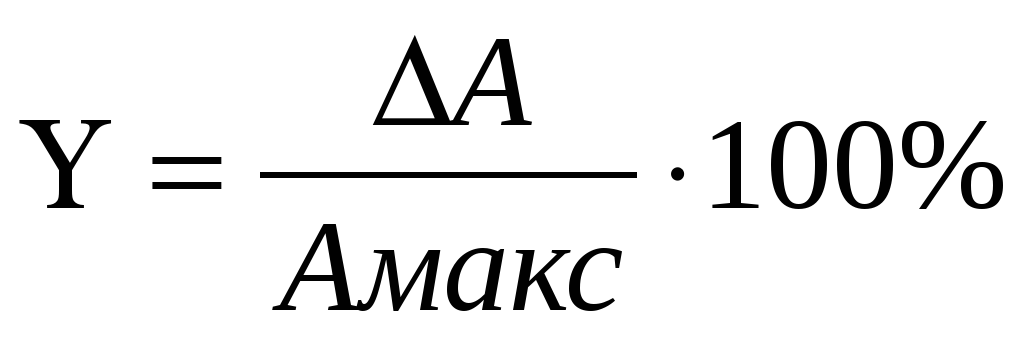
Сопротивление шунта
RШ = RА / Р-1 (Ом)
6 .Добавочное сопротивление
RДОБ = RV * ( Р-1) (Ом)
Коэффициент трансформации по току:
Кi = I 1/ I2
8 Коэффициент трансформации по напряжению:
КU = U 1 /U2
9. Ток сети:
IC = Ki * I (А)
Напряжение сети:
UC = KU* U (В)
Активная мощность сети:
PC = Ki * KU *P (Вт)
Реактивная мощность сети :
Q = U*I* sinφ (Вар)
Полная мощность сети:
S = U*I (ВА)
14. Полное сопротивление сети :
ZC = UC/ IC (Ом)
15 Коэффициент мощности:
Cosφ = PC / SC
Номинальная постоянная счетчика:
СНОМ = W НОМ/ NНОМ (Вт*с/об)
Действительная постоянная счетчика:
С = (U*I*t / N) (Вт*с/об)
18 Поправочный коэффициент:
К= С / СНОМ
Относительная погрешность счетчика
Β = [(СНОМ – С) /CНОМ] * 100%
















